Читать онлайн «Теорема Лапласа» — Бетев Сергей Михайлович — RuLit
Ровная и спокойная речь свидетельницы, казалось, не доходила до Хоминой. Светлана Владимировна положила ногу на ногу, обхватила колени ладонями и думала о чем-то своем. Иван Петрович только подивился ее самообладанию, которое вначале она, казалось, утратила. Когда лента кончилась, Хомина не шелохнулась. Она продолжала думать.
– Что вы на это ответите? – спросил он тогда.
– Она сказала все правильно, вы же сами слышали: мне было неудобно говорить о выигрышах потому, что я фининспектор. А насчет наших отношений с Юрием, так это ее собственное мнение, на которое я даже не обижаюсь. Каждый понимает людей по-своему.
– Ну что ж… Я думаю, на сегодня разговора хватит, – сказал Иван Петрович.
– Я могу быть свободна? – спросила она с облегчением.
– Нет, – вздохнул он. – Вынужден разочаровать вас. Я принял решение о вашем аресте.
– Вынужден разочаровать вас. Я принял решение о вашем аресте.
– Аресте?
– Да.
– Но я на работе!..
– Думаю, что это уже не имеет значения. – И, видя, как ужас против воли сковывает ее всю, добавил с сожалением:– Закон есть закон, Светлана Владимировна.
Первый день допросов ободрил Ивана Петровича, но не настолько, чтобы он всецело занялся Хоминой. Напротив, он готовился к новым неожиданностям, и они не замедлили явиться.
В тот же день к вечеру он получил справку о премиальных Хоминой, а предусмотрительный помощник приобщил к ней еще и выписку из приказов о ее командировках. Премии Хомина получала почти ежемесячно. Это были разные суммы, но факт оставался фактом, какая-то часть ее показания приобретала неопровержимые доказательства. Более того, выписка из приказов о командировках могла стать в ее руках тоже средством защиты, если она сумеет ею воспользоваться. И во время распространения пятого, и во время распространения шестого выпусков Хомина выезжала в командировки по месту продажи обнаруженных у нее билетов.
Встречаясь с ней на допросах, Иван Петрович старался получить лишь более определенные ответы на вопросы, заданные при первом разговоре, намеренно не раскрывая главных сведений, которыми располагал.
К его удивлению, Хомина сама сочла нужным объяснить, что сто билетов до ее отпуска были подброшены ей во время работы ликвидационной комиссии. Не учитывать этого заявления он не мог, потому что о показаниях Пустынина по этому поводу Хомина знать не могла.
Но во всем этом деле имелась одна особенность. Хомина не была преступницей уголовного пошиба, ведомственной проходимкой или мошенницей. Она пошла на преступление, несомненно, впервые. Все, кто ее окружал и кого ей удалось сделать прямыми или косвенными участниками своего злоупотребления, оказались людьми, также далекими от подобных вещей. И это сумело благотворно отразиться на всем следствии, так как избавляло Упорова от траты времени на беседы со свидетелями об их гражданском долге. С первой встречи с ним стала откровенной Аня Куркова.
Все это Иван Петрович понимал и поэтому несколько изменил свое отношение к Пустынину.
Во время второй встречи он долго говорил с ним о Хоминой, ни словом не обмолвившись по существу дела. Со Светланой они познакомились на юге, потом, когда она развелась со своим прежним мужем, решили жить вместе. Не зарегистрировались, оказывается, потому, что развод Хоминой по первому браку был не оформлен. Иван Петрович почувствовал, как хорошо относится Пустынин и к жене, и к приемной дочери. Сейчас, когда они говорили о девочке, особенно бросалась в глаза неподдельная тревога о ней, которую Пустынин по-мужски неумело старался скрыть.
Со Светланой они познакомились на юге, потом, когда она развелась со своим прежним мужем, решили жить вместе. Не зарегистрировались, оказывается, потому, что развод Хоминой по первому браку был не оформлен. Иван Петрович почувствовал, как хорошо относится Пустынин и к жене, и к приемной дочери. Сейчас, когда они говорили о девочке, особенно бросалась в глаза неподдельная тревога о ней, которую Пустынин по-мужски неумело старался скрыть.
Не ускользнуло от внимания Упорова и другое. По каким-то маленьким штрихам, хотя бы по тому, что при всяком случае Пустынин непременно вспоминал Хомину, Иван Петрович убедился, что он занимал в семье подчиненное место, ходил, как говорят, «под пятой» у жены. Он, видимо, так привык полагаться всегда и во всем на нее, что сейчас, без нее, в разговоре со следователем чувствовал себя неуверенно.
Хомина находилась под арестом уже третий день, когда из Москвы пришла телеграмма, в которой сообщалось, что в указанную запросом неделю в сберегательной кассе № 5287 Москвы, расположенную в магазине «Детский мир», предъявлялся билет, выигравший ковер стоимостью восемьдесят четыре рубля. Это был единственный билет, относящийся по территориальности к Камышловскому району Свердловской области.
Это был единственный билет, относящийся по территориальности к Камышловскому району Свердловской области.
В тот же день Иван Петрович спросил на допросе Пустынина:
– Юрий Михайлович, из каких побуждений вы сделали ложное заявление о принадлежности вам билетов, украденных в магазине «Подарки»?
– Эти билеты покупал я, – ответил Пустынин после некоторого молчания.
– Вы хотите искренне помочь своей жене, и я понимаю вас в простом человеческом смысле, – сказал ему Иван Петрович. – Но если учитывать, что ложь мстит за себя любому, кто избирает ее защитницей, то как бы вы поступили в таком случае?
– Я ведь давал объяснение по этому поводу, – попытался уйти от ответа Пустынин. Письменное…
– Об этом я и говорю,
– Что же еще нужно?
– Вы называли в объяснении место, где покупали билеты…
– Да, в пассаже.
– Как же вы могли в пассаже купить билеты, которые продавались в Верхней Салде?
– Какая Верхняя Салда?! – растерянно посмотрел на него Пустынин.
– Прочтите в этом письме строки, подчеркнутые красным карандашом, – сказал ему Иван Петрович, передавая письмо фабрики Гознак.
Прочитав, Пустынин посмотрел на письмо как на похоронную.
– Нашлись, что ли, билеты? – спросил он.
– Так ведь их необязательно и находить, – ответил с улыбкой Иван Петрович. – Вы же сами передали следователю номера, отмеченные на таблице в газете.
– Какой кошмар! – сказал он тихо.
– Говорить по существу будем, Пустынин? – жестко осведомился Иван Петрович.
– Какой кошмар!
– Билеты эти нельзя было купить ни в пассаже, ни на вокзале, как утверждала ваша жена.
– Их принесла Светлана, – подавленно признался Пустынин.
– Минуточку, Юрий Михайлович, я достану бланк протокола допроса…
В следствии наступал перелом.
На другой день Упоров обрушил на Хомину почти весь груз имеющихся улик. После того как она письменно подтвердила свои показания о месте приобретения билетов шестого выпуска, он познакомил ее с письмом фабрики Гознак. И когда она наконец ухватилась за утверждение, что билеты приобрела в командировках, он показал пять ее заявлений с категорическим отказом вспомнить место покупки и предъявил показания Пустынина. Наконец Иван Петрович решился на последнее: он вызвал в управление Куркову. Пока она сидела у его помощника, он познакомил Хомину с ее объяснением.
И когда она наконец ухватилась за утверждение, что билеты приобрела в командировках, он показал пять ее заявлений с категорическим отказом вспомнить место покупки и предъявил показания Пустынина. Наконец Иван Петрович решился на последнее: он вызвал в управление Куркову. Пока она сидела у его помощника, он познакомил Хомину с ее объяснением.
И натолкнулся на решительное, злое противодействие:
– Никакого пианино я не выигрывала. Никакой Ани Курковой среди моих знакомых нет, – отрезала Хомина.
Она отвернулась. Но Иван Петрович долго смотрел на нее. И когда понял, что она чувствует его взгляд, всей кожей чувствует его молчаливое презрение, поднял трубку и сказал:
Онлайн-уроки TutorOnline по теории вероятностей Взрослый
Русский языкРусская литератураАнглийский языкНемецкий языкМатематикаИстория РоссииОбществознаниеГеографияБиологияФизикаХимияИспанский языкФранцузский языкВсеобщая историяИнформатика и ИКТЛитературное чтениеВысшая математикаПольский языкТурецкий языкИтальянский языкКитайский языкРусский язык как иностранныйЭкономикаПрограммированиеЛогикаШахматыАнглийский язык IELTS TOEFLТеоретическая механикаМатематическая статистикаЭконометрикаМастерство актерскоеПравоЯпонский языкКорейский языкPhotoshopТеория вероятностейПодготовка к школеЖивописьРисованиеРКИ для детей-билингвовРиторикаЛогистикаПсихологияИгра на гитареИстория БеларусиУправление человеческими ресурсами
10 класс1 курс2 курсВзрослыйНе указан
Применить фильтр
Урок 1. 18. Теоремы сложения и умножения вероятностей.
18. Теоремы сложения и умножения вероятностей.
Просмотреть
Урок 1.12. Аксиоматическое определение вероятности.
Просмотреть
Урок 1.10. Ограниченность классического и статистического определений вероятности, геометрической вероятности при описании реальных явлений.
ПросмотретьУрок 1.6. Составные события, действия над событиями.
Просмотреть
Урок 3.6. Теорема Муавра-Лапласа.
Просмотреть
Урок 3.7. Теорема Пуассона.
Просмотреть
Урок 3.4. Центральная предельная теорема.
Просмотреть
Урок 3.1. Массовые явления и закон больших чисел.
Просмотреть
Урок 2.17. Связь между дифференциальной и интегральной функцией распределения.
Просмотреть
Урок 2.16. Функция плотности распределения и ее свойства.
Просмотреть
Урок 2.11. Биномиальное распределение, распределение Пуассона.
Просмотреть
Урок 2.12. Система двух случайных величин.
Просмотреть
Урок 2.13. Закон распределения вероятностей дискретной двумерной величины.
Просмотреть
Урок 2.7. Математическое ожидание и дисперсия, их свойства.
Просмотреть
Урок 2.8. Моменты случайных величин.
Просмотреть
Урок 2.9. Примеры законов распределения дискретных и непрерывных случайных величин.
Просмотреть
Урок 2.10. Распределение функций случайных аргументов.
Просмотреть
Урок 2.4. Интегральная функция распределения и ее свойства.
Просмотреть
Урок 2.5. Плотность распределения вероятностей.
Просмотреть
Урок 2.6. Числовые характеристики случайных величин (математическое ожидание, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты, мода, медиана, коэффициенты асимметрии и эксцесса) и их свойства.
Просмотреть
Урок 2.1. Дискретные случайные величины.
Просмотреть
Урок 2.2. Закон распределения дискретной случайной величины.
Просмотреть
Урок 2.3. Многоугольник распределения.
Просмотреть
Урок 1.22. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.
Просмотреть
Урок 1.21. Локальная и интегральная теоремы Лапласа.
Просмотреть
Теорема о конечном значении
Введение в теорему о конечном значении
Теорема об окончательном значении используется для определения окончательного значения во временной области путем применения только нулевой частотной составляющей к представлению системы в частотной области.
Преобразование Лапласа непрерывного сигнала во временной области \(x(t)\):
| $$\mathscr{L} \left[ x\left( t \right) \right]=X\left(s\right)$$ 9{-ст}\,дт$$ |
Теорема об окончательном значении утверждает:
| $$\lim_{t\to \infty}x\left( t \right)=\lim_{s\to 0}{sX \left( s \right)}$$ |
Исключения
В некоторых случаях теорема об окончательном значении точно предсказывает конечное значение, хотя окончательного значения во временной области может и не быть. Это относится к колебательным системам, то есть системам без демпфирования, и неустойчивым системам, у которых один или несколько полюсов расположены в правой полуплоскости.
Это относится к колебательным системам, то есть системам без демпфирования, и неустойчивым системам, у которых один или несколько полюсов расположены в правой полуплоскости.
Итог двух проверок:
- Все ненулевые корни знаменателя \(X(s)\) должны иметь отрицательные действительные части (см. эту статью: Стабильность передаточной функции — интересные факты о полиномиальной форме )
- \(X(s)\) не должен иметь более одного полюса в начале координат.
Пример 1
Найдите окончательное значение во временной области следующего сигнала в форме области Лапласа: 9{2}}= \lim_{s \to 0}\frac{1}{s} = \infty$$
Полюс находится в правой половине плоскости: теорема о конечном значении неприменима (хотя результат тот же — передаточная функция имеет неограниченный выход).
Веб-симулятор Проверьте (переместите область действия на соответствующую передаточную функцию). Обратите внимание, что преобразование Лапласа ступенчатой функции равно \(1/s\):
Пример 2
Найдите окончательное значение во временной области следующего сигнала в форме области Лапласа:
$$Y \влево( s \вправо) = \frac{s-20}{s \влево( s+8 \вправо)}$$
Ответ:
$$\lim_{t\to \infty}y\left( t \right)= \lim_{s \to 0}sY \left( s \right)= \lim_{s \to 0} \frac{ s \left(s-20\right)}{s \left( s+8 \right)} = \lim_{s \to 0} \frac{s-20}{s+8} = \frac{-20 {8}=-2,5$$
Веб-симулятор Проверьте (переместите область действия на соответствующую передаточную функцию). Обратите внимание, что преобразование Лапласа ступенчатой функции равно \(1/s\):
Обратите внимание, что преобразование Лапласа ступенчатой функции равно \(1/s\):
Пример 3
Найдите окончательное значение во временной области следующего сигнала в форме области Лапласа:
$$Y \влево( s \вправо) = \frac{s+20}{s \влево( s-8 \вправо)}$$
Ответ:
$$\lim_{t\to \infty}y\left( t \right)= \lim_{s \to 0}sY \left( s \right)= \lim_{s \to 0} \frac{ s \left(s+20\right)}{s \left( s-8 \right)} = \lim_{s \to 0} \frac{s+20}{s-8} = \frac{20} {-8}=-2,5 (неверно)$$
Полюс находится в правой половине плоскости: теорема о конечном значении неприменима.
Веб-симулятор Проверьте (переместите область действия на соответствующую передаточную функцию). Обратите внимание, что преобразование Лапласа ступенчатой функции равно \(1/s\):
Пример 4
Найдите окончательное значение во временной области следующего сигнала в форме области Лапласа:
$$Y \влево( s \вправо) = \frac{1}{s \влево( s^{2}+81 \вправо)}$$ 9{2}+81 \right)}= \frac{1}{81}(неверно)$$
Система не демпфирована (все ненулевые корни знаменателя должны иметь отрицательные действительные части).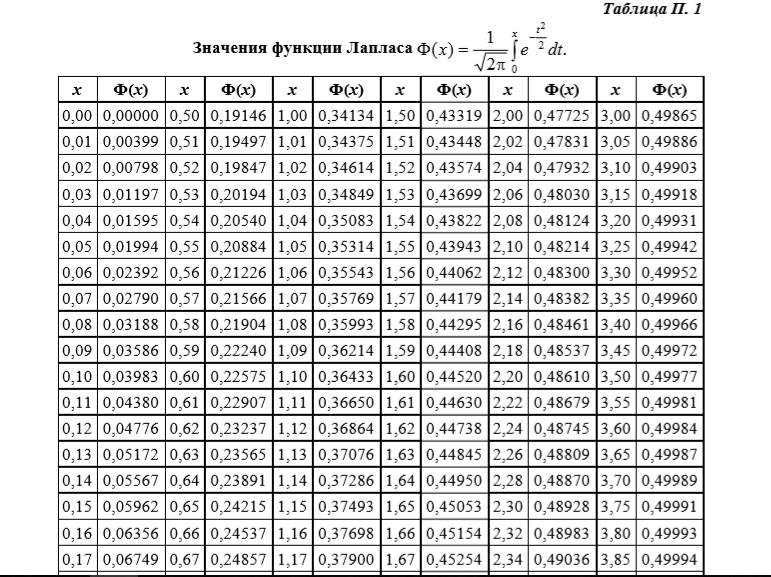
Веб-симулятор Проверьте (переместите область действия на соответствующую передаточную функцию). Обратите внимание, что преобразование Лапласа ступенчатой функции равно \(1/s\):
Пример 5
Найдите окончательное значение во временной области следующего сигнала в форме области Лапласа: 9\infty 1\,dx\left( t \right)=x\left( \infty \right)-x\left( 0 \right)$$
Отмена \(x(0)\):
| $$\lim_{s \to 0}sX\left( s \right) =x\left( \infty \right)$$ |
Дискретно-временная форма теоремы о начальном значении
Теорема о конечном значении утверждает:
| $$\lim_{k\to \infty}x\left[ k \right]=\lim_{z\to 1}{(z-1)X \left( z \right)}$$ 9{-ст}$$ |
«Z» становится 1 на бесконечное время.
Подробнее о соединении домена Лапласа и домена Z здесь: ОТНОШЕНИЕ МЕЖДУ S/Z-ПЛОСКОСТЯМИ И ВРЕМЕННОЙ ОБЛАСТЬЮ
Ссылки
- http://wikis.controltheorypro.com/index.php?title=Final_Value_Theorem
- Статья в Википедии о теореме 9 об окончательном значении0044
- http://lpsa.swarthmore.edu/LaplaceXform/FwdLaplace/LaplaceProps.html
Версия
Версия этой статьи от 04.02.2018.
Автор(ы)
ТС
Дополнительная литература
Реализация пропорционального контроллераВ MatLab, DSP и FPGA.
Блок-схема системы управленияОсновы потока сигналов.
Моделирование систем с помощью передаточных функций
Введение в динамические системы.
Демонстрация ряда Фурье
Это все синусоидальные волны.
Метод расширения полных функций Бернштейна оператора Лапласа
Метод расширения полных функций Бернштейна оператора Лапласа
Скачать PDF
Скачать PDF
- Открытый доступ
- Опубликовано:
- Матеуш Квасьницкий 1 и
- Яцек Муха 1
Журнал эволюционных уравнений том 18 , страницы 1341–1379 (2018)Цитировать эту статью
607 доступов
13 цитирований
- 9{1 — \alpha} \nabla _{t,x})\).
 Мы приводим аналогичный результат для всех полных функций Бернштейна от \(-\Delta \), используя спектральную теорию струн Крейна. Приведены два примера приложений: теорема Куранта–Гильберта об узловых линиях для гармонических расширений собственных функций нелокальных операторов Шрёдингера \(\psi (-\Delta ) + V(x)\), а также оценка сверху для собственные значения этих операторов. Здесь \(\psi \) — полная функция Бернштейна, а V — ограничивающий потенциал.
Мы приводим аналогичный результат для всех полных функций Бернштейна от \(-\Delta \), используя спектральную теорию струн Крейна. Приведены два примера приложений: теорема Куранта–Гильберта об узловых линиях для гармонических расширений собственных функций нелокальных операторов Шрёдингера \(\psi (-\Delta ) + V(x)\), а также оценка сверху для собственные значения этих операторов. Здесь \(\psi \) — полная функция Бернштейна, а V — ограничивающий потенциал.Скачайте, чтобы прочитать полный текст статьи
Литература
В. Амброзио, Решения в основных состояниях для нелинейного уравнения с псевдорелятивистским оператором Шредингера . Дж. Матем. физ. 57 (2016): 051502.
Статья MathSciNet Google Scholar
В. Арендт, А. Ф. М. тер Эльст, М. Варма, Дробные степени секторальных операторов через оператор Дирихле-Неймана .
 Комм. Уравнения в частных производных, в печати, https://doi.org/10.1080/03605302.2017.1363229.
Комм. Уравнения в частных производных, в печати, https://doi.org/10.1080/03605302.2017.1363229.Артикул MathSciNet Google Scholar
Р. Баньюэлос, Т. Кульчицки, Процесс Коши и задача Стеклова . Дж. Функц. Анальный. 211(2) (2004): 355–423.
Артикул MathSciNet Google Scholar
Т. Бычковский, Ю. Малецкий, М. Рызнар, Попадание в полупространства бесселевско-броуновскими диффузиями . Потенциальный анал. 33(1) (2010): 47–83.
Артикул MathSciNet Google Scholar
Л. Каффарелли, Л. Сильвестр, Проблема расширения, связанная с дробным лапласианом . Комм. Уравнения в частных производных 32 (7) (2007): 1245–1260.
Артикул MathSciNet Google Scholar
«>
Р. Кармона, У. К. Мастерс, Б. Саймон, Релятивистские операторы Шредингера: асимптотическое поведение собственных функций . Дж. Функц. Анальный. 91 (1990): 117–142.
Артикул MathSciNet Google Scholar
С.-Ю. А. Чанг, М. дель Мар Гонсалес, Дробный лапласиан в конформной геометрии . Доп. Мат. 226(2) (2011): 1410–1432.
Артикул MathSciNet Google Scholar
Z.-Q. Чен, М. Фукусима, Дж. Ин, Следы симметричных марковских процессов и их характеристики . Анна. Вероятно. 34 (3) (2006): 1052–1102.
Артикул MathSciNet Google Scholar
З. К. Чен, Р. Сонг, Двусторонние оценки собственных значений подчиненного броуновского движения в ограниченных областях . Дж. Функц. Анальный. 226 (2005): 90–113.

Артикул MathSciNet Google Scholar
Р. Д. ДеБласси, Время первого выхода двумерного симметричного устойчивого процесса из клина . Анна. Вероятно. 18 (1990): 1034–1070.
Артикул MathSciNet Google Scholar
Р. Д. ДеБласси, Частные уравнения высших порядков и симметричные устойчивые процессы . Вероятно. Области, связанные с теорией 129 (2004): 495–536.
MathSciNet МАТЕМАТИКА Google Scholar
М. Демут, Дж. А. ван Кастерен, Стохастическая спектральная теория для самосопряженных операторов Феллера . Спрингер Базель АГ (2000).
Глава Google Scholar
К. Донати-Мартин, М. Йор, Некоторые явные кериновые представления некоторых субординаторов, включая гамма-процесс .
 Опубл. RIMS, Киотский университет. 42 (2006): 879–895.
Опубл. RIMS, Киотский университет. 42 (2006): 879–895.Б. Дыда, А. Кузнецов, М. Квасьницкий, Дробный оператор Лапласа и G-функция Мейера Конструктивное приближение. 45(3) (2017): 427–448.
Артикул MathSciNet Google Scholar
Х. Дым, Х. П. МакКин, Гауссовские процессы, теория функций и обратная спектральная задача . Academic Press, Нью-Йорк-Сан-Франциско-Лондон, 1976.
МАТЕМАТИКА Google Scholar
Б. Дыда, А. Кузнецов, М. Квасьницкий, Собственные значения дробного оператора Лапласа в единичном шаре . Дж. Лондон Матем. соц. 95 (2017): 500–518.
Артикул MathSciNet Google Scholar
Р. Л. Франк, Границы собственных значений дробного лапласиана: обзор . Препринт, 2016 г.
 , arXiv: 1603.09736.
, arXiv: 1603.09736.Р. Л. Франк, М. дель Мар Гонсалес, Д. Д. Монтичелли, Дж. Тан, Проблема расширения дробного лапласиана CR . Доп. Мат. 270 (2015), 97–137.
Артикул MathSciNet Google Scholar
Р. Л. Франк, Э. Ленцманн, Единственность нелинейных основных состояний для дробных лапласианов в \(\mathbf{R}\). Акта Математика. 210(2) (2013): 261–318
Статья MathSciNet Google Scholar
Р. Л. Франк, Э. Х. Либ, Р. Зайрингер, Неравенства Харди-Либа-Тирринга для дробных операторов Шредингера . Дж. Амер. Мат. соц. 21(4) (2008): 925–950.
Артикул MathSciNet Google Scholar
Р. Л. Франк, Э. Ленцманн, Л. Сильвестр, Единственность радиальных решений для дробного лапласиана .
 Комм. Чистое приложение Мат. 69 (9) (2015): 1671–1726.
Комм. Чистое приложение Мат. 69 (9) (2015): 1671–1726.Артикул MathSciNet Google Scholar
Дж. Э. Гале, П. Дж. Миана, П. Р. Стинга, Проблема продолжения и дробные операторы: полугруппы и волновые уравнения . Дж. Эвол. Уравнения 13 (2013): 343–368.
Артикул MathSciNet Google Scholar
Дж. Гудман, Д. Спектор, Некоторые замечания о граничных операторах расширений Бесселя . Дискретная непрерывная динам. Сис. сер. С 11(3) (2018): 493–509.
Артикул MathSciNet Google Scholar
И. С. Градштейн, И. М. Рыжик, Таблица интегралов, рядов и произведений . А. Джеффри, Д. Цвиллингер (редакторы), Academic Press, (2007).
К. Р. Грэм, М. Зворски, Матрица рассеяния в конформной геометрии .
 Изобретать. Мат. 152 (1) (2003): 89–118.
Изобретать. Мат. 152 (1) (2003): 89–118.Артикул MathSciNet Google Scholar
Ф. Хиросима, Т. Ичиносе, Дж. Лоринци, Представление интеграла по траекториям для операторов Шредингера с функциями Бернштейна лапласиана . Преподобный Матем. Phys 24(6) (2012): 1250013.
Статья MathSciNet Google Scholar
Ф. Хиросима, Дж. Лоринци, Граница Либа–Тирринга для операторов Шредингера с функциями Бернштейна лапласиана . Комм. стох. Анальный. 6(4) (2012): 589–602.
МАТЕМАТИКА Google Scholar
Л. Хёрмандер, Анализ линейных дифференциальных операторов в частных производных. III . Grundlehren der mathematischen Wissenschaften, Vol. 275, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1985.
«>К. Калета, Т. Кульчицки, Внутренняя ультрасжимаемость для операторов Шредингера на основе дробного лапласиана Потенциальный анал. 33 (2010): 313–339.
Артикул MathSciNet Google Scholar
К. Калета, Дж. Лоринци, Точечные оценки собственных функций и внутренние свойства типа ультрасжимаемости полугрупп Фейнмана-Каца для класса процессов Леви . Анна. Проб. 43 (2015): 1350–1398.
Артикул Google Scholar
К. Калета, Й. Лоринци, Спад собственных функций для нелокальных операторов Шрёдингера с затухающими потенциалами .
 Потенциальный анал. 46 (2017): 647–688.
Потенциальный анал. 46 (2017): 647–688.Артикул MathSciNet Google Scholar
П. Ким, Р. Сонг, З. Вондрачек, О гармонических функциях для следовых процессов . Мат. Нахр. 284 (14–15) (2011): 1889–1902.
Артикул MathSciNet Google Scholar
С. Котани, С. Ватанабе, Спектральная теория струн Крейна и обобщенные диффузионные процессы . В кн.: Функциональный анализ в марковских процессах , изд. М. Фукусима, лекция. Обратите внимание на математику. 923, Springer, Берлин, 1982, стр. 235–259.
Т. Кульчицкий, М. Квасьницкий, Ю. Малецкий, А. Стош, Спектральные свойства процесса Коши на полупрямой и интервале . проц. Лондонская математика. соц. 101 (2) (2010): 589–622.
Артикул MathSciNet Google Scholar
«>М. Квасьницкий, Спектральный анализ подчиненных броуновских движений на полуоси . Студия математики. 206(3) (2011): 211–271.
Артикул MathSciNet Google Scholar
М. Квасьницкий, Собственные значения дробного оператора Лапласа в интервале . Дж. Функц. Анальный. 262(5) (2012): 2379–2402.
Артикул MathSciNet Google Scholar
М. Квасьницкий, Десять эквивалентных определений дробного оператора Лапласа . Фракт. Расчет заявл. Анальный. 20(1) (2017): 7–51.
Артикул MathSciNet Google Scholar
«>Э. Х. Либ, Х.-Т. Яу, Устойчивость и нестабильность релятивистской материи . Комм. Мат. физ. 118(2) (1988): 177–213.
Артикул MathSciNet Google Scholar
Й. Лоринци, Й. Малецкий, Спектральные свойства безмассового релятивистского гармонического осциллятора . Дж. Дифференц. Уравнения 253 (2012): 2846–2871.
Артикул MathSciNet Google Scholar
М. Мариас, Теория Литтлвуда–Пэли–Стейна и диффузии Бесселя . Бык. науч. Мат. 111(3) (1987): 313–331.
MathSciNet МАТЕМАТИКА Google Scholar
«>Дж. Питман, М. Йор, Столкновение, занятие и обратное локальное время одномерных диффузий: мартингальные и экскурсионные подходы . Бернулли 9 (2003): 1–24.
Артикул MathSciNet Google Scholar
Л. Ронкаль, П. Р. Стинга, Дробный лапласиан на торе . коммун. Контемп. Мат. 18(3) (2016): 1550033.
Статья MathSciNet Google Scholar
К. Сато, Процессы Леви и бесконечно делимые распределения . Кембриджский университет Пресса, Кембридж (1999).
МАТЕМАТИКА Google Scholar
«>П. Р. Стинга, Дж. Л. Торреа, Проблема расширения и неравенство Харнака для некоторых дробных операторов . Комм. Частичная разл. Уравнения 35 (2010): 2092–2122.
Артикул MathSciNet Google Scholar
Р. Ян, О расширениях более высокого порядка для дробного лапласиана . Препринт, 2013 г., arXiv: 1302.4413.
Веб-сайт Media-wiki для нелокальных уравнений, с.в. Extension Technique , https://www.ma.utexas.edu/mediawiki/index.php/Extension_technique, по состоянию на 17 мая 2017 г. Факультет чистой и прикладной математики, Вроцлавский университет науки и техники, ул. Wybrzeże Wyspiańskiego 27, 50-370, Вроцлав, Польша
Матеуш Квасьницкий и Яцек Муха
- Матеуш Квасьницкий
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jacek Mucha
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
N. Jacob, F.-Y. Ван, Собственные значения высшего порядка для нелокальных операторов Шрёдингера . Комм. Чистое приложение Анальный. 17(1) (2018): 191–208.
МАТЕМАТИКА Google Scholar
М. Квасьницкий, Внутренняя ультрасжимаемость стабильных полугрупп на неограниченных открытых множествах . Потенциальный анал. 31(1) (2009): 57–77.
Артикул MathSciNet Google Scholar
Д. Ленц, П. Столлманн, Д. Вингерт, Компактность полугрупп Шрёдингера . Мат. Нахр. 283(1) (2010): 94–103.
Артикул MathSciNet Google Scholar
С. А. Молчанов, Е. Островский, Симметричные устойчивые процессы как следы вырожденных диффузионных процессов . Теор. Проб. заявл. 14 (1) (1969): 128–131.
Артикул MathSciNet Google Scholar
Р. Шиллинг, Р. Сонг, З. Вондрачек, Функции Бернштейна: теория и приложения . Исследования по математике. 37, De Gruyter, Berlin, 2012.
Авторы
Автор, ответственный за корреспонденцию
Матеуш Квасьницкий.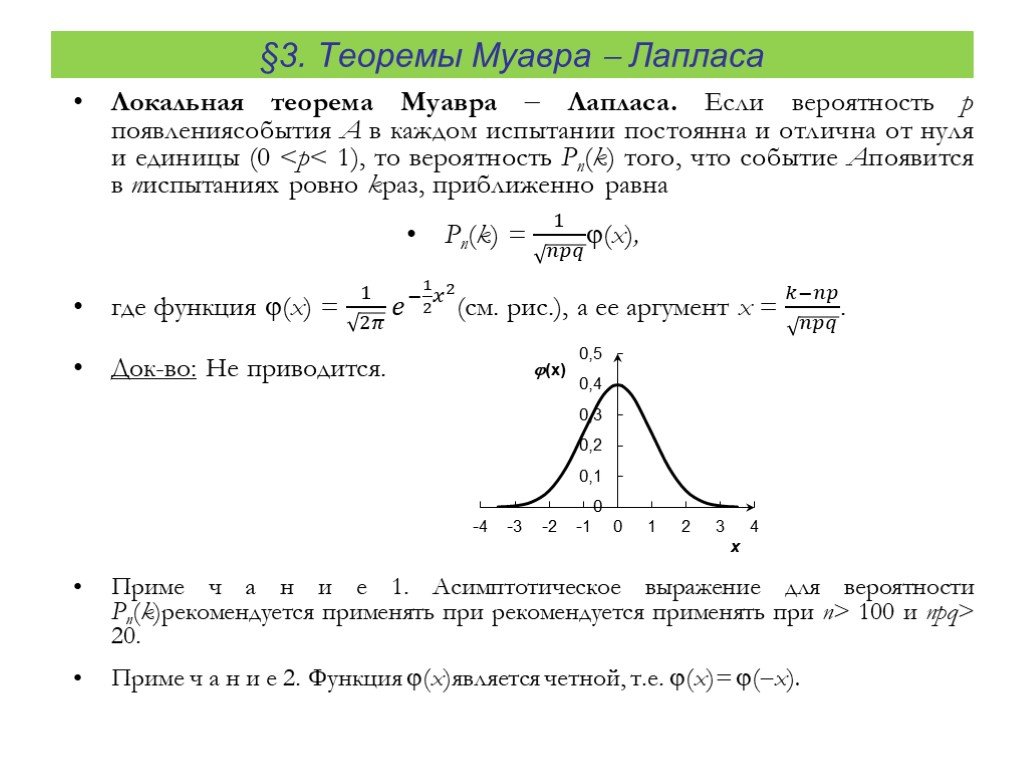

 Мы приводим аналогичный результат для всех полных функций Бернштейна от \(-\Delta \), используя спектральную теорию струн Крейна. Приведены два примера приложений: теорема Куранта–Гильберта об узловых линиях для гармонических расширений собственных функций нелокальных операторов Шрёдингера \(\psi (-\Delta ) + V(x)\), а также оценка сверху для собственные значения этих операторов. Здесь \(\psi \) — полная функция Бернштейна, а V — ограничивающий потенциал.
Мы приводим аналогичный результат для всех полных функций Бернштейна от \(-\Delta \), используя спектральную теорию струн Крейна. Приведены два примера приложений: теорема Куранта–Гильберта об узловых линиях для гармонических расширений собственных функций нелокальных операторов Шрёдингера \(\psi (-\Delta ) + V(x)\), а также оценка сверху для собственные значения этих операторов. Здесь \(\psi \) — полная функция Бернштейна, а V — ограничивающий потенциал. Комм. Уравнения в частных производных, в печати, https://doi.org/10.1080/03605302.2017.1363229.
Комм. Уравнения в частных производных, в печати, https://doi.org/10.1080/03605302.2017.1363229.
 Опубл. RIMS, Киотский университет. 42 (2006): 879–895.
Опубл. RIMS, Киотский университет. 42 (2006): 879–895. , arXiv: 1603.09736.
, arXiv: 1603.09736. Комм. Чистое приложение Мат. 69 (9) (2015): 1671–1726.
Комм. Чистое приложение Мат. 69 (9) (2015): 1671–1726. Изобретать. Мат. 152 (1) (2003): 89–118.
Изобретать. Мат. 152 (1) (2003): 89–118. Потенциальный анал. 46 (2017): 647–688.
Потенциальный анал. 46 (2017): 647–688.