| Доказательства теорем о свойствах описанной около треугольника окружности |
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | пересекаются в одной точке . | |
| | ||
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного середина гипотенузы . | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
, | ||
| Площадь треугольника | S = 2R 2 sin A sin B sin C , | |
| Радиус описанной окружности | Для любого треугольника справедливо равенство: |
| Серединные перпендикуляры к сторонам треугольника |
Все серединные перпендикуляры , проведённые к сторонам произвольного треугольника, |
| Окружность, описанная около треугольника |
Около любого треугольника можно описать окружность . Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. |
| Центр описанной около остроугольного треугольника окружности |
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы . |
| Центр описанной около тупоугольного треугольника окружности |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c
– стороны треугольника, A , B , С
– углы треугольника, R
– радиус описанной окружности. |
| Площадь треугольника |
Для любого треугольника справедливо равенство: S = 2R 2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. |
| Радиус описанной окружности |
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. |
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O
лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность . Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Вам понадобится
- Треугольник с заданными параметрами
- Циркуль
- Линейка
- Угольник
- Таблица синусов и косинусов
- Математические понятия
- Определение высоты треугольника
- Формулы синусов и косинусов
- Формула площади треугольника
Инструкция
Начертите треугольник с нужными параметрами.
Проведите ко всем сторонам треугольника и найдите точку их пересечения. Обозначьте высоты как h с соответствующими сторонам индексами. Найдите точку их пересечения и обозначьте ее О. Она и будет являться центром окружности. Таким образом, радиусами этой окружности будут являться отрезки ОА, ОВ и ОС.
Радиус найти по двум формулам. Для одной вам необходимо сначала вычислить . Она равна всех сторон треугольника на синус любого из углов, деленному на 2.
В этом случае радиус описанной окружности вычисляется по формуле
Для другой достаточно длину одной из сторон и синус противолежащего угла.
Вычислите радиус и опишите треугольника окружность.
Полезный совет
Вспомните, что такое высота треугольника. Это перпендикуляр, проведенный из угла к противолежащей стороне.
Площадь треугольника может быть представлена и как произведение квадрата одной из сторон на синусы двух прилежащих углов, деленное на удвоенный синус суммы этих углов.
S=а2*sinβ*sinγ/2sinγ
Источники:
- таблица с радиусами описанной окружности
- Радиус окружности, описанной около равностороннего
Считается описанной вокруг многоугольника в том случае, если она касается всех его вершин. Что примечательно, центр подобной окружности совпадает с точкой пересечения перпендикуляров, проведенных из середин сторон многоугольника. Радиус описанной окружности полностью зависит от того многоугольника, вокруг которого она описана.
Вам понадобится
- Знать стороны многоугольника, его площадь/периметр.
Инструкция
Обратите внимание
Вокруг многоугольника можно описать окружность только в том случае, если он правильный, т.е. все его стороны равны и все его углы равны.
Тезис, гласящий, что центром описанной вокруг многоугольника окружности является пересечение его серединных перпендикуляров, справедлив для всех правильных многоугольников. 1/2.
1/2.
Для многоугольников не всегда возможно выяснить соотношение радиусов вписанных и и длин его сторон. Чаще ограничиваются построением таких окружностей около многоугольника, а затем физического радиуса окружностей с помощью измерительных приборов или векторного пространства.
Для построения описанной окружности выпуклого многоугольника строят биссектрисы двух его углов, на их пересечении лежит центр описанной окружности. Радиусом будет расстояние от точки пересечения биссектрис до вершины любого угла многоугольника. Центр вписанной на пересечении перпендикуляров, построенных вовнутрь многоугольника из центров сторон (эти перпендикуляры срединными). Достаточно построить два таких перпендикуляра. Радиус вписанной окружности равен расстоянию от точки пересечения срединных перпендикуляров до стороны многоугольника.
Видео по теме
Обратите внимание
В произвольно заданный многоугольник нельзя вписать окружность и описать окружность вокруг него.
Полезный совет
В четырехугольник можно вписать окружность, если a+c = b+d, где a, b, с, d — стороны четырехугольника по порядку. 2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.
2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.
Видео по теме
Три точки, однозначно определяющие треугольник в Декартовой системе координат — это его вершины. Зная их положение относительно каждой из координатных осей можно вычислить любые параметры этой плоской фигуры, включая и ограничиваемую ее периметром площадь . Это можно сделать несколькими способами.
Инструкция
Используйте формулу Герона для расчета площади треугольника . В ней задействованы размеры трех сторон фигуры, поэтому вычисления начините с . Длина каждой стороны должна быть равна корню из суммы квадратов длин ее проекций на координатные оси. Если обозначить координаты A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃), длины их сторон можно выразить так: AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Для упрощения расчетов введите вспомогательную переменную — полупериметр (Р). Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Рассчитайте площадь (S) по формуле Герона — извлеките корень из произведения полупериметра на разность между ним и длиной каждой из сторон. В общем виде ее можно записать так: S = √(P*(P-AB)*(P-BC)*(P-AC)) = √(P*(P-√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²))*(P-√((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²))*(P-√((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²)).
Для практических расчетов удобно пользоваться специализированными -калькуляторами. Это скрипты, размещенные на серверах некоторых сайтов, которые проделают все необходимые расчеты на основе координат, введенных вами в соответствующую форму. Единственный такого сервиса — он не дает объяснений и обоснований для каждого шага вычислений. Поэтому, если вас интересует только конечный результат, а не вычисления в общем виде, перейдите, например, на страницу http://planetcalc.ru/218/.
В поля формы введите каждую координату каждой из вершин треугольника — они здесь как Ax, Ay, Az и т.д. Если треугольник задан двухмерными координатами, в поля — Az, Bz и Cz — пишите ноль. В поле «Точность вычисления» установите нужное число знаков после запятой, кликая мышкой плюса или минуса. Помещенную под формой оранжевую кнопку «Рассчитать» нажимать не обязательно, вычисления будут произведены и без этого. Ответ вы найдете рядом с надписью «Площадь треугольника » — она размещена сразу под оранжевой кнопкой.
Источники:
- найдите площадь треугольника с вершинами в точках
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.

Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим
Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.
Или, иными словами, радиус окружности, в которую вписан треугольник.
Как найти радиус окружности, описанной около треугольника – общая формула
Общая формула выглядит следующим образом: R = abc/4√p(p – a)(p – b)(p – c), где R – радиус описанной окружности, p – периметр треугольника поделенный на 2 (полупериметр). a, b, c – стороны треугольника.
Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 – 3)(8 – 6)(8 – 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.
Ответ: R = 126/16√5
Как найти радиус окружности, описанной около равностороннего треугольника
Для нахождения радиуса окружности, описанной около равностороннего треугольника, существует довольно простая формула: R = a/√3, где a – величина его стороны.
Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.
Найти радиус описанной окружности.
Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.
Ответ: R = 5/√3.
Как найти радиус окружности, описанной около прямоугольного треугольника
Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b – катеты и c – гипотенуза. Если сложить квадраты катетов в прямоугольном треугольнике, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.
Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
В данном выражение 5 – длина гипотенузы.
Ответ: R = 2.5.
Как найти радиус окружности, описанной около равнобедренного треугольника
Формула выглядит следующим образом: R = a²/√(4a² – b²), где a – длина бедра треугольника и b – длина основания.
Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.
Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² – 8²).
R = 49/√(196 – 64) = 49/√132. Ответ можно записать прямо так.
Ответ: R = 49/√132
Онлайн ресурсы для вычисления радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться онлайн калькуляторами, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост. Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.
Построение правильных многоугольников. Построение правильных вписанных многоугольников
Для начала разберемся с том, какую окружность можно назвать вписанной в треугольник. Это вам не просто взять и нарисовать в треугольнике фигуру. Ту окружность можно назвать вписанной в треугольник, у которой есть три точки на дуге, соприкасающихся с тремя гранями треугольника.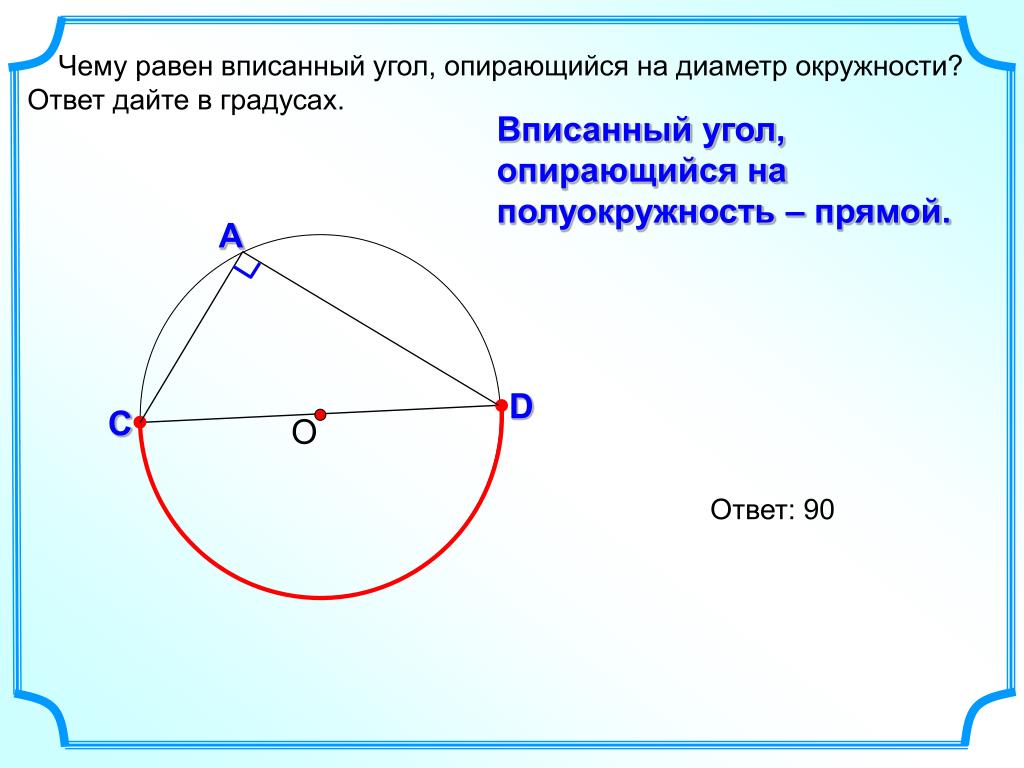
Из этого определения следует, что в каждый треугольник можно вписать лишь одну единственную возможную окружность, центр которой находится на пересечении трех биссектрис внутренних углов данного треугольника.
Теперь подробнее о том, как вписать окружность в треугольник:
- Находим вершины треугольника, как помним, их три.
- Из каждой вершины необходимо с помощью циркуля провести окружности, можно произвольного радиуса.
- Теперь найдите точку пересечения двух окружностей (эта точка должна находиться на стороне треугольника, которая противоположна делимому углу) и соединяем с делимым углом.
- Такую операцию необходимо провести с каждым из трех углов. У вас получатся в результате три пересекающиеся биссектрисы.
- Центр окружности вписанной в треугольник будет находиться в точки пересечения его биссектрис.
- Далее при помощи циркуля рисуем окружность с центром в полученной точке.
Как вписать треугольник в окружность
Вписанным в окружность треугольником называют треугольник, у которого три вершины соприкасаются с окружностью. Тогда окружность называют описанной вокруг треугольника.
Тогда окружность называют описанной вокруг треугольника.
Из этого следует, что радиус этой окружности — это отрезок, соединяющий центр описанной окружности и вершину треугольника. Поэтому для того, чтобы вписать треугольник в окружность необходимо обозначить три точки на окружности и соединить их отрезками.
Внимание, только СЕГОДНЯ!
ДРУГОЕ
Часто в геометрии приходится сталкиваться с описанными окружностями и их радиусами. Это ведет к простому вопросу: как…
Как начертить треугольник?Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих…
Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом…
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин,…
Как разделить окружность на части?Для того чтобы разделить отрезок или угол на равные части, особых навыков не…
Чему равен радиус описанной окружности?Описанной окружностью многоугольника называется такая окружность, которая…
Делить окружность на равное количество частей — это не пустое занятие, нужное лишь для того, чтобы усложнить вам жизнь…
Кто-то из нас математику в школе просто прогуливал, кто-то проболел, а кто-то подзабыл за давностью школьных лет, но…
Диаметром окружности называют отрезок прямой, которая соединяет две наиболее удаленные друг от друга точки окружности,…
Каждый школьник в начальных классах пытался узнать, что такое треугольник и что такое периметр ттреугольника. Попробуем…
Попробуем…
Задачи на геометрические построения весьма хорошо развивают пространственное и логическое мышление и потому являются одной из основных частей школьной программы обучения. Как и в любой предметной области, существуют типовые и нетиповые задачи. К типовым задачам можно отнести, например, построение равностороннего треугольника . В процессе построения треугольник оказывается вписанным в окружность . Но как быть, если нужно вписать равносторонний треугольник в окружность , которая уже построена?
Вам понадобится
- — линейка;
- — карандаш;
- — циркуль.
Инструкция
Постройте хорду заданной окружности. При помощи линейки начертите отрезок так, чтобы он пересекал окружность в двух точках. Пусть это будут точки A и B. Желательно, чтобы эти точки были расположены на достаточном удалении друг от друга.
Постройте перпендикуляр, пересекающий отрезок AB и делящий его точкой пересечения на две равные части. Установите между ножками циркуля расстояние, несколько меньшее длины отрезка AB, но заведомо большее длины половины этого отрезка. Установите иглу циркуля в точку A. Вычертите окружность . Установите иглу циркуля в точку B. Вычертите еще одну окружность . Проведите отрезок через точки пересечения вычерченных окружностей так, чтобы он пересек отрезок AB в одной точке (пусть это будет точка C) и первоначальную окружность в двух точках (пусть это будут точки D и E).
Установите между ножками циркуля расстояние, несколько меньшее длины отрезка AB, но заведомо большее длины половины этого отрезка. Установите иглу циркуля в точку A. Вычертите окружность . Установите иглу циркуля в точку B. Вычертите еще одну окружность . Проведите отрезок через точки пересечения вычерченных окружностей так, чтобы он пересек отрезок AB в одной точке (пусть это будет точка C) и первоначальную окружность в двух точках (пусть это будут точки D и E).
Постройте перпендикуляр, пересекающий отрезок DE и делящий его точкой пересечения на две равные части способом, аналогичным описанному во втором шаге. Пусть построенный отрезок пересекает окружность в точках F и G, а отрезок DE в точке O. Точка O будет являться центром окружности.
Установите расстояние между ножками циркуля равным радиусу окружности. Поместите иглу циркуля в точку D. Поместите конец другой ножки циркуля в точку O.
Найдите точки двух углов равностороннего треугольника , вписанного в окружность .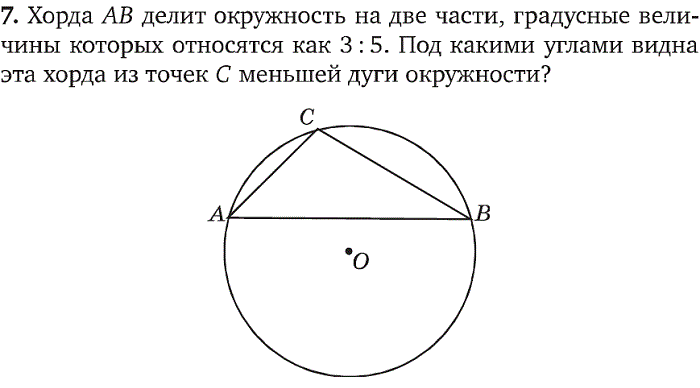 Не изменяя положения ножки циркуля с иглой (в точке D) и расстояния между ножками циркуля, установленные на предыдущем шаге, начертите окружность . Эта окружность пересечет первоначальную окружность в двух точках. Пусть это будут точки H и I.
Не изменяя положения ножки циркуля с иглой (в точке D) и расстояния между ножками циркуля, установленные на предыдущем шаге, начертите окружность . Эта окружность пересечет первоначальную окружность в двух точках. Пусть это будут точки H и I.
Впишите равносторонний треугольник в окружность . Попарно соедините отрезками точки E, H и I. Треугольник со сторонами EH, HI и EI будет равносторонним и вписанным в заданную изначально окружность .
Согласно определению, если все вершины многоугольника принадлежат окружности, он называется «вписанным». Построить на бумаге такую фигуру несложно, особенно если все составляющие ее стороны имеют одинаковую длину. Для правильного треугольника такое построение может быть выполнено несколькими способами, а выбор наиболее удобного зависит от имеющихся инструментов.
Вам понадобится
- Бумага, карандаш, циркуль, линейка, калькулятор, транспортир.
Инструкция
Если у вас есть возможность использовать при построении транспортир, начните с выбора произвольной точки на окружности, которая должна стать одной из вершин правильного треугольника .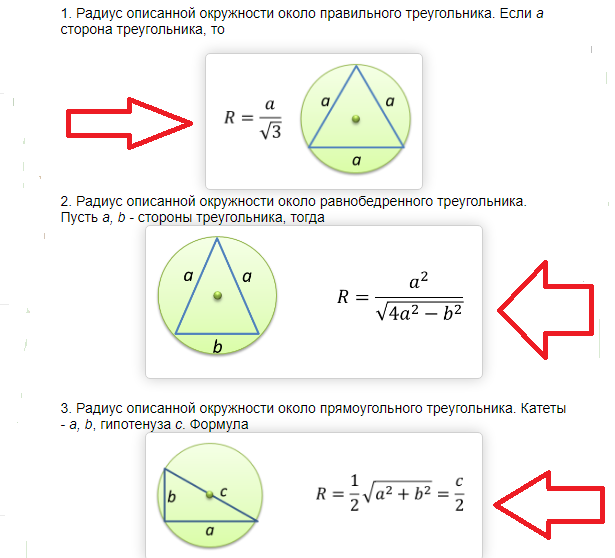 Обозначьте ее, например, буквой А.
Обозначьте ее, например, буквой А.
Начертите вспомогательный отрезок, соединив точку А с центром окружности. К этому отрезку приложите транспортир таким образом, чтобы нулевое деление совпало с центром круга, и поставьте вспомогательную точку у отметки 120°. Через эту точку проведите еще один вспомогательный отрезок с началом в центре круга и окончанием на пересечении с окружностью . Точку пересечения обозначьте буквой В — это вторая вершина вписанного треугольника .
Повторите предыдущий шаг, но транспортир прикладывайте ко второму вспомогательному отрезку, а точку пересечения с окружностью обозначьте буквой С. Больше транспортир не понадобится.
Соедините точки А и В, В и С, С и А. На этом построение правильного треугольника вписанного в окружность будет завершено.
Если транспортира нет, но есть циркуль и калькулятор, то начните с вычисления длины стороны треугольника . Вы наверняка знаете, что ее можно выразить через радиус описанной окружности, умножив его на отношение тройки к квадратному корню из тройки, то есть примерно на 1,732050807568877. Округлите это число до нужной степени точности и умножьте на радиус круга.
Округлите это число до нужной степени точности и умножьте на радиус круга.
Отметьте произвольную точку на окружности и обозначьте ее буквой А — это первая вершина правильного треугольника .
Отложите на циркуле найденную на пятом шаге длину стороны треугольника и начертите вспомогательный круг с центром в точке А. Точки пересечения двух окружностей обозначьте буквами В и С — это две другие вершины вписанного в круг правильного треугольника .
Соедините точки А и В, В и С, С и А и построение будет завершено.
Внимание, только СЕГОДНЯ!
Инструкция
Способ первый. Если вы хотите начертить в окружности правильный треугольник, из ее центра необходимо провести 3 отрезка ОВ, ОС и ОМ под углом 120о друг к другу. Точка О будет совпадать с центром окружности, а точки В, С и М будут находиться на самой окружности. Соедините эти точки между собой и получите равносторонний треугольник ВСМ.
Способ второй. Вам необходимо начертить в окружности треугольник, зная только две его стороны. Выберите на окружности точку О, которая будет являться вершиной треугольника АОС, а известные стороны будут АО и ОС. Из точки О отмерьте отрезок ОА так, чтобы точка А находилась на окружности. Таким же способом начертите отрезок ОС. Соединив точки А и С, получите необходимый треугольник.
Вам необходимо начертить в окружности треугольник, зная только две его стороны. Выберите на окружности точку О, которая будет являться вершиной треугольника АОС, а известные стороны будут АО и ОС. Из точки О отмерьте отрезок ОА так, чтобы точка А находилась на окружности. Таким же способом начертите отрезок ОС. Соединив точки А и С, получите необходимый треугольник.
Способ третий. Необходимо начертить в окружности треугольник, зная одну сторону и угол, прилегающий к этой стороне. Допустим, что в треугольнике АВС известна сторона АВ и угол ВАС. Начертите отрезок АВ так, чтобы точки А и В лежали на окружности, затем отмерьте угол ВАС и проведите отрезок АС так, чтобы точка С так же находилась на окружности. Соедините точки С и В для окончания построения треугольника.
Способ четвертый. Имеется некий треугольник ТМР. Необходимо нарисовать вокруг него окружность таким образом, чтобы он был вписан в окружность. Проведите перпендикуляры из середины каждой стороны треугольника. Точка их пересечения – точка О, будет являться центром окружности. Соедините точку О с любой вершиной треугольника ТМР, получившийся отрезок будет радиусом окружности.
Точка их пересечения – точка О, будет являться центром окружности. Соедините точку О с любой вершиной треугольника ТМР, получившийся отрезок будет радиусом окружности.
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
Рассмотрим способ с линейкой и циркулем. Построим треугольник АВС. С помощью линейки начертите линию АВ, это будет одна из сторон треугольника , а точки А и В его вершинами.
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Если все вершины треугольник а лежат на одной окружности, то в этом случае он называется вписанным, а окружность, соответственно — описанной вокруг него. Построить треугольник на известной окружности очень просто, но как вписать треугольник в круг, если изначально существует именно он?
Построить треугольник на известной окружности очень просто, но как вписать треугольник в круг, если изначально существует именно он?
Вам понадобится
- — циркуль;
- — бумага;
- — карандаш;
- — линейка.
Инструкция
Для любого треугольника всегда возможно построить описанную окружность, поскольку эта кривая однозначно определяется тремя заданными точками.
Чтобы это обнаружить, достаточно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, должны быть решениями системы из трех уравнений второй степени с тремя неизвестными.
Эта система будет иметь единственное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она вовсе не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следовательно, этот случай можно даже не рассматривать. Итак, решение заведомо существует.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.

Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию.
 Обозначаем его буквами АС.
Обозначаем его буквами АС. - Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам.
 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон.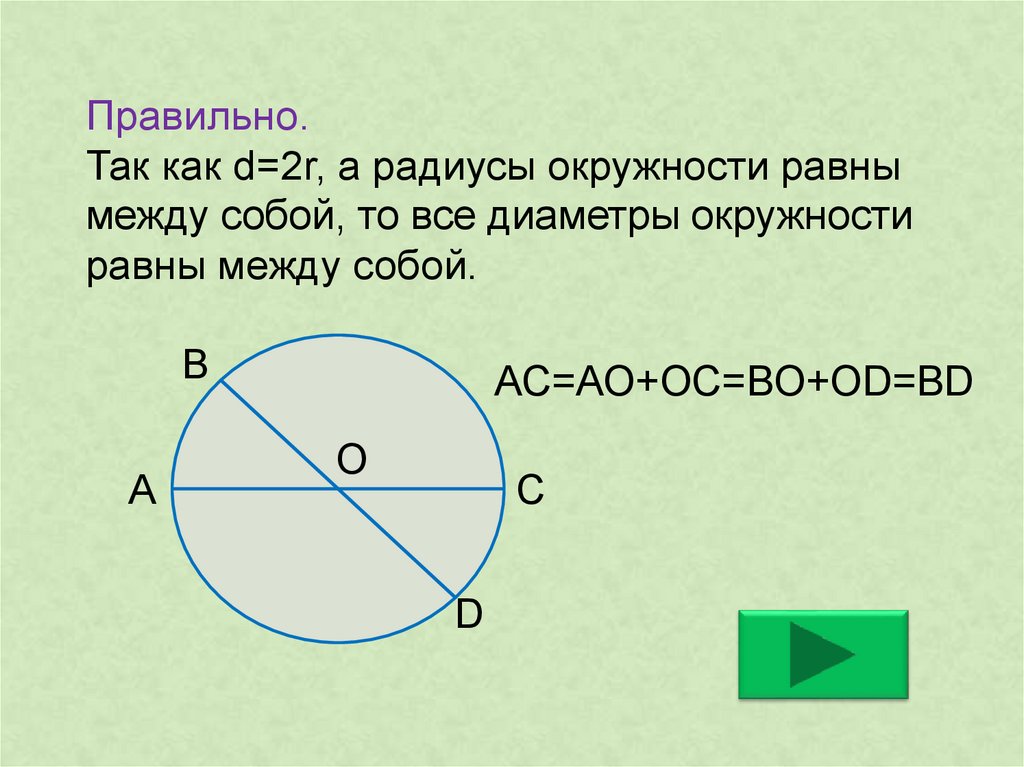 Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Ещё больше интересного
как начертить треугольник, как начертить треугольник в окружности, как начертить прямоугольный треугольник, как начертить циркулем треугольник, как начертить вписанный треугольник, как начертить описанный треугольник:Из нашей статьи вы узнаете, как начертить треугольник, а именно как изобразить следующие треугольники: разносторонний, равнобедренный, равносторонний, прямоугольный, тупоугольный, остроугольный, вписанный, описанный вокруг окружности, при помощи циркуля и линейки.
Какая связь между двумя кругами?
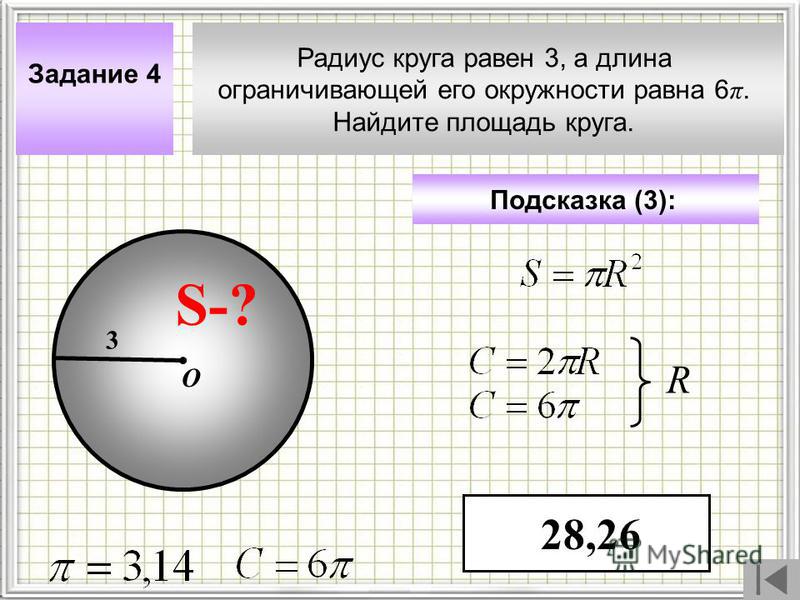
Окружность — это плоская фигура, ограниченная единственной изогнутой линией, и все прямые линии, проведенные из любой точки внутри круга к ограничивающей линии, равны. Круг — это фигура, состоящая из многих компонентов. Основными компонентами для определения окружности являются длина окружности, радиус, диаметр и центр окружности.
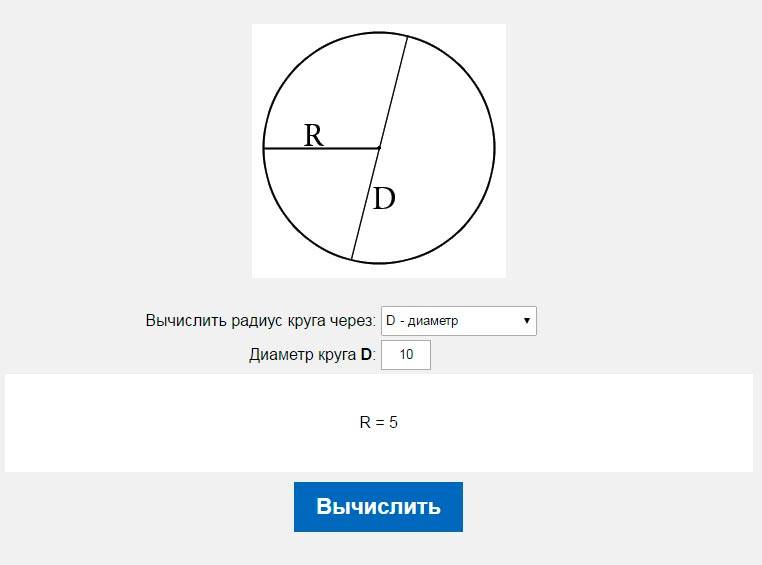
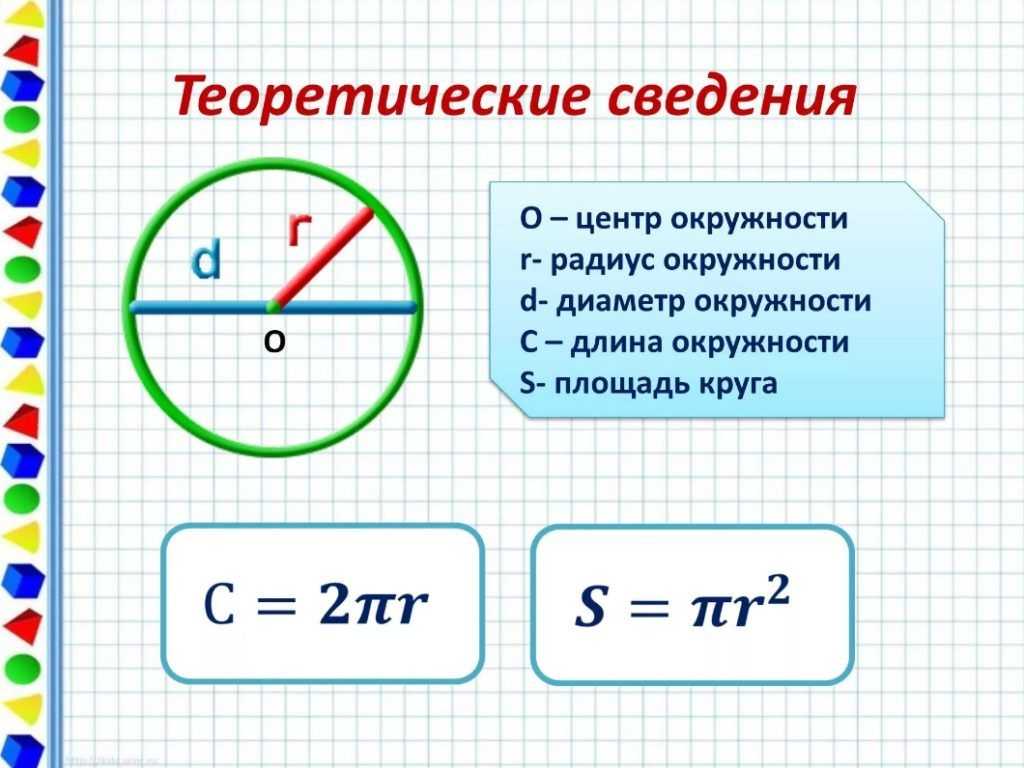
Что такое радиус? Радиус — это отрезок, соединяющий центр круга или сферы с его периметром или границей в геометрии.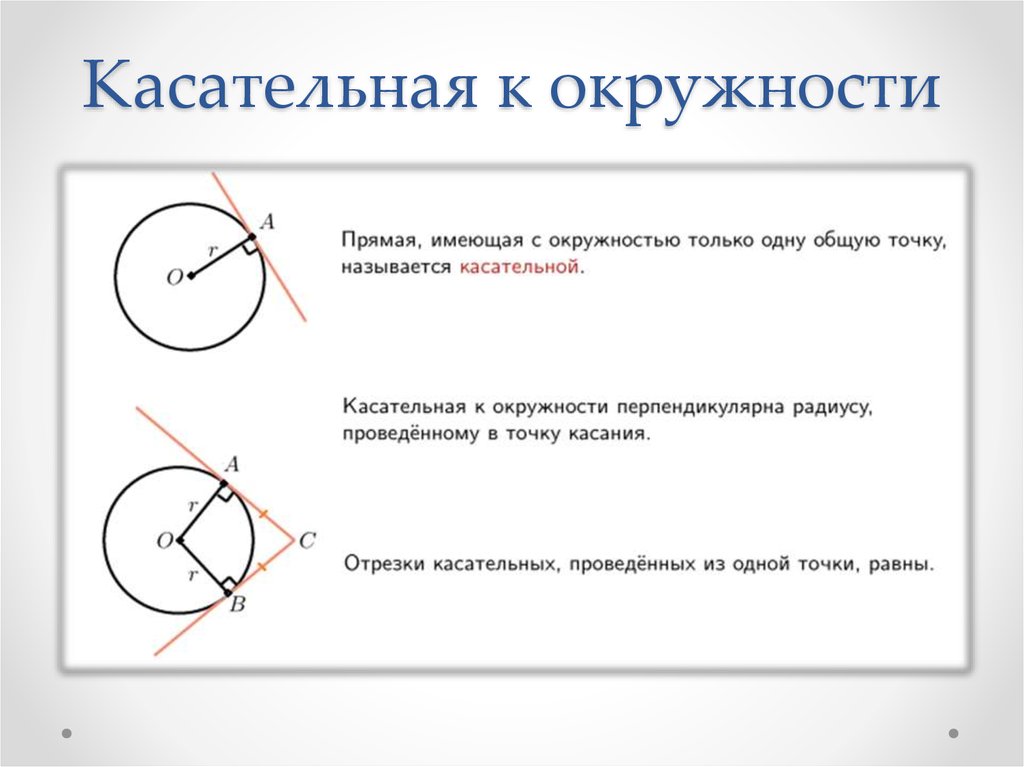 Обычно обозначается аббревиатурой «р». Множественное число слова «радиус» — это «радиусы», которое используется при одновременном обсуждении нескольких радиусов. Диаметр — это самый длинный отрезок в круге или сфере, соединяющий любые точки на противоположной стороне от центра, а радиус — это половина длины диаметра. Его можно записать как d/2, где d — диаметр круга или сферы.
Обычно обозначается аббревиатурой «р». Множественное число слова «радиус» — это «радиусы», которое используется при одновременном обсуждении нескольких радиусов. Диаметр — это самый длинный отрезок в круге или сфере, соединяющий любые точки на противоположной стороне от центра, а радиус — это половина длины диаметра. Его можно записать как d/2, где d — диаметр круга или сферы.
Давайте сначала кратко рассмотрим различные части круга-
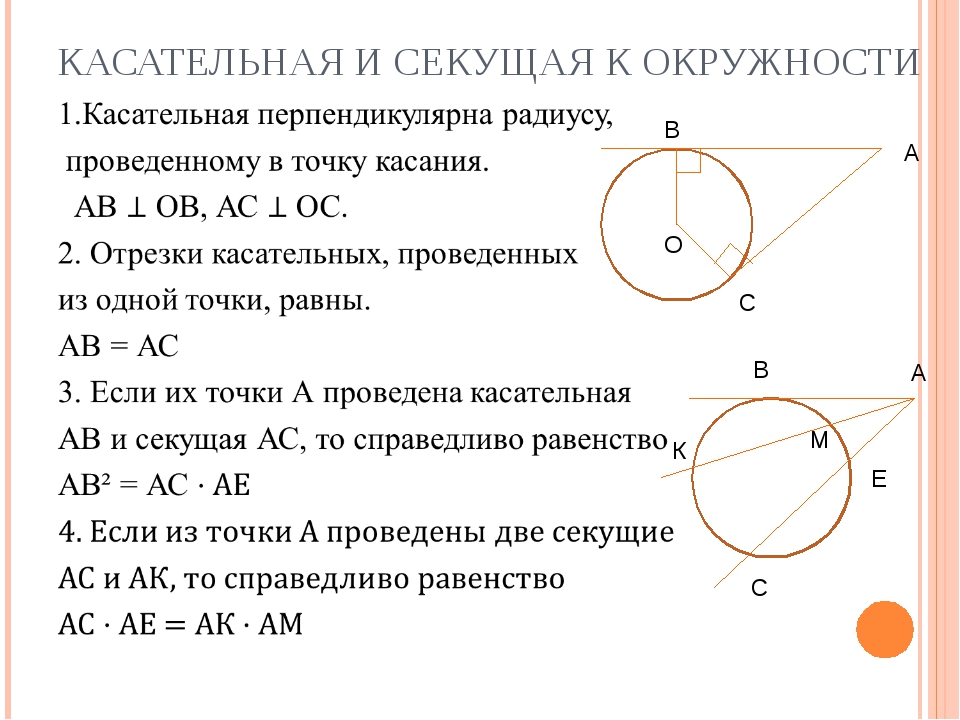
- Секущая: это линия, которая пересекает круг в двух уникальных местах.
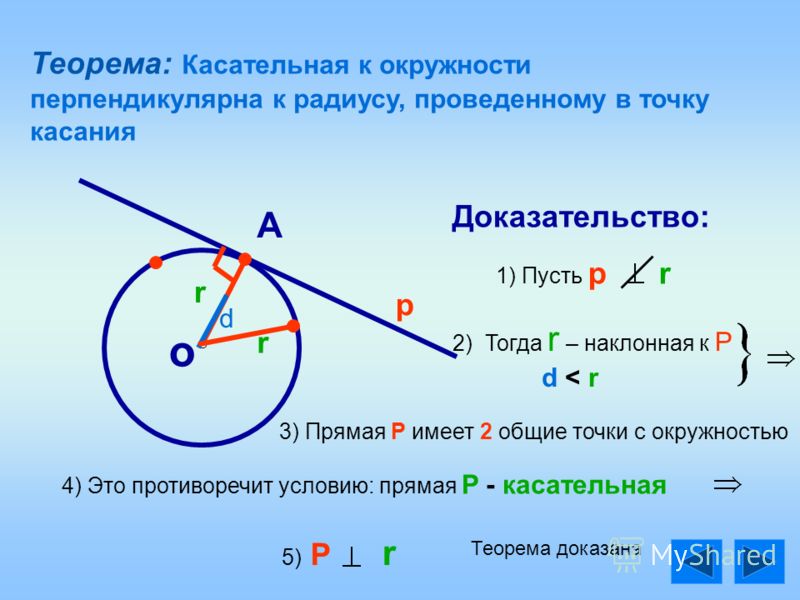
- Касательная: Линия, которая касается окружности точно в одной точке. Касательная к окружности — это линия, которая касается окружности в одной точке и бесконечно тянется.
- Хорда: хорда окружности — это отрезок, соединяющий две точки на окружности окружности. В круге можно найти любое количество хорд. Диаметр окружности – это ее наибольшая хорда.
- Сегмент: Сегмент окружности представляет собой часть окружности, описанную хордой и дугой.

- Дуга: Дуга является частью или частью окружности круга.
- Сектор: Сектор круга – это площадь, ограниченная двумя радиусами и дугой круга.
Когда мы рассматриваем круг, они будут иметь разный радиус, диаметр и центр. Предположим, что две окружности имеют радиусы r1 и r2 соответственно.
Две окружности в одной плоскостиДве окружности, лежащие в одной плоскости, могут пересекаться, описываться, разделяться, вписываться и включаться при соблюдении различных условий, которые заключаются в следующем. Рассмотрим две окружности радиусами r1 и r2. Пусть расстояние, разделяющее их центр, равно d.
- Две окружности будут касаться друг друга, если расстояние между их центрами равно сумме их радиусов или разнице между их радиусами. Они могут быть обозначены как окружности, соприкасающиеся снаружи и внутри. Два круга соприкоснутся, если расстояние между их центрами «d» равно сумме их радиусов или разнице между их радиусами.
 Математически мы можем представить это как,
Математически мы можем представить это как,
D = R 1 — R 2 или D = R 1 + R 2 9003
- 9 + R 2 9003
- . сумма двух радиусов, d = r 1 + r 2 , видно, что они имеют только одну точку пересечения между собой. Две окружности будут иметь общую касательную.
- Когда расстояние между их центрами равно разнице двух радиусов, d = r 1 – r 2 , видно, что они разделяют только одну точку. Две окружности будут иметь общую касательную. Один из кругов находится внутри другого круга. Математически
- Две окружности пересекутся в двух точках, если разница между их радиусами меньше, чем расстояние, разделяющее их центры. Это также можно определить, если сумма их радиусов больше, чем расстояние, разделяющее их центры, которое определяется как «d».
 Две компланарные окружности, т.е. лежащие в одной плоскости, будут иметь две точки пересечения. Математически это можно представить как
Две компланарные окружности, т.е. лежащие в одной плоскости, будут иметь две точки пересечения. Математически это можно представить как - 2
- . большой круг равен расстоянию, разделяющему их центры. Это можно понять по следующей схеме. Математически это можно определить как
d = r 1
- Один из кругов лежит в другом, когда расстояние между центрами равно радиусу маленького круга. Это можно понять по следующей схеме. Математически
d = r 2
- Если две окружности имеют общий центр независимо от их радиуса, то они называются концентрическими окружностями. Это круги, имеющие общий центр. Область между двумя концентрическими окружностями разного радиуса называется кольцом. Любые две окружности можно сделать концентрическими путем инверсии, выбрав центр инверсии в качестве одной из ограничивающих точек.
 Это можно определить математически как
Это можно определить математически как
d = 0
ЗаключениеКогда две окружности компланарны, т.е. лежат в одной плоскости и имеют разный радиус и разделены расстоянием от центра одной до другой, они могут пересекаться в нуле, одной или двух точках которые мы узнали в статье выше. Окружности могут описывать, пересекать, описывать, разделять, вписывать и включать, следуя различным условиям, которые мы прочитали в статье. Общая разница между различными случаями полностью зависит от радиуса двух окружностей и расстояния, разделяющего их центры.
геометрия — Круг с бесконечным радиусом является линией
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 42к раз
$\begingroup$
Меня интересует следующая диаграмма:
Изображение подразумевает, что круг бесконечного радиуса является линией.
 Интуитивно я это понимаю, но мне было интересно, можно ли эту проблему сформулировать и доказать формально? При каком определении «окружности» и «линии» это верно?
Интуитивно я это понимаю, но мне было интересно, можно ли эту проблему сформулировать и доказать формально? При каком определении «окружности» и «линии» это верно?Спасибо!
- геометрия
- круги
- бесконечность
- инверсионная геометрия
$\endgroup$
5
$\begingroup$
Окружность радиуса $r$ с центром в точке $(r,0)$ имеет параметрическую форму $$ \begin{массив}{}x=r(1-\cos(\theta/r))&y=r\sin(\theta/r)\end{массив}\tag{1} $$ предел кривой в $(1)$ при $r\to\infty$ равен $$ \begin{массив}{}x=0&y=\theta\end{массив}\tag{1} $$ что является вертикальной линией на вашем изображении.
Приложение:
В инверсивной геометрии круги и линии считаются одним и тем же. Обратной окружностью, проходящей через центр инверсии, является линия, не проходящая через центр, и наоборот.
 Обратной линией, проходящей через начало координат, является сама линия.
Обратной линией, проходящей через начало координат, является сама линия.На следующем изображении красный и зеленый круги обратны по отношению к серому кругу. Обратите внимание, что когда красный кружок проходит через центр инверсии, зеленый кружок становится линией.
$\endgroup$
1
$\begingroup$
Большинство людей подходят к этому с точки зрения проективной геометрии. Я подойду к этому с дифференциальная геометрическая точка зрения вместо этого, так как я чувствую, что могу дать более интуитивное понимание с этой точки зрения. К сожалению, я не могу говорить о $-\infty = \infty$ с этой точки зрения, не касаясь стереографической проекции или проективизации, но я все равно не думаю, что это суть понимания.
Для плавной кривой (т. е. без резких поворотов) на плоскости существует понятие ее кривизны; это числовая величина, определенная в каждой точке кривой, которая, за неимением лучшей формулировки, описывает, насколько изогнута кривая в этой точке.
 Если вы представляете себя на велосипеде, едущим по кривой со скоростью $10$ миль в час, то там, где кривизна очень велика, вы поворачиваете очень быстро. Там, где кривизна мала, вы вращаетесь не очень быстро, а там, где кривизна равна нулю, вы вообще не поворачиваетесь.
Если вы представляете себя на велосипеде, едущим по кривой со скоростью $10$ миль в час, то там, где кривизна очень велика, вы поворачиваете очень быстро. Там, где кривизна мала, вы вращаетесь не очень быстро, а там, где кривизна равна нулю, вы вообще не поворачиваетесь.Из этого интуитивного описания легко догадаться, что прямая линия везде имеет кривизну $0$, и на самом деле это однозначно характеризует прямые линии. Вы также можете показать, если сделаете надлежащие точные определения, что круг радиуса $R$ имеет постоянную кривизну $1/R$, и это также однозначно характеризует круги. Если вы знаете какую-нибудь физику, это тесно связано с тем фактом, что равномерное круговое движение является результатом постоянного ускорения по направлению к центру. По существу существует только два вида кривых постоянной кривизны: линии (нулевая кривизна) и окружности (ненулевая кривизна).
Утверждение о том, что линия представляет собой бесконечно большой круг, может быть оформлено в терминах кривизны.
 Для каждого $R>0$ пусть $C_R$ будет окружностью радиуса $R$; тогда она имеет кривизну $1/R$. Тогда в пределе при $R\to\infty$ кривизна достигает $0$. В некотором смысле, в точке «$R=\infty$» мы получаем кривизну «$1/\infty = 0$», прямую линию. То, как это интерпретируется более формально, состоит в том, что по мере того, как $R\to\infty$, маленькие сегменты окружности $C_R$ становятся все более и более приближенными к прямым линиям. Вооружившись этой интерпретацией, мы можем изменить выделенное жирным шрифтом утверждение: существует только один вид кривых постоянной кривизны: окружности, в том числе бесконечные (прямые).
Для каждого $R>0$ пусть $C_R$ будет окружностью радиуса $R$; тогда она имеет кривизну $1/R$. Тогда в пределе при $R\to\infty$ кривизна достигает $0$. В некотором смысле, в точке «$R=\infty$» мы получаем кривизну «$1/\infty = 0$», прямую линию. То, как это интерпретируется более формально, состоит в том, что по мере того, как $R\to\infty$, маленькие сегменты окружности $C_R$ становятся все более и более приближенными к прямым линиям. Вооружившись этой интерпретацией, мы можем изменить выделенное жирным шрифтом утверждение: существует только один вид кривых постоянной кривизны: окружности, в том числе бесконечные (прямые). Приложение: Это только один из способов увидеть утверждение, что линии — это «бесконечные круги». Другой распространенный способ думать об этом — в контексте проективной геометрии, где линии могут «стать кругами», «замыкая их» добавлением «бесконечно удаленных точек». Кроме того, вы можете думать о них в контексте инверсионной геометрии (геометрии отображения $z\mapsto 1/\overline{z}$ на комплексной плоскости) и более общих преобразований Мёбиуса, которые в целом имеют тенденцию отображать линии и окружности в другие линии и круги; если принять соглашение, что линия представляет собой бесконечный круг, то можно сказать, что преобразования Мёбиуса отображают круги в круги, что делает их описание несколько более аккуратным.
 92}{r}-2x=0$$
92}{r}-2x=0$$и пусть $r\to \infty$, вы обнаружите, что вы получаете уравнение $x=0$, которое является точно вертикальной осью…
$\endgroup$
$\begingroup$
Ну, это верно для обычной евклидовой плоскости. Это неверно в обычной гиперболической плоскости. «Предел» окружностей, проходящих через общую точку, по мере неограниченного роста радиуса, является орициклом. Иногда это пишется horocircle.
На приведенном выше изображении было бы два орицикла, касающихся вашей линии в точке $C$, по одному с каждой стороны от линии.
Как бы то ни было, об этом можно рассказать еще много страниц. Может быть, мне следует просто сказать, что существует «внутренне присущее» аксиоматическое определение гиперболической плоскости, модернизированное Давидом Гильбертом. Вы, вероятно, впервые встретитесь с некоторыми моделями, наиболее популярными из которых являются диск Пуанкаре, верхняя полуплоскость Пуанкаре, модель Бельтрами-Клейна, модель однолистного гиперболоида в трехмерном пространстве Минковского.
 Первые два и четвертый связаны со ссылкой на Википедию.
Первые два и четвертый связаны со ссылкой на Википедию.$\endgroup$
3
$\begingroup$
Круга бесконечного радиуса не существует. Может оказаться полезным использовать фразу «круг бесконечного радиуса» в качестве сокращения для некоторого предельного случая семейства кругов увеличивающегося радиуса, и (как показывают другие ответы) этот предел может дать вам прямую линию.
$\endgroup$
1 92} — ф}$$ Для случая $a=b=0$ ваше уравнение описывает линию, и ваш радиус становится бесконечным из-за деления на ноль. Обратите внимание, что определение также включает окружности с мнимым радиусом, у которых нет точек на реальной плоскости. Вы можете исключить их, ограничив диапазон параметров.
Интерпретируя точки вашей плоскости как комплексные числа, вы можете определить, что четыре точки лежат на общей окружности или прямой, если их отношение является действительным числом.
 Используя это определение, линия — это просто круг, и единственное разумное значение, которое можно присвоить его радиусу, — это $\infty$.
Используя это определение, линия — это просто круг, и единственное разумное значение, которое можно присвоить его радиусу, — это $\infty$.Преобразование Мёбиуса преобразует окружности и линии комплексной плоскости (или комплексные линии, в зависимости от того, как вы используете слово) $\mathbb C$ в другие окружности и линии. Таким образом, приведенное выше определение круга подходит и для этих преобразований. Существует научная тема под названием «Геометрия Мёбиуса», в которой для описания линий и окружностей используются четырехмерные векторы. В этой настройке линия снова является частным случаем круга, и выполнение любого вычисления радиуса приведет к бесконечности.
Вы можете немного расширить геометрию Мёбиуса, чтобы получить геометрию Ли, где четные точки являются частными случаями окружностей, а именно с нулевым радиусом. Преобразования Ли могут преобразовывать обычные круги в линии или точки и наоборот.
Окружность можно определить как линию постоянной кривизны без конечных точек.
 2$. Существуют коники с вещественными коэффициентами, вырождающиеся в пару прямых. Одна из них — линия на бесконечности, инцидентная двум указанным выше точкам, а другая может быть конечной линией. Поэтому, если ваша коника не вырождается в двойную линию на бесконечности, вы получаете одну линию как конечную часть коники, которая по определению является кругом. Вы можете вычислить центр этого круга, используя указанные выше точки, и результатом будет бесконечная точка, указывающая на бесконечный радиус. 92$ для положительного бесконечного гипердействительного числа $r$ дает окружность бесконечного радиуса в гиперреальной плоскости. Можно взять конечную часть $F$ окружности, т. е. точки с конечными обеими координатами. Тогда стандартной частью $F$ является прямая, а именно ось $y$.
2$. Существуют коники с вещественными коэффициентами, вырождающиеся в пару прямых. Одна из них — линия на бесконечности, инцидентная двум указанным выше точкам, а другая может быть конечной линией. Поэтому, если ваша коника не вырождается в двойную линию на бесконечности, вы получаете одну линию как конечную часть коники, которая по определению является кругом. Вы можете вычислить центр этого круга, используя указанные выше точки, и результатом будет бесконечная точка, указывающая на бесконечный радиус. 92$ для положительного бесконечного гипердействительного числа $r$ дает окружность бесконечного радиуса в гиперреальной плоскости. Можно взять конечную часть $F$ окружности, т. е. точки с конечными обеими координатами. Тогда стандартной частью $F$ является прямая, а именно ось $y$.$\endgroup$
$\begingroup$
Стандартное определение окружности — это геометрическое место на расстоянии r от центра O .
 Очевидно, что линия на евклидовой плоскости не является окружностью. Но действительно ли мы видим центр, чтобы проверить, является ли часть кривой частью некоторого круга? Нет, потому что на евклидовой плоскости линия постоянной ненулевой кривизны является критерием окружности (рассматриваем только кривые с одним знаком кривизны, т.е. все хорды должны лежать по одну сторону от кривой). Например, мы можем проверить, постоянна ли кривизна Менгера для всех троек различных точек. Если это так и является отличной от нуля величиной, то наша кривая представляет собой часть круга. Существуют разные определения кривизны, например, дифференциально-геометрическое, но не важно, какое определение мы используем, если оно работает для небольшого участка кривой. Локальное определение кривизны подразумевает локальный критерий окружности. На евклидовой плоскости окружности с очень малой кривизной (т. е. с большим радиусом) локально почти неотличимы от прямых линий, где прямые — это линии нулевой кривизны.
Очевидно, что линия на евклидовой плоскости не является окружностью. Но действительно ли мы видим центр, чтобы проверить, является ли часть кривой частью некоторого круга? Нет, потому что на евклидовой плоскости линия постоянной ненулевой кривизны является критерием окружности (рассматриваем только кривые с одним знаком кривизны, т.е. все хорды должны лежать по одну сторону от кривой). Например, мы можем проверить, постоянна ли кривизна Менгера для всех троек различных точек. Если это так и является отличной от нуля величиной, то наша кривая представляет собой часть круга. Существуют разные определения кривизны, например, дифференциально-геометрическое, но не важно, какое определение мы используем, если оно работает для небольшого участка кривой. Локальное определение кривизны подразумевает локальный критерий окружности. На евклидовой плоскости окружности с очень малой кривизной (т. е. с большим радиусом) локально почти неотличимы от прямых линий, где прямые — это линии нулевой кривизны.
Как связаны между собой два определения r,O -окружностей и линий постоянной кривизны? Мы видим, на евклидовой плоскости, каждая (незавершенная) линия постоянной кривизны является либо r,O -окружностью, либо прямой линией.
У нас есть еще две однородные геометрии плоскости: эллиптическая геометрия и геометрия Лобачевского. У них тоже есть расстояния, и там тоже работает дифференциальная геометрия. В любой из этих геометрий и прямые линии, и r,O -окружности имеют постоянную кривизну, но как они связаны? В эллиптической геометрии нет r,O -окружностей с r > πR /2 (где R — константа) и, что любопытно, окружности радиусом πR /2 совпадают с прямыми ( большие круги). Так, в эллиптической геометрии, (незавершенных) линий постоянной кривизны и r,O -окружностей определяют один и тот же класс кривых.
В геометрии Лобачевского существуют противоположные условия: имеется r,O -окружностей для любых r > 0, но любая r,O -окружностей имеет кривизну больше 1/ R , где R постоянная (извините, не помню точную зависимость кривизны по р ).

- + R 2 9003
- 9 + R 2 9003
- 9
R 1 — R 2


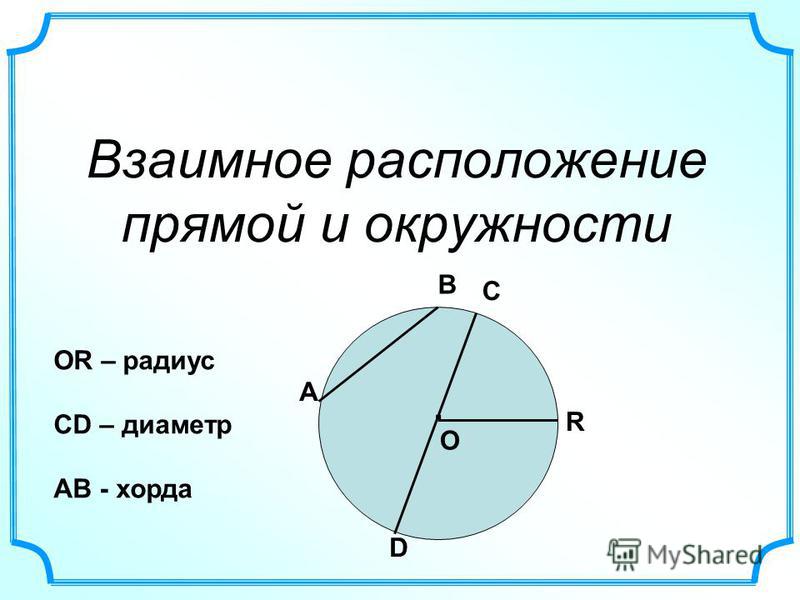
 Для этого сначала нужно найти радиус для вписанной окружности по формуле: R = S/p, где S обозначает площадь треугольника, а р – его полупериметр, p приравнивается к (a + b + c)/2. После того, как известен радиус, нужно воспользоваться первой формулой. Либо же сразу подставить все значения в формулу D = 2S/p.
Для этого сначала нужно найти радиус для вписанной окружности по формуле: R = S/p, где S обозначает площадь треугольника, а р – его полупериметр, p приравнивается к (a + b + c)/2. После того, как известен радиус, нужно воспользоваться первой формулой. Либо же сразу подставить все значения в формулу D = 2S/p.
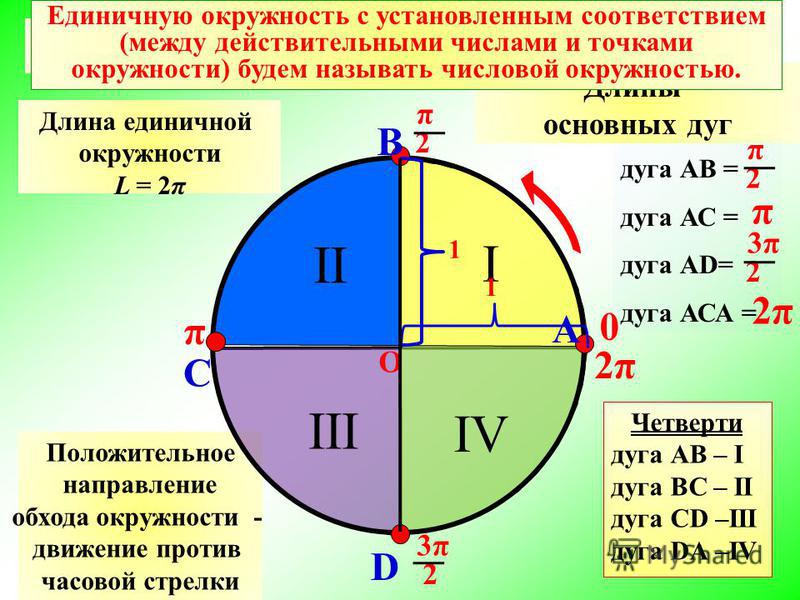

 Обозначаем его буквами АС.
Обозначаем его буквами АС.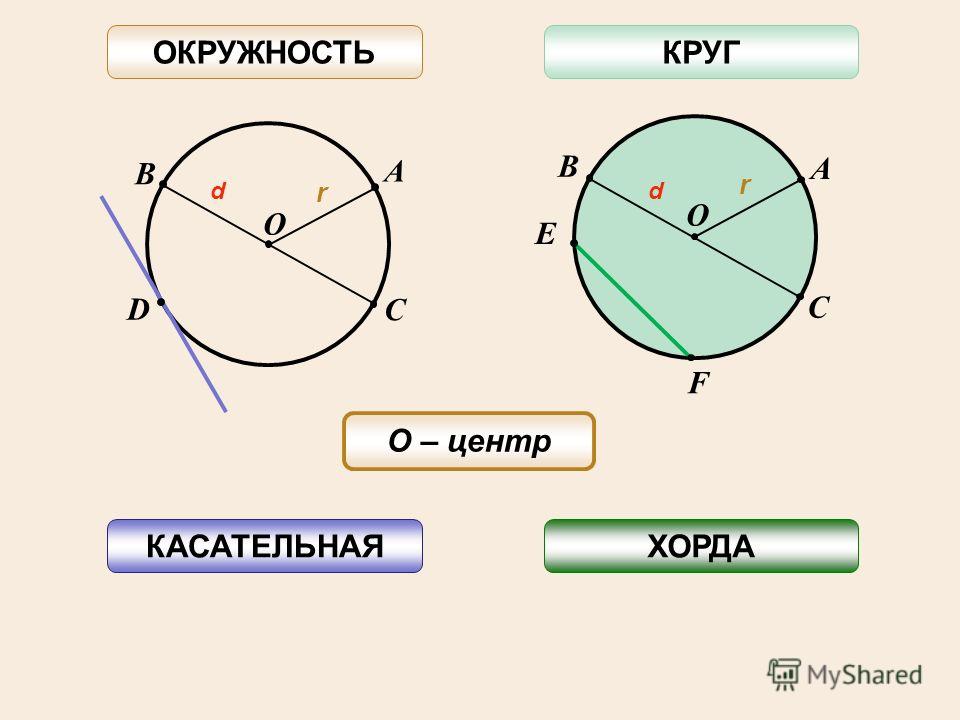 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник.
 Математически мы можем представить это как,
Математически мы можем представить это как, Две компланарные окружности, т.е. лежащие в одной плоскости, будут иметь две точки пересечения. Математически это можно представить как
Две компланарные окружности, т.е. лежащие в одной плоскости, будут иметь две точки пересечения. Математически это можно представить как Это можно определить математически как
Это можно определить математически как Интуитивно я это понимаю, но мне было интересно, можно ли эту проблему сформулировать и доказать формально? При каком определении «окружности» и «линии» это верно?
Интуитивно я это понимаю, но мне было интересно, можно ли эту проблему сформулировать и доказать формально? При каком определении «окружности» и «линии» это верно? Обратной линией, проходящей через начало координат, является сама линия.
Обратной линией, проходящей через начало координат, является сама линия.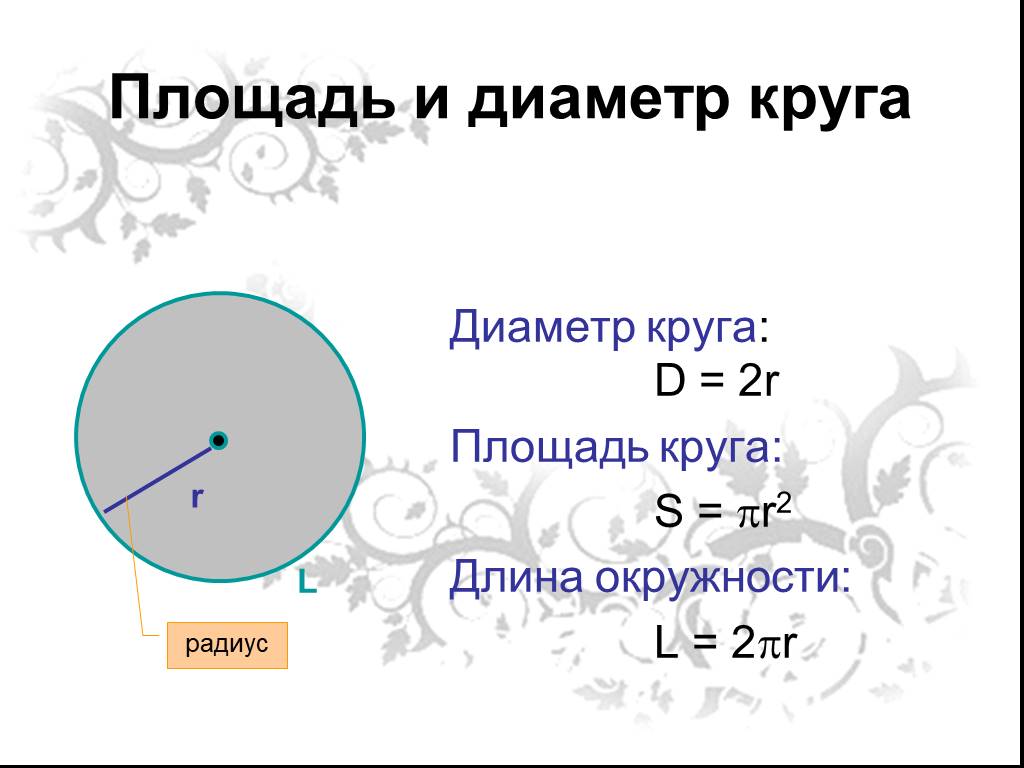 Если вы представляете себя на велосипеде, едущим по кривой со скоростью $10$ миль в час, то там, где кривизна очень велика, вы поворачиваете очень быстро. Там, где кривизна мала, вы вращаетесь не очень быстро, а там, где кривизна равна нулю, вы вообще не поворачиваетесь.
Если вы представляете себя на велосипеде, едущим по кривой со скоростью $10$ миль в час, то там, где кривизна очень велика, вы поворачиваете очень быстро. Там, где кривизна мала, вы вращаетесь не очень быстро, а там, где кривизна равна нулю, вы вообще не поворачиваетесь. Для каждого $R>0$ пусть $C_R$ будет окружностью радиуса $R$; тогда она имеет кривизну $1/R$. Тогда в пределе при $R\to\infty$ кривизна достигает $0$. В некотором смысле, в точке «$R=\infty$» мы получаем кривизну «$1/\infty = 0$», прямую линию. То, как это интерпретируется более формально, состоит в том, что по мере того, как $R\to\infty$, маленькие сегменты окружности $C_R$ становятся все более и более приближенными к прямым линиям. Вооружившись этой интерпретацией, мы можем изменить выделенное жирным шрифтом утверждение: существует только один вид кривых постоянной кривизны: окружности, в том числе бесконечные (прямые).
Для каждого $R>0$ пусть $C_R$ будет окружностью радиуса $R$; тогда она имеет кривизну $1/R$. Тогда в пределе при $R\to\infty$ кривизна достигает $0$. В некотором смысле, в точке «$R=\infty$» мы получаем кривизну «$1/\infty = 0$», прямую линию. То, как это интерпретируется более формально, состоит в том, что по мере того, как $R\to\infty$, маленькие сегменты окружности $C_R$ становятся все более и более приближенными к прямым линиям. Вооружившись этой интерпретацией, мы можем изменить выделенное жирным шрифтом утверждение: существует только один вид кривых постоянной кривизны: окружности, в том числе бесконечные (прямые). 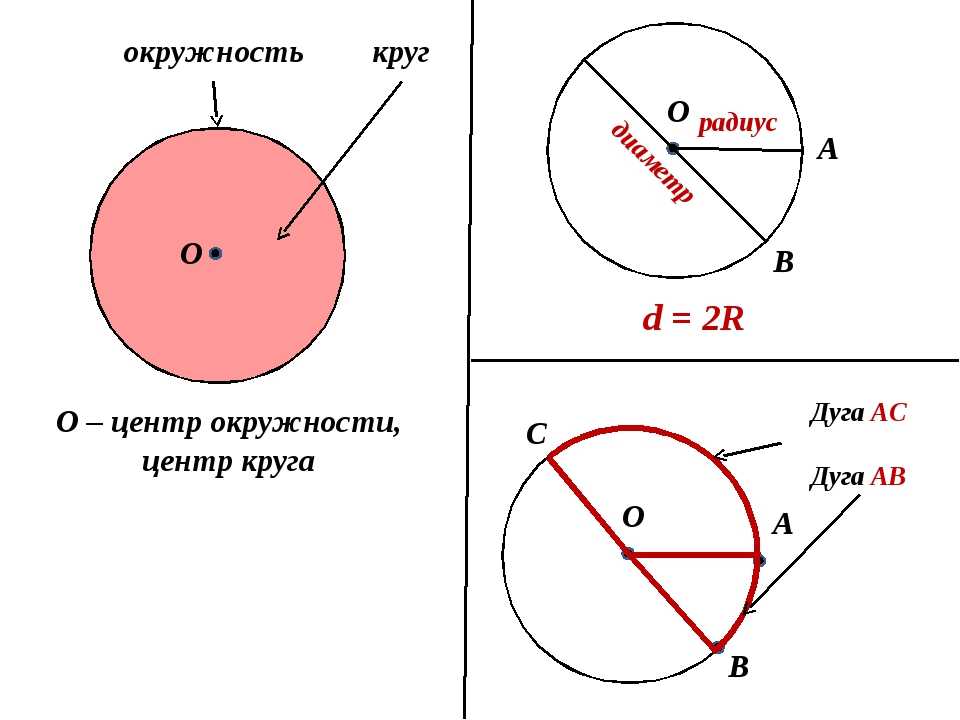 92}{r}-2x=0$$
92}{r}-2x=0$$ Первые два и четвертый связаны со ссылкой на Википедию.
Первые два и четвертый связаны со ссылкой на Википедию. Используя это определение, линия — это просто круг, и единственное разумное значение, которое можно присвоить его радиусу, — это $\infty$.
Используя это определение, линия — это просто круг, и единственное разумное значение, которое можно присвоить его радиусу, — это $\infty$. 2$. Существуют коники с вещественными коэффициентами, вырождающиеся в пару прямых. Одна из них — линия на бесконечности, инцидентная двум указанным выше точкам, а другая может быть конечной линией. Поэтому, если ваша коника не вырождается в двойную линию на бесконечности, вы получаете одну линию как конечную часть коники, которая по определению является кругом. Вы можете вычислить центр этого круга, используя указанные выше точки, и результатом будет бесконечная точка, указывающая на бесконечный радиус. 92$ для положительного бесконечного гипердействительного числа $r$ дает окружность бесконечного радиуса в гиперреальной плоскости. Можно взять конечную часть $F$ окружности, т. е. точки с конечными обеими координатами. Тогда стандартной частью $F$ является прямая, а именно ось $y$.
2$. Существуют коники с вещественными коэффициентами, вырождающиеся в пару прямых. Одна из них — линия на бесконечности, инцидентная двум указанным выше точкам, а другая может быть конечной линией. Поэтому, если ваша коника не вырождается в двойную линию на бесконечности, вы получаете одну линию как конечную часть коники, которая по определению является кругом. Вы можете вычислить центр этого круга, используя указанные выше точки, и результатом будет бесконечная точка, указывающая на бесконечный радиус. 92$ для положительного бесконечного гипердействительного числа $r$ дает окружность бесконечного радиуса в гиперреальной плоскости. Можно взять конечную часть $F$ окружности, т. е. точки с конечными обеими координатами. Тогда стандартной частью $F$ является прямая, а именно ось $y$. Очевидно, что линия на евклидовой плоскости не является окружностью. Но действительно ли мы видим центр, чтобы проверить, является ли часть кривой частью некоторого круга? Нет, потому что на евклидовой плоскости линия постоянной ненулевой кривизны является критерием окружности (рассматриваем только кривые с одним знаком кривизны, т.е. все хорды должны лежать по одну сторону от кривой). Например, мы можем проверить, постоянна ли кривизна Менгера для всех троек различных точек. Если это так и является отличной от нуля величиной, то наша кривая представляет собой часть круга. Существуют разные определения кривизны, например, дифференциально-геометрическое, но не важно, какое определение мы используем, если оно работает для небольшого участка кривой. Локальное определение кривизны подразумевает локальный критерий окружности. На евклидовой плоскости окружности с очень малой кривизной (т. е. с большим радиусом) локально почти неотличимы от прямых линий, где прямые — это линии нулевой кривизны.
Очевидно, что линия на евклидовой плоскости не является окружностью. Но действительно ли мы видим центр, чтобы проверить, является ли часть кривой частью некоторого круга? Нет, потому что на евклидовой плоскости линия постоянной ненулевой кривизны является критерием окружности (рассматриваем только кривые с одним знаком кривизны, т.е. все хорды должны лежать по одну сторону от кривой). Например, мы можем проверить, постоянна ли кривизна Менгера для всех троек различных точек. Если это так и является отличной от нуля величиной, то наша кривая представляет собой часть круга. Существуют разные определения кривизны, например, дифференциально-геометрическое, но не важно, какое определение мы используем, если оно работает для небольшого участка кривой. Локальное определение кривизны подразумевает локальный критерий окружности. На евклидовой плоскости окружности с очень малой кривизной (т. е. с большим радиусом) локально почти неотличимы от прямых линий, где прямые — это линии нулевой кривизны.