Числовые и буквенные выражения / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
Чтение числовых выражений
12 + 9 — сумма
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 8) — к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
14 — 6 = 8
18 — 9 = 9
8 < 9, значит,
14 — 6 < 18 — 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
2 класс
Задание 64, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 68. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы
Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 56, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 100, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 111, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 31, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 40, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 50, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 61, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 7, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 13, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 3, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 4, Моро, Волкова, Рабочая тетрадь, 1 часть
© 2019 — budu5.com, Буду отличником!
budu5.com
Числовые, буквенные выражения и выражения с переменными: определения, примеры
В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
Числовые выражения
С самый первых уроков математики школьники начинают знакомство с числовыми выражениями. Выражение содержит числа, и действия над этими числами. Возьмем простейшие примеры для счета: 5+2; 3-8; 1+1. Все это — числовые выражения. Если выполнить действия, указанные в выражении, то получится его значение.
Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.
Учитывая все сказанное, дадим определение. Что такое числовое выражение?
Определение. Числовое выражениеЧисловые выражения — это комбинация чисел, арифметических действий, знаков дробных черт, корней, логарифмов, тригонометрических и других функций, а также скобок и иных математических символов.
Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.
Поясним данное определение.
Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:
- натуральные числа: 6, 173, 9,
- целые числа: 18, 0, 64,
- рациональные числа:
обыкновенные дроби 13, 34,
смешанные числа 618, 8957,
периодические и непериодические десятичные дроби 9,78, 8,556 - иррациональные числа: π, e,
- комплексные числа: i=-1.
Во-вторых, арифметические действия. то известные нам еще из курса начальной школы сложение, умножение, вычитание и деление. Знаки «+», «-«, «
zaochnik.com
Числовые и буквенные выражения. Значение выражения
Числовые выражения
Числовое выражение – это запись, составленная со смыслом, в которой числа обозначены цифрами (в неё также могут входить знаки арифметических действий и скобки). Числовые выражения так же называются арифметическими выражениями.
7 – числовое выражение
7 — 2 · + : 1 – бессмысленный набор символов
Вычислить значение выражения – это значит выполнить все арифметические действия, указанные в выражении. Действия выполняются в определённом порядке, в зависимости от самих действий и присутствия в выражении скобок. Про порядок выполнения действий можно прочитать тут:
Значение числового выражения – это число, получившееся после выполнения всех вычислений.
Пример 1. Найдите значение числового выражения 4 + 3
Решение:
4 + 3 = 7
Ответ: 7.
Пример 2. Найдите значение числового выражения 4 · 3
Решение:
4 · 3 = 12
Ответ: 12.
Буквенные выражения
Буквенное выражение – это числовое выражение, в котором числа могут быть обозначены и цифрами и буквами. Буквенные выражения так же называются алгебраическими выражениями.
При обозначении чисел буквами обычно используют строчные (маленькие) буквы латинского алфавита:
7 · a – буквенное выражение
a – (b + c) – буквенное выражение
Чаще всего в буквенных выражениях разные числа обозначены разными буквами, но например в выражении:
a = b
подразумевается что a и b являются одним и тем же числом.
Значение буквенного выражения – это число, получившееся после выполнения всех вычислений. Действия в буквенных выражениях выполняются после подстановки вместо букв их численных значений.
Пример. Найдите значение буквенного выражения 2 · a + 3 при a = 7.
Решение:
2 · 7 + 3 = 14 + 3 = 17
Ответ: 17.
В буквенных выражениях знак умножения между числом и буквой, а так же между буквами, не пишут, поэтому считается, что:
7 · a = 7a и x · y = xy
Если в записи выражения одна и та же буква, например a, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны иметь ввиду одно и тоже число.
Пример. Найдите значение буквенного выражения 5x — 2x при x = 4.
Решение:
5 · 4 — 2 · 4 = 20 — 8 = 12
Ответ: 12.
В арифметике буквенные обозначения употребляют, когда необходимо выразить, что некоторое свойство (или правило) принадлежит не каким-нибудь отдельным числам, а является общим для любых чисел. Например:
a + b = b + a
Данное равенство показывает нам, что, как бы мы не переставляли слагаемые, сумма от этого не изменится. Подставив вместо букв любые числа, мы можем в этом убедиться сами:
1 + 2 = 2 + 1
naobumium.info
Буквенные выражения
Цели урока:
- Познакомить детей с новым математическим понятием “Буквенные выражения”, научить читать, записывать, находить значения математических выражений.
- Совершенствовать вычислительные навыки и умения решать составные задачи.
- Развивать логическое мышление, внимание, речь учащихся, умения делать выводы. Учить рассуждать, используя ранее изученные знания.
- Воспитывать любовь к животным, стремление помогать им.
Оборудование:
- Индивидуальные карточки.
- Аудиозапись “Голоса птиц”.
- Образец написания цифры 7.
- Проектор.
- Компьютер.
ХОД УРОКА
I. Организационный момент
– Сегодня на уроке нас ожидает необычные приключения, потому что мы отправляемся в математический лес. Путешествуя по нему, вы познакомитесь с новым видом выражений, покажете свои вычислительные навыки и умение решать задачи изученных видов, В лесу нужно быть всегда предельно внимательными, а уж в математическом лесу тем более.
Здравствуй, лес, необычный лес,
Полный математических чудес
Что узнаем мы с тобою?
Надо думать головою.
Как узнать да как найти.
Все, что мы увидим, вы будете записывать в дневники наблюдений (в тетради).
II. Проверка домашнего задания
(с. 62, № 13).Учитель заранее выполняет на доске рисунок.
– На лужайке от цветка к цветку ползли две улитки.
Какую фигуру образовал путь каждой улитки? Узнать, какое расстояние проползла каждая из них, вам поможет домашнее задание. Что вы находите, определяя расстояние, пройденное улитками? (Периметр.)
– Как найти периметр?
– На сколько больше проползла вторая улитка, чем первая? (На 25 мм.)
– Как узнали?
– Почему результат находили вычитанием?
III. Каллиграфическая минутка.
– Запишем в дневник наблюдений, какое сегодня число.
Посмотрите, какой необычный цветок распустился на полянке. Какие цифры вы нашли на нем? Учитель открывает рисунок, заранее выполненный им на доске.
– Давайте зарисуем его элементы в наши дневники наблюдений. Учитель показывает образец правильного написания цифр 7.
– Какое число мы записали?
IV. Сообщение темы и целей урока
– Прочитайте запись на доске.
5 + 3
14-(8 + 3)
7-4
– Как одним словом назвать эти записи? (выражения)
– Что такое выражение? (примеры)
– В выражениях присутствуют числа, значит эти выражения называются? (числовые)
– Что значит найти значение выражения? (решить, записанные на доске примеры)
– Сегодня мы с вами познакомимся еще с одним видом выражений и научимся находить значения этих выражений.
– Прочитайте тему урока. (Тема: ………… выражения)
– Мы не можем полностью прочитать тему сегодняшнего урока, т.к. лесное чудовище зашифровала слово.
Чтобы тему урока узнать,
Надо вычислить и расшифровать.
V. Устный счет.
9 12 15 18 21 24 25 27 35 выражения
У 10 + 2 = 12
Б 29 – 20 = 9
Е 40– 5 = 35
Ы 21 + 6 = 27
Е 14 + 7 = 21
Н 16 + 8 = 24
Н 20+ 5 = 25
В 48 – 30 = 18
К 10+5 = 15
Поставьте числа в порядке возрастания.
– Тропинка раздвоилась, в вдалеке виден чей-то домик. Для того чтобы узнать, кто там живет, вышлем на каждую тропинку по разведчику. Учитель вызывает к доске 2-х учеников. Они выполняют вычисления и записывают в окошко домика полученный результат.
– Кто живет в домике? (Ежик.)
– А ежик приготовил вам задание:
Послушайте задачу.
Ежик по лесу гулял,
Всех грибами угощал.
Пять грибов он дал лисице,
Двадцать зайцу
И про белку не забыл –
Тридцать белых подарил.
Посмотрел в корзину… пусто,
И ежу вдруг стало грустно.
Сколько грибов было в корзине ежа? Покажите мне ответы (55 грибов,) Как узнали?
VI. Подготовительная работа к изучению нового материала.
1. Устно.
– Посмотрите какая – то карточка на пенёчке со странной записью. (2 + ?)
– Вы встречали такие записи? (И да, и нет).
– Как это понять? ( В окошко вставляли число так, чтобы равенство было верным).
– А как вы думаете, можно подставить число в эту запись?
– Давайте попробуем подставить числа, которые принесли наши зверята.
– Читают числовые выражения
– Какой сделаем вывод? (Если в окошки подставлять разные числа, получатся разные числовые выражения).
VII. Объяснение нового материала.
– Мудрые Математики решили заменить окошки латинскими буквами для обозначения любого числа. Латинские буквы вы постепенно выучите . Они у нас на таблице. Давайте и мы подставим в запись букву.
– Что получили? (Выражение)
– Что есть в нашем выражении? (Латинская буква).
– Значит, как правильнее назвать? (Буквенное выражение).
– Как называются выражения, в записях которых присутствуют латинские буквы?
– Хором.
– Мы будем учиться читать, записывать и находить значения буквенных выражений.
Вывешиваю алфавит. Находим сходство в написании букв латинского, русского, английского алфавитов.
Читаем буквы. В записи буквенных выражений используются строчные буквы латинского алфавита.
– Давайте проверим, совпадает наш вывод с выводом в учебнике? (читаем вывод на стр. 64)
– Научимся писать некоторые буквы латинского алфавита.
– Запишем свои наблюдения:
(учитель пишет с объяснением на доске, а дети в тетради.)
a, b, c, d, k.
– Чтение 1 учеником вслух, а остальные следят.
– Как читаются буквенные выражения? (Так же, как и числовые).
VIII. Физкультминутка
Звери устали и приглашают на прогулку в лес. (Включается грамзапись пения птиц).
Мы выходим с вами в лес.
Сколько здесь вокруг чудес!
Вдруг мы видим: из куста
Выпал птенчик из гнезда.
Тихо птенчика берём
И в гнездо его кладём
На полянку мы выходим
Много ягод там находим.
На лужайке, на лужайке
Мы попрыгаем, как зайки.
Впереди из-за куста
Смотрит рыжая лиса.
Мы лисичку обхитрим,
На носочках убежим.
Стоп. Немножко отдохнём.
Снова в школу мы зайдём.
– Скольких животных мы встретили в лесу? (3)
IХ. Закрепление.
Упражнения в чтении и записи буквенных выражений
Работа в парах. У каждой пары листок с заданием: вставить вместо “окошка” букву латинского алфавита, прочитать.
На доске рисунок ежа. Дети выходят к доске, читают буквенные выражения и вешают на спинку ежа
– Вот мы узнали, что такое буквенное выражение, научились их читать. А теперь научимся их решать, №2 страница 65.
– Прочитайте. Как вы думаете, как их будем решать?
– Прочитаем план решения буквенных выражений:
1) прочитать;
2) записать;
3) подставить в выражения;
4) вычислить.
– Читаем выражение. Сумма k и 7. Запишем. Если k=10, то подставим вместо k -10, получим выражение 10 + 7 = 17
– Если k = 7, подставим вместо k – 7, запишем выражение 7+7=14.
– Второе выражение решает ученик у доски, а остальные в тетрадях.
| k – 7 | |
| k = 10 | 10 – 7 = 3 |
| k = 7 | 7 – 7 = 0 |
Х. Физкультминутка
Звери устали и приглашают на прогулку в лес. (Включается грамзапись пения птиц).
Мы выходим с вами в лес.
Сколько здесь вокруг чудес
Вдруг мы видим: из куста
Выпал птенчик из гнезда.
Тихо птенчика берём
И в гнездо его кладём
На полянку мы выходим
Много ягод там находим.
На лужайке, на лужайке
Мы попрыгаем, как зайки.
Впереди из-за куста
Смотрит рыжая лиса.
Мы лисичку обхитрим,
На носочках убежим.
Стоп. Немножко отдохнём
Снова в школу мы зайдём.
– Скольких животных мы встретили в лесу? (3)
ХI. Работа над пройденным материалом.
1) Карточки: Вычислить значение выражения
2) – В школе ждут наши друзья. Белочка просит решить задачу и ответить , сколько у неё осталось запасов на зиму?
Решение задачи № 3 стр. 65.
Прочитать.
Белочка запасла грибы на зиму: 60 рыжиков и 40 маслят. 10 грибов она уже отдала бельчатам. Сколько грибов у неё осталось?
– О чём задача?
– О каких грибах?
– Что это за грибы? (съедобные).
– Что известно в задаче?
– Что надо узнать?
– Как запишем краткое условие?
(Ученик диктует, учитель вывешивает краткую запись на плакате).
Было – 60 гр. И 40 гр.
Отдала – 40 гр.
Осталось – ?
– Решить задачу самостоятельно. Кто решит, встаньте. Подумайте, а можно ли решить её другим способом.
1 сп. – (60 + 40) – 10 = 90 (гр.)
2 сп. – (60 – 10) +40 = 90 (гр.)
3 сп. – (40 – 10) + 60 = 90 (гр.)
Вывод. Ответ одинаков, значит можно решать задачу любым способом, кому как удобно.
ХII. Итог урока.
– А теперь на карточках выполните задания
– А вам понравился урок?
– Что вам понравилось?
– Что нового узнали?
– Повторите план решения буквенных выражений.
– Звери благодарят вас за помощь. Дарят вам пятёрки.
Домашнее задание.
№ 4 стр.65 (найти разные способы решения задачи, кто сколько сможет).
Придумать своё буквенное выражение и предложить завтра на уроке своему соседу найти его значение.
urok.1sept.ru
Числовые и буквенные выражения. Формулы
Как найти периметр прямоугольника, стороны которого равны 3 см и 5 см (рис. 67)?
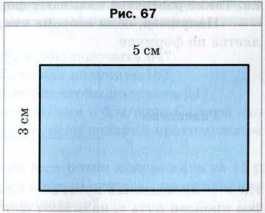
Отвечая на этот вопрос, вы можете сделать такую запись: 2 * 3 + 2 * 5.
Такая запись представляет собой числовое выражение.
Приведем еще несколько примеров числовых выражений: 12 : 4 − 1, (5 + 17) + 11, (19 − 7) * 3. Эти выражения составлены из чисел, знаков арифметических действия и скобок.
Заметим, что не всякая запись, составленная из чисел, знаков арифметических действия и скобок является числовым выражением. Например, запись +) +3 − (2 представляет собой бессмысленный набор символов.
Завершив решение задачи о периметре прямоугольника, получим ответ 16 см. В таких случаях говорят, что число 16 является значением выражения 2 * 3 + 2 * 5.
А чему равен периметр прямоугольника, стороны которого равны 3 см и a см? Ответом будет выражение 2 * 3 + 2 * a.
Запись 2 * 3 + 2 * a представляет собой буквенное выражение.
Приведем еще несколько примеров буквенных выражений: (a + b) + 11, 5 + 3 * x, n : 2 − k * 5. Эти выражения составлены из чисел, букв, знаков арифметических действий и скобок.
Как правило, в буквенных выражениях знак умножения пишут только между числами. В остальных случаях его опускают. Например, вместо 5 * y, m * n, 2 * (a + b) соответственно пишут 5y, mn, 2(a + b).
Пусть стороны прямоугольника равны a см и b см. В этом случае буквенное выражение для нахождения его периметра выглядит так: 2a + 2b.
Подставим в это выражение вместо букв a и b соответственно числа 3 и 5. Получим числовое выражение 2 * 3 + 2 * 5, которое мы уже записывали для нахождения периметра прямоугольника. Если же вместо a и b подставить, например, числа 4 и 9, то получим числовое выражение 2 * 4 + 2 * 9. Вообще, из одного буквенного выражения можно получить бесконечно много числовых выражений.
Обозначим периметр прямоугольника буквой P. Тогда равенство
P = 2a + 2b
можно использовать для нахождения периметра любого прямоугольника. Такие равенства называют формулами.
Например, если сторона квадрата равна a, то его периметр вычисляется по формуле:
P = 4a
Равенство
s = vt
где s − пройденный путь, v − скорость движения, а t − время, за которое пройден путь s, называют формулой пути.
Пример 1. Собранные в саду яблоки фермер разложил в пять ящиков по a кг и в b ящиков по 20 кг. Скоько килограммов яблок собрал фермер? Вычислите значение полученного выражения при a = 18, b = 9.
Решение.
В пяти ящиках содержится 5a кг яблок, а в b ящиках − 20b кг. Всего фермер собрал (5a + 20b) кг яблок.
Если a = 18, b = 9, то получаем: 5 * 18 + 20 * 9 = 90 + 180 = 270 (кг).
Ответ: (5a + 20b) кг, 270 кг.
Пример 2. Найдите, ползуясь формулой пути, скорость, с которой поезд прошел 324 км за 6 ч.
Решение.
Поскольку s = vt, то v = s : t. Тогда можно записать v = 324 : 6 = 54 (км/ч).
Ответ: 54 км/ч.
Пример 3. Буратино купил m булочек по 2 сольдо и торт за 5 сольдо. Составим формулу для вычисления стоимости покупки и найдите эту стоимость, если:
1) m = 4;
2) m = 12.
Решение.
За m булочек Буратино заплатил 2m сольдо.
Обозначив стоимость покупки буквой k, получаем формулу k = 2m + 5.
1) Если m = 4, то k = 2 * 4 + 5 = 13;
2) если m = 12, то k = 2 * 12 + 5 = 29.
Ответ: k = 2m + 5, 13 сольдо, 29 сольдо.
reshalka.com
Значение числового, буквенного выражения и выражения с переменными
В процессе разбора тем о числовых, буквенных выражениях и выражениях с переменными следует обратить внимание на понятие значение выражения. Ниже дадим определение этому термину, рассмотрим примеры.
Что такое значение числового выражения
Мы знакомимся с числовыми выражениями с самого начала школьного обучения. Да и почти сразу начинает использоваться понятие «значение числового выражения». Так обозначают выражения, составляющие которого – числа, соединяемые знаками арифметических действий: плюс, минус, умножить, разделить.
Определение 1Значение числового выражения – это конечное число, получаемое в результате выполнения заданных действий в исходном числовом выражении.
Например, простейшее числовое выражение 2+3. Оно задает необходимость выполнить сложение натуральных чисел, в результате чего получается число 5, которое и будет служить значением числового выражения 2+3.
Зачастую в словосочетании «значение числового выражения» слово «числовое» не употребляют, поскольку в любом случае понятно, значение какого выражения рассматривается.
Определение, которое мы дали выше, верно для числовых выражений и более сложной структуры, изучаемых в старших классах. Также нужно сказать о том, что возможно встретить такие числовые выражения, значение которых указать нет возможности: в некоторых выражениях задаются действия, которые нельзя выполнить. К примеру, деление на нуль не определено, а значит указать значение выражения, к примеру, 5:(9-9) невозможно. Такие числовые выражения называют выражениями, не имеющими смысла.
В основном интерес вызывает не само числовое выражение, а его значение. Практически всегда существует задача по нахождению значения заданного выражения, которая так и обозначается: «найти значение выражения». В соответствующей статье можно детально изучить сам процесс нахождения значения числовых выражения разного рода с примерами.
Значение буквенного выражения и выражения с переменными
Кроме числовых, интерес представляют и буквенные выражения – те выражения, составляющими которого являются, в том числе, одна или несколько букв. Буквы в буквенном выражении обозначают разные числа, и при замене букв на числа получается числовое выражение.
Определение 2Значения букв – числа, которые заменяют эти буквы в буквенном выражении. Тогда значение буквенного выражения при заданных значениях букв – это значение полученного числового выражения.
Таким образом, речь идет не о значении буквенного выражения, как такового, а о его значении, когда заданы (определены) конкретные значения букв.
Например, рассмотрим буквенное выражение 3·x + y. Допустим также, что заданы некоторые зн
zaochnik.com
Числовые и буквенные выражения. Формулы
Представим себе такую историю.
– Паша, я вчера смотрел чемпионат мира «Формулы-1»! – рассказывал Саша. – Это такое зрелище! Ты только представь себе: болиды «Формулы-1» могут развить скорость аж до четырёхсот километров в час. Вот бы мне так погонять!
– Саша, ты что? – перебил Паша. – Это очень опасная скорость. И чтобы научиться так ездить, нужно многие годы тренироваться. А ты знаешь, что в математике тоже есть формулы?
– Формулы? – удивился Саша. – Ты хочешь сказать, что цифры устраивают гонки?
– Нет, Саша! Ты такой смешной! – засмеялся Паша. – Математические формулы совсем другие. Но лучше всех нам о них расскажет только Электроша.
– Ребята, прежде чем я вам расскажу о формулах, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим о формулах, – предложил Электроша, – но прежде вам нужно разобраться в понятиях «числовое выражение» и «буквенное выражение».
Чтобы в них разобраться, ответьте мне на вопрос: как найти периметр прямоугольника, стороны которого равны, например, 4 и 8 см?
– Ну это же все знают, – начал Саша. – Периметр прямоугольника – это сумма длин всех его сторон. Тогда периметр нашего прямоугольника равен 4 + 8 + 4 + 8.
– Саша, – перебил Паша, – но в прямоугольнике же две пары равных сторон. Значит, вычислить периметр нашего прямоугольника можно было следующим образом: 2 умножить на 4 плюс 3 умножить на 8.
– Не спорьте, ребята, – сказал Электроша. – Вы оба правы! Периметр прямоугольника можно вычислить и первым, и вторым способом. Записи, которые вы составили, называют числовыми выражениями.
Запомните! Числовое выражение – это выражение, составленное из чисел, знаков арифметических действий и скобок.
– Электроша, а вот такая запись тоже будет числовым выражением? – решил спросить Саша.
– Нет, Саша, – ответил Электроша. – Важно понимать, что не всякая запись, составленная из чисел, знаков арифметических действий и скобок, будет являться числовым выражением. Запись, которую показал нам Саша, представляет собой бессмысленный набор символов.
В записи выражений никогда не применяются знаки равенств и неравенств.
– А теперь, может, вы мне скажете, чему же равен периметр нашего прямоугольника? – спросил Электроша.
– Периметр прямоугольника равен 24 см, – ответили мальчишки.
– Правильно! – подтвердил Электроша. – Число, которое получают в результате выполнения всех действий в числовом выражении, называют значением этого выражения.
Выражение не имеет значения, если какое-либо из действий в нём нельзя выполнить.
– А теперь скажите, чему равен периметр прямоугольника, стороны которого равны, например, 4 см и а см?
– Периметр этого прямоугольника будет равен 2 умножить на 4 плюс 5 умножить на а, – ответил Паша.
– Молодец! – похвалил Пашу Электроша. – Запись «2 умножить на 4 плюс 2 умножить на а» называют буквенным выражением.
Запомните! Буквенное выражение – это выражение, которое составлено из чисел, букв, знаков арифметических действий и скобок.
Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют ещё переменными. Если в буквенное выражение вместо буквы подставить число и выполнить все действия, то получим значение буквенного выражения.
Давайте вместо а в нашем буквенном выражении подставим число 10. Получим числовое выражение 2 умножить на 4 плюс 2 умножить на 10 равно 28. В этом случае число 28 является значением нашего буквенного выражения при а = 10.
– А буквенные выражения всегда имеют значения? – спросили мальчишки.
– Хороший вопрос! – ответил Электроша. – Буквенное выражение может не иметь значения в случае, если при подстановке значений букв в буквенное выражение получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называют некорректным для натуральных чисел. Говорят также, что значение такого выражения не определено для натуральных чисел, а само выражение не имеет смысла.
Например, найдём значение буквенного выражения а – b при а = 20, b = 25.
– Электроша, но 20 меньше 25, – заметили ребята, – а в вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.
– Правильно вы заметили, – сказал Электроша. – В таком случае говорят, что выражение не имеет смысла при указанных а и b.
Как правило, в буквенных выражениях числовой множитель (коэффициент) пишут перед буквой, а знак умножения ставят только между числами. Например, вместо 2 умножить на а пишут просто 2а. Или вместо выражения 2 умножить на сумму чисел а и b пишут 2(a + b).
– А теперь скажите, чему равен периметр прямоугольника, стороны которого равны а см и b см?
– Периметр такого прямоугольника можно вычислить выражением 2а + 2b, – сказал Паша.
– Молодец! – похвалил Электроша. – Если мы подставим в это выражение вместо букв а и b соответственно числа 4 и 8, то получим числовое выражение 2 умножить на 4 плюс 2 умножить на 8. Это числовое выражение мы уже записывали для нахождения периметра первого прямоугольника. Если вместо букв а и b мы подставим, например, числа 4 и 10, то получим числовое выражение 1 умножить на 4 плюс 2 умножить на 10. Такое числовое выражение мы тоже уже записывали для вычисления периметра второго прямоугольника.
– Так что, Электроша, вместо чисел а и b можно подставлять разные числа? – спросили ребята.
– Да! – ответил Электроша. – Из одного буквенного выражения можно получить бесконечно много различных числовых выражений.
Если периметр прямоугольника обозначить буквой P, то получим равенство P = 2а + 2b. Такое равенство можно использовать для нахождения периметра любого прямоугольника. Такие равенства называют формулами.
– А! – воскликнул Саша. – Теперь понятно, про какие формулы говорил Паша.
Запомните! Правило, записанное в виде равенства двух буквенных выражений, называется формулой.
– Вы уже знакомы с некоторыми формулами, – продолжил Электроша. – Может, назовёте их?
– Если сторона квадрата равна а, то его периметр можно вычислить по формуле P = 4а, – начал Саша.
– А я ещё знаю формулу пути: S = vt, – продолжил Паша. – Здесь S – это пройденный путь, v – скорость движения, а t – время, за которое пройден путь S.
– Какие вы молодцы! – похвалил ребят Электроша. – А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: в каждый из овалов впишите значения буквенного выражения два эм плюс десять при значении буквы эм, указанном в соответствующем уголке фигуры.
Решение: начнём с первого уголка фигуры. Здесь m = 5. Подставим число 5 вместо m в буквенное выражение 2m + 10. Посчитаем. Получим 20. В следующем уголке записано число 0. Подставим его вместо буквы m в выражение. Получим 2 умножить на 0 плюс 10. Посчитаем и получим 10. Следующее число 10. Подставим его в выражение вместо буквы m. Получим 30. В следующем уголке записано число 105. Подставим его в выражение. Посчитаем и получим 220. И последнее число 15. Подставим его в выражение и посчитаем. Получим 40.
Следующее задание: заполните таблицу.
Решение: в первой строчке нам известно, что пешеход прошёл 8 минут со скоростью 70 м/мин. Воспользуемся формулой пути. Подставим в неё известные нам скорость и время. Посчитаем и получим, что пешеход прошёл 560 метров. В следующей строчке нам известно, что велосипедист за 2 часа проехал 24 км. Нужно узнать, с какой скоростью он ехал. Из формулы пути выразим скорость. Подставим наши данные в формулу. Посчитаем и получим, что скорость велосипедиста 12 км/ч. И в последней строчке нам известно, что автомобиль ехал со скоростью шестьдесят километров в час и проехал 240 км. Нужно узнать, сколько времени ехал автомобиль. Выразим из формулы пути время. Подставим в формулу известные значения. Посчитаем и получим, что автомобиль ехал 4 часа.
– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.
Итак, Наташа купила в подарок своей маме шоколадное сердечко. Сколько весит эта шоколадка, если каждый квадратик весит 10 г?
Решение: сердечко состоит из 32 целых квадратиков и из 16 половинок квадратиков. Так как целый квадратик весит 10 г, то половинка квадратика весит 5 г. А тогда вес всего шоколадного сердечка можно найти так: 32 умножить на 10 + 16 умножить на 5. Посчитаем и получим, что сердечко весит 400 г.
videouroki.net
