Сочетания | Наука собственными силами
Свойства сочетаний
Числа Ckn обладают целым рядом замечательных свойств. Эти свойства можно доказать по-разному. Можно доказывать алгебраически – прямо воспользоваться формулой (8)
Но можно эти же свойства доказывать и чисто комбинаторными соображениями.
Свойствo 1
(9).
Алгебраическое доказательство:
В формулу для Ckn верхним индексом подставим (n-k). Получим
Однако намного изящнее комбинаторное доказательство:
Что значит «выбрать n-k предметов из n»? Это все равно что «указать k предметов, которые не будут выбраны». Т.е. выбрать n-k предметов из n можно столькими же способами, что и k предметов.
Этим свойством удобно пользоваться, когда верхний индекс ненамного меньше нижнего.
Сравните, к примеру, два способа вычисления C57:
напрямую используя формулу (8):
или применяя формулу (9):
Не правда ли, второй проще?
Свойство 2
(10).
Алгебраическое доказательство:
Запишем правую часть, используя формулу (8) для числа сочетаний:
Приведем к общему знаменателю, равному n!∙(n-k)!:
Однако и здесь комбинаторное доказательство намного красивее:
Все сочетания из n по k (их количество равно Ckn ) можно разбить на два класса: содержащие элемент под номером n и не содержащие его.
Выбрать из n элементов k штук, включая n-й – это все равно, что из оставшихся n-1 элементов выбрать k-1. Это можно сделать Ck-1n-1 способами.
Если же n-й элемент в сочетание не входит, то все k элементов нужно выбирать из оставшихся n-1 элементов. Это можно сделать Ckn-1 способами.
Так как каждое сочетание из n по k входит или в один, или в другой класс, но не в оба сразу, можно применить правило суммы, и получить доказываемое равенство:
(10).
Свойство 3
(11).
Доказательство (комбинаторное):
В левой части равенства стоит количество всех сочетаний из n элементов (независимо от числа элементов в самих сочетаниях).
О каждом элементе мы можем принять решение: брать его в сочетание или не брать. Т.е. для каждого элемента есть два варианта решения: «да» и «нет». Будем для обозначения того или иного сочетания класть на каждый элемент монетку, причем «да» будем обозначать орлом, а «нет» – решкой. Таким образом, каждому сочетанию из n элементов будет соответствовать ряд из n монет.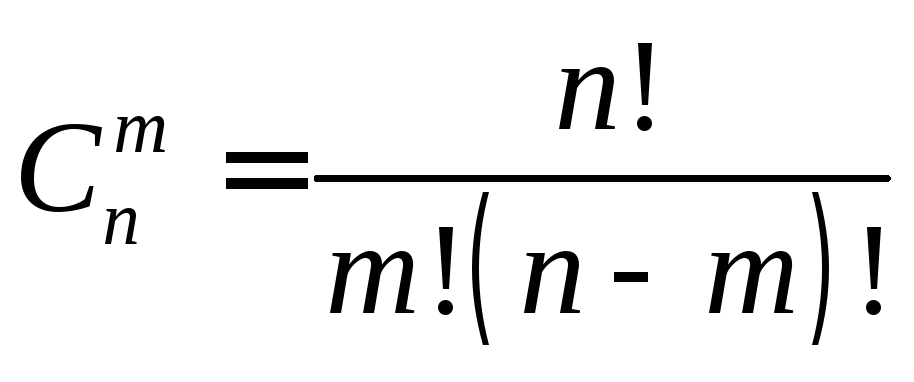
В разделе «Основные законы комбинаторики» мы доказали, что для n монет возможны 2n вариантов распределения орлов и решек. Поэтому количество всех сочетаний из n элементов равно 2n, что и требовалось доказать.
Перейти к следующей главе →
Страницы: 1 2 3
Термопара TW-N(K) 4.8-300-1.5 м-1/8
Описание Термопара TW-N(K) 4.8-300-1.5 м-1/8
•Термопара TW-N(K) 4.8-300-1.5 m-1/8 длинна 300 мм, резъба 1/8. провод 1.5 м. термопары из никросил-нисиловые (никельхромникель-никелькремниевые) ТНН — Тип N.
Сравнение термопар
Таблица ниже описывает свойства нескольких различных типов термопары. В пределах колонок точности, T представляет температуру горячего соединения, в градусах Цельсия. Например, термопара с точностью В±0.0025Г—T имела бы точность В±2.5 В°C в 1000 В°C.| Тип термопары | Температурный диапазон °C (длительно) | Температурный диапазон °C (кратковременно) | Класс точности 1 (°C) | Класс точности 2 (°C) | IEC Цветовая маркировка |
| K | 0 до +1100 | −180 до +1300 | ±1. ±0.004×T от 375 °C до 1000 °C |
±2.5 от −40 °C до 333 °C ±0.0075×T от 333 °C до 1200 °C |
|
| J | 0 до +700 | −180 to +800 | ±1.5 от −40 °C до 375 °C ±0.004×T от 375 °C до 750 °C |
±2.5 от −40 °C до 333 °C ±0.0075×T от 333 °C до 750 °C |
|
| N | 0 до +1100 | −270 to +1300 | ±1.5 от −40 °C до 375 °C ±0.004×T от 375 °C до 1000 °C |
±2.5 от −40 °C до 333 °C ±0.0075×T от 333 °C до 1200 °C |
С этим товаром смотрят
Оставить отзыв о «Термопара TW-N(K) 4.8-300-1.5 м-1/8»
Ваши знания будут оценены пользователями сайта, если Вы авторизуетесь перед написанием отзыва.
| Ваше имя:* | |
| Заголовок:* | |
| Оценка товара: | |
| Достоинства: | |
| Недостатки: | |
| Комментарий:* | |
| В целом Ваш отзыв: | Положительный Отрицательный |
Алгоритм для возврата всех комбинаций k элементов из n
Искусство компьютерного программирования, том 4: Fascicle 3 содержит множество таких алгоритмов, которые могут лучше соответствовать вашей конкретной ситуации, чем то, что я описываю.
Коды Грея
Проблема, с которой вы столкнетесь, конечно же, с памятью, и довольно быстро у вас будут проблемы с 20 элементами в вашем наборе — 20 C 3 = 1140. И если вы хотите повторить над набором лучше всего использовать модифицированный алгоритм кода Грея, чтобы вы не удерживали их все в памяти. Они генерируют следующую комбинацию из предыдущей и избегают повторений. Их много для разных целей. Хотим ли мы максимизировать различия между последовательными комбинациями? минимизировать? и так далее.
Некоторые из оригинальных статей, описывающих коды Грея:
- Некоторые пути Гамильтона и алгоритм минимального изменения
- Алгоритм генерации комбинации смежных обменов
Вот некоторые другие документы, посвященные этой теме:
- Эффективная реализация алгоритма генерации комбинаций Eades, Hickey, Read Adjacent Interchange (PDF, с кодом на Паскале)
- Комбинированные генераторы
- Обзор комбинаторных кодов Грея (PostScript)
- Алгоритм кодов Грея
Chase’s Twiddle (algorithm)
Phillip J Chase, `Algorithm 382: Combinations of M out of N Objects’ (1970)
Алгоритм в C.
..
Вы также можете ссылаться на комбинацию по ее индексу (в лексикографическом порядке). Понимая, что индекс должен быть некоторым изменением справа налево на основе индекса, мы можем построить что-то, что должно восстанавливать комбинацию.
Итак, у нас есть набор {1,2,3,4,5,6}… и нам нужны три элемента. Допустим {1,2,3} мы можем сказать, что разница между элементами равна единице и по порядку и минимальна. {1,2,4} имеет одно изменение и является лексикографически номером 2. Таким образом, количество «изменений» на последнем месте составляет одно изменение в лексикографическом порядке. Второе место с одним изменением {1,3,4} имеет одно изменение, но на него приходится больше изменений, поскольку оно находится на втором месте (пропорционально количеству элементов в исходном наборе).
Метод, который я описал, это деконструкция, как кажется, от множества к индексу, нам нужно сделать обратное, что намного сложнее. Вот как Баклз решает проблему. Я написал немного C для их вычисления с небольшими изменениями — я использовал индекс наборов, а не диапазон чисел для представления набора, поэтому мы всегда работаем от 0 до n.
- Поскольку комбинации неупорядочены, {1,3,2} = {1,2,3} — мы упорядочиваем их как лексикографические.
- Этот метод имеет неявный 0, чтобы начать набор для первой разницы.
Указатель комбинаций в лексикографическом порядке (McCaffrey)
Есть и другой способ: его концепция легче понять и запрограммировать, но без оптимизации Buckles. К счастью, он также не создает повторяющихся комбинаций:
Набор, максимизирующий , где .
Например: 27 = С(6,4) + С(5,3) + С(2,2) + С(1,1) . Итак, 27-я лексикографическая комбинация из четырех вещей: {1,2,5,6}, это индексы любого набора, который вы хотите посмотреть. Пример ниже (OCaml), требуется выбрать функцию , оставить читателю:
(* это найдет комбинацию [x] списка [set] при взятии [k] элементов *)
пусть комбинация_маккаффери устанавливает k x =
(*функция максимизации -- максимизировать a, равное aCb *)
(* вернуть наибольшее значение c, где c < i, и выбрать (c, i) <= z *)
пусть rec максимизирует a b x =
если (выбрать a b ) <= x тогда a еще максимизировать (a-1) b x
в
позвольте повторить итерацию n x i = сопоставить i с
| 0 -> []
| я ->
пусть max = максимизирует n i x в
max :: iterate n (x - (выберите max i)) (i-1)
в
если x < 0, то сбой с "ошибками" иначе
пусть idxs = iterate (набор List.
length) x k в
List.map (List.nth set) (List.sort (-) idxs)
length) x k в
List.map (List.nth set) (List.sort (-) idxs)
Небольшой и простой итератор комбинаций
Следующие два алгоритма предназначены для дидактических целей. Они реализуют итератор и (более общую) общую комбинацию папок.
Они максимально быстрые, имеют сложность O( k .
Мы начнем с итератора, который будет вызывать предоставленную пользователем функцию для каждой комбинации
let iter_combs n k f =
пусть rec iter v s j =
если j = k, то f v
иначе для i = s to n - 1 do iter (i::v) (i+1) (j+1) сделано в
итер [] 0 0
Более общая версия будет вызывать предоставленную пользователем функцию вместе с переменной состояния, начиная с начального состояния. Поскольку нам нужно передать состояние между разными состояниями, мы не будем использовать цикл for, а вместо этого воспользуемся рекурсией,
let fold_combs n k f x =
пусть rec петля i s c x =
если я < п, то
петля (i+1) s c @@
пусть c = i::c и s = s + 1 и i = i + 1 в
если s < k, то петля i s c x иначе f c x
иначе х в
цикл 0 0 [] х
комбинаторика - Почему ${n \выбрать k} = {n \выбрать n-k}$?
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 16 тысяч раз
$\begingroup$
Говорят, что $${n \choose k}={n \choose n-k}.
$$
Кто-нибудь может объяснить, что это значит?
Среди многих задач, использующих это доказательство, вот пример:
В английском алфавите $26$ букв, из которых $5$ — гласные (и $21$ — гласные). согласные буквы).
Сколько $5$-буквенных слов можно составить, используя $3$ разных согласных? и $2$ разных гласных?
Я понимаю, где ответ говорит, что у нас есть:
$$P(21,3) = 21\times 20\times 19 = 7980\ ,$$
и
$$P(5,2) = 5 \times4 = 20\ .$$
Мы получаем перестановки для каждой категории. Теперь мы должны расставить их по $5$ местам, но там сказано, что это делается вычислением:
$$C(5,3)$$
и далее поясняется:
В каждом случае остальные буквы будут гласными.
(Разве мы не должны проверить этот случай?)
Это заканчивается умножением всех трех вместе: $C(5,3)\times P(21,3)\times P(5,2)$
- комбинаторика
- интуиция
$\endgroup$
1
$\begingroup$
$$
\начать{выравнивать}
\dbinom{6}{2} & \longleftrightarrow \dbinom{6}{6-2} \\[8pt]
AB & \longleftrightarrow CDEF \\
AC & \longleftrightarrow BDEF \\
AD & \longleftrightarrow BCEF \\
AE & \longleftrightarrow BCDF \\
AF & \longleftrightarrow BCDE \\
BC & \longleftrightarrow ADEF \\
BD & \longleftrightarrow ACEF \\
BE & \longleftrightarrow ACDF \\
BF & \longleftrightarrow ACDE \\
CD & \longleftrightarrow ABEF \\
CE & \longleftrightarrow ABDF \\
CF & \longleftrightarrow ABDE \\
DE & \longleftrightarrow ABCF \\
DF & \longleftrightarrow ABCE \\
EF & \longleftrightarrow ABCD
\end{выравнивание}
$$
Способов выбрать 2$ из 6$ ровно столько же, сколько способов выбрать 6-2$ из 6$, потому что каждому способу выбора 2$ из 6$ соответствует способ выбора 6-2$ из 6$.
$\endgroup$
1
$\begingroup$
Рассмотрим набор из $n$ объектов. Выбор $k$ из них для включения в набор эквивалентен выбору $n-k$ для исключения.
Редактировать: Рассмотрим школьную игру в вышибалы с красной и синей командами. Всего учеников $n$, а в синей команде $k$ учеников. Так как каждый ученик играет, в красной команде $n-k$ учеников.
Поскольку учитель физкультуры необъективен, он позволяет синей команде сначала выбрать всех своих игроков. У них есть $\binom{n}{k}$ способы сделать это. После этого у красной команды нет выбора . Они должны выбрать всех оставшихся $n-k$ учеников.
Было бы равное количество способов сделать это, если бы учитель был склонен к красному цвету, поэтому $\binom{n}{k} = \binom{n}{n-k}$.
$\endgroup$
4
$\begingroup$
Когда у нас есть $n$ объектов на выбор, и мы решили включить $k$ из них, существует ${n\choose k}$ способов выбора этих объектов.
Однако в то же время мы выбираем , а не , чтобы включить $n-k$ объектов, и есть ${n \выбрать n-k}$ способов исключить эти объекты. Таким образом, мы имеем, что ${n \выберите k} = {n \выберите n-k}$.
$\endgroup$
2 9{n-к} = 0, $$
как действительные для произвольных $x$ и $y$ получаем
$$ {n \выберите k} = {n \выберите n-k} $$
Физический смысл - действительно...
Даны $(k)$ белых шаров и $(n-k)$ черных шаров, мы можем составить $\displaystyle n \choose \displaystyle k$ перестановки.
Даны $(n-k)$ белых шаров и $(k)$ черных шаров, мы можем составить $\displaystyle n \choose \displaystyle n-k$ перестановки.
Оба случая симметричны (черный шар $\leftrightarrow$ белый шар), поэтому
$$ {n \выберите k} = {n \выберите n-k} $$
$\endgroup$
0
$\begingroup$
Вы можете использовать определение $\binom{n}{k}=\frac{n!}{k!(n-k)!}$ :
$\binom{n}{n-k}=\frac{n !}{(n-k)!(n-(n-k))!}=\frac{n!}{(n-k)!(n-n+k)!}=\frac{n!}{(n-k)!( k)!}=\frac{n!}{k!(n-k)!}=\binom{n}{k}$
По моему опыту, это самое простое доказательство, которое я нашел без необходимости проходить через много комбинаторных аргументов.