Тема 1. Определители, матрицы, системы
Определитель (число), детерминант – числовая характеристика для квадратной матрицы.
П равила вычисления определителей второго и третьего порядка:
Определителем второго порядка, соответствующим матрице А, называется число
Аналогично, для определителя третьего порядка:
Определители третьего порядка вычисляются по правилу Саррюса: одно из трех слагаемых, входящих в правую часть со знаком плюс, есть произведение элементов главной диагонали матрицы, каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента их противоположного угла матрицы, а слагаемые со знаком минус, строятся таким же образом, но относительно побочной диагонали.
Свойства определителей:
При транспонировании матрицы определитель не изменяется
При перестановке каких-либо двух строк/столбцов определитель меняет знак
Если в определителе есть кратное строке/столбцу, то коэффициент пропорциональности можно вынести за знак определителя
Если есть нулевая строка/столбец, то определитель равен 0
Если в определителе есть 2 одинаковых столбца/строки, то определитель равен 0
Определитель не изменится, если к любой строке/столбцу прибавить любой другой столбец/строку с любым коэффициентом
Определитель равен сумме произведений элементов каких-либо строк/столбцов на их алгебраическое дополнение
Если все элемента какого-либо ряда определителя, кроме одного, равны 0, то определитель равен этому, не равному нулю элементу, умноженному на его алгебраическое дополнение
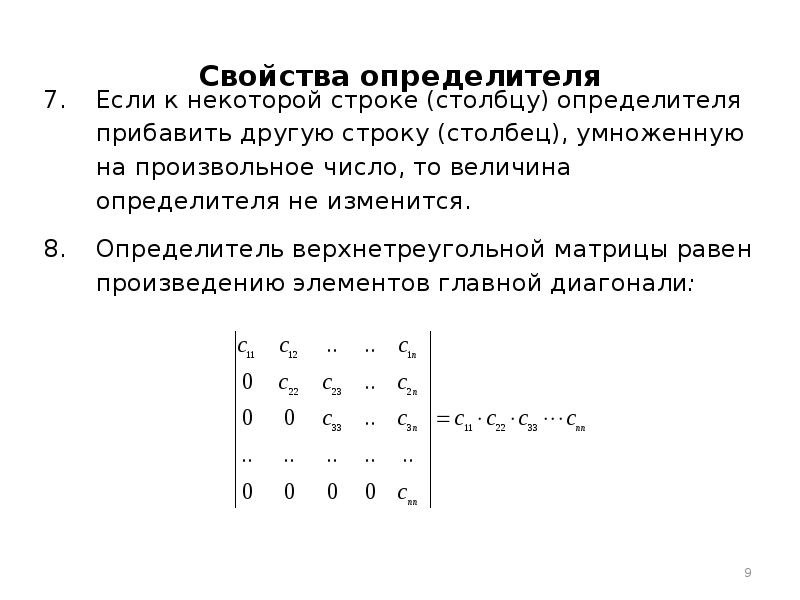
Определитель треугольной матрицы равен произведению элементов его главной диагонали
Миноры и алгебраические дополнения
Минор – к ai,j называется определитель, получившийся
из данной матрицы путем вычеркивания
i-строки и j-столбца.
Алгебраические дополнения – к элементу ai,j называется Aij=(-1)i+j* Mij, если i+j – четное, то Aij= Mij, если нечетное — Aij=- Mij,
Теорема Лапласа
Определитель можно разложить по любой строке/столбцу – он равен сумме произведений элементов любой строки/столбца на свое алгебраическое дополнение.
Вычисление определителей высших порядков, правило треугольника.
Правило треугольника:
Разложение по алгебраическому дополнению:
Приведение к треугольному виду:
Преобразование, когда все элементы, лежащие по одну сторону одной из его диагоналей, становятся равными 0. А определитель матрицы равен произведению элементов на его диагонали.
*****************************************************************************************************
Матрица – упорядоченная по строкам и столбцам совокупность элементов, матрица размером m x n – прямоугольная таблица из чисел aij, состоящая из m строк и n столбцов.
Виды матриц:
Квадратная (m=n)
Прямоугольная (m>n или n>m)
Строчная (m=1)
Столбцовая (n=1)
Диагональная (A=diag (a,b,c) = )
Единичная (A=diag (a,b,c) = )
Основные операции с матрицами и их свойства
Операции (А, В):
А+В=В+А
А+(В+С)=(А+В)+С
α(А+В)=αА+αВ
(αβ)А=α(βА)
Транспонирование матрицы – все строки матрицы меняются на столбцы с такими же номерами
- Для любой квадратной матрицы можно сосчитать определитель
Умножение матриц – матрица С, элемент которой, стоящий в i-строке и j-столбце, равен сумы произведений соответственных элементов i-строки матрицы А и j-столбца матрицы В. Умножать можно те матрицы, для которых число столбцов первого сомножителя совпадает с числом строк второго.
Для любой квадратной невырожденной (определитель не равен 0) матрицы можно найти обратную матрицу
, А* из алгебраических дополнений.
Аn=А*А…А
Свойства:
А(В+С)=АВ+АС
А(ВС)=(АВ)С
α(АВ)=(αА)В
(АВ)Т=ВТ АТ
(А+В)Т=АТ+ВТ
Определитель квадратной матрицы
по
Определитель квадратной матрицы (до матриц 3 × 3), свойства определителей, миноры, сомножители и применение определителей при нахождении площади треугольника
Для вычисления обратной матрицы требуется определитель. Для каждой квадратной матрицы A существует единичное скалярное значение, известное как определитель A , обозначаемый как det A или |A|.
Если det(A)=0, матрица называется единственной . Определитель содержит те же элементы, что и матрица, которые заключены между вертикальными чертами вместо скобок в скалярном уравнении. Если A = [ A ] является одним элементом (1×1), то определитель определяется как значение элемента
Тогда | А | =det A = a 11
Если A равно (n x n), его определитель может быть определен в терминах порядка (n-1) или меньше.
Определитель A = $\lbrack \begin{matrix}
3 & -2 & \\
17 & 11 & \\
\end{matrix}
\rbrack $ записывается как $\vert \begin{matrix }
3 & -2 & \\
17 & 11 & \\
\end{matrix}
\vert $. Для определителей второго порядка мы используем следующую формулу:
Если A является матрицей размера n x n, а одна строка и один столбец удалены, результирующая матрица представляет собой (n-1) x (n-1) подматрица A .
Определитель такой подматрицы называется минором A и обозначается m ij , где i и j соответствуют удаленным строке и столбцу соответственно. Это означает, что m ij является минором элемента a ij в A .
Кофактор C ij элемента а IJ определяется как:
, когда сумма ряд № I и столбец J ровно, C IJ = M IJ и когда I + 20192020202020202019202019202019201920201920 10. . нечетно, c ij =-m ij
Определитель матрицы n x n A можно записать как: элементы первой строки из A и их соответствующие кофакторы.
Для использования миноров для вычисления определителей третьего порядка каждый член одной строки умножается на его минор.
Знаки товара чередуются, начиная со второго товара. В приведенном ниже определении показано расширение с использованием элементов первого for определителя. Однако можно использовать ЛЮБУЮ строку.
Пример. Оценить определитель A = $\lbrack \begin{matrix}
2 & 3 & 4 & \\
6 & 5 & 7 & \\
1 & 2 & 8 & \\
\end{matrix}
\rbrack $
Пример: найти определитель
Кофакторы первой строки:
определитель третьего порядка.
- ШАГ 1: Запишите первые два столбца справа от определителя, как показано ниже.
- ШАГ 2: Проведите диагональ от каждого элемента в верхнем ряду вниз и вычислите произведение чисел на каждой диагонали.
- ШАГ 3: Теперь проведите диагональ от каждого элемента в нижнем ряду вверх и вычислите произведение чисел на каждом.
- Чтобы найти значение определителя, сложите произведения первого набора диагоналей, а затем вычтите произведения второго набора диагоналей.
- Значение: aei + bfg + cdh – gec – hfa – idb
Определители используются для вычисления площади треугольника, когда известны координаты трех вершин.
Площадь треугольника, вершины которого имеют координаты (a, b), (c, d), (e, f), можно найти по формуле:
Пример: Найдите площадь треугольника, вершины которого имеют координаты (-4, -1), (3, 2), (4, 6).
Присвойте значения a, b, c, d, e и f в приведенной выше формуле: a = -4, b = -1, c = 3, d = 2, e = 4, f = 6
Теперь используйте диагональный метод и добавьте нижние продукты и вычтите верхние продукты: -8 + (-4) + 18 – 8 – (-24) –(-3) = 25. Значение определителя равно 25. И когда мы применяем это к формуле площади, мы получаем ½ (25) = 12,5. Площадь треугольника равна 12,5 квадратных единиц.
Когда один или несколько элементов определителя неизвестны, но известно значение определителя, мы можем использовать расширение, чтобы найти значения переменной.
Пожалуйста, поделитесь
Свойства определителей
Свойства определителейМайкл Френдли
2022-12-08
Сначала мы делаем это на простых числовых примерах.
а затем с помощью геометрических диаграмм.Создать матрицу 2 x 2
A <- matrix(c(3, 1,
2, 4), nrow=2, byrow=ИСТИНА)
А ## [1] [2] ## [1,] 3 1 ## [2,] 2 4
det(A)
## [1] 10
2. транспонировать -> det (A) без изменений
det( t(A))
## [1] 10
3. умножить строку * k -> k * det(A)
Обратите внимание, что для умножения строк на различных констант требуется диагональная матрица слева. 92 * дет(А)
## [1] 90
5. det (A B) -> det(A) * det(B)
Определитель произведения есть произведение определителей. то же самое верно для любого количества терминов в матричном произведении.
B <- матрица(с(4, 2,
3, 5), nrow=2, byrow=ИСТИНА)
B ## [1] [2] ## [1,] 4 2 ## [2,] 3 5
det(A %*% B)
## [1] 140
det(A) * det(B)
## [1] 140
6.
пропорциональные строки или столбцы -> det() == 0 Здесь мы просто добавляем дополнительную копию столбца 1 матрицы, поэтому С[3] == С[1] . Определитель равен 0, потому что столбцы
линейно зависимы.
C <- матрица(c(1, 5,
2, 6,
4, 4), nrow=3, byrow=ИСТИНА)
C <- cbind(C, C[1])
C ## [1] [2] [3] ## [1,] 1 5 1 ## [2,] 2 6 2 ## [3,] 4 4 4
дет(С)
## [1] 0
7. Добавить кратные одной строки в другую -> det без изменений
Это принцип, лежащий в основе одной из элементарных строк операции.
А[2,] <- А[2,] - 2*А[1,] дет(А)
## [1] 10
8. Геометрическая интерпретация
Многие аспекты матриц и векторов имеют геометрическую интерпретацию.
Для матриц \(2 \times 2\)
определитель - это площадь параллелограмма, заданного формулой
строки (или столбцы), нанесенные на график в 2D-пространстве. (Для \(3 \times 3\) матриц определитель равен 
)
A <- матрица(c(3, 1,
2, 4), nrow=2, byrow=ИСТИНА)
А ## [1] [2] ## [1,] 3 1 ## [2,] 2 4
det(A)
## [1] 10
В пакете matlib есть несколько полезных функций
( vectors() ) для рисования геометрических диаграмм.
библиотека (matlib)
хлим <- с(0,6)
илим <- с(0,6)
пар(мар=с(3,3,1,1)+.1)
график (xlim, ylim, тип = "n", xlab = "X1", ylab = "X2", asp = 1)
сумма <- А[1,] + А[2,]
# нарисуйте параллелограмм, определяемый строками A
многоугольник( rbind(c(0,0), A[1,], sum, A[2,]), col=rgb(1,0,0,.2))
векторы (A, метки = c ("a1", "a2"), pos.lab = c (4,2))
векторы (сумма, происхождение = A [1,], col = "серый")
векторы (сумма, происхождение = A [2,], col = "серый")
# добавить несколько аннотаций
text(0,6, "det(A) - площадь его векторов-строк", pos=4)
текст (среднее (A [ 1]), среднее (A [ 2]), "det (A)", cex = 1,25) Простой визуальный
доказательство этого факта об определителях, но его легче всего увидеть в
случай диагональной матрицы, где векторы-строки ортогональны, поэтому
площадь - это просто высота x ширина.
(D <- 2 * diag(2))
## [1] [2] ## [1,] 2 0 ## [2,] 0 2
det(D)
## [1] 4
Постройте это как прежде:
par(mar=c(3,3,1,1)+.1)
график (с (0,2), с (0,2), тип = "n", xlab = "X1", ylab = "X2", asp = 1)
сумма <- D[1,] + D[2,]
многоугольник( rbind(c(0,0), D[1,], sum, D[2,]), col=rgb(0,1,0,.2))
векторы (D, метки = c ("d1", "d2"), pos.lab = c (3,4))
векторы (сумма, происхождение = D [1,], col = "серый")
векторы (сумма, происхождение = D [2,], col = "серый")
текст (среднее (D [ 1]), среднее (D [ 2]), "det (D)", cex = 1,25) Наконец, мы также можем понять, почему определитель равен нулю, когда строки или столбцы пропорциональны.
(B <- matrix(c(1, 2, 2, 4), 2,2))
## [1] [2] ## [1,] 1 2 ## [2,] 2 4
det(B)
## [1] 0
Такие векторы называются коллинеарными . Они заключают нет площадь .
пар(mar=c(3,3,1,1)+.1)
график (с (0,4), с (0,4), тип = "n", xlab = "X1", ylab = "X2", asp = 1)
векторы(B, метки=c("b1", "b2"), pos.