Sin a sin b sin c sin a b c: Теорема синусов — Тригонометрия

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )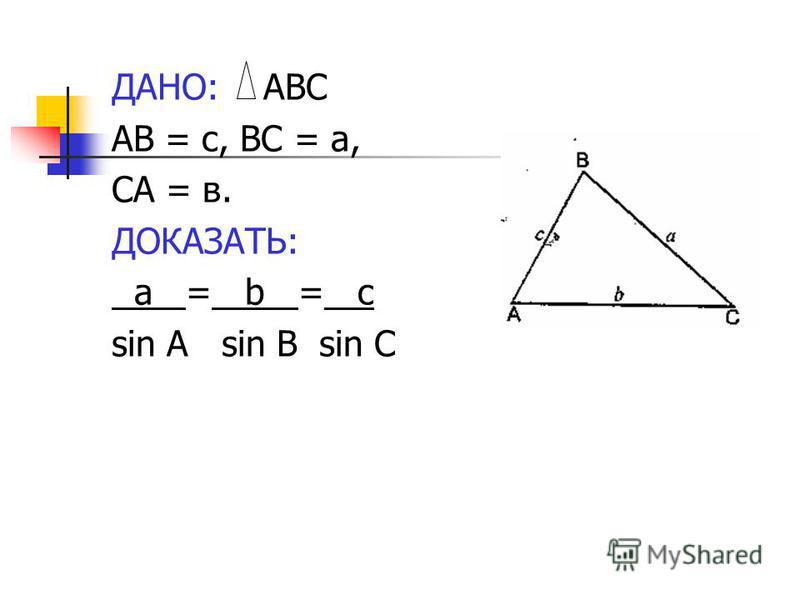
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение
tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значение
sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95
Найти точное значение		sin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

тригонометрия — Для $\треугольника ABC$ докажите $(\sin A + \sin B)( \sin B +\sin C)( \sin C + \sin A) > \sin A \sin B \sin C$

спросил

6 лет, 6 месяцев назад

Изменено 6 лет, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

В $\треугольнике$ ABC докажите, что $$( \sin A + \sin B )( \sin B + \sin C )( \sin C + \sin A) > \sin A \sin B \sin C$$

Я пробовал формулу А. М.-Г.М. отношения с $\sin A$, $\sin B$ и $\sin C$, но на самом деле это не помогает. Итак, каково правильное доказательство?

  • тригонометрия
  • неравенство
  • треугольники

$\endgroup$

$\begingroup$

Почему?

При $\sin A,\sin B,\sin C>

0,$

$$\dfrac{\sin A+\sin B}2\ge\sqrt{\sin A\sin B}$$

$$\имплицит (\sin A+\sin B)(\sin B+\sin C )(\sin C+\sin A)\ge8\sin A\sin B\sin C$$, что определенно равно $>\sin A\sin B\sin C$

$\endgroup$

0

$\begingroup$

Пока этот треугольник евклидов, все значения sin положительны (или, может быть, 0, но это несложно). Когда вы перемножите эти факторы, вы получите $\sin A \sin B \sin C+$..(другие положительные вещи), что определенно больше, чем $\sin A \sin B \sin C$

$\endgroup$

$\begingroup$

Пусть стороны треугольника равны $a,b,c. $ Пусть $R$ — радиус описанной окружности треугольника Имеем $$0< 2 R=(\sin A)/a=(\sin B)/b =(\sin C)/c.$$ Таким образом, неравенство эквивалентно $$(a+b)(b+c)(c+a)>a b c.$$

В треугольнике $a+ b>c>0$ и $b+c>a>0$ и $c+a>b>0 .$ Итак, $(a+b)(b+c)(c+a)>c a b.$

Альтернативное доказательство: в треугольнике все синусы углов положительны. Если вы расширите свой исходный левый стержень, у вас будет 8 положительных членов, и каждый из них равен правому сердцу!

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

тригонометрия — Если $ a,b,c\in \left(0,\frac{\pi}{2}\right)\;,$ Тогда докажите, что $\frac{\sin (a+b+c)} {\ грех а + \ грех б + \ грех с}

спросил

Изменено 6 лет, 1 месяц назад

Просмотрено 348 раз

$\begingroup$

Если $\displaystyle a,b,c\in \left(0,\frac{\pi}{2}\right)\;,$ Докажите, что $\displaystyle \frac{\sin (a+b+c )}{\sin a+\sin b+\sin c}<1$

$\bf{Мой\; Try::}$ Используя $$\sin(a+\underbrace{b+c}) = \sin a\cdot \cos (b+c)+\cos a\cdot \sin (b+c)$$

$$ = \sin a\cdot (\cos b\cos c-\sin b\sin c)+\cos a(\sin b\cos c+\cos b\sin c)$$

$$ = \sin a\cos b\cos c-\sin a\sin b\sin c+\cos a \sin b\cos c+\cos a\cos b\sin c$$

Теперь, как я могу решить это после этого, требуется помощь , спасибо

  • тригонометрия

$\endgroup$

$\begingroup$

$\sin(a) + \sin(b) > \sin(a+b)$, если $(a,b)\in (0, \pi)\ подразумевает $

$\sin(a + b +c ) <= \sin(a) + \sin(b + c) < \sin(a) + \sin(b) + \sin(c)$

$\endgroup$

6

$\begingroup$

Используя $$\sin (a+b+c)-\sin a-\sin b-\sin c $$

$$= 2\cos\left(\frac{2a+b+c}{2 }\right)\sin \left(\frac{b+c}{2}\right)-2\sin\left(\frac{b+c}{2}\right)\cos \left(\frac{ b-c}{2}\справа)$$

Итак, $$ = 2\sin\left(\frac{b+c}{2}\right)\left[\cos\left(\frac{2a+b+c}{2}\right)-\ cos \left(\frac{b-c}{2}\right)\right]$$

$$ = -4\sin \left(\frac{a+b}{2}\right)\sin \left( \frac{b+c}{2}\right)\sin \left(\frac{a+c}{2}\right)<0,$$

Bcz, учитывая $\displaystyle a,b,c \in \left(0,\frac{\pi}{2}\right)$.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *