Nothing found for Blog Wp-content Uploads 2016 12 Fizika_ege_test Pdf
Настоящая Политика конфиденциальности определяет, каким образом Центр подготовки к ЕГЭ и ОГЭ Годограф собирает, использует, хранит и раскрывает информацию, полученную от пользователей на веб-сайте godege.ru («Сайт»). Данная политика конфиденциальности относится и к Сайту, всем поддоменам Сайта и всем продуктам и услугам, предлагаемым Центр подготовки к ЕГЭ и ОГЭ Годограф .
Эта страница содержит сведения о том, какую информацию мы или третьи лица могут получать, когда Вы пользуетесь нашим Сайтом. Мы надеемся, что эти сведения помогут Вам принимать осознанные решения в отношении предоставляемой нам информации о себе.
Настоящая Политика конфиденциальности распространяется непосредственно на этот Сайт и на информацию, получаемую с его помощью. Она не распространяется ни на какие другие сайты и не применима к веб-сайтам третьих лиц, которые могут содержать упоминание о нашем Сайте и с которых могут делаться ссылки на Сайт, а так же ссылки с этого Сайта на другие сайты сети Интернет.
Получаемая информация
Когда Вы посещаете Сайт, мы определяем IP адрес, имя домена с которого Вы к нам пришли (например, «yandex.ru») и страну регистрации данного ip , а так же фиксируем все переходы посетителей с одной страницы Сайта на другую.
Сведения, которые мы получаем на Сайте, могут быть использованы для того, чтобы облегчить пользование Сайтом. Сайт собирает только общую информацию, которую Ваш браузер предоставляет добровольно при посещении Сайта.
Сайт применяет стандартную технологию «cookies» («куки») для настройки стилей отображения Сайта под параметры экрана монитора. «Куки» представляет собой данные с веб-сайта, который сохраняет на жестком диске Вашего же компьютера. В «cookies» содержится информация, которая может быть необходимой для настройки Сайта, — для сохранения Ваших установок вариантов просмотра и сбора статистической информации по Сайту, т.е. какие страницы Вы посетили, что было загружено, имя домена интернет-провайдера и страна посетителя, а также адреса сторонних веб-сайтов, с которых совершен переход на Сайт и далее.
Также данную технологию использует установленные на Сайте счетчики компании Yandex/Rambler/Google и т.п.
Технология «Cookies» не содержит никаких личных сведений относительно Вас. Чтобы просматривать материал без «cookies», Вы можете настроить свой браузер таким образом, чтобы она не принимала «cookies», либо уведомляла Вас об их посылке (настройки браузеров различны, поэтому советуем Вам получить справку в разделе «Помощь» и выяснить как изменить установки браузера по «cookies»).
Кроме того, Сайт использует стандартные возможности (журналы) веб-сервера для подсчета количества посетителей и оценки технических возможностей хост-сервера, рейтинги и счетчики посещаемости от сторонних организаций (yandex.ru, top100.rambler.ru, top.mail.ru и др.). Мы используем эту информацию для того, чтобы определить сколько человек посещает Сайт и расположить страницы наиболее удобным для пользователей способом, обеспечить соответствие Сайта с используемыми Вами браузерам, и сделать содержание Сайта максимально полезным для посетителей.
Также мы можем собирать личную идентификационную информацию от пользователей, когда пользователь посещает наш Сайт, регистрируется на Сайте, оформляет заказ, заполняет формы и в связи с другой активностью на Сайте. Пользователя могут попросить при необходимости указывать имя, электронный адрес, номер телефона, данные кредитной карты. Пользователи могут, однако, посещать наш Сайт анонимно. Мы собираем личную идентификационную информацию пользователей, только если они добровольно предоставляют нам такую информацию. Пользователи всегда могут отказаться в предоставлении личной идентификационной информации, за исключением случаев, когда это может помешать пользоваться отдельными функциями Сайта.
Как мы используем собранную информацию
Центр подготовки к ЕГЭ и ОГЭ Годограф может собирать и использовать личную информацию пользователей для следующих целей:
— Для улучшения обслуживания клиентов.
Предоставляемая вами информация помогает нам реагировать на запросы клиентов более эффективно;
— Чтобы персонализировать пользовательский опыт. Мы можем использовать информацию для определения кто из посетителей Сайта наиболее заинтересован в услугах и ресурсах предоставляемых на нашем Сайте;
— Для улучшения нашего Сайта. Мы можем использовать обратную связь, которую Вы предоставляете, чтобы улучшить наши продукты и услуги;
— Чтобы отправлять пользователям информацию, которую они согласились получать на темы, которые, как мы думаем, будут представлять для них интерес;
— Чтобы отправить периодические сообщения электронной почты, которые могут включать новости компании, обновления, информацию о продуктах и услугах и т.
д. Если пользователь хотел бы отказаться от получения последующих писем, мы включаем подробное описание инструкции по тому, как отписаться в нижней части каждой электронной почты или пользователь может связаться с нами через наш Сайт. Как мы защищаем вашу информацию
Мы принимаем соответствующие меры безопасности по сбору, хранению и обработке собранных данных для защиты их от несанкционированного доступа, изменения, раскрытия или уничтожения Вашей личной информации (имя пользователя, пароль, информация транзакции и данные, хранящиеся на нашем Сайте).
Общий доступ к личной информации
Мы не продаем, не обмениваем или не даем в аренду личную информацию пользователей. Мы можем предоставлять общие агрегированные демографические данные, не связанные с личной информацией, нашими партнерами и рекламодателями для целей, описанных выше. Мы можем использовать сторонних поставщиков услуг, чтобы помочь нам управлять нашим бизнесом и Сайтом или управлять деятельностью от нашего имени, например, проведение рассылки или статистические и иные исследования.
Мы можем делиться этой информацией с этими третьими лицами для ограниченных целей при условии, что Вы дали нам соответствующие разрешения.
Изменения в политике конфиденциальности
Центр подготовки к ЕГЭ и ОГЭ Годограф имеет право по своему усмотрению обновлять данную политику конфиденциальности в любое время. В этом случае мы опубликуем уведомление на главной странице нашего Сайта и сообщим Вам об этом по электронной почте. Мы рекомендуем пользователям регулярно проверять эту страницу для того, чтобы быть в курсе любых изменений о том, как мы защищаем личную информацию, которую мы собираем. Используя Сайт, Вы соглашаетесь с принятием на себя ответственности за периодическое ознакомление с Политикой конфиденциальности и изменениями в ней.
Ваше согласие с этими условиями
Используя этот Сайт, Вы выражаете свое согласие с этой политикой. Если Вы не согласны с этой политикой, пожалуйста, не используйте наш Сайт. Ваше дальнейшее использование Сайта после внесения изменений в настоящую политику будет рассматриваться как Ваше согласие с этими изменениями.
Отказ от ответственности
Помните, политика конфиденциальности при посещении сторонних Сайтов третьих лиц, не подпадает под действия данного документа. Администрация Сайта не несет ответственности за действия других веб-сайтов.
Как с нами связаться
Если у Вас есть какие-либо вопросы по политике конфиденциальности, использованию Сайта, или иным вопросам, связанным с Сайтом, пожалуйста, свяжитесь с нами по адресу: Центр подготовки к ЕГЭ и ОГЭ Годограф
godege.ru
переулок Васнецова 9 строение 2, 5 этаж г. Москва
+7 (495) 970-99-66
[email protected]
404 Not Found
404 Not Found
|
|
Ответ
Подтверждено
232,2 тыс.
{2}}=Vq\9{2}}m}}\left( \dfrac{1}{B} \right) \\
& \Rightarrow r=\sqrt{\dfrac{2mV}{q}}\left(\dfrac{1}{ B} \right) \\
\end{align}$
Следовательно, правильный ответ на поставленный выше вопрос — вариант c.
Примечание:
Следует отметить, что первоначально заряд находился в состоянии покоя до того, как мы фактически начали его ускорять через разность потенциалов V. Отсюда мы можем заключить, что вся энергия будет равна разности между начальной и конечная кинетическая энергия заряда. Частица фактически начинает двигаться по круговой траектории, поскольку векторное произведение, взятое между v и B, представляет собой поворот двух векторов.
Недавно обновленные страницы
Большинство эубактериальных антибиотиков получены из биологии ризобия класса 12 NEET_UG
Биоинсектициды саламин были извлечены из класса 12 Biology NEET_UG
Какое из следующих утверждений, касающихся Baculovirussess, Neet_ug
. Какое из следующих утверждений, касающихся Baculoviruses, Neet_ug
.
муниципальные канализационные трубы не должны быть непосредственно 12 класса биологии NEET_UG
Очистка сточных вод выполняется микробами A B Удобрения 12 класса биологии NEET_UG
Иммобилизация фермента – это конверсия активного фермента класса 12 биологии NEET_UG
Большинство эубактериальных антибиотиков получают из биологического класса Rhizobium 12 NEET_UG
Саламиновые биоинсектициды были извлечены из биологического класса А 12 NEET_UG
12 класс биологии NEET_UG
Канализационные или городские канализационные трубы не должны быть напрямую 12 класс биологии NEET_UG
Очистка сточных вод выполняется микробами A B Удобрения 12 класс биологии NEET_UG
Иммобилизация фермента — это преобразование активного фермента класса 12 биологии NEET_UG
Тенденции сомнений 46 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 Следующая →
AP Физика C Электричество Справка » Экзамен по электричеству и магнетизму
Тонкий стержень длиной L лежит в плоскости xy и несет линейную плотность заряда, где колеблется от 0 до .
Рассчитайте потенциал в точке на оси Y.
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте линейную плотность заряда и элемент длины , где каждая точка от точки. Таким образом, потенциал равен
Сообщить об ошибке
Равномерно заряженное кольцо радиуса несет полный заряд. Рассчитайте потенциал на расстоянии от центра по оси кольца.
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте линейную плотность заряда и элемент длины. Расстояние от каждой точки на кольце до точки на оси равно . Наконец, проинтегрируйте от до , чтобы получить
Сообщить об ошибке
Равномерно заряженная квадратная рамка со стороной несет полный заряд .
Вычислите потенциал в центре квадрата.
Вы можете использовать интеграл:
Возможные ответы:
Правильный ответ:
Объяснение:
Рассчитайте потенциал с одной стороны стержня, а затем умножьте его на , чтобы получить общий потенциал со всех четырех сторон. Сориентируйте полосу по оси x так, чтобы ее конечные точки находились в точке , и используйте линейную плотность заряда . Таким образом, потенциал равен
Сообщить об ошибке
Рассмотрим сферическую оболочку с радиусом и зарядом . Какова величина электрического поля в центре этой сферической оболочки?
Возможные ответы:
Правильный ответ:
Ноль
Пояснение:
Согласно теореме об оболочках, полное электрическое поле в центре заряженной сферической оболочки всегда равно нулю.
В этот момент любые линии электрического поля приведут к симметрии, компенсируя друг друга и создавая в этой точке чистое поле, равное нулю.
Сообщить об ошибке
Заряд неизвестного значения удерживается вдали от других зарядов. Линии его электрического поля и некоторые линии электрического эквипотенциала (V 1 и V 2 ) показаны на диаграмме.
Второй точечный заряд, известный как отрицательный, расположен в точке А на диаграмме. В каком направлении будет свободно двигаться второй, отрицательный заряд?
Возможные ответы:
Он останется неподвижным
В сторону точки А
В сторону точки С
В сторону первоначального заряда Q
Правильный ответ:
В сторону точки С
Объяснение:
Первоначальный заряд Q отрицателен, на что указывает направление линий электрического поля на диаграмме.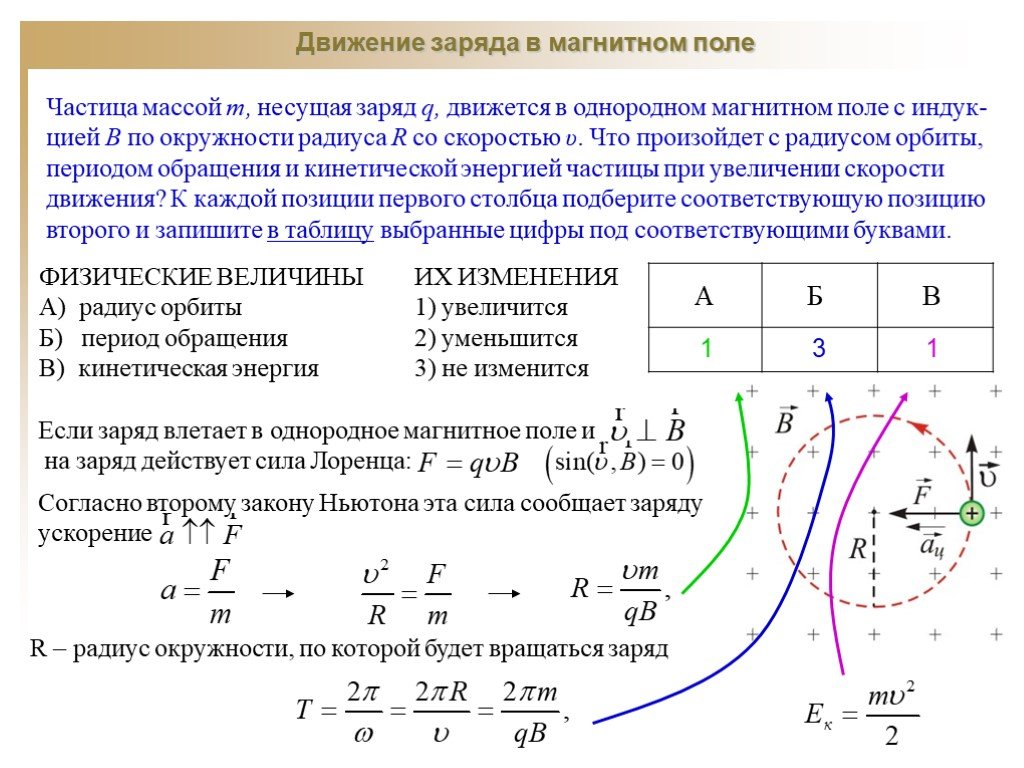
Отрицательный точечный заряд любой величины, помещенный в точку А, заставит оба заряда ощущать друг на друга силу взаимного отталкивания. Следовательно, второй заряд будет отталкиваться первоначальным отрицательным зарядом с силой, направленной радиально вдоль линии, соединяющей центр Q и точку A, что приводит к свободному движению к C. Кроме того, точка B находится на линии эквипотенциала с точкой А; отрицательные точечные заряды будут перемещаться из областей с более низким электрическим потенциалом в области с более высоким электрическим потенциалом (против направления силовых линий электрического поля), поэтому точка B не является жизнеспособным ответом.
Сообщить об ошибке
Путешествующий протон входит в однородное магнитное поле и подвергается воздействию магнитной силы, заставляя его двигаться по круговой траектории. Принимая магнитное поле за , каков радиус этого кругового пути (показан красным)?
Возможные ответы:
Правильный ответ:
Пояснение:
Для расчета магнитной силы одиночного заряда мы используем , где — заряд протона, — его скорость, — однородное магнитное поле.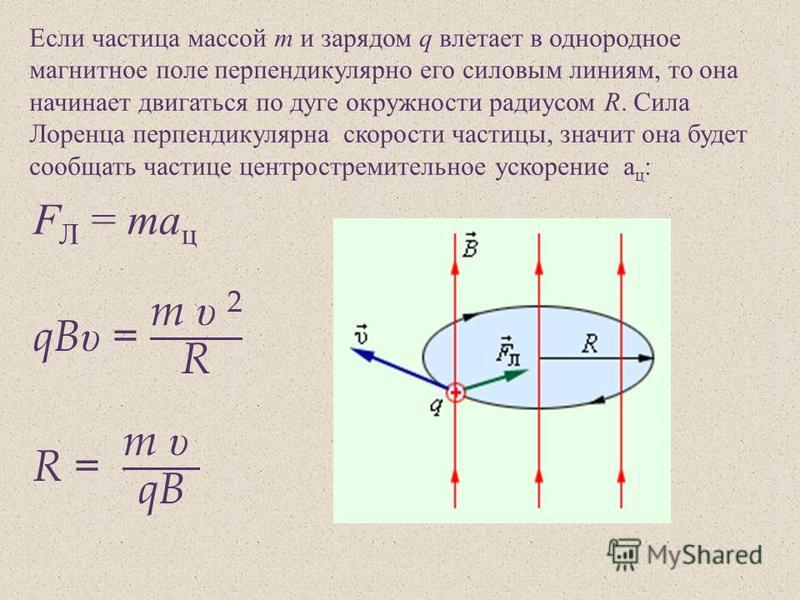
Поскольку эта магнитная сила заставляет протон двигаться по круговой траектории, мы приравниваем это уравнение магнитной силы к уравнению центростремительной силы.
– масса протона и – радиус кругового пути. Решите для .
Используя значения, указанные в вопросе, мы можем найти радиус.
Сообщить об ошибке
Что из следующего лучше всего описывает суммарный магнитный поток через замкнутую сферу в присутствии магнита?
Возможные ответы:
Положительный, только если северный полюс магнита находится в пределах поверхности
Верно несколько других вариантов
Отрицательный, только если северный полюс магнита находится в пределах поверхности
Ноль вне зависимости от ориентации магнита
Нуль, только если магнит полностью заключен в поверхность
Правильный ответ:
Ноль независимо от ориентации магнита
Объяснение:
Чистый магнитный поток (или чистое поле, втекающее и вытекающее) через любую замкнутую поверхность всегда должен быть равен нулю.
Это связано с тем, что у силовых линий магнитного поля нет начальной или конечной точки, поэтому любая силовая линия, идущая на поверхность, также должна выходить. Другими словами, «магнитных монополей не существует».
Сообщить об ошибке
Частица с зарядом и массой движется со скоростью перпендикулярно однородному магнитному полю, . Каков период обращения частицы в поле?
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Установите магнитную силу равной центростремительной силе, так как магнитная сила направлена к центру кругового пути частицы, а центростремительная сила определяется как результирующая сила, направленная к центростремительной силе. центр кругового пути.
Переставить, чтобы изолировать скорость:
Определите расстояние, , пройденное за один оборот, которое является окружностью окружности радиуса :
Подставьте это расстояние и скорость в , чтобы решить за период :
Сообщить об ошибке
Рассмотрим петлю с током с током, радиусом и центром.
Частица с зарядом пролетает через центр и влетает в страницу со скоростью . Какова полная электромагнитная сила, действующая на частицу в момент ее пролета через петлю, в терминах заданных переменных?
Возможные ответы:
Правильный ответ:
Пояснение:
Правильный ответ — ноль. Чтобы вычислить силу магнитного поля, действующую на движущуюся заряженную частицу, мы используем векторное произведение. Мы знаем, что если магнитное поле параллельно вектору скорости частицы, то создаваемая сила равна нулю.
Поскольку наше магнитное поле в этом случае движется в том же направлении, что и скорость частицы, мы знаем, что магнитная сила на частице равна нулю.
Сообщить об ошибке
Рассмотрим два длинных прямых проводника с током на расстоянии друг от друга, по каждому из которых течет ток определенной величины в противоположных направлениях.
Если два описанных провода не удерживаются на месте, какое движение произойдет в результате возбужденных магнитных полей?
Возможные ответы:
Провода будут вращаться по часовой стрелке
Провода будут вращаться против часовой стрелки
Провода будут двигаться навстречу друг другу
Провода будут удаляться друг от друга
Провода останутся на месте
Правильный ответ:
Провода будут удаляться друг от друга
Объяснение:
Ответ заключается в том, что провода будут двигаться друг от друга. Используя наше правило правой руки, мы знаем, что магнитные поля, создаваемые каждым проводом, имеют одинаковое направление, пока их токи противоположны. Снова используя правило правой руки для определения направления силы, действующей на каждый провод со стороны магнитного поля, с которым они взаимодействуют, мы получим силу, направленную от другого провода для каждого провода.