Математика. Ее содержание, методы и значение. Том 1
Математика. Ее содержание, методы и значение. Том 1
ОглавлениеПРЕДИСЛОВИЕГлава I. ОБЩИЙ ВЗГЛЯД НА МАТЕМАТИКУ § 1. ОСОБЕННОСТИ МАТЕМАТИКИ § 2. АРИФМЕТИКА § 3. ГЕОМЕТРИЯ § 4. АРИФМЕТИКА И ГЕОМЕТРИЯ § 5. ЭПОХА ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ § 6. МАТЕМАТИКА ПЕРЕМЕННЫХ ВЕЛИЧИН § 7. СОВРЕМЕННАЯ МАТЕМАТИКА § 8. СУЩНОСТЬ МАТЕМАТИКИ § 9. ЗАКОНОМЕРНОСТИ РАЗВИТИЯ МАТЕМАТИКИ Глава II. АНАЛИЗ § 2. ФУНКЦИЯ Графики функций. § 3. ПРЕДЕЛ § 4 НЕПРЕРЫВНЫЕ ФУНКЦИИ § 5. ПРОИЗВОДНАЯ Примеры вычисления производных. § 6. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Производная суммы. Производная произведения. Производная частного. Производная обратной функции. Таблица производных. Нахождение производной функции от функции. § 7. МАКСИМУМ И МИНИМУМ. ИССЛЕДОВАНИЕ ГРАФИКОВ ФУНКЦИЙ Отыскание наибольших и наименьших значений функции. Производные высших порядков. Смысл второй производной. Выпуклость и вогнутость. Признаки максимумов и минимумов.  Исследование графиков функций.§ 8. ПРИРАЩЕНИЕ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ Теорема о среднем и примеры ее применения. § 9. ФОРМУЛА ТЕЙЛОРА Формула Тейлора. Ряд Тейлора. § 10. ИНТЕГРАЛ Определенный интеграл. Связь дифференциального и интегрального исчисления. § 11. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. ТЕХНИКА ИНТЕГРИРОВАНИЯ § 12. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Неявное задание функции. Геометрическое изображение. Частные производные и дифференциал. Дифференцирование неявных функций. Задачи на максимум и минимум. Формула Тейлора. Относительный максимум и минимум. § 13. ОБОБЩЕНИЯ ПОНЯТИЯ ИНТЕГРАЛА Контурные и поверхностные интегралы. § 16. РЯДЫ Сходимость ряда. Ряды функций. Равномерно сходящиеся ряды. Степенные ряды. Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ § 2. ДВЕ ОСНОВНЫЕ ИДЕИ ДЕКАРТА Идея сопоставления уравнениям с двумя неизвестными линий на плоскости. Основные задачи, решаемые аналитической геометрией, и определение аналитической геометрии.  2.§ 6. ОБЩАЯ ТЕОРИЯ ДИАМЕТРОВ НЬЮТОНА § 7. ЭЛЛИПС, ГИПЕРБОЛА И ПАРАБОЛА Уравнение эллипса и его фокальное свойство. Законы движения планет. Эллипс инерции. Гипербола и ее фокальное свойство. Парабола и ее директрисса. Свойство касательной к параболе. Директриссы эллипса и гиперболы. Конические сечения. Парабола как график пропорциональности квадрату и гипербола как график обратной пропорциональности. § 8. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ 2-Й СТЕПЕНИ К КАНОНИЧЕСКОМУ ВИДУ Формулы преобразования координат. Приведение любого уравнения 2-й степени к одному из 9 канонических видов. § 9. ЗАДАНИЕ СИЛ, СКОРОСТЕЙ И УСКОРЕНИЙ ТРОЙКАМИ ЧИСЕЛ. ТЕОРИЯ ВЕКТОРОВ Арифметизация сил, скоростей и ускорений, введенная Лагранжей. Алгебра векторов. Скалярное произведение и его свойства. § 10. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ. УРАВНЕНИЕ ПОВЕРХНОСТИ В ПРОСТРАНСТВЕ И УРАВНЕНИЯ ЛИНИИ Уравнение плоскости и уравнения прямой. Общее уравнение 2-й степени с тремя переменными и 17 его канонических видов.  Эллипсоид. Гиперболоиды и конус 2-го порядка. Параболоиды. § 11. ПРЕОБРАЗОВАНИЯ АФФИННЫЕ И ОРТОГОНАЛЬНЫЕ Эллипс как результат «сжатия» окружности. Пример решения более сложной задачи. Важнейшие применения аффинных преобразований Формулы аффинных преобразований. Ортогональные преобразования. § 13. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ Применение основной теоремы плоской перспективы в аэрофотосъемке. Проективная плоскость. Проективные отображения; основная теорема. Проективная геометрия. Запись проективных преобразований формулами. § 14. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Проективные преобразования круга в себя. ЗАКЛЮЧЕНИЕ Глава IV. АЛГЕБРА (ТЕОРИЯ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ) § 2. АЛГЕБРАИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЯ Разложение многочлена на множители и формулы Виета. Теорема о симметрических многочленах. Работы Лагранжа. Открытие Абеля. Теория Галуа. Приложение теории Галуа к вопросу о разрешимости геометрической задачи циркулем и линейкой.  Две основные нерешенные задачи, связанные с теорией Галуа. § 3. ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ Теория комплексных чисел. Поверхность модуля многочлена. О возрастании модуля многочлена при удалении от начала. Существование минимумов поверхности M. Лемма Даламбера. § 4. ИССЛЕДОВАНИЕ РАСПОЛОЖЕНИЯ КОРНЕЙ МНОГОЧЛЕНА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ Простые и кратные корни многочлена. Теорема Ролля и некоторые ее следствия. Правило знаков Декарта. Теорема Штурма. Задача Гурвица. § 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КОРНЕЙ |
Краткая методичка для математиков и не только: «Чем приращение отличается от дифференциала» — Современные математики
Дифференциал — это не очень маленькое приращение. Это приращение эквивалентное нулю. То есть, оно неотличимо от нуля (Леонард Эйлер) относительно той величины, приращение которой рассматривается. То есть, либо есть приращение, но нет дифференциала и нет производной.
Либо есть дифференциал и есть производная, но нет приращения. И то, и другое вместе — это отклонение рассудка от адекватного восприятия реальности. Либо — профанация, когда люди вызубрили нечто, но не понимают сути.
Как это пощупать «на пальцах»? Есть понятия несоизмеримые. Например, длина не соизмерима с площадью. То есть, площадь сама по себе величина измеримая. Длина, тоже, сама по себе измерима. Но длина и площадь — величины несоизмеримые. У отрезка нет площади. Его площадь равна нулю. Но у него есть длина. Она нулю не равна. Опять же, перейдем к площади круга и длине окружности.
Длина окружности — функция радиуса. Площадь круга — функция радиуса. Если рассматривать эти функции отдельно друг от друга, то они совершенно независимы и существуют независимо друг от друга. То есть, это самостоятельные функции.
Но если использовать алгоритм дифференцирования: «Производная — есть предел отношения приращения функции к приращению аргумента, при устремлении последнего к нулю», то функция площади круга, как функция длины отрезка, назыаемого радиусом будет связана с функцией длины окружности, как функция этого же аргумента.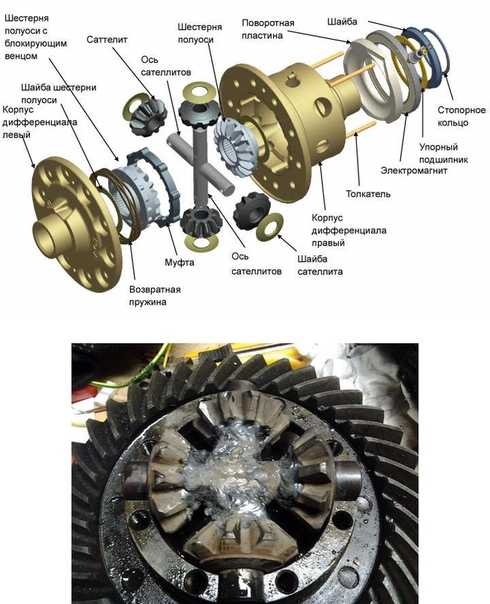
Еще раз. Сами по себе это две самостоятельные функции. Но, при использозовании действия «дифференцирования», одна из этих функций станет структурным элементом другой функции. Для чего это нужно? Для адекватного описания действительности. Потому, что почти все объекты действительного мира меняют свои размеры именно интегрированием.
Приведу схематичный пример. Например, ствол дерева увеличивается объемно, в размерах, путем действия интегрирования. Объем этого ствола можно продифференцировать по радиусу на части по аналогу рулона туалетной бумаги и получить части ствола в виде множества частей одного типа. Если ствол распилить на части бессистемно но на одинаковые по объему части, то это позволит получить множество частей свола разного типа.. Это действие называется делением.
Схематичный пример действий дифференцирования и интегрирования расположен на рисунке в начале статьи.
Это схема. Эту схему можно мысленно превратить в математическую модель.
Если Вы будете интегрировать площадь круга по дифференциалу радиуса, то можно получить объем конуса высотой, равной радиусу основания конуса. Это будет выглядеть следующим образом. Вначале будет точка — радиус равен нулю. Смотрим на пирамидку на рисунке. Почти такую же мы будем составлять мысленно из колечек того же радиуса, какой будет и высота пирамидки.
То есть, на точку «надеваем» колечко на том же самом расстоянии, что и радиус самого колечка, потому, что мы интегируем площади колечек именно по дифференциалу длины того отезка, который называется радиусом. Надеваем все больше колечек, выполняя исходное обязательное условие: Радиус каждого очень тонкого колечка равен расстоянию от первоначальной точки (вершины «пирамидки») до этого колечка. Будем получать объем пирамидки, равный интегралу площади колечек по диференциалу радиуса. Я, надеюсь, схема понятна. Именно эта модель вынесена в заголовок моего блога.
Теперь, вернемся к заявленной теме статьи. Что такое неопределенность «ноль, деленный на ноль» или что такое бесконечность? Это модели нашего разума, а не модели реальности.
Если часть площади круга представить как кольцо, ограниченное внутренней окружностью и внешней, то площадь кольца и будет приращением функции площади круга. Расстояние можду этими двумя окружностями и будет приращением аргумента.
Теперь ключевой момент. Радиус — это длина отрезка. Отрезок имеет длину. Точка длины не имеет. Это несоизмеримые объекты. Длина точки, как и ее площадь равны нулю. Круг имеет площадь, то есть, это интеграл длин окружностей по дифференциалу радиуса. Каждая окружность имеет длину, но не имеет площади. Для части площади круга, как приращения его площади площадь окружности равна нулю. Размер точки как для длины окружности так и для площади круга тоже равен нулю.
Если площадь кольца начать мысленно сжимать, то есть устремить друг к другу внешнюю окружность к внутренней, то пределом площади такого кольца станут две окружности, расположенные рядом. То есть, между ними не «влезет» другая окружность. Это будет элементарное приращение площади круга. Что с радиусом? Его длина станет элементарной и будет находиться между двумя соседними точками.
Это и будет элементарным приращением аргумента.
Теперь самый важный момент. Две отдельные точки, находящиеся рядом — не есть длина. Две окружности, находящиеся рядом — не есть площадь. Что делает длиной две соседние точки и площадью две соседние окружности? Дифференциал! Это величина меньшего порядка, чем точка, так же, как точка величина меньшего порядка, чем длина и так же, как длина — величина меньшего порядка, чем площадь! Я уже показывал как геометрически представить себе дифференциал. По-моему это в серии статей о том, что такое, на самом деле, неопределенный интеграл. Кому будет интересно — найдет…
Все величины геометрических объектов — относительны точке. Все численные величины относительны единице измерения. Вот мы и подошли к основе «структурного анализа». Что такое сама точка? Я уже показывал определение точки, данное Рене Декартом. Точка, В МАТЕМАТИКЕ — объект относительный, а не абсолютный, как и число.
P.S. Можно, конечно, написать учебник. В котором подробно все изложить с иллюстрациями и определениями.
Но отечественным математикам это не нужно. Они сами это написали. Ну и хрен с ними… Пусть интеллектуально опускают детей идиотизмами типа: производная — есть скорость изменения функции. Раз родителям этих детей все равно. Бредовые шаблоны встраиваются мозгом в систему видения мира…
В чем разница между дифференциалом и производной?
Сначала вы должны изучить понятие функции, чтобы понять разницу между дифференциалом и производной функции.
Одной из фундаментальных идей математики является понятие функции, которое описывает связь между набором входов и набором потенциальных выходов, где каждый вход соединяется с одним выходом. Независимая переменная — это одна переменная, а зависимая — другая.
В математике переменные — это любые физически изменяющиеся объекты. Разница между дифференциалом и производной заключается в том, что если есть изменение скорости одной переменной для другой переменной, мы называем это производной.
С другой стороны, дифференциальное уравнение представляет собой соответствующее уравнение, которое математически выражает отношения между переменными.
Давайте изучим основные определения и разницу между дифференциалом и производной:
Содержание
Что такое производная?
Скорость, с которой функция изменяется в определенный момент времени, называется производной.
Например, наклон линии, определяющий скорость ее изменения, постоянен вдоль всей линии. Производная сообщает нам, каков наклон параболы в конкретной точке, потому что наклон параболы колеблется.
Другой способ изобразить производную — использовать наклон линии, касательной к кривой в определенной точке. Получение производной — это процесс дифференцирования. Дифференциальные уравнения и производные часто используются вместе.
Нахождение производных осуществляется посредством процесса дифференцирования. Они используются для обозначения наклона касательной линии. Производные количественно определяют крутизну наклона функции за определенный интервал времени.
Производная интеграла
Результатом дифференцирования результата интеграла является производная интеграла.
Поскольку дифференцирование интеграла должно давать саму исходную функцию, интегрирование — это процесс нахождения «анти» производной.
Когда нижний предел интеграла является константой, а его верхний предел — просто переменной, его производная — это сама функция. Другими словами, где «a» — константа, d/dx ∫ a x f(t) dt = f(x).
Подробнее: В чем разница между похожими и непохожими дробями?
Что такое дифференциал?
Источник: CuemathДифференциальные уравнения — это ветвь исчисления, отображающая малейшие изменения некоторых переменных величин. Производные и их функции являются частью дифференциальных уравнений.
Основные разделы исчисления включают дифференциальную и интегральную ветви. Окружающая среда, в которой мы живем, полна постоянно меняющихся, взаимосвязанных величин.
Символ дифференциала, бесконечно малой величины, часто равен dy/dx.
Поскольку производная отражает наклон функции на бесконечно малом интервале, сравнимом с одной точкой, ее часто рассматривают как частное дифференциалов, таких как dy/dx, dy/dx.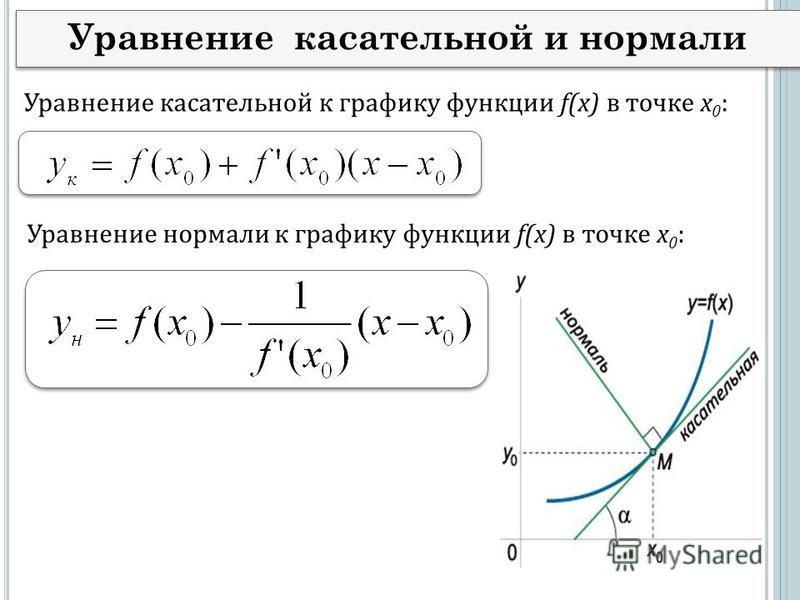
Разница между дифференциалом и производной
Основное различие между дифференциалом и производной приведено ниже:
Основное различие между дифференциалом и производной заключается в том, что производная относится к скорости изменения функции, относится к фактическому изменению функции.
Другой способ определить производные — рассмотреть отношение функции и переменных дифференциалов.
Другое различие между дифференциалом и производной состоит в том, что дифференциал представляет собой изменение переменной (дх) . Напротив, производная — это изменение функции (dy/dx) (dy/dx) (dx) .
Производная представляет собой отношение дифференциалов, поскольку функция представляет отношение между двумя переменными. Дифференциалы показывают фактическое изменение значения с помощью линейной карты, тогда как производные представляют то же изменение с помощью карты наклона.
Дифференциал Против. Производная
С точки зрения взаимосвязей термины дифференциал и производная тесно связаны друг с другом. Переменные — это изменяющиеся объекты в математике, и скорость, с которой одна переменная изменяется по отношению к другой, известна как производная.
Дифференциальные уравнения описывают отношения между этими переменными и их производными. Нахождение производной — это процесс дифференцирования.
Сравнение между дифференциалом и производной заключается в том, что дифференциал функции представляет собой фактическое изменение функции, тогда как производная представляет собой скорость, с которой выходное значение изменяется по отношению к входному значению.
Представление дифференциала Vs. Производная
Дифференциалы могут быть представлены как dx, dy и т. д., где dx представляет небольшое изменение x, dy представляет небольшое изменение y. Дифференциал dy может быть выражен следующим образом при сопоставлении изменений связанных величин, где y является функцией x:
Наклон функции в любой заданной точке является ее производной и может быть представлен как d/dx.
Например, мы можем записать производную sin(x) как:
d/dx sin(x) = sin(x)' = cos(x)
Связь между производной и дифференциалом
Дифференциация — это метод вычисления производной или скорости, с которой выход y функции изменяется в зависимости от изменяющейся переменной x.
Проще говоря, производная — это скорость изменения у относительно х.
Это соотношение представляет y = f(x) , что означает, что y является функцией x.
Функция, значение которой определяет наклон функции f(x) там, где она задана и f(x) дифференцируема, называется производной от f(x). Он говорит о наклоне графика в определенном месте.
В чем разница между дифференциалом и производной?
Выделение основных различий между дифференциалом и производной в следующей таблице:
| Производная | Дифференциальная |
|---|---|
Скорость изменения переменных в дифференциальном уравнении представлена производной. | Дифференциалы показывают наименьшие вариации величин переменных. |
| Вычисляется наклон графика в конкретной точке. | Вычисляется для нахождения линейной разности. |
| Простые производные просто показывают, насколько быстро зависимая переменная изменяется по отношению к независимой переменной. | Производные — это инструмент, используемый при решении дифференциальных уравнений. Дифференциальные уравнения также имеют производные. |
| Известно, как функционально соотносятся различные переменные. | Между переменными нет известных функциональных взаимосвязей. |
| Существует много производных степеней и различных репрезентативных формул. Наиболее часто используемая формула для производной: d/dx | Для выражения дифференциальных уравнений можно использовать многочисленные формулы. Одна из наиболее часто используемых формул: dy/dx = f. (x) |
Заключение
Дифференциал и производная различаются функциями, которые они выполняют, и значениями, которые каждая из них представляет.
Разница между дифференциалом и производной заключается в том, что дифференциалы описывают незначительные изменения в различных количествах, например, площадь тела.
Позволяет вычислить отношения зависимых и независимых переменных уравнения.
Узнайте больше: В чем разница между площадью и периметром?
Разница между дифференциалом и производной
Понимание математических понятий может быть трудным, и одна из самых запутанных задач в исчислении — это понимание разницы между дифференциалом и производной. Эти два тесно связаны, но не могут использоваться взаимозаменяемо; каждый из них имеет свое собственное применение. В этом сообщении блога мы углубимся в то, что делает их уникальными, чтобы вы могли получить четкое представление о том, когда использовать тот или иной термин. Если вы надеетесь освежить некоторые термины или узнать больше о производных и дифференциалах в первый раз, этот пост должен предоставить вам всю необходимую информацию.
Что такое дифференциал?
Что такое производная?
Разница между дифференциалом и производной
Заключение
Что такое дифференциал?
- Дифференциальная математика — раздел прикладной математики, изучающий поведение функций и их производных при изменении независимых переменных. Дифференциальная математика опирается на такие понятия, как пределы, производные, приближения и интегрирование, для анализа поведения конкретной функции.
- Дифференциальные уравнения включают изучение физических систем, свойства которых зависят от дифференцируемых функций. Дифференциальная математика составляет важную часть современной техники и физики, а ее методы используются во многих различных областях, таких как вычислительные финансы, машинное обучение, наука о данных и метеорология.
- Дифференциальные уравнения также широко используются в моделях роста населения и эпидемиологических исследованиях.
Дифференциальная математика — сложный, но мощный инструмент, который становится все более важным во многих научных дисциплинах.
Дифференциальная математика — сложный, но мощный инструмент, который становится все более важным во многих научных дисциплинах.Что такое производная?
- Производная — это фундаментальное математическое понятие, относящееся к идее определения скорости изменения одной величины по отношению к другой. Производные представлены символами, называемыми символами дифференциального оператора (обозначаются ∂), а производные вычисляются, показывая затронутую область по отношению к конкретному аспекту.
- Производные находят применение во многих областях, таких как статистика, экономика, физика и химия, или практически в любой другой области, связанной со сбором и анализом данных.
- Производные можно использовать для построения сложных уравнений или просто использовать в качестве аналитического инструмента для более эффективного понимания и интерпретации данных. Производные могут выявить закономерности и тенденции, которые в противном случае могут быть невидимы без этого типа анализа.
Разница между дифференциалом и производной
Дифференциал и производная — это два связанных математических понятия, которые часто путают, но они отличаются друг от друга. Дифференциалы измеряют скорость изменения между выходом и входом процесса, в то время как производные измеряют скорость изменения выхода в результате небольших изменений на входе.
- Дифференциалы обеспечивают общую меру, в то время как производные требуют дополнительной информации, такой как конкретная точка или граница, и могут давать более точные результаты.
- Дифференциальные уравнения пытаются найти ответы на вопросы, связанные с изменением некоторой переменной во времени, в то время как производные пытаются предсказать, как одна переменная будет реагировать на изменение других переменных в задаче.
- Дифференциалы и производные — невероятно важные компоненты математики, помогающие ученым понять и предсказать определенные явления в природе.
Заключение
Термины «дифференциал» и «производная» часто используются взаимозаменяемо, но на самом деле они имеют разные значения.