Чем характеризуется вектор: ВЕКТОР | Энциклопедия Кругосвет

Вектор

В математике и физике, вектор является величиной, которая характеризуется своим направлением, а также численным значением. Когда же используются векторы и зачем они нужны? Векторы используют для записи тех величин, которые обыкновенными числами записать невозможно. Допустим, нам необходимо описать положение предмета относительно некоторой точки. Разумеется, мы можем вычислить расстояние между точкой и предметов и записать его обыкновенным числом, но это не будет полной характеристикой. А вот если мы запишем данную величину вектором, то помимо расстояния, мы будем еще знать направление, в котором данный предмет находится относительно заданной точки.

Графически все векторы изображаются, как направленные отрезки определенной заданной длины.

Что же такое свободные векторы? По-другому свободные векторы можно еще назвать и равными. Это такие векторы, у которых совпадает, как модульная величина (то есть отрезок по значению одинаковый), так и направление.

А теперь поговорим не много о действиях над векторами. Зачем вообще придумали слаживать вектора? На самом-то деле, просто решили, что можно вывести один вектор, который бы оказывал тоже воздействие, что и два других вектора. Как вы догадались, два других вектора, это наши слагаемые, а один вектор, который оказывает такое же воздействие – это наша сумма. Вектора складываются несколькими способами, в математики они называются «правилами». Первый – «правило треугольника», второй – «правило «параллелограмма». Стоит отметить и то, что мы можем сложить и три, и четыре , и пять векторов, но делать это надо постепенно, то есть попарно.

Координаты вектора с началом в точке A(x   1 , y   1 , z   1 )

и концом в точке B(x   2 , y   2 , z   2 )

→ AB   (x   2 — x   1 , y   2 — y   1 , z   2 — z   1 )

Координаты суммы векторов → a   (x   1 , y   1 , z   1 ) и → b   (x   2 , y   2 , z   2 )

→ a   + → b   = → c   (x   1 + x   2 , y   1 + y   2 , z   1 + z   2 )

Свойства сложения векторов

→ a   + → b   = → b   + → a

( → a   + → b   ) + → c   = → a   + ( → b   + → c   )

→ a   + → 0   = → a

→ a   + (- → a   ) = → 0

Координаты произведения вектора на число

λ * → a   (x, y, z) = → c   (λx, λy, λz)

Свойства умножения

(λμ) → a   = λ(μ → a   )

(λ + μ) * → a   = λ → a   + μ → a

λ( → a   + → b   ) = λ → a   + λ → b

0 * → a   = λ → 0   = → 0

Скалярное произведение векторов

→ a   (x   1 , y   1 , z   1 ) и → b   (x   2 , y   2 , z   2 )

→ a   * → b   = x   1 x   2 + y   1 y   2 + z   1 z   2 = | → a   | * | → b   | * cos( → a   , → b   )

Косинус угла между векторами

→ a   (x   1 , y   1 , z   1 ) и → b   (x   2 , y   2 , z   2 )

cos( → a   , → b   ) = → a * → b   | → a   | * | → b   | = x   1 x   2 + y   1 y   2 + z   1 z   2 √ x 2 1 + y 2 1 + z 2 1 * √ x 2 2 + y 2 2 + z 2 2

Свойства скалярного произведения

→ a   * → b   = → b   * → a

→ a   * → a   ≥ 0

→ a   * → a   = | → a   | 2

→ a   ( → b   + → c   ) = → a   * → b   + → a   * → c

(λ → a   ) → b   = λ( → a   → b   )

Длина вектора → a   (x, y, z)

| → a   | = √ x 2   + y 2   + z 2

Осторожно, Вектор!

Автор статьи — Чернов Н. С.

При изучении Физики приходится иметь дело с векторными величинами. Знание основ векторной алгебры является не только необходимым условием успешного и оптимального решения практических задач, но подчас и фундаментом для правильного толкования многих физических понятий.

К сожалению (и удивлению) приходится констатировать, что подавляющее большинство учебников и учебных пособий уделяют недостаточно внимания этому важнейшему вопросу, хотя многие книги по физике и начинаются с изучения основ векторной алгебры.

Это проявляется, во-первых, в неполном охвате ее основных положений, во-вторых, в необоснованном усложнении (либо, наоборот, в упрощении) некоторых понятий, и, в-третьих, в непоследовательном применении или вообще не использовании ранее данных понятий. На что, на мой взгляд, следует обратить внимание учителей?

Важнейшим условием успешного преподавания Физики является обязательное предварительное изучение основ векторной алгебры. Без всякого преувеличения следует еще раз подчеркнуть: от этого будет зависеть успех всего дела! Не следует жалеть затраченных на это изучение часов: эти часы в дальнейшем «возвратятся» в результате того, что с применением методов векторного анализа, некоторые вопросы потребуют меньшего времени на их изучение.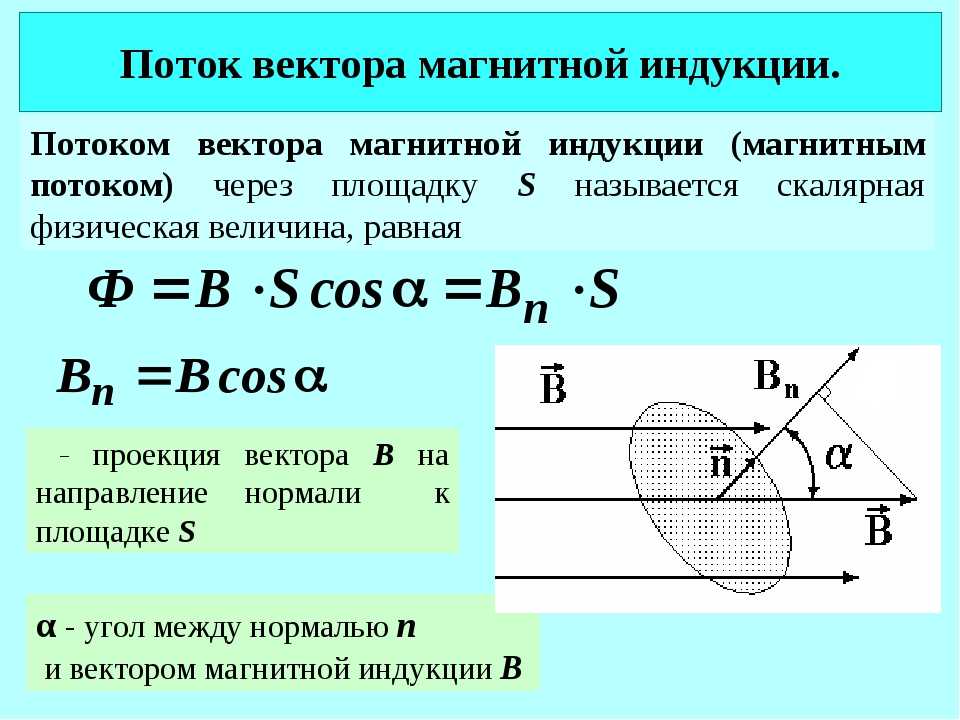

Экономится также время, затраченное учениками на повторение пройденного материала. Но самое главное заключается в том, что учащиеся осваивают единый мощнейший метод изучения тех разделов и тем всех без исключения разделов физики, где встречаются векторные величины (механика, электростатика, электродинамика, магнетизм).

Какие же основные понятия и действия над векторными величинами учащиеся должны знать перед изучением основного курса? Перечислю их.

1. Понятие о векторных и скалярных величинах.
2. Сложение векторов.
3. Вычитание векторов.
4. Умножение вектора на скаляр.
5. Умножение векторов: а) скалярное умножение, б) векторное умножение.
6. Проекции векторов: а) скалярная проекция, б) векторная проекция.
7. Нахождение модуля вектора по его проекциям.

Кратко остановимся на каждом из этих пунктов.

Понятие о векторных и скалярных величинах.

Об определении скалярных величин. Часто говорят, что скаляры – это величины, для характеристики которых достаточно указания только числовой меры, то есть это такие свойства изучаемых объектов, которые полностью характеризуются числом (положительным или отрицательным). Возможно, такого определения будет достаточно, учитывая, что определение скалярных величин дается, в основном для их, если так можно сказать, «противопоставления» векторам, для того, чтобы сделать акцент на главном свойстве векторной величины – направлении. Однако преподаватель должен знать, что такое определение скаляров является неполным. Нужно еще указать, что числовое значение скалярной величины

не зависит от выбора системы координат и начала отсчета времени.

В соответствии с этим определением не являются скалярными величины, использованные в следующих предложениях: «Санкт-Петербург расположен на 30-м градусе восточной долготы», «Знаменитые «Начала» Ньютон опубликовал в 1687 году», «Сейчас 12 часов по Московскому времени», «Точка А имеет координаты 5 ,0, 0».

Действительно, выбрав иное начало отсчета (пулковский меридиан вместо гринвичского, сотворение мира вместо Рождества Христова, среднеевропейское время вместо московского, иную координатную систему, мы получили бы совсем иные числа: ноль градусов, 7195 год (а сам Ньютон получил бы 5675 год) и т. д.

Наоборот, в последующих утверждениях мы имеем дело с типичными скалярами: «Санкт-Петербург на 30 градусов восточнее Лондона», «Сегодня продолжительность дня в Москве составляет 12 часов», «Знаменитые «Начала» Ньютон опубликовал в возрасте 44 лет», «Расстояние между точками А и О равно 5».

Таким образом, всякому скаляру может быть поставлено в соответствие число, но не всякое число может являться скаляром. Другое дело, что при первоначальном изучении векторной алгебры на эти «тонкости» может быть и не следует заострять внимание учеников, но преподаватель это знать должен.

Об определении векторных величин. Вектором называют величину, характеризуемую числовым значением, направлением в пространстве и складывающейся с другой, себе подобной величиной геометрически.

Следует обязательно подчеркнуть, что последняя часть определения является не свойством вектора, что нередко утверждается, но именно неотъемлемой частью определения. Два первых требования необходимы, но недостаточны. В незнании этого заложен источник многочисленных ошибок.

Рассмотрим такую физическую величину как сила тока. Эта величина характеризуется, как известно, числом ( I = Δq/Δt) и направлением (от плюса к минусу). Однако известно, что токи в точке, где цепь разветвляется, складываются алгебраически, а не геометрически (первый закон Кирхгофа). Вот и получается, что сила тока, оказывающаяся вектором по «урезанному» определению, в действительности является скаляром. Поэтому следует избегать таких неточных, а, значит, и неправильных определений.

Вообще говоря, определения не могут быть правильными или неправильными, точными или неточными (запрещается только их внутренняя противоречивость). Кто, например, может запретить автору любой книги считать, что скаляр – это просто любое число, а вектор – это величина, характеризующаяся числом и направлением? Никто не может! Это – его право. Точно также автору никто не может запретить понимать под числом пи не 3,14…, а, например, 8,395 или измерять расстояние не в метрах, а в попугаях. Находясь в этой своей, если так можно сказать, «понятийной системе координат», автор может весьма комфортно себя чувствовать, делая одно открытие за другим. Но при общении с другими исследователями, находящимися в другой «понятийной системе», ему постоянно придется объяснять, что именно он понимает под тем или иным определением (термином, буквой…).

Даже при обозначении какой-то физической величины или действия над ней многие стараются использовать такие символы (буквы, знаки умножения, сложения, интегрирования и т.д.), которые «приняты на вооружение» большинством физиков. Так, общепринято обозначать заряд буквой q, массу – буквой m, и т. д. Даже в таких «мелочах», когда вместо общепринятого обозначения площади буквой S, некоторые авторы используют буквы A или F (а такое встречается в книгах по технической механике), многие испытывают психологический дискомфорт. А чего уж говорить, если речь идет об определении каких-то категорий, процессов… Тут и запутаться недолго. В общем, не такая уж это и безобидная вещь – пренебрежение общепринятыми соглашениями. Попробуйте, эксперимента ради, предложить ученикам измерять скорость в попугаях, деленных на секунду или под пи понимать число 8,395. Я догадываюсь, какова будет их реакция.

Во избежание ничем не оправданной путаницы, преподаватель должен жестко подходить к тому, что написано на «ярлыке», который мы наклеиваем на то или иное свойство изучаемого объекта. Все сказанное относится и к определению скалярных и векторных величин. Для них разработан соответствующий математический аппарат, им можно сопоставить конкретные физические свойства. Конечно, с течением времени некоторые понятия корректируются, уточняются, но всегда в рамках общих соглашений. Однако на сегодняшний день все определения, отличающиеся по содержанию от общепринятых, будут являться неточными и неверными.

Что касается обозначения векторных величин, то следует предостеречь учеников от такого их обозначения, когда над буквой вектора ставится черточка. И, хотя такой символ векторной величины давно ушел в прошлое, все-таки иногда его можно еще встретить. Черточкой над буквой принято обозначать средние значения величин, а для обозначения векторов применяется только стрелка над буквой (речь, конечно, идет о рукописном варианте, в печатном варианте буквы, обозначающие векторы имеют жирный шрифт).

Сложение векторов. Основным правилом сложения векторных величин является «правило многоугольника». На него и надо сделать акцент, а не на «правило параллелограмма». Причем следует подчеркнуть, что слагаемые векторы могут быть как угодно ориентированы в пространстве. При таком подходе теряет смысл раздельно излагать, например, плоскую и пространственную системы сил. Кроме того, следует внушить студентам, что изучаемые действия над векторами – это действия над абстрактными образами (грубо говоря, просто над стрелками). В векторной алгебре никакой вектор не наделяется никаким физическим содержанием.

Но студенты также должны понимать, что эти абстрактные образы являются обобщением конкретных свойств многих физических объектов. Изучив действия над математическими образами, учащимся не составит никакого труда перенести эти действия на реальные свойства: скорости, силы, напряженности полей и т. д.

После такого подхода к изучению действий над векторами иногда приходится слышать от самих учеников такой, например, вопрос: «Зачем же тогда в учебниках каждый раз заново изучается операция сложения (вычитания, проектирования…) скоростей, сил, расположенных на плоскости, сил, расположенных в пространстве, сложение моментов и т. д.), если все они складываются по одним и тем же правилам, разработанным для «математических» векторов?». Вот и подумайте, как отвечать на подобные справедливые вопросы, а заодно и над тем, сколько часов в дальнейшем сэкономит такая изначальная «массированная векторная подготовка», и на сколько стали бы тоньше учебники, если их как следует «выжать».

При изучении именно сложения векторов следует особо подчеркнуть, что в основе изучаемой науки лежит эксперимент. Отнести ту или иную физическую величину к скалярам или векторам можно только на основе экспериментов (сложение электрических токов, о чем я уже говорил – тому пример). Распространенные суждения типа «Силы (ускорения, скорости и т. д.) складываются геометрически, так как это – векторы» принципиально ошибочны. Причина и следствие здесь поменялись местами, телега поставлена впереди лошади. Следует говорить: «Установлено опытом, что сила характеризуется числовым значением, направлением и складывается с другой силой по правилу параллелограмма. Следовательно, сила – вектор и, описывая силы, можно использовать разработанный для векторов математический аппарат».

Вычитание векторов. Здесь вначале надо дать определение обратного (противоположного) вектора, а затем просто заменить операцию вычитания операцией сложения. При таком подходе обычно у учащихся не возникает никаких вопросов. Но именно при изучении вычитания векторов самое время будет сказать ученикам о том, что не бывает ни положительных, ни отрицательных векторов. Знак же «минус» перед символическом обозначении вектора указывает только на то, что речь идет об обратном векторе, но вовсе не о том, что бывают отрицательные (а, значит, и положительные) векторы.

Векторы в отличие от скаляров бессмысленно также сравнивать между собой, используя понятия «больше» или «меньше», то есть записи: а < b или a > b лишены смысла (к модулям векторов это, конечно, не относится). Надо всегда помнить, что вектор – сложный объект, который одновременно характеризуется и величиной и направлением. Поэтому, если кто-то надумает сравнивать между собой векторы по признаку «больше – меньше», то тогда ему придется сравнивать по этому признаку не только модули векторов, но и их направления, а это, согласитесь, бессмысленно. А вот равными между собой векторы быть могут. Это – такие векторы, которые имеют одинаковые модули и одинаковые направления.

Умножение вектора на скаляр. В большинстве учебников дается следующее определение этой операции: «При умножении вектора а на скаляр k получается новый вектор kа, который имеет модуль в |k| раз больший модуля данного вектора. Направлен вектор kа в сторону вектора а, если k > 0 и в противоположную сторону, если k < 0». Очевидно, следует говорить, что модуль нового вектора не в | k | раз больше, а в | k | раз отличается от модуля исходного вектора. Думаю, что это уточнение пояснений не требует.

Скалярное умножение векторов. Эта операция встречается при введении понятия работы, потока вектора, при решении задач. Обычно трудностей в понимании этого действия не вызывает. Следует только обратить внимание учеников на обозначение этой операции (точка, но не косой крест, либо круглые скобки, в которые помещаются перемножаемые векторы). Полезно показать, что скалярное произведение вектора самого на себя даст квадрат его модуля (это пригодится, когда, например, будет рассматриваться вопрос о кинетической энергии).

Векторное произведение двух векторов. На эту операцию следует обратить особое внимание, во-первых, в силу ее важности при изучении некоторых понятий механики и электротехники, а, во-вторых, в силу некоторых затруднений ее усвоения учениками. Видимо, последнее соображение и заставляет авторов некоторых учебников закрывать глаза на ее применение, подчас, несмотря на то, что в начале курса эта операция иногда рассматривается. В результате некоторые важнейшие физические понятия извращаются до неузнаваемости. Судите сами.

Фундаментальное понятие момента силы относительно точки во всех школьных учебниках, а также практически во всех учебниках для техникумов и колледжей трактуется следующим образом (возможны несущественные отличия). «Моментом силы относительно точки называется взятое со знаком плюс или минус произведение модуля силы F на кратчайшее расстояние L от точки до линии действия силы, то есть М = ± FL».

Посмотрите на эту формулу и задумайтесь, что же это за величина такая момент силы: вектор это или скаляр? То, что автор такой записи не считает это понятие вектором сразу видно хотя бы по обозначению этой величины (над символом нет стрелки, и он не выделен жирным шрифтом). Символ ± тоже говорит не в пользу векторного характера момента силы (векторы не бывают ни положительными, ни отрицательными), да и произведение модуля силы на расстояние (сугубо скалярные величины) тем более не позволяет считать момент силы вектором.

Думаете, момент силы – это скаляр? Вынужден разочаровать: здесь положение ничем не лучше, чем с векторным статусом этого понятия: уж очень знак минус смущает. Действительно, откуда он мог взяться, если перемножаются сугубо положительные величины? Так что же это за величина-то такая? Это знают только авторы, предлагающие такое определение момента (да и то сомневаюсь в их толковом ответе). И все потому, что они просто не поверили в возможность ученика понять операцию векторного произведения двух векторов в применении, как к математическим образам, так и к физическим понятиям. Зато эти же авторы нисколько не стесняются проявить свои математические познания, предлагая, например, бедным студентам техникумов и колледжей рассчитывать перемещения сечений балок с помощью так «необходимого» студентам интеграла Мора, отечески «успокаивая» их тем, что это проще, чем решать двойные интегралы, формулы которых зачем-то приводятся. Кому нужна эта математическая бахрома, если вы не можете дать четкого и толкового определения, в общем-то, несложного, но чрезвычайно важного физического понятия?

Вернемся к моменту силы относительно точки. Конечно, это – вектор, и об этом все давным-давно знают. И равен этот вектор векторному произведению радиус-вектора точки приложения силы относительно полюса на вектор силы, то есть M = r x F. И направление этого вектора легко определяется по известному (даже ученикам) правилу буравчика. А вот, что касается плюса или минуса, то это уже зависит от направления оси, на которую я буду проектировать вектор M. И речь тут уже идет, как вы понимаете, не о моменте силы и не о его модуле, а о проекции этого вектора, и знаки эти зависят только от моей воли, а не от того, как уверяют авторы, поворачивает ли момент наше тело по или против хода часовой стрелки, поскольку направление оси, на которую проектируется вектор момента, я выбираю по своей прихоти.

Не забывайте также, что «намудрив» с понятием момента силы (хотели, как лучше…), авторам уже ничего не остается, как нести такую же ересь и в отношении момента пары сил. А ведь ученикам еще и задачи порешать не мешало бы для закрепления данного понятия. Как же их решать, если само понятие момента, данное этими авторами, вовсе этим понятием не является?

Вот и получается, что лучше уж совсем ничего не знать о моменте силы, чем иметь такие знания.

Не лучшим образом обстоит дело и с понятием угловой скорости, которая тоже «как на грех» является вектором. И связь между тремя векторами: вектором линейной скорости v, вектором угловой скорости ω и радиус-вектором r вращающейся точки тоже определяется правилом векторного произведения, а именно v = ω x r.

Кстати, многие авторы умалчивают о том, что угловая скорость – вектор тоже, видимо, по причине их беспокойства непонятливостью учеников. Ведь здесь же надо им как-то объяснить, почему сами углы векторами не являются, а вот их дифференциалы – почему-то векторы. Куда проще написать, что ω = φ/t, чем ω = dφ/dt. Но ведь всегда может найтись (и слава Богу!) какой-нибудь любознательный ученик, который возьмет да и спросит: «Линейная скорость – это вектор (Вы нам сами об этом говорили), а как насчет угловой скорости? Тоже ведь скорость как-никак…». И ведь бывает, спрашивают!

Ну, и, конечно, следует сказать учащимся, как обозначается векторное произведение: либо косым крестом, в отличие от точки, как в случае скалярного произведения, либо перемножаемые векторы помещаются в квадратные скобки. Одновременное применение и креста и квадратных скобок, то есть [axb] используется крайне редко.

Скалярная проекция вектора на ось. Необходимость изучения этой операции очевидна. Дело в том, что некоторые физические законы имеют векторный характер, а при решении тех или иных практических задач часто бывает необходимо получить конкретное число. Переход от векторов к их модулям без проектирования и нахождения проекций в большинстве случаев невозможен. Поэтому студенты должны не только знать, что такое проекция вектора, но и уметь ее находить.

Учащиеся также должны понимать, что, когда говорят «проекция вектора», имеют в виду скалярную проекцию. Слово «скалярная» в определении обычно опускается. И в то же время, эта проекция скаляром не является (хотя и называется скалярной проекцией), несмотря на утверждения многих авторов, что проекция вектора – это скаляр. Дело в том, что эта проекция зависит от выбора системы координат, и в разных системах проекции одного и того же вектора будут разными. Скаляр же – величина инвариантная по отношению к любым координатным системам.

О проектировании векторов говорится во всех учебниках, без этого просто невозможно изучение предмета. Другое дело, что большинство авторов идут по самому неоптимальному пути: проекции вводятся для конкретных физических образов (скоростей, сил и т. д.), вместо того, чтобы в самом начале курса рассмотреть вектор (и все, что с ним связано) как математический образ. Если этого не сделать, то студенты оказываются в положении, когда они «за деревьями не видят леса». Однако мы об этом уже говорили. Сейчас же я покажу, как некоторые авторы используют понятие проекции вектора на ось при изучении некоторых вопросов механики.

Приведу фрагмент изложения вопроса о растяжении и сжатии, взятый из одного из учебников по технической механике для техникумов. «…целесообразно договориться о правиле знаков для проекций внешних сил при определении нормальной силы в сечении: проекции внешних сил, направленных от сечения, положительны и, наоборот, проекции внешних сил, направленных к сечению, отрицательны». Авторы считают этот договор настолько важным, что сочли необходимым выделить курсивом некоторые слова и фразы своего предложения.

О чем, собственно, договор? А договор, по сути, о том, чтобы поставить жирный крест на понятии проекции вектора и его правильном использовании. Действительно, даже школьнику понятно, что бессмысленно говорить о проекции, не определив ось, на которую это проектирование выполняется. Авторы же этим грубо пренебрегают. Далее. Рассматриваемые авторами силы, направленные «от сечения», действуют в противоположных направлениях, поэтому они никак не могут иметь один и тот же знак своих проекций. То же самое касается и сил, направленных «к сечению».

Зачем выдумывать какое-то «правило знаков», когда можно (и нужно!) просто-напросто выбрать любую ось и спроектировать на нее все необходимые силы? Получается, что вместо стройного и последовательного изложения курса, перед нами предстает мозаичная картина несвязанных между собой «правил», ничего не дающих, кроме путаницы в головах учащихся.

Векторная проекция вектора на ось. Введение этого понятия связано с необходимостью знания студентами основной формулы векторной алгебры, которая, в свою очередь, используется как при решении задач, так и при изложении некоторых тем. Кроме того, векторная проекция используется и при разложении вектора на составляющие.

Проще всего ввести это понятие как произведение скалярной проекции вектора на орт соответствующей оси. Обозначение векторной проекции такое же, как и скалярной, но с «векторной атрибутикой». Например, если дан вектор а, то его скалярная проекция, например, на ось Х обозначается как ax, а векторная будет иметь обозначение ax (в рукописном варианте, как известно, вместо жирного написания буквы над ней ставится стрелка).

Следует приучать учеников к корректному использованию обозначений, связанных с векторными величинами. В частности, нужно обратить их внимание на традиционно существующую «чехарду» в обозначениях векторов, их составляющих и модулей, когда речь идет о нормальных и тангенциальных ускорениях. В литературе нередко и сам вектор нормального ускорения, и его проекция на нормаль, и модуль обозначаются одним и тем же символом аn. Аналогично и для касательного ускорения. Студенты должны знать, что:

a_τ — это вектор касательного ускорения,

a_n — это вектор нормального ускорения.

a_τ и an являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,

a_τ — это проекция (скалярная!) касательного ускорения на касательную ось,

a_n — это проекция (скалярная!) нормального ускорения на ось нормали,

| a_τ |- это модуль вектора касательного ускорения,

| a_n | — это модуль вектора нормального ускорения.

Нахождение модуля вектора по его проекциям. С точки зрения математики, тут все просто: модуль вектора равен корню квадратному из суммы квадратов его проекций. По сути – это обычная теорема Пифагора. Необходимость в применении этой формулы возникает всегда, когда в задаче нужно найти модуль какой-то векторной величины, например, силы. По ходу решения задачи находятся проекции, а потом и сам модуль. Здесь важно приучить студентов неукоснительно применять данную формулу, даже, если вектор имеет одну составляющую с положительной проекцией на выбранную ось.
Такая «дотошность» приучит студентов к математической и физической строгости, к пониманию того, что никаких «мелочей» и никакого «заметания мусора под ковер» в науке нет и быть не должно.

Все изложенное, конечно, не является чем-то новым для преподавателей тех дисциплин, где встречаются векторные величины. Математическую сторону поднятых вопросов знают преподаватели математики.

Целью же этой статьи является привлечение учителей к критическому анализу учебников и пособий с точки зрения поднятых вопросов и к пониманию необходимости единого подхода в применении методов векторного анализа. А это возможно при углублении межпредметных связей, на что должны обратить внимание преподаватели математики и физики конкретного учебного заведения.

Чернов Николай Сергеевич

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

 

Please enable JavaScript to view the

Применение векторов в повседневной жизни

6

Введение

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.

Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.

Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.

История возникновения понятия вектор

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.

Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др. , характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]

Векторы в математике

Вектором называется направленный отрезок, который имеет начало и конец.[1]

Вектор с началом в точке А и концом в точке В принято обозначать как  АВ. Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например .

Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Действительно, каждый направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства: скажем, вектор АВ естественно определяет перенос, при котором точка А перейдет в точку В, также и обратно, параллельный перенос, при котором А переходит в В, определяет собой единственный направленный отрезок АВ.

Длиной вектора АВ называется длина отрезка АВ, её обычно обозначают АВ. Роль нуля среди векторов играет нулевой вектор, у которого начало и конец совпадают; ему, в отличие от других векторов, не приписывается никакого направления.

Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.

Операции над векторами

Модуль вектора

Модулем вектора АВ называется число, равное длине отрезка АВ. Обозначается, как АВ. Через координаты вычисляется, как:

=+ +

Сложение векторов

В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

){\displaystyle {\vec {a}}+{\vec {b}}=(a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z})}

Для геометрического построения вектора суммы {\displaystyle {\vec {c}}={\vec {a}}+{\vec {b}}}c = используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов {\displaystyle {\vec {a}}} и {\displaystyle {\vec {b}}} некоторой точки будет тем же, что применение сразу одного переноса {\displaystyle {\vec {a}}+{\vec {b}}}, соответствующего этому правилу. Для сложения двух векторов{\displaystyle {\vec {a}}} и {\displaystyle {\vec {b}}} по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:

Правило многоугольника

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же {\displaystyle n} векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом {\displaystyle n}- го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Правило параллелограмма

Для сложения двух векторов {\displaystyle {\vec {a}}} и {\displaystyle {\vec {b}}} по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Вычитание векторов

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

‚ {\displaystyle {\vec {a}}-{\vec {b}}=(a_{x}-b_{x},a_{y}-b_{y},a_{z}-b_{z})}

Для получения вектора разности {\displaystyle {\vec {c}}={\vec {a}}-{\vec {b}}} начала векторов соединяются и началом вектора {\displaystyle {\vec {c}}} будет конец {\displaystyle {\vec {b}}}, а концом — конец {\displaystyle {\vec {a}}}. Если записать, используя точки векторов, то AC-AB=BC{\displaystyle {\overrightarrow {AC}}-{\overrightarrow {AB}}={\overrightarrow {BC}}}.

Умножение вектора на число

Умножение вектора {\displaystyle {\vec {a}}} на число {\displaystyle \alpha 0}, даёт сонаправленный вектор с длиной в {\displaystyle \alpha } раз больше. Умножение вектора {\displaystyle {\vec {a}}} на число {\displaystyle \alpha , даёт противоположно направленный вектор с длиной в {\displaystyle \alpha } раз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:

{\displaystyle \alpha {\vec {a}}=(\alpha a_{x},\alpha a_{y},\alpha a_{z})}

Скалярное произведение векторовСкалярное

Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними.

Применение векторов в смежных наукахВекторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии

Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.

Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.

Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.

Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.

Векторы в повседневной жизни

 Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как  пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора  при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.  

Векторы в знаках дорожного движения

        Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.

Заключение

 Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.

Выводы

1. Каждый человек постоянно сталкивается с векторами в повседневной жизни.

2. Векторы необходимы нам для изучения не только математики, но и других наук.

3. Каждый должен знать, что такое вектор.

Источники

1. Башмаков М.А. Что такое вектор?-2-е изд., стер.- М.: Квант, 1976.-221с. 

2. Выгодский М.Я. Справочник по элементарной математике.-3-е изд., стер. — М.: Наука, 1978.-186с.

3. Гусятников П.Б. Векторная алгебра в примерах и задачах.-2-е изд., стер.- М.: Высшая школа, 1985.-302с.

4. Зайцев В.В. Элементарная математика. Повторительный курс.-3-е изд., стер. — М.: Наука,1976.-156с.

5. Коксетер Г.С. Новые встречи с геометрией.-2-е изд., стер. — М.: Наука,1978.-324с.

6. Погорелов А.В. Аналитическая геометрия.- 3-е изд., стер. — М.: Квант,1968.-235с.

ВЕКТОРНОЕ ИСЧИСЛЕНИЕ • Большая российская энциклопедия

ВЕ́КТОРНОЕ ИСЧИСЛЕ́НИЕ, раз­дел ма­те­ма­ти­ки, в ко­то­ром изу­ча­ют­ся век­то­ры евк­ли­до­ва про­стран­ст­ва и опе­ра­ции над ни­ми.

Воз­ник­но­ве­ние В. и. свя­за­но с по­треб­но­стя­ми ме­ха­ни­ки и фи­зи­ки. Ос­но­вы В. и. бы­ли за­ло­же­ны ис­сле­до­ва­ния­ми У. Га­миль­то­на и Г. Грас­сма­на (1844–1850). Их идеи бы­ли ис­поль­зо­ва­ны Дж. К. Мак­свел­лом в его ра­бо­тах по элек­три­че­ст­ву и маг­не­тиз­му. Совр. вид В. и. при­дал Дж. Гиббс. Зна­чительный вклад в раз­ви­тие В. и. внёс М. В. Ос­т­ро­град­ский.

Векторная алгебра

Век­то­ром на­зы­ва­ет­ся на­прав­лен­ный от­ре­зок пря­мой, у ко­то­ро­го один ко­нец (точ­ка $A$) счи­та­ет­ся на­ча­лом, дру­гой (точ­ка $B$) – кон­цом век­то­ра. Обыч­но век­то­ры обо­зна­ча­ют­ся $AB, \overline{AB}, \overrightarrow{AB}, \boldsymbol a, \bar a, \vec a$, или про­сто $a$. Век­тор, на­ча­ло и ко­нец ко­то­ро­го сов­па­да­ют, на­зы­ва­ет­ся ну­ле­вым и обыч­но обо­зна­ча­ет­ся $\boldsymbol 0$ или 0. Ха­рак­те­ри­сти­ка­ми век­то­ра яв­ля­ют­ся его мо­дуль (дли­на), ко­то­рый ра­вен дли­не от­рез­ка $AB$ (обо­зна­ча­ет­ся $|AB|$), и на­прав­ле­ние от $A$ к $B$. Ну­ле­во­му век­то­ру при­пи­сы­ва­ют лю­бое на­прав­ле­ние. Все ну­ле­вые век­то­ры счи­та­ют­ся рав­ны­ми. Век­тор еди­нич­ной дли­ны на­зы­ва­ет­ся еди­нич­ным век­то­ром или ор­том. Век­то­ры на­зы­ва­ют­ся кол­ли­не­ар­ны­ми, ес­ли они ле­жат ли­бо на од­ной пря­мой, ли­бо на па­рал­лель­ных пря­мых, и ком­пла­нар­ны­ми, ес­ли они ле­жат на од­ной плос­ко­сти. Век­тор на­зы­ва­ет­ся сво­бод­ным, ес­ли его на­чаль­ная точ­ка мо­жет быть вы­бра­на про­из­воль­но. Обыч­но два век­то­ра на­зы­ва­ют­ся рав­ны­ми, ес­ли они кол­ли­не­ар­ны, име­ют оди­на­ко­вую дли­ну и оди­на­ко­во на­прав­ле­ны.

Кро­ме сво­бод­ных век­то­ров в ме­ха­нике и фи­зи­ке час­то рас­смат­ри­ва­ют­ся век­то­ры, ко­то­рые ха­рак­те­ри­зу­ют­ся мо­ду­лем, на­прав­ле­ни­ем и по­ло­же­ни­ем на­чаль­ной точ­ки (точ­кой при­ло­же­ния). Та­кие век­то­ры на­зы­ва­ют­ся свя­зан­ны­ми. Свя­зан­ные век­то­ры счи­та­ют­ся рав­ны­ми, ес­ли они име­ют не толь­ко рав­ные мо­дули и оди­на­ко­вые на­прав­ле­ния, но и об­щую точ­ку при­ло­же­ния. Мно­же­ст­во рав­ных ме­ж­ду со­бой век­то­ров, рас­по­ло­жен­ных на од­ной пря­мой, на­зы­ва­ет­ся сколь­зя­щим век­то­ром. За­да­ние сколь­зя­ще­го или свя­зан­но­го век­то­ра мо­жет быть за­ме­не­но за­да­ни­ем двух сво­бод­ных век­торов. В В. и. рас­смат­ри­ва­ют­ся толь­ко сво­бод­ные век­то­ры.

В век­тор­ной ал­геб­ре рас­смат­ри­ва­ют­ся ли­ней­ные опе­ра­ции над век­то­ра­ми, т. е. сло­же­ние век­то­ров и ум­но­же­ние век­то­ра на дей­ст­ви­тель­ное чис­ло.

Рис. 1.

Рис. 2.

Рис. 3.

Сум­мой $a+b$ век­то­ров $a$ и $b$ на­зы­ва­ет­ся век­тор, иду­щий из на­ча­ла век­то­ра $a$ в ко­нец век­то­ра $b$ при ус­ло­вии, что на­ча­ло век­то­ра $b$ при­ло­же­но к кон­цу век­то­ра $a$ (рис.  1), этот век­тор ра­вен так­же диа­го­на­ли па­рал­ле­ло­грам­ма, по­стро­ен­но­го на век­то­рах $a$ и $b$ (рис. 2). По­строе­ние сум­мы не­сколь­ких век­то­ров по­ка­зано на рис. 3.

Про­из­ве­де­ни­ем $\alpha a$ век­то­ра $a$ и чис­ла $\alpha$ на­зы­ва­ет­ся век­тор, кол­ли­не­ар­ный век­то­ру $a$, имею­щий дли­ну $|\alpha|\cdot |a|$ и на­прав­ле­ние, сов­па­даю­щее с на­прав­ле­ни­ем $a$ при $\alpha > 0$ и про­ти­во­по­лож­ное при $\alpha < 0$. Ес­ли $\alpha =0$ или/и $a=0$, то $\alpha a = 0$.

Век­тор $-1\cdot a$ на­зы­ва­ет­ся про­ти­во­по­лож­ным век­то­ру $a$ и обо­зна­ча­ет­ся $-a$.

Опе­ра­ции сло­же­ния век­то­ров и ум­но­же­ния век­то­ра на чис­ло об­ла­да­ют свой­ст­ва­ми $a+b = b+a, (a+b)+c = a+(b+c), a+0 = a, a+(-a) = 0, 1\cdot a=a, \alpha(\beta a) = (\alpha\beta)a, \alpha(a+b) = \alpha a +\alpha b, (\alpha +\beta)a = \alpha a +\beta a$, где $a,b,c$ – век­то­ры, а $\alpha$ и $\beta$ – дей­ст­ви­тель­ные чис­ла. Раз­но­стью $a-b$ век­то­ров $a$ и $b$ на­зы­ва­ет­ся век­тор $x$ та­кой, что $x+b = a, x = a+(-b)$.  Мно­же­ст­во всех век­то­ров евк­ли­до­ва про­стран­ст­ва с вве­дён­ны­ми в нём опе­ра­ция­ми сло­же­ния и ум­но­же­ния на чис­ло об­ра­зу­ет век­тор­ное про­стран­ст­во.

В век­тор­ной ал­геб­ре час­то ис­поль­зу­ют­ся по­ня­тия ли­ней­ной за­ви­си­мо­сти и ли­ней­ной не­за­ви­си­мо­сти век­то­ров. Век­то­ры $a_1, \ldots , a_n$ на­зы­ва­ют­ся ли­ней­но за­ви­си­мы­ми, ес­ли су­ще­ст­ву­ют чис­ла $\alpha_1, \ldots , \alpha_n$, из ко­то­рых хо­тя бы од­но от­лич­но от нуля, та­кие, что ли­ней­ная ком­би­на­ция $\alpha_1 a_1 + \ldots + \alpha_n a_n = 0$, т. е. сум­ма век­то­ров в ле­вой час­ти это­го ра­вен­ст­ва рав­на ну­ле­во­му век­то­ру. В про­тив­ном слу­чае век­то­ры $a_1, \ldots, a_n$ на­зы­ва­ют­ся ли­ней­но не­за­ви­си­мы­ми.

Рис. 4.

В ме­ха­ни­ке и фи­зи­ке обыч­но ис­поль­зу­ют­ся дву­мер­ные и трёх­мер­ные век­тор­ные про­стран­ст­ва. В трёх­мер­ном про­стран­ст­ве су­ще­ст­ву­ют трой­ки ли­ней­но не­за­ви­си­мых век­то­ров, лю­бые че­ты­ре век­то­ра ли­ней­но за­ви­си­мы; в дву­мер­ном про­стран­ст­ве, т.  е. на плос­ко­сти, су­ще­ст­ву­ют па­ры ли­ней­но не­за­ви­си­мых век­то­ров, лю­бые три век­то­ра ли­ней­но за­ви­си­мы. Ли­ней­но не­за­ви­си­мые век­то­ры $e_1, e_2, e_3$ трёх­мер­но­го евк­ли­до­ва про­стран­ст­ва об­ра­зу­ют ба­зис, т. е. лю­бой век­тор $a$ мо­жет быть един­ст­вен­ным об­ра­зом пред­став­лен в ви­де $a = a_1e_1 + a_2e_2 + a_3e_3$, где $a_1, a_2, a_3$ – чис­ла, на­зы­вае­мые ко­ор­ди­на­та­ми (ком­по­нен­та­ми) век­то­ра $a$ в дан­ном ба­зи­се. Век­тор $a$ c ко­ор­ди­на­та­ми $a_1, a_2, a_3$ час­то за­пи­сы­ва­ют в ви­де $a=(a_1,a_2, a_3)$. Три вза­им­но ор­то­го­наль­ных (пер­пен­ди­ку­ляр­ных) век­то­ра, дли­ны ко­то­рых рав­ны еди­ни­це и ко­то­рые обыч­но обо­зна­ча­ют $i, j, k,$ об­ра­зу­ют т. н. ор­то­нор­ми­ро­ван­ный ба­зис. Ес­ли на­ча­ла этих век­то­ров по­мес­тить в не­ко­то­рую точ­ку $O$, то по­лу­чит­ся де­кар­то­ва пря­мо­уголь­ная сис­те­ма ко­ор­ди­нат в трёх­мер­ном про­стран­ст­ве (рис. 4). Ука­зан­ным вы­ше ли­ней­ным опе­ра­ци­ям над век­то­ра­ми со­от­вет­ст­ву­ют ана­ло­гич­ные опе­ра­ции над их ко­ор­ди­на­та­ми: ес­ли век­то­ры $a$ и $b$ име­ют ко­ор­ди­на­ты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$, то сум­ма $a+b$ этих век­то­ров име­ет ко­ор­ди­на­ты $(a_1 + b_1, a_2 + b_2, a_3 + b_3)$, а век­тор $\alpha a$ име­ет ко­ор­ди­на­ты $(\alpha a_1,\alpha a_2, \alpha a_3)$.

Раз­ви­тие и при­ме­не­ние век­тор­ной ал­геб­ры тес­но свя­за­ны с разл. век­тор­ны­ми про­из­ве­де­ния­ми: ска­ляр­ным, век­тор­ным и сме­шан­ным. Ска­ляр­ным про­из­ве­де­ни­ем век­то­ров $a$ и $b$ на­зы­ва­ет­ся чис­ло, обо­зна­чае­мое $(a, b)$, рав­ное про­из­ве­де­нию длин этих век­то­ров на ко­си­нус уг­ла $\varphi$ ме­ж­ду ни­ми:

$$(a, b) = |a| |b| \cos \varphi$$

Ска­ляр­ным про­из­ве­де­ни­ем вы­ра­жа­ет­ся, напр., ра­бо­та си­лы $F$ на пря­мо­ли­ней­ном пу­ти $s$, ко­то­рая рав­на $|F| |s| \cos \varphi$, где $\varphi$ – угол ме­ж­ду век­то­ра­ми $F$ и $s$.

Cкалярное про­из­ве­де­ние об­ла­да­ет сле­дую­щи­ми свой­ст­ва­ми:

$$(a, b) = (b, a) , \quad (\alpha a, b) = \alpha (a, b),$$ $$(a+b, c) = (a, c) + (b, c), \quad (a, a) \geq 0,$$

где $a, b, c$ — век­то­ры, $\alpha$ — чис­ло; в по­след­нем не­ра­вен­ст­ве ра­вен­ст­во име­ет ме­сто лишь при $a = 0$. Ес­ли в ор­то­нор­ми­ро­ван­ном ба­зи­се $i, j, k$ век­то­ры $a$ и и $b$ име­ют со­от­вет­ст­вен­но ко­ор­ди­на­ты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$,  то

$$(a, b) = a_1b_1 + a_2b_2 + a_3b_3,$$ $$|a| = \sqrt {a_1^2 + a_2^2 + a_3^2},$$ $$|b| = \sqrt {b_1^2 + b_2^2 + b_3^2},$$ $$\cos \varphi = \frac {a_1b_1 + a_2b_2 +a_3b_3}{\sqrt {a_1^2 + a_2^2 + a_3^2}\sqrt {b_1^2 + b_2^2 + b_3^2}}$$

Рис. 5.

При оп­ре­де­ле­нии век­тор­но­го про­из­ве­де­ния ис­поль­зу­ет­ся по­ня­тие ле­вой и пра­вой упо­ря­до­чен­ных троек век­то­ров. Упо­ря­до­чен­ная трой­ка век­то­ров $a, b, c$ ($a$ — пер­вый, $b$ — вто­рой, $c$ — тре­тий век­то­ры), при­ве­дён­ных к об­ще­му на­ча­лу и не ле­жа­щих в од­ной плос­ко­сти, на­зы­ва­ет­ся пра­вой (ле­вой), ес­ли они рас­по­ла­га­ют­ся так, как рас­по­ла­га­ют­ся со­от­вет­ст­вен­но боль­шой, ука­за­тель­ный и сред­ний паль­цы пра­вой (ле­вой) ру­ки. На рис. 5 изо­бра­же­ны сле­ва – пра­вая, а спра­ва – ле­вая трой­ки век­то­ров.

Век­тор­ным про­из­ве­де­ни­ем век­то­ров $a$ и $b$ на­зы­ва­ет­ся век­тор, обо­зна­чае­мый $[a ,b]$, та­кой, что дли­на век­то­ра $[a, b]$ рав­на про­из­ве­де­нию длин век­то­ров $a$ и $b$ на си­нус уг­ла $\varphi$ ме­ж­ду ни­ми, и ес­ли $a$ и $b$ не­кол­ли­не­ар­ны, то век­тор $[a, b]$ пер­пен­ди­ку­ля­рен век­то­рам $a$ и $b$ и на­прав­лен так, что трой­ка век­то­ров $a, b, [a, b]$ яв­ля­ет­ся пра­вой. В слу­чае, ес­ли $a$ и $b$ кол­ли­не­ар­ны, то $[a, b] = 0$. Век­тор­ное про­из­ве­де­ние об­ла­да­ет сле­дую­щи­ми свой­ст­ва­ми:

$$[a ,b] = — [b, a], \quad [(\alpha a), b] = \alpha [a, b],$$ $$[c, (a + b)] = [c, a] + [c, b],$$ $$[a, [b, c]] = b(a, c) — c(a, b),$$ $$([a, b], [c, d]) = (a, c)(b, d) — (a, d)(b, c),$$

где $a, b, c, d$ — век­то­ры, $\alpha$ — чис­ло.

Ес­ли в ор­то­нор­ми­ро­ван­ном ба­зи­се $i, j, k$, об­ра­зую­щем пра­вую трой­ку, век­то­ры $a$ и $b$ име­ют со­от­вет­ст­вен­но ко­ор­ди­на­ты $(a_1, a_2, a_3)$ и $(b_1, b_2, b_3)$, то

$$[a,b] = (a_2b_3 — a_3b_2, a_3b_1 — a_1b_3, a_1b_2 — a_2b_1),$$

или

$$[a, b] = \begin {vmatrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$$

По­ня­тие век­тор­но­го про­из­ве­де­ния при­ме­ня­ет­ся в разл. за­да­чах ме­ха­ни­ки и фи­зи­ки. Напр., мо­мент си­лы $F$, при­ло­жен­ной к точ­ке $M$, от­но­си­тель­но точ­ки $O$ ра­вен век­тор­но­му про­из­ве­де­нию $[\overline{OM}, F]$.

Сме­шан­ным про­из­ве­де­ни­ем век­то­ров $a, b$ и $c$ на­зы­ва­ет­ся чис­ло, обо­зна­чае­мое $abc$, рав­ное ска­ляр­но­му про­из­ве­де­нию $([a, b], c)$ век­то­ра $[a, b]$ на век­тор $c$.  Сме­шан­ное про­из­ве­де­ние век­то­ров $a, b$ и $c$, не па­рал­лель­ных од­ной плос­ко­сти, рав­но объ­ё­му па­рал­ле­ле­пи­пе­да, по­стро­ен­но­го на при­ве­дён­ных к об­ще­му на­ча­лу век­то­рах $a, b$ и $c$, взя­то­му со зна­ком плюс, ес­ли трой­ка $a, b, c$ пра­вая, и со зна­ком ми­нус, ес­ли трой­ка ле­вая. Ес­ли век­то­ры $a, b$ и $c$ па­рал­лель­ны од­ной плос­ко­сти, то $abc = 0$. Спра­вед­ли­вы так­же ра­вен­ст­ва $abc = bca = cab$. Ес­ли ко­ор­ди­на­ты век­то­ров $a, b$ и $c$ в ор­то­нор­ми­ро­ван­ном ба­зи­се $i, j, k$, об­ра­зую­щем пра­вую трой­ку, суть $(a_1, a_2, a_3), (b_1, b_2, b_3)$ и $(c_1, c_2, c_3)$, то

$$abc = \begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end {vmatrix}$$

Вектор-функции скалярных аргументов

Рис. 6.

В ме­ха­ни­ке, фи­зи­ке, диф­фе­рен­ци­аль­ной гео­мет­рии ши­ро­ко ис­поль­зу­ет­ся по­ня­тие век­тор-функ­ции од­но­го или не­сколь­ких ска­ляр­ных ар­гу­мен­тов. Ес­ли ка­ж­до­му зна­че­нию пе­ре­мен­ной $t$ из не­ко­то­ро­го мно­же­ст­ва $\{t\}$ ста­вит­ся в со­ответ­ст­вие оп­ре­де­лён­ный век­тор $r$, то го­во­рят, что на мно­же­ст­ве $\{t\}$ за­да­на век­тор-функ­ция (век­тор­ная функ­ция) $r = r(t)$.  Т. к. век­тор $r$ оп­ре­де­ля­ет­ся ко­ор­ди­на­та­ми $(x, y, z)$ в ба­зи­се $i, j, k$, то за­да­ние век­тор-функ­ции $r = r(t)$ эк­ви­ва­лент­но за­да­нию трёх ска­ляр­ных функ­ций $x = x(t), y = y(t), z=z(t)$.

По­ня­тие век­тор-функ­ции ста­но­вит­ся на­гляд­ным, ес­ли об­ра­тить­ся к го­до­гра­фу этой функ­ции, т. е. мно­же­ст­ву кон­цов всех век­то­ров $r(t)$, при­ло­жен­ных к на­ча­лу ко­ор­ди­нат $O$ (рис. 6). Ес­ли при этом рас­смат­ри­вать ар­гу­мент $t$ как вре­мя, то век­тор-функ­ция $r(t)$ пред­став­ляет со­бой за­кон дви­же­ния точ­ки $M$, дви­жу­щей­ся по кри­вой $L$ – го­до­гра­фу функ­ции $r(t)$.

При изу­че­нии век­тор-функ­ций важ­ную роль иг­ра­ет по­ня­тие про­из­вод­ной. Это по­ня­тие вво­дит­ся сле­дую­щим об­ра­зом: ар­гу­мен­ту $t$ да­ёт­ся при­ра­ще­ние $\Delta t \neq 0$ и век­тор $\Delta r = r(t + \Delta t) — r(t)$ (на рис. 6 это век­тор ) ум­но­жа­ет­ся на $1 /{\Delta t}$. Пре­дел вы­ра­же­ния $\Delta r /{\Delta t}$ при $\Delta t \to 0$ на­зы­ва­ет­ся про­из­вод­ной век­тор-функ­ции $r(t)$ и обо­зна­ча­ет­ся $r'(t)$ или $dr/{dt}$. {\prime}].$$

В диф­фе­рен­ци­аль­ной гео­мет­рии век­тор-функ­ции од­но­го ар­гу­мен­та ис­поль­зу­ют­ся для за­да­ния кри­вых. Для за­да­ния по­верх­но­стей поль­зу­ют­ся век­тор-функ­ция­ми двух ар­гу­мен­тов.

Векторный анализ

В ме­ха­ни­ке, фи­зи­ке и гео­мет­рии ши­ро­ко ис­поль­зу­ют­ся по­ня­тия ска­ляр­ных и век­тор­ных по­лей. Темп-ра не­рав­но­мер­но на­гре­той пла­сти­ны и плот­ность не­од­но­род­но­го те­ла пред­став­ля­ют со­бой фи­зич. при­ме­ры со­от­вет­ст­вен­но плос­ко­го и про­стран­ст­вен­но­го ска­ляр­ных по­лей. При­ме­ра­ми век­тор­но­го по­ля яв­ля­ют­ся мно­же­ст­во всех век­то­ров ско­ро­стей час­тиц ус­та­но­вив­ше­го­ся по­то­ка жид­ко­сти, по­ле си­лы тя­же­сти и на­пря­жён­ность элек­трич. по­ля.

Для ма­те­ма­тич. за­да­ния ска­ляр­ных и век­тор­ных по­лей ис­поль­зу­ют­ся со­от­вет­ст­вен­но ска­ляр­ные и век­тор­ные функ­ции. Плот­ность те­ла пред­став­ля­ет со­бой ска­ляр­ную функ­цию точ­ки, а по­ле ско­ро­стей час­тиц ус­та­но­вив­ше­го­ся по­то­ка жид­ко­сти – век­тор­ную функ­цию точ­ки. Для гео­мет­рич. ха­рак­те­ри­сти­ки ска­ляр­но­го по­ля ис­поль­зу­ют­ся по­ня­тия ли­ний и по­верх­но­стей уров­ня. Ли­ни­ей уров­ня плос­ко­го ска­ляр­но­го по­ля на­зы­ва­ет­ся ли­ния, на ко­то­рой функ­ция, за­даю­щая по­ле, име­ет по­сто­ян­ное зна­че­ние. Ана­ло­гич­но оп­ре­де­ля­ет­ся по­верх­ность уров­ня про­стран­ст­вен­но­го ска­ляр­но­го по­ля. При­ме­ра­ми ли­ний уров­ня мо­гут слу­жить изо­тер­мы – ли­нии уров­ня ска­ляр­но­го по­ля тем­пе­ра­тур не­рав­но­мер­но на­гре­той пла­сти­ны.

Пусть $M$ – про­из­воль­ная точ­ка на ли­нии (по­верх­но­сти) уров­ня ска­ляр­но­го по­ля. При дви­же­нии точ­ки $M$ по ли­нии (по­верх­но­сти) уров­ня функ­ция $f$, за­даю­щая по­ле, не ме­ня­ет­ся, а макс. из­ме­не­ние функ­ции $f$ про­ис­хо­дит при сме­ще­нии по нор­ма­ли к этой ли­нии (по­верх­но­сти) в точ­ке $M$. Это из­ме­не­ние ха­рак­те­ри­зу­ет­ся с по­мо­щью т. н. гра­ди­ен­та ска­ляр­но­го по­ля. Гра­ди­ент пред­став­ля­ет со­бой век­тор, на­прав­лен­ный по нор­ма­ли к ли­нии (по­верх­но­сти) уров­ня в точ­ке $M$ в сто­ро­ну воз­рас­та­ния $f$ в этой точ­ке. Ве­ли­чи­на гра­ди­ен­та рав­на про­из­вод­ной функ­ции $f$ в ука­зан­ном на­прав­ле­нии. Гра­ди­ент обо­зна­ча­ет­ся сим­во­лом $grad \:f$. В ба­зи­се $i, j, k$ гра­ди­ент $grad \:f$ име­ет ко­ор­ди­на­ты $(\partial f/{\partial x}, \partial f/{\partial y}, \partial f/{\partial z})$ (для плос­ко­го по­ля $(\partial f/{\partial x}, \partial f/{\partial y})$). Гра­ди­ент ска­ляр­но­го по­ля пред­став­ля­ет со­бой век­тор­ное по­ле.

Рис. 8.

Рис. 7.

Для век­тор­ных по­лей вво­дят­ся по­ня­тия век­тор­ной ли­нии, век­тор­ной труб­ки, цир­ку­ля­ции, ди­вер­ген­ции и вих­ря (ро­то­ра). Пусть в не­ко­то­рой об­лас­ти $\Omega$ за­да­но век­тор­ное по­ле с по­мо­щью век­тор­ной функ­ции $a= a(M)$ пе­ре­мен­ной точ­ки $M$ из $\Omega$. Ли­ния $L$ в об­лас­ти $\Omega$ на­зы­ва­ет­ся век­тор­ной ли­ни­ей, ес­ли век­тор ка­са­тель­ной в ка­ж­дой её точ­ке $M$ на­прав­лен по век­то­ру $a(M)$ (рис. 7). Ес­ли по­ле $a$ – по­ле ско­ро­стей час­тиц ста­цио­нар­но­го по­то­ка жид­ко­сти, то век­тор­ные ли­нии это­го по­ля – тра­ек­то­рии час­тиц жид­ко­сти. Часть про­стран­ст­ва в $\Omega$, со­стоя­щая из век­тор­ных ли­ний, на­зы­ва­ет­ся век­тор­ной труб­кой (рис. 8). В слу­чае век­тор­но­го по­ля ско­ро­стей час­тиц ста­цио­нар­но­го по­то­ка жид­ко­сти век­тор­ная труб­ка есть часть про­стран­ст­ва, ко­то­рую «за­ме­та­ет» при сво­ём пе­ре­ме­ще­нии не­ко­то­рый объ­ём жид­ко­сти.

Пусть $AB$ – не­ко­то­рая глад­кая ли­ния в $\Omega, l$ – дли­на ду­ги, от­счи­ты­вае­мая от точ­ки $A$ до пе­ре­мен­ной точ­ки $M$ этой ли­нии, $t$ – еди­нич­ный век­тор ка­са­тель­ной к $AB$ в $M$. Цир­ку­ля­ци­ей по­ля $a$ вдоль кри­вой $AB$ на­зы­ва­ет­ся ве­ли­чи­на

$$\int _{AB} (a, t) dl.$$

Ес­ли $a$ – си­ло­вое по­ле, то цир­ку­ля­ция $a$ вдоль $AB$ пред­став­ля­ет со­бой ра­бо­ту это­го по­ля вдоль пу­ти $AB$.

Ди­вер­ген­ци­ей век­тор­но­го по­ля $a$, имею­ще­го в ба­зи­се $i, j, k$ ко­ор­ди­на­ты $P, Q, R$, на­зы­ва­ет­ся сум­ма

$$\partial P/{\partial x} + \partial Q/{\partial y} + \partial R/{\partial z},$$

ко­то­рая обо­зна­ча­ет­ся $\mathrm{div}\:a$.  Напр., ди­вер­ген­ция гра­ви­та­ци­он­но­го по­ля, соз­да­вае­мо­го не­ко­то­рым рас­пре­де­ле­ни­ем масс, рав­на объ­ём­ной плот­но­сти $\rho (x, y, z)$ это­го по­ля, ум­но­жен­ной на $4\pi$.

Вихрь (ро­тор) век­тор­но­го по­ля $a$ пред­став­ля­ет со­бой век­тор­ную ха­рак­тери­сти­ку вра­ща­тель­ной со­став­ляю­щей это­го по­ля, вихрь по­ля $a$, обо­зна­чае­мый $\mathrm{rot} \:a$, ра­вен

$$\left ( \frac {\partial R}{\partial y} — \frac {\partial Q}{\partial z}, \frac {\partial P}{\partial z} — \frac {\partial R}{\partial x}, \frac {\partial Q}{\partial x} — \frac {\partial P}{\partial y}  \right).$$

На­хо­ж­де­ние гра­ди­ен­та ска­ляр­но­го по­ля, ди­вер­ген­ции и вих­ря век­тор­но­го по­ля обыч­но на­зы­ва­ют осн. диф­фе­рен­ци­аль­ны­ми опе­ра­ция­ми век­тор­но­го ана­ли­за. Спра­вед­ли­вы сле­дую­щие фор­му­лы, свя­зы­ваю­щие эти опе­ра­ции:

$$\mathrm {grad} (fh) = f\: \mathrm {grad}\:h + h\:\mathrm {grad}\: f, $$ $$ \mathrm {div} (fa) = (a, \mathrm {grad}\: f) + f\: \mathrm {div}\: a,$$ $$\mathrm {rot} (fa) = f\: \mathrm {rot}\: a + [\mathrm {grad}\: f, a],$$ $$\mathrm {div} [a, b] = (b, \mathrm {rot}\: a) — (a, \mathrm {rot}\: b),$$

где $f$ и $h$ – ска­ляр­ные, а $a$ и $b$ – век­тор­ные по­ля. Век­тор­ное по­ле $a$ на­зы­ва­ет­ся по­тен­ци­аль­ным по­лем, ес­ли это по­ле пред­став­ля­ет со­бой гра­ди­ент не­ко­то­ро­го ска­ляр­но­го по­ля $f$. При этом по­ле $f$ на­зы­ва­ет­ся по­тен­циа­лом век­тор­но­го по­ля $a$. Для то­го что­бы по­ле $a$, ко­ор­ди­на­ты ко­то­ро­го $P, Q, R$ име­ют не­пре­рыв­ные ча­ст­ные про­из­вод­ные, бы­ло по­тен­ци­аль­ным, не­об­хо­ди­мо и дос­та­точ­но, что­бы в ка­ж­дой точ­ке об­лас­ти $\Omega$ вихрь это­го по­ля был ра­вен ну­лю. Ес­ли в од­но­связ­ной об­лас­ти $\Omega$ за­да­но по­тен­ци­аль­ное по­ле $a$, то по­тен­ци­ал $f$ это­го по­ля мо­жет быть най­ден по фор­му­ле

$$f(M) = \int_{AM} (a, t) dl,$$

в ко­то­рой $AM$ – лю­бая глад­кая кри­вая, со­еди­няю­щая фик­си­ро­ван­ную точ­ку $A$ из $\Omega$ с точ­кой $M, t$ – еди­нич­ный век­тор ка­са­тель­ной к кри­вой $AM$ и $l$ – дли­на ду­ги $AM$, от­счи­ты­вае­мая от точ­ки $A$.

Век­тор­ное по­ле $a$ на­зы­ва­ет­ся со­ле­нои­даль­ным, или труб­ча­тым, ес­ли это по­ле пред­став­ля­ет со­бой вихрь не­ко­то­ро­го по­ля $b$.  При этом по­ле $b$ на­зы­ва­ет­ся век­тор­ным по­тен­циа­лом по­ля $a$. Для то­го что­бы по­ле $a$ бы­ло со­ле­нои­даль­ным, не­об­хо­ди­мо и дос­та­точ­но, что­бы в ка­ж­дой точ­ке об­лас­ти $\Omega$ ди­вер­ген­ция это­го по­ля бы­ла рав­на ну­лю. Век­тор­ное по­ле $a$, для ко­то­ро­го $\mathrm {div} \:a = 0, \mathrm {rot} \: a = 0$, на­зы­ва­ет­ся гар­мо­ни­че­ским.

В век­тор­ном ана­ли­зе важ­ную роль иг­ра­ют ин­те­граль­ные со­от­но­ше­ния: Ост­ро­град­ско­го фор­му­ла, име­нуе­мая так­же ос­нов­ной фор­му­лой век­тор­но­го ана­ли­за, и Сто­кса фор­му­ла.

Вектор — виды, свойства и операции над отрезками » Kupuk.net

Если величина характеризуется числовым значением и определенным направлением, она называется вектором. Он обозначается двумя большими буквами с верхней чертой (если есть начало и конец), реже — маленьким строчным символом (когда есть только точка старта). Например, AB или a. Параметр нашел широкое применение не только в геометрии, но и прикладных науках.

Основные понятия

Определение вектора подразумевает отрезок, который имеет начало и направление. Координаты — это значения его первой и последней точки:

• X1 Y1.
• X2 Y2.

Формула будет выглядеть следующим образом: V=(X1-X2; Y1-Y2). Есть и нулевой вектор, когда координаты начала и конца совпадают. По факту, это всего лишь точка, и обычно ей не приписывают определенной направленности. В этом ключевое отличие от остальных.

Еще одним основным понятием является длина вектора. Формула по координатам: | V |=| T1-T2|. Рассматривают также проекцию на ось. Это направленная прямая, равная произведению исходного параметра на косинус образовавшегося угла. Также она может быть нулевой, если изначальный отрезок располагается перпендикулярно координатам.

Виды векторов

У отрезков с направлениями существуют определенные модификации, которые и формируют их виды. Векторы могут различаться. Однако если у них единая ориентация, хотя отличные начало и конец, их рассматривают в качестве одной из следующих групп:

• Нулевой. Здесь начальная и конечная точка идентичны, а длина равна нулю.
• Коллинеарные. Они располагаются либо параллельно друг другу, либо на одной прямой.
• Сонаправленные. Это подгруппа коллинеарных векторов, когда ориентация отрезка совпадает.
• Противоположно направленные. В данном случае коллинеарные отрезки будут ориентированы в разные стороны.
• Равные. Должны иметь не только идентичную длину, но и быть направленными в одну сторону.
• Единичные. Векторы с одной длиной, независимо от направления.
• Компланарные. Отрезки лежат в параллельных плоскостях либо в одной из них.

Также различают свободные, скользящие и фиксированные векторы. В первом случае совпадает направление и длина. Во втором — лежат на одной прямой. Иногда отрезки могут полностью или частично накладываться друг на друга. И в третьем наблюдаются полностью идентичные показатели — ориентация, начало, конец.

Операции над отрезками

Любые геометрические свойства векторов можно перенести на систему координат — как двоичную, так и троичную. Впоследствии приобретаются алгебраические характеристики, что упрощает способы вычисления. Можно привести в пример несколько классических операций:

• Модуль. Это то же самое, что и длина.
• Сложение. Высчитывается путем суммирования координатных слагаемых.
• Модуль суммы. Вычисляется посредством теоремы косинусов.
• Вычитание. Высчитывается путем получения разности соответствующих координатных показателей.
• Модуль разности. Здесь также задействуется теорема косинусов, однако перед угловой величиной ставится знак минус.
• Умножение на число. Если показатель имеет положительное значение, то вектор будет сонаправленным, больше в указанное количество раз. Если отрицательное, то противоположно ориентированным.
• Скалярное произведение. Вычисляется через геометрические характеристики. В формуле присутствует значение косинуса — рассматривается угол, который образуется, если отрезки наложить друг на друга, но направление оставить прежним.
• Векторное произведение. Для вычисления задействуется трехмерное пространство. Чтобы получить результат, необходимо чертить перпендикулярно расположенный вектор (относительно двух других).

Сложнее всего выполняются операции по произведению. Здесь задействуются алгебраические и геометрические свойства. Удобнее видеть чертеж, ориентироваться по нему. Когда отрезки наложены друг на друга либо имеется перпендикуляр (в трехмерном пространстве), выводить математические значения намного проще.

Правила сложения

Чтобы геометрически построить сложение векторов, задействуются разные методы. Независимо от способа, результат одинаковый. Поэтому таковой подбирается в зависимости от условий задачи:

• Правило треугольника. Оно следует из переноса отрезков. На плоскости один накладывается на другой, образуя угол. Конечные точки тоже соединяются между собой, чтобы получилась законченная геометрическая фигура. Вектор суммы задается именно этой новой линией.
• Правило многоугольника. Задействуется аналогичным предыдущему образом, когда необходимо получить сумму сразу нескольких отрезков. Также называют правилом ломаной. Векторы переносятся параллельно на плоскости, чтобы соединиться в геометрическую фигуру. Замыкающая грань становится результатом математического действия.
• Правило параллелограмма. В соответствии с ним чертится фигура, гранями которой становятся два отрезка. Диагональ является результатом сложения.

Правилом параллелограмма пользуются, когда векторы расположены в разных плоскостях. Трехмерное пространство усложняет процесс вычисления, но правильный чертеж позволяет вывести точные алгебраические свойства, построить пример. Также рассматриваемый способ задействуется, если необходимо, чтобы все линии выходили из одного угла.

Признаки компланарности

Если векторы располагаются параллельно друг другу либо исходят из одной точки, то они называются компланарными. При этом объединить в группу можно множество отрезков. Также действует правило, что для двух элементов всегда найдется равноудаленная плоскость, что относит их к соответствующей группе. Существует три условия:

• Три вектора будут таковыми, если их общее произведение имеет нулевое значение.
• Когда отрезки линейно зависимы, они тоже являются компланарными.
• N -ое количество компланарное, когда линейно независимы только два из них.

Большинство задач в отношении этого свойства основываются на доказательстве компланарности двух и более отрезков. Когда есть три вектора и один из них нулевой, это уже теорема, от которой отталкиваются иные решения и подтверждения.

Геометрические свойства

Может показаться, что векторы представляют собой обычные отрезки. Однако они помогают выводить подсчеты и алгебраические характеристики в разных прикладных и математических науках. У них следующие геометрические свойства:

• Поскольку отрезки представляют собой прямые, любое правило будет действительным как для плоскостного, так и для пространственного расположения.
• В геометрии широко используется понятие свободного вектора. Это означает, что его начало и/или конец можно будет продлить для упрощения расчетов.
• Нахождение в пространстве — расплывчатое понятие. Учитывая форму отрезка, его рассматривают как в двухмерном, так и в трехмерном виде.
• От движения итоговые значения не зависят. Их можно передвигать в пространстве и на плоскости, образуя иные геометрические фигуры в совокупности линий.
• Для сравнения используют равенства или неравенства. Задействуется ось координат, если необходимо — трехмерная. Когда располагаются совершенно в разных сторонах, имеют отличные начала и концы, все равно могут быть одинаковыми.
• Решения задач выполняются геометрически и алгебраически. Задействовать только один способ не удастся.

Для выполнения тех или иных операций можно воспользоваться онлайн-калькулятором. Удобная форма заполнения позволяет получить результат быстро. Вычислительная техника самостоятельно подбирает удобный способ подсчета, строит геометрический чертеж, выводит алгебраические свойства. Некоторые системы могут выдать не только результат, но и пошаговое решение.

Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность.

Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение

		Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Поделиться:    Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение (произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости. Взаимное расположение векторов. Разложение вектора по координатным векторам. Понятие вектора. Коллинеарные векторы: Действия с векторами. Сложение векторов. Свойства сложения векторов (суммы векторов): Действия с векторами. Вычитание векторов (разность векторов): Действия с векторами. Умножение вектора на число. Свойства умножения вектора на число. Критерий коллинеарности векторов: Действия с векторами. Скалярное умножение векторов (скалярное произведение). Проекция вектора на вектор, разложение вектора по неколлинеарным векторам: Координаты вектора на плоскости — показывают координаты центрального вектора (вектора, с началом в центре координат), равного данному: Действия с векторами в координатах на плоскости. Сложение, вычитание (разность), умножение на число, скалярное умножение (произведение): Взаимное расположение векторов. Угол между векторами, перпендикулярные векторы, параллельные векторы = коллинеарные векторы: Разложение вектора по координатным векторам (ортам): Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Введение в векторы — Math Insight

Определение вектора

Вектор — это объект, который имеет как величину, так и направление. Геометрически мы можем изобразить вектор как направленный отрезок линии, длина которого равна величине вектора и со стрелкой, указывающей направление. Направление вектора от хвоста к голове.

Два вектора одинаковы, если они имеют одинаковую величину и направление. Это означает, что если мы возьмем вектор и переместим его в новое положение (не поворачивая его), то вектор, который мы получим в конце этого процесса, будет тем же вектором, который у нас был в начале.

Два примера векторов представляют силу и скорость. И сила, и скорость имеют определенное направление. Величина вектор будет указывать силу силы или скорость, связанную со скоростью.

Мы обозначаем векторы жирным шрифтом, как в $\vc{a}$ или $\vc{b}$. Особенно при письме от руки, где нельзя легко писать полужирным шрифтом, люди иногда обозначают векторы стрелками, как в $\vec{a}$ или $\vec{b}$ или используют другие обозначения. Здесь нам не нужно будет использовать стрелки. Обозначим величину вектора $\vc{a}$ через $\|\vc{a}\|$. Когда мы хотим сослаться на число и подчеркнуть, что это не вектор, мы можем назвать это число скаляром. Мы будем обозначать скаляры с курсивом, как в $a$ или $b$.

Вы можете изучить понятие величины и направления вектора, используя приведенный ниже апплет. Обратите внимание, что перемещение вектора не меняет вектор, так как положение вектора не влияет на величину или направление. Но если вы растянете или повернете вектор, перемещая только его голову или хвост, величина или направление изменятся. (Этот апплет также показывает координаты вектора, о которых вы можете прочитать на другой странице.)

Величина и направление вектора. Синяя стрелка обозначает вектор $\vc{a}$. Два определяющих свойства вектора, величина и направление, показаны красной полосой и зеленой стрелкой соответственно. Длина красной полосы — это величина $\|\vc{a}\|$ вектора $\vc{a}$. Зеленая стрелка всегда имеет длину единицу, но ее направление совпадает с направлением вектора $\vc{a}$. Единственным исключением является случай, когда $\vc{a}$ является нулевым вектором (единственным вектором с нулевой величиной), для которого направление не определено. Вы можете изменить любой конец $\vc{a}$, перетащив его мышью. Вы также можете переместить $\vc{a}$, перетащив середину вектора; однако изменение положения $\vc{a}$ таким образом не меняет вектор, так как его величина и направление остаются неизменными.

Дополнительная информация об апплете.

Существует одно важное исключение для векторов, имеющих направление. ноль вектор, обозначенный полужирным шрифтом $\vc{0}$, является вектором нулевой длины. Поскольку у него нет длины, он не указывает ни в каком конкретном направлении. Существует только один вектор нулевой длины, поэтому мы можем говорить о нулевом векторе .

Операции над векторами

Ряд операций над векторами можно определить геометрически без ссылка на любую систему координат. Здесь мы определяем сложение, вычитание и умножение скаляром. На отдельных страницах мы обсуждаем два разных способа умножения двух векторов: скалярное произведение и перекрестное произведение.

Сложение векторов

По двум векторам $\vc{a}$ и $\vc{b}$ образуем их сумму $\vc{a}+\vc{b}$ следующим образом. Сдвигаем вектор $\vc{b}$ до тех пор, пока его хвост не совпадет с головой вектора $\vc{a}$. (Напомним, что такой перевод не меняет вектор.) Тогда направленный отрезок из хвоста $\vc{a}$ в начало $\vc{b}$ представляет собой вектор $\vc{a}+\vc{b}$. 2}=20\sqrt{2}$ миль в час относительно земли.

Добавление векторов удовлетворяет двум важным свойствам.

1. Коммутативный закон, который гласит, что порядок сложения не имеет значения: $$\vc{a}+\vc{b}=\vc{b}+\vc{a}.$$ Этот закон также называется законом параллелограмма, как показано на рисунке ниже. изображение. Два ребра параллелограмма определяют $\vc{a}+\vc{b}$, а другая пара ребер определяет $\vc{b}+\vc{a}$. Но обе суммы равны равна той же диагонали параллелограмма.

2. Ассоциативный закон, утверждающий, что сумма трех векторов не зависит от того, какая пара векторов добавляется первой: $$(\vc{a}+\vc{b})+\vc{c} = \vc{a} + (\vc{b}+\vc{c}).$$

Вы можете изучить свойства сложения векторов с помощью следующего апплета. (Этот апплет также показывает координаты векторов, о которых вы можете прочитать на другой странице.)

Сумма двух векторов. Сумма $\vc{a}+\vc{b}$ вектора $\vc{a}$ (синяя стрелка) и вектора $\vc{b}$ (красная стрелка) показана зеленой стрелкой . Поскольку векторы не зависят от их начального положения, обе синие стрелки представляют один и тот же вектор $\vc{a}$, а обе красные стрелки представляют один и тот же вектор $\vc{b}$. Сумму $\vc{a}+\vc{b}$ можно составить, поместив хвост вектора $\vc{b}$ в начало вектора $\vc{a}$. То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.

Дополнительная информация об апплете.

Вычитание вектора

Перед определением вычитания мы определяем вектор $-\vc{a}$, который является противоположностью $\vc{a}$. Вектор $-\vc{a}$ — это вектор с той же величиной, что и $\vc{a}$, но направленной в противоположном направлении.

Мы определяем вычитание как сложение с противоположным вектором: $$\vc{b}-\vc{a} = \vc{b} + (-\vc{a}). $$ Это эквивалентно переворачиванию вектора $\vc{a}$ при применении вышеуказанные правила добавления. Вы видите, как вектор $\vc{x}$ в ниже рисунок равен $\vc{b}-\vc{a}$? Обратите внимание, как это то же самое как утверждается, что $\vc{a}+\vc{x}=\vc{b}$, как и при вычитании скалярные числа.

Скалярное умножение

Имея вектор $\vc{a}$ и действительное число (скаляр) $\lambda$, мы можем сформировать вектор $\lambda\vc{a}$ следующим образом. Если $\lambda$ положительна, то $\lambda\vc{a}$ — это вектор, направление которого совпадает с направлением $\vc{a}$, а длина равна $\lambda$, умноженной на длину $ \vc{а}$. В этом случае умножение на $\lambda$ просто растягивает (если $\lambda>1$) или сжимает (если $0

Если, с другой стороны, $\lambda$ отрицательно, то мы должны взять напротив $\vc{a}$ перед его растяжением или сжатием. Другими словами, вектор $\lambda\vc{a}$ указывает направление, противоположное вектору $\vc{a}$, а длина $\lambda\vc{a}$ равна $|\lambda|$, умноженной на длину $\vc{a}$. Независимо от знака $\lambda$, мы наблюдаем, что величина $\lambda\vc{a}$ в $|\lambda|$ умножается на величину $\vc{a}$: $\| \лямбда \vc{а}\| = |\лямбда| \|\vc{a}\|$.

Скалярные умножения удовлетворяют многим из тех же свойств, что и обычное умножение.

1. $s(\vc{a}+\vc{b}) = s\vc{a} + s\vc{b}$ (распределительный закон, форма 1)
2. $(s+t)\vc{a} = s\vc{a}+t\vc{a}$ (распределительный закон, форма 2)
3. $1\vc{a} = \vc{a}$
4. $(-1)\vc{a} = -\vc{a}$
5. $0\vc{a} = \vc{0}$

В последней формуле ноль слева — это число 0, а ноль справа — это вектор $\vc{0}$, уникальный вектор, длина которого равна нулю.

Если $\vc{a} = \lambda\vc{b}$ для некоторого скаляра $\lambda$, то мы говорим что векторы $\vc{a}$ и $\vc{b}$ параллельны. Если $\lambda$ отрицательно, некоторые люди говорят, что $\vc{a}$ и $\vc{b}$ антипараллельны, но мы не использовать этот язык.

Мы смогли описать векторы, сложение векторов, вычитание векторов и скалярное умножение без привязки к какой-либо системе координат. Преимущество такого чисто геометрического рассуждения состоит в том, что наши результаты справедливы в целом, независимо от какой-либо системы координат, в которой живут векторы. Однако иногда полезно выражать векторы через координаты, как обсуждалось на странице о векторах в стандартных декартовых системах координат на плоскости и в трехмерном пространстве.

Компонент вектора

Вектор — это величина, которая имеет как величину, так и направление. Перемещение, скорость, ускорение и сила — это векторные величины, которые мы уже обсуждали в учебнике по физике. В первых двух модулях все векторы, которые мы обсуждали, были просто направлены вверх, вниз, влево или вправо. Когда существовала диаграмма свободного тела, изображающая силы, действующие на объект, каждая отдельная сила была направлена ​​в одном измерении — либо вверх, либо вниз, либо влево, либо вправо. Когда объект имел ускорение и мы описали его направление, оно было направлено на одно измерение — вверх или вниз или влево или вправо. Теперь в этом блоке мы начинаем видеть примеры векторов, которые направлены в двух измерениях — вверх и вправо, на север и запад, на восток и юг и т.д.

Что такое компонент?

В ситуациях, когда векторы направлены под углом к ​​обычным осям координат, будет использован полезный математический прием, чтобы преобразуем вектор в две части, каждая из которых направлена ​​по осям координат. Например, вектор, направленный на северо-запад, можно рассматривать как состоящий из двух частей — северной части и западной части. Вектор, направленный вверх и вправо, можно представить как состоящий из двух частей — восходящей части и правой части.

Любой вектор, направленный в двух измерениях, можно рассматривать как имеющий влияние в двух разных направлениях. То есть его можно представить состоящим из двух частей. Каждая часть двумерного вектора известна как компонент . Компоненты вектора отображают влияние этого вектора в заданном направлении. Совместное влияние двух компонентов эквивалентно влиянию одного двумерного вектора. Один двумерный вектор можно заменить двумя компонентами.

 

Угловой Векторы имеют две составляющие

Если собачья цепь Фидо растянута вверх и вправо и туго натянута его хозяином, то сила натяжения в цепи имеет две составляющие — направленную вверх и правую составляющую. Для Фидо влияние цепи на его тело равносильно влиянию на его тело двух цепей — одной, тянущей вверх, и другой, тянущейся вправо. Если бы одна цепь была заменена двумя цепями. с каждой цепью, имеющей величину и направление компонентов, тогда Фидо не будет знать разницы. Это не потому, что Фидо тупой (беглый взгляд на его фото показывает, что он точно не тот), а потому, что совокупное влияние двух составляющих эквивалентно влиянию одного двумерного вектора.

 

 

  Рассмотрим картину, подвешенную к стене с помощью двух проволок, натянутых вертикально и горизонтально. Каждый провод оказывает на изображение силу натяжения, чтобы выдержать его вес. Поскольку каждый провод растягивается в двух измерениях (как по вертикали, так и по горизонтали), сила натяжения каждого провода имеет две составляющие — вертикальную составляющую и горизонтальную составляющую. Сосредоточившись на проводе слева, мы могли бы сказать, что провод имеет левую и восходящую составляющие. Это означает, что провод слева можно заменить двумя проводами, один из которых тянется влево, а другой — вверх. Если заменить один провод двумя проводами (каждый из которых имеет величину и направление компонентов), то это не повлияет на стабильность изображения. Совместное влияние двух компонентов эквивалентно влиянию одного двумерного вектора.

 

 

 

Рассмотрим самолет, который летит из международного аэропорта О’Хара в Чикаго в пункт назначения в Канаде. Предположим, что самолет летит так, что вектор его результирующего смещения направлен на северо-запад. Если это так, то смещение плоскости имеет две составляющие — составляющую в северном направлении и составляющую в западном направлении. Это означает, что у самолета было бы такое же водоизмещение, если бы он летел в Канаду двумя сегментами — один был направлен строго на север, а другой — строго на запад. Если бы единственный вектор смещения был заменен этими двумя отдельными векторами смещения, то пассажиры в самолете оказались бы в одном и том же конечном положении. Совместное влияние двух компонентов эквивалентно влиянию одиночного двумерного смещения.

 

Любой вектор, направленный в двух измерениях, можно рассматривать как имеющий две разные компоненты. Компонент одного вектора описывает влияние этого вектора в заданном направлении. В следующей части этого урока мы исследуем два метода определения величины компонентов. То есть мы будем исследовать , какое влияние оказывает вектор в заданном направлении.

Следующий раздел:

Перейти к следующему уроку:

Что такое вектор? — PMC

1. Гусман М.Г., Харрис Э. 2015. Денге. Ланцет 385, 453–465. ( 10.1016/S0140-6736(14)60572-9) [PubMed] [CrossRef] [Google Scholar]

2. Гублер Д.Дж. 2007. Продолжающееся распространение вируса западного нила в западном полушарии. клин. Заразить. Дис. 45, 1039–1046. ( 10.1086/521911) [PubMed] [CrossRef] [Google Scholar]

3. Sambri V, et al. 2013. Вирус Западного Нила в Европе: возникновение, эпидемиология, диагностика, лечение и профилактика. клин. микробиол. Заразить. 19, 699–704. (10.1111/1469-0691.12211) [PubMed] [CrossRef] [Google Scholar]

4. Maltezou HC, et al. 2010. Конго-крымская геморрагическая лихорадка в Европе: текущая ситуация требует готовности. евронаблюдение 15, 48–51. [PubMed] [Google Scholar]

5. Реускен С., Хейман П. 2013. Факторы, способствующие появлению хантавируса в Европе. Курс. мнение Вирол. 3, 92–99. ( 10.1016/j.coviro.2013.01.002) [PubMed] [CrossRef] [Google Scholar]

6. Wilson AJ, Mellor PS. 2009. Синий язык в Европе: прошлое, настоящее и будущее. Фил. Транс. Р. Соц. Б 364, 2669–2681. ( 10.1098/rstb.2009.0091) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

7. Gatherer D, Kohl A. 2016. Вирус Зика: ранее медленная пандемия быстро распространяется по Америке. Дж. Генерал Вирол. 97, 269–273. ( 10.1099/jgv.0.000381) [PubMed] [CrossRef] [Google Scholar]

8. Rizzoli A, Hauffe HC, Carpi G, Vourc’h GI, Neteler M, Rosa R. 2011. Боррелиоз Лайма в Европе. евронаблюдение 16, 2–9. [Google Scholar]

9. Weaver SC, Lecuit M. 2015. Вирус чикунгунья и глобальное распространение болезни, переносимой комарами. Н. англ. Дж. Мед. 372, 1231–1239 гг.. ( 10.1056/NEJMra1406035) [PubMed] [CrossRef] [Google Scholar]

10. Европейский центр профилактики и контроля заболеваний. 2014. Ежегодный эпидемиологический отчет за 2014 г. — новые и трансмиссивные болезни. Стокгольм, Швеция: ECDC. [Google Scholar]

11. Хотез П.Дж. 2016. Грядущие бедствия Южной Европы: трансмиссивные забытые тропические болезни. PLoS Негл. Троп. Дис. 10, e0004243 ( 10.1371/journal.pntd.0004243) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

12. 2009. Ищу руководство по ТБ. Вет. Рек. 164, 477 (10.1136/vr.164.16.477) [CrossRef] [Google Scholar]

13. Леонард Д. 2014. Контроль туберкулёза крупного рогатого скота. Вет. Рек. 174, 535–536. ( 10.1136/vr.g3414) [PubMed] [CrossRef] [Google Scholar]

14. Roberts T, O’Connor C, Nuñez-Garcia J, de la Rua-Domenech R, Smith NH. 2014. Необычный кластер инфекции Mycobacterium bovis у кошек. Вет. Рек. 174, 326 ( 10.1136/vr.102457) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

15. Центры по контролю и профилактике заболеваний. 2016. Бешенство: домашние животные. Атланта, Джорджия: Центры по контролю и профилактике заболеваний (CDC). [Google Scholar]

16. Pinaud S, et al. 2016. Переход от клеточных к гуморальным реакциям способствует врожденной иммунной памяти у улитки-переносчика Biomphalaria glabrata . PLoS Патог. 12, e1005361 ( 10.1371/journal.ppat.1005361) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

17. Barbosa FS, Olivier L. 1958. Исследования улиток-переносчиков бильгарциоза мансони в северо-восточной Бразилии. Бык. Всемирный орган здравоохранения. 18, 895–908. [Бесплатная статья PMC] [PubMed] [Google Scholar]

18. 2015. Трансмиссивные болезни в Канаде. Можно. коммун. Дис. Респ. 41, 117–154. См. http://www.phac-aspc.gc.ca/publicat/ccdr-rmtc/15vol41/dr-rm41-06/assets/pdf/15vol41_06-eng.pdf. [Бесплатная статья PMC] [PubMed] [Google Scholar]

19. Kuno G, Chang G-JJ. 2005. Биологическая передача арбовирусов: пересмотр и новое понимание компонентов, механизмов и уникальных признаков, а также тенденций их эволюции. клин. микробиол. преп. 18, 608–637. ( 10.1128/cmr.18.4.608-637.2005) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

20. Гибсон Д.Р., Флинн Н.М., Пералес Д. 2001. Эффективность программ обмена шприцев в снижении поведения, связанного с риском заражения ВИЧ, и сероконверсии ВИЧ среди потребителей инъекционных наркотиков. СПИД 15, 1329–1341. ( 10.1097/00002030-200107270-00002) [PubMed] [CrossRef] [Google Scholar]

21. Ангелакис Э., Ажар Э.И., Биби Ф., Ясир М., Аль-Гамди А.К., Ашши А.М., Эльшеми А.Г., Рауль Д. 2014. Бумажные деньги и монеты как потенциальные переносчики инфекционных заболеваний. Фут. микробиол. 9, 249–261. ( 10.2217/fmb.13.161) [PubMed] [CrossRef] [Google Scholar]

22. Всемирная организация здравоохранения. 2016. Трансмиссивные болезни. В информационных бюллетенях ВОЗ. Женева, Швейцария: ВОЗ; См. http://www.who.int/mediacentre/factsheets/fs387/en/. [Google Scholar]

23. Центры по контролю и профилактике заболеваний. 2016. Словарь терминов. Атланта, Джорджия, США: CDC. [Google Scholar]

24. Лафферти К.Д., Курис А.М. 2002. Трофические стратегии, разнообразие животных и размер тела. Тенденции Экол. Эвол. 17, 507–513. ( 10.1016/s0169-5347(02)02615-0) [CrossRef] [Google Scholar]

25. Semenza JC, Menne B. 2009. Изменение климата и инфекционные заболевания в Европе. Ланцет Инфекция. Дис. 9, 365–375. ( 10.1016/S1473-3099(09)70104-5) [PubMed] [CrossRef] [Google Scholar]

26. Европейский центр профилактики и контроля заболеваний. 2016. Трансмиссивные болезни. В темах Здоровье. Сольна, Швеция: Европейский центр профилактики и контроля заболеваний; См. http://ecdc.europa.eu/en/healthtopics/climate_change/health_effects/Pages/vector_borne_diseases.aspx. [Академия Google]

27. Межправительственная группа экспертов по изменению климата. 2007. Изменение климата 2007: воздействия, адаптация и уязвимость. Вклад Рабочей группы II в Четвертый оценочный отчет Межправительственной группы экспертов по изменению климата (редакторы М.Л. Парри, О.Ф. Канзиани, Дж.П. Палутикоф, П.Дж. ван дер Линден, К.Э. Хэнсон). Кембридж, Великобритания: Издательство Кембриджского университета. См. http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_wg2_report_impacts_adaptation_and_vulnerability.htm.

28. Молинье Д.Х. 2003. Общие темы в меняющихся сценариях трансмиссивных болезней. Транс. R Соц. Троп. Мед. Гиг. 97, 129–132. ( 10.1016/S0035-9203(03)-6) [PubMed] [CrossRef] [Google Scholar]

29. Гублер Д.Дж. 1998. Возрождение трансмиссивных болезней как глобальная проблема здравоохранения. Эмердж. Заразить. Дис Дж. 4, 442 (10.3201/eid0403.980326) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

30. Центры по контролю и профилактике заболеваний. 2016. Отдел трансмиссивных болезней (DVBD). Атланта, Джорджия, США: CDC. [Академия Google]

31. Hu C, et al. 2008. Инфекции иммуногенными трипаносомами снижают репродуктивную способность цеце: потенциальное влияние различных штаммов паразитов на структуру популяции переносчиков. PLoS Негл. Троп. Дис. 2, e192 (10.1371/journal.pntd.0000192) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

32. Cator LJ, George J, Blanford S, Murdock CC, Baker TC, Read AF, Thomas МБ. 2013. «Манипуляция» без паразита: измененное пищевое поведение комаров не зависит от заражения малярийными паразитами. проц. Р. Соц. Б 280, 20130711 ( 10.1098/rspb.2013.0711) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

33. Cator LJ, Pietri JE, Murdock CC, Ohm JR, Lewis EE, Read AF, Luckhart S, Thomas MB. 2015. Иммунный ответ и передача сигналов инсулина изменяют пищевое поведение комаров, повышая потенциал передачи малярии. науч. Респ. 5 (10.1038/srep11947) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

34. Sanders CJ, Selby R, Carpenter S, Reynolds DR. 2011. Высотный полет Culicoides мокрецы. Вет. Рек. 169, 208 (10.1136/vr.d4245) [PubMed] [CrossRef] [Google Scholar]

35. Randolph SE. 1998. Клещи не насекомые: последствия противопоставления биологии переносчиков для потенциала передачи. Паразитол. Сегодня 14, 186–192. ( 10.1016/S0169-4758(98)01224-1) [PubMed] [CrossRef] [Google Scholar]

36. Diekmann O, Heesterbeek JAP, Roberts MG. 2010. Построение матриц нового поколения для сегментарных моделей эпидемий. Дж. Р. Соц. Интерфейс 7, 873–885. ( 10.1098/rsif.2009.0386) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

37. Hartemink NA, Randolph SE, Davis SA, Heesterbeek JAP. 2008. Базовый репродуктивный номер для сложных систем заболеваний: определение R ₀ для клещевых инфекций. Являюсь. Нац. 171, 743–754. ( 10.1086/587530) [PubMed] [CrossRef] [Google Scholar]

38. Добсон А., Фуфопулос Дж. 2001. Новые инфекционные патогены диких животных. Фил. Транс. Р. Соц. Лонд. Б 356, 1001–1012. ( 10.1098/rstb.2001.0900) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

39. Добсон А. 2004. Динамика популяций возбудителей с несколькими видами хозяев. Являюсь. Нац. 164, С64–С78. ( 10.1086/424681) [PubMed] [CrossRef] [Google Scholar]

40. Fenton A, Streicker DG, Petchey OL, Pedersen AB. 2015. Все хосты созданы равными? Разделение вклада видов-хозяев в устойчивость паразитов в сообществах с несколькими хозяевами. Являюсь. Нац. 186, 610–622. ( 10.1086/683173) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

41. Гандон С. 2004. Эволюция многохозяинных паразитов. Эволюция 58, 455–469. ( 10.1111/j.0014-3820.2004.tb01669.x) [PubMed] [CrossRef] [Google Scholar]

42. Холт Р.Д., Добсон А.П., Бегон М., Бауэрс Р.Г., Шаубер Э.М. 2003. Расселение паразитов в принимающих сообществах. Экол. лат. 6, 837–842. ( 10.1046/j.1461-0248.2003.00501.x) [CrossRef] [Google Scholar]

43. Андерсон Р.М., Мэй Р.М. 1991. Инфекционные болезни человека: динамика и борьба. Оксфорд, Великобритания: Издательство Оксфордского университета. [Академия Google]

44. Ализон С., ван Баален М. 2008. Компромисс между передачей и вирулентностью при трансмиссивных болезнях. Теор. Народ. биол. 74, 6–15. (10.1016/j.tpb.2008.04.003) [PubMed] [CrossRef] [Google Scholar]

45. Андерсон Р.М., Мэй Р.М. 1978 год. Регуляция и стабильность популяционных взаимодействий хозяина и паразита: I. Регуляторные процессы. Дж. Аним. Экол. 47, 219–247. ( 10.2307/3933) [CrossRef] [Google Scholar]

46. Макдональд Г. 1957. Эпидемиология и борьба с малярией. Лондон, Великобритания: Издательство Оксфордского университета. [Академия Google]

47. Шаубер Э.М., Остфельд Р.С. 2002. Моделирование последствий снижения компетентности резервуара и демографического оборота в экологии болезни Лайма. Экол. заявл. 12, 1142–1162. ( 10.2307/3061042) [CrossRef] [Google Scholar]

48. Шмидт К.А., Остфельд Р.С. 2001. Биоразнообразие и эффект разбавления в экологии болезней. Экология 82, 609–619. ( 10.2307/2680183) [CrossRef] [Google Scholar]

49. Dubey JP. 2008. История Toxoplasma gondii — первые 100 лет. Дж. Юкар. микробиол. 55, 467–475. ( 10.1111/j.1550-7408.2008.00345.x) [PubMed] [CrossRef] [Google Scholar]

50. Бегон М., Беннетт М., Бауэрс Р.Г., Френч Н.П., Хейзел С.М., Тернер Дж. 2002. Уточнение условий передачи в моделях хозяин-микропаразит: количество, плотность и площадь. Эпидемиол. Заразить. 129, 147–153. ( 10.1017/s0950268802007148) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

51. Fenton A, Fairbairn JP, Norman R, Hudson PJ. 2002. Паразитарная передача: примирение теории и реальности. Дж. Аним. Экол. 71, 893–905. ( 10.1046/j.1365-2656.2002.00656.x) [CrossRef] [Google Scholar]

52. Маккаллум Х., Барлоу Н., Хоун Дж. 2001. Как следует моделировать передачу патогена? Тенденции Экол. Эвол. 16, 295–300. ( 10.1016/S0169-5347(01)02144-9) [PubMed] [CrossRef] [Google Scholar]

53. Вайшер Б., Браун Д. 2000. Введение в нематоды: общая нематология. София, Болгария: Издательство Pensoft. [Google Scholar]

54. Перкинс С.Е., Фентон А. 2006. Гельминты как переносчики возбудителей у позвоночных хозяев: теоретический подход. Междунар. Дж. Паразитол. 36, 887–894. (10.1016/j.ijpara.2006.04.001) [PubMed] [CrossRef] [Google Scholar]

55. Lund EE, Burtner RH. 1957. Инфекционность яиц Heterakis gallinae с яиц Histomonas meleagridis . Эксп. Паразитол. 6, 189–193. ( 10.1016/0014-4894(57)

-0) [PubMed] [CrossRef] [Google Scholar]

56. Лунд Э.Э., Вер Э.Э., Эллис Д.Дж. 1966 год. Передача дождевыми червями Heterakis и Histomonas индейкам и курам. Дж. Паразитол. 52, 899–902. ( 10.2307/3276528) [PubMed] [CrossRef] [Google Scholar]

57. André AvS, et al. 2002. Роль эндосимбиотических бактерий Wolbachia в патогенезе речной слепоты. Наука 295, 1892–1895 гг. ( 10.1126/science.1068732) [PubMed] [CrossRef] [Google Scholar]

58. Aitken MM, Jones PW, Hall GA, Hughes DL, Brown GTH. 1981. Реакции крупного рогатого скота, инфицированного и свободного от трематод, на экспериментальное повторное заражение Salmonella dublin . Рез. Вет. науч. 31, 120–126. [PubMed] [Google Scholar]

59. Brady MT, O’Neill SM, Dalton JP, Mills KHG. 1999. Фасциола hepatica подавляет защитный Th2-ответ против Bordetella pertussis . Заразить. Иммун. 67, 5372–5378. [Бесплатная статья PMC] [PubMed] [Google Scholar]

60. Randolph SE, Miklisová D, Lysy J, Rogers DJ, Labuda M. 1999. Заболеваемость по совпадению: модели заражения клещами грызунов способствуют передаче вируса клещевого энцефалита. Паразитология 118, 177–186. ( 10.1017/s0031182098003643) [PubMed] [CrossRef] [Google Scholar]

61. Лашарм-Лора Л., Солсбери В., Хамфри Т.Дж., Стаффорд К., Перкинс С.Е. 2009. Бактерии, выделенные из паразитических нематод, — потенциальный новый переносчик патогенов? Окружающая среда. Здоровье 8, S17 (10.1186/1476-069x-8-s1-s17) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

62. Lacharme-Lora L, Perkins SE, Humphrey TJ, Hudson PJ, Salisbury В. 2009. Использование биолюминесцентных бактериальных биосенсоров для изучения роли свободноживущих гельминтов как резервуаров и переносчиков Salmonella . Окружающая среда. микробиол. 1, 198–207. ( 10.1111/j.1758-2229.2009.00031.x) [PubMed] [CrossRef] [Google Scholar]

63. Kaplan EH, Khoshnood K, Heimer R. 1994. Сокращение количества игл, инфицированных ВИЧ, возвращено в программу обмена игл в Нью-Хейвене: смена клиентов или обмен игл? Являюсь. Дж. Общественное здравоохранение 84, 1991–1994. (10.2105/ajph.84.12.1991) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

64. Anderson RM, May RM. 1982. Коэволюция хозяев и паразитов. Паразитология 85, 411–426. ( 10.1017/S0031182000055360) [PubMed] [CrossRef] [Google Scholar]

65. Франк С.А. 1996. Модели вирулентности паразитов. Q. Преподобный Биол. 71, 37–78. ( 10.1086/419267) [PubMed] [CrossRef] [Google Scholar]

66. Choisy M, Brown SP, Lafferty KD, Thomas F. 2003. Эволюция трофической передачи у паразитов: зачем добавлять промежуточных хозяев? Являюсь. Нац. 162, 172–181. ( 10.1086/375681) [PubMed] [CrossRef] [Google Scholar]

67. Пулин Р. 1994. Эволюция паразитарных манипуляций поведением хозяина — теоретический анализ. Паразитология 109, С109–С118. ( 10.1017/S0031182000085127) [PubMed] [CrossRef] [Google Scholar]

68. Mideo N, Alizon S, Day T. 2008. Связь динамики внутри и между хозяевами в эволюционной эпидемиологии инфекционных заболеваний. Тенденции Экол. Эвол. 23, 511–517. ( 10.1016/j.tree.2008.05.009) [PubMed] [CrossRef] [Google Scholar]

69. Mideo N, Day T. 2008. Об эволюции репродуктивной сдержанности при малярии. проц. Р. Соц. Б 275, 1217–1224. ( 10.1098/rspb.2007.1545) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

70. McKenzie FE, Bossert WH. 1998. Оптимальная продукция гаметоцитов Plasmodium falciparum . Дж. Теор. биол. 193, 419–428. ( 10.1006/jtbi.1998.0710) [PubMed] [CrossRef] [Google Scholar]

71. Koella JC, Antia R. 1995. Оптимальная схема репликации и передачи паразитов с двумя стадиями жизненного цикла. Теор. Народ. биол. 47, 277–291. ( 10.1006/tpbi.1995.1012) [CrossRef] [Google Scholar]

72. Bell AS, Huijben S, Paaijmans KP, Sim DG, Chan BHK, Nelson WA, Read AF, Borrmann S. 2012. Повышенная передача лекарственно-устойчивых паразитов комарам после медикаментозного лечения малярии грызунов. ПЛОС ОДИН 7, e37172 ( 10.1371/journal.pone.0037172) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

73. Huijben S, Nelson WA, Wargo AR, Sim DG, Drew DR, Read AF. 2010. Химиотерапия, экология внутри хозяина и приспособленность лекарственно-устойчивых малярийных паразитов. Эволюция 64, 2952–2968. ( 10.1111/j.1558-5646.2010.01068.x) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

74. Paul REL, Bonnet S, Boudin C, Tchuinkam T, Robert V. 2007. Агрегация малярийных паразитов ограничивает уровень заражения комарами. Заразить. Жене. Эвол. 7, 577–586. ( 10.1016/j.meegid.2007.04.004) [PubMed] [CrossRef] [Google Scholar]

75. Грейшар М., Мидео Н., Рид А., Бьорнстад О. 2016. Прогнозирование оптимальных инвестиций в передачу малярийных паразитов. Эволюция 70, 1542–1558. ( 10.1111/evo.12969) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

76. Pollitt LC, Churcher TS, Dawes EJ, Khan SM, Sajid M, Basanez MG, Colegrave N, Reece SE. 2013. Затраты на скученность при передаче малярийных паразитов. Эвол. заявл. 6, 617–629. ( 10.1111/eva.12048) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

77. Ари Ф. и др. 2014. Молекулярный маркер резистентной к артемизинину малярии Plasmodium falciparum . Природа 505, 50–55. ( 10.1038/nature12876) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

78. Straimer J, et al. 2015. Мутации K13-пропеллера придают устойчивость к артемизинину у клинических изолятов Plasmodium falciparum . Наука 347, 428–431. ( 10.1126/science.1260867) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

79. Миотто О и др. 2015. Генетическая архитектура резистентного к артемизинину Plasmodium falciparum . Нац. Жене. 47, 226–234. (10.1038/ng.3189) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

80. Molina-Cruz A, et al. 2013. Ген малярийного паразита человека Pfs47 опосредует уклонение от иммунной системы комаров. Наука 340, 984–987. ( 10.1126/science.1235264) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

81. Mideo N, et al. 2016. Инструмент глубокого секвенирования для разделения показателей элиминации после противомалярийного лечения при поликлональных инфекциях. Эвол. Мед. Здравоохранение 2016, 21–36. ( 10.1093/emph/eov036) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

82. St Laurent B, et al. 2015. Клинические изоляты Plasmodium falciparum , устойчивые к артемизинину, могут инфицировать различных комаров-переносчиков в Юго-Восточной Азии и Африке. Нац. коммун. 6, 8614 (10.1038/ncomms9614) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

83. Mellor PS, Boorman J. 1980. Размножение вируса блютанга у Culicoides nubeculosus (meigen), одновременно инфицированных вирусом и микрофиляриями Onchocercacercais (Райе и Генри). Анна. Троп. Мед. Паразитол. 74, 463–469. ( 10.1080/00034983.1980.11687368) [PubMed] [CrossRef] [Google Scholar]

84. Turell M, Rossignol P, Spielman A, Rossi C, Bailey CL. 1984. Усиленная передача арбовирусов комарами, которые одновременно проглатывают микрофилярии. Наука 225, 1039–1041. ( 10.1126/science.6474165) [PubMed] [CrossRef] [Google Scholar]

85. Shaw AE, et al. 2012. Дрозофила меланогастр в качестве модельного организма для репликации и тропизма вируса блутанга. Дж. Вирол. 86, 9015–9024. ( 10.1128/jvi.00131-12) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

86. Antonovics J, Wilson AJ, Forbes MR, Hauffe HC, Kallio ER, Leggett HC, Longdon B, Okamura Б., Саит С.М., Вебстер Дж.П. 2017. Эволюция режима передачи. Фил. Транс. Р. Соц. Б 372, 20160083 ( 10.1098/rstb.2016.0083) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

87. Barnett HC. 1962. Инкриминация членистоногих как переносчиков болезней. В проц. XI межд. Конгресс энтомологов стр. 341–345. Вена.

88. Ламбрехтс Л., Скотт Т.В. 2009. Способ передачи и эволюция вирулентности арбовирусов у комаров-переносчиков. проц. Р. Соц. Б 276, 1369–1378. ( 10.1098/rspb.2008.1709) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

89. Box GEP. 1979. Надежность в стратегии построения научной модели. В книге «Надежность в статистике» (редакторы Лаунер Р.Л., Уилкинсон Г.Н.), стр. 201–236. Лондон, Великобритания: Академическая пресса. [Академия Google]

ЧТО ТАКОЕ ВЕКТОР? – Sacramento-Yolo Mosquito & Борьба с переносчиками

Многие люди могут не знать, что такое «Борьба с переносчиками» и почему это важно. Переносчик – это насекомое или животное, передающее заболевание другим животным или человеку. По сути, переносчик — это переносчик болезни. Примеры распространенных переносчиков включают комаров, клещей, клещей и блох.

Частью нашей работы является наблюдение, мониторинг и контроль над переносчиками таких заболеваний, как вирус Западного Нила и болезнь Лайма. Кроме того, мы работаем с другими государственными агентствами и учреждениями, чтобы информировать общественность о переносчиках, болезнях, которые они переносят, и о методах профилактики.

Adulticides – Средства, используемые для сокращения популяций взрослых комаров, они могут содержать один или несколько активных ингредиентов и наносятся с помощью ручных опрыскивателей, опрыскивателей, установленных на грузовиках, или самолетов. Для немедленного уменьшения количества взрослых комаров в районе можно использовать антиадалциды.
Биологическая борьба – Альтернативный метод борьбы с вредителями, в котором используются естественные враги вредителей, включая хищников, паразитов и болезнетворные организмы.
BTI ( Bacillus thuringiensis ) – Встречающаяся в природе бактерия, обитающая в почве, содержащая споры, содержащие токсины, которые специально нацелены и воздействуют только на личинок комаров, мошек и грибных комаров. BTI не токсичен для людей и одобрен для использования в органическом земледелии.
Химическая борьба – Химическая борьба – это использование специальных химических соединений (инсектицидов), которые уничтожают взрослых и неполовозрелых комаров. Он применяется, когда другие методы не могут удержать численность комаров ниже допустимого уровня или когда необходимы меры экстренной борьбы для быстрого прерывания или прекращения передачи болезни человеку.
CO2 Ловушка с наживкой – CO2 является важным компонентом выдыхаемого воздуха и является аттрактантом для самок комаров, ищущих хозяина. Эти ловушки могут быть заполнены сухим льдом или сжатым газом CO2.
Энцефалит – Воспаление головного мозга, часто вызываемое вирусом, может вызывать легкие гриппоподобные симптомы или отсутствие симптомов при at. Энцефалит также может привести к более тяжелым гриппоподобным симптомам, судорогам или проблемам с органами чувств или движениями и редко может быть опасным для жизни.
Gravid – беременные, несущие яйца или молодняк.
Gravid Traps – ловушка, использующая грязную воду для привлечения самок комаров, ищущих место для откладывания яиц. В нашем округе на эти ловушки в основном попадается Culex pipiens .
Ларвициды – Ларвициды – это продукты, используемые для сокращения численности неполовозрелых комаров. Они могут быть биологическими или химическими по происхождению, наноситься непосредственно на воду и контролировать комаров, предотвращая появление взрослых личинок комаров.
Малярия – вызывается паразитами, которые атакуют красные кровяные тельца, разрушая их при бесполом размножении. Он передается человеку в первую очередь комарами Anopheles и может передаваться через общие иглы, переливание крови или трансплацентарные инфекции. Комары заражаются, питаясь другими людьми, которые являются носителями паразита.
Лужи/пробы комаров – Комары отлавливаются и собираются с поля. Собранные самки затем объединяются по видам. Каждый образец содержит от одного до максимум 50 комаров на образец. Каждый образец тестируется на наличие вирусов энцефалита Сент-Луиса, западного энцефаломиелита лошадей и вирусов Западного Нила с помощью полимеразной цепной реакции (ПЦР) TaqMan в реальном времени.
Световая ловушка для Нью-Джерси . Отлавливает взрослых комаров, отслеживает сезонную численность и отслеживает действия по борьбе с комарами.
Паразит – Организм, который живет и питается на другом растении или животном или в нем (известный как хозяин). Обычно паразит наносит вред хозяину. Паразиты — одни из самых злейших вредителей; но когда паразиты помогают людям, атакуя и контролируя вредителей, которые могут нанести вред сельскохозяйственным культурам или животным, они становятся формой биологической борьбы.
Физический контроль – физическое воздействие или изменение мест обитания комаров, что приводит к сокращению или устранению численности комаров.
Хоботок – длинная ротовая часть взрослого комара.
Дозорные куриные стаи . Округ использует контрольные куриные стаи для выявления передачи арбовирусов, переносимых комарами, таких как вирус Западного Нила (ВЗН), западный конский энцефаломиелит (ВЭЭ) или энцефалит Сент-Луиса (СКВ). В течение нескольких дней после укуса комара, зараженного одним из этих вирусов, у цыплят вырабатываются специфические антитела к этому вирусу. Они не заболевают и не умирают. Образцы крови у цыплят обычно берут сотрудники лаборатории и проверяют на наличие этих антител.
Вирус энцефалита Сент-Луиса (SLEV) – передается человеку при укусе инфицированного комара. Большинство людей, инфицированных SLEV, не имеют явных признаков заболевания. Начальные симптомы заболевших включают лихорадку, головную боль, тошноту, рвоту и усталость. Тяжелое нейроинвазивное заболевание (часто сопровождающееся энцефалитом, воспалением головного мозга) чаще встречается у пожилых людей. В редких случаях это может привести к длительной инвалидности или смерти. Специфического лечения инфекции SLEV не существует; лечение основано на симптомах.
Сверхмалый объем (размер капель) – Этот высококонцентрированный раствор может содержать только активный ингредиент; применяется не разбавляя. Эти решения требуют специального оборудования для применения в сверхмалых объемах. Применение УМО часто осуществляется с самолетов или с наземного оборудования для борьбы со взрослыми комарами.
Клещ – кровососущий наружный паразит млекопитающих, птиц и рептилий. Некоторые клещи могут передавать заболевания людям и животным. Основным переносчиком болезни Лайма в округах Сакраменто и Йоло является Ixodes pacificus, , также известный как западный черноногий клещ. Клещи обычно встречаются на травянистых участках, в кустарниках или в лесистых местностях. Они ждут на верхушках растительности человека или другого животного-хозяина (это называется «поиски»). Когда хозяин касается его, клещ вступает в контакт, ищет подходящее место и начинает процесс кормления.
Переносчик – животное или насекомое, способное передавать болезнь людям или другим животным или считающееся вредным для общественного здравоохранения.
Вирус Западного Нила – это заболевание, передающееся человеку, птицам, лошадям и другим животным при укусе зараженного комара. Комары заражаются от инфицированных птиц при заборе крови и могут впоследствии передавать его при укусах животных или людей. Вакцин для профилактики или лекарств для лечения ВЗН не существует. К счастью, у большинства людей, инфицированных ВЗН, симптомы отсутствуют. Примерно у 1 из 5 инфицированных людей появляется лихорадка, головная боль, утомляемость, увеличение лимфатических узлов и другие симптомы. Примерно у 1 из 150 инфицированных развивается серьезное заболевание, иногда со смертельным исходом.
Западный лошадиный энцефалит – вирусное заболевание, передающееся людям и лошадям через укус инфицированного комара. Вирус представляет собой альфавирус и тесно связан с вирусами восточного энцефалита лошадей и венесуэльского энцефалита лошадей.
Вирус Зика — преимущественно распространяется через укус инфицированного комара ( Aedes aegypti или Aedes albopictus ). Хотя в Калифорнии не было зарегистрировано случаев передачи вируса Зика комарами, инфицированные путешественники ежегодно возвращаются в штат. При наличии комаров, способных передавать вирус Зика, всегда существует возможность местной передачи.

Что такое вектор? – Объяснение и примеры

Векторы эффективно передают информацию о математическом или физическом элементе. В частности:

Векторы — это математические величины, используемые для представления объектов, которые имеют как величину, так и направление.

Вы когда-нибудь задумывались, чем скорость отличается от скорости, а масса отличается от веса? Подсказка: ответ связан с векторами! Мы рассмотрим эти и другие вопросы при обсуждении следующих векторных тем в этой статье:

• Определение вектора
• Введение в векторы

 

Определение вектора

В физике и математике вектор определяется как:

».

Используя приведенное выше определение, мы можем видеть, что представление векторов требует наличия двух компонентов, а именно:

• Величина (или размер)
• Направление

 

Знакомство с векторами

Исторически векторы использовались в геометрии, физике и механике. Однако со временем векторы стали широко использоваться во многих областях, включая линейную алгебру, инженерию, информатику, структурный анализ и навигацию.

Поскольку векторы выражают два понятия, а именно величину и направление, они могут создавать множество математических моделей для различных задач и сценариев.

В этом разделе мы познакомимся со следующими важными концепциями векторов:

• Геометрическое и математическое представление векторов
• Скаляры и векторы
• Различные типы векторов

Геометрическое и математическое представление векторов can141 900 быть геометрически представлены прямыми стрелками определенной длины, указывающими в определенном направлении с определенными начальными и конечными точками. Длина вектора представляет его величину, тогда как направление указывает его направление относительно набора координат. Изображение ниже является примером геометрического представления вектора.

Рассмотрим следующий рисунок, где A — вектор. |А| представляет его длину (или величину), а стрелка, указывающая из точки a в точку b, представляет его направление. Точка a называется начальной или начальной точкой, а точка b называется конечной или конечной точкой вектора A . Хотя в этом примере вектор показан в двух измерениях, он также может иметь три, четыре и более измерения.

Величина вектора в основном такая же, как длина отрезка ab. Направление вектора в основном совпадает с направлением стрелки.

Алгебраически вектор можно представить в виде упорядоченной пары. Это представление называется вектор-столбцом. На изображении ниже вектор OA представлен как вектор-столбец.

OA = (2,3)

Это означает, что вектор смещен от начала координат на две точки по горизонтали (ось X) и четыре точки по вертикальной оси (ось Y).

Векторы часто обозначаются жирным шрифтом, например , или 9.0107 A.  Если жирный шрифт невозможен, например, при написании заметок от руки, вектор представляется буквой со стрелкой над ней.

Векторы и скаляры

Физические и математические величины классифицируются либо как векторы, либо как скаляры. Хотя они связаны, векторы и скаляры используются в разных ситуациях.

Скалярная величина

Скалярная величина имеет величину, но не направление.

Скаляры представляются простыми буквами, такими как a или A, и обычно состоят из действительных чисел. Некоторыми распространенными примерами скаляров являются время, скорость, энергия, масса, объем, площадь и высота.

Величина вектора

Величина вектора имеет как величину, так и направление.

В отличие от скалярных величин, которые имеют только одну компоненту, векторные величины состоят из двух компонент. Некоторые распространенные примеры векторов включают скорость, смещение и ускорение.

Чтобы лучше понять разницу между скалярными и векторными величинами, рассмотрим несколько примеров:

Определите, является ли данная величина вектором или скаляром.

V = 10 м, Восток

Чтобы классифицировать эту величину, нам нужно рассмотреть определения векторов и скаляров и выяснить, сколько у нее компонентов. Сначала разложим заданную величину на части. Данная величина имеет модульную составляющую | В| = 10м. Он также указывает на Восток. Следовательно, мы можем заключить, что данная величина является вектором, так как имеет две составные части.

A = 5 см

В этом примере присутствует только компонент магнитуды. Поскольку нет упоминания о направлении, эта величина является скаляром.

Величина скаляра A равна 5 см.

Различные типы векторов

Различные типы векторов, используемые в математике, включают в себя:

• нулевой вектор
• . Ко-начальные векторы
• Коллинеарные векторы
• Копланарные векторы

Каждый из этих типов векторов очень важен и имеет различные применения. Их описания можно найти ниже.

Нулевой вектор

Вектор называется нулевым вектором, если его модуль равен нулю. Нулевой вектор начинается и заканчивается в одной и той же точке, что означает, что он имеет координаты (0,0). Он также не имеет определенного направления. Например:  A = (0,0) и A = 0 — это разные способы записи нулевых векторов.

Единичный вектор

Единичный вектор — это вектор, длина или величина которого равна 1. Нахождение единичного вектора с тем же направлением, что и у другого вектора, может быть полезным инструментом, и мы называем его нормализованным вектором. Такой вектор находится делением заданного вектора на его величину:

Y шляпа = Y/ |Y|

Примечание. Помните, что единичные векторы равны друг другу, только если они указывают в одном направлении.

Равный вектор

Два или более вектора называются равными, если они имеют одинаковую величину и направлены в одном направлении. Два вектора, A и B, на изображении, показанном ниже, равны, так как их величина и направление одинаковы.

Вектор смещения

Если точка X смещена (перемещена) из одной позиции в другую позицию Y, то смещение между двумя точками можно представить в виде вектора смещения. В этом случае вектор смещения будет записан как ХУ.

Отрицательное значение вектора

Два вектора с одинаковой величиной, но противоположным направлением называются отрицательными по отношению друг к другу. Пусть a и b — два вектора с одинаковой величиной. Если направление b противоположно направлению a, , то a и b являются отрицательными значениями друг друга. Соотношение между этими двумя векторами:

a = -b

Вектор положения

Вектор положения используется для указания положения объекта в трехмерных декартовых координатах относительно заданной контрольной точки.

Совместно начальные векторы

Два или более вектора, имеющие одинаковую начальную или начальную точку, называются совместно начальными векторами. На изображении, приведенном ниже, векторы AC и AB являются совместными начальными векторами.

Коллинеарные векторы

Векторы, параллельные друг другу или лежащие на одной прямой, называются коллинеарными векторами.

Копланарные векторы

Два или более трехмерных вектора, лежащих в одной плоскости, называются копланарными векторами.

Примеры

В этом разделе мы обсудим некоторые примеры векторных задач и их пошаговые решения.

Пример 1

Выразите заданный вектор AD , как показано на изображении ниже, в виде вектора-столбца.

Решение

По определению вектор-столбец выражается как упорядоченная пара. Из рисунка видно, что AD начинается в точке A и заканчивается в точке D. Он смещен на 3 единицы вправо по оси x и на 4 единицы вверх по оси y.

Таким образом, заданный вектор AD , записанный как вектор-столбец:

AD = (3,4)

ниже как вектор-столбец.

Решение

По определению вектор-столбец выражается как упорядоченная пара. Из рисунка видно, что UV начинается в точке U и заканчивается в точке V. Он смещен на 3 единицы вправо по оси x и на 2 единицы вниз по оси y.

Таким образом, заданный вектор UV , записанный как вектор-столбец, имеет вид:

UV = (5, -2)

Обратите внимание, что отрицательный знак указывает на то, что вектор движется вниз по оси y.

Пример 3

Идентифицирует данную величину как скалярную или векторную.

S = 40 минут

Решение

Данная величина является скалярной, поскольку имеет только величину и не имеет направления. Его величина |S| = 40.

Пример 4

Определите данную величину как скалярную или векторную.

OW = (2,-3)

Решение

Данная величина является вектором. Он выражается как вектор-столбец, OW, , где O — начальная точка, а W — конечная точка. Это показывает, что перевод из O в W осуществляется на 2 точки вправо по горизонтальной оси и на 3 точки вниз по оси Y.

Пример 5

Идентифицирует данную величину как скалярную или векторную.

V = 0

Решение

Данная величина является вектором. Величина вектора V задается как |V| = 0, так что на самом деле это нулевой вектор. Таким образом, направление этого вектора не указано, поскольку нулевой вектор не имеет направления.

Пример 6

Идентифицирует данную величину как скалярную или векторную.

F = 20N, вниз

Решение

Данная величина является вектором. Величина вектора F, равна |F| = 20, а направление указано как нисходящее.

Практические вопросы

Определите следующие величины как векторы или скаляры и определите их величины и направления. 92, вертикально вверх.

S = 20 см при 60 градусах

W = (2,5)

V = 20 миль в час, северо-восток

Выразите данный вектор изображения в виде столбца PQ 90 вектор.

Выразите заданный вектор MN , как показано на изображении ниже, в виде вектора-столбца.

Ответы

1. Вектор: Величина |X| = 2 м, а направление указано как север.
92)
2. Вектор: Магнитуда |V|= 20 миль в час, направление указано как северо-восток.
3. Вектор PQ можно представить в виде упорядоченной пары:

PQ = (5,5).

Это означает, что вектор PQ начинается в точке P и заканчивается в точке Q. Он смещен на 5 точек вправо по горизонтальной оси и на 5 точек вверх.

12. Вектор MN можно представить в виде упорядоченной пары:

MN = (-2, -4).

Это означает, что вектор MN начинается в точке M и заканчивается в точке N. Он переносится на 2 точки влево по горизонтальной оси и на 4 точки вниз по оси y.

Предыдущий урок | Главная страница | Следующий урок

Что такое векторный файл?

Вы когда-нибудь загружали изображение с веб-сайта и обнаруживали, что это векторный файл? Но что такое векторный файл? А для чего вы используете векторные файлы?

Что такое векторный файл?

Векторный файл или векторное изображение создается с использованием математических формул, задающих точки на сетке. Размер сетки и точек изображения можно регулировать бесконечно, поскольку точки могут перемещаться в соответствии с математической формулой без деформации или пикселизации (как это происходит с другими типами изображений).

Ваш смартфон или камера не захватывает векторные изображения. Вместо этого он захватывает растровые изображения, которые используют тысячи или миллионы пикселей для построения изображения. Поскольку фиксированное количество пикселей создает изображение, изменение размера требует, чтобы каждый пиксель растягивался и сохранял качество, чего они не могут сделать.

Следовательно, если вы попытаетесь растянуть фотографию до большого размера, она станет нечеткой и потеряет качество. Вы можете уменьшить изображение до небольшого размера без потери качества, потому что пиксели могут сжиматься.

История векторных файлов

Векторные файлы тоже существуют уже довольно давно. Векторные графические дисплеи были впервые использованы как часть системы ПВО США SAGE, позволяя операторам отображать местоположение союзных и вражеских самолетов на одной карте, используя ряд входных данных. До этого операторы вручную наносили местоположения векторов, обновляли карту и затем передавали информацию пилотам.

Была игровая приставка, в которой использовалась исключительно векторная графика. Vectrex была домашней консолью со встроенным монохромным ЭЛТ-монитором, что было редкостью во время ее выпуска в 1919 году.82. Консоль рисовала постоянный поток изображений по осям X и Y, обновляя их в ответ на действия пользователя. Он также поставлялся с разноцветными накладками на экран, которые создавали ощущение изменения цвета игры.

Термин «векторное изображение» в настоящее время относится к двухмерным компьютерным изображениям и широко используется в печатных СМИ и дизайнерских работах.

Что такое расширения векторных файлов?

Расширения векторных файлов отличают файлы векторных изображений от других типов файлов изображений. Например, фотографии могут использовать JPEG, PNG или RAW, каждый из которых определяет некоторые характеристики изображения внутри файла, в частности, использование растровых изображений. То же самое относится и к расширениям векторных файлов, которые могут определять характеристики содержимого и программы, используемой для создания векторного файла.

Наиболее распространенные расширения векторных файлов:

• .AI Указывает Adobe Illustrator Файл изображения
• .EPS Остается для Encapsulated Postscript , который немного более старый, но все еще полезный файл вектора
• .SVV. Файл векторной графики , который представляет собой формат файла векторного изображения на основе XML, широко используемый в Интернете

Является ли PDF форматом векторного файла?

Вы можете использовать PDF как формат векторного файла, абсолютно. Но это зависит от исходного создания файла, поскольку PDF также может функционировать как растровый файл.

Зачем использовать векторный файл?

Файлы векторных изображений универсальны, что делает их полезными для нескольких целей, особенно в печати и дизайнерских работах. Например, если вы разрабатываете логотип для своего бизнеса, вы хотите использовать один и тот же логотип на нескольких платформах и в печатных СМИ без потери качества и ущерба имиджу.

Если вы используете растровый формат, каждый раз, когда вы пытаетесь изменить логотип, есть большая вероятность, что конечный продукт будет зернистым или нечетким, особенно если вы попытаетесь увеличить его.

То же самое верно, если вы скопируете изображение из социальной сети и попытаетесь распечатать его. Платформы социальных сетей сжимают изображения в стандартных растровых форматах, чтобы уменьшить размер на своих серверах и ускорить обслуживание. Но если вы попытаетесь распечатать скопированное изображение как фотографию, оно, скорее всего, будет выглядеть пиксельным или иметь низкое качество.

Принимая во внимание, что если вы используете векторное изображение для своего логотипа (или любой другой дизайнерской работы), вы можете масштабировать изображение вверх и вниз по своему усмотрению без ущерба для качества.

Как открыть векторный файл?

Существует множество программ, которые могут открыть файл векторного изображения для просмотра, например бесплатный инструмент для редактирования изображений Irfanview.

Однако Irfanview (как и многие инструменты для просмотра изображений) не может редактировать векторные файлы. Для этого вам понадобится инструмент для редактирования векторов, например Adobe Illustrator. Хотя Adobe Illustrator является одним из лучших инструментов для работы с векторными изображениями на рынке, он является дорогим вариантом для большинства людей, особенно если вы хотите создать или отредактировать только один файл.

Итак, имея это в виду, ознакомьтесь с лучшими бесплатными альтернативами Adobe Illustrator для векторного редактирования.

Можете ли вы преобразовать другие форматы в векторный файл?

Можно преобразовать формат файла растрового изображения в формат векторного файла для создания векторного файла, но результаты будут различаться в зависимости от исходного файла. Допустим, вы создаете красивый новый логотип в виде растрового файла, но затем хотите преобразовать его в векторный файл, чтобы упростить масштабирование вверх и вниз. Вы можете преобразовать файл в векторный тип, сохранив изображение и уменьшив вероятность нечеткости или других проблем с качеством.

Успех выходного файла зависит от программы, которую вы используете для преобразования в векторное изображение. Например, некоторые онлайн-конвертеры растровых изображений в векторные не будут правильно захватывать изображение или выдавать файл очень низкого качества. Принимая во внимание, что такие программы, как Adobe Illustrator и Inkscape, специализируются на создании и редактировании векторных изображений и поставляются с обширным набором инструментов для автоматического преобразования.

Пример преобразования векторного файла

Следующие изображения иллюстрируют преобразование изображения из растра в вектор. На первом изображении показаны глаза Рю из серии Street Fighter в виде растра. Обратите внимание на пикселизацию:

Вот как выглядят глаза после векторизации:

Мелкие детали удаляются из растрового изображения и сглаживаются в математические формы, которыми легче манипулировать в больших форматах.

No related posts.