Чему модуль x равен: Уравнения с модулями. Модули

Чему равен модуль х 2. Как решать уравнения с модулем: основные правила

Инструкция

Если модуль представлен в виде непрерывной функции, то значение ее аргумента может быть как положительным, так и отрицательным: |х| = х, х ≥ 0; |х| = — х, х

Модуль нулю, а модуль любого положительного числа – ему . Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.

Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.

Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.

Возведенный в степень аргумент одновременно находится под знаком корня того же порядка – он решается при помощи : √a² = |a| = ±a.

Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >

Модуль нуля равен нулю, а модуль любого положительного числа – ему самому. Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.

Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя целое положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.

Отрицательным модуль быть не может, поэтому любое отрицательное число преобразуется в положительное: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.

Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается изменение порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.

Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т.к. оно будет влиять на знак выражения.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

А вычисляется в соответствии с такими правилами:

Для краткости записи применяют |а| . Так, |10| = 10; — 1 / 3 = | 1 / 3 |; | -100| =100 и т. д.

Всякой величине х соответствует достаточно точная величина |х |.

И значит тождество у = |х | устанавливает у как некоторую функцию аргумента х .

График этой функции представлен ниже.

Для x > 0 |x | = x , а для x x |= —x ; в связи с этим линия у = |x | при x > 0 совмещена с прямой у =х (биссектриса первого координатного угла), а при х у = -х (биссектриса второго координатного угла).

Отдельные уравнения включают в себя неизвестные под знаком модуля .

Произвольные примеры таких уравнений — |х — 1| = 2, |6 — 2х | =3х + 1 и т. д.

Решение уравнений содержащих неизвестную под знаком модуля базируется на том, что если абсолютная величина неизвестного числа х равняется положительному числу а, то само это число х равняется или а, или -а.

Например :, если |х | = 10, то или х =10, или х = -10.

Рассмотрим решение отдельных уравнений .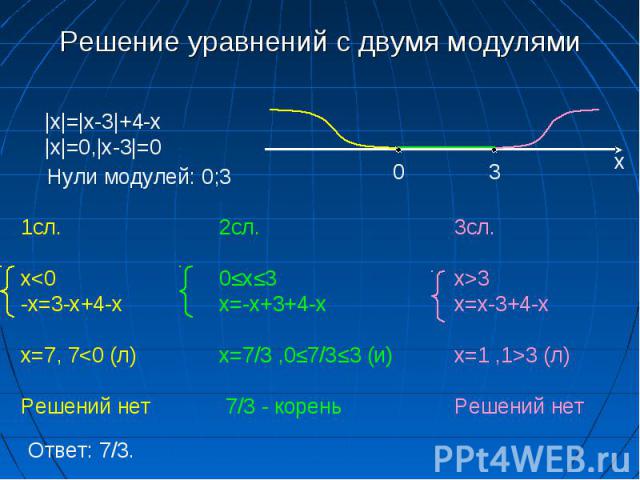

Проанализируем решение уравнения |х — 1| = 2.

Раскроем модуль тогда разность х — 1 может равняться или + 2, или — 2. Если х — 1 = 2, то х = 3; если же х — 1 = — 2, то х = — 1. Делаем подставновку и получаем, что оба эти значения удовлетворяют уравнению.

Ответ. Указанное уравнение имеет два корня: x 1 = 3, x 2 = — 1.

Проанализируем решение уравнения | 6 — 2х | = 3х + 1.

После раскрытия модуля получаем: или 6 — 2х = 3х + 1, или 6 — 2х = — (3х + 1).

В первом случае х = 1, а во втором х = — 7.

Проверка. При х = 1 |6 — 2х | = |4| = 4, 3x + 1 = 4; от суда следует, х = 1 — корен ь данного уравнения .

При x = — 7 |6 — 2

x | = |20| = 20, 3x + 1= — 20; так как 20 ≠ -20, то х = — 7 не является корнем данного уравнения.

Ответ. У уравнения единственный корень: х = 1.

Уравнения такого типа можно решать и графически .

Так решим, например , графически уравнение |х- 1| = 2.

Первоначально выполним построение графика функции у = |x — 1|. Первым начертим график функции у =х- 1:

Ту часть этого графика , которая расположена выше оси х менять не будем. Для нее х — 1 > 0 и потому |х -1|=х -1.

Часть графика, которая расположена под осью х , изобразим симметрично относительно этой оси. Поскольку для этой части х — 1 х — 1|= — (х — 1). Образовавшаяся в результате линия (сплошная линия) и будет графиком функции

у = |х —1|.

Эта линия пересечется с прямой у = 2 в двух точках: M 1 с абсциссой -1 и М 2 с абсциссой 3. И, соответственно, у уравнения |х — 1| =2 будет два корня: х 1 = — 1, х 2 = 3.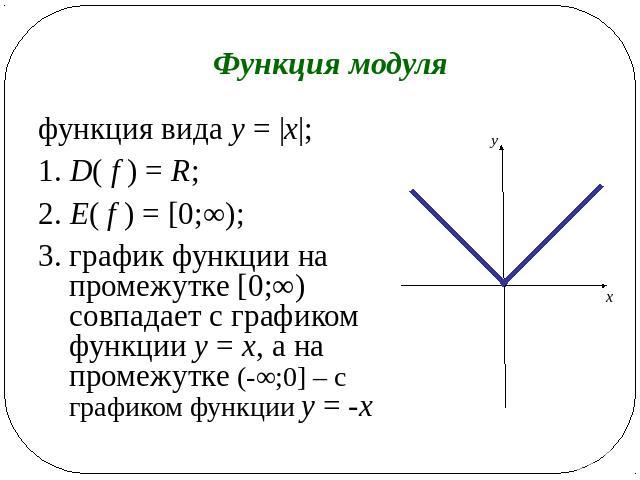

Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

{±c, если с > 0

Если |x| = c, то x = {0, если с = 0

{нет корней, если с

1) |x| = 5, т. к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

2) |x 2 – 5| = 11, т.к. 11 > 0, то

x 2 – 5 = 11 или x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 нет корней

3) |x 2 – 5x| = -8 , т.к. -8

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x) .

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3

2) |x – 1| = 1 – x 2 .

1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:

(1 – x)(1 + x) ≥ 0

2. Решение:

x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 или x = 1 x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1.

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 или x = 4 x = 2 или x = 1

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:

|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1 x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5.

Рассмотрим еще один пример:

x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому

|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2 или |x| = 1

Нет корней x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или 3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5 или 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 или x + 1 = -2. Нет корней.

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам. Заработай деньги с помощью своих знаний на https://teachs.ru !

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

Модуль комплексного числа

Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi , поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi .

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a , потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x|

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.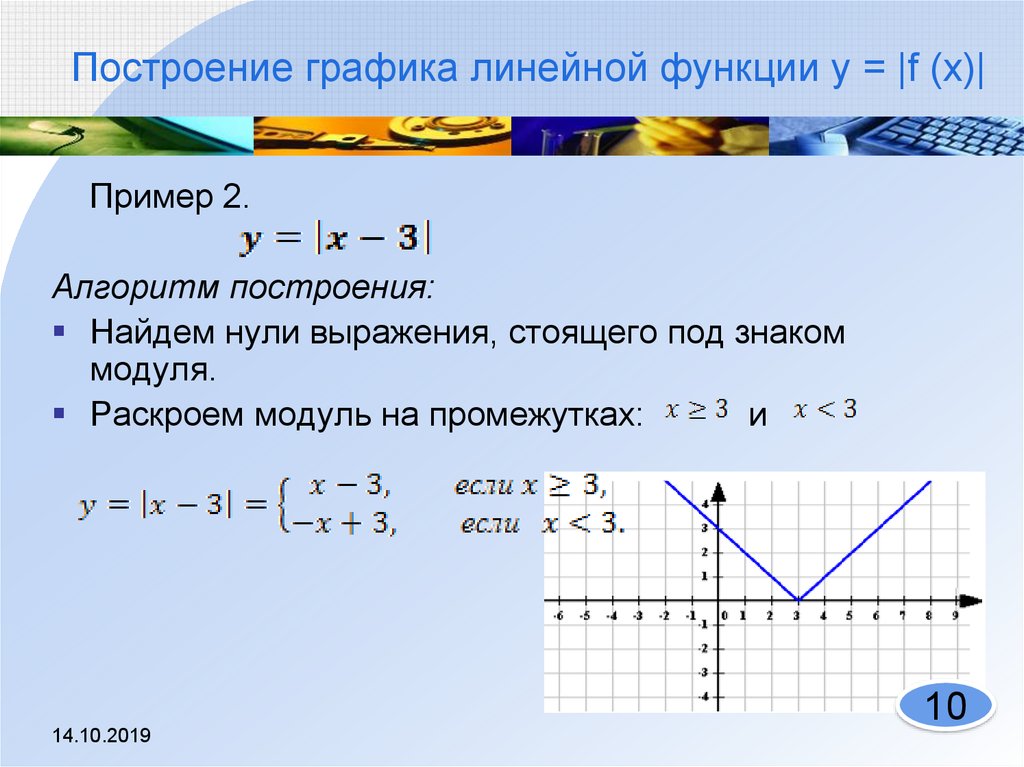

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2 .

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2 .

Ответ: 2 и −2 .

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0 . Получено: x = –2 .

Это означает, что –2 – поворотная точка.

Разделим интервал на 2 части:

1. для x + 2 ≥ 0

[−1; + ∞).

1. для х + 2

Общим ответом для этих двух неравенств является интервал (−∞; –3].

Окончательное решение – объединение ответов отдельных частей:

x ∈ (–∞; –3] ∪ [–1; + ∞).

Ответ: x ∈ (–∞; –3] ∪ [–1; + ∞) .

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x 1 = 3; x 2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке.

Ответ: x = 0 .

Модуль суммы

Модуль разности

Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Известно свойство:

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение : из рисунка видно, что график симметричен относительно оси Y.

Пример 2 . Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)) .

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

Пример 1 . Решить методом интервалов.

Решение:

кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн для чайников 🫖🤓

Учитель очень удивится увидев твоё верное решение😉

Введите уравнение с неизвестным, для которого требуется найти корни.

Решим уравнение с неизвестным x
(если данное уравнение калькулятор способен решить).

Левая и правая части уравнения теперь совмещены в одну. 2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Абсолютное значение — общее руководство по математическим навыкам

Что это значит?

Определения:

Абсолютное значение (или модуль) | х | действительного числа x является неотрицательным значением x независимо от его знака.

Например, абсолютное значение 5 равно 5, а абсолютное значение -5 также равно 5. Абсолютное значение числа можно рассматривать как его расстояние от нуля по линии действительных чисел. Кроме того, абсолютная величина разности двух действительных чисел есть расстояние между ними.

Абсолютное значение обладает следующими четырьмя фундаментальными свойствами:

Неотрицательность $$|a| ≥ 0$$ Положительная определенность $$|a| = 0 ⇔ a = 0$$ Мультипликативность $$|ab| = |a||b|$$ Субаддитивность $$|a + b| ≤ |а| + |b|$$

Другие важные свойства абсолютного значения включают:

Идемпотентность (абсолютное значение абсолютного значения является абсолютным значением) $$||a|| = |a|$$ Симметрия $$|-a| = |a|$$ Тождество неразличимых (эквивалентно положительной определенности) $$|a — b| = 0 ⇔ a = b$$ Неравенство треугольника (эквивалентное субаддитивности) $$|a — b| ≤ |а — с| + |c — b|$$ Сохранение деления (эквивалентно мультипликативности) $$|a  /  b| = |а| /  |б| \space\space if \space\space b ≠ 0$$ (эквивалент субаддитивности) $$|a — b| ≥ ||а| — |b||$$

Два других полезных свойства, касающихся неравенств: $$|a| ≤ b ⇔ -b ≤ a ≤ b$$ $$|a| ≥ b ⇔ a ≤ -b \space или \space b ≤ a$$

Эти соотношения можно использовать для решения неравенств, включающих абсолютные значения. Например: $$|x — 3| ≤ 9 ⇔ -9 < x - 3 < 9$$ $$⇔ -6 < x < 12$$

Источник:en.wikipedia.org/wiki/Absolute_value

 Как это выглядит?

Абсолютное значение 5 равно 5, это расстояние от 0,5 единиц.

Абсолютное значение -5 равно 5, это расстояние от 0,5 единиц.

$$|x| = 2 $$

$$|x| > 2$$

$$Для \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$

|7| = 7 означает, что абсолютное значение 7 равно 7.

|-7| = 7 означает, что абсолютное значение -7 равно 7.

|-2 — x| означает абсолютное значение -2 минус x.

-|х| означает отрицательное значение абсолютного значения x.

Тебе пригодится…

Абсолютное значение действительных чисел встречается в самых разных математических установках, например, абсолютное значение также определяется для комплексных чисел, кватернионов, упорядоченных колец, полей и векторных пространств. В реальной жизни абсолютное значение тесно связано с понятиями величины, расстояния и нормы. Подобно глубине океана, времени: 500 г. до н.э. в отличие от 500 г. н.э.

  Видео

Абсолютное значение и числовые строки

Смотреть видео Академии Хана »
Продолжительность: 5:39

  Видео

Абсолютное значение целых чисел

Смотреть видео Академии Хана »
Продолжительность: 2:22

  Видео

Уравнения абсолютного значения

Смотреть видео Академии Хана »
Продолжительность: 10:41

Практические задачи

Абсолютные значения »

Уравнения абсолютных значений »

Модульная функция — формула, график, свойства, примеры

Модульная функция дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В математике модуль действительного числа x задается функцией модуля , обозначаемой |x|. Это дает неотрицательное значение x. Модуль или абсолютное значение числа также рассматривается как расстояние числа от начала координат или нуля.

В этой статье мы узнаем об определении функции модуля, вычислении модуля для чисел, переменных и многочленов, а также решенных примерах и вопросах функции модуля.

1.	Что такое функция модуля?
2.	Формула функции модуля
3.	Домен и диапазон функции модуля
4.	Применение модульной функции
5.	График функции модуля
6.	Свойства функции модуля
7.	Производная и интеграл функции модуля
8.	Часто задаваемые вопросы о модульной функции

Что такое функция модуля?

Функция модуля , которую также называют функцией абсолютного значения, дает модуль или абсолютное значение числа независимо от того, является ли число положительным или отрицательным. Он всегда дает неотрицательное значение любого числа или переменной. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → (0,∞) и x ∈ R.

|x| — модуль x, где x — действительное число. Если x неотрицательно, то f(x) будет иметь то же значение x. Если x отрицательно, то f(x) будет величиной x, то есть f(x) = -x, если x отрицательно. Подытожим приведенную ниже формулу функции модуля.

Формула функции модуля

Значение функции модуля всегда неотрицательно. Если f(x) является функцией модуля, то мы имеем:

• Если x положителен, то f(x) = x
• Если х = 0, то f(x) = 0
• Если х < 0, то f(x) = -x

Это означает, что если значение x больше или равно 0, то функция модуля принимает фактическое значение, но если x меньше 0, функция принимает фактическое значение ‘x’ с минусом.

Домен и диапазон функции модуля

Мы можем применить функцию модуля к любому вещественному числу. Диапазон функции модуля — это набор неотрицательных действительных чисел, который обозначается как (0, ∞), а область определения функции модуля — R (где R относится к набору всех действительных чисел). Следовательно, область определения функции модуля составляет R , а диапазон равен (0,∞).

Применение модульной функции

Теперь, когда мы знаем формулу функции модуля, давайте рассмотрим несколько примеров, чтобы понять ее применение. Шаги для расчета функции модуля приведены ниже:

Пример: Рассмотрим функцию модуля f(x) = |x|.

• Если x = − 3, то y = f(x) = f(−3) = −(−3) = 3, здесь x меньше 0.
• Если x = 3, то y = f(x) = f(3) = 3, здесь x больше 0
• Если x = 0, то y = f(x) = f(0) = 0, здесь x равно 0

Обратите внимание, что здесь f(-3) = f(3). Другими словами, |3| = |-3| = 3.

График функции модуля

Теперь давайте посмотрим, как построить график для функции модуля. Давайте рассмотрим x как переменную, принимающую значения от -5 до 5. Вычисляя модуль для положительных значений «x», линия на графике представляет собой «y = x», а для отрицательных значений «x» на графике изображена линия «y = -x».

х	f(x) = |x|
-5	5
-4	4
-3	3
-2	2
-1	1
0	0
1	1
2	2
3	3
4	4
5	5

Свойства функции модуля

Теперь, когда у нас есть формула для функции модуля и график функции модуля, давайте теперь исследуем свойства функции модуля:

Производная и интеграл функции модуля

Поскольку мы знаем, что функция модуля f(x) = |x| равно x, если x > 0, и -x, если x < 0, поэтому производная функции модуля равна 1, если x > 0, и -1, если x < 0. Производная функции модуля не определена для x = 0. Следовательно, производная модульной функции может быть записана как d(|x|)/dx = x/|x| , для всех значений x и x, не равных 0.

Используя формулу функции модуля и формулы интегрирования, интеграл функции модуля равен (1/2)x ² + C, если x ≥ 0, и его интеграл равен -(1/2)x ² + C, если x < 0. Таким образом, интегрирование функции модуля можно представить как:

• ∫|x| dx = (1/2)x ² + C, если x ≥ 0
• ∫|х| dx = -(1/2)x ² + C, если x < 0

Важные замечания о функции модуля

• Функция модуля также называется функцией абсолютного значения и представляет собой абсолютное значение числа. Обозначается |x|.
• Областью определения модульных функций является множество всех действительных чисел.
• Диапазон функций модуля — это набор всех действительных чисел, больших или равных 0.
• Вершина графика модулей y = |x| равно (0,0).
• Вершина функции модуля y = a |x — h| + k равно (h, k).

Тема, связанная с функцией модуля

• Модуль комплексного числа
• Калькулятор абсолютного значения
• Калькулятор модов

Часто задаваемые вопросы о модульной функции

Что такое функция модуля?

Функция модуля дает модуль или абсолютное значение числа независимо от того, является число положительным или отрицательным. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → R и x ∈ R. Это также называется функцией абсолютного значения.

Что такое домен и диапазон функции модуля?

Областью определения функции модуля является R (где R относится к набору всех положительных действительных чисел), а диапазон функции модуля представляет собой набор неотрицательных действительных чисел, который обозначается как (0,∞).

Что такое интегрирование модульной функции?

Интегрирование функции модуля зависит от значения x. Это:

• ∫|x| dx = (1/2)x ² + C, если x ≥ 0
• ∫|х| dx = -(1/2)x ² + C, если x < 0

Как дифференцировать функцию модуля?

Имеем f(x) = |x| равно x, если x > 0, и -x, если x < 0, следовательно, производная модульной функции равна 1, если x > 0, и -1, если x < 0. Производная модульной функции не определена для x = 0 Подводя итог, можно сказать, что производная функции модуля |x| равно x/|x|, где x не равно 0.

Всегда ли функция модуля положительна?

Модуль положительного числа положителен. Модуль отрицательного числа получается при игнорировании знака минус. Таким образом, функция модуля всегда положительна.

Почему функция модуля не дифференцируема?

Функция модуля |x| не дифференцируема при x = 0, так как график Mod(x) имеет острую точку при x = 0. Кроме того, левый и правый предел производной не равны при x = 0.

Как вы решаете задачи на модульную функцию?

Задачи модульных функций можно решить, применяя модуль к неотрицательному числу, а отрицательное число всегда дает одно и то же число.