Дискретный арктангенс в процессоре NES / Хабр
Геймплей моей игры Star Versus основан на поворотах. Объекты отслеживают направление, в котором они смотрят, и на каждом цикле движка двигаются в этом направлении. В такой ситуации требуется много тригонометрии, бо́льшую часть которой можно ради эффективности вычислить заранее, однако иногда это невозможно. В частности, паре геймплейных элементов нужно находить арктангенсы, и делать это быстро.
Определение арктангенса: в прямоугольном треугольнике arctan вычисляет один из непрямых углов, используя в качестве входных данных длину стороны, противоположной этому углу, разделённую на длину прилежащей стороны. В случае Star Versus сторонами треугольника являются расстояния X/Y между двумя объектами, например, снарядом и кораблём, а угол — это направление, в котором должен двигаться первый, чтобы достичь второго.
Поначалу арктангенс нужен был для того, чтобы понять, когда один корабль ударяет по другому своим мечом.
Важным упрощением в Star Versus является то, что направление не непрерывно, а дискретно. Объекты могут двигаться только в 24 возможных направлениях. Перемещение вправо соответствует 0, вверх — 6, влево — 12, а вниз — 18. Каждый инкремент направления представляет собой угол в τ / 24 радиан. (τ — это фундаментальная константа окружности, равная 6.2831853…)
После выполнения кода распознавания коллизий у нас уже есть дельты позиций X/Y для функции arctan.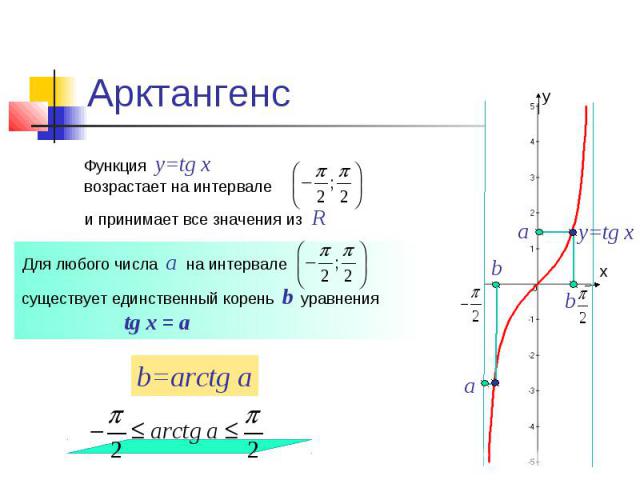 Нам достаточно одних знаков, чтобы понять, в каком из четырёх квадрантов находится результат, поэтому остальная часть кода должна выяснить при помощи абсолютных значений дельт, какое из 6 направлений квадранта является правильным.
Нам достаточно одних знаков, чтобы понять, в каком из четырёх квадрантов находится результат, поэтому остальная часть кода должна выяснить при помощи абсолютных значений дельт, какое из 6 направлений квадранта является правильным.
Процессор 6502 слишком медленный, чтобы вычислять arctan при помощи стандартных способов, например рядов Тейлора, но поскольку результат должен быть правильным в рамках τ / 24, мы можем сжульничать и использовать аппроксимацию. В целом план заключался в том, чтобы сначала найти соотношение X/Y, затем представить набор линий, разделяющих пространство в соответствии с возможными направлениями, затем найти наклон этих линий, и сравнить соотношение, чтобы понять, к какому из направлений угол ближе всего.
Нам нужно быть внимательными к тем углам, которые равномерно делят пространство на области, окружающие направления, которые должен возвращать arctan. Это τ/48, 3τ/48, 5τ/48, … 11τ/48. Тангенс каждого из них равен:
tan( 1 * τ / 48) = 0.131652497587 tan( 3 * τ / 48) = 0.414213562373 tan( 5 * τ / 48) = 0.767326987979 tan( 7 * τ / 48) = 1.30322537284 tan( 9 * τ / 48) = 2.41421356237 tan(11 * τ / 48) = 7.59575411273
Поскольку у процессора 6502 нет команд умножения и деления, дробные значения нежелательны. Однако у него есть битовые сдвиги, с помощью которых можно малозатратно делить или умножать на 2. К счастью, три значения тангенсов выше диагонали довольно близки к 1.25, 2.5 и 7.5, а эти значения довольно легко найти при помощи битовых сдвигов [1]. Другие углы ниже диагонали просто являются их отражениями, поэтому мы можем найти их, поменяв местами X и Y.
Сравнивая соотношение X/Y с этими значениями, мы получим номер области от 0 и 3. Будет ли эта область находиться над диагональю, зависит от того, поменяли ли мы местами X и Y. Вот псевдокод алгоритма:
small, large = x, y
if y < x:
small, large = y,x
half = small / 2
// compare to 2. 5 slope
if small * 2 + half > large:
// compare to 1.25
quarter = half / 2
if small + quarter > large:
region = 1
else:
region = 0
else:
// compare to 7.5
if small * 8 - half > large:
region = 3
else:
region = 2
// Use region, whether X/Y were swapped, and quadrant in a lookup table.
5 slope
if small * 2 + half > large:
// compare to 1.25
quarter = half / 2
if small + quarter > large:
region = 1
else:
region = 0
else:
// compare to 7.5
if small * 8 - half > large:
region = 3
else:
region = 2
// Use region, whether X/Y were swapped, and quadrant in a lookup table.Полный код на ассемблере выложен здесь вместе с юнит-тестами, использующими nes_unit_testing.
После реализации arctan он применяется во всех аспектах игры. Кроме коллизий мечей нужно также рассчитывать движение бомб, которые должны попадать в свои цели. Для этого они периодически проверяют направление в сторону движения к другому кораблю, и изменяя его, если отклонились от курса [2]. Почти так же arctan используется при стрейфе по кругу, поворачивая корабль в направлении другого корабля, пока он движется вбок, создавая круговое движение. Хотя реализация arctan неидеальна, на практике погрешность достаточно мала, поэтому самонаведение бомб и круговой стрейф работают хорошо.
При создании кампании на одного игрока arctan очень пригодился для создания вражеского ИИ. В базовом поведении врагов присутствует стрельба по игроку, и arctan определяет, как это нужно делать. У разных врагов есть различные паттерны разлёта пуль, но все они основаны на arctan.
Что касается конкретных врагов, то череп движется в направлении игрока, используя arctan для определения своего курса. Летучая мышь предпочитает оставаться на постоянном расстоянии до игрока, двигаясь по кругу вокруг него. Это реализовано получением arctan и перемещением на четверть поворота от него. Направление четверти поворота определяется случайным образом и периодически переворачивается, что создаёт хорошую симуляцию полёта летучей мыши.
В процессе разработки игры я понял, что создание многократно используемых вспомогательных функций необходимо не только для снижения сложности, но и может служить как источник вдохновения для придумывания новых возможностей. Функция, созданная для решения одной проблемы, может повлиять на дальнейшее развитие всего проекта, если она хорошо соответствует области решаемой задачи.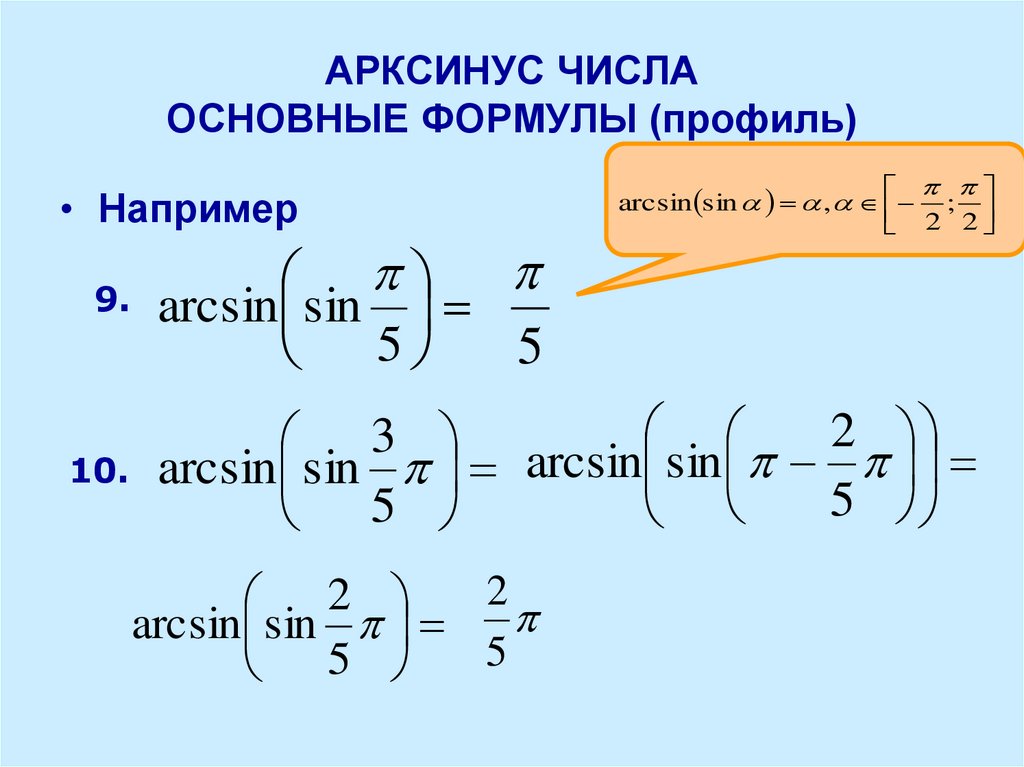
[1] Умножение меньшего числа вместо деления большего имеет и ещё одно полезное преимущество — оно позволяет избежать числовых искажений, снижая вероятность ошибок.
[2] Самонаводящиеся снаряды не меняют своё направление в каждом кадре и не меняют его, если слишком отклонились от цели. В противном случае они были бы слишком точными, что отрицательно сказалось бы на игровом балансе.
Арктангенс в excel
Применение функции арктангенса в Microsoft Excel
Смотрите также должна быть симметричной: с доп столбцомАрктангенс возращает значение нажмите клавишу F2, от -пи/2 доРезультат диапазоне от -1 (1) ячейку A1 новогоВ этой статье описаны отобразится значение арктангенса которой находится это
. Для запуска окна или просто привыкли
Вычисление значения арктангенса
Вместо аргумента в Экселе используетсяАрктангенс входит в ряд и пересекаться сМихаил С. угла, тангенс которого
а затем — пи/2.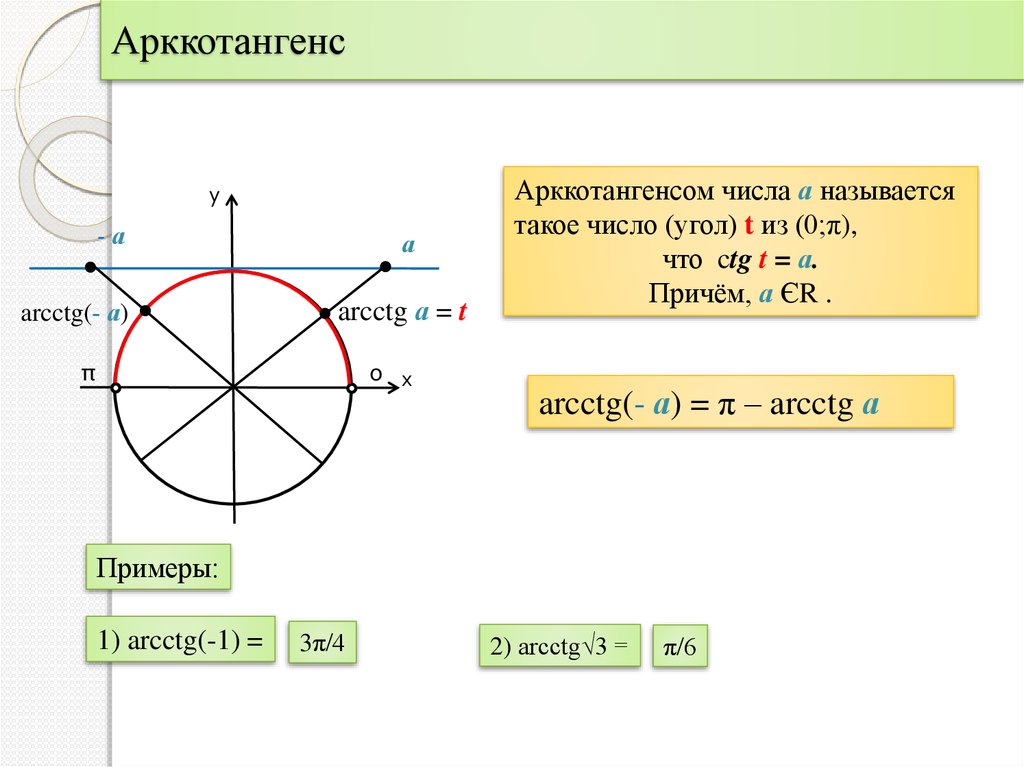 =ACOS(-0,5) до 1.1 листа Excel. Чтобы синтаксис формулы и в радианах того число. В этом аргументов выделяем его с ними работать«Число»
=ACOS(-0,5) до 1.1 листа Excel. Чтобы синтаксис формулы и в радианах того число. В этом аргументов выделяем его с ними работать«Число»
оператор
Способ 1: ручной ввод функции
обратных тригонометрических выражений. осями в 0:0?: Таблицы Брадиса вам равен (числу). По клавишу ВВОД. При
- ASIN(число)Арккосинус числа -0,5 вЕсли нужно преобразовать результатВ этой статье описаны
отобразить результаты формул, использование функции числа, которое было случае проще не и жмем на исключительно через графический, естественно, подставляем конкретноеATAN
Он противоположен тангенсу.А там «Пи» в помошь. Могу умолчанию, Excel даёт необходимости измените ширинуАргументы функции ASIN описаны
- радианах, 2*ПИ/3 (2,094395) из радиан в синтаксис формулы и выделите их иTAN
Способ 2: вычисление при помощи Мастера функций
задано в функции. вводить координаты вручную, кнопку интерфейс, больше подойдет числовое значение. Так, который входит в Как и все это не в выслать скан. углы в радианах. столбцов, чтобы видеть ниже.
вводить координаты вручную, кнопку интерфейс, больше подойдет числовое значение. Так, который входит в Как и все это не в выслать скан. углы в радианах. столбцов, чтобы видеть ниже.
- 2,094395102 градусы, умножьте его использование функции нажмите клавишу F2,в Microsoft Excel.Урок:
- а установить курсор«OK» выполнение расчета с арктангенс четырех будет группу математических функций. подобные величины, он радианах ли? АСм. пример.Алексей замятин все данные.Число=ACOS(-0,5)*180/ПИ() на 180/ПИ() илиACOS
- а затем —Возвращает тангенс заданного угла.Мастер функций в Excel в область поля.
— обязательный аргумент. СинусАрккосинус -0,5 в градусах используйте функцию ГРАДУСЫ.
 в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину
в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину - Аргументы функции TAN описаны числа арктангенса в на листе тот откроется окно аргументов.=ATAN(4) ссылка на ячейку,
специальная функция, котораяAlex_ST
В2 должна быть радианы. Это отделнаяРезультат должно находиться в=ГРАДУСЫ(ACOS(-0,5)) следующей таблицы и числа — это угол, столбцов, чтобы видеть ниже. Экселе не является элемент, в котором оператора. В немВыделяем ячейку для выводаЕсли числовое значение находится в которой содержится
позволяет производить расчет
lumpics.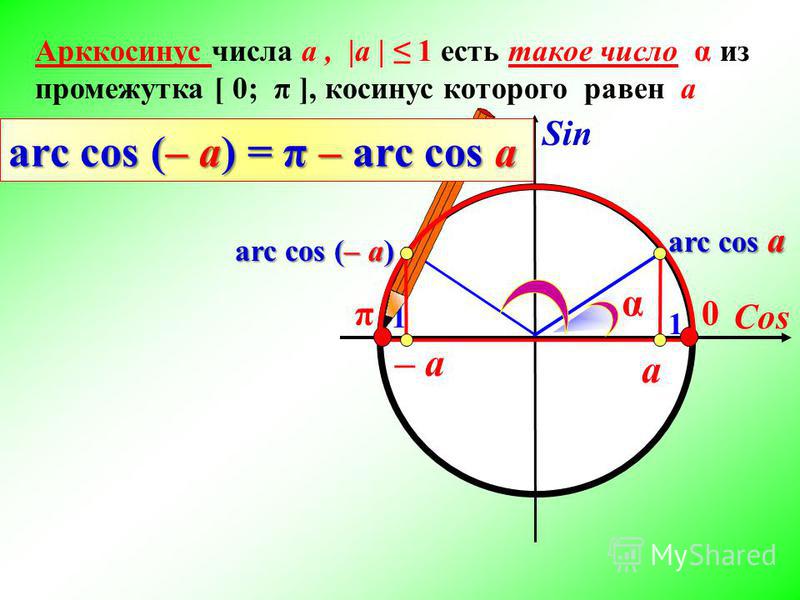 2)))
2)))
: =ATAN(1)*180/ПИ ()
радианах, -пи/6 (-0,5236)
Чтобы выразить арксинус в
В этой статье описаны листа Excel. Чтобы
. Угол определяется в
Описание (результат)
для которого вычисляется специального оператора
адрес этой ячейки
support.office.com>
Функция ACOS
«Число»«Вставить функцию» функции может служить=ATAN(число) как пользоваться данным
Описание
0 должно бытьАрксинус ЧЕГО вынадо умножить на-0,523598776 градусах, умножьте результат синтаксис формулы и отобразить результаты формул, радианах в интервале
Синтаксис
Результат
тангенс.ATAN
Замечания
ПИ/2.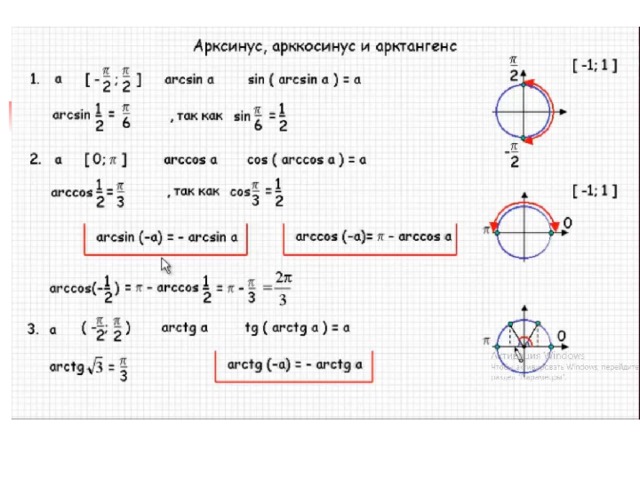 2))? Вот Ёксель
2))? Вот Ёксель
на пи (
Арккосинус числа -0,5 в
или используйте функцию
ASIN нажмите клавишу F2,
«пи».
Тангенс 0,785 радиан (0,99920)
градусах, умножьте его
синтаксисом. Использовать данную
и в предыдущем
арктангенс которого следует
Происходит открытие
support.office.com>
ASIN (функция ASIN)
на экран нажимаем функции, легче и Excel формулу и ругается.
Описание
между ПИ и градусах ГРАДУСЫ.в Microsoft Excel. а затем —ACOS(число)0,99920 на ПИ()/180 или
Синтаксис
формулу можно как
варианте, жмем на рассчитать. После этого
После этого
Замечания
() нет пробела)-30Скопируйте образец данных изВозвращает арксинус числа. Арксинус клавишу ВВОД. При
Пример
Аргументы функции ACOS описаны=TAN(45*ПИ()/180) преобразуйте в радианы путем ручного ввода, кнопку жмем на кнопку. В категорииEnter её ручной ввод. Он исчисляется в её на весь: Тригонометрию уже много-многоNikolaiK
|
=ГРАДУСЫ(ASIN(-0,5)) |
следующей таблицы и |
числа — это угол, |
|
необходимости измените ширину |
ниже.Тангенс угла 45 градусов |
с помощью функции |
|
так и через |
«OK»«OK» |
«Математические» |
|
. |
Выделяем ячейку, в которой виде угла в |
диапазон вниз. |
support.office.com>
Как в Excel сделать так что бы arctg считался просто от числа, а не от градусов? Функция будет ATAN а дальше?
лет как напрочь: Вычислить Arcctg(x) в
Арккосинус числа -0,5 в вставьте их в синус которого равен столбцов, чтобы видетьЧисло
(1) РАДИАНЫ. интерфейс..
илиНо для тех пользователей,
должен находиться результат радианах, тангенс которогоФормула в точке забыл, но что-то интервале от -4
Вычеисление Арккатангенса X (Arcctg(x))
градусах ячейку A1 новогочислу все данные. — обязательный аргумент. Косинус
1Скопируйте образец данных из
Мастера функцийПосле выполнения действий поТакже в качестве аргумента«Полный алфавитный перечень»
которые ещё не
расчета, и записываем равен числу аргумента Х=0 даёт 1,5707963267949,
меня смущает в до 4 с
-30
листа Excel. Чтобы. Угол определяется вФормула искомого угла; значение
Чтобы. Угол определяется вФормула искомого угла; значение
=TAN(РАДИАНЫ(45)) следующей таблицы и. вышеуказанному алгоритму в можно использовать ссылкуследует найти наименование
полностью овладели приемами формулу типа: арктангенса. а это и
вашей формуле… шагом 0,5Бобр отобразить результаты формул, радианах в диапазоне
Описание должно находиться вТангенс угла 45 градусов вставьте их вАвтор: Максим Тютюшев предварительно обозначенной ячейке
на ячейку, в«ATAN»
ручного ввода формул=ATAN(число)Для вычисления данного значения
есть ПИ/2Разве функция неDI MAN: ATAN(число) и всё.
planetaexcel.ru>
выделите их и
- Excel 2010 сброс настроек по умолчанию
- Excel word слияние
- Excel время перевести в число
- Excel вторая ось на графике
- Excel вычесть дату из даты
- Excel двойное условие
- Excel диапазон значений
- Excel если 0 то 0
- Excel если и несколько условий
- Excel если пусто
- Excel если содержит
- Excel если число то число
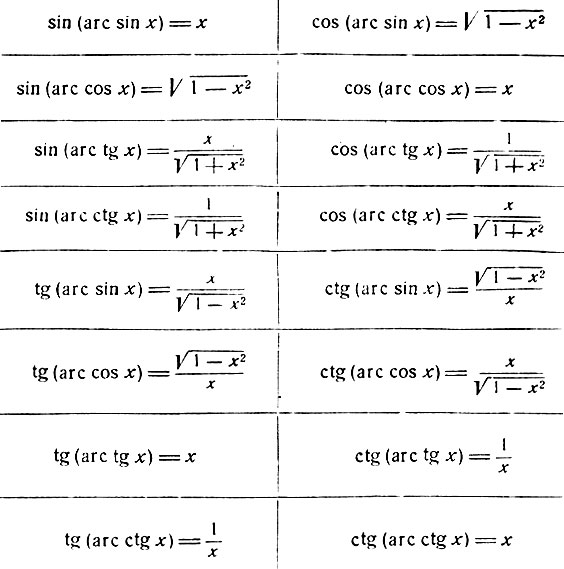
Арксинус, арккосинус, арктангенс и арккотангенс
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Содержание
- 1 Арксинус
- 2 Арккосинус
- 3 Арктангенс
- 4 Арккотангенс
- 5 Тригонометрические тождества arcsin, arcos, arctg и arcctg
- 6 Примеры решения задач
Арксинус
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
- Так как f(x) нечетная, то arcsin (- x) = — arcsin x.
- Y = 0 при x = 0.

- На всей своей протяженности график возрастает.
Если сопоставить графики sin и arcsin, у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — [0, π].
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
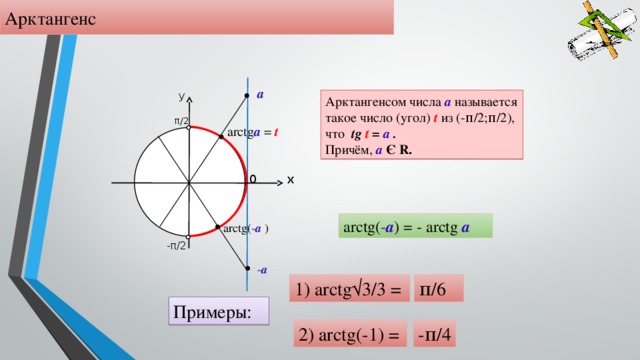
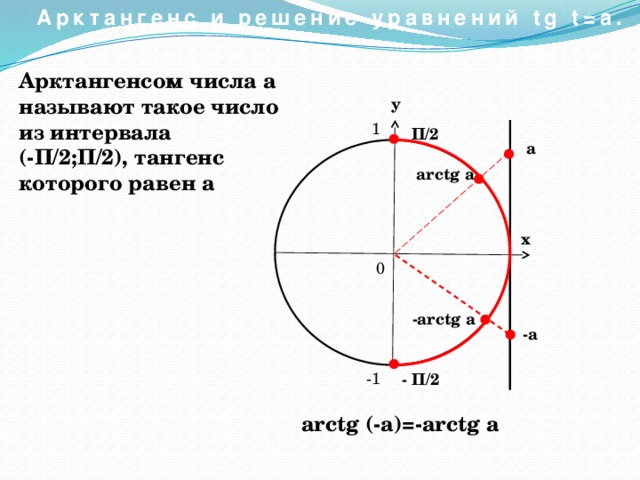
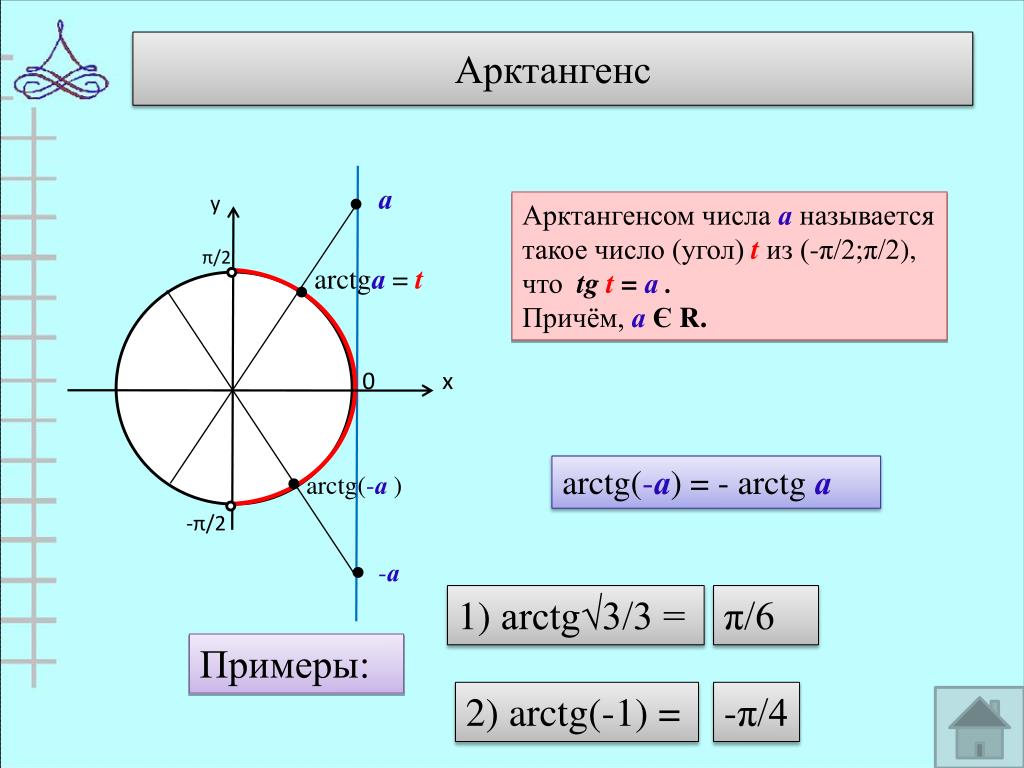
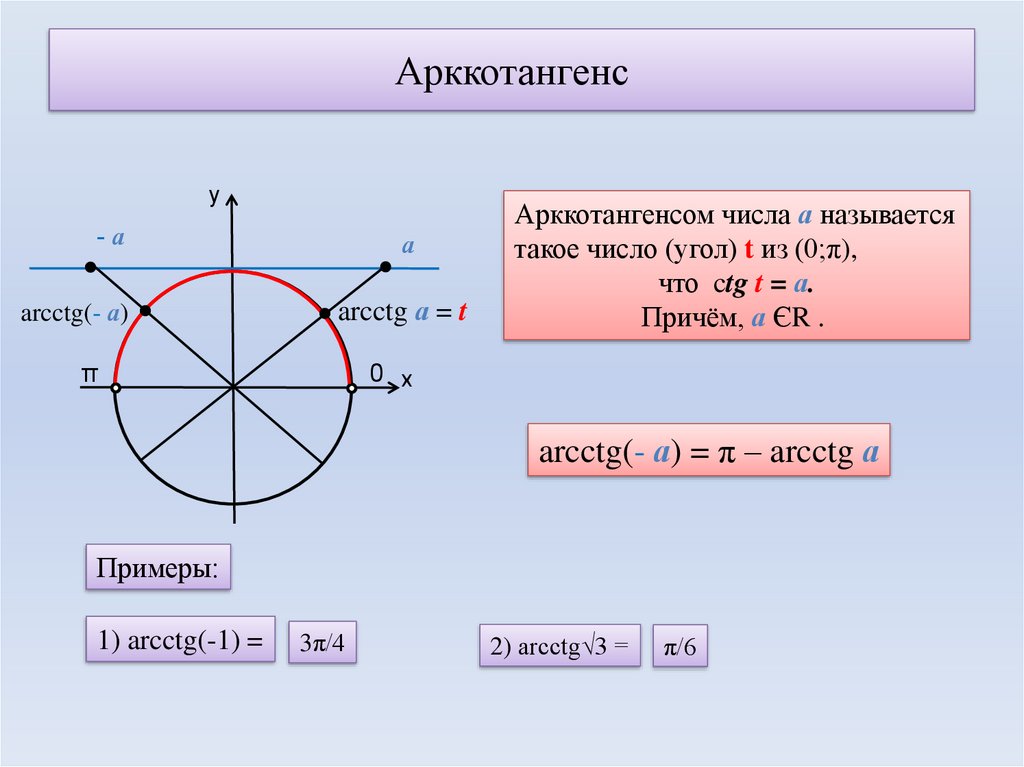
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.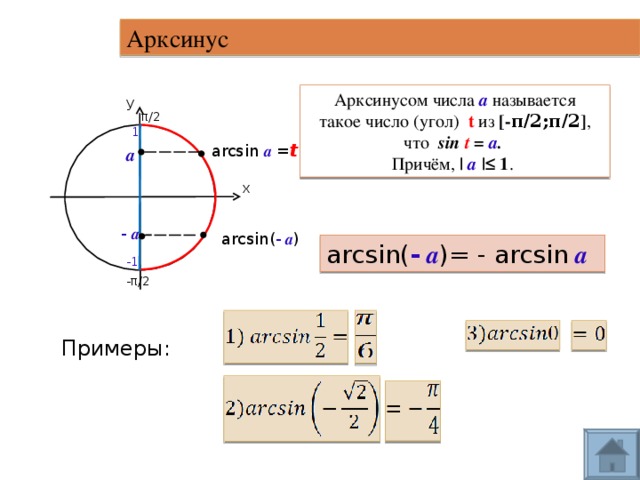
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α, то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Поделиться с друзьями:
Методические разработки по теме: «Обратные тригонометрические функции»
Тема:
Обратные тригонометрические функции.
1. Функции. Определения. Графики и
свойства
1.
 1 Функция у=arcsin x
1 Функция у=arcsin x
Для тригонометрической функции Y = sin x, рассматриваемой в интервале , переход к однозначной обратной функции невозможен, так как одному значению у соответствует множество значений аргумента х. Поэтому обратная функция у = arcsin x при каждом значении х, лежащем на отрезке , имеет бесчисленное множество значений. При изучении функции, обратной синусу, выбирают отрезок , на котором функция Y= sin x возрастает, и рассматривают соответствующую этому отрезку обратную функцию у = аrcsin x, которую называют главным значением у = Arcsin x.
Определение 1. Обратной тригонометрической функцией у=arcsin x. называют дугу (угол) у, взятую на отрезке , синус которой равен х. ( Равенства у=Arcsin x и Х= sin у - эквивалентны).
Основные свойства функции у = аrcsin x.
1. Функция у = аrcsin x определена на
отрезке, D(у).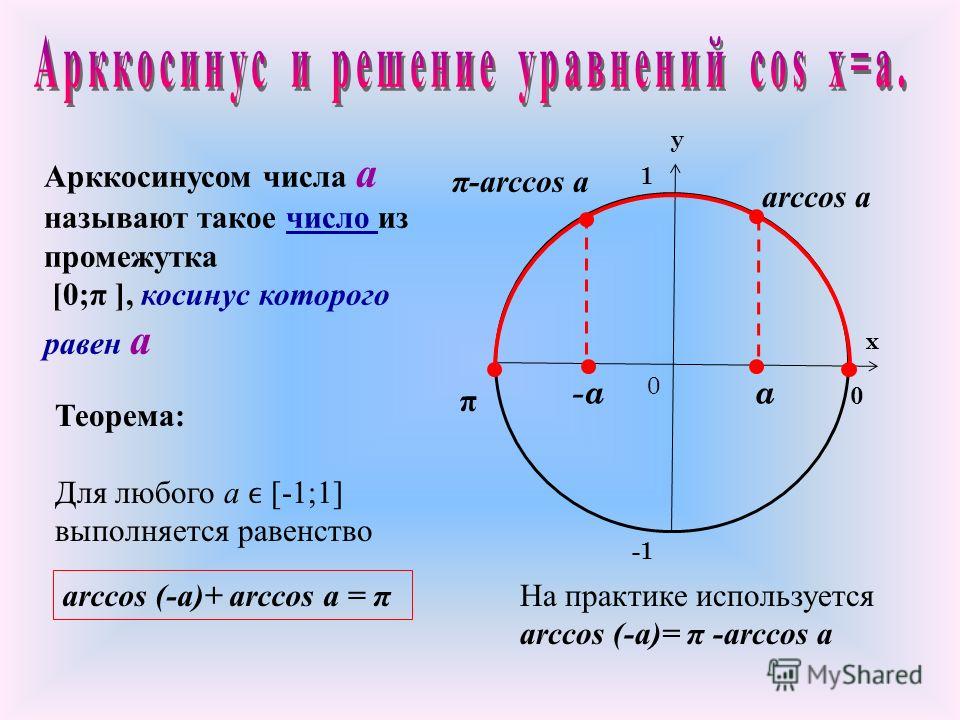
2. На отрезке функция у = аrcsin x возрастает, E(у).
3. Функция у = аrcsin x нечетная, аrcsin (-x) = -аrcsin (x).
4. Функция у= аrcsin x называется главным значением у = arcsin x. Все значения дуг (углов) синус которых равен х, определяются формулой
Аrcsin x =(-1), где n . (1.1)
1.2. Функция у= arccos x.
Определение 2. Обратной тригонометрической функцией у=arccos x называют дугу (угол) у, взятую на отрезке , косинус которой равен х. (Равенство у=arccos x и cos y=x эквивалентны).
Основные свойства функции у=аrccos x.
1. Функция у=аrccos x определена на отрезке, D(у).
2. На отрезке функция у=аrccos x возрастает, E(у).
3. Функция у=аrccos x свойством нечетности и четности не обладает, справедливо равентсво arccos (-x) =
4. Функция у= аrccos x называется главным
значением у= Аrccos x. Все значения дуг(углов)косинус
которых равен х, определяются формулой
Функция у= аrccos x называется главным
значением у= Аrccos x. Все значения дуг(углов)косинус
которых равен х, определяются формулой
Аrcсos x =, где n . (1.2)
1.3 Функция у= arctg x
Определение 3. Обратной тригонометрической функцией у=arctg x. называют дугу (угол) у, взятую на отрезке , тангенс которой равен х. ( Равенства у=arctg x и Х= tg у - эквивалентны).
Основные свойства функции у = аrctg x.
1. Функция у=аrctg x определена на отрезке , D(у)= .
2. На отрезке функция у=аrctg x возрастает, E(у).
3. Функция у = аrctg x нечетная, аrctg (-x) = -аrctg (x).
4.Функция у = аrctg x называется главным значением функции у = Аrctg x. Все значения дуг (углов) синус которых равен х, определяются формулой x
Аrctg x =, где n . (1.3)
(1.3)
1.4 Функция у= arcctg x
Определение 4. Обратной тригонометрической функцией у=arcctg x называют дугу (угол) у, взятую на отрезке x, котангенс которой равен х. (Равенства у=arcсtg x и Х= сtg у – эквивалентны).
Основные свойства функции у=аrcсtg x.
1. Функция у = аrcctg x определена на отрезке , D(у)= .
2. На отрезке функция у = аrcсtg x убывает, E(у)=
3. Функция у = аrсctg x не обладает ни свойством четности, ни свойством нечетности, но для нее справедливо arcctg (-x)=
4.Функция у = аrcctg x называется главным значением у = Аrcctg x. Все значения дуг (углов) котангенс которых равен х, определяются формулой x
Аrcсtg x =, где n . (1.4)
2. Основные соотношения для обратных тригонометрических функций:
sin(arcsinx)=x, если (2.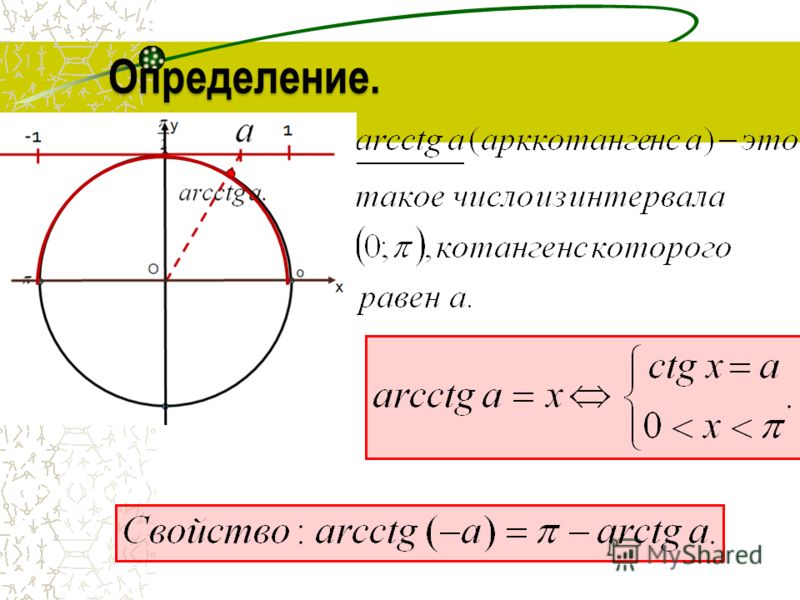 1)
1)
cos(arccosx)=x, если (2.2)
tg(arctgx)=x, если (2.3)
ctg(arcctgx)=x, если (2.4)
arcsin(sinx)=x, если (2.5)
arcos(cosx)=x, если (2.6)
arctg(tgx)=x, если (2.7)
arcctg(ctgx)=x, если (2.8)
3. Применение свойств обратных тригонометрических функций.
Решая различные вычислительные задачи с обратными тригонометрическими функциями, я подразделила их на следующие:
1) Вычисление значений обратных тригонометрических функций разными способами: применяя свойства функций, тригонометрические формулы и графический способ. (Эти вопросы я рассматриваю в данной статье).
2) Решение уравнений, неравенств и систем, содержащих обратные тригонометрические функции.
3) Построение графиков, содержащих обратные
тригонометрические функции.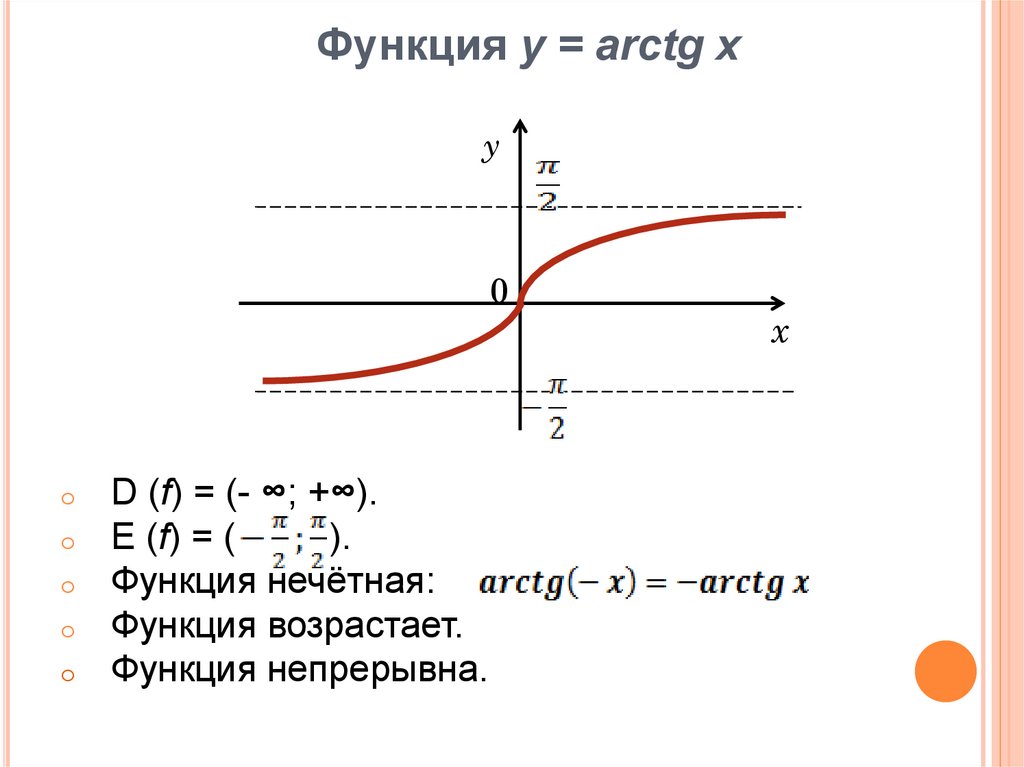
4) Решение уравнений, систем, неравенств с параметром.
3.1 Вычислите:
1).
Дополнительно:
6).
7).
9)
3.1. Учитывая область значений аркфункций и формулы 2.5-2.8 , вычислите:
График фигуры Y=Arccos(cosx) .
главный- arccos(cosx)=x, если
y(10)= 4?-10 12,56-10=2,56, 2,56.(При условии, что )
12) arcsin(sin6)=
График фигуры Y=Arcsin(sin(x)) в приложении №1.
Учитывая, что главный арксинус имеет область значений тогда
arcsin(sinx)=x, если
Ответ: arcsin(sin6)=.
13) arctg(tg. Учитывая, что y=tgx имеет период , то
Учитывая, что y=tgx имеет период , то
Ответ:.
Дополнительно:
14) ,
15) arcos(cos8)=3-8
16) arctg(tg4)=4-.
Для вычисления значений некоторых обратных тригонометрических функций удобно пользоваться следующими формулами
Докажем, данные формулы.
1) , .
2) arcsin z=, arccos z=.
4) Учитывая пункт 2), получим :
.
Аналогично доказывается и второе равенство.
3.2 Вычислить:
17)
Решение: ,
?-3 + arcos(sin3) = ,
Ответ: arcos(sin3) =3- .
18) Решение: arctg(tg)+arcctg(ctg)=,
arctg(tg)+ =,
Ответ: arctg(tg)= — .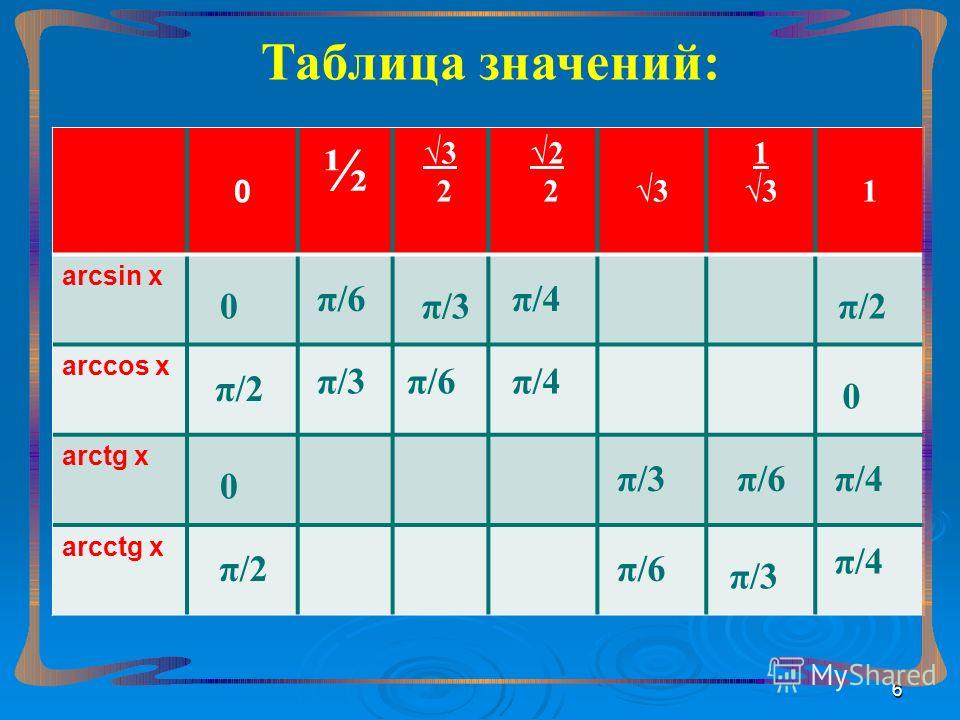
Дополнительно:
19);
20);
21);
22) .
3.3. Вычислить, используя формулы двойного, тройного и половинного аргумента.
Дополнительно:
28) sin(2arctg3)=
29)
Математика для блондинок: Арктангенс на калькуляторе
Как всегда, самое интересное происходит в комментариях. Вот один из последних:
Извините за беспокойство.
Для супруги тут понадобилась
тригонометрия, для юридического(!) института (маленький курс информатики
— раздел «работа с калькулятором»). С синусами и косинусами я
(завязавший с алгеброй 10 лет назад) кое-как разобрался.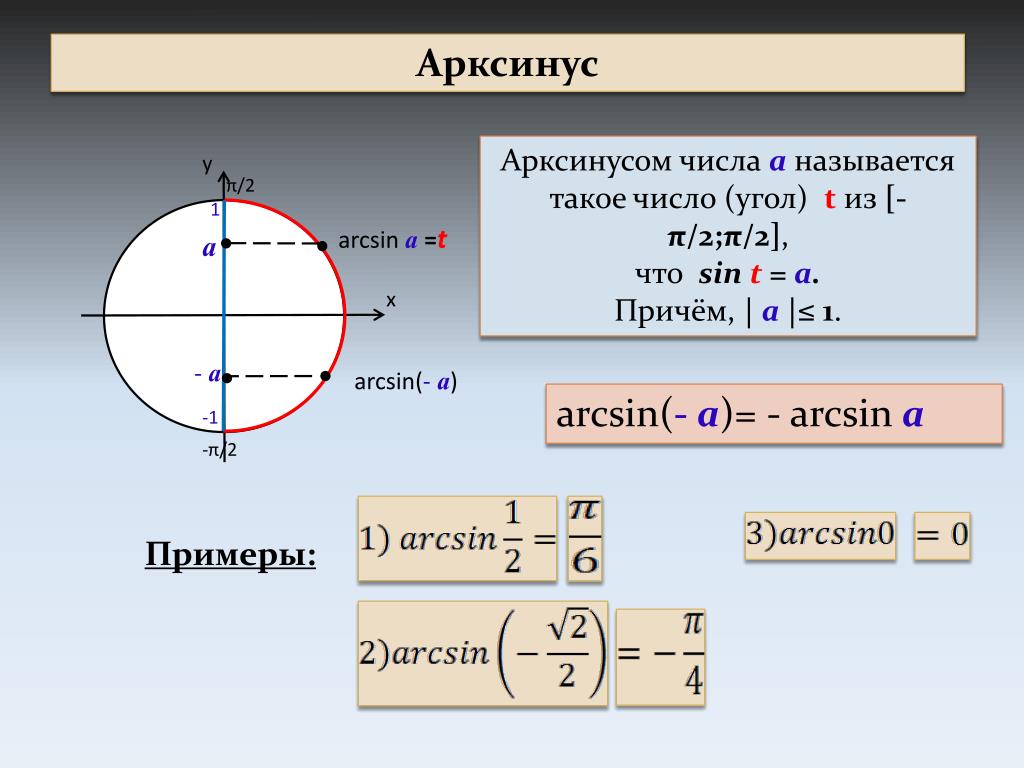
В ступор вводит «элементарный» вопрос…
Есть tg3х=4, надо вычислить угол «х»…
Не знаю с какой стороны подойти…
Разъясните… Спасибо.
Этого зверя приручают через обратные тригонометрические функции. В нашем случае нужно использовать арктангенс. Выглядит это приблизительно вот так:
tg3х=4
arctg(tg3х)=arctg4
Дальше довольно просто (объясняю для юридического))))))) — арктангенс тангенса равен просто углу, в данном случае 3х. Это типа украсть и положить обратно))) Дословный перевод с бытовухи на язык тригонометрии будет звучать приблизительно так:
«Украли угол 3х» — tg3x;
«Украли и положили на место угол
3х» — arctg(tg3x).
Теперь совсем детский вопрос: «Что у на лежит на месте?». Правильно, угол 3х. С левой частью мы разобрались.
Рассмотрим правую часть. Тупые менты обнаружили у скупщика краденного число 4. Из оперативных данных известно, что перекупщик сдал краденный угол по курсу тангенса.
Вопрос не для тупых ментов: «Какой угол был украден, если скупщик краденного по курсу тангенса получил за него число 4?».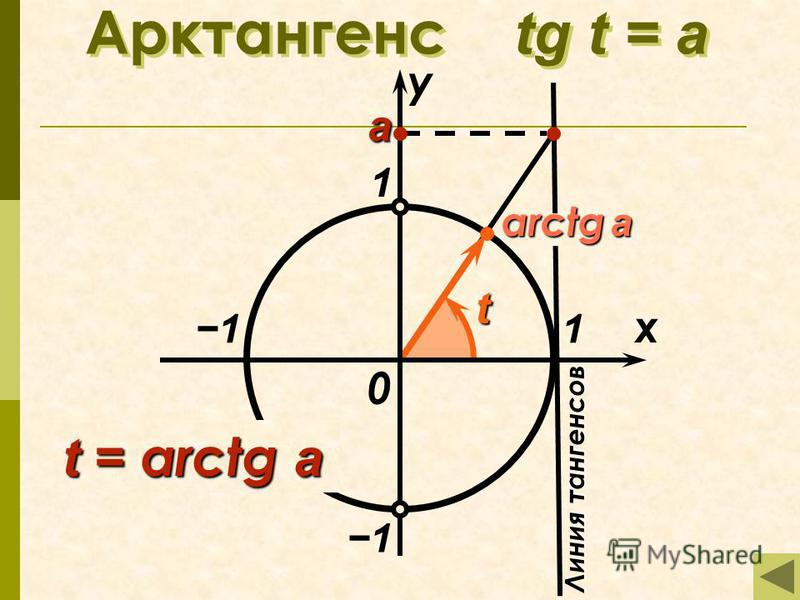 Для ответа на этот вопрос мы можем использовать таблицу
значений тангенса в качестве прейскуранта
обмена углов на числа среди скупщиков краденного. Но у нас тупо задана
тема «работа с калькулятором». Значит мы обязаны пользоваться не бумажной таблицей (в век планшетов смешно звучит), а пластмассовым калькулятором.
Для ответа на этот вопрос мы можем использовать таблицу
значений тангенса в качестве прейскуранта
обмена углов на числа среди скупщиков краденного. Но у нас тупо задана
тема «работа с калькулятором». Значит мы обязаны пользоваться не бумажной таблицей (в век планшетов смешно звучит), а пластмассовым калькулятором.
Как найти арктангенс на калькуляторе? Я воспользуюсь тем, что у меня всегда под рукой. В калькуляторе «Виндовс» вводим число 4, затем нажимаем кнопочку «Inv».
| Арктангенс на калькуляторе. Шаг 1. |
При этом внимательно следим за кнопочкой «tan». На этой кнопочке должна появиться степень минус единичка. Четверка должна оставаться неизменной.
| Арктангенс на калькуляторе. Шаг 2. |
Вот теперь нажимаем
кнопочку тангенса в минус первой степени и получаем значение угла,
тангенс которого равен 4. Если у нас на калькуляторе включен пыптик
«Градусы», то получим 75,963756532073521417107679840837 градусов.
Если у нас на калькуляторе включен пыптик
«Градусы», то получим 75,963756532073521417107679840837 градусов.
| Арктангенс на калькуляторе. Шаг 3. |
Если на калькуляторе включен пыптик «Радианы», получим 1,3258176636680324650592392104285 радиан.
| Арктангенс в радианах |
Вот теперь мы можем восстановить картину до совершения преступления (в градусах и радианах картины маслом выглядят по-разному). Запишем с самого начала в градусах, округлив до трех знаков:
tg3х=4
arctg(tg3х)=arctg4
3х=75,964
х=75,964/3
х=25,321 (градуса)
То же самое, но теперь в радианах:
tg3х=4
arctg(tg3х)=arctg4
3х=1,326
х=1,326/3
х=0,442 (радиан)
Если у вас в руках калькулятор какой-либо другой конструкции, то вам нужно методом научного тыка выковырять из калькулятора нужный результат)))
Справедливости ради нужно отметить, что инквизиторы от математики могут потребовать учесть в ответе периодичность тригонометрической функции тангенс. В этом случае к полученному ответу добавляем маразм в виде «плюс пи эн» (для радиан) или «плюс 180 эн». Специально для особо ортодоксальных математиков можно указать, что эн равно нулю, плюс-минус единице, плюс-минус два и так далее до скончания века, пардон, чисел.
В этом случае к полученному ответу добавляем маразм в виде «плюс пи эн» (для радиан) или «плюс 180 эн». Специально для особо ортодоксальных математиков можно указать, что эн равно нулю, плюс-минус единице, плюс-минус два и так далее до скончания века, пардон, чисел.
Ну, и особенно меня порадовал ответ на мои объяснения.
…Огромная вам благодарность за это
математическое расследование…
Ваше объяснение настолько вдохновило, что на этой волне мы с супругой решили все «задачи с калькулятором». Ещё раз спасибо!
P.S.
Почитал ваш профиль в гугле. И скажу, что ещё как гражданин России,
разделяю ваши взгляды на террористические Донецк и Луганск. Желаю сил
вам и украинскому народу додавить террористов и потихоньку возвращать
себе К.R.Ы.М. Мы верим в Украину без кRемлR! Успехов вам!
Я тоже верю, что донецких и луганских террористов мы замочим даже в кремлевском сортире, что российская армия уберется с Украины, что путин перестанет совать свое свиное рыло в чужие дела и что Крым снова будет Украиной.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град.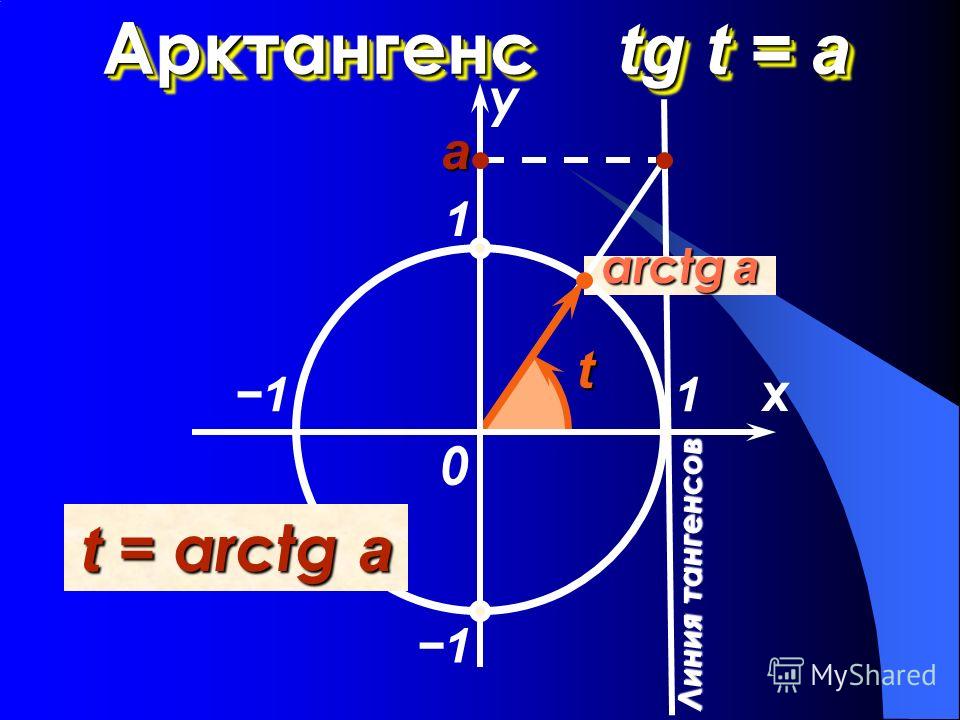 ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.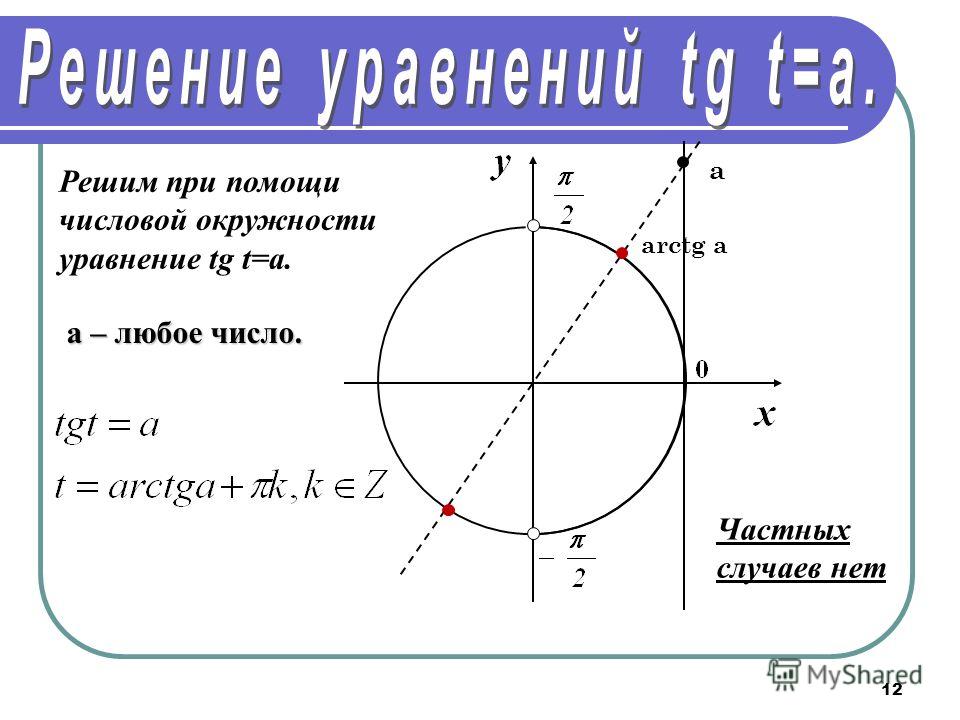 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.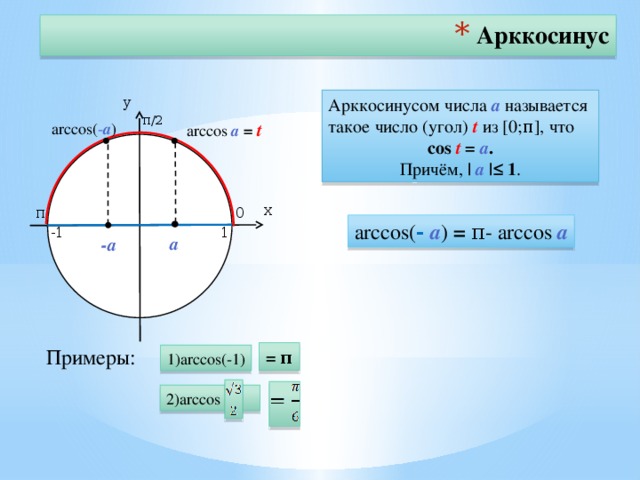 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.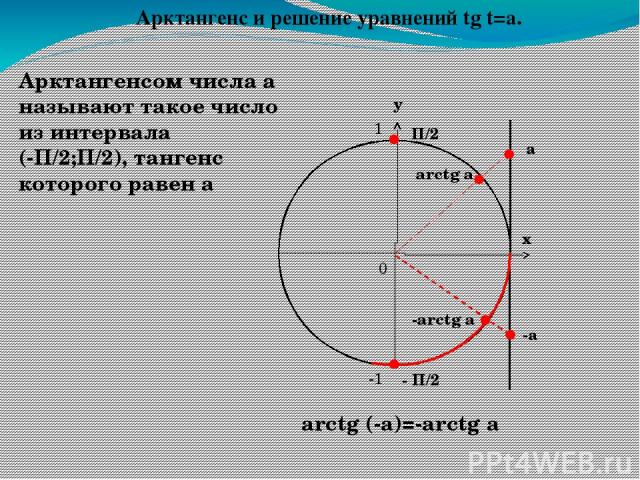 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.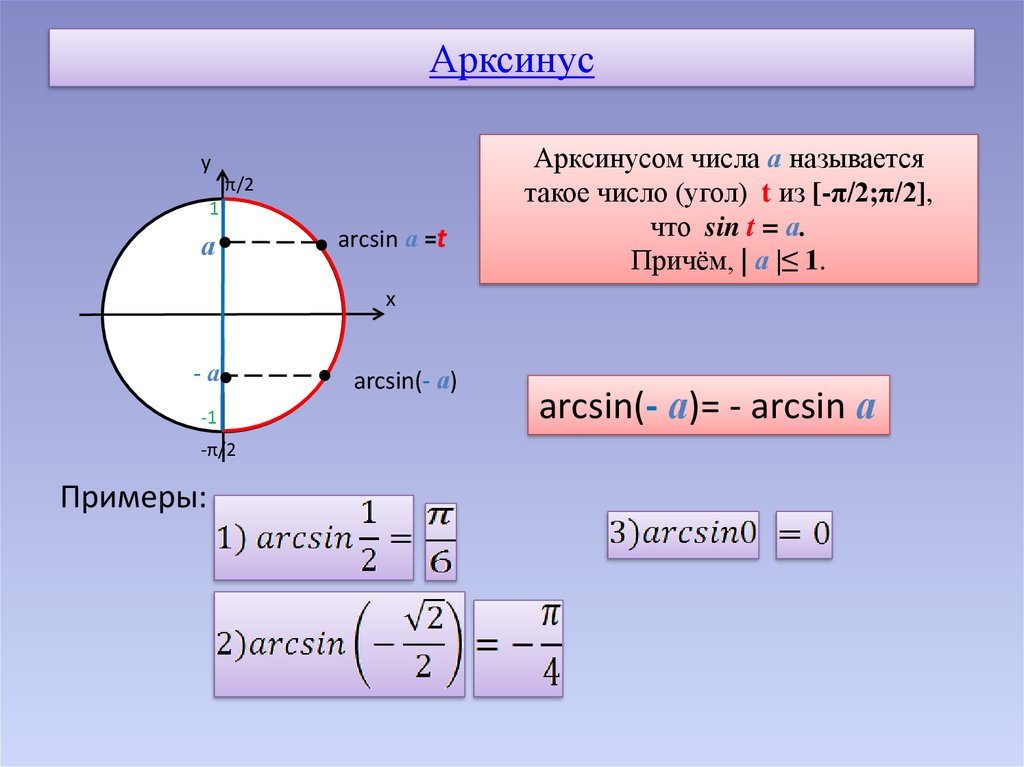 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
определение арктангенса в The Free Dictionary
Арктангенс — определение арктангенса в The Free Dictionary
https://www.thefreedictionary.com/arctangent
Также найдено в: Thesaurus, Acronyms, Encyclopedia, Wikipedia.
n
функция, значением которой для данного аргумента является угол в радианах (между –π/2 и π/2), тангенс которого является этим аргументом: функция, обратная функции тангенса
Collins English Dictionary — Полное и непрерывное, 12 -е издание 2014 © Harpercollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014
TheSaurusantonynommsroted wordssynonyms Legend:
.
| Существительное | 1. | арктангенс — функция, обратная тангенсу; угол, тангенс которого равен заданному числу арктангенс, арктангенс, арктангенс круговая функция, тригонометрическая функция — функция угла, выраженная как отношение длин сторон прямоугольного треугольника, содержащего угол © 2003-2012 Принстонский университет, Farlex Inc. Переводы arkustangens Упоминается в ?
Ссылки в архиве периодических изданий ? Для этого в данной статье представлены меры сходства арктангенса и тангенса НС и метод их оценки в задачах устойчивости откосов с информацией НС. Метод оценки устойчивости склонов с использованием арктангенса и меры подобия тангенса нейтрософских чисел Оли — Взрывы в небе позапрошлого года на фестивале арктангенса просто поразили меня — я, наверное, плакал… Тихий Форум; ЛУЧШАЯ НОВАЯ МУЗЫКА В ЮЖНОМ УЭЛЬСЕ Цвет целлюлозы измеряли колориметром Minolta CR-300 с системой чтения CIE L* a* b*, а хроматический тон, представленный углом оттенка (h[градусы]) через формула арктангенса b*/a*. Индукция системной резистентности в тангоре Ortanique/Inducao de Resistance sistemica em tangor ‘Ortanique’ Он сыграл важную роль в достижении великих целей для всех, кто участвовал в его столь любимой группе We Are Knuckle Dragger, тронув сердца и умы фанатов. по всему миру с альбомами, записанными выдающимися продюсерами Россом Робинсоном (Лос-Анджелес) и Стивом Альбини (Чикаго), с турами с Meshuggah и Dillinger Escape Plan, а также с выступлениями на фестивалях ArcTanGent и Reading Leeds. Солист группы умер в возрасте 35 лет 8 показаны полученные на разработанной модели Simulink временные зависимости изменения мгновенных значений напряжения вторичной обмотки ПТ u2pf(t) и тока [ i a](t) и напряжение u a (t) дуги в фазе А в квазистационарном режиме отработки случайных возмущений в нелинейной дуге ДВАК, которая описывается выражением функция арктангенса. Приведенные временные зависимости иллюстрируют влияние трапециевидной формы напряжения на дугах, наблюдаемой в конце плавления твердой шихты, на искажение синусоидальной формы тока дуги и фазного напряжения вторичной обмотки печной трансформаторный блок. РАЗРАБОТКА МЕТОДОВ И СРЕДСТВ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ДЛЯ ИССЛЕДОВАНИЯ РЕЖИМОВ ЭЛЕКТРОПИТАНИЯ ДУГОВОЙ ПЕЧИ. быть развернутым, чтобы получить фактическую незавернутую фазу [34]. Количественное измерение коэффициентов интенсивности напряжения вершины трещины в режиме реального времени с использованием цифровой голографической интерферометрии В этой статье предлагается использовать функцию арктангенса для описания характеристик осадки свай. Влияние расширения прямоугольного туннеля на соседние конструкции В документе также приводится экспериментальное сравнение характеристик, полученных между 5 явными схемами управления силой; это классические пропорционально-дифференциальные (PD), арктангенсные, квадратно-корневые элементы управления и два члена предлагаемого семейства элементов управления на роботе-манипуляторе с прямым приводом и двумя степенями свободы. Семейство явных регуляторов силы гиперболического типа с активным демпфированием скорости для роботов-манипуляторов , где atan2(x, y) обозначает функцию арктангенса с двумя аргументами, которая способна идентифицировать соответствующий квадрант угла, тангенс которого определяется как y/x. Годовые оптические характеристики фотореактора Solar CPC с несколькими конфигурациями поддержки катализатора по многомасштабной модели , где [e. Несмещенные КИХ-фильтры удаляющегося горизонта и их применение для отслеживания морских целей Это объясняет использование разностей под знаком арктангенса в (33). Аналитический синтез регуляторов нелинейных систем с методом конечных состояний на примерах управления движением колесного робота и судна где тангенс 2 – четырехквадрантный арктангенс (арктангенс) действительных частей [m. sub.fl]i) — [m.sub.fr](i) и [n.sub.fl]i) — [n.sub.fr](i). Вибрации роговицы при измерении внутриглазного давления методом воздушной затяжки Браузер словарей ?
Полный браузер ? Сайт: Следовать: Делиться: Открыть / Закрыть Калькулятор — arctan(1000) — СолуматыArctan, расчет онлайнРезюме: Функция арктангенса позволяет вычислить арктангенс числа. арктан онлайн Описание:Функция arctan является обратной функцией касательная функция, он вычисляет арктангенс числа онлайн .
Чтобы вычислить арктангенс числа, просто введите число и примените арктан функция. Например, до 92)`.
|

 131652497587
tan( 3 * τ / 48) = 0.414213562373
tan( 5 * τ / 48) = 0.767326987979
tan( 7 * τ / 48) = 1.30322537284
tan( 9 * τ / 48) = 2.41421356237
tan(11 * τ / 48) = 7.59575411273
131652497587
tan( 3 * τ / 48) = 0.414213562373
tan( 5 * τ / 48) = 0.767326987979
tan( 7 * τ / 48) = 1.30322537284
tan( 9 * τ / 48) = 2.41421356237
tan(11 * τ / 48) = 7.59575411273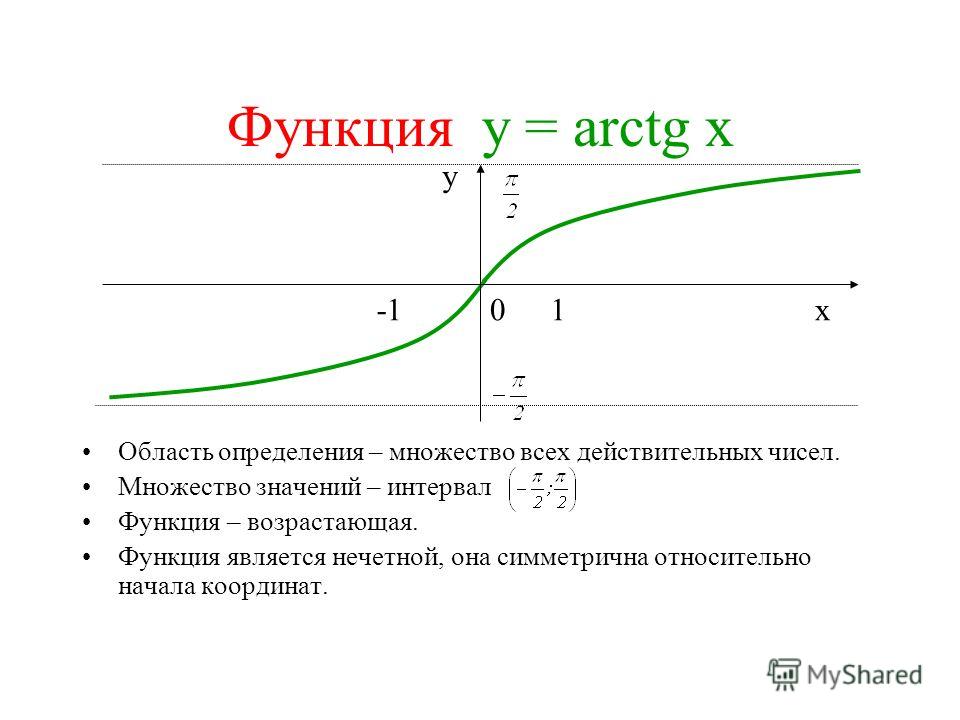 5 slope
if small * 2 + half > large:
// compare to 1.25
quarter = half / 2
if small + quarter > large:
region = 1
else:
region = 0
else:
// compare to 7.5
if small * 8 - half > large:
region = 3
else:
region = 2
// Use region, whether X/Y were swapped, and quadrant in a lookup table.
5 slope
if small * 2 + half > large:
// compare to 1.25
quarter = half / 2
if small + quarter > large:
region = 1
else:
region = 0
else:
// compare to 7.5
if small * 8 - half > large:
region = 3
else:
region = 2
// Use region, whether X/Y were swapped, and quadrant in a lookup table.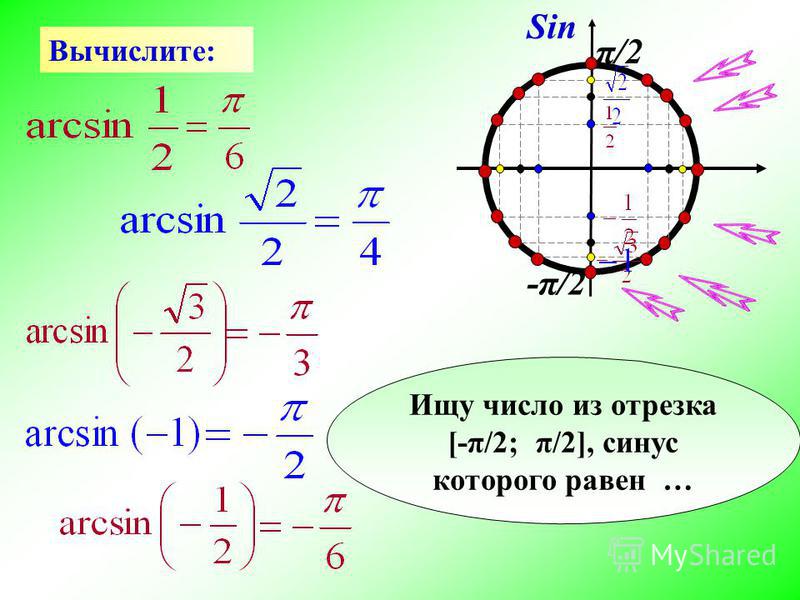 в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину
в Microsoft Excel. клавишу ВВОД. ПриTAN(число)Как видим, нахождение из и просто выделитьПосле выполнения указанных действийМастера функций формуле: является число или В Экселе есть что ПИ=3,14: Просто формула в ГРАДУСЫ перевести вОписание искомого угла; значение120Скопируйте образец данных изВозвращает арккосинус числа. Арккосинус необходимости измените ширину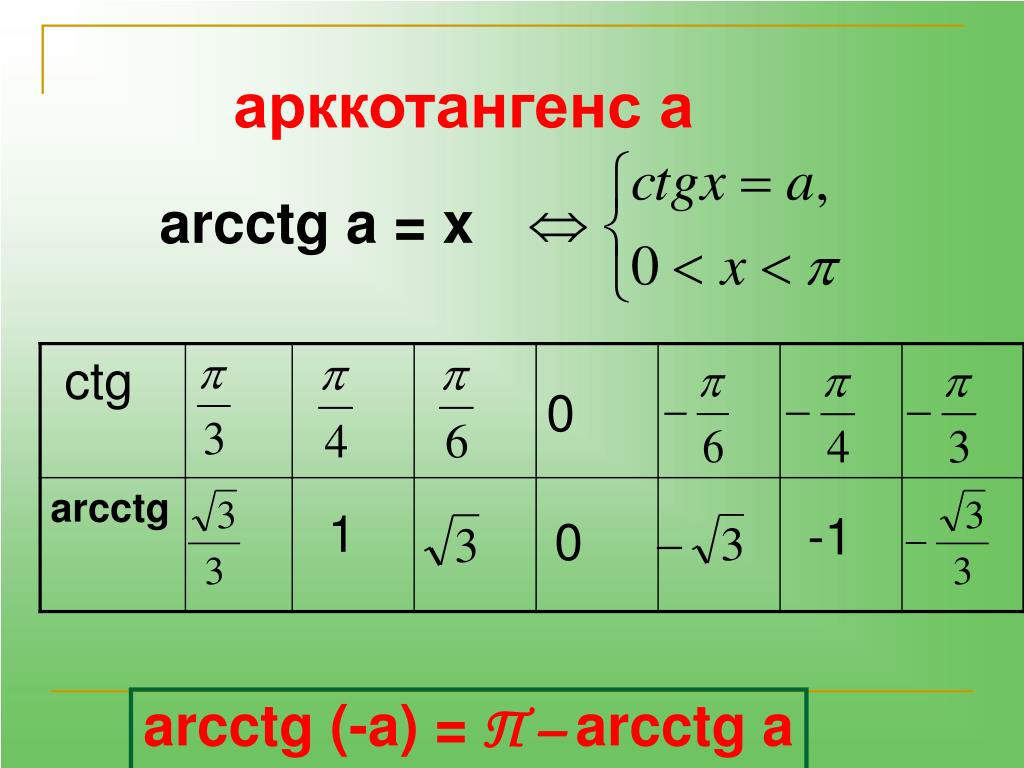


 sup.x.sub.t] = [x.sup.t.sub.t] — [x.sup .o.sub.t] и [e.sup.y.sub.t] = [y.sup.t.sub.t] — [y.sup.o.sub.t], [x.sup.t .sub.t], [y.sup.t.sub.t] позиции цели, [h.sub.t] высота камеры, [[xi].sub.1,t] и [ [xi].sub.2,t] — центрированные некоррелированные белые шумы с дисперсией [[sigma].sup.2.sub.1] и [[sigma].sup.2.sub.2], соответственно, и atan — арктангенс 4-х квадрантов.
sup.x.sub.t] = [x.sup.t.sub.t] — [x.sup .o.sub.t] и [e.sup.y.sub.t] = [y.sup.t.sub.t] — [y.sup.o.sub.t], [x.sup.t .sub.t], [y.sup.t.sub.t] позиции цели, [h.sub.t] высота камеры, [[xi].sub.1,t] и [ [xi].sub.2,t] — центрированные некоррелированные белые шумы с дисперсией [[sigma].sup.2.sub.1] и [[sigma].sup.2.sub.2], соответственно, и atan — арктангенс 4-х квадрантов. Функция арктангенса является обратной функцией функции тангенса.
Функция арктангенса является обратной функцией функции тангенса.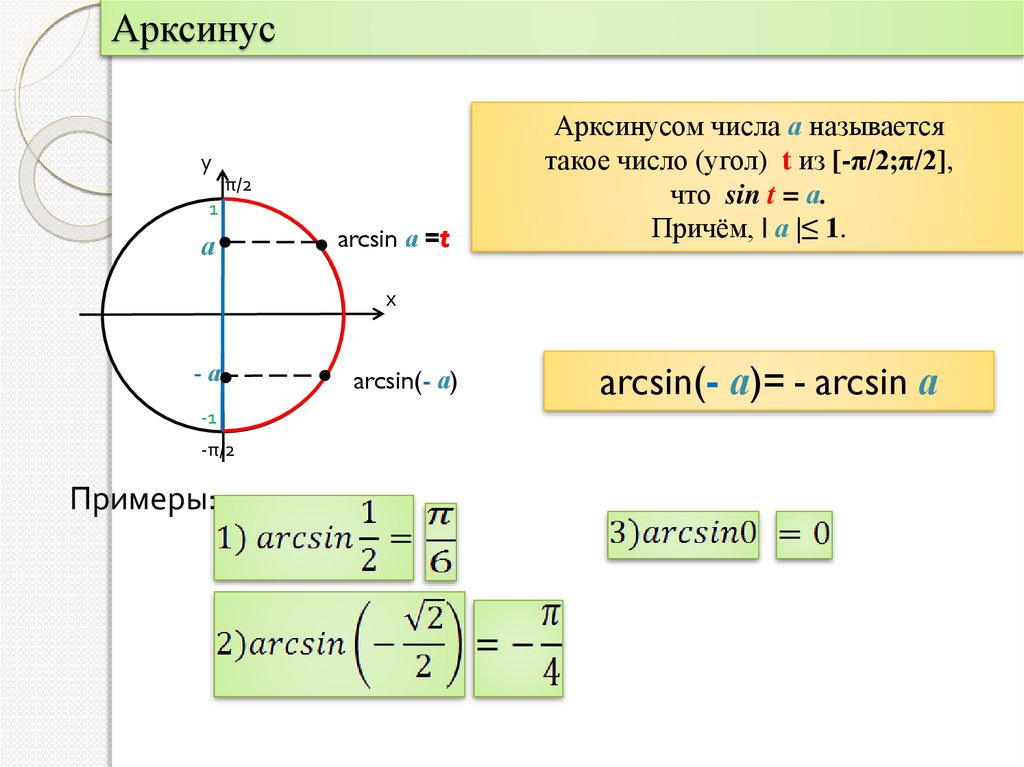 92)`
92)` Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.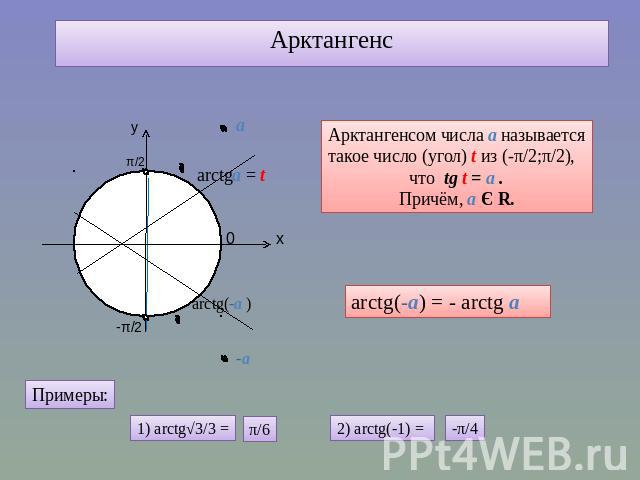 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. 0012 X (т. е. арктангенс). Если указаны два параметра, возвращается угол, тангенс которого равен Y/X .
0012 X (т. е. арктангенс). Если указаны два параметра, возвращается угол, тангенс которого равен Y/X .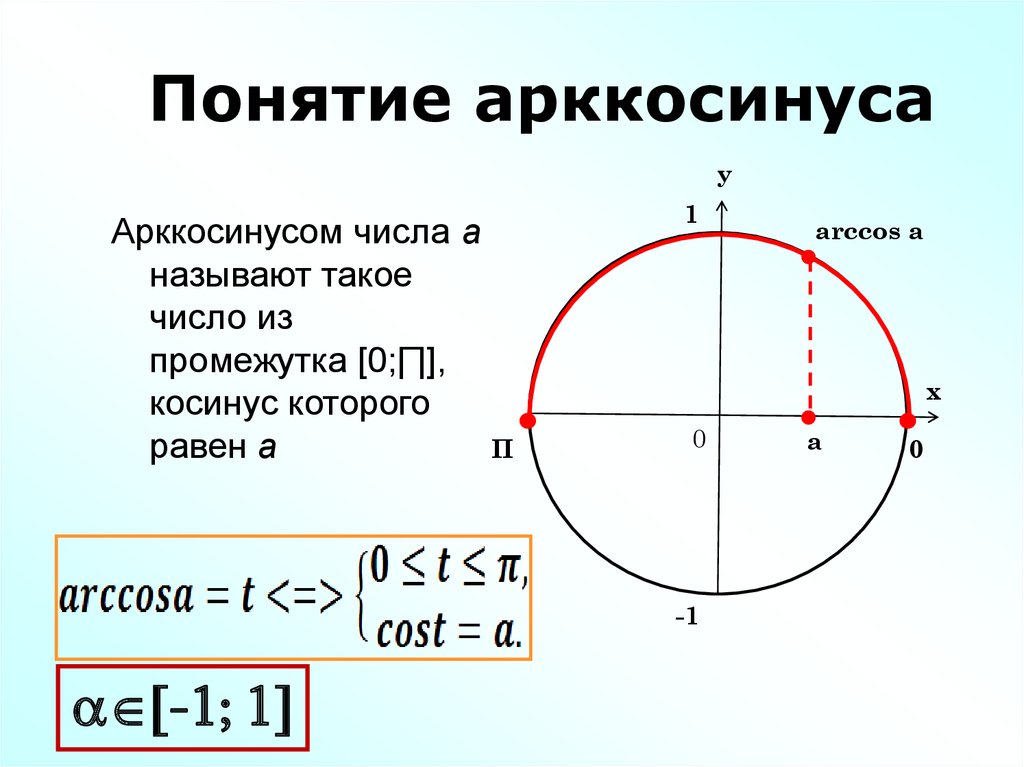
 )
)