Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
 4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.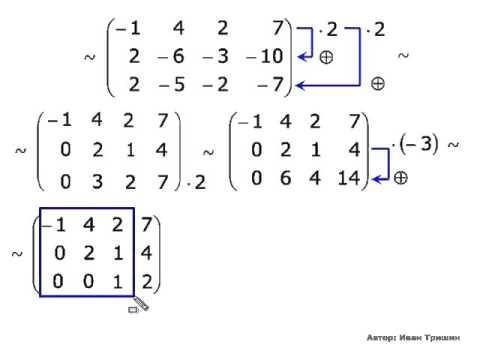
 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.

 The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)4. Метод гаусса
Рассмотрим еще один метод решения систем линейных алгебраических уравнений – метод Гаусса, который применим к любой системе линейных алгебраических уравнений. Иногда этот метод называют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.
Итак, пусть задана система mлинейных алгебраических уравнений сnнеизвестными:
(6)
В матричном виде система (6) записывается АХ=В, где А – прямоугольная матрица размера mn:
А=,
а Х и В – матрицы-столбцы: Х=,
В=.
Если в результате преобразований матрицы системы получится треугольная матрица, то система будет иметь вид:
где
Из последнего уравнения можно найти , а затем, подставляя найденноев предпоследнее уравнение, найтии т.д. В итоге будем иметьединственноерешение,, …,. В этом случае ранг матрицы А системы уравнений равенn.
Если в результате преобразований матрицы системы получится трапециевидная матрица, то система примет вид:
где
В этом случае k<n, следовательно, система уравнений будет неопределенной, то есть будет иметьбесконечное множество решений, так как она содержитn–kсвободных переменных:
Придавая свободным
переменным
,,
…,произвольные значения, будем иметь
каждый раз новое решение исходной
системы уравнений, то есть решений будет
бесконечное множество. В этом случае
ранг матрицы А системы равенk.
В этом случае
ранг матрицы А системы равенk.
Если в результате преобразований получено уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.
Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициентыотличны от нуля. Если же какой-либо из этих коэффициентов равен нулю, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.
В заключение отметим, что метод Гаусса применяется и для однородных систем линейных алгебраических уравнений. В этом случае, если получаем треугольный вид системы уравнений, то она будет иметь единственное (нулевое) решение == …==0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.
При решении системы
линейных алгебраических уравнений
методом Гаусса удобно выписать расширенную
матрицу системы и все преобразования
выполнять над строками и столбцами
расширенной матрицы.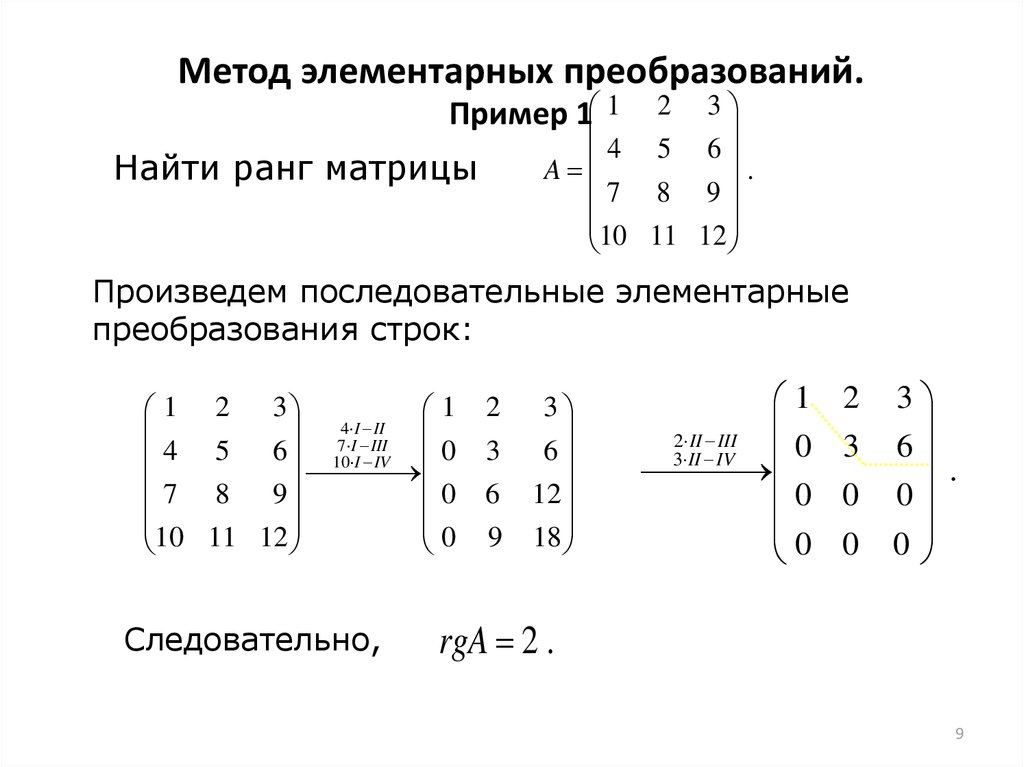
Рассмотрим примеры решения систем линейных алгебраических уравнений методом Гаусса.
Пример 1.
Решение.
Выпишем расширенную матрицу системы:
~ (не меняя первую строку, вычтем из второй
строки первую, из третьей вычтем первую строку, умноженную
на 3) ~ ~ (первую и вторую строки не меняем,
а из третьей вычтем вторую, умноженную на 4) ~ .
Получили матрицу А треугольного вида, причем на диагонали элементы отличны от нуля. Следовательно, ранг матрицы А равен 3, ранг расширенной матрицы также равен 3, и по теореме Кронекера-Капелли исходная система совместна, причем имеет единственное решение. Получим это решение.
Согласно последней матрице исходную систему можно записать в виде:
Из последнего
уравнения имеем, что
=
–1. Подставляяво
второе уравнение, получимПодставляяи
Подставляяво
второе уравнение, получимПодставляяи
в первое уравнение, получим
Ответ:
Пример 2.
Решение.
Выпишем расширенную матрицу системы:
~ (первую и четвертую строки не меняем, из
второй строки вычтем первую, умноженную на 3, из третьей строки вычтем
первую) ~ ~ (первую и вторую строки не меняем, из третьей строки вычтем вторую, умноженную на, а из четвертой вычтем вторую, умноженную на) ~~
~ (первую, вторую и третью строки не меняем, к четвертой строке
прибавим третью) ~ .
В итоге получили трапециевидную матрицу А. Следовательно, если бы последняя строка расширенной матрицы была нулевой, то исходная система уравнений имела бы бесконечное множество решений.
Так как она дает
уравнение
,
которое не имеет решения, то исходная
система является несовместной, то есть
не имеет решений.
Пример 3.
Решение.
Выпишем расширенную матрицу системы:
~ ~ (разделим третью
строку на 2)~~ (так как три строки одинаковые, то
две из них можно отбросить) ~ .
В итоге получили трапециевидную матрицу. Следовательно, исходная система уравнений неопределенная, то есть имеет бесконечное множество решений. Заметим, что ранг матрицы А равен двум.
Соответствующая система уравнений имеет вид:
В качестве свободных («лишних») переменных примем переменные и, так как минорсоответствует переменными. Получим:
Следовательно,
Подставим в первое уравнение:
Таким образом,
найдено решение исходной системы
линейных алгебраических уравнений.
Обозначив, получим решение исходной системы
Придаваяпроизвольные числовые значения, каждый раз будем иметь новое решение системы.
Более подробное изложение методов решения систем ЛАУ можно найти в книгах [ 1-4 ].
Метод Гаусса — определение с примерами решения
Содержание:
- Опишем метод Гаусса подробнее
- Примеры с решением
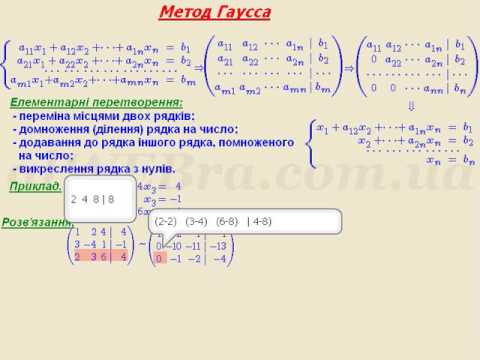
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений (4.3)
Процесс решения по методу Гаусса состоит из двух этапов. На нервом этапе (прямой ход) система приводится к i ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где
Коэффициенты называются главными элементами системы. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Прямой ход. Будем считать, что элемент (если то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля). Преобразуем систему (4.3), исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы).
Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы.
Затем умножим обе части первого уравнения на и сложим с третьим уравнением сиап стемы. Продолжая этот процесс, получим эквивалентную систему
Здесь
новые значения коэффициентов и правых частей, которые полу чаю юя после первого шага. Аналогичным образом, считая главным элементом исключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее.
Продолжаем этот процесс, пока это возможно. Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы. Второй этап {обратный ход) заключается в решении ступенчатой системы.
Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное через остальные неизвестные Затем подставляем значение в предпоследнее уравнение системы и выражаем затем находим Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.
Возможно вам будут полезны данные страницы:
Разложение в ряд Тейлора |
Матричные уравнения: пример решения |
Метод Жордана Гаусса |
Метод Крамера: пример решения |
Замечания: 1.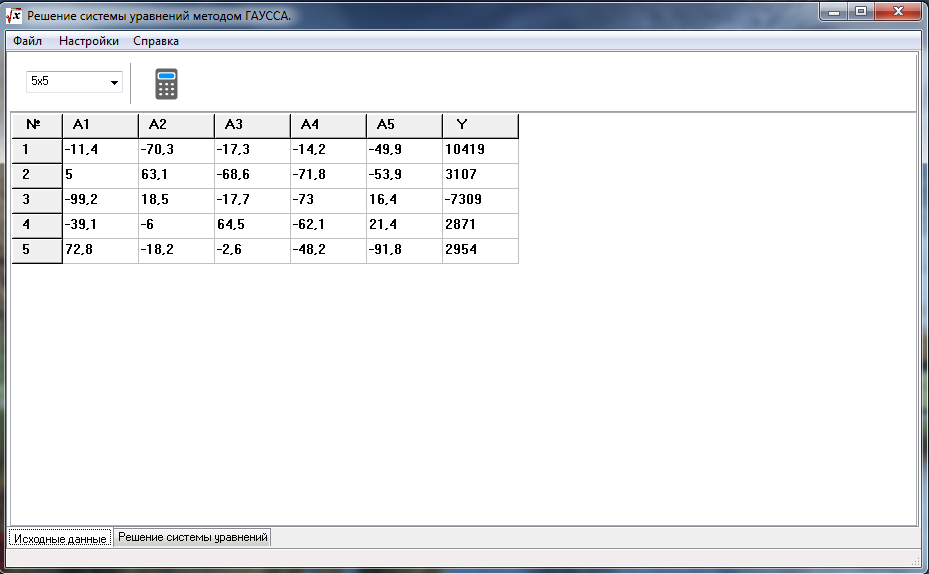 Если ступенчатая система оказывается треугольной, т. е. то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения далее поднимаясь по системе вверх, найдем все остальные неизвестные На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).
Если ступенчатая система оказывается треугольной, т. е. то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения далее поднимаясь по системе вверх, найдем все остальные неизвестные На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).
Примеры с решением
Пример 4.4.
Решить систему методом Гаусса:
Решение:
В результате элементарных преобразований над расширенной матрицей системы
исходная система свелась к ступенчатой:
Поэтому общее решение системы: Если положить, например, то найдем одно из частных решений этой системы
Пример 4.5.
Решить систему методом Гаусса:
Решение:
Произведем элементарные преобразования над строчками расширенной матрицы системы:
Полученная матрица соответствует системе
Осуществляя обратный ход, находим Рассмотрим решение системы (1. 25) т линейных уравнений с п неизвестными. Заметим, что матрица коэффициентов системы не обязательно должна быть квадратной.
25) т линейных уравнений с п неизвестными. Заметим, что матрица коэффициентов системы не обязательно должна быть квадратной.
Предлагаемые методы решения систем линейных алгебраических уравнений сводятся к элементарным преобразованиям над уравнениями системы.
Преобразования Гаусса удобно проводить, осуществляя преобразования не самих уравнений, а строк матрицы их коэффициентов.
Рассмотрим матрицу
(1.33) называемую расширенной матрицей системы (1.25), так как в нее, кроме коэффициентов матрицы А системы (1.25), дополнительно включен столбец свободных членов В. Метод Гаусса (метод последовательного исключения неизвестных. Рассмотрим систему (1.25) в случае
Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы (1.33) приводится к равносильной матрице ступенчатого вида по алгоритму поиска ранга матрицы (см. пример 1.13). Это и есть прямой ход метода Гаусса.
На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.
Пример 1.18.
Решить систему уравнений методом Гаусса:
Решение:
Расширенная матрица системы имеет вид
Используя элементарные преобразования (см. пример 1.14), сведем эту матрицу к ступенчатой, не забывая при этом, что теперь в строке уже не три, а четыре элемента.
Вспомнив, что до черты стоят коэффициенты системы уравнений, а после нее — столбец свободных членов, выпишем получившуюся систему уравнений:
Теперь применим обратный ход метода Гаусса. Из последнего 4 2 тл уравнения полученной системы найдем
Из второго уравнения найдем Аналогично найдем из первого уравнения, подставив в него уже наиденные два неизвестных
Получим решение системы
Предлагаем читателю убедиться, что найденные числа образуют решение данной системы. Расширенная матрица системы. Ступенчатая матрица. Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:
Расширенная матрица системы. Ступенчатая матрица. Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:
Матрица содержит т горизонтальных рядов, называемых строками, и вертикальных рядов, называемых столбцами, числа называются ее элементами. Таким образом, первый индекс элемента — это номер строки (номер уравнения системы (1.1)), а второй индекс — номер столбца (или номер неизвестного коэффициентом при котором является уравнении системы (1.1)).
Например, матрица
квадратная матрица 3-го — единичная матрица 2-го порядка. Если к матрице А добавить столбец из свободных членов, то получим так называемую расширенную матрицу А* системы, содержащую всю информацию о системе:
Для системы из примера 1.1 матрицей системы является а расширенной матрицей этой системы является матрица На практике элементарным преобразованиям подвергают не саму систему, а ее расширенную матрицу.
Преобразованиям двух типов над системой (1.1) соответствуют два типа элементарных преобразований над строками матрицы 1-й тип — перестановка местами двух любых ее строк; 2-й тип — сложение соответствующих элементов двух любых строк, все элементы одной из которых предварительно умножены на одно и то же число.
Целью элементарных преобразований является приведение расширенной матрицы системы (1.1) к так называемой ступенчатой форме.
Определение 1.6. Матрица называется ступенчатой, если для нее выполняются следующие условия: 1) если какая-либо строка данной матрицы состоит из нулей, то и все последующие строки также состоят из нулей; 2) если — первый ненулевой элемент строки, а — первый ненулевой элемент строки,то Так, например, матрица
является ступенчатой.
Матрица из одной строки считается ступенчатой по определению. Теорема 1.2. Любую матрицу Л конечным числом элементарных преобразований первого и второго типов можно преобразовать в ступенчатую матрицу.
Пример 1.7.
Привести к ступенчатому виду матрицу
Решение:
Выполним следующие элементарные преобразования над матрицей
1) к элементам второй строки прибавим элементы первой строки и из элементов третьей строки вычтем элементы первой строки, в результате преобразуется к виду: — расширенная матрица системы.
2) переставим вторую и третью строки:
3) из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, получим:
На приведении расширенной матрицы системы (1.1) к ступенчатой матрице основан метод Гаусса, или метод последовательного исключения неизвестных. Система линейных уравнений с расширенной ступенчатой матрицей называется ступенчатой системой, по теореме 1.1 она будет равносильна соответствующей системе в форме (1.1). Приведение системы (1.1) к ступенчатой форме называется прямым ходом метода Гаусса.
Решение полученной ступенчатой системы называется обратным ходом метода Гаусса. Он может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего уравнения ступенчатой системы, так и в форме преобразования матрицы к ступенчатой матрице специального вида.
Пример 1.8.
Решить методом Гаусса систему уравнений
Решение:
Прямой ход метода Гаусса. В примере 1.7 матрица при помощи элементарных преобразований приведена к ступенчатой матрице
Теперь матрице сопоставим систему, для которой она будет расширенной матрицей:
Обратный ход метода Гаусса. 1-й способ. Имеем: . 2-й способ.
Умножим последнюю строку матрицы на 1 /5, сложим со второй строкой, после чего к первой строке прибавим последнюю, умноженную на (-2), с целью получить нули в третьем столбце:
Напишем систему с расширенной матрицей
Ответ: система совместная и определенная, она имеет единственное решение:
Решение систем линейных уравнений методом гаусса
Содержание
- Введение 2
- Понятие матрицы 5
- Немного из биографии Гаусса 6
- Решение систем линейных уравнений методом Гаусса 7
- Проведение обучающего эксперимента 12
- Заключение 14
- Список используемой литературы 15
ВВЕДЕНИЕ
Увлечение математикой начинается с размышления над какой-то интересной задачей или проблемой.
Часто на уроках математики мы решаем различные уравнения. Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных алгебраических уравнений. Способы решения систем линейных уравнений – очень интересная и важная тема. В седьмом классе на уроках алгебры мы использовали такие способы, как сложение, подстановка и графический.
Нужно заметить, что не всегда системы линейных уравнений удобно решать данными способами. Мы решили выяснить существуют ли другие методы решения систем линейных уравнений. Изучив данную тему, мы выяснили, что существуют такие методы, как: метод Крамара, метод Гаусса, метод обратной матрицы.
Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Выдающегося немецкого математика Карла Фридриха Гаусса (1777–1855) современники называли «королём математики». Ещё в раннем детстве он проявлял незаурядные математические способности.
На примерах был изучен и исследован алгоритм решения систем линейных уравнений методом Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Процесс решения по методу Гаусса состоит из двух этапов, называемых прямым и обратным ходом. На первом этапе система приводится к треугольному виду, а на втором (обратный ход) идет последовательное определение неизвестных из указанной треугольной системы.
Метод Гаусса — один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры. Поэтому поиск решения системы линейных уравнений методом Гаусса имеет не только важное значение, но и является частью алгоритма решения многих задач, что позволяет говорить об актуальности изучения метода Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных.
Актуальность:
Системы линейных алгебраических уравнений имеют широкое применение в решении многих задач практического приложения математики. Данная тема в школьном курсе алгебры не изучается, чтобы изучить данную тему, необходимо познакомиться с понятиями матрицы, матрица системы и расширенная матрица системы. Получение новых знаний и нового опыта способствует развитию личности, формирует некоторые особенности мышления и оказывает влияние на отношение к миру.
Цель работы:
Научиться решать системы уравнений с помощью метода Гаусса
и применять этот метод на практике, ознакомить и научить одноклассников решать системы уравнений методом Гаусса.
Задачи исследования
1. Познакомиться с понятием «матрица» и «матрица системы».
2. Изучить метод Гаусса.
3. Научиться применять метод Гаусса на практике.
Объект(изучения): Метод Гаусса
Предмет: Системы линейных уравнений с двумя и более переменными.
Методы исследования: анализ, обобщение, эксперимент, опрос.
Гипотезы: С помощью данного метода увеличивается скорость решения систем линейных уравнений. Метод Гаусса можно изучать на уроках алгебры в 7 — 8 классах как дополнительный метод решения систем уравнений с двумя и более переменными.
Глава I
ПОНЯТИЕ МАТРИЦЫ
Матрицей размера mn, где m — число строк, n — число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i — номер строки, а j — номер столбца
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.
Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае.
НЕМНОГО ИЗ БИОГРАФИИ ГАУССА
Иога́нн Карл Фри́дрих Га́усс (1777 — 1855) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков».
С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре, теории чисел, дифференциальной и неевклидовой геометрии, теории вероятностей, а также в механике, астрономии, физике и геодезии.
Гаусс чрезвычайно строго относился к своим печатным трудам и никогда не публиковал даже выдающиеся результаты, если считал свою работу над этой темой незавершённой. Изучение архива Гаусса показало, что он медлил с публикацией ряда своих открытий, и в результате его опередили другие математики. Вот неполный перечень упущенных им трудов.
- Неевклидова геометрия
- Эллиптические функции
- Метод наименьших квадратов
- Закон распределения простых чисел
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса представляет собой специальный алгоритм последовательного исключения неизвестных из уравнений системы. В этом алгоритме обычно различают два этапа:
В этом алгоритме обычно различают два этапа:
Первый этап называется прямой ход,
Второй этап – обратный ход.
Цель прямого хода метода Гаусса заключается в приведение матрицы системы к треугольному виду, когда в результате некоторых элементарных преобразований уравнений системы на главной диагонали матрицы системы будут располагаться ненулевые элементы, а все элементы ниже главной диагонали будут равны нулю. В результате наших преобразований должна получаться система, равносильная исходной системе линейных уравнений. Преобразования, которые позволяют свести исходную систему к треугольной, сохраняя равносильность, называются элементарными. Что будем понимать под элементарными преобразованиями?
Определение. Элементарными преобразованиями уравнений системы называют следующие преобразования:
1) перестановка местами двух любых уравнений;
2) умножение обеих частей какого-либо уравнения на любое число, не равное нулю;
3) прибавление к обеим частям одного из уравнений соответствующих частей любого другого уравнения;
4) перестановка (перенумерация) неизвестных системы.
Примем без доказательства, что все перечисленные преобразования приводят к системам, которые равносильны (эквивалентны) исходной системе линейных уравнений.
Удобно в методе Гаусса работать не с самой системой линейных уравнений, а с основой системы – расширенной матрицей.
Элементарным преобразованиям системы соответствуют следующие элементарные преобразования расширенной матрицы:
1. умножение произвольной строки на любое число, отличное от нуля;
2. прибавление к произвольной строке матрицы любой другой строки матрицы;
3. перестановка местами любых двух строк;
4. перестановка местами любых двух столбцов матрицы системы;
5. транспонирование.
Решение системы уравнений с двумя переменными
Пример 1. Решим систему:
Решение:
Ответ: (-4; 1)
Решение системы уравнений с тремя переменными
Пример 2. Решим систему:
Решение:
Ответ: (-3; 8; 0)
Пример 3.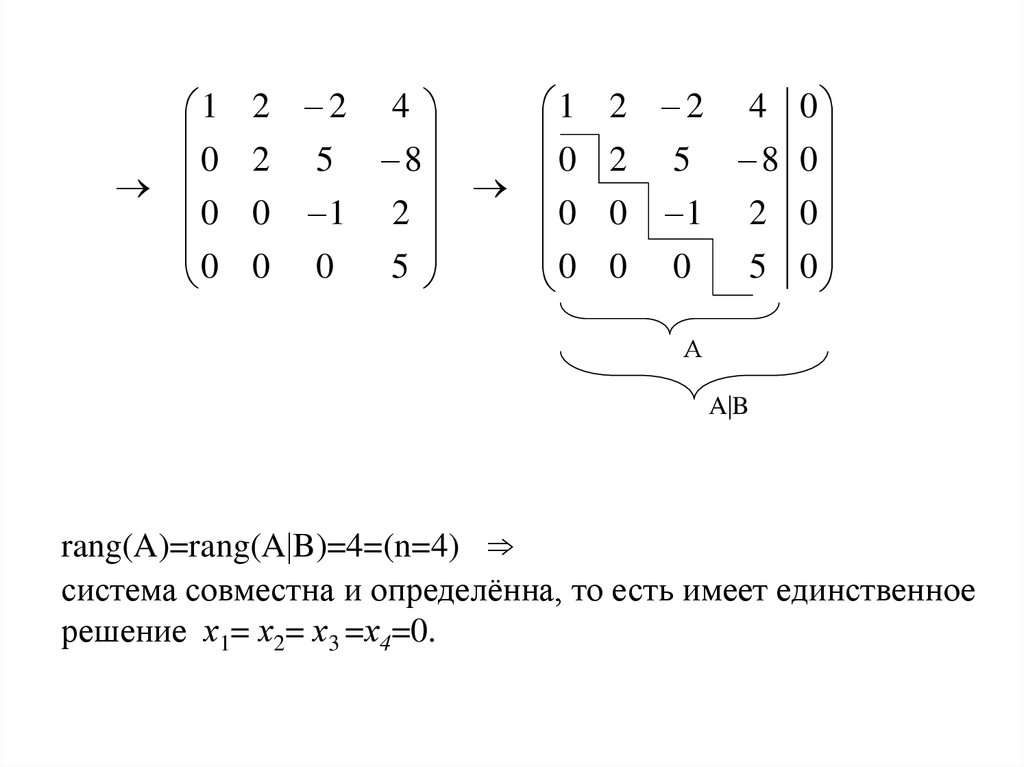 Решим систему:
Решим систему:
Решение:
Ответ: (1; 2; 3).
Пробуем применять изученное к решению задач:
Кондитерская фабрика производит продукцию трех видов: торты, пирожные и рулеты. Для их производства используется сырье трех типов: мука 1 кг, сахар 1 кг, молоко 1 л. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей:
Найти ежедневный объем выпуска каждого вида продукции.
Решение. Пусть ежедневно фабрика выпускает х1 тортов, х2 пирожных и х3 рулетов. Составим систему уравнений.
Составим расширенную матрицу системы :
Ответ: фабрика выпускает ежедневно 50 тортов, 200 пирожных и 95 рулетов.
Глава II
Проведение обучающего эксперимента
Одной из целей моего проекта является научить одноклассников решать системы уравнений методом Гаусса, для чего на спецкурсе по математике я показала и рассказала им о своей работе и предложила совместно решить несколько систем, состоящих из двух строк, методом Гаусса. Ребят заинтересовал данный метод, они с интересом слушали меня, а потом совместно решали системы уравнений данным методом. Далее ребятам были предложены системы уравнений и заданы следующие вопросы:
Ответ: Ответ:
Ответ: Ответ:
Ответ: Ответ:
Ответ:
1. Знакомы ли вы с методом Гаусса?
2. Применяете и вы этот метод?
3. Хотите ли вы что б этот метод был в школьной программе ?
4. Будете ли вы решать системы этим методом?
5. Считаете ли вы этот метод простым ?
Ответы на которые вы можете видеть на диаграмме.
Заключение.
Метод Гаусса позволяет решать любые системы линейных уравнений и существенно сократить время нахождения решений систем линейных уравнений. Метод Гаусса доступен для его изучения учащимся 7 — 8 классов при решении систем линейных уравнений
Метод Гаусса доступен для его изучения учащимся 7 — 8 классов при решении систем линейных уравнений
У меня получилось самой освоить данный метод и передать свои знания одноклассникам. Таким образом, поставленные мною цели и задачи выполнены. И ещё метод Гаусса прост тем, как мне кажется, что для его освоения не требуется много знаний. А также для матриц ограниченного размера метод Гаусса менее трудоёмкий по сравнению с другими методами, поэтому в будущем я планирую его активно применять при решении систем уравнений.
ЛИТЕРАТУРА
- Основы высшей математики: Учеб. пособие для вузов/В.С. Шипачев; под ред.акад. А.Н. Тихонова. —5-е изд.,стер. — М. Высш. Шк., 2003. — 279с.
- Высшая математика для экономистов: учебное пособие для студентов экономических специальностей высших учебных заведений /Н.Ш Кремер, Б.А. Путко. — М.: Банки и биржи ЮНИТИ, 1997. – 239с.
- Математика. Задачник : учеб. Пособие для образоват. Учреждений нач. и сред. Проф. образования / М.
 И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.
И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с. - http://mathprofi.ru/metod_gaussa_dlya_chainikov.html
- https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0
- https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB_%D0%A4%D1%80%D0%B8%D0%B4%D1%80%D0%B8%D1%85
- https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0
Метод Гаусса для решения систем линейных уравнений (стр. 1 из 2)
1. Система линейных алгебраических уравнений
1.1 Понятие системы линейных алгебраических уравнений
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
где числа aij называются коэффициентами системы, числа bi – свободными членами, aij и bi (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x1,…, xn – неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа xn. Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;
В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа xn. Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;
– вектор-столбец из неизвестных xj.
– вектор-столбец из свободных членов bi.
Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов
1.2 Решение системы линейных алгебраических уравнений
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.
Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
Всякое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.
2. Метод исключения Гаусса
2.1 Сущность метода исключения Гаусса
Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.
1. Прямой ход.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид:
,
где
Коэффициенты aii называются главными (ведущими) элементами системы.
1-й шаг.
Будем считать, что элемент
(если a11=0, переставим строки матрицы так, чтобы a11 не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).
Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).
Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на
). Затем умножим обе части первого уравнения на
и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на
). Таким образом, последовательно умножаем первую строку на число
и прибавляем к i-й строке, для i=2, 3, …, n.
Продолжая этот процесс, получим эквивалентную систему:
Здесь
– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:
Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a11
0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а22(1) (если a22(1)
0) и т. д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.
д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.
Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида
то это свидетельствует о несовместности системы.
На этом прямой ход метода Гаусса заканчивается.
2. Обратный ход.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.
Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).
2.2 Примеры решения СЛАУ методом Гаусса
В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.
Пример 1. Решить СЛАУ 3-го порядка.
Обнулим коэффициенты при
во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:
Оценка уровня подготовки | ||
Балл (оценка) | Вербальный аналог | |
90-100 | 5 | отлично |
80-89 | 4 | хорошо |
70-79 | 3 | удовлетворительно |
менее 70 | 2 | неудовлетворительно |
Матрицы и исключение Гаусса
Обратная замена
Напомним, что линейная система уравнений состоит из набора двух или более линейных уравнений с одинаковыми переменными. Линейная система, состоящая из трех уравнений стандартной формы, расположенных так, что переменная x не входит ни в одно уравнение после первого, а переменная y не входит ни в одно уравнение после второго, называется верхнетреугольной формой A. линейная система, состоящая из уравнений стандартной формы с тремя переменными, расположенных так, что переменная x не появляется после первого уравнения, а переменная y не появляется после второго уравнения. Например,
Обратите внимание, что система образует треугольник, в котором каждое последующее уравнение содержит на одну переменную меньше. В общем,
линейных систем в верхне треугольной форме{a1x+b1y=c1b2y=c2 {a1x+b1y+c1z=d1b2y+c2z=d2c3z=d3
переменных, а затем обратно заменить, чтобы решить для оставшихся переменных.
Пример 1
Решите: {3x−y=72y=−2.
Решение:
Напомним, что решения линейных систем с двумя переменными, если они существуют, представляют собой упорядоченные пары ( x , y ). Мы можем легко определить значение y , используя второе уравнение.
2y=-2y=-1
Затем используйте первое уравнение 3x-y=7 и тот факт, что y=-1, чтобы найти x .
3x−y=73x−(−1)=73x+1=73x=6x=2
Ответ: (2,−1)
Пример 2
Решите: {x−6y+2z=163y−9z=5z=−1.
Решение:
Напомним, что решения линейных систем с тремя переменными, если они существуют, представляют собой упорядоченные тройки ( x , y , z ). Используйте второе уравнение 3y−9z=5 и тот факт, что z=−1, чтобы найти y .
3y-9z=53y-9(-1)=53y+9=53y=-4y=-43
Затем подставьте y и z в первое уравнение.
x−6y+2z=16x−6(−43)+2(−1)=16x+8−2=16x+6=16x=10
Ответ: (10,−43,−1)
Попробуйте! Решите: {4x−y+3z=12y−9z=−23z=2.
Ответ: (14, 2, 23)
(нажмите, чтобы посмотреть видео)
Матрицы и исключение Гаусса
Целью этого раздела является разработка метода, упрощающего процесс решения линейных систем. Начнем с определения матрицы. Прямоугольный массив чисел, состоящий из строк и столбцов, который представляет собой прямоугольный массив чисел, состоящий из строк и столбцов. Учитывая линейную систему в стандартной форме, мы создаем матрицу коэффициентов. Матрица коэффициентов линейной системы в стандартной форме, записанная так, как они появляются, выстроены в линию без переменных или операций. записав коэффициенты в том виде, в котором они появляются, без переменных или операций, как показано ниже.
Матрица линейной системы {a1x+b1y+c1z = d1a2x+b2y+c2z = d2a3x+b3y+c3z = d3 ⇒ [a1b1c1a2b2c2a3b3c3]
. Каждая из них представляет собой коэффициенты в равновесиях и союзники. Кроме того, если мы включим столбец, представляющий константы, мы получим то, что называется расширенной матрицей. Матрица коэффициентов с включенным столбцом констант. Для линейной системы с двумя переменными
Матрица коэффициентов с включенным столбцом констант. Для линейной системы с двумя переменными
Линейная система увеличенная матрица {a1x+b1y = c1a2x+b2y = c2 ⇔ [a1b1 | c1a2b2 | c2]
и для линейной системы с тремя переменными, мы имеем
Линейная система Уполномоченная матрица {A1x+b1y+c1z = d1z = d11 +b2y+c2z = d2a3x+b3y+c3z = d3 ⇔ [a1b1c1 | d1a2b2c2 | d2a3b3c3 | d3]
Примечание : пунктирная вертикальная линия обеспечивает визуальное разделение между коэффициенной матрицей и колонкой константов. В других ресурсах по алгебре, с которыми вы можете столкнуться, это иногда опускается.
Пример 3
Постройте расширенную матрицу, которая соответствует: {9x−6y=0−x+2y=1 .
Решение:
Эта система состоит из двух линейных уравнений в стандартной форме; следовательно, коэффициенты в матрице появляются так же, как и в системе.
{9x — 6y = 0 — x+2y = 1 ⇔ [9–6 | 0,12 | 1]
Пример 4
Создайте дополненную матрицу, которая соответствует: {x+2y -4z = 52x+y −6z=84x−y−12z=13 .
Решение:
Поскольку уравнения приведены в стандартной форме, коэффициенты появляются в матрице так же, как и в системе.
{x+2y — 4z = 52x+y — 6z = 84x — y -12z = 13 ⇔ [12–4 | 521–6 | 84 —1 —12 | 13]
Матрица находится в верхней треугольной форме, если все элементы ниже ведущего ненулевого элемента в каждой последующей строке равны нулю. Например,
Обратите внимание, что элементы ниже главной диагонали равны нулю, а коэффициенты выше образуют треугольную форму. В целом,
Верхняя треугольная форма [A1B10B2] [A1B1C10B2C200C3]
Это важно, потому что в этом разделе мы наметим процесс, с помощью которого могут быть сделаны определенные операции для получения эквивалентной линейной системы в верхней треугольной форме. с помощью обратной замены. Обзор процесса представлен ниже:
Когда система находится в форме верхнего треугольника, мы можем использовать обратную подстановку, чтобы легко решить ее. Важно отметить, что представленные здесь расширенные матрицы представляют собой линейные системы уравнений в стандартной форме.
Следующие элементарные операции над строкамиОперации, которые можно выполнить для получения эквивалентных линейных систем. в результате получаются расширенные матрицы, представляющие эквивалентные линейные системы:
- Любые две строки можно поменять местами.
- Каждый элемент в строке может быть умножен на ненулевую константу.
- Любая строка может быть заменена суммой этой строки и кратной другой.
Примечание: Эти операции согласуются со свойствами, используемыми в методе исключения.
Чтобы эффективно решить систему линейных уравнений, сначала постройте расширенную матрицу. Затем примените соответствующие элементарные операции над строками, чтобы получить расширенную матрицу в верхнетреугольной форме. В этой форме эквивалентная линейная система может быть легко решена с помощью обратной замены. Этот процесс называется устранением Гаусса. Этапы, используемые для получения эквивалентной линейной системы в форме верхнего треугольника, чтобы ее можно было решить с помощью обратной подстановки, названной в честь Карла Фридриха Гаусса (1777–1855).
Рисунок 3.1
Carl Friedrich Gauss (Wikipedia)
Шаги решения линейного уравнения с двумя переменными с помощью метода исключения Гаусса перечислены в следующем примере.
Пример 5
Решите, используя матрицы и метод исключения Гаусса: {9x−6y=0−x+2y=1 .
Решение:
Перед началом этого процесса убедитесь, что уравнения в системе имеют стандартную форму.
Шаг 1 : Построить соответствующую расширенную матрицу.
{9x−6y=0−x+2y=1 ⇔ [9−6|0−12|1]
Шаг 2 В этом случае нам нужно только исключить первый элемент второй строки, −1. Для этого умножьте второй ряд на 9 и прибавьте его к первому ряду.
Теперь используйте это, чтобы заменить вторую строку.
[9−6|0012|9]
В результате получается расширенная матрица в форме верхнего треугольника.
Шаг 3 : Преобразуйте обратно в линейную систему и решите с помощью обратной подстановки. В этом примере у нас
В этом примере у нас
[9–6 | 0012 | 9] ⇒ {9x — 6y = 012y =
Решите второе уравнение для y ,
12y = 9y = 912y = 34
. первое уравнение для нахождения x ,
9x−6y=09x−6(34)=09x−92=09x=92x=12
Ответ: (12, 34)
Шаги по использованию исключения Гаусса для решения линейное уравнение с тремя переменными перечислены в следующем примере.
Пример 6
Решить с помощью матриц и исключения Гаусса: {x+2y−4z=52x+y−6z=84x−y−12z=13 .
Решение:
Перед началом этого процесса убедитесь, что уравнения в системе имеют стандартную форму.
Шаг 1 : Построить соответствующую расширенную матрицу.
{x+2y — 4z = 52x+y — 6z = 84x — y -12z = 13 ⇒ [12–4 | 521 - 6 | 84 —1 —12 | 13]
Шаг 2 : Примените элементарную рядовые операции для получения верхней треугольной формы. Начнем с удаления первого элемента второй строки, в данном случае 2. Для этого умножьте первую строку на −2, а затем добавьте ее ко второй строке.
[12−4 |521−6 |84−1−12 |13]⇒×(−2)−2−48−10+21−680−32−2
Используйте это, чтобы заменить вторую строку.
[12−4 |50−32 |−24−1−12 |13]
Затем удалите первый элемент третьей строки, в данном случае 4, умножив первую строку на −4 и добавив ее к третий ряд.
[12−4 |50−32 |−24−1−12 |13]⇒×(−4)−4−816−20+4−1−12130−94−7
Используйте это для замены третьего строка.
[12−4 |50−32 |−20−94 |−7]
В результате получается расширенная матрица, в которой элементы ниже первого элемента первой строки равны нулю. Затем удалите второй элемент в третьей строке, в данном случае −9.. Умножьте вторую строку на −3 и прибавьте к третьей строке.
Используйте это, чтобы заменить третью строку, и мы увидим, что получили матрицу в форме верхнего треугольника.
[12−4 |50−32 |−200−2 |−1]
Шаг 3 : Преобразовать обратно в линейную систему и решить с помощью обратной подстановки. В этом примере мы имеем
[12–4 | 50–32 | −200–2 | −1] ⇒ {x+2y -4z = 5–3y+2z = −2-2Z = −1
Ответ: Читателю остается убедиться, что это решение (5,1,12).
Примечание: Обычно работа, связанная с заменой строки путем умножения и сложения, выполняется на стороне с использованием черновой бумаги.
Пример 7
Решите, используя матрицы и метод исключения Гаусса: {2x−9y+3z=−18x−2y−3z=−8−4x+23y+12z=47 .
Решение:
Начнем с преобразования системы в расширенную матрицу коэффициентов.
{2x — 9y+3z = −18x —2y — 3z = −8–4x+23y+12z = 47 ⇒ [2–93 | −181–2 — 3 | −8−42312 | 47]
операции со строками упрощаются, если ведущим ненулевым элементом в строке является 1. По этой причине начните с замены первой и второй строк.
Замените вторую строку суммой −2, умноженной на первую и вторую строки.
Замените третью строку суммой четырех значений, умноженных на первую и третью строки.
Затем разделите строку 3 на 15.
Поменяйте местами строку 3 и строку 2.
Затем замените строку 3 на сумму 5, умноженную на вторую и третью строки.
В результате получается матрица в форме верхнего треугольника. Матрица находится в форме эшелона строк. Матрица имеет треугольную форму, где старший ненулевой элемент каждой строки равен 1. Если она находится в верхнем треугольном виде, где старший ненулевой элемент каждой строки равен 1. Мы можем получить эту форму, заменив третью строку на результат деления на 9.
Матрица находится в форме эшелона строк. Матрица имеет треугольную форму, где старший ненулевой элемент каждой строки равен 1. Если она находится в верхнем треугольном виде, где старший ненулевой элемент каждой строки равен 1. Мы можем получить эту форму, заменив третью строку на результат деления на 9.
Преобразовать в систему линейных уравнений и решить методом обратной подстановки.
[1−2−3 |−8010 |1001 |13] ⇒ {x−2y−3z=−8y=1z=13
Здесь y = 1 и z=13. Подставьте в первое уравнение, чтобы найти x .
x−2y−3y=−8x−2(1)−3(13)=−8x−2−1=−8x−3=−8x=−5
Ответ: Следовательно, решение (−5, 1, 13).
Техническое примечание : Многие современные калькуляторы и системы компьютерной алгебры могут выполнять исключение Гаусса. Сначала вам нужно будет узнать, как ввести матрицу. Затем используйте функции калькулятора, чтобы найти форму эшелона строк. Мы рекомендуем вам провести некоторые веб-исследования по этой теме для вашей конкретной модели калькулятора.
Попробуйте! Решите методом исключения Гаусса: {x−3y+2z=164x−11y−z=692x−5y−4z=36 .
Ответ: (6, −4, −1)
(нажмите, чтобы посмотреть видео)
Напомним, что некоторые непротиворечивые линейные системы зависимы, то есть имеют бесконечно много решений. А некоторые линейные системы не имеют одновременного решения; это несовместимые системы.
Пример 8
Решите, используя матрицы и метод исключения Гаусса: {x−2y+z=42x−3y+4z=74x−7y+6z=15 .
Решение:
Начнем с преобразования системы в расширенную матрицу коэффициентов.
{x -2y+z = 42x — 3y+4z = 74x — 7y+6z = 15 ⇒ [1–21 | 42–34 | 74–76 | 15]
Замените строку второй на −2 (строка 1) +(строка 2) и заменить третью строку на −4(строка 1)+(строка 3).
[1−21 |4012 |−1012 |−1]
Заменить третью строку на −1(строка 2)+(строка 3).
[1−21 |4012 |−1000 |0]
Последняя строка указывает, что это зависимая система, поскольку преобразование расширенной матрицы обратно в уравнения дает
{x−2y+z=4y+2z=−10x+0y+0z=0
Обратите внимание, что ряд нулей соответствует следующему тождеству:
0x+0y+0z=00=0 ✓
In В этом случае мы можем выразить бесконечное множество решений через z . Из второй строки имеем следующее:
Из второй строки имеем следующее:
y+2z=−1y=−2z−1
А из первого уравнения
x−2y+z=4x−2(−2z−1)+z= 4x+5z+2=4x=−5z+2
Решения принимают вид (x, y, z)=(−5z+2,−2z−1, z), где z — любое действительное число.
Ответ: (−5z+2,−2z−1,z)
Зависимые и несогласованные системы можно идентифицировать в расширенной матрице коэффициентов, когда все коэффициенты в одной строке равны нулю.
Если ряду нулей соответствует нулевая константа, то матрица представляет собой зависимую систему. Если константа отлична от нуля, то матрица представляет собой противоречивую систему.
Попробуйте! Решить с помощью матриц и исключения Гаусса: {5x−2y+z=−310x−y+3z=0−15x+9y−2z=17 .
Ответ: Ø
(нажмите, чтобы посмотреть видео)
Ключевые выводы
- Линейная система в форме верхнего треугольника может быть легко решена с помощью обратной подстановки.
- Увеличенная матрица коэффициентов и исключение Гаусса могут быть использованы для упрощения процесса решения линейных систем.

- Чтобы решить систему с использованием матриц и исключения Гаусса, сначала используйте коэффициенты для создания расширенной матрицы. Примените элементарные операции над строками, чтобы получить матрицу в верхнем треугольном виде. Преобразуйте матрицу обратно в эквивалентную линейную систему и решите ее с помощью обратной замены.
Тематические упражнения
{5x−3y=2y=−1
{3x+2y=1y=3
{х-4у=12у=-3
{х-5у=310у=-6
{4x−3y=−167y=0
{3x−5y=−104y=8
{2x+3y=−13y=2
{6x−y=−34y=3
{х-у=02у=0
{2х+у=23у=0
{х+3у-4г=1у-3г=-2г=3
{x−5y+4z=−1y−7z=10z=−2
{х-6у+8г=23у-4г=-42г=-1
{2x−y+3z=−92y+6z=−23z=2
{10x−3y+z=1311y−3z=92z=−6
{3x−2y+5z=−244y+5z=34z=−12
{х-у+2г=12у+г=13г=-1
{х+2у-г=2у-3г=16г=1
{х-9у+5г=-32у=103г=27
{4x − z=33y−2z=−12z=−8
Часть A: обратная замена
Решите с помощью обратной замены.
{х+2у=34х+5у=6
{6x+5y=43x+2y=1
{х-2у=12х-у=1
{х-у=2-х+у=-1
{−x+8y=32y=2
{3x−2y=4−y=5
{3x-2y+7z=84x-5y-10z=6-x-3y+2z=-1
{x−y−z=02x−y+3z=−1−x+4y−3z=−2
{х-9у+5г=-32у=103г=27
{4x−z=33y−2z=−12z=−8
{8x+2y=-13-2y+z=112x-5z=-18
{x−3z=2y+6z=42x+3y=12
{х-5у=22х-у=1
{х-2у=-1х+у=1
{10x−7y=15−2x+3y=−3
{9x−10y=23x+5y=−1
{3x+5y=82x−3y=18
{5x−3y=−147x+2y=−1
{9x+15y=53x+5y=7
{6x−8y=1−3x+4y=−1
{х+у=0х-у=0
{7x-3y=03x-7y=0
{2x−3y=4−10x+15y=−20
{6x−10y=20−3x+5y=−10
{х+у-2г=-1-х+2у-г=1х-у+г=2
{x−y+z=−2x+2y−z=6−x+y−2z=3
{2x-y+z=2x-y+z=2-2x+2y-z=-1
{3x−y+2z=7−x+2y+z=6x+3y−2z=1
{х-3у+г=6-х-у+2г=42х+у+г=3
{4x−y+2z=12x−3y+2z=7−2x+3y+4z=−16
{2x−4y+6z=−43x−2y+5z=−25x−y+2z=1
{3x+6y+9z=62x−2y+3z=0−3x+18y−12z=5
{-x+y-z=-23x-2y+5z=13x-5y-z=3
{х+2у+3г=43х+8у+13г=212х+5у+8г=16
{2x−4y−5z=3−x+y+z=13x−4y−5z=−4
{5x−3y−2z=43x−6y+4z=−6−x+2y−z=2
{-2x-3y+12z=44x-5y-10z=-1-x-3y+2z=0
{3x−2y+5z=104x+3y−3z=−6x+y+z=2
{х+2у+г=-3х+6у+3г=7х+4у+2г=2
{2x−y+z=14x−y+3z=52x+y+3z=7
{2x+3y-4z=03x-5y+3z=-105x-2y+5z=-4
{3x-2y+9z=2-2x-5y-4z=35x-3y+3z=15
{8x+2y=-13-2y+z=112x-5z=-18
{x−3z=2y+6z=42x+3y=12
{9x+3y-11z=62x+y-3z=17x+2y-8z=3
{3x−y−z=4−5x+y+2z=−36x−2y−2z=8
{2x−4y+3z=153x−5y+2z=185x+2y−6z=0
{3x−4y−3z=−144x+2y+5z=12−5x+8y−4z=−3
Часть B: Матрицы и исключение Гаусса
Построить соответствующую расширенную матрицу (не решать).
Решить с помощью матриц и метода исключения Гаусса.
Исследуйте и обсудите историю исключения Гаусса.
 Кому приписывают первую разработку этого процесса? Опубликуйте что-нибудь интересное, связанное с этой историей.
Кому приписывают первую разработку этого процесса? Опубликуйте что-нибудь интересное, связанное с этой историей.Исследовать и обсудить историю современной матричной записи. Кому приписывают разработку? В каких областях они используются сегодня? Опубликуйте свои выводы на доске обсуждений.
Часть C: Дискуссионная доска
Ответы
(-15,-1)
(-5,-32)
(−4, 0)
(−32,23)
(0, 0)
(−8, 7, 3)
(-6,-2,-12)
(85,0,−3)
(73,23,−13)
(−3, 5, 9)
[12 |345 |6]
[1−2 |12−1 |1]
[−18 |302 |2]
[3−27 |84−5−10 |6−1−32 |−1]
[1−95 |−3020 |10003 |27]
[820 |−130−21 |1120−5 |−18]
(13,−13)
(32,0)
(6, −2)
Ø
(0, 0)
(х, 23х-43)
(2, 3, 3)
(0, 1, 3)
(1, −1, 2)
(12,12,−12)
Ø
(-7, -13, 7)
(1,0,12)
(−8,−12z+52,z)
(−1,2,1)
(−32,−12, 0)
Ø
(2, −2, 1)
Ответ может отличаться
[1/3] Полное руководство по исключению Гаусса | Адам Дхалла
Часть 1 из 3: Что это значит и как мы [люди] его вычисляем, развороты, сингулярные случаи, обмен строками и понимание геометрии с использованием диапазонных и линейных комбинаций.

Эта серия может выступать своего рода конспектом лекций 1–4 проф. Класс Гилберта Стрэнга 18.06 на MIT OCW, а также некоторые дополнительные лакомые кусочки интуиции, которые я смог собрать.
Продолжая свой личный путь изучения линейной алгебры, я хотел бы поделиться, в основном из своих эгоистичных соображений (написание концепций заставляет их придерживаться ) интуиция по фундаментальной концепции линейной алгебры: использование матричных обозначений для решения системы уравнений.
Исключение по Гауссу является начальной концепцией многих курсов линейной алгебры для первого года обучения. Это краткое объяснение предназначено для того, чтобы помочь любому, кто изучает один из этих курсов, узнать об исключении Гаусса и, что более важно (мы потратим на это больше времени), разложить эту систему на множители в виде A = LU.
Я бы порекомендовал иметь четкое представление об основах исключения Гаусса (и всех концепциях ниже), хотя я все равно рассмотрю его.
Содержание:
Это подробное руководство, но если вы ищете конкретные лакомые кусочки информации, воспользуйтесь этими ссылками:
- Почему наш классический способ решения линейных систем не работает
- Мотивация для исключения Гаусса
- Верхний треугольник
- Исключение по Гауссу в системе (2 x 2)
- Исключение по Гауссу в системе (3 x 3)
- Развороты
- Временное разбиение и замена строк (не единичные)
- Перманентный пробой, т. е. сингулярный случай
- Случай сингулярной системы #1: Бесконечные решения
- Случай сингулярной системы #2: Нет решений
- Геометрический вид сингулярного случая
Почему наш классический способ решения линейных систем не работает ‘t Work
Мы хорошо знакомы с линейными системами уравнений, может быть, со средней школы — не позже, чем на втором курсе старшей школы.
Было несколько способов их решения — вы могли использовать одно уравнение для решения некоторого неизвестного, а затем заменить это неизвестное его новым значением в другом уравнении. это называется замена.
это называется замена.
Вы также можете исключить целых уравнений, добавляя и вычитая сами уравнения.
И хотя исключение Гаусса немного ближе ко второму, с любым из этих методов все же есть проблема. Оба они работают в небольших системах с 2 или 3 уравнениями и неизвестными, но когда вы доберетесь до больших систем, вам понадобится методическая и надежная формула, которая работает со всеми системами.
Когда вы решаете большие системы, это делает компьютер. Довольно сложно заставить компьютер выполнять либо исключение, либо замену так, как нас учили классически, поскольку методы отличаются от уравнения.
Эта потребность в методической формуле является причиной существования исключения Гаусса.
Мотивация исключения по Гауссу
Исключение по Гауссу — это способ методичного и предсказуемого решения системы уравнений с использованием матриц.
Давайте рассмотрим пример системы и решим ее методом исключения.
Очевидно, нам не нужна линейная алгебра, чтобы решить это. Черт возьми, мы можем решить это с первого взгляда. Ответ совершенно очевиден: x = y = 1. Но чем больше у нас неизвестных и уравнений, тем сложнее становится экспоненциально.
Мы можем хранить всю эту информацию в одной матрице и двух векторах, матрице, в которой хранятся все наши коэффициенты A, векторе неизвестных x и наших ответах b.
Если мы умножим это, мы получим ту же систему уравнений. Что еще более важно, мы действительно можем избавиться от векторов x и y во время исключения, поскольку они не несут никакой информации. Мы знает , что система 2 x 2 и, следовательно, имеет два неизвестных.
Таким образом, мы можем создать дополненную матрицу из A и b.
Справа от пунктирной линии – наша матрица коэффициентов, слева – наши ответы.Вышеприведенное можно прочитать как два уравнения: 1x + 1y = 2 и 2x + 1y = 3 (если представить, что вектор x и y все еще существует — или, проще, просто представить соответствующее неизвестное, сидящее рядом к каждому коэффициенту
Аналогичным образом можно выполнить исключение в этой матричной форме. Что мы хотим сделать, так это превратить матрицу коэффициентов A в U — то, что мы называем верхним треугольником .
Что мы хотим сделать, так это превратить матрицу коэффициентов A в U — то, что мы называем верхним треугольником .
Верхний треугольный
Верхний треугольный (U) — особый вариант матрицы, в которой под диагональю только нули. Верхние треугольные узоры встречаются только в квадратных матрицах. Ниже приведены (2 x 2), (3 x 3) и (4 x 4) верхние треугольные матрицы.
Причина, по которой верхнетреугольные матрицы предпочтительны при решении систем уравнений, заключается в том, что они облегчают их решение. Давайте на мгновение представим систему уравнений с три уравнения и три неизвестных.
слева формат Ax+b, а справа дополненный стиль. Оба эквивалентны.Если матрица коэффициентов уже находится в форме верхнего треугольника , как показано выше, система становится очень простой для решения. Вы можете решить ее снизу вверх. Нижний элемент просто указывает, что это такое.
В верхнем треугольнике это то, во что превращается ваша система.
Теперь мы можем легко решать снизу вверх. Мы можем легко вычислить, что z должно быть, и мы можем подставить это значение z в приведенное выше уравнение, чтобы легко найти d . Это называется обратной заменой .
Это может быть легче понять на конкретном примере. Посмотрим еще один верхний треугольник в формате Ax = b и дополненный.
слева — формат Ax+b, а справа — дополненный стиль. Оба эквивалентны.Соответствующая система уравнений (она должна быть у вас в голове, когда вы это видите) выглядит так.
Мы можем легко понять это снизу вверх. Мы можем с первого взгляда увидеть, что z равно 3, и затем мы можем подставить это в уравнения выше ( обратная замена) и найти каждую переменную по одной, что делает это довольно легко. Мы можем узнать, что y must = 1 и x = 2.
Исключение по Гауссу в системе (2 x 2)
Давайте теперь вернемся к нашему примеру, чтобы лучше понять, куда мы хотим двигаться. Мы хотим каким-то образом превратить матрицу коэффициентов слева в число 9.0005 верхняя треугольная матрица , которую легко решить.
Мы хотим каким-то образом превратить матрицу коэффициентов слева в число 9.0005 верхняя треугольная матрица , которую легко решить.
То, как мы это делаем, напоминает нашу классическую стратегию ликвидации. Чтобы создать верхнюю треугольную матрицу (2 x 2), мы хотим, чтобы место, занимаемое нашей двойкой, было занято 0. Нам все равно, какие числа — помните, верхний треугольник имеет только 0 ниже диагонали. Это единственные критерии.
Мы делаем наше первое исключение , чтобы преобразовать это 2 в 0. Мы умножаем первую строку нашей матрицы коэффициентов [ 1 1 ] и вычитаем ее из нижней строки [ 2 1 ], выбирая множитель, который отменяет 2
Если это поможет, думайте об этом так же, как об уничтожении старой школы — мы делаем то же самое. Правильный множитель для умножения первой строки равен 2. После умножения нашей первой строки на 2, мы получаем [ 2 2 ], который затем вычитаем из второй строки, чтобы получить нашу обновленную матрицу.
Но, заметьте, мы не меняли правую сторону! И вы будете полностью правы. Как и в классическом исключении, мы делаем то же самое действие умножения и вычитания с левой стороны. Итак, мы умножаем первое число 2 на наш множитель 2 и вычитаем его из 3, чтобы получить -1.
Обратите внимание, что наша верхняя строка не меняется, когда мы умножаем ее и вычитаем из следующей строки, изменяется только строка ниже. Это также напоминает то, как мы делаем классическое исключение — мы используем уравнение как инструмент для упрощения других уравнений — мы не изменяем само исходное уравнение.
А теперь смотри! У нас есть упрощенная система с верхним треугольником в качестве матрицы коэффициентов. Записав это снова в полном виде, получим:
Где U — верхний треугольник, x неизвестная матрица, и c, наша модифицированная «правая сторона» (ранее b ).
Просто напомним. Мы перешли от Ax = b к Ux = c , преобразовав нашу матрицу A (исключение) в верхний треугольный U, применив то же преобразование к b, чтобы сохранить согласованность с обеих сторон равенства. Итак, эти две совершенно равнозначные системы.
Итак, эти две совершенно равнозначные системы.
Исключение Гаусса в системе (3 x 3)
Давайте немного попрактикуемся с исключением Гаусса в менее тривиальной форме, в матрице (3 x 3). Снова используем конкретный пример. Скажем, мы хотели решить эту систему.
Выглядит довольно устрашающе. Обратите внимание, что пробел в первой строке соответствует первому уравнению, не включающему z. Во-первых, давайте преобразуем его в эквивалентную матричную форму и расширенную матрицу Ax = b и A | б.
Теперь мы можем преобразовать нашу матрицу коэффициентов в верхний треугольник, выполнив ряд шагов, аналогичных тем, которые выполняются для матрицы (2 x 2).
Чтобы превратить нашу матрицу в верхний треугольник, мы хотим, чтобы три точки в левом нижнем углу (в настоящее время занятые 4, 2 и 2) были равны 0. Опять же, нас не волнуют числа на диагонали и над ней. — они могут быть какими угодно.
Наш первый шаг состоит в том, чтобы сделать 4 во второй строке, первом столбце равным нулю аналогичным образом. Множитель, на который мы умножаем первую строку перед вычитанием, равен 2, поэтому 2 в первой строке отменяет 4 во второй строке. Затем мы вычитаем это 2 x [ 2 3 0 ] = [ 4 6 0 ] из второй строки.
Множитель, на который мы умножаем первую строку перед вычитанием, равен 2, поэтому 2 в первой строке отменяет 4 во второй строке. Затем мы вычитаем это 2 x [ 2 3 0 ] = [ 4 6 0 ] из второй строки.
Затем мы делаем то же самое вычисление с правой стороны, умножая 8 на 2 и вычитая его из 9, получая -7.
На один шаг ближе от нашего А к У!Наш следующий шаг — удалить 2 в левом нижнем углу. Мы сделаем это, снова умножив первую строку, но на этот раз вычтя ее из третья строка , выбрав множитель, который будет умножаться на 2 из первой строки и отменять 2 в третьей строке.
Этот множитель равен всего 1. Мы умножаем нашу первую строку на 1 x [ 2 3 0 ] = [ 2 3 0 ], которую затем вычитаем из [ 2 2 3 ]. [ 2 2 3 ] — [ 2 3 0 ]= [ 0 -1 3].
И не забудьте сделать то же самое с правой стороны — взять 8, умножить на 1 и вычесть из 9, чтобы получить 1.
Теперь обратите внимание, что мы очистили все числа ниже диагонали в первом столбце. нам сделано с этим столбцом.
Прежде чем мы перейдем к очистке этого -1 во втором столбце, я хотел бы указать кое-что об исключениях, которые мы делали.
Pivots
До сих пор мы основывали наш выбор множителя на том, что умножается на 2 (первая строка, первый столбец) и исключается на числа под ним. Именно так мы определяем наш множитель. Это делает его важным, в любом случае в этой колонке. Мы называем это число точкой разворота . Точнее, первая опорная точка, , так как это первая из трех опорных точек в нашем уравнении.
Это три точки опоры в нашей матрице прямо сейчас. Я подчеркиваю важность этой части прямо сейчас — мы не рассматриваем опорные точки, пока не получим для них . Вы увидите, что наша третья опорная точка, 3, больше не будет 3, как только мы выполним еще один шаг исключения. Таким образом, мы на самом деле не думаем о опорных точках, пока не доберемся до них, поскольку этапы исключения часто изменяют ряды под ними, а вместе с ними и опорные точки.
Повороты станут более важными позже. А пока вернемся к нашему примеру.
Теперь нам нужно избавиться от -1 в третьей строке, во втором столбце. (3, 2 позиция). Для этого мы используем наш -секундный пивот. Поскольку первый столбец полностью состоит из нулей и не повлияет на наши вычисления, мы можем думать об этом почти как о нахождении верхнего треугольника системы 2 x 2 .
Как и раньше, мы смотрим на нашу вторую строку и видим, на какое число мы должны ее умножить, чтобы -1 во второй строке уравнялось с -1 в третьей строке. Этот множитель равен 1, , так как при умножении получится -1 (-1 x 1), а при вычитании из следующей строки прибавится к 0 (-1- -1 = -1 + 1 = 0).
Опять же, мы делаем то же самое вычисление с правой частью, умножая наше -7 на 1 и вычитая его из 1, чтобы получить 8 (1—7 = 1 + 7 = 8).
Теперь наша исходная матрица A стала верхним треугольником U, а наша правая часть изменилась с b, исходной правой стороны, на c, модифицированную.
Теперь ее можно легко решить восходящим путем с помощью обратной подстановки.
Начав снизу с z = 1, и расширив вверх, мы получим ответ z = 1 , y = 2 и x = 2.
Чтобы лучше понять исключение Гаусса, мы должны задайте критический вопрос: когда алгоритм исключения Гаусса не работает? Возможны два случая. Временный сбой и постоянный сбой .
Нули могут никогда не существовать в положении точки вращения. Когда это происходит, элиминация прекращается либо временно, либо навсегда.
Посмотрим как.
Временная разбивка и обмен строками (не в единственном числе)
Когда ноль существует где-либо, кроме последней разворотной точки , мы имеем временную разбивку. т. е. они неособы и имеют единственное решение.
Когда в опорной позиции стоит ноль, мы не можем исключить 2 или 5 из первого столбца, потому что нет ничего, на что мы могли бы умножить 0, чтобы исключить 2 или 5, поскольку 0 x любое число = 0.
Что делать мы делаем, чтобы решить эту проблему? А обмен строками. Так как число в первом опорном разряде равно 0, мы можем поменять местами первую и вторую строки, чтобы ноль больше не доставлял нам хлопот.
Теперь мы можем умножить нашу опорную точку. В качестве дополнительного бонуса нам не нужно исключать число в позиции (2, 1), поскольку оно уже равно 0.
Та же проблема может возникнуть и во втором столбце. Скажем, мы начинаем с довольно скромной (3 x 3) матрицы, такой как эта:
После того, как мы использовали исключение, чтобы избавиться от первого столбца (4), у нас осталась проблема.
Второй стержень превратился в 0! Мы можем сделать то же самое, чтобы исправить это, но на этот раз обмен строками между строками 2 и 1. Это исправляет систему, а также решает ее.
Помните, что при замене строк в расширенной матрице мы также должны поменять местами правую часть b.
Это имеет большой смысл, если вы думаете об этом с точки зрения уравнений. Совершенно очевидно, что изменение порядка уравнений требует, чтобы вы меняли ответы. Взглянув на это уравнение, вы поймете, что это совершенно очевидно.
Совершенно очевидно, что изменение порядка уравнений требует, чтобы вы меняли ответы. Взглянув на это уравнение, вы поймете, что это совершенно очевидно.
Итак, когда поломка становится постоянной?
Постоянный сбой, т. е. единичный случай
Когда мы сталкиваемся с постоянным сбоем, это происходит потому, что либо недостаточно информации в системе, либо противоречивая информация в системе. Первый создает бесконечных решений, а второй создает без решений.
Переходим к делу: поломка необратима, когда последний опорный пункт равен нулю. Логически это логично. Когда вы находитесь в последней строке и сталкиваетесь с нулем, под ней больше нет строк, на которые можно было бы переключиться, и вы не можете переключиться на строку выше (это разрушит верхнюю треугольную форму, к которой вы строите).
Случай сингулярной системы № 1: Бесконечные решения
Давайте рассмотрим их в матрицах (2 x 2), так как это довольно легко понять. Вот система, которая является единственной.
Вот система, которая является единственной.
Обратите внимание, что когда мы делаем исключение, мы получаем:
О нет, последняя опорная точка равна 0, что означает, что она единственная. Давайте посмотрим, что это означает в виде системы уравнений.
Мы можем ясно видеть, что эта система уравнений имеет бесконечных решений. Поскольку второе уравнение оценивается как 0 = 0, что верно независимо от значений x и y , у нас остается одно уравнение для описания двух неизвестных, что дает бесконечное количество примеров.
Оглядываясь назад на исходную систему, становится ясно, почему у нас бесконечное количество примеров.
Второе уравнение не добавляет никакой информации в нашу систему. Это просто первое уравнение, умноженное на два. У нас остается то же количество информации, как если бы у нас было только одно уравнение, и у нас недостаточно ограничений, чтобы найти единственное значение 9.0005 х и г.
Это происходит во множестве ситуаций. Короче говоря, эта проблема бесконечных решений возникает, когда одно (или несколько) наших уравнений составляют из некоторой комбинации других уравнений в системе.
Вот два менее очевидных примера подобного случая с бесконечным числом ответов.
В обоих этих случаях мы получаем два уравнения для описания 3 неизвестных. Этого недостаточно, и мы таким образом получаем бесконечное количество решений.Сингулярный системный случай #2: Нет решений
Второй тип постоянной поломки, когда мы получаем без решений, очень похож. По сути, это когда левая часть нашей системы представляет собой некоторую комбинацию друг друга, а правая часть содержит противоречивую информацию. Давайте посмотрим, что это означает на простом примере 2 x 2.
Это идентично системе, которую мы исследовали в случае бесконечных решений, за исключением того, что я изменил 12 в b в 13.
Возможно, вы уже видите, к чему все идет. Давайте воспользуемся методом исключения Гаусса, чтобы упростить систему уравнений. В итоге мы получим следующее:
Давайте воспользуемся методом исключения Гаусса, чтобы упростить систему уравнений. В итоге мы получим следующее:
Если мы запишем это в виде уравнения, мы увидим, что оно содержит противоречивую информацию.
0 не равно 1. Таким образом, это уравнение неверно для любых неизвестных x или y. Эта система не имеет решений.
Этот тип сингулярного случая без решения возникает, когда левая часть представляет собой некоторую комбинацию друг друга, как здесь, но правые части не совпадают с той же комбинацией. Раньше у нас были бесконечные решения, потому что правая часть совпадала, и мы получили 0 = 0. Но поскольку мы изменили левую часть и по-разному изменили правую часть, в некотором смысле у нас нет решений вместо бесконечного числа. количество.
Два других наших примера в бесконечном случае становятся примерами для случаев отсутствия решения, если мы просто изменим правые части, чтобы сделать их несовместимыми.
Действительно, замена 9 и 10 на любое другое число, которое не равно 9 или 10, не приведет к решению.
Но как определить, является ли система единственной, не пройдя весь путь исключения? Это, как и многие концепции линейной алгебры, требует геометрического понимания.
Геометрический вид особого случая
Эта часть требует хорошего понимания комбинаций span и linear. Если вы сомневаетесь в этом, это видео все объясняет.
Кроме того, мы должны смотреть как на изображение строки , так и на представление столбца матрицы. Это предполагает рассмотрение матрицы не как системы уравнений, а как векторов в пространстве. Если вы не знакомы с обоими из них, смотрите, эта лекция великолепно освещает все это.
Вот очень быстрое обновление одной картинки для изображения строки и изображения столбца.
При использовании представления строки для анализа системы (2 x 2) единичный случай может означать две разные вещи. Давайте использовать те же примеры, что и в прошлый раз.
В более высоких измерениях появляется все больше и больше способов пересечения плоскостей, которые либо дают бесконечное количество решений, либо не дают их вообще. Например, в 3D две плоскости могут пересекаться для решения, но 3-я плоскость не пересекается, что приводит к тому, что решений для системы в целом нет — или плоскости могут пересекаться, но все они могут быть прямыми вертикальными — вызывая целая вертикальная линия бесконечных решений.
Например, в 3D две плоскости могут пересекаться для решения, но 3-я плоскость не пересекается, что приводит к тому, что решений для системы в целом нет — или плоскости могут пересекаться, но все они могут быть прямыми вертикальными — вызывая целая вертикальная линия бесконечных решений.
Но теперь давайте посмотрим на это с точки зрения линейных комбинаций и охвата в столбце формы нашей системы, чтобы получить больше интуиции.
Обратите внимание, что источником проблемы в обоих этих особых случаях является то, что векторы являются коллинеарными, и поэтому могут описывать только одну линию как комбинацию: их диапазон одномерен и существует только на линии они делят.
Трехмерным геометрическим аналогом этого будут два из трех трехмерных векторов (a, b, c) и (e, f, g), существующих на одних и тех же плоскость, приводит к тому, что диапазон трех векторов в сумме оказывается только в плоскости, которую они разделяют — если ответ, также трехмерный вектор, не существует на плоскости (что с точки зрения вероятности вероятно), нет решения. И если ответ существует ли на плоскости , существует бесконечное количество комбинаций трех векторов, чтобы получить этот ответ.
И если ответ существует ли на плоскости , существует бесконечное количество комбинаций трех векторов, чтобы получить этот ответ.
Вернемся к 2D-системам — мы определили, что проблема в том, что они имеют коллинеарных векторов. Как определить это заранее? Это простой тест.
Возьмите столбцы вашей матрицы A и поместите их в виде линейной комбинации. Есть ли способ для комбинации векторов объединиться, чтобы сформировать нулевой вектор, где x ≠ y ≠ 0?
Почему это работает как лакмусовая бумажка, если система содержит зависимые векторы? Ну, если есть способ, который мы можем найти, чтобы компенсировать векторы, используя комбинации других векторов в системе, это означает, что один из векторов должен состоять из некоторой комбинации других.
И, очевидно, мы не учитываем x = y = 0, так как это будет работать для любой линейной комбинации. Здесь есть ненулевой ответ, а именно:
Таким образом, мы можем решить систему уравнений, используя матричные обозначения, чтобы создать матрицу коэффициентов A. Мы помещаем это либо в Ax = b или дополненная форма для решения. Преобразуем эту матрицу A в легко разрешимую верхнетреугольную U , используя исключение умножения-вычитания в строках по обе стороны от знака равенства (поворот b в c по другую сторону знака равенства).
Мы помещаем это либо в Ax = b или дополненная форма для решения. Преобразуем эту матрицу A в легко разрешимую верхнетреугольную U , используя исключение умножения-вычитания в строках по обе стороны от знака равенства (поворот b в c по другую сторону знака равенства).
Затем мы используем обратную замену для решения системы снизу вверх.
Это вся информация, которую вам нужно знать, чтобы провести и понять процесс ликвидации. Есть много более эффективных и интересных способов выполнить это устранение, о которых я расскажу в следующих двух статьях.
В следующей статье мы рассмотрим эти преобразования, исключения и замены строк как 9Умножение матриц 0005 — по сути, , поиск матриц, на которые мы можем умножить наше A, чтобы выполнить исключение так же, как мы только что сделали это вручную.
Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия, в настоящее время участвует в STEM и бизнес-стипендии TKS . Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды. Чтобы не отставать,
Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды. Чтобы не отставать,
Следуйте за ним I nstagram и его LinkedIn . Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Глава 6 Метод исключения Гаусса для решения одновременных линейных уравнений
6.1 Цели обучения
После успешного завершения этого урока вы должны уметь
(1). написать алгоритм для решения системы одновременных линейных уравнений с использованием наивного метода исключения Гаусса
(2). решить набор одновременных линейных уравнений, используя наивное исключение Гаусса.
(3). используйте шаги прямого исключения метода исключения Гаусса, чтобы найти определитель квадратной матрицы,
(4). перечислить теоремы, связанные с определителем матриц,
(5). связывают нулевое и ненулевое значение определителя квадратной матрицы с наличием или отсутствием обратной матрицы.
связывают нулевое и ненулевое значение определителя квадратной матрицы с наличием или отсутствием обратной матрицы.
(6). перечислить подводные камни наивного метода исключения Гаусса
(7). показывают подводные камни наивного метода исключения Гаусса на примерах
(8). напишите алгоритм для решения системы одновременных линейных уравнений с использованием исключения Гаусса с частичным поворотом.
(9). решить систему одновременных линейных уравнений методом исключения Гаусса с частичным поворотом
6.2 Как система уравнений решается численно методом исключения Гаусса?
Одним из самых популярных методов решения одновременных линейных уравнений является метод исключения Гаусса. Подход предназначен для решения общего набора \(n\) уравнений и \(n\) неизвестных
\[\begin{split} &a_{11}x_{1} + a_{12}x_{2} + a_{13}x_{3} + \ldots + a_{1n}x_{n} = b_{1}\\ &a_{21}x_{1} + a_{22}x_{2} + a_{23}x_ {3} + \ldots + a_{2n}x_{n} = b_{2}\\ &\vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ &a_ {n1}x_{1} + a_{n2}x_{2} + a_{n3}x_{3} + \ldots + a_{{nn}}x_{n} = b_{n} \end{split}\ ]
Исключение Гаусса состоит из двух шагов
Прямое исключение неизвестных: На этом этапе неизвестные исключаются в каждом уравнении, начиная с первого уравнения.
 Таким образом, уравнений сводятся к одному уравнению и одному неизвестному в каждом уравнении.
Таким образом, уравнений сводятся к одному уравнению и одному неизвестному в каждом уравнении.Обратная замена: На этом шаге, начиная с последнего уравнения, находятся все неизвестные.
6.3 Прямое устранение неизвестных:
На первом шаге прямого исключения первое неизвестное \(x_{1}\) удаляется из всех строк ниже первой строки. Первое уравнение выбирается в качестве основного уравнения для исключения \(x_{1}\). Таким образом, чтобы исключить \(x_{1}\) во втором уравнении, нужно разделить первое уравнение на \(a_{11}\) (отсюда и название опорного элемента), а затем умножить его на \(a_{21}\ ). Это то же самое, что умножить первое уравнение на \(a_{21}/a_{11}\), чтобы получить
\[a_{21}x_{1} + \frac{a_{21}}{a_{11 }}a_{12}x_{2} + \ldots + \frac{a_{21}}{a_{11}}a_{1n}x_{n} = \frac{a_{21}}{a_{11} }b_{1}\] 9{(n — 1)}}\]
6.5 Пример 1
Восходящая скорость ракеты указана в таблице 1 для трех разных моментов времени. {2} + a_{2}t + a_{3},5 \leq т \leq 12\]
{2} + a_{2}t + a_{3},5 \leq т \leq 12\]
Коэффициенты \(a_{1},a_{2},and_{3}\) для приведенного выше выражения равны
\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \\ \end{bmatrix} = \begin{bmatrix} 106,8 \ \ 177.2 \\ 279.2 \\ \end{bmatrix}\]
Найдите значения \(a_{1},a_{2} и\ a_{3}\), используя наивный метод исключения Гаусса. Найдите скорость в \(t = 6,7,5,9,11\) секунд.
Решение
Расширенная матрица:
\[\begin{bmatrix} 25 & 5 & 1 & | & 106,8 \ 64 & 8 & 1 & | & 177,2 \ 144 & 12 & 1 & | & 279.2 \\ \end{bmatrix}\]
Прямое исключение неизвестных
Поскольку есть три уравнения, будет два шага прямого исключения неизвестных.
Первый шаг
Разделите строку \(1\) на \(25\), а затем умножьте ее на \(64\), то есть умножьте строку \(1\) на \(64/25 = 2,56) \).
\[\left( \begin{matrix} \left\lbrack 25 \right. \ & \ 5 & \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ |\ \ \ \ \ \\ \end {matrix}106.8\rbrack \right) \times 2.56\ \text{дает строку 1 как}\]
\ & \ 5 & \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ |\ \ \ \ \ \\ \end {matrix}106.8\rbrack \right) \times 2.56\ \text{дает строку 1 как}\]
\[\begin{matrix} \left\lbrack 64 \right.\ & 12.8 & 2.56 \\ \end{ matrix}\ \ \ \ \ |\ \ 273.408\rbrack\]
Вычесть результат из строки \(2\)
\[\frac{\begin{matrix} \ \ \ \lbrack\begin{matrix} 64 & \ \ \ \ 8 & \ \ \ \ \ 1 \\ \end{matrix}\ \ \ \ \ |\ \ & 177.2\rbrack \\- \lbrack\begin{matrix} 64 & 12.8 & 2.56 \\ \ конец {матрица}\ \ | & 273.408\rbrack \\ \end{matrix}}{\ \ \ \begin{matrix} \begin{matrix} 0 & — 4.8 & — 1.56 \\ \end{matrix} & — 96.208 \\ \end{matrix}}\]
чтобы получить результирующие уравнения как
\[\left\lbrack \begin{matrix} 25 & 5 & 1 \\ 0 & — 4,8 & — 1,56 \\ 144 & 12 & 1 \\ \end{matrix} \ \ \ \ \ \ \ \ \begin{matrix} | \ \ \ \ \ \ \ 106.8 \\ \ |\ — 96.208 \\ |\ \ \ \ \ \ \ 279.2 \\ \end{matrix} \right\rbrack\]
Разделить строку \(1\) на \ (25\), а затем умножьте его на \(144\), то есть умножьте строку \(1\) на \(144/25 = 5,76\).
\[\left( \begin{matrix} \left\lbrack 25 \right.\ & \ \ \ \ 5 & \ \ \ 1 \\ \end{matrix} \ \ \ \ \ \ |\ \ \ \ \ \ \ \ \ 106.8\rbrack \right) \times 5.76\ \text{дает строку 1 как}\]
\[\left\lbrack \begin{matrix} 144 & 28.8 & 5.76 \\ \end{matrix} \ \ \ \ \right|\ \ \ \ \ \ 615.168\rbrack\]
Вычесть результат из строки \(3\)
\[\frac{\begin{matrix} \ \ \ \ \lbrack\begin{matrix} 144 & 12 & \ \ \ \ \ \ 1 \\ \end{matrix}\ \ \ \ | & 279.2\rbrack \\ — \begin{matrix} \lbrack 144 & 28.8 & 5.76 \\ \end{matrix}\ \ \ | & 615.168\rbrack \\ \end{matrix}}{\ \ \ \ \begin{matrix} \begin{matrix} 0 & — 16,8 & — 4,76 \\ \end{matrix} & — 335,968 \\ \end{matrix}}\]
чтобы получить результирующие уравнения как
\[\left\lbrack \begin{matrix} 25 & 5 & 1 \\ 0 & — 4,8 & — 1,56 \\ 0 & — 16,8 & — 4,76 \\ \end{matrix}\ \ \ \ \ \ \ \ \ \begin{matrix} |\ \ \ \ \ \ \ \ \ 106,8 \\ |\ \ — 96,208 \\| — 335,968 \\ \end{matrix} \right\rbrack\]
Второй шаг
Теперь разделим строку \(2\) на \(-4,8\) и затем умножим на \(-16,8\), то есть умножьте строку \(2\) на \(-16,8/-4,8 = 3,5\).
\[\left( \left\lbrack 0 — 4,8\ \ — 1,56\ \ \ \ \ \ \ \ \ \\right|\ \ \ — 96,208\rbrack\ \right) \times 3,5\ \text{дает Строка 2 как}\]
\[\слева\lbrack 0 — 16,8\ — 5,46\ \ \ \ \ \ \ \ \ \ \right| — 336,728\rbrack\]
Вычесть результат из строки \(3\)
\[\frac{\begin{matrix} \ \ \ \ \ \lbrack\begin{matrix} 0 & -16,8 & -4,76\ \\ \end{matrix} \ \ \ \ \ | & -335.968\rbrack \\ \ -\ \lbrack \begin{matrix} 0 & -16,8 & -5,46\ \\ \end{matrix}\ \ \ \ \ | & -336.728\rbrack \\ \end{matrix}}{\begin{matrix} \ \ \ \ \ \begin{matrix} 0 & \ \ \ \ \ \ \ 0 & \ \ \ \ \ \ 0.7 \end{ матрица} & \ \ \ \ \ \ \ \ \ \ \ 0,76 \ \ \ \end{matrix}}\]
, чтобы получить результирующие уравнения как
\[\left\lbrack \begin{matrix} 25 & 5 & 1 \\ 0 & — 4,8 & — 1,56 \\ 0 & 0 & 0,7 \\ \end{matrix} \ \ \ \ \ \ \ \begin{matrix} |\ \ \ \ \ \ 106,8 \\ \ \ |\ — 96,208 \\ |\ \ \ \ \ \ \ \ 0,76 \\ \end{matrix} \right\rbrack \]
\[\begin{bmatrix} 25 & 5 & 1 \\ 0 & — 4,8 & — 1,56 \\ 0 & 0 & 0,7 \\ \end{bmatrix}\begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \\ \end{bmatrix} = \begin{bmatrix} 106,8 \\ — 96. 208 \\ 0.76 \\ \end{bmatrix}\]
208 \\ 0.76 \\ \end{bmatrix}\]
Обратная замена
Из третьего уравнения
\[0.7a_{3} = 0.76\]
\[\begin{split} a_{3 } &= \frac{0.76}{0.7}\\ &= 1.08571 \end{split}\]
Подставляя значение \(a_{3}\) во второе уравнение,
\[- 4.8a_{ 2} — 1,56a_{3} = — 96,208\]
\[\begin{split} a_{2} &= \frac{- 96,208 + 1,56a_{3}}{- 4,8}\\ &= \frac {- 96,208 + 1,56 \ умножить на 1,08571}{- 4,8}\\ &= 19.6905\end{split}\]
Подставляя значения \(a_{2}\) и \(a_{3}\) в первое уравнение,
\[25a_{1} + 5a_{2} + a_{3} = 106,8\]
\[\begin{split} a_{1} &= \frac{106,8 — 5a_{2} — a_{3}}{25}\\ &= \frac{106,8 — 5 \times 19,6905 — 1,08571}{25}\\ &= 0,2
\end{split}\]
Следовательно, вектор решения равен
\[\begin{bmatrix} a_{1} \\ a_{2} \ \ a_{3} \\ \end{bmatrix} = \begin{bmatrix} 0,2
\\ 19,6905 \\ 1,08571 \\ \end{bmatrix}\] 9{2} \\ 6 & 7.5 & 9 & 11 \\ 1 & 1 & 1 & 1 \end{bmatrix}\\ &= \left\lbrack 0,2
\ \ 19,6905 \ \ 1,08571 \right\rbrack\begin{bmatrix} 36 & 56. 25 & 81 & 121 \\ 6 & 7.5 & 9 & 11 \\ 1 & 1 & 1 & 1 \end{bmatrix}\\ &= \left\lbrack 129.686 \ \ 165.104\ \ 201.828 \ \ 252.828 \right \rbrack \end{split}\]
25 & 81 & 121 \\ 6 & 7.5 & 9 & 11 \\ 1 & 1 & 1 & 1 \end{bmatrix}\\ &= \left\lbrack 129.686 \ \ 165.104\ \ 201.828 \ \ 252.828 \right \rbrack \end{split}\]
\[v(6) = 129,686\ м/с\]
\[v(7,5) = 165,1\ 04\ м/с\]
\[v(9 ) = 201,828\ м/с\]
\[v(11) = 252,828\ м/с\]
6.6 Можно ли использовать наивные методы исключения Гаусса для нахождения определителя квадратной матрицы?
Одним из наиболее эффективных способов найти определитель квадратной матрицы является использование следующих двух теорем об определителе матриц в сочетании с наивным исключением Гаусса.
Теорема 1:
Пусть \(\lbrack A\rbrack\) — матрица \(n \times n\). Тогда, если \(\lbrack B\rbrack\) является матрицей \(n \times n\), которая является результатом добавления или вычитания кратного одной строки в другую строку, тогда \(det(A) = det(B) \) (То же самое относится и к операциям со столбцами). 9{n}a_{{ii}} \end{split}\]
Из этого следует, что если мы применим шаги прямого исключения метода исключения Наивного Гаусса, определитель матрицы останется прежним согласно теореме 1.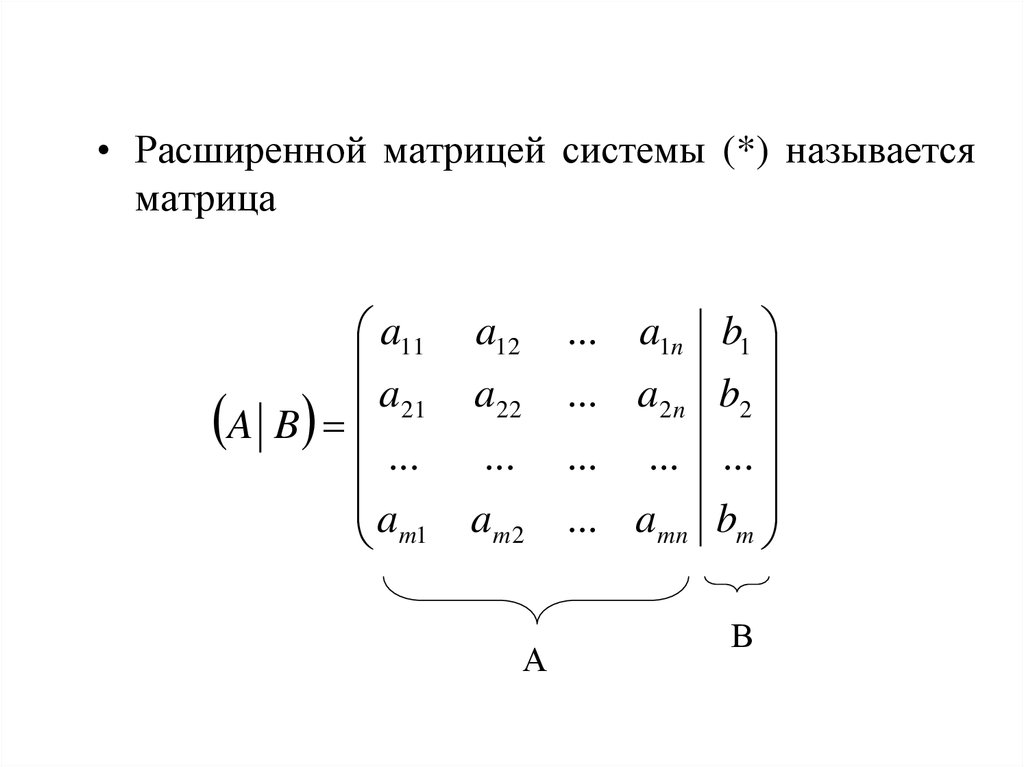 Тогда, поскольку в конце шагов прямого исключения результирующая матрица является верхнетреугольной, определитель будет дан теоремой 2.
Тогда, поскольку в конце шагов прямого исключения результирующая матрица является верхнетреугольной, определитель будет дан теоремой 2.
6.6.1 Пример 2
Найдите определитель
{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\]
Решение
Помните, что в примере 1 мы выполнили шаги прямого исключения неизвестных, используя метод наивного исключения Гаусса на \(\lbrack A\rbrack\), чтобы получить
\[\left\lbrack B \right \rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 0 & — 4,8 & — 1,56 \\ 0 & 0 & 0,7 \\ \end{bmatrix}\]
Согласно теореме 2
\[\begin {split} det(A) &= det(B)\\ &= 25 \times ( — 4.8) \times 0.7\\ &= — 84.00 \end{split}\]
6.7 Что делать, если я не могу найти определитель матрицы, используя метод исключения Наивного Гаусса, например, если я получаю проблемы деления на ноль во время метода исключения Наивного Гаусса?
Ну, можно применить исключение Гаусса с частичным поворотом. Однако определитель полученной верхней треугольной матрицы может отличаться знаком. Следующая теорема применяется в дополнение к предыдущим двум, чтобы найти определитель квадратной матрицы.
Однако определитель полученной верхней треугольной матрицы может отличаться знаком. Следующая теорема применяется в дополнение к предыдущим двум, чтобы найти определитель квадратной матрицы.
Теорема 3:
Пусть \(\lbrack A\rbrack\) будет матрицей \(n \times n\). Тогда, если \(\lbrack B\rbrack\) является матрицей, полученной в результате замены одной строки другой строкой, то \(det(B) = — det(A)\).
6.7.1 Пример 3
Найдите определитель числа
\[\lbrack A\rbrack = \begin{bmatrix} 10 & — 7 & 0 \\ — 3 & 2,099 & 6 \\ 5 & — 1 & 5 \\ \end{bmatrix}\]
Решение
Конец шагов прямого исключения исключения Гаусса с частичным поворотом, мы получим
\[\lbrack B\rbrack = \begin{bmatrix} 10 & — 7 & 0 \\ 0 & 2,5 & 5 \\ 0 & 0 & 6,002 \\ \end{bmatrix}\]
\[\begin {split} \det\left( B \right) &= 10 \times 2.5 \times 6.002\\ &= 150.05 \end{split}\]
Так как строки были переключены один раз во время шагов прямого исключения метода Гаусса с частичным поворотный,
\[\begin{split} \det\left( A \right) &= — det(B)\\ &= — 150. 05 \end{split}\]
05 \end{split}\]
6.7.2 Пример 4 9{- 1}\ \lbrack A\rbrack\).
6.8 Есть ли подводные камни метода наивного исключения Гаусса?
Да, в наивном методе исключения Гаусса есть две ловушки.
Деление на ноль: Деление на ноль может происходить в начале \(n — 1\) шагов прямого исключения.
Например,
\[5x_{2} + 6x_{3} = 11\]
\[4x_{1} + 5x_{2} + 7x_{3} = 16\]
\[9x_{1 } + 2x_{2} + 3x_{3} = 15\]
приведет к делению на ноль на первом шаге прямого исключения, поскольку коэффициент при \(x_{1}\) в первом уравнении равен нулю, что очевидно, когда мы записываем уравнения в матричной форме.
\[\begin{bmatrix} 0 & 5 & 6 \\ 4 & 5 & 7 \\ 9 & 2 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 11 \\ 16 \\ 15 \\ \end{bmatrix}\]
А как насчет приведенных ниже уравнений: Является ли деление на ноль проблемой? ?
\[5x_{1} + 6x_{2} + 7x_{3} = 18\]
\[10x_{1} + 12x_{2} + 3x_{3} = 25\]
\[20x_{ 1} + 17x_{2} + 19x_{3} = 56\]
Записано в матричной форме,
\[\begin{bmatrix} 5 & 6 & 7 \\ 10 & 12 & 3 \\ 20 & 17 & 19 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 18 \\25 \\ 56 \ \ \end{bmatrix}\]
нет проблемы деления на ноль на первом шаге прямого исключения. Поворотным элементом является коэффициент \(x_{1}\) в первом уравнении, 5, и это ненулевое число. Однако в конце первого шага прямого исключения мы получаем следующие уравнения в матричной форме 9{nd}\) шаг прямого исключения, коэффициент \(x_{2}\) в уравнении 2 будет использоваться в качестве опорного элемента. Этот элемент равен нулю и, следовательно, создаст проблему деления на ноль.
Поворотным элементом является коэффициент \(x_{1}\) в первом уравнении, 5, и это ненулевое число. Однако в конце первого шага прямого исключения мы получаем следующие уравнения в матричной форме 9{nd}\) шаг прямого исключения, коэффициент \(x_{2}\) в уравнении 2 будет использоваться в качестве опорного элемента. Этот элемент равен нулю и, следовательно, создаст проблему деления на ноль.
Поэтому важно учитывать, что возможность деления на ноль может возникнуть в начале любого шага прямого исключения.
Ошибка округления: Наивный метод исключения Гаусса подвержен ошибкам округления. Это верно, когда имеется большое количество уравнений по мере распространения ошибок. Кроме того, если есть вычитание чисел друг из друга, это может привести к большим ошибкам. См. пример ниже.
6.8.1 Пример 5
Вспомните пример 2, где мы использовали простое исключение Гаусса для решения
\[20x_{1} + 15x_{2} + 10x_{3} = 45\]
\[- 3x_{1 } — 2,249x_{2} + 7x_{3} = 1,751\]
\[5x_{1} + x_{2} + 3x_{3} = 9\]
с использованием шести значащих цифр с отсечением в ваших вычислениях? Повторите задачу, но теперь используйте в своих вычислениях пять значащих цифр с отсечкой.
Решение
Запись в матричной форме
\[\begin{bmatrix} 20 & 15 & 10 \\ — 3 & — 2,249 & 7 \\ 5 & 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{ 2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 1.751 \\ 9 \\ \end{bmatrix}\]
Прямое исключение неизвестных
Первый шаг
Разделите ряд 1 на 20, а затем умножьте его на –3, то есть умножьте ряд 1 на \(- 3/20 = — 0,15\).
\[\begin{pmatrix} \begin{bmatrix} 20 & 15 & 10 \\ \end{bmatrix} & \left\lbrack 45 \right\rbrack \\ \end{pmatrix} \times — 0.15\ \text {дает строку 1 как}\]
\[\begin{matrix} \left\lbrack — 3 \right.\ & — 2.25 & \left. \ — 1,5 \right\rbrack \\ \end{matrix} \ \ \ \ \ \ \ \ \left\lbrack — 6,75 \right\rbrack\]
Вычесть результат из строки 2
\[\frac{\ begin{matrix} \ \ \lbrack\begin{matrix} -3 & \ \ \ -2.249 & \ \ \ \ \ 7 \\ \end{matrix}\ \ \ \ \ \ | & 1.751\rbrack \\ — \begin{matrix} \lbrack -3 & \ \ \ \ -2. 25 \ \ -1.5 \ \ \\ \end{matrix}\ \ \ | & -6.75\rbrack \\ \end{matrix}}{\ \ \ \ \begin{matrix} \begin{matrix} 0 & \ \ \ \ \ 0.001 & \ \ \ \ 8.5 \\ \end{matrix} & \ \ \ \ \ 8.501 \end{matrix}}\]
25 \ \ -1.5 \ \ \\ \end{matrix}\ \ \ | & -6.75\rbrack \\ \end{matrix}}{\ \ \ \ \begin{matrix} \begin{matrix} 0 & \ \ \ \ \ 0.001 & \ \ \ \ 8.5 \\ \end{matrix} & \ \ \ \ \ 8.501 \end{matrix}}\]
, чтобы получить результирующие уравнения в виде
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & 0,001 & 8,5 \\ 5 & 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{ 1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 8.501 \\ 9 \\ \end{bmatrix}\]
Разделить строку 1 на 20 а затем умножьте его на \(5\), то есть умножьте строку 1 на \(5/20 = 0,25\).
\[\begin{pmatrix} \begin{bmatrix} 20 & 15 & 10 \\ \end{bmatrix} & \left\lbrack 45 \right\rbrack \\ \end{pmatrix} \times 0.25\ \text{ дает строку 1 как}\]
\[\begin{matrix} \left\lbrack 5 \right.\ & 3.75 & \left. \ 2.5 \right\rbrack \\ \end{matrix} \ \ \ \ \ \ \ \ \left\lbrack 11.25 \right\rbrack\]
Вычесть результат из строки 3
\[\frac{\begin{ матрица} \ \ \lbrack\begin{matrix} 5 & \ \ \ \ \ \ 1 & \ \ \ \ \ \ 3 \\ \end{matrix}\ \ \ \ \ \ \ | & 9\rbrack \\ — \begin{matrix} \lbrack 5 & \ \ \ \ 3. 75 \ \ \ \ \ 2.5 \ \ \\ \end{matrix}\ \ \ | & 11.25\rbrack \\ \end{matrix}}{\ \ \ \begin{matrix} \begin{matrix} 0 &\ -2.75 \ \ \ \ \ \ 0.5 \\ \end{matrix} & \ -2.25 \ конец{матрица}}\]
75 \ \ \ \ \ 2.5 \ \ \\ \end{matrix}\ \ \ | & 11.25\rbrack \\ \end{matrix}}{\ \ \ \begin{matrix} \begin{matrix} 0 &\ -2.75 \ \ \ \ \ \ 0.5 \\ \end{matrix} & \ -2.25 \ конец{матрица}}\]
, чтобы получить результирующие уравнения в виде
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & 0,001 & 8,5 \\ 0 & — 2,75 & 0,5 \\ \end{bmatrix}\begin{bmatrix} x_ {1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 8,501 \\ — 2,25 \\ \end{bmatrix}\]
Второй шаг
Теперь для второго шага прямого исключения мы будем использовать строку 2 в качестве сводного уравнения и исключить строку 3: столбец 2.
Разделить строку 2 на \(0,001\), а затем умножить на \(-2,75\ ), то есть умножьте строку 2 на \(- 2,75/0,001 = — 2750\).
\[\begin{pmatrix} \begin{bmatrix} 0 & 0,001 & 8,5 \\ \end{bmatrix} & \left\lbrack 8,501 \right\rbrack \\ \end{pmatrix} \times — 2750\ \text {дает строку 2 как}\]
\[\begin{matrix} \left\lbrack 0 \right.\ & — 2.75 & \left. \ — 23375 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \left\lbrack — 23377. 75 \right\rbrack\]
75 \right\rbrack\]
Перезапись до 5 значащих цифр с отсечением
\[\begin{ матрица} \left\lbrack 0 \right.\ & — 2.75 & \left. \ — 23375 \right\rbrack \\ \end{matrix} \ \ \ \ \ \ \ \ \left\lbrack — 23377 \right\rbrack\]
Вычесть результат из строки 3
\[\frac{\begin{matrix} \ \ \lbrack\begin{matrix} 0 & \ \ \ \ \ \ -2,75 & \ \ \ \ \ \ 0,5 \\ \ конец {матрица}\ \ \ \ \ \ \ | & -2.25\rbrack \\ — \begin{matrix} \lbrack 0 & \ \ \ \ -2.75 \ \ \ \ \ -23375 \ \ \\ \end{matrix}\ \ \ | & -23377\rbrack \\ \end{matrix}}{\begin{matrix} \begin{matrix} 0 &\ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ 23375 \\ \end{matrix} & \ \ \ \ \ \ \ \ 23374 \end{matrix}}\]
Перезапись в пределах 6 значащих цифр с отсечением
\[\begin{matrix} \left\lbrack 0 \right.\ & 0 & \left. \ 23375 \right\rbrack \\ \end{matrix} \ \ \ \ \ \ \ \ \left\lbrack — 23374 \right\rbrack\]
чтобы получить результирующие уравнения как
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & 0,001 & 8,5 \\ 0 & 0 & 23375 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \ end{bmatrix} = \begin{bmatrix} 45 \\ 8. 501 \\ 23374 \\ \end{bmatrix}\]
501 \\ 23374 \\ \end{bmatrix}\]
Это конец шагов прямого исключения.
Обратная подстановка
Теперь мы можем решить приведенные выше уравнения с помощью обратной подстановки. Из третьего уравнения
\[\begin{split} 23375x_{3} &= 23374\\ x_{3} &= \frac{23374}{23375}\\ &= 0,99995 \end{split}\]
Подстановка значения \(x_{3}\) во второе уравнение
\[0,001x_{2} + 8,5x_{3} = 8,501\]
\[\begin{split} x_{2} & = \frac{8,501 — 8,5x_{3}}{0,001}\\ &= \frac{8,501 — 8,5 \times 0,99995}{0,001}\\ &= \frac{8,501 — 8,499575}{0,001}\\ &= \frac{8,501 — 8,4995}{0,001}\\ &= \frac{0,0015}{0,001}\\ &= 1,5 \end{split}\]
Подстановка значения \ (x_{3}\) и \(x_{2}\) в первом уравнении,
\[20x_{1} + 15x_{2} + 10x_{3} = 45\]
\[\begin{ split} x_{1} &= \frac{45 — 15x_{2} — 10x_{3}}{20}\\ &= \frac{45 — 15 \times 1,5 — 10 \times 0,99995}{20}\\ &= \frac{45 – 22,5 – 9,9995}{20}\\ &= \frac{22,5 – 9,9995}{20}\\ &= \frac{12,5005}{20}\\ &= \frac{12,500}{ 20}\\ &= 0,625 \end{split}\]
Следовательно, решение
\[\begin{split} \left\lbrack X \right\rbrack &= \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \ end{bmatrix}\\ &= \begin{bmatrix} 0,625 \\ 1,5 \\ 0,99995 \\ \end{bmatrix} \end{split}\]
Сравните это с точным решением
\[\left\ lbrack X \right\rbrack = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}\]
6.
 9 Какие существуют способы улучшения наивного метода исключения Гаусса?
9 Какие существуют способы улучшения наивного метода исключения Гаусса?Как видно из примера 3, ошибки округления были большими, когда использовались пять значащих цифр, а не шесть значащих цифр. Одним из методов уменьшения ошибки округления может быть использование более значащих цифр, то есть использование двойной или учетверенной точности для представления чисел. Однако это не позволило бы избежать возможных ошибок деления на ноль в наивном методе исключения Гаусса. Чтобы избежать деления на ноль, а также уменьшить (но не устранить) ошибку округления, предпочтительным методом является исключение Гаусса с частичным поворотом. 9{{th}}\) строка, \(k \leq p \leq n\), затем поменяйте местами строки \(p\) и \(k\).
Другие этапы прямого исключения аналогичны методу наивного исключения Гаусса. Шаги обратной замены остаются точно такими же, как и в методе наивного исключения Гаусса.
6.11 Пример 6
В предыдущих двух примерах мы использовали наивное исключение Гаусса для решения
\[20x_{1} + 15x_{2} + 10x_{3} = 45\]
\[- 3x_{1 } — 2,249x_{2} + 7x_{3} = 1,751\]
\[5x_{1} + x_{2} + 3x_{3} = 9\]
с использованием пяти и шести значащих цифр с отсечением в вычислениях. Используя пять значащих цифр с отсечением, было найдено решение
Используя пять значащих цифр с отсечением, было найдено решение
\[\begin{split} \left\lbrack X \right\rbrack &= \begin{bmatrix} x_{1} \\ x_{2} \\ x_{ 3} \\ \end{bmatrix}\\ &= \begin{bmatrix} 0,625 \\ 1,5 \\ 0,99995 \\ \end{bmatrix} \end{split}\]
Это отличается от точного решения
\[\begin{split} \left\lbrack X \right\rbrack &= \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix}\\ & = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \end{split}\]
Найдите решение, используя исключение Гаусса с частичным поворотом, используя пять значащих цифр с отсечением в ваших вычислениях.
Решение
\[\begin{bmatrix} 20 & 15 & 10 \\ — 3 & — 2,249 & 7 \\ 5 & 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{1 } \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 1,751 \\ 9 \\ \end{bmatrix}\]
Прямое устранение неизвестных
Теперь для первого шага прямого исключения абсолютное значение элементов первого столбца ниже строки 1 равно
\[\слева| 20 \вправо|,\влево| — 3 \вправо|,\влево| 5 \right|\]
или
\[20,\ 3,\ 5\]
Итак, наибольшее абсолютное значение находится в строке \(1\). Таким образом, согласно исключению Гаусса с частичным поворотом, переключение между строками \(1\) и строками \(1\) дает
Таким образом, согласно исключению Гаусса с частичным поворотом, переключение между строками \(1\) и строками \(1\) дает
\[\begin{bmatrix} 20 & 15 & 10 \\ — 3 & — 2,249 & 7 \\ 5 & 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 1,751 \\ 9 \\ \end{bmatrix}\]
Разделите строку \(1\) на \(20\), а затем умножьте ее на \(-3\), то есть умножьте строку \(1\) на \(\displaystyle — 3/20 = — 0,15\ ).
\[\begin{pmatrix} \begin{bmatrix} 20 & 15 & 10 \\ \end{bmatrix} & \left\lbrack 45 \right\rbrack \\ \end{pmatrix} \times — 0.15\ \text {дает строку 1 как}\]
\[\begin{matrix} \left\lbrack — 3 \right.\ & — 2.25 & \left. \ — 1,5 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \ \left\lbrack — 6,75 \right\rbrack\]
Вычесть результат из строки \(2\)
\[\frac{\begin{matrix} \\\lbrack\begin{matrix} -3 & \\\ -2,249 & \\\\\ 7 \\ \end{matrix}\ \ \ \ \ \ | & 1.751\rbrack \\ — \begin{matrix} \lbrack -3 & \ \ \ \ -2. 25 \ \ -1.5 \ \ \\ \end{matrix}\ \ \ | & -6.75\rbrack \\ \end{matrix}}{\ \ \ \ \begin{matrix} \begin{matrix} 0 & \ \ \ \ \ 0.001 & \ \ \ \ 8.5 \\ \end{matrix} & \ \ \ \ \ 8.501 \end{matrix}}\]
25 \ \ -1.5 \ \ \\ \end{matrix}\ \ \ | & -6.75\rbrack \\ \end{matrix}}{\ \ \ \ \begin{matrix} \begin{matrix} 0 & \ \ \ \ \ 0.001 & \ \ \ \ 8.5 \\ \end{matrix} & \ \ \ \ \ 8.501 \end{matrix}}\]
чтобы получить результирующие уравнения как
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & 0,001 & 8,5 \\ 5 & 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 8,501 \\ 9\\ \end{bmatrix}\]
Разделите строку \(1\) на \(20\), а затем умножьте ее на \(5\), то есть умножьте строку \(1\) на \(5/ 20 = 0,25\).
\[\begin{pmatrix} \begin{bmatrix} 20 & 15 & 10 \\ \end{bmatrix} & \left\lbrack 45 \right\rbrack \\ \end{pmatrix} \times 0.25\ \text{ дает строку 1 как}\]
\[\begin{matrix} \left\lbrack 5 \right.\ & 3.75 & \left. \ 2.5 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \ \left\lbrack 11.25 \right\rbrack\]
Вычесть результат из строки \(3\)
\[\displaystyle \frac{\begin{matrix} \ \ \lbrack\begin{matrix} 5 & \ \ \ \ \ \ 1 & \ \ \ \ \ \ 3 \\ \end{matrix}\ \ \ \ \ \ \ | & 9\rbrack \\ — \begin{matrix} \lbrack 5 & \ \ \ \ 3. 75 \ \ \ \ \ 2.5 \ \ \\ \end{matrix}\ \ \ | & 11.25\rbrack \\ \end{matrix}}{\ \ \ \begin{matrix} \begin{matrix} 0 &\ -2.75 \ \ \ \ \ \ 0.5 \\ \end{matrix} & \ -2.25 \ end{matrix}}\]
75 \ \ \ \ \ 2.5 \ \ \\ \end{matrix}\ \ \ | & 11.25\rbrack \\ \end{matrix}}{\ \ \ \begin{matrix} \begin{matrix} 0 &\ -2.75 \ \ \ \ \ \ 0.5 \\ \end{matrix} & \ -2.25 \ end{matrix}}\]
, чтобы получить результирующие уравнения в виде
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & 0,001 & 8,5 \\ 0 & — 2,75 & 0,5 \\ \end{bmatrix }\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ 8,501 \\ — 2,25 \\ \end{bmatrix} \]
Это конец первого шага прямого исключения.
Теперь для второго шага прямого исключения абсолютное значение элементов второго столбца ниже строки 1 равно
\[\left| 0,001 \вправо|,\влево| — 2.75 \right|\]
или
\[0.001,\ 2.75\]
Итак, наибольшее абсолютное значение находится в строке \(3\). Таким образом, строка \(2\) меняется местами со строкой \(3\), чтобы получить
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & — 2,75 & 0,5 \\ 0 & 0,001 & 8,5 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 45 \\ — 2,25 \\ 8,501 \\ \ конец{bmatrix}\]
Разделите строку \(2\) на \(-2,75\), а затем умножьте ее на \(0,001\), то есть умножьте строку \(2\) на \(0,001/ — 2,75 = — 0,00036363\).
\[\begin{pmatrix} \begin{bmatrix} 0 & — 2,75 & 0,5 \\ \end{bmatrix} & \left\lbrack — 2,25 \right\rbrack \\ \end{pmatrix} \times — 0,00036363\ \text{дает строку 2 как}\]
\[\begin{matrix} \left\lbrack 0 \right.\ & 0.00099998 & \left. \ — 0.00018182 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \ \left\lbrack 0.00081816 \right\rbrack\]
Вычесть результат из строки \(3\)
\[\displaystyle \frac{\begin{matrix} \ \ \ \lbrack \begin{matrix} 0 & \ \ \ \ \ \ \ \ \ \ \ 0,001 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 8.5 \\ \end{matrix} \ \ \ \ \ \ \ \ \ \ \ \ \ \ | & 8.501\rbrack \\ — \begin{matrix} \lbrack 0 & \ \ \ \ 0.00099998 \ \ \ \ \ -0.00018182 \ \ \\ \end{matrix}\ \ \ | & 0.00081816\rbrack \\ \end{matrix}}{\ \ \begin{matrix} \ \begin{matrix} 0 &\ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 8.50018182 \\ \end{matrix} & \ \ \ \ \ \ \ \ \ 8.50018184 \end{matrix}}\]
Перезапись в пределах \(5\) значащих цифр с отсечением
\[\begin{matrix} \left\lbrack 0 \right. \ & 0 & \left. \ 8.5001 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \ \left\lbrack 8.5001 \right\rbrack\]
\ & 0 & \left. \ 8.5001 \right\rbrack \\ \end{matrix}\ \ \ \ \ \ \ \ \left\lbrack 8.5001 \right\rbrack\]
чтобы получить результирующие уравнения как
\[\begin{bmatrix} 20 & 15 & 10 \\ 0 & — 2,75 & 0,5 \\ 0 & 0 & 8,5001 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \ end{bmatrix} = \begin{bmatrix} 45 \\ — 2,25 \\ 8,5001 \\ \end{bmatrix}\]
Обратная замена
\[8.5001x_{3} = 8.5001\]
\[\begin{split} x_{3} &= \frac{8.5001}{8.5001}\\ &= 1 \end{ split}\]
Подстановка значения \(x_{3}\) в строке \(2\)
\[- 2,75x_{2} + 0,5x_{3} = — 2,25\]
\[ \begin{split} x_{2} &= \frac{- 2,25 — 0,5x_{2}}{- 2,75}\\ &= \frac{- 2,25 — 0,5 \times 1}{- 2,75}\\ &= \frac{- 2,25 — 0,5}{- 2,75}\\ &= \frac{- 2,75}{- 2,75}\\ &= 1\end{split}\]
Подстановка значений \(x_{3}\) и \(x_{2}\) в строке 1
\[20x_{1} + 15x_{2} + 10x_{3} = 45\]
\ [\begin{split} x_{1} &= \frac{45 — 15x_{2} — 10x_{3}}{20}\\ &= \frac{45 — 15 \times 1 — 10 \times 1}{ 20}\\ &= \frac{45 — 15 — 10}{20}\\ &= \frac{30 — 10}{20}\\ &= \frac{20}{20}\\ &= 1 \ end{split}\]
6.
 12 Метод исключения Гаусса для решения одновременных линейных уравнений Викторина
12 Метод исключения Гаусса для решения одновременных линейных уравнений Викторина(1). Цель шагов прямого исключения в методе наивного исключения Гаусса состоит в том, чтобы свести матрицу коэффициентов к (а) матрице _____________.
(A) диагональная
(B) идентификационная
(C) нижняя треугольная
(D) верхняя треугольная
(2). Деление на ноль во время шагов прямого исключения в наивном гауссовском исключении системы уравнений \(\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack\) подразумевает матрица коэффициентов \(\left\lbrack A \right\rbrack\)
(A) обратима
(B) несингулярна
(C) может быть сингулярной или неособой
(D) — единственное число
(3). Используя компьютер с четырьмя значащими цифрами с отсечением, наивное решение исключения Гаусса для
\[\begin{matrix} 0,0030x_{1} + 55,23x_{2} = 58,12 \\ 6,239x_{1} — 7,123x_{2} = 47,23 \\ \конец{матрица}\] равно
(A) \(x_{1} = 26,66;\ x_{2} = 1,051\)
(B) \(x_{1} = 8,769;\ x_{2} = 1,051\)
( C) \(x_{1} = 8,800;\ x_{2} = 1,000\)
(D) \(x_{1} = 8,771;\ x_{2} = 1,052\)
(4). Используя компьютер с четырьмя значащими цифрами с отсечением, метод исключения Гаусса с частичным поворотом решает
Используя компьютер с четырьмя значащими цифрами с отсечением, метод исключения Гаусса с частичным поворотом решает
\[\begin{matrix} 0,0030x_{1} + 55,23x_{2} = 58,12 \\ 6,239x_{1} — 7,123x_{2} = 47,23 \\ \end{matrix}\] равно
(A) \(x_{1} = 26,66;\ x_{2} = 1,051\)
(B) \(x_{1} = 8,769;\ x_{2} = 1,051\)
(C) \(x_{1} = 8,800;\ x_{2} = 1,000\)
(D) \(x_{1} = 8,771;\ x_{2} = 1,052\)
(5). В конце шагов прямого исключения наивного метода исключения Гаусса для следующих уравнений 9{2} + {bt} + c\) для аппроксимации профиля скорости.
| \(v(t)\) | \((м/с)\) | 0 | 227.04 | 362,78 | 517,35 | 602,97 | 901,67 | (A) 225} & {15} & {1} \\ {400} & {20} & {1} \\ \end{bmatrix}\begin{bmatrix} {a} \\ {b} \\ {c} \\ \end{bmatrix}{=}\begin{bmatrix} {227.

 И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.
И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.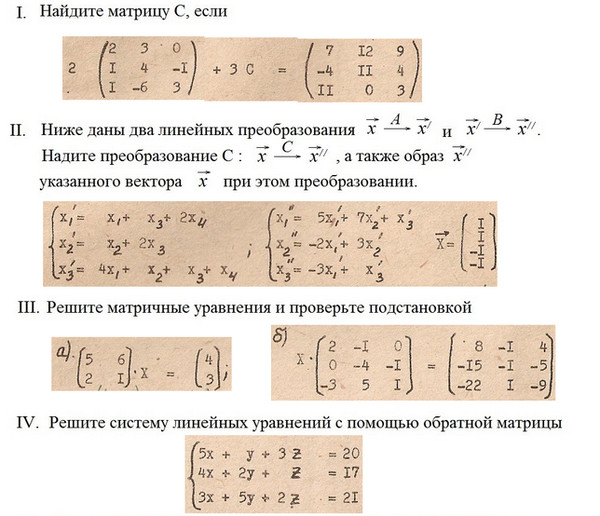 Этот способ заключается в обнулении элементов основной расширенной матрицы системы уравнений, находящихся под главной диагональю.
Этот способ заключается в обнулении элементов основной расширенной матрицы системы уравнений, находящихся под главной диагональю. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число. Для этого вычтем из них первую строчку, умноженную на и , соответственно:
Для этого вычтем из них первую строчку, умноженную на и , соответственно: ru/education/sys_lin_eq/gauss.html
ru/education/sys_lin_eq/gauss.html
 Кому приписывают первую разработку этого процесса? Опубликуйте что-нибудь интересное, связанное с этой историей.
Кому приписывают первую разработку этого процесса? Опубликуйте что-нибудь интересное, связанное с этой историей. Таким образом, уравнений сводятся к одному уравнению и одному неизвестному в каждом уравнении.
Таким образом, уравнений сводятся к одному уравнению и одному неизвестному в каждом уравнении. 04} \\ {362.78} \\ {517.35} \\ \end{bmatrix}\)
04} \\ {362.78} \\ {517.35} \\ \end{bmatrix}\) Используйте наивный метод исключения Гаусса для решения
Используйте наивный метод исключения Гаусса для решения
 второй столбец, коэффициенты неизвестного z в третий столбец и константы в четвертый столбец.
второй столбец, коэффициенты неизвестного z в третий столбец и константы в четвертый столбец.

 Так как последнее уравнение имеет только одно неизвестное, и, следовательно, мы можем легко найти его значение:
Так как последнее уравнение имеет только одно неизвестное, и, следовательно, мы можем легко найти его значение: Это тема, обычно представленная в основах матричной алгебры .
Это тема, обычно представленная в основах матричной алгебры .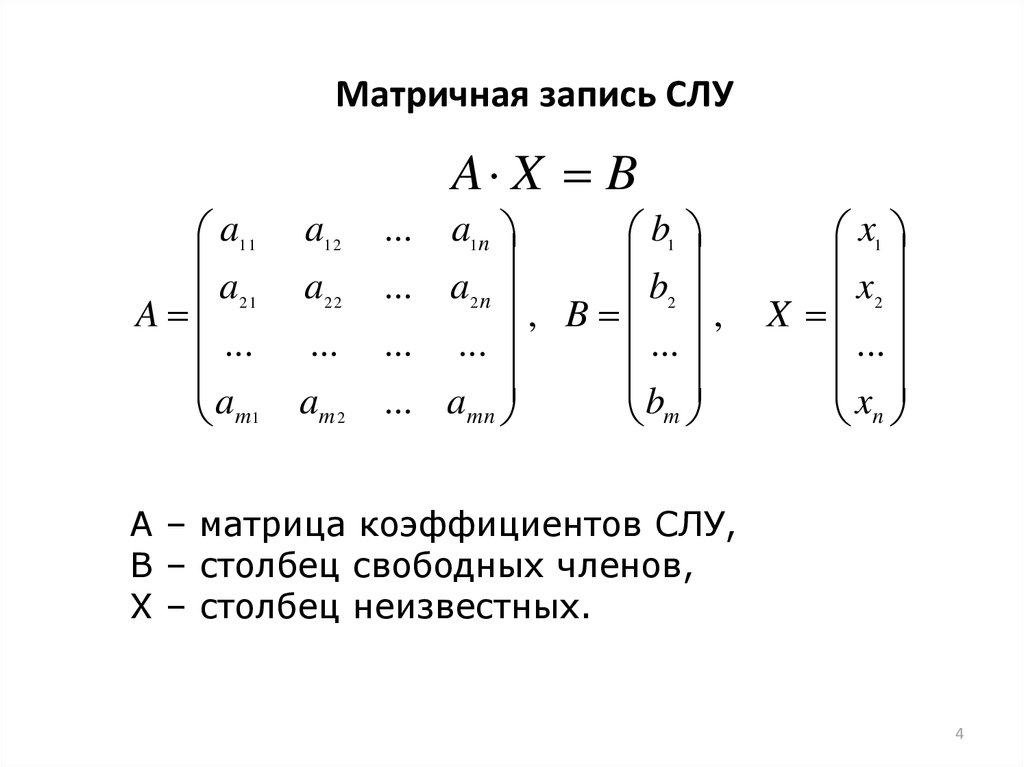 Компьютеры широко используют его для эффективной оценки потенциально тысяч переменных.
Компьютеры широко используют его для эффективной оценки потенциально тысяч переменных.




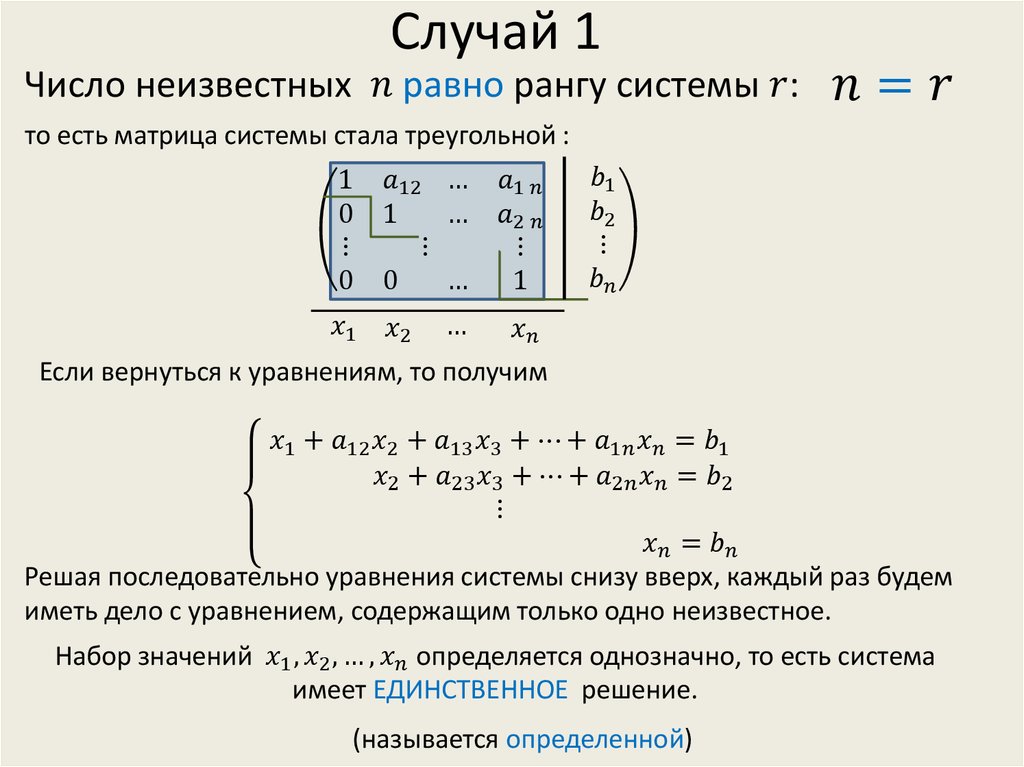 Кроме того, графически несовместная система представлена тремя непересекающимися плоскостями.
Кроме того, графически несовместная система представлена тремя непересекающимися плоскостями.  .
.
 Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Когда система записывается в такой форме, мы называем ее расширенной матрицей. третий столбец. Очень важно, чтобы каждое уравнение было записано в стандартной форме ax+by+cz=dax+by+cz=d, чтобы переменные выровнялись. Когда в уравнении отсутствует переменный член, коэффициент равен 0,9.0013
третий столбец. Очень важно, чтобы каждое уравнение было записано в стандартной форме ax+by+cz=dax+by+cz=d, чтобы переменные выровнялись. Когда в уравнении отсутствует переменный член, коэффициент равен 0,9.0013


 С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.
С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.



 Затем замените строку 2 результатом.
Затем замените строку 2 результатом. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.
Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.


 [A].
[A]. 1050.12 | 12 0001 335]
1050.12 | 12 0001 335] % интерес. Таким образом,
% интерес. Таким образом, x+y+z=10 000. Замена y = 1000y = 1000 и z = 6000, z = 6000, мы получаем
x+y+z=10 000. Замена y = 1000y = 1000 и z = 6000, z = 6000, мы получаем



 40.20.10.60.10.7 | 0,20,8–0,8][–0,10,3–0,1–0,40.20.10.60.10,7 | 0,20,8−0,8]
40.20.10.60.10.7 | 0,20,8–0,8][–0,10,3–0,1–0,40.20.10.60.10,7 | 0,20,8−0,8]



