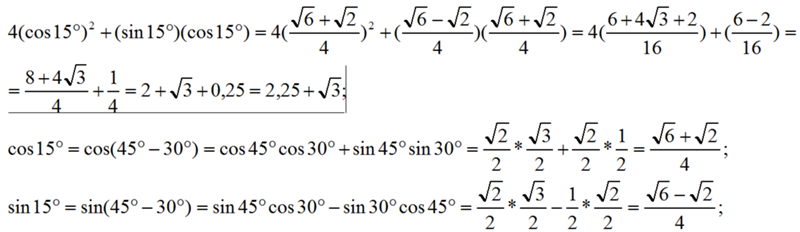Косинус суммы двух углов
Докажем следующие две формулы:
cos (α + β) = cos α cos β — sin α sin β, (1)
cos (α — β) = cos α cos β + sin α sin β. (2)
Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2π:
0 < α < 2π, 0 < β < 2π;
2) α > β .
Пусть положительная часть оси 0х является общей начальной стороной углов α и β.
Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α — β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.
В системе координат х0у точка М имеет координаты (cos α, sin α), а точка N — координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:
d12 = (cos α — cos β)2 + (sin α — sin β)2 = cos2 α — 2 cos α cos β +
+ cos2β + sin2 α — 2sin α sin β + sin2 β = 2 (1 — cos α cos β — sin α sin β).
При вычислениях мы воспользовались тождеством
sin2 φ + cos2 φ = 1.
Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β.
В этой системе координат точка М имеет координаты (cos (α — β), sin (α — β)), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:
Поэтому квадрат расстояния между ними равен:
d22 = [cos (α — β) — 1] 2 + [sin (α — β) — 0]2 = cos2 (α — β) — 2 cos (α — β) + 1 +
+ sin2 (α — β) = 2 [1- cos(α — β)].
Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому
d12 = d22
или
2 (1 — cos α cos β — sin α sin β) = 2 [1- cos(α — β)].
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β.
Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2r, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π . Поэтому можно считать, что 0 < α < 2π, 0 < β < 2π.
Поэтому можно считать, что 0 < α < 2π, 0 < β < 2π.
Не существенным оказывается и условие α > β. Действительно, если α < β, то β >α; поэтому, учитывая четность функции cos х, получаем:
cos (α — β) = cos (β — α) = cos β cos α + sin β sin α,
что по существу совпадает с формулой (2). Таким образом, формула
cos (α — β) = cos α cos β + sin α sin β
верна для любых углов α и β. В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:
cos (α + β) = cos [α — ( — β)] =cos α cos (-β) + sin α sin (-β) =
= cos α cos β — sin α sin β,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
1) cos 75° = cos (30° + 45°) = cos 30° • cos 45°-sin 30°-sin 45° =
\( \frac{\sqrt3}{2}\cdot\frac{\sqrt2}{2} — \frac{1}{2}\cdot\frac{\sqrt2}{2}=\frac{\sqrt6 — \sqrt2}{4} \)
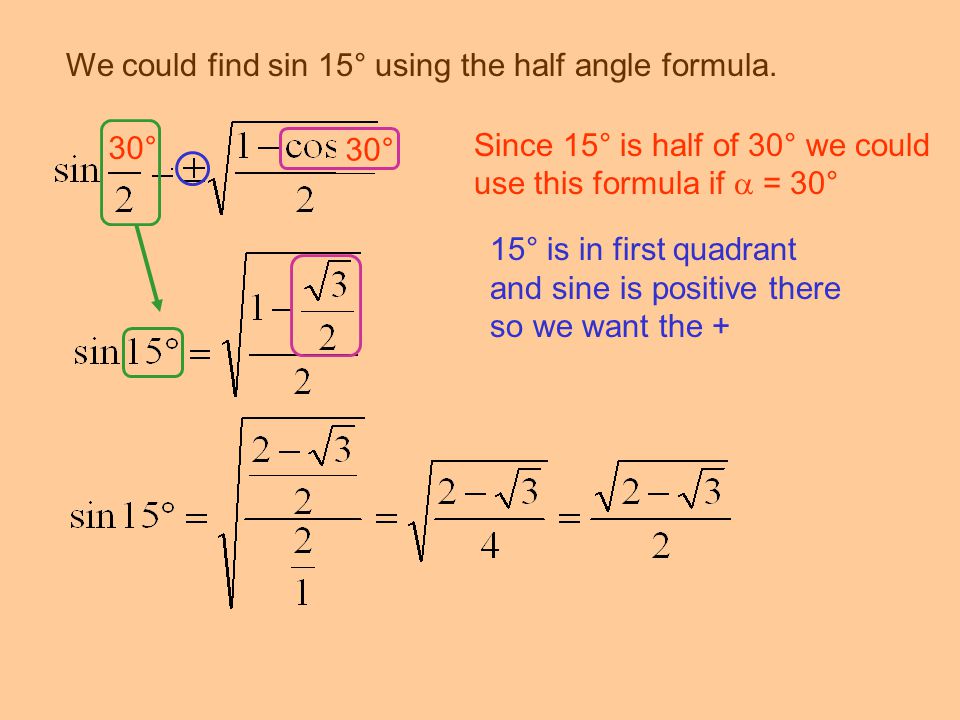
2) cos 15° = cos (45° — 30°) = cos 45° • cos 30° + sin 45°• sin 30° =
\( \frac{\sqrt2}{2}\cdot\frac{\sqrt3}{2} + \frac{\sqrt2}{2}\cdot\frac{1}{2}=\frac{\sqrt6 + \sqrt2}{4} \)
История о том, как прочитать 120 тысяч анекдотов и не рассмеяться раньше времени / Хабр
Кейс изучения средств тематического моделирования для датасета анекдотов на русском языке. Датасет не размечен, поэтому в данной работе делается предварительное выделение топиков объединяющих анекдоты, с использованием различных методов:
Датасет не размечен, поэтому в данной работе делается предварительное выделение топиков объединяющих анекдоты, с использованием различных методов:
использованных для различных способов векторизации токенов датасета.
Но обо всем по порядку.
Два слова зачем и почему мне это надо
Данная работа возникла под влиянием курса по NLP . Признаюсь, меня завораживает магия, которая возникает с использованием инструментов NLP при превращении слов и предложений в векторы несущие смыслы.
Мой эксперимент, это способ приобщиться, к сообществу этих волшебников со своей пока еще скромной волшебной палочкой. В своей работе я использую Data Science и Machine Learning, при анализе данных и разработке алгоритмов обработки, там все конечно безумно интересно для пытливого ума, но NLP это другое…. это игра на поле ИИ и это то, что изменит жизнь человечества навсегда и к чему еще нужно подготовиться.
Вместо введения: что такое тематическое моделирование
Тематическая модель (topic model)модель коллекции текстовых документов, которая определяет, к каким темам относится каждый документ коллекции. Алгоритм построения тематической модели получает на входе коллекцию текстовых документов. На выходе для каждого документа выдаётся числовой вектор, составленный из оценок степени принадлежности данного документа каждой из тем. Размерность этого вектора, равная числу тем, может либо задаваться на входе, либо определяться моделью автоматически. Предполагается, что каждый документ может относиться к одной или нескольким темам. Темы отличаются друг от друга различной частотой употребления слов. Требуется найти эти темы, то есть определить число тем, распределения частот слов, характерное для каждой темы, тематику каждого документа — в какой степени он относится к каждой из тем.
Алгоритм построения тематической модели получает на входе коллекцию текстовых документов. На выходе для каждого документа выдаётся числовой вектор, составленный из оценок степени принадлежности данного документа каждой из тем. Размерность этого вектора, равная числу тем, может либо задаваться на входе, либо определяться моделью автоматически. Предполагается, что каждый документ может относиться к одной или нескольким темам. Темы отличаются друг от друга различной частотой употребления слов. Требуется найти эти темы, то есть определить число тем, распределения частот слов, характерное для каждой темы, тематику каждого документа — в какой степени он относится к каждой из тем.
Входом для модели является коллекция документов, а выходом — набор векторов, каждый из которых содержит оценки вероятности принадлежности документа к каждой теме. Фундаментально с основами тематического моделирования можно ознакомиться, например, вот здесь, и конечно в курсе К. В. Воронцова.
В. Воронцова.
Тематическое моделирование (topic modeling) — построение тематической модели.
Целью построения тематической модели может быть как непосредственно выявление множества латентных тем, так и решение различных дополнительных задач.
Типичные приложения тематического моделированияанализ коллекций научных статей; анализ новостных потоков; рубрикация коллекций изображений, видео, музыки; аннотация генома и другие задачи биоинформатики; коллаборативная фильтрация, в рекомендательных системах
В работе https://habr.com/ru/company/otus/blog/503398/ мне понравилась структура исследования, которой я пытался следовать и в своей работе.
Этот открытый урок Анализ текстовых данных тематическое моделирование комментариев Вконтакте // Бесплатный урок OTUS был тем мотиватором, который дал мне силы и терпение подготовить данный пост, но и позволил вставить свои 5 копеек.
Библиотеки, функции, данные
В статье не будет представлен весь код исследования, но пытливые умы смогут восстановить ход работы опираясь на мой GitHub. _`{|}~—»«…–’
filter_token = rus_stops + list (punctuation)
from pymorphy2 import MorphAnalyzer
parser = MorphAnalyzer()
text = input_text.lower()
tokenized_text = word_tokenize(text)
clean_text = [word for word in tokenized_text if word not in filter_token]
lemmatized_text = [parser.parse(word)[0].normal_form for word in clean_text]
_`{|}~—»«…–’
filter_token = rus_stops + list (punctuation)
from pymorphy2 import MorphAnalyzer
parser = MorphAnalyzer()
text = input_text.lower()
tokenized_text = word_tokenize(text)
clean_text = [word for word in tokenized_text if word not in filter_token]
lemmatized_text = [parser.parse(word)[0].normal_form for word in clean_text]
С ее помощью мы переведем слова в начальную форму и получим данные для формирования «мешка слов».
токенизированные и лемматизированные документы из исходного датасета
Импортируем библиотеку Gensim и ее необходимые функции
import gensim from gensim import corpora, models from ast import literal_eval
Используем функцию corpora для получения словаря из лемматизированного текста. После создания словаря лучше всего отфильтровать те слова, которые встречаются в слишком большом количестве текстов, и те, которые встречаются в слишком маленьком количество текстов. Для этого используем метод  После удаления лишних слов ужимаем словарь в размерах (убираем пропуски) с помощью метода compactify.
После удаления лишних слов ужимаем словарь в размерах (убираем пропуски) с помощью метода compactify.
dictionary = gensim.corpora.Dictionary(ds_line["text_processed"].values) # составляем словарь из терминов
print('Размер словаря до фильтрации: {}'.format(len(dictionary)))
dictionary.filter_extremes(no_below=3, no_above=0.4, keep_n=3*10**6)
dictionary.compactify()
print('Размер словаря после фильтрации: {}'.format(len(dictionary)))
print(dictionary) Примеры полученного словаря и его размера
Создаем корпус анализируемых текстов, на основе полученного словаря
corpus = [dictionary.doc2bow(text) for text in ds_line['text_processed']]
Дополнительно, к такому прямолинейному варианту получения словаря и корпуса, воспользуемся и альтернативным вариантом получения словаря и корпуса, опираясь на разбиения исходного текста на биграммы (попарной последовательности токенов в предложении) , идеи и инструменты почерпнуты из Анализ текстовых данных. ..
..
Не буду здесь останавливаться на всех достоинствах подхода выделения токенов с использованием биграмм, но придумавший его, прозорливо учел смысловую связку последовательности слов, которая влияет и на их ценность для векторизации, в отличие от простого «мешка слов».
# Build the bigram models texts=(ds_line["text_processed"]) bigram = models.Phrases(texts, min_count=3, threshold=5) bigram_mod = models.phrases.Phraser(bigram) texts_bi = make_bigrams(texts) dictionary_bi = corpora.Dictionary(texts_bi) # составляем словарь из терминов с учетом биграмм слов предлжений print('Размер словаря до фильтрации: {}'.format(len(dictionary_bi))) dictionary_bi.filter_extremes(no_below=3, no_above=0.4, keep_n=3*10**6) print('Размер словаря после фильтрации: {}'.format(len(dictionary_bi))) corpus_bi = [dictionary_bi.doc2bow(text) for text in texts_bi] # составляем корпус документов по словарю полученному с использованием биграмм
размер словаря построенного по биграммам
пример полученных словарей
Вопрос «Хорошо или плохо большой размер словаря?»Чем больше словарь тем большую детализацию сравнения можно получить, обратная сторона длинного словаря — усложнение расчетов с большемерными векторами.
Во всем нужен баланс
Формирование тем, на основании модели Latent Dirichlet allocation (LDA) из Gensim
Latent Dirichlet allocation (LDA)модель матричного разложения, при которой предполагается, что распределение тематик имеет в качестве априори распределения Дирихле.
алгоритмы матричного разложения направлены на получение так матриц W и H , при котором их матричное произведение приведет с заданной точностью к матрице V. В нашем случае W это матрица — документ — токен, а соответственно: W это матрица документ — топик. а H топики — токены
Распределение Дирихле является обобщением Бета‑распределения на многомерный случай
Получаем и сохраняем модели для двух вариантов пар corpus,dictionary.
количество number_topics пока выберем произвольно равным 20, вопрос числа топиков открытый.
ldamodel_base=lda_model_gensim(corpus,dictionary,number_topics)
ldamodel_base.save('lda_20_base')
ldamodel_bi=lda_model_gensim(corpus_bi,dictionary_bi,number_topics)
ldamodel_bi.
save('lda_20_bi')Более точно на вопрос достаточного числа топиков отвечает дополнительное, достаточно ресурсоемкое исследование, по расчету такого показателя модели как когерентность, в контексте тематического моделирования, это величина характеризует степень неслучайной схожести тем.
Чем больше показатель когерентности, тем более связаны токены в топиках между собой и тем лучше модель.UDP моделирование с помощью векторизации через эмбеддинги, предложило вариант 180 тем, мне кажется избыточно но…. реальное число и правда больше 20.
А для начала — 20 и точка.
Визуализация полученных моделей топиков
Модели построены, а теперь хотелось бы взглянуть на то, что у нас получилось.
В библиотеке Gensim есть встроенная интерактивная визуализация расстояния между темами. Её можно использовать для того, чтобы оценить, насколько пересекаются между собой полученные темы и какие токены в какие топики попадают и в какой пропорции.
В рамках самой статьи, я могу привести только картинку, иллюстрирующую как выглядит этот замечательный инструмент.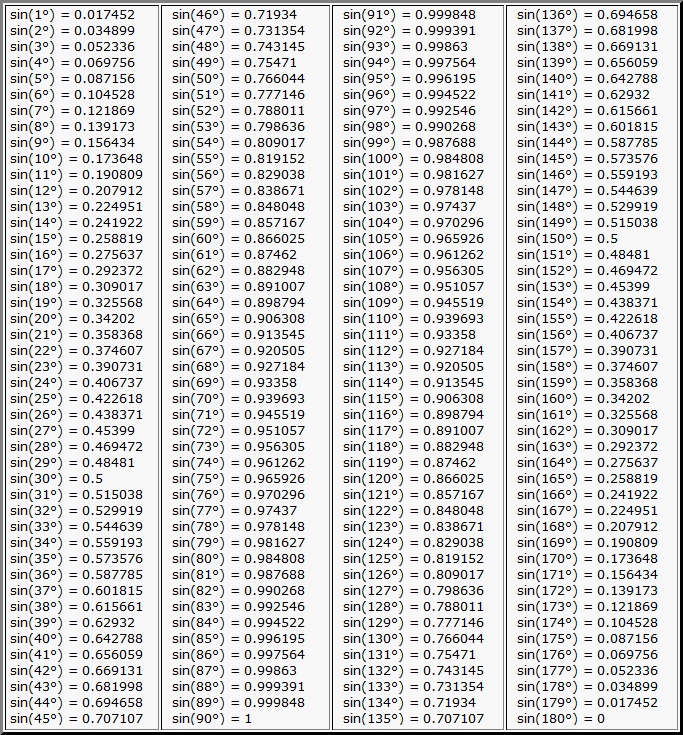
gensimvis
Тот же, кто хочет «поиграться» с полученными моделями для двух вариантов:
«base» — непосредственно из BOW
«bi» — из биграмм
может обратиться к соответствующему разделу GitHub.
Для большей наглядности, наряду с динамической «игровой» моделью визуализации полученных топиков, воспользуемся еще одним инструментом, чтобы увидеть получившиеся топики: построим облака токенов входящих в топики, полученные в каждой из моделей.
Приведу, несколько пар полученных изображений. Кроме того, часть, наиболее интересных «облаков» представлены в отдельных файлах в GitHub.
видно, топики с одинаковыми номерами содержат разный набор ключевых токенов, это объясняется стохастической природой формирования топиков моделями.
Небольшой разведочный анализ полученного результата
Возникает вопрос можно ли топики полученных с разными входными данными (словари и корпусы) согласовать между собой?
Предлагаю проверить следующую идею: назначим каждому документу наиболее подходящий (вероятный) для него топик, каждой из моделей( base и bi) и определим «устойчивые» — наиболее популярные пары топиков, которые назначаются одному документу.
ds_line["lda_base"] = ds_line["text_processed"].apply(get_topic, lda=ldamodel_base) ds_line["lda_bi"] = ds_line["text_processed"].apply(get_topic, lda=ldamodel_bi) ds_line["topic_base"] = ds_line["lda_base"].str[0] ds_line["probability_base"] = ds_line["lda_base"].str[1] del ds_line["lda_base"] ds_line["topic_bi"] = ds_line["lda_bi"].str[0] ds_line["probability_bi"] = ds_line["lda_bi"].str[1] del ds_line["lda_bi"] del ds_line["text_processed_new"] del ds_line["text_processed"]
Итоговый dataframe это выглядит так:
видны id топиков и вероятности совпадения топика текста документа
Оценим степень совпадения топиков полученных для моделей
Поскольку, как мы видим, значение для probability в некоторых случаях бывает не высокое, то ограничимся только теми записями у которых оно выше 0.5 (т.е. один топик присвоен гарантированно правильно)
ds_line_lite=ds_line[(ds_line['probability_base']>0.5)&(ds_line['probability_bi']>0.5)] ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index() ds_top.columns=['topic_base', 'topic_bi', 'rec_counts'] ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index() ds_top.columns=['topic_base', 'topic_bi', 'rec_counts']
Видно что разница между минимальным (1) и максимальным значением (181)
для более наглядной визуализации полученного результата воспользуемся функцией десятичного логарифма от rec_counts
ds_top['log']=np.log10(ds_top['rec_counts'])
topics_base_bi = pd.pivot_table(ds_top,
index='topic_base',
values='log',
columns='topic_bi',
fill_value=0)
topics_base_bi_np=topics_base_bi.valuesИ построим представления близости между топиками с различными индексами c использованием инструментов визуализации plotly и seabon
fig = px.imshow(topics_base_bi,width=600, height=600, labels = dict(y = "Топики Base", x = "Топики Bi", color = "Legend")) #fig.update_xaxes(side = "top") fig.show()
plt.rcParams['figure.figsize']=15,15 sns.heatmap(topics_base_bi, annot=True, fmt=".1f")
визуализация сходства топиков — значения выше 2 (жёлтые и светло-жёлтые квадраты), может быть признаком сходства топиков.
Сравним облака топиков для различных значений десятичного логарифма числа общих записей
Значение = 2.25
plotWordCloud_Gensim(topic_number=7, topics=lda_topics_base,head='Топики base ') plotWordCloud_Gensim(topic_number=7, topics=lda_topics_bi,head='Топики bi ')
Как видим они визуально похожи и выделяют сходные токены
Значение = 2.23
plotWordCloud_Gensim(topic_number=5, topics=lda_topics_base,head='Топики base ') plotWordCloud_Gensim(topic_number=10, topics=lda_topics_bi,head='Топики bi ')
Видно наличие общих токенов но их вес в облаках различен
plotWordCloud_Gensim(topic_number=9, topics=lda_topics_base,head='Топики base ') plotWordCloud_Gensim(topic_number=9, topics=lda_topics_bi,head='Топики bi ')
Значение = 0 (общих записей нет)
видно что совпадение слов в топиках отсутствует
Как видно, идея сравнения работает, у нас есть возможность, если понадобится, обеспечить «сведение» топиков полученных в разных моделях. С другой стороны, следует отметить, что полученные выше результат относится лишь к 3% от общего числа документов (9*394=3546).
С другой стороны, следует отметить, что полученные выше результат относится лишь к 3% от общего числа документов (9*394=3546).
Снижение порога для probability до уровня 0.4 или 0.3 — увеличило бы число учитываемых документов, но снижало бы достоверность отнесения документов к одному топику и это потребует дополнительную доработку для получения результирующих данных.
Можно переходить к первым выводам.
Зафиксируем краткий вывод:
Библиотека Gensim позволяет получать топики тематического моделирования, для чего использовалась векторизация типа «мешок слов», а также использованы различные алгоритмы оптимизации количество токенов словаря.
Визуальный анализ — heatmap сравнения топиков полученных с различающимися входными данными показывает, что число совпадающих топиков, получаемых в различных моделях (base и bi) в Gensim не превышает 50% (10-11). Тем самым эти совпадающие топики можно считать ядром топиков нашего массива документов.
В дальнейшем необходимо провести более углублённый анализ получивших топиков на степень их близости к смысловому содержанию группируемых анекдотов, для чего, было бы правильно, привлечь обратную связь от людей.
Далее, в исследовательских целях испробуем другой способ векторизации на базе весов TF-IDF, для чего обратимся к библиотеке Sklearn.
Используем библиотеку Sklearn, для тематического моделирования
В библиотеке Sklearn для векторизации, наряду с BOW использую и метод получения весов TF-IDF для токенов в предложениях текста.
TF-IDF (TF — term frequency, IDF — inverse document frequency) — статистическая мера, используемая для оценки важности слова в контексте документа, являющегося частью коллекции документов или корпуса.IDF (inverse document frequency — обратная частота документа) — инверсия частоты, с которой некоторое слово встречается в документах коллекции. Учёт IDF уменьшает вес широкоупотребительных слов. Для каждого уникального слова в пределах конкретной коллекции документов существует только одно значение IDF.
Учёт IDF уменьшает вес широкоупотребительных слов. Для каждого уникального слова в пределах конкретной коллекции документов существует только одно значение IDF.
Воспользуемся функцией Tfidfvectorizer. Модель Tfidfvectorizer создает представление исходного массива текстов в виде разреженной матрицы размерности NхM (N — количество текстов, M — мощность словаря), при этом словарь фильтруется отсечением токены имеющих малые значения величины (веса) TF-IDF.
Импортируем данные подготовленные при работе с Gensim, чтобы избежать повторения этапов токенизации и лемматизации. Модель TfidfVectorizer позволяет создавать словари с заранее ограниченной длинной и без такого ограничения. Для нашего исследования ограничение снято.
from sklearn.feature_extraction.text import TfidfVectorizer #no_features = 300 #tfidf_vectorizer = TfidfVectorizer(max_df=0.95, min_df=2, max_features=no_features, stop_words=filter) tfidf_vectorizer = TfidfVectorizer(max_df=0.95, min_df=2, stop_words=filter_token) tfidf = tfidf_vectorizer.fit_transform(ds_line["text_processed_new"].values.astype('U')) tokens_sklearn = tfidf_vectorizer.get_feature_names_out() print('Длина словаря',len(tokens_sklearn))
Мощность (длина) получившегося словаря сопоставима с той, что была получена для моделей в Gensim.
Модели получения тем используемые в Sklearn
Библиотека Sklearn для тематического моделирования предоставляет 2 алгоритма:
С первым LatentDirichletAllocation, мы уже знакомы.
Второй вариант Non-Negative Matrix Factorization.
Non-Negative Matrix Factorization (NMF)Статистический метод, который использует для матричного разложения метод факторного анализа с обязательным ограничением на неотрицательность значений векторов разложения.
Обычно число столбцов матрицы W и число строк матрицы H в NMF выбирается так, что произведение WH становится приближением к V. Полное разложение матрицы V тогда состоит из двух неотрицательных матриц W и H, а также из остаточной матрицы U, такой, что V=WH + U. Элементы остаточной матрицы могут быть и положительными, и отрицательными.
Элементы остаточной матрицы могут быть и положительными, и отрицательными.
Используем в нашем анализе оба подхода
from sklearn.decomposition import NMF, LatentDirichletAllocation no_topics = 20 no_top_words=10
тренируем модели
# Model lda_tfidf lda_tfidf = LatentDirichletAllocation(n_components=no_topics, max_iter=5, learning_method='online', learning_offset=50.,random_state=1024).fit(tfidf) # Model NMF nmf = NMF(n_components=no_topics, random_state=1024, l1_ratio=.5, init='nndsvd').fit(tfidf)
из полученных моделей вычислим индексы топиков с максимальным значением функции плотности распределения и произведем присвоение этого индекса каждому из документов, аналогично тому, как это было сделано для моделей в Gensim.
top_lda=topics_max(tfidf,lda_tfidf)
top_nmf=topics_max(tfidf,nmf)
ds_topic=pd.read_csv('/content/anekdot_topics.csv')
ds_topic['topic_nmf']=top_nmf[:,1]
ds_topic['probability_nmf']=top_nmf[:,0]
ds_topic['topic_lda']=top_lda[:,1]
ds_topic['probability_lda']=top_lda[:,0]Визуализация топиков полученных по моделям nmf и lda_tf-idf
токены топиков для модели lda
токены топиков для модели NMF
Аналогично с моделями из Gensim, построим облака полученных токенов
for i in range(20):
plotWordCloud_2(topic_number=i, topics=topic_lda)
plotWordCloud_2(topic_number=i, topics=topic_nmf) Полученные облака, собраны в файл.
По аналогии со сравнительным анализом проведенным для моделей из Gensim, интересно сравнить и «синхронизировать» топики формируемые разными подходами и особенностями библиотек между моделями из Gensim и Sklearn соответственно. Можно пойти по проторенной ранее дорожке, через анализ мощности множеств для пар топиков, но предлагаю воспользоваться другим подходом, который я остроумно условно назвал «методом 20 века», по шкале NLP (21 век это конечно GPT 😊).
Используем предобученных векторы эмбеддингов слов, входящих в топики. Это позволит нам решить несколько задач:
Нежно прикоснуться к эмбеддингам
Учесть при векторизации топика не только исходные значения токенов, из которых он состоит, но и близость по смыслу (соответственно значению вектора) токенов размещающихся в общих, с исходным токеном, кластере.
Вперед, на эмбеддинги
Для получения эмбеддингов используем модель «маленький BERT» (rubert-tiny) . Выбор именно этой модели вызван, в большей степени ресурсными ограничениям, но с другой стороны «зачем платить дважды», если мы «почувствуем разницу» используя небольшую модель, не не почувствуем, то другое дело :(.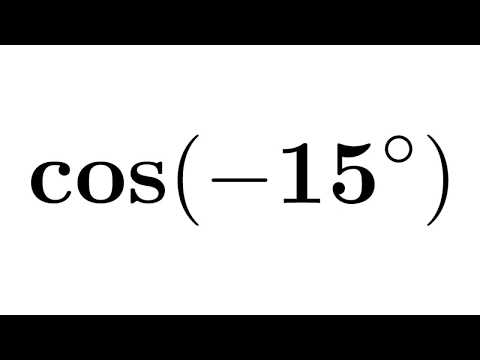
Из rubert-tiny получим модель и токенизатор на основе предобученных эмбеддингов.
import torch
from transformers import AutoTokenizer, AutoModel
tokenizer = AutoTokenizer.from_pretrained("cointegrated/rubert-tiny")
model = AutoModel.from_pretrained("cointegrated/rubert-tiny")
# model.cuda() # на случай если у вас есть GPUПолучив предобученные эмбеддинги воспользуемся ими и сравним полученные ранее топики. На текущий момент нет никаких специальных предпосылок чтобы выбрать какие модели взять взять для сравнения, поэтому выберем пару наугад: topic_base (Gensim) и topic_nmf (Sklearn). Дополнительно, из ресурсных соображений ограничимся 15 первыми токенами каждого из топиков.
Что мы получим в результате ?312 мерный вектора эмбеддингов обобщающих 15 первых токенов входящих в описание топика.
В качестве способа сравнения полученных векторов, осуществим попарный расчет косинусного расстояния для топиков различных моделей. Косинусное расстояние, а именно косинус угла между сравниваемыми векторами, имеет для нас прозрачный результат — для коллинеарных векторов, cos будет равен 1, для ортогональных 0.
Косинусное расстояние, а именно косинус угла между сравниваемыми векторами, имеет для нас прозрачный результат — для коллинеарных векторов, cos будет равен 1, для ортогональных 0.
Поехали.
plt.rcParams['figure.figsize']=15,15
topic_sim=[]
for i in range(20):
v1 = ' '.join(topic_base[topic_base['topic']==i]['topic_word'].values[:15])
v1_emb=embed_bert_cls(v1, model, tokenizer)
# print(v1)
for m in range(20):
sim_work=[]
v2 = ' '.join(topic_nmf[topic_nmf['topic']==m]['topic_word'].values[:15])
v2_emb=embed_bert_cls(v2, model, tokenizer)
sim=similarity(v1_emb, v2_emb)
sim_work.append(i)
sim_work.append(m)
sim_work.append(sim)
topic_sim.append(sim_work)
#topic_sim
topic_sim_ds=pd.DataFrame(topic_sim,columns=['base','nmf','cos_sim'])
glue = topic_sim_ds.pivot('base', 'nmf', 'cos_sim')
sns.heatmap(glue, annot=True, fmt=".1f") Визуализация результатов расчета косинусной близости
Посмотрим на пары топиков признанных близкими:
plotWordCloud_Sklearn(topic_number=0, topics=topic_nmf) plotWordCloud_Gensim(topic_number=16, topics=lda_topics_base,head='Топики base ')
Топики практически идентичны
plotWordCloud_Sklearn(topic_number=2, topics=topic_nmf) plotWordCloud_Gensim(topic_number=3, topics=lda_topics_base,head='Топики base ')
Высокая и наглядная близость топиков
plotWordCloud_Sklearn(topic_number=17, topics=topic_nmf) plotWordCloud_Gensim(topic_number=12, topics=lda_topics_base,head='Топики base ')
Полагаю, эти два топика яркое отражение особенности формирования эмбеддингов топиков — популярные токены не совпадают, синонимически топики оказались близки
Подведем итоги по проделанному и уведенному
Были опробованы две наиболее популярные библиотеки для задачи для тематического моделирования.

Представлены два метода оценки близости топиков из разных моделей. Метод базирующийся на частотности пар топиков относимых к одному документу показал, что однозначное отнесение корректно лишь в 3% случаев, что является косвенным свидетельство того, что выбранное число исходных топиков 20, не достаточно для эффективной кластеризации и требует дополнительных исследований.
В дополнение к вывод п.2 можно сделать заключение, что топики получаемые, при различающихся способах формирования ключевых данных — словарей топиков и алгоритмов векторизации, отличаются, но пересекаются в 50% случаев, получаемое множество пересечения можно признать ядром топиков для данного датасета.
Привлечение методов учета предобученных эмбеддингов позволяет «сводить» топики получаемые по разным моделям, с учетом смысловой синонимичности токенов входящих топики.
Получены и сохранены топики для 4 моделей тематического моделирования. Сохраненные топики можно использовать как для дальнейшего сравнения, так и проведения разметки данных на степень релевантности.

Для каждого документа получены значения топиков к которым он может быть отнесен.
Что можно и нужно сделать дальше:
С использованием BERT или «хорошо утрамбованного» в маленькую модель (из 2Гб в 24 Мб) FastText на основании инструкции, сделать эмбеддинги каждого анекдота, и проверить алгебру открытую в w2v при сложении и вычитании анекдотов с весами.
Целесообразно изменить процедуру присвоения топиков к текстам, через проверку близости основе сравнения векторов эмбеддингов для текста и топиков.
Оценить несколькими разными методами значение предельного числа тем.
Найти площадку для привлечения к разметке любопытных и сочувствующих.
Дообучить модели BERT, на корпусе анекдотов, может быть это где-то пригодится.
Замахнуться на анекдоты на других языках.
Когда-нибудь научить большую языковую модель отличать смешное от несмешного и рассказывать анекдоты в тему.

…А анекдоты то будут?
Анекдоты конечно будут. Для желающих есть небольшая функция «генератор анекдотов», отображающая анекдоты, по соответствующему топику и модели.
joke_generator(ds_line,9,10,'topic_nmf')
С помощью нее, можно получить, к примеру, такое:
10 анекдотов к топику с id 9 модели «topic_nmf»
Да, и пожалуй пойду почитаю и другие анекдоты. Всем спасибо.
Кстати, по этой ссылке вы можете абсолютно бесплатно посмотреть запись вебинара про современные применения NLP.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Значения sin 15, cos 15, tan 15 | грех 15 потому что 15
от promath
Присоединяйтесь к нашему каналу Telegram. Значения sin 15°, cos 15° и tan 15° очень важны в теории тригонометрии. Мы найдем их значения в этом посте.
Теперь найдем значение sin 15 градусов.
Значение sin 15
Значение $\sin 15$ будем вычислять по формуле сложных углов синусоидальных функций. Мы будем использовать следующую формулу:
sin(A-B) = sin A cos B – cos A sin B
Обратите внимание, что $\sin 15 = \sin(45 -30)$
$= \sin 45 \cdot \cos30 – \cos 45 \cdot \sin 30$
$= \dfrac{1}{\sqrt{2}} \cdot \dfrac{\sqrt{3}}{2} – \dfrac{1}{\sqrt{2}} \cdot \ dfrac{1}{2}$
$= \dfrac{\sqrt{3}}{2\sqrt{2}} – \dfrac{1}{2\sqrt{2}}$
$= \dfrac {\sqrt{3}-1}{2\sqrt{2}}$
Таким образом, значение sin 15 равно (√3−1)/2√2.
Теперь найдем значение cos 15.
Значение cos 15 92}$
Извлекая квадратный корень с обеих сторон, получаем, что
$\cos 15 = \dfrac{\sqrt{3}+1}{2\sqrt{2}}$
Итак, мы получили значение от cos 15, что равно (√3+1)/2√2.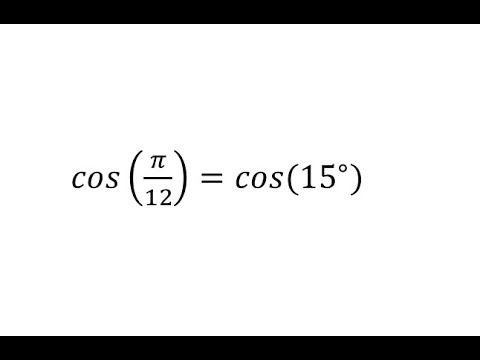
также прочитайте:
SINX = 0 Общее решение
SIN 15 COS 15
Вопрос: Найдите значение SIN 15 COS 15.
Ответ:
9911991119911911991111111111111111111111111111111119111911911 гг. 15$ и $\cos 15$ мы можем вычислить значение произведения $\sin 15 \cos 15.$Поскольку мы знаем выше, что sin 15 = (√3-1)/2√2 и cos 15 = (√3+1)/2√2, мы получаем, что
sin 15 cos 15 = (√3 -1)/2√2 × (√3+1)/2√2
= [(√3-1)(√3-1)] / (2√2) 2
= [(√ 3) 2 – 12] / 8 по формуле а 2 -b 2
= (3-1)/8
= 2/8 = 1/4
Значение тангенса 9 17
(Метод 1 нахождения tan 15:) Сначала найдем значение $\tan 15$, используя значения $\sin 15$ и $\cos 15.$ 92}$
$=\dfrac{4-2\sqrt{3}}{3-1}$
$=\dfrac{2(2-\sqrt{3})}{2}$
$ =2-\sqrt{3}$
Таким образом, значение tan 15 равно 2-√3.
(Метод 2 нахождения тангенса 15:) Далее мы найдем значение $\tan 15$, используя формулу разности двух углов для тангенса.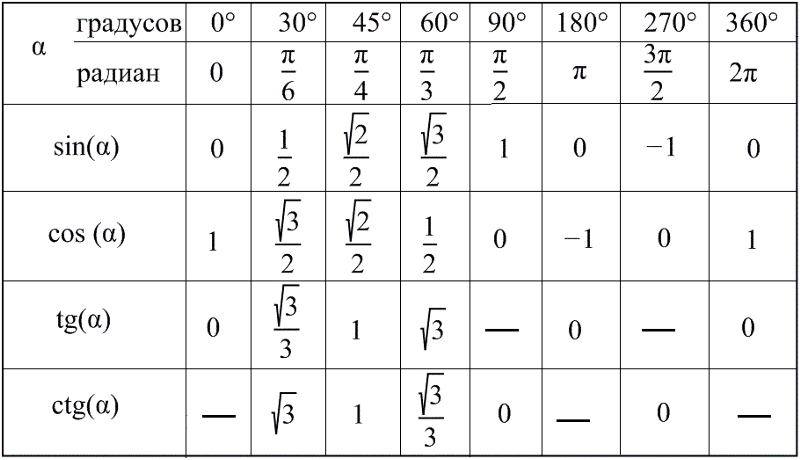

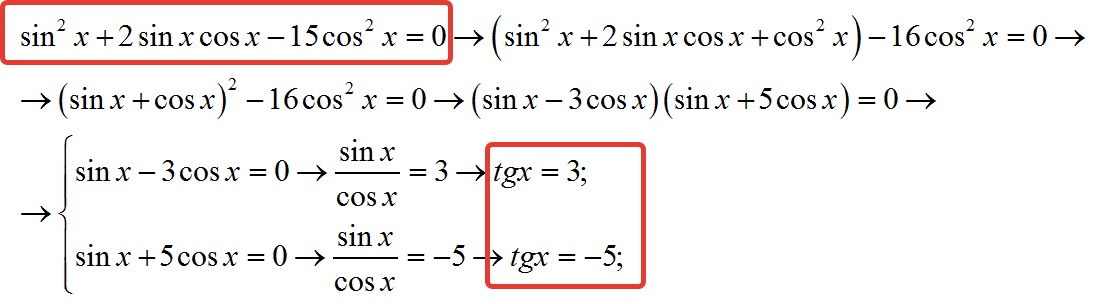
 5)&(ds_line['probability_bi']>0.5)]
ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index()
ds_top.columns=['topic_base', 'topic_bi', 'rec_counts']
ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index()
ds_top.columns=['topic_base', 'topic_bi', 'rec_counts']
5)&(ds_line['probability_bi']>0.5)]
ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index()
ds_top.columns=['topic_base', 'topic_bi', 'rec_counts']
ds_top=ds_line_lite.groupby(['topic_base','topic_bi'])['text_base'].count().reset_index()
ds_top.columns=['topic_base', 'topic_bi', 'rec_counts'] imshow(topics_base_bi,width=600, height=600, labels = dict(y = "Топики Base", x = "Топики Bi", color = "Legend"))
#fig.update_xaxes(side = "top")
fig.show()
imshow(topics_base_bi,width=600, height=600, labels = dict(y = "Топики Base", x = "Топики Bi", color = "Legend"))
#fig.update_xaxes(side = "top")
fig.show() fit_transform(ds_line["text_processed_new"].values.astype('U'))
tokens_sklearn = tfidf_vectorizer.get_feature_names_out()
print('Длина словаря',len(tokens_sklearn))
fit_transform(ds_line["text_processed_new"].values.astype('U'))
tokens_sklearn = tfidf_vectorizer.get_feature_names_out()
print('Длина словаря',len(tokens_sklearn))