Функция y = ctg x, её свойства и график катангенса с примерами
- Развертка котангенса движения точки по числовой окружности в функцию от угла
- Свойства функции y=ctgx
- Примеры
п.1. Развертка котангенса движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности на горизонтальной касательной, проведенной через точку (0;1), отображаются значения котангенсов соответствующих углов (см. §3 данного справочника).
Рассмотрим, как изменяется котангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=ctgx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.
В результате получаем график y=ctgx для для всех x из области допустимых значений.
График котангенса называют «тагненцоидой», термин «котангенцоида» не используют.
Часть графика c \(0\lt x\lt\pi\) называют главной ветвью графика котангенса.
п.2. Свойства функции
y=ctgx1. Область определения \(x\ne\pi k\) — множество действительных чисел, кроме точек, в которых \(sinx=0\).
2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb{R}\)
3. Функция нечётная $$ ctg(-x)=-ctgx $$
4. Функция периодическая с периодом π $$ ctg(x+\pi k)=ctgx $$
5. Функция стремится к \(-\infty\) при приближении слева к точкам \(x=\pi k\).
Приближение к точке a слева записывается как \(x\rightarrow a-0\) $$ \lim_{x\rightarrow \pi k-0} ctgx=-\infty $$ Функция стремится к \(+\infty\) при приближении справа к точкам \(x=\pi k\).
Приближение к точке a справа записывается как \(x\rightarrow a+0\) $$ \lim_{x\rightarrow \pi k+0} ctgx=+\infty $$ Нули функции \(y_{0}=0\) достигаются в точках \(x_0=\frac\pi2+\pi k\)
6.
Функция убывает на всей области определения.
7. Функция имеет разрывы в точках \(x=\pi k\), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами \((\pi k;\ \pi+\pi k)\) функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=ctgx на заданном промежутке:
a) \(\left[\frac{2\pi}{3}; \pi\right)\) $$ y_{min}=\lim_{x\rightarrow\pi-0}ctgx=-\infty,\ \ y_{max}=ctg\left(\frac{2\pi}{3}\right)=-\frac{1}{\sqrt{3}} $$ б) \(\left(0; \frac{\pi}{4}\right]\) $$ y_{min}=ctg\left(\frac{\pi}{4}\right)=1,\ \ y_{max}=\lim_{x\rightarrow +0}ctgx=+\infty $$ в) \(\left[\frac{7\pi}{6}; \frac{7\pi}{4}\right]\) $$ y_{min}=ctg\left(\frac{7\pi}{4}\right)=-1,\ \ y_{max}=ctg\left(\frac{7\pi}{6}\right)=\sqrt{3} $$
Пример 2. Решите уравнение:
a) \(ctgx=-\sqrt{3}\)
Бесконечное множество решений: \(x=\frac{5\pi}{6}+\pi k,\ k\in\mathbb{Z}\)
б) \(ctg\left(x+\frac\pi2\right)=0\)
\(x+\frac\pi2=\frac\pi2+\pi k\)
Бесконечное множество решений: \(x=\pi k,\ k\in\mathbb{Z}\)
в) \(ctg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{8}+\frac{\pi k}{2},\ k\in\mathbb{Z}\)
г) \(ctg\left(\frac{x}{3}-1\right)=-1\)
\(\frac{x}{3}-1=-\frac{\pi}{4}+\pi k\)
\(\frac{x}{3}=1-\frac{\pi}{4}+\pi k\)
Бесконечное множество решений: \(x=3-\frac{3\pi}{4}+3\pi k,\ k\in\mathbb{Z}\)
Пример 3.
3
2+n-72)=1/(n+9)Детская кроватка 0 градусов — Найдите значение детской кроватки 0 градусов
LearnPracticeDownload
Значение детской кроватки 0 градусов не определено (∞) . Раскладушка 0 градусов в радианах записывается как раскладушка (0° × π/180°), то есть раскладушка (0π) или раскладушка (0). В этой статье мы обсудим способы нахождения значения cot 0 градусов на примерах.
- Детская кроватка 0°: не определено(∞)
- Cot 0° в радианах: cot (0π) или cot (0 . . .)
Каково значение детской кроватки 0 градусов?
Значение кроватки 0 градусов равно ∞. Cot 0 градусов также можно выразить с помощью эквивалента заданного угла (0 градусов) в радианах (0 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180° )
⇒ 0 градусов = 0° × (π/180°) рад = 0π или 0 . .
.
∴ кроватка 0° = кроватка(0) = не определено(∞)
Объяснение:
Для кроватки 0 градусов угол 0° лежит на положительной оси x. Таким образом, значение кроватки 0° = undefined(∞)
Поскольку функция котангенса является периодической функцией, мы можем представить cot 0° как cot 0 градусов = cot(0° + n × 180°), n ∈ Z.
⇒ раскладушка 0° = раскладушка 180° = раскладушка 360° и так далее.
Методы определения значения кроватки 0 градусов
Значение кроватки 0° задано как undefined(∞). Мы можем найти значение кроватки 0 градусов по:
- Используя Unit Circle
- Использование тригонометрических функций
Детская кроватка 0 градусов с использованием единичного круга
Чтобы найти значение кроватки 0 градусов с помощью единичного круга:
- Нарисуйте единичный радиус окружности ‘r’, образующий угол 0° с положительной осью x.
- Раскладушка 0 градусов равна x-координате(1), деленной на y-координату(0) точки пересечения (1, 0) единичной окружности и r.
Следовательно, значение кроватки 0° = x/y = undefined(∞).
Cot 0° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cot 0 градусов как:
- cos(0°)/sin(0°)
- ± cos 0°/√(1 — cos²(0°))
- ± √(1 — sin²(0°))/sin 0°
- ± 1/√(сек²(0°) — 1)
- ± √(cosec²(0°) — 1)
- 1/тангенс 0°
Мы можем использовать тригонометрические тождества для представления cot 0° как
- tan (90° — 0°) = tan 90°
- -тангенс (90° + 0°) = -тангенс 90°
- -кроватка (180° — 0°) = -кроватка 180°
Примечание. Поскольку 0° лежит на положительной оси x, конечное значение cot 0° будет неопределенным (∞).
☛ Также проверьте:
- кроватка 34 градуса
- кроватка 75 градусов
- кроватка 1 градус
- кроватка 10 градусов
- кроватка 0 градусов
- кроватка 53 градуса
Примеры использования детской кроватки 0 градусов
Пример 1: Упрощение: 4 (cot 0°/tan 45°)
Решение:
Мы знаем cot 0° = ∞ и tan 45° = 1
⇒ 4 (кот 0°/тангенс 45°) = ∞Пример 2.
Найдите значение cot 0°, используя cos 0° и sin 0°. Решение:
Мы знаем, cot 0° = cos 0°/sin 0°
= 1/0 = не определено (∞)Пример 3: Найдите значение (cos (0°) cosec (0°) sec (0°))/2. [Подсказка: используйте cot 0° = ∞]
Решение:
Используя формулы тригонометрии,
(cos (0°) cosec (0°) sec (0°))/2 = cos (0°)/(2 sin (0°) cos (0°))
Используя формулу sin 2a,
2 sin (0°) cos (0°) = sin (2 × 0°) = sin 0°
⇒ cos (0°) / sin (0°) = кроватка 0°
⇒ (cos (0°) cosec (0°) sec (0°))/2 = ∞
Найдите значение cot 0°, используя cos 0° и sin 0°. перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о детской кроватке 0 градусов
Что такое детская кроватка 0 градусов?
Cot 0 градусов — значение котангенса тригонометрической функции для угла, равного 0 градусов.
Значение кроватки 0° не определено или ∞.
Каково значение Cot 0 градусов в терминах Sin 0°?
Используя тригонометрические тождества, мы можем записать кроватку 0° через sin 0° как кроватку(0°) = √(1 — sin²(0°))/sin 0° . Здесь значение sin 0° равно 0,
Как найти 0° с помощью других тригонометрических функций?
Используя формулу тригонометрии, значение cot 0° может быть выражено через другие тригонометрические функции следующим образом:
- cos(0°)/sin(0°)
- ± cos 0°/√(1 — cos²(0°))
- ± √(1 — sin²(0°))/sin 0°
- ± 1/√(сек²(0°) — 1)
- ± √(cosec²(0°) — 1)
- 1/тангенс 0°
☛ Также проверьте: таблицу тригонометрии
Как найти значение 0 градусов?
Значение cot 0 градусов можно рассчитать, построив угол 0° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности. Значение кроватки 0° равно координате x(1), деленной на координату y (0).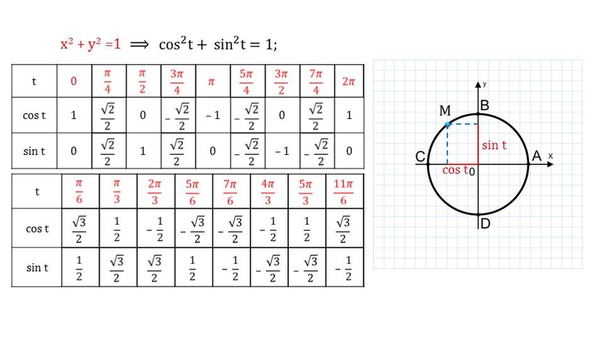
∴ кроватка 0° = undefined(∞)
Каково значение кроватки 0° в терминах сек 0°?
Мы можем представить функцию котангенса через функцию секанса, используя тригонометрические тождества, cot 0° можно записать как 1/√(sec²(0°) — 1). Здесь значение sec 0° равно 1,
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Таблица котангенсов | Кубенс
Таблица котангенсов записывается в таблицу расчетных значений котангенсов углов от 0° до 360°. С помощью таблицы котангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Чтобы узнать значение тангенса искомого угла, достаточно найти его в таблице.
С помощью таблицы котангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора.
Чтобы найти значение котангенса искомого угла, достаточно воспользоваться таблицей.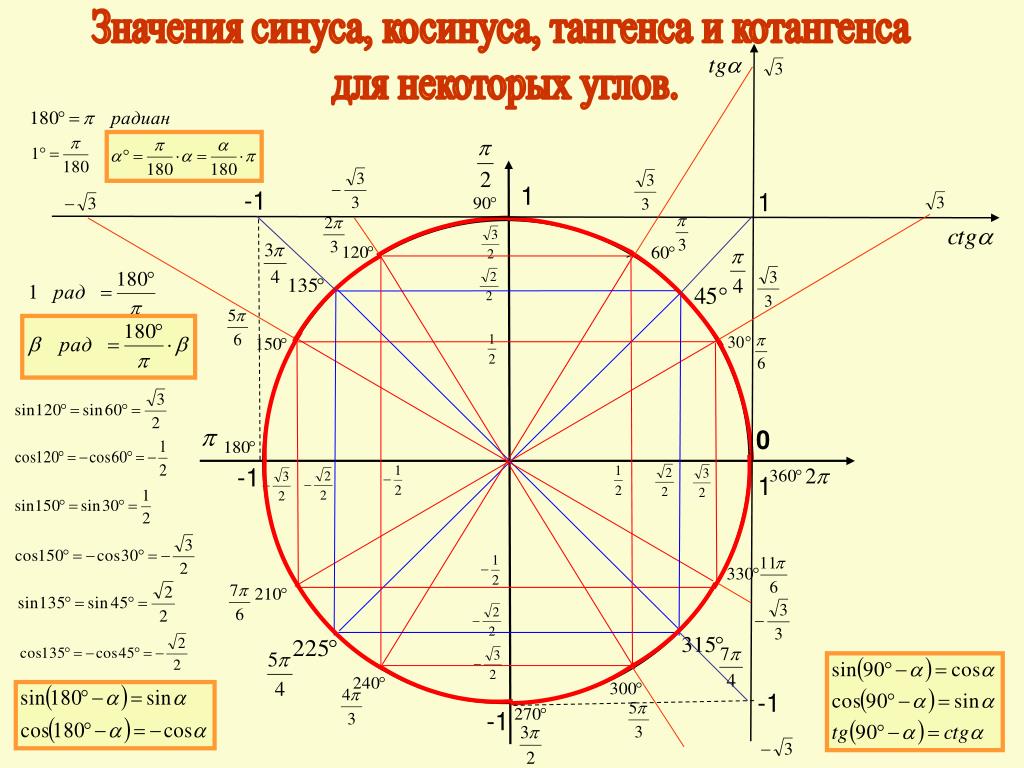
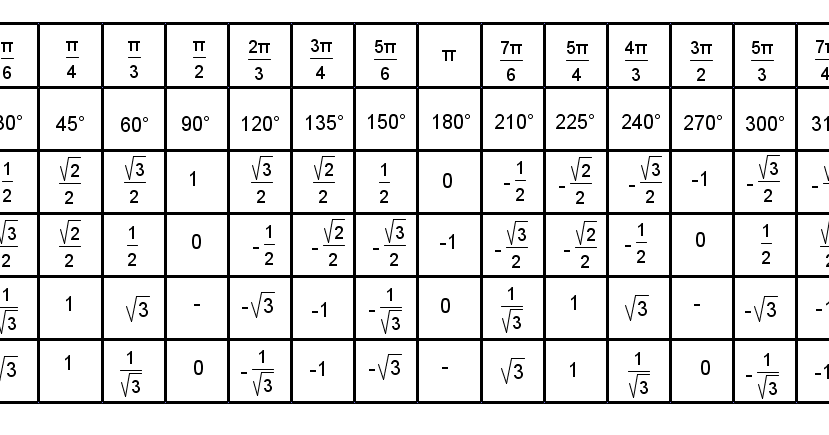
Табличный котангенс в радианах
| α | 0 | №/6 | №/4 | №/3 | №/2 | № | 3π/2 | 2π |
| КТГ α |
Таблица котангенсов , наряду с таблицей косинусов и диаграммой синусов и таблицей тангенсов изучается в начале тригонометрии. Без понимания таблицы котангенсов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. По сути это только показатели отношения различных сторон прямоугольного треугольника друг к другу, они могут помочь в решении большинства задач, результат которых сводится к решениям прямоугольных треугольников.
Котангенс одной из основных тригонометрических функций.
Таблица углов котангенсов от 0° до 180°
Таблица углов котангенсов от 0° до 180°
| ctg(0°) = ∞ ctg( 1°) = 57,28996 ctg(2°) = 28,63625 ctg(3°) = 19,08114 ctg(4°) = 14,30067 ctg(5°) = 11,43005 ctg(6°) = 9,51436 ctg(7°) = 8,1443 5 ctg(8°) = 7,11537 ctg(9°) = 6,31375 ctg(10°) = 5,67128 ctg(11°) = 5,14455 ctg(12°) = 4,70463 ctg( 13°) = 4,33148 ctg (14°) = 4,01078 ctg(15°) = 3,73205 ctg(16°) = 3,48741 ctg(17°) = 3,27085 ctg(18°) = 3,07768 ctg(19°) = 2. КТГ(20 °) = 2,74748 ctg(21°) = 2,60509 ctg(22°) = 2,47509 ctg(23°) = 2,35585 ctg(24°) = 2,24604 ctg(25°) = 2,1 4451 ctg(26°) = 2,0503 ctg(27°) = 1,96261 ctg(29°) = 1,80405 ctg(30°) = 1,73205 ctg(31°) = 1,66428 ctg(32°) = 1,60033 ctg(33°) = 1,53986 ctg g(34°) = 1,48256 ctg (35°) = 1,42815 ctg(36°) = 1,37638 ctg(37°) = 1,32704 ctg(38°) = 1,27994 ctg(39°) = 1,2349 ctg(40°) = 1 .  19175 КТГ(41 °) = 1,15037 ctg(42°) = 1,11061 ctg(43°) = 1,07237 ctg(44°) = 1,03553 ctg(45°) = 1 ctg(46°) ) = 0,96569 ctg(47 °) = 0,93252 ctg(48°) = 0,9004 ctg(49°) = 0,86929 ctg(50°) = 0,8391 ctg(51°) = 0,80978 ctg(52°) = 0,78129 ctg(53°) = 0,75355 900 23 ctg(54°) = 0,72654 ctg(55°) = 0,70021 ctg(56°) = 0,67451 ctg(57°) = 0,64941 ctg(58°) = 0,62487 ctg(59°) = 0,60086 ctg(60°) ) = 0,57735 | ctg(61°) = 0,55431 ctg(62°) = 0,53171 ctg(63°) = 0,50953 ctg(64°) = 0,48773 ctg(65°) = 0,46631 ctg(66°) = 0,44523 ctg (67°) = 0,42447 ctg(68°) = 0,40403 ctg(69°) = 0,38386 ctg(70°) = 0,36397 ctg(71°) = 0,34433 ctg(72°) = 0,32492 ctg(73°) = 0,30573 ctg g(74°) = 0,28675 ctg (75°) = 0,26795 ctg(76°) = 0,24933 ctg(77°) = 0,23087 ctg(78°) = 0,21256 ctg(79°) = 0,19438 ctg(80°) = 0,17633 ктг(81 °) = 0,15838 ctg(82°) = 0,14054 ctg(83°) = 0,12278 ctg(84°) = 0,1051 ctg(85°) = 0,08749 ctg(86°) = 0,06 993 ctg(87°) = 0,05241 ctg(88°) = 0,03492 ctg(89°) = 0,01746 ctg(90°) = 0 ctg(91°) = -0,01746 ctg(92°) = -0,03492 ctg(93°) = -0,05241 ctg(94°) ) = -0,06993 ctg(95°) = -0,08749 ctg(96°) = -0,1051 ctg(97°) = -0,12278 ctg(98°) = -0,14054 ctg(99°) = -0,15838 ctg г(100° ) = -0,17633 керн (101°) = -0,19438 кр (103°) = -0,23087 кр (104°) = -0,24933 кр (105°) = -0,26795 ctg(106°) = -0,28675 ctg(107°) = -0,30573 ctg(108°) = -0,32492 кр(109°) = -0,34433 кр(110°) = -0,36397 кр(111°) = -0,38386 кр(112°) = -0,40403 кр(113°) = -0,42447 КТГ(114 °) = -0,44523 керн (115°) = -0,46631 кр (116°) = -0,48773 кр (117°) = -0,50953 кр (118°) = -0,53171 кр (119°) = -0,55431 ctg(120°) = -0,57735 | ctg(121°) = -0,60086 ctg(122°) = -0,62487 ctg(123°) = -0,64941 ctg(124°) = -0,67451 ctg(125°) = -0,70021 9 0023 ctg(126° ) = -0,72654 ctg(127°) = -0,75355 ctg(128°) = -0,78129 ctg(129°) = -0,80978 ctg(130°) = -0,8391 ctg(131°) = -0,86929 ctg(132°) = -0,9004 9002 3 ctg(133° ) = -0,93252 керр (134°) = -0,96569 кр (135°) = -1 кр (136°) = -1,03553 кр (137°) = -1,07237 кр (138°) = — 1,11061 керн(139°) = -1,15037 кр(140°) = -1,19175 кр(141°) = -1,2349 кр(142°) = -1,27994 кр(143°) = -1.  32704 КТГ(144 °) = -1,37638 ctg(145°) = -1,42815 ctg(146°) = -1,48256 ctg(147°) = -1,53986 ctg(148°) = -1,60033 ctg(149°) = -1,66428 ctg(150°) = -1,73205 ctg(151°) = -1,80405 90 023 ctg(152° ) = -1,88073 центра (153°) = -1,96261 центра (154°) = -2,0503 центра (155°) = -2,14451 центра (156°) = -2,24604 центра (157°) = -2,35585 ctg(158°) = -2,47509 ctg(159°) = -2,60509 ctg(160°) = -2,74748 ctg(161°) = -2, ctg(162°) = -3,07768 ctg г(163°) = -3,27085 ctg(164°) = -3,48741 ctg(165°) = -3,73205 ctg(166°) = -4,01078 ctg(167°) = -4,33148 ctg(168°) = -4,70463 ctg(169°) = -5,14455 центра (172°) = -7,11537 центра (173°) = -8,14435 центра (174°) = -9,51436 центра (175°) = -11,43005 центра (176°) ) = -14,30067 ctg(177°) = -19,08114 ctg(178°) = -28,63625 ctg(179°) = -57,28996 ctg(180°) = ∞ |
Котангенс 0 (котангенс нуля)
равно (до бесконечности)
1 котангенс (и котангенс единицы)
равный
3 котангенс (и котангенс три)
равный
90 котангенс (и котангенс 90 градусов)
(равный нулю)
30 котангенс ( и котангенс 30 градусов)
равен
45 котангенс (и котангенс 45 градусов)
равен
Котангенс 60 (котангенс 60 градусов)
равен
Таблица котангенсы углов от 181° до 360°
| ctg(181°) = 57,28996 ctg(182°) = 28,63625 ctg(183°) = 19,08114 ctg(184°) = 14,3006 7 ctg(185°) = 11,43005 ctg(186°) = 9,51436 ctg(187°) = 8,14435 ctg(188°) = 7,11537 ctg(189°) = 6,31375 ctg(190°) = 5,67128 ctg(191°) = 5,14455 ctg(192°) = 4,70463 ctg(193°) = 4,33148 ctg(194°) = 4,01078 ctg(195°) = 3,73205 ctg(196°) = 3,48741 ctg(197°) = 3,27085 9 0023 ctg(198°) = 3,07768 ctg(199°) = 2, ctg(200°) = 2,74748 ctg(201°) = 2,60509 ctg(202°) = 2,47509 ctg(203°) = 2,35585 90 023 ctg(204°) = 2,24604 ctg (205°) = 2,14451 центра (206°) = 2,0503 центра (207°) = 1,96261 центра (208°) = 1,88073 центра (209°) = 1,80405 центра (21) 0°) = 1,73205 ctg(211 °) = 1,66428 цир. 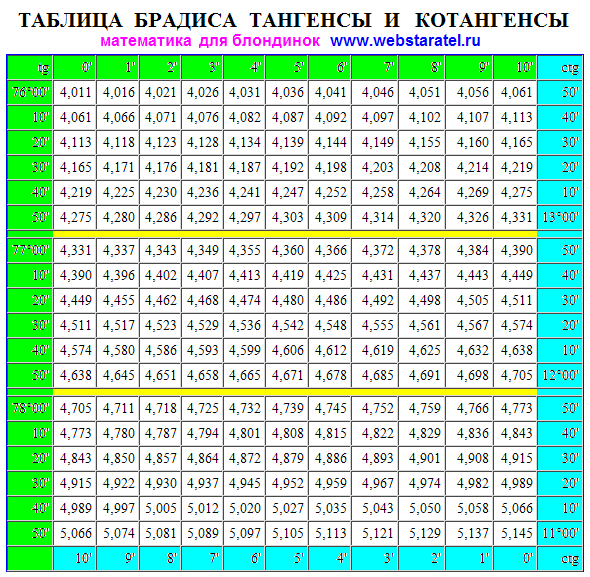 (212°) = 1,60033 цир. (213°) = 1,53986 цир. = 1,37638 ctg(217°) = 1,32704 ctg(218°) = 1,27994 ctg(219°) = 1,2349 ctg(220°) = 1,19175 ctg(221°) = 1,15037 ctg(222°) = 1,11061 ctg(223°) = 1,07237 ctg(224°) = 1,03553 ctg(225°) = 1 ctg(226°) = 0,96569 ctg(227°) = 0,93252 ctg(228°) = 0,9004 ctg(229°) = 0,86929 90 023 ctg(230°) = 0,8391 ctg(231°) = 0,80978 ctg(232°) = 0,78129 ctg(233°) = 0,75355 ctg(234°) = 0,72654 ctg(235°) = 0,70021 ctg g(236°) = 0,67451 ctg( 237°) = 0,64941 ctg(238°) = 0,62487 ctg(239°) = 0,60086 ctg(240°) = 0,57735 | ctg(241°) = 0,55431 ctg(242°) = 0,53171 ctg(243°) = 0,50953 ctg(244°) = 0,48773 ctg(245°) = 0,46631 9 0023 ctg(246°) = 0,44523 ctg (247°) = 0,42447 ctg(248°) = 0,40403 ctg(249°) = 0,38386 ctg(250°) = 0,36397 ctg(251°) = 0,34433 ctg(2) 52°) = 0,32492 ctg(253 °) = 0,30573 ctg(254°) = 0,28675 ctg(255°) = 0,26795 ctg(256°) = 0,24933 90,23087 023 ctg(262°) = 0,14054 ctg (263°) = 0,12278 центра (264°) = 0,1051 центра (265°) = 0,08749 центра (266°) = 0,06993 центра (267°) = 0,05241 центра (26) 8°) = 0,03492 ctg(269 °) = 0,01746 ctg(270°) = 0 ctg(271°) = -0,01746 ctg(272°) = -0,03492 ctg(273°) = -0,05241 ctg (274°) = -0,06993 ctg(275°) = -0,08749 ctg(276°) = -0,1051 ctg(277°) = -0,12278 ctg(278°) = -0,14054 ctg(279°) = -0,15838 ctg(280°) = -0,17633 90 023 ctg(281° ) = -0,19438 центра (282°) = -0,21256 центра (283°) = -0,23087 центра (284°) = -0,24933 центра (285°) = -0,26795 центра (286°) = -0,28675 ctg(287°) = -0,30573 ctg(288°) = -0,32492 ctg(289°) = -0,34433 ctg(290°) = -0,36397 ctg(291°) = -0,38386 ctg г(292°) = -0,40403 ctg(293°) = -0,42447 ctg(294°) = -0,44523 ctg(295°) = -0,46631 ctg(296°) = -0,48773 ctg(297°) = -0,50953 ctg(298°) = -0,53171 ctg(299°) = -0,55431 90 023 ctg(300° ) = -0,57735 | ctg(301°) = -0,60086 ctg(302°) = -0,62487 ctg(303°) = -0,64941 ctg(304°) = -0,67451 ctg(305°) = -0,70021 9 0023 ctg(306° ) = -0,72654 керн(307°) = -0,75355 кр(308°) = -0,78129 кр(309°) = -0,80978 кр(310°) = -0,8391 кр(311°) = -0,86929 ctg(312°) = -0,9004 ctg(313°) = -0,93252 ctg(314°) = -0,96569 ctg(315°) = -1 ctg(316°) = -1,03553 ctg(317°) = -1,07237 ctg(318°) = -1,11061 контрольных точек (319°) = -1,15037 ctg(320°) = -1,19175 ctg(321°) = -1,2349 ctg(322°) = -1,27994 ctg(323°) = -1,32704 ctg(32) 4°) = -1,37638 ctg(325°) = -1,42815 ctg(326°) = -1,48256 ctg(327°) = -1,53986 ctg(328°) = -1,60033 ctg(329°) = -1 .  |