Формула cos 2: Формулы двойного аргумента (базовый уровень) — урок. Алгебра, 10 класс.

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )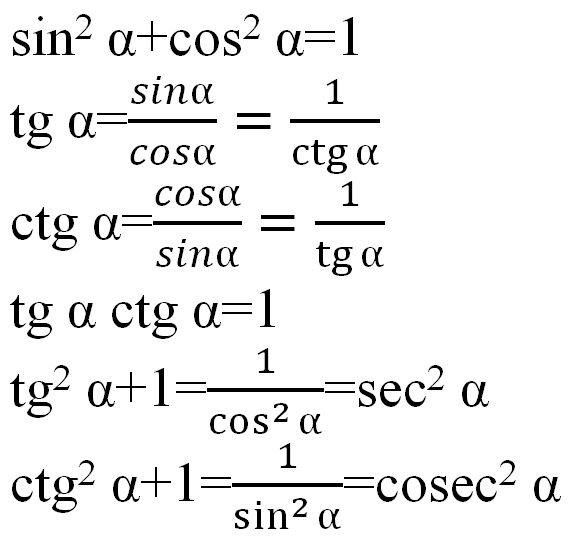
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )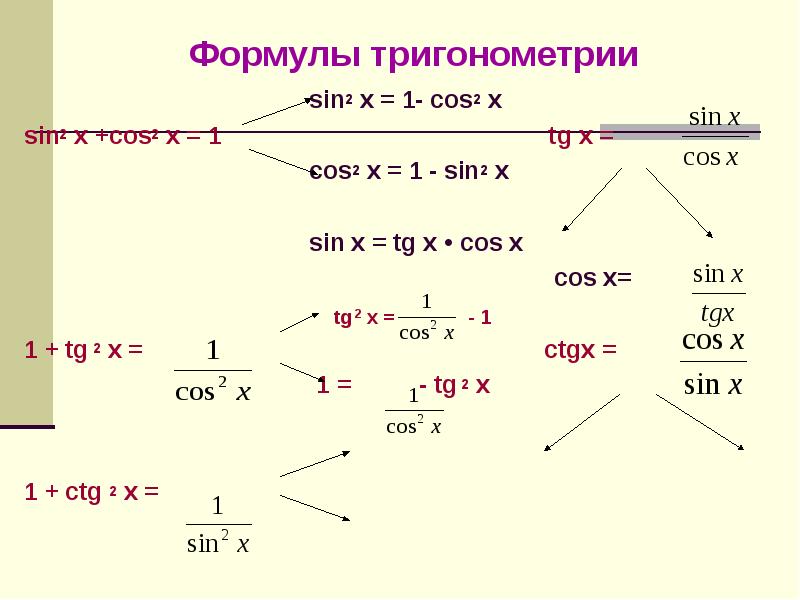
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град.
)
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93
Найти точное значение		cos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значение arcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Урок алгебры в 10-м классе по теме «Формулы двойного аргумента»

Цели урока:

Образовательные – вывести формулы тригонометрии, позволяющие выразить sin 2x, cos 2x, tg 2x через sinx, cosx, tgx, показать многообразие их применения.

Развивающие – вырабатывать навыки и умения использовать полученные формулы в тригонометрических преобразованиях, развивать математическое мышление учащихся, умение видеть и применить изученные тождества, развивать умения самостоятельной учебно-познавательной деятельности, развивать культуру речи и любознательность.

Воспитательные – побуждать учащихся к преодолению трудностей в процессе умственной деятельности, к самоконтролю и самоанализу.

Ожидаемый результат: Каждый учащийся должен знать вывод формул двойного аргумента и уметь применять их для преобразований тригонометрических выражений на уровне обязательных результатов обучения.

Тип урока: Урок ознакомления с новым материалом.

План урока:

  1. Организационно-мотивационный этап.
  2. Актуализация имеющихся знаний и личного опыта учащихся (устная работа).
  3. Изучение нового материала.
  4. Домашнее задание.
  5. Итог урока.
  6. Закрепление изученного материала (контрольный срез).

Ход урока

Презентация.

1. Организационно-мотивационный этап.

Сегодня на уроке мы выведем формулы тригонометрии – формулы двойного аргумента и рассмотрим многообразие их применения. Эпиграфом нашего урока будут слова Бернардо Больцано “Формула подчас кажется более мудрой, чем выдумавший ее человек”.

2. Актуализация имеющихся знаний и личного опыта учащихся (устная работа).

Вспомним формулу синус суммы, косинус суммы и тангенс суммы аргументов. Вызываются 3 учащихся, которые на 3 досках записывают отдельно эти формулы:

sin(x +y) = sinxcosy + cosxsiny;
cos(x+y) = cosxcosy – sinxsiny;
tg(x+y) = .
Далее учащиеся устно работают с места.

№1 Упростить:

а)
б)
в)
г)

№2 Вычислить:

а)
б)
в)
г)
д)

3. Изучение нового материала.

Сейчас мы выведем с вами тригонометрические формулы двойного аргумента и рассмотрим многообразие их применения.

Если положить в формулах, записанных вами в начале урока на доске x= y, то получаем:

1)

sin(x+y) = sinxcosy + cosxsiny
sin2x = sinxcosx + sinxcosx = 2sinxcosx

2)

cos(x+y) = cosxcosy – sinxsiny
cos2x = cosxcox – sinxsinx = cos2x – sin2x

3)

tg(x+y) =
tg2x =

Каждую из 3-х формул выводит 1 ученик.

Рассмотреть варианты применения данных формул.

  • sin10x = 2sin5x*cos5x
  • sin
  • cos(8x – 14y) = cos2(4x – 7y) – sin2(4x – 7y)
  • tg
  • 2sin7xcos7x = sin14x
  • cos23,5t — sin23,5t = cos7t

А теперь докажем два тождества, используя доказанную в начале урока формулу cos 2x = cos 2x – sin2x

1. Доказать тождество:

cos2x = 1 – 2sin2x
cos2x = cos2x – sin2x = (1 — sin2x) — sin2x = 1 — 2 sin2x
cos2x = 1 — 2 sin2x

2. Доказать тождество:

cos2x = 2cos2x – 1
cos2x = cos2x – sin2x = cos2x – (1 — cos2x) = 2cos2x – 1
cos2x = 2cos2x – 1

3. Выразить sin2x из равенства:

cos2x = 1 — 2sin2x
2 sin2x = 1 – cos2x
sin2x =

4. Выразить cos2x из равенства:

cos2x = 2cos2x – 1
cos2x+1 = 2cos2x
2cos2x = cos2x+1
cos2x =

Итак, выполняя №1 и №2, мы получили еще два варианта формулы двойного аргумента, а выполняя №3 и №4, вывели формулы понижения степени.

4. Домашнее задание.

  • §21
  • №21. 1 – 21.6 (а)
  • №21.9 (а)

5. Итог урока.

  1. Что нового узнали на уроке?
  2. Довольны ли вы своей работой на уроке?

6. Закрепление изученного материала. Контрольный срез.

Учащиеся выполняют работу на карточках с дифференцированными заданиями по теме урока (самопроверка).

1 вариант.

№1 Упростите, продолжив решение, и выберите правильный ответ:

а)

Ответ:

1) 4/3;
2) 4/3cosx;
3) 2/3;
4) 4/3ctgx.

б)

Ответ:

1) cos20;
2) 2cos20;
3) ctg20;
4) другой ответ.

№2 Упростите и выберите правильный ответ:

а)

Ответ:

1) 3tgx;
2) 3sinx;
3) 1.5sinx;
4) 3tg2x.

б) cos2t – cos2t =

Ответ:

1) sin2t;
2) -sin2 t;
3) 2cos2 t+sin2 t;
4) другой ответ.

2 вариант.

№1 Упростите, продолжив решение, и выберите правильный ответ:

а)

Ответ:

1) -3tg2x;
2) 3sin2 x;
3) 6 tgx;
4) 3tg2 x.

б)

Ответ:

1) 3/2;
2) 2/3;
3) 2/3sin2x;
4) другой ответ.

№2 Упростите и выберите правильный ответ:

а)

Ответ:

1) tg2x;
2) 2sinx;
3) 1/2sinx;
4) 1/2 + tgx.

б) cos2t + sin2t =

Ответ:

1) cos2t;
2) 2sint;
3) cost-sint;
4) другой ответ.

Проверяются верные ответы.

1 вариант:

№1 а) 1; б) 2.
№2 а) 2;б) 1.

2 вариант:

№1 а) 4; б) 2.
№2 а) 3; б) 1.

Учащиеся поднимают руку, кто при выполнении работы сделал 2 ошибки, затем – кто одну ошибку и, наконец, кто не сделал ни одной ошибки, выполнил всё полностью и верно.

Молодцы ребята, отлично поработали.

Ученики сдают карточки на проверку учителю.

На следующих двух уроках мы с вами продолжим изучение применения формул двойного аргумента в тригонометрических преобразованиях.

Спасибо всем за урок!

Формула Cos 2x — объяснение, примеры решений и часто задаваемые вопросы

  • Формула
  • Формула Cos 2x

В прямоугольном треугольнике тригонометрическое отношение угла объясняет взаимосвязь между углом и длиной его сторон. . Но тогда что такое cos 2x? Формула косинуса 2x или Cos 2x также является одной из таких тригонометрических формул, которая также известна как формула двойного угла. Она называется формулой двойного угла, потому что в ней есть двойной угол. Именно по этой причине он управляется выражениями для тригонометрических функций суммы и разности двух чисел (углов) и связанными с ними выражениями. Теперь, когда мы знаем, что такое формула cos 2x, мы можем двигаться вперед и узнать некоторые более важные вещи о тригонометрии, а также узнать, что такое формула cos2x.

Тригонометрия и прямоугольный треугольник

В прямоугольном треугольнике гипотенуза, основание (прилежащее) и перпендикуляр (противоположный), т. е. три стороны прямоугольного треугольника, откуда тригонометрические отношения получены. В математике есть три основных тригонометрических отношения, которые также известны как тригонометрические тождества. Мы можем найти недостающие углы и недостающие стороны прямоугольного треугольника с помощью тригонометрических соотношений. В прямоугольном треугольнике один угол равен 90 градусов, а два других угла по 45 градусов каждый. Три стороны прямоугольного треугольника

  • Гипотенуза: Гипотенуза противоположна 90 градусам и является самой длинной стороной треугольника.

  • Перпендикуляр (противоположный): это сторона, противоположная неизвестному углу, представленному как θ, и перпендикулярная основанию (то есть угол между основанием и перпендикуляром составляет 90 градусов).

  • Основание (смежное): это основание, на котором покоится треугольник, и оно также содержит оба угла, т. е. 9{2}\]

    Что такое функция косинуса?

    Отношение стороны, примыкающей к углу (θ), к гипотенузе (самой длинной стороне) в треугольнике определяется как косинус угла. Теперь вопрос, какова формула cos2x?

    Cos θ = Adjacent/Hypotenuse

    Тригонометрическая формула Cos2x

    Теперь, если вам интересно, что такое формула cos2x, позвольте мне сказать вам, что у нас есть пять формул cos x.

      9{2} a + sin a — 1 = 0\],

      Факторизация этого квадратного уравнения с переменной sin a

      (2 sin a — 1)(sin a + 1) = 0

      2 sin a — 1 = 0 или sin a + 1 = 0

      sin a = 1/2 или sin a = −1

      разность двух чисел, а также родственное выражение. В статье будут разработаны прочные основы тригонометрии.

      Дата последнего обновления: 02 мая 2023

      •

      Всего просмотров: 292,5k

      •

      Просмотров сегодня: 7,73k

      Недавно обновленные страницы

      Diagonal of Формула квадрата — значение, вывод и примеры решения

      Формула дисперсионного анализа — Определение, полная форма, статистика и примеры

      Формула среднего — Методы отклонения, примеры решений и часто задаваемые вопросы

      Формула доходности в процентах — APY, атомная экономика и пример решения

      Формула серии — Определение, примеры решения и часто задаваемые вопросы

      Формула площади поверхности квадратной пирамиды – определение и вопросы

      Диагональ квадратной формулы – значение, вывод и примеры решения

      Формула ANOVA – определение, полная форма, статистика и примеры

      Формула среднего значения – методы отклонения, примеры решения и Часто задаваемые вопросы

      Формула процентной доходности — APY, атомная экономика и пример решения

      Формула серии

      — определение, примеры решения и часто задаваемые вопросы

      Формула площади поверхности квадратной пирамиды — определение и вопросы

      Актуальные темы

      функций — Что такое cos²(x)?

      спросил

      Изменено 6 лет, 4 месяца назад

      Просмотрено 21к раз

      $\begingroup$

      Мне это кажется странным.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *