Чему равен синус 50: сколько будет sin50 градусов? — ответ на Uchi.ru

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34
Упростить		sin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )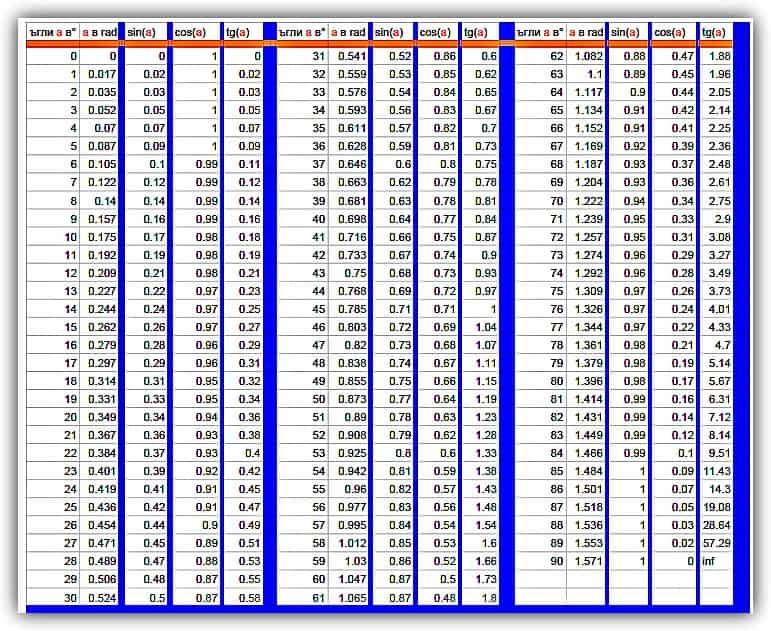
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )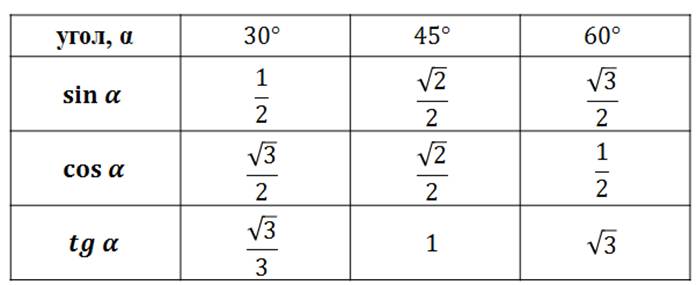
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )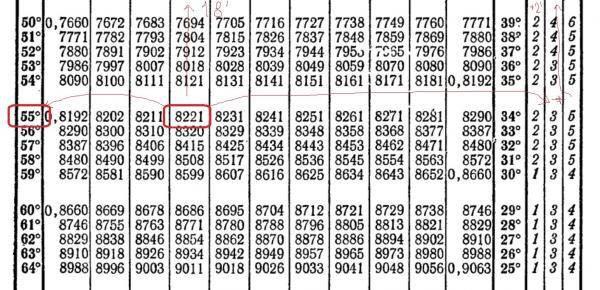
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94
Найти точное значение		arcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы
88 град.

Как найти синус 10 градусов? — Хабр Q&A

Если надо просто вычислить, то калькулятор в помощь.
Если самому и без оценки, то разложи синус в ряд и посчитай столько членов, какая точность нужна.

Ответ написан

Комментировать

Приближенные значения обычно смотрят в таблицах или получают в калькуляторах.

Ещё есть такая формула (ряды Тейлора):
sin(x) ~= x5/5! + x3/3! + x
где x в радианах:

Если стоит задача именно без техники примерно найти sin(10°) можно воспользоваться бумагой, карандашом, линейкой и циркулем. sin() угла в прямоугольном треугольнике это отношение противолежащего катета к гипотенузе. Если нарисовать окружность радиуса 1, то sin() будет равен самой длине противолежащего катета.

Нарисуйте окружность радиусом, скажем, 10 см (будем считать 1 = 10см). Отмерьте угол в 1/18 полукруга (прямой угол разделить на три части и ещё раз на три). Опустите перпендикуляр из точки на окружности на горизонтальную ось. Его длина, делёная на 10см будет значением синуса.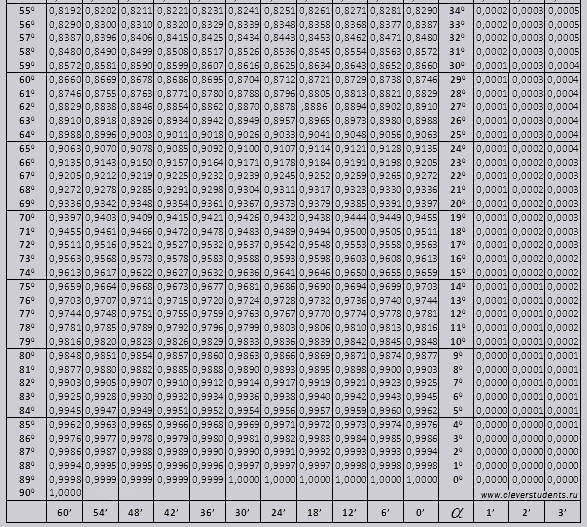

Ответ написан

Воспользуйтесь формулами синусов и косинусов суммы и приведите sin3X к f(sinX), а потом решите полученное уравнение

Ответ написан

Комментировать

Комментировать

Синус 30 гр = 0.5 далее через формулу тройного угла легко найти точный ответ. Никакие ряды не надо, известен точный результат в радикалах. А да, получится уравнение 3-ей степени, которое вам придётся решить. Но ничё, оно решается, по формулам Кардано. Какой сейчас сказать не могу, не помню формулу тройного угла.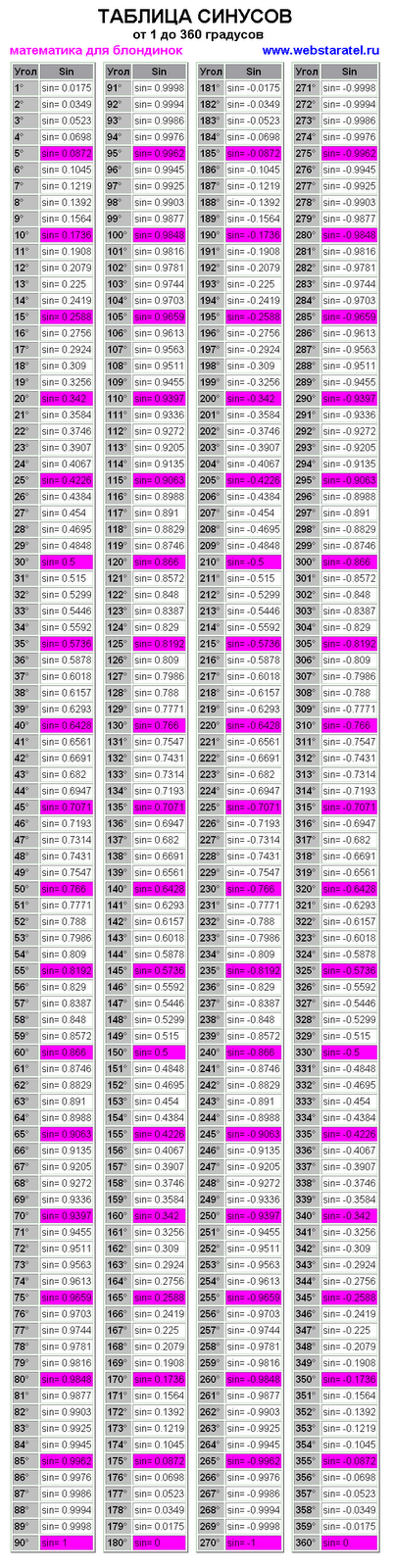 .. поищите в гугле… Кстати Тейлор плохой вариант. его базис неортогонален в функ пространстве. Поэтому ошибки начинают расти при увеличении числа членов. Синус собственно это вектор в бесконечномерном функциональном пространстве. Мы ищем его координаты. Для тейлора они известны и для Чебышева тоже. Уже всё давно подсчитано и не только ждя этих двух базисов. Но для синуса, периодической ограниченной фунции они не годятся. Но увеличение числа членов по разложению по Чебышеву уже стабильно повышает точность в отличие от Тейлора. Было бы веселее посчитать синус 6 градусов в радикалах… Хе-хе…

Ответ написан

Комментировать

По формуле Кардано получается неприводимый случай, когда вещественный корень выражается в комплексных радикалах, но не выражается в вещественных. 3 = 1/2, где x — синус 10 градусов) Q меньше нуля, следовательно у нас три действительных корня. Казалось бы, всё хорошо, но эти корни получаются из комплексных чисел, а до этого вам из этих чисел нужно кубический корень извлечь, что делается по второй формуле Муавра, в свою очередь которая основыается на тригонометрическом представлении комплексных чисел. И в итоге у вас синус 10 градусов равен… синусу 10 градусов… Такие дела

Ответ написан

Комментировать

Калькулятор — sin(50) — Солуматы

Sin, расчет онлайн

Резюме:

Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.

sin online

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.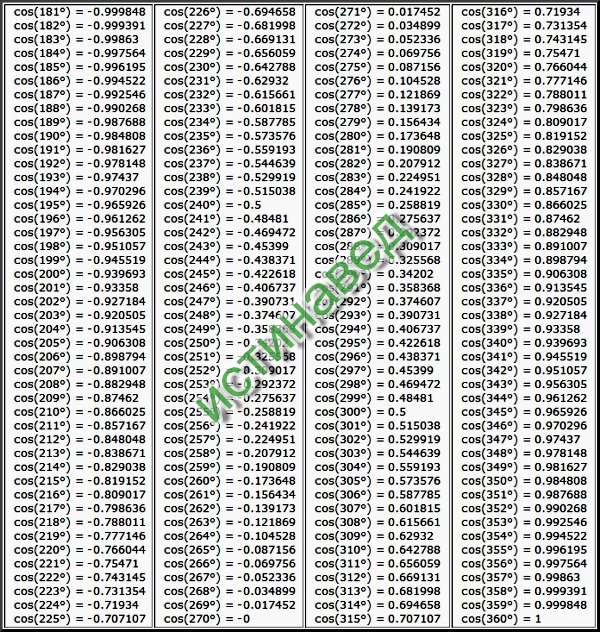

Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.

  1. Расчет синуса

    2. Вычисление синуса угла в радианах

    Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

    Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.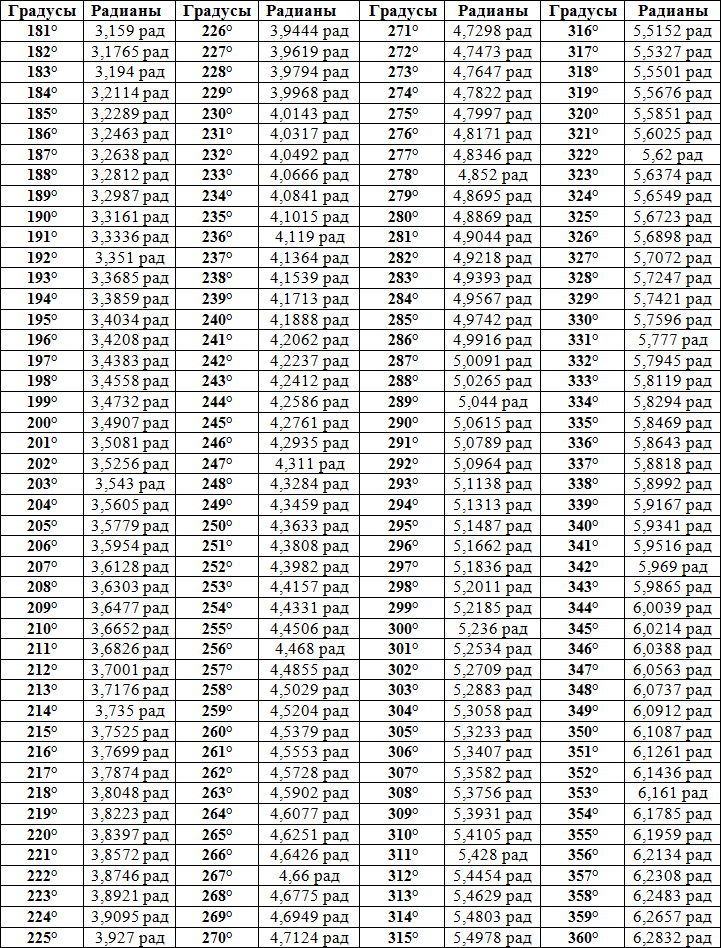

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.

    Вычислить синус угла в градусах

    Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

    Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.

    Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

  2. Таблица специальных синусоидальных значений

    3. Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :

    sin(`2*pi`) `0`
    sin(`pi`) `0`
    sin(`pi/90 `2`)7
    sin(`pi/4`) `sqrt(2)/2`
    sin(`pi/3`) `sqrt(3)/2`
    sin(`pi/6`) `1/2`
    sin(`2*pi/3`) `sqrt(3) /2`
    sin(`3*pi/4`) `sqrt(2)/2`
    sin(`5*pi/6`) `1/2`
    sin(`0`) `0`
    sin(`-2*pi`) `0`
    sin(`-pi`) 7 0907 8 ` sin(`pi/2`) `-1`
    sin(`-pi/4`) `-sqrt(2)/2`
    sin(`-pi/3`) `-sqrt(3)/2`
    sin(`-pi/6`) `-1/2`
    sin(`-2*pi/3`) `-sqrt(3)/2`
    sin( `-3*pi/4`) `-sqrt(2)/2`
    sin(`-5*pi/6`) `-1/2`

  3. Основные свойства

    4. `AA x в RR, k в ZZ`,

  • `sin(-x)= -sin(x)`
  • `sin(x+2*k*pi)=sin(x)`
  • `sin(pi-x)=sin(x)`
  • `sin(pi+x)=-sin(x)`
  • `sin(pi/2-x)=cos(x)`
  • `sin(pi/2+x)=cos(x)`

  • Производная синуса

    • Производная синуса равна cos(x).

  • Первообразная синуса

    • Первообразная синуса равна -cos(x).

  • Свойства функции синуса

    • Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.

  • Уравнение с синусом

    • Калькулятор имеет решатель, который позволяет решать уравнение с синусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.

    Синтаксис:

    sin(x), где x — мера угла в градусах, радианах или градах.

    Примеры:

    sin(`0`), возвращает 0

    Производный синус:

    можно использовать калькулятор производной, который позволяет вычислить производную функции синуса

    производная sin(x) является производной(`sin(x)`)=`cos(x)`

    Синус первообразной :

    Калькулятор первообразной позволяет вычислить первообразную функции синуса.

    Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`

    Предел синуса :

    Калькулятор предела позволяет вычислить пределы функции синуса.

    предел sin(x) is limit(`sin(x)`)

    Обратная функция синуса :

    обратная функция синуса — это функция арксинуса, отмеченная как arcsin.

    Графический синус :

    Графический калькулятор может отображать синусоидальную функцию в заданном интервале.

    Свойство функции синуса:

    Функция синуса является нечетной функцией.

    Расчет онлайн с синусом (sine)

    См. также

    Список связанных калькуляторов:

    • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
    • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
    • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
    • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
    • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
    • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
    • Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
    • Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
    • Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
    • Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
    • Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
    • Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

    Напоминания о курсах, калькуляторы, упражнения и игры: тригонометрические функции, действительные функции

     

    Чистый синусоидальный инвертор 5000 Вт

    Описание продукта

    Обзор :

    Чистый синусоидальный инвертор мощностью 5000 Вт — промышленного класса — 12 В постоянного тока, 50 и 60 Гц и теперь имеет двойную розетку GFCI и сертифицирован FCC. Этот продукт также включает в себя вентилятор с терморегулированием, обеспечивающий повышенную эффективность и меньший уровень шума. Он будет продолжать выдавать стабильную, чистую синусоидальную мощность и поддерживать выходное напряжение, даже если напряжение батареи снижается. Высокая выходная мощность достигается за счет привода DSP (Digital Signal Process). Этот инвертор идеально подходит для работы с нелинейными нагрузками (такими как двигатели с регулируемой скоростью и небольшие компрессоры). Чистая синусоидальная мощность также предпочтительна для принтеров LaserJet, чувствительной электроники, компьютерных серверов, микроволновых печей, медицинского оборудования, любого с печатной платой и зарядными устройствами для аккумуляторных дрелей. Внешний датчик напряжения аккумулятора позволит вам контролировать емкость аккумулятора и энергопотребление.

    Этот инвертор мощностью 5000 Вт может использоваться для автономных домашних систем резервного питания, солнечных батарей, лодок, рабочих транспортных средств и жилых автофургонов.

    Особенности:

    • 5000 Вт непрерывная мощность
    • 10000 Вт. Эффективный выход при низком напряжении
    • 2 — Двойная розетка GFCI
    • Разъем клеммной колодки переменного тока прямого подключения и
    • Кабель для дополнительного дистанционного выключателя
    • Изолированное заземление и нейтраль
    • Защита от короткого замыкания (GFCI и
    • Прерыватель переменного тока)
    • Выключатель
    • вентиляторы с терморегулированием
    • Вольтметр постоянного тока в комплекте
    • Руководство по эксплуатации
    • Техническая поддержка в течение всего срока службы
    • Гарантия 1 год Замена деталей и работ

    Технические характеристики

    • DC Входное напряжение 13,2 В (10,5 В 15 В)
    • Выходное напряжение Нет нагрузки 120VAC +/- 3%
    • Непрерывное 5000 Вт
    • SURGE 1000000 (1/2 SECOD)
    • SURGE 1000000 (1/2 SECOD)
    • SURGE 1000000 (1/2 SECOD)
    • (1/2 Second)
    • .

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *