Чему равен вертикальный угол: Что такое вертикальные углы? Ответ на webmath.ru

alexxlab / / Разное

Содержание

Смежные и вертикальные углы. Перпендикулярные прямые [wiki.eduVdom.com]

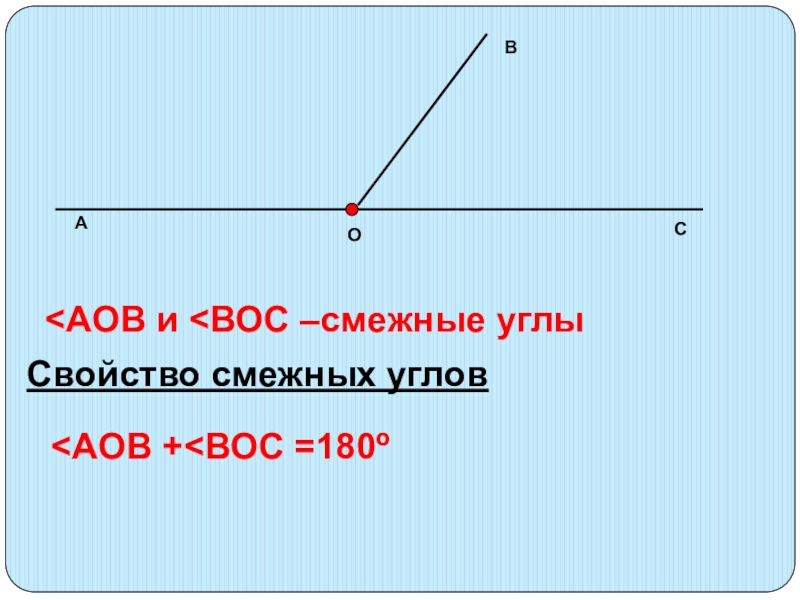
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.


Сумма смежных углов равна 180°

Рис.1

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.


Вертикальные углы равны

Рис.2

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).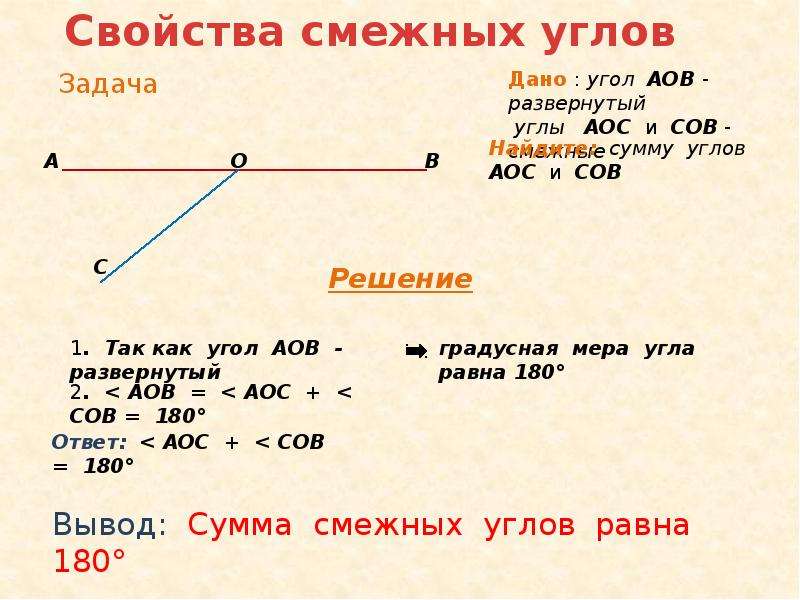

Теорема 2. Вертикальные углы равны.

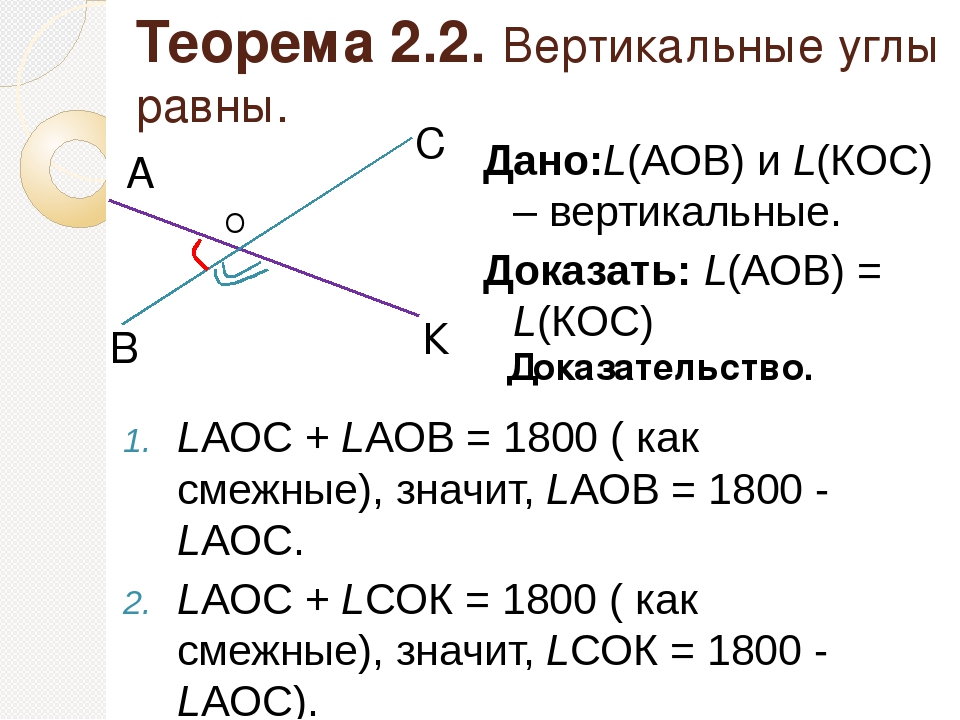
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.


Рис.3

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.


АН — перпендикуляр к прямой

Рис.4

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.


Чертежный угольник

Рис.5

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание.

Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.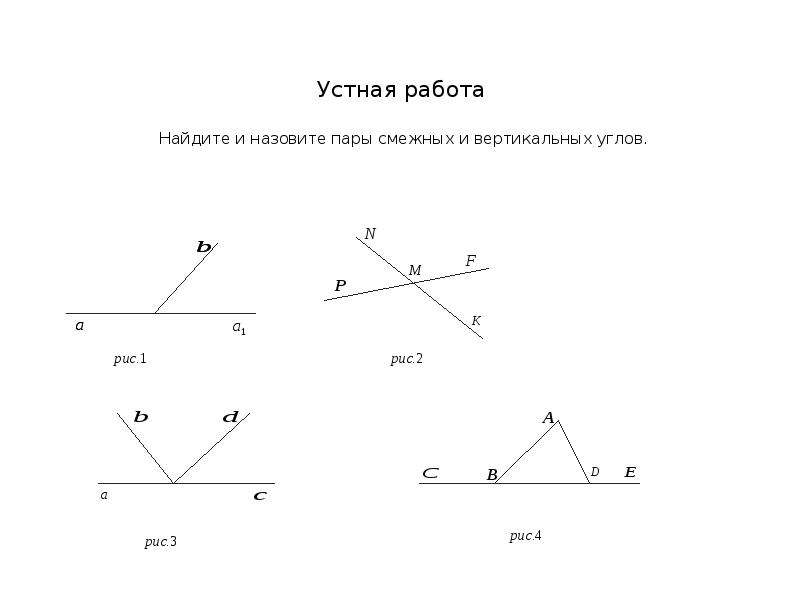
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Факт 1. \circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.


 

Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.


 

Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.


 

Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

 

Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.


 

Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.


 

Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.


 

Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.


 

Факт 11.
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.

\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

Смежные и вертикальные углы | Геометрия

Смежные углы

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).

∠ABD  и  ∠DBC  — это смежные углы,  AC  — прямая, луч  BD  — общая сторона углов и наклонная к прямой  AC,  ∠ABC  — развёрнутый угол,  B  — основание наклонной.

Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину:

Сумма смежных углов

Любые два смежных угла составляют в сумме развёрнутый угол. Развёрнутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.

∠ABD + ∠DBC = 2d,

где  d  — это обозначение прямого угла  (d = 90°).

Вертикальные углы

Вертикальные углы — это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов:

∠AOB  и  ∠COD,  а также  ∠AOD  и  ∠BOC  — вертикальные углы.

Равенство вертикальных углов

Вертикальные углы равны между собой. Рассмотрим вертикальные углы  1  и  3:

Сумма  ∠1  и  ∠2  равна развёрнутому углу  (180°).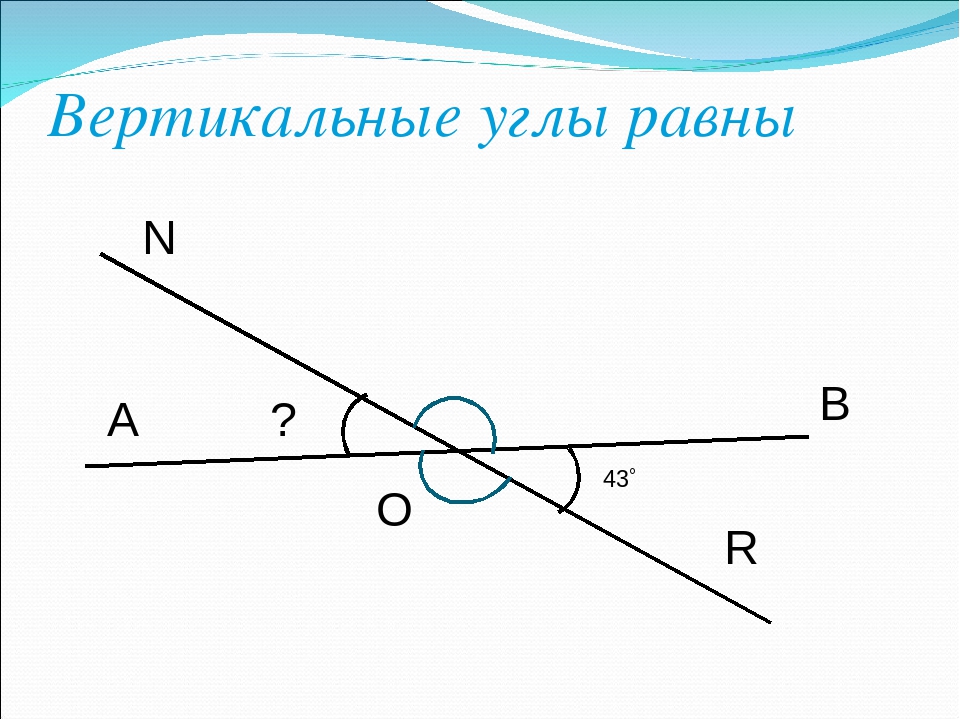   Сумма 

∠2  и  ∠3  тоже равна развёрнутому углу  (180°).  Значит:

∠1 + ∠2 = ∠2 + ∠3

Следовательно,  ∠1 = ∠3.  Равенство вертикальных углов доказано.

Смежные и вертикальные углы

1. Смежные углы.

Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.

Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.

Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.

Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).

Смежные углы могут иметь самые разнообразные положения (рис. 74).

Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°

Отсюда прямой угол можно определить как угол, равный своему смежному углу.

Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.

Например, если один из смежных углов равен 54°, то второй угол будет равен:

180° — 54° = l26°.

2. Вертикальные углы.

Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС— вертикальные; углы АОЕ и СОF — также вертикальные.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.

Таким же образом можно вычислить, чему равны ∠3 и ∠4.

∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;

∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).

Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.

Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.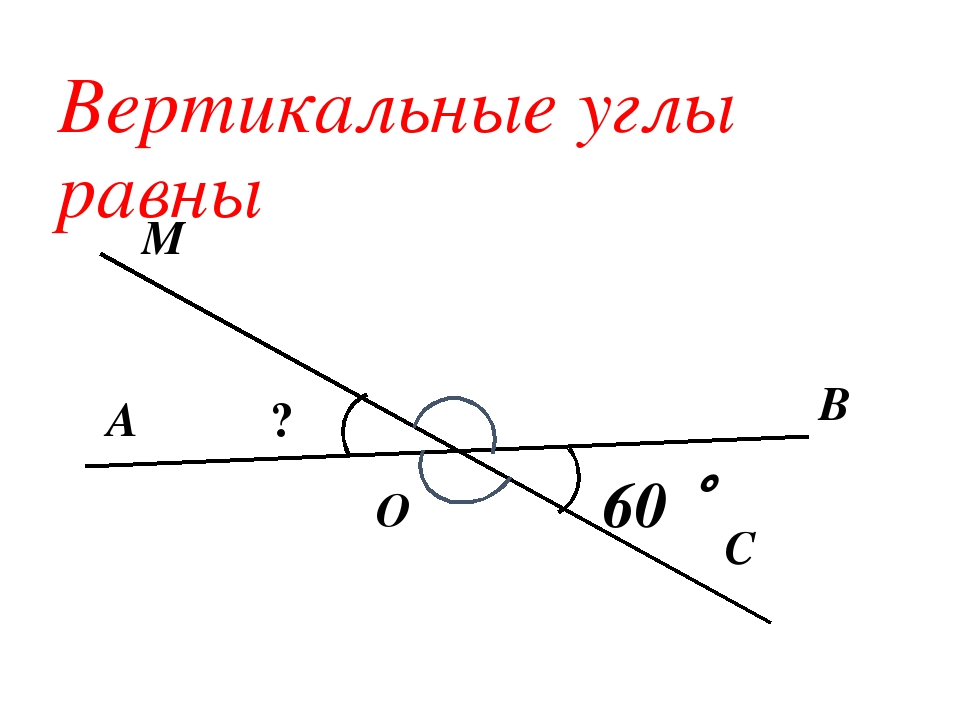

Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.

Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.

Доказательство можно провести следующим образом (рис. 78):

∠a + ∠c = 180°;

∠b + ∠c = 180°;

(так как сумма смежных углов равна 180°).

Отсюда

∠a + ∠c = ∠b + ∠c

(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).

В это равенство входит один и тот же угол с.

Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b, т. е. вертикальные углы равны между собой.

3. Сумма углов, имеющих общую вершину.

На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

Вертикальные углы. Перпендикулярные прямые. 7-й класс

Проверка понимания учащимися нового материала.

– Откройте учебник на стр.25 №65(а, б).

– Читаем задание под буквой а.

Найдите неразвёрнутые углы, образованные при пересечении 2-х прямых если:

а) сумма двух из них равна 114°.

Дано: а и в – прямые, а пересекает в, 1+3=114°

Найдите: 1, 2, 3, 4.

Решение.

– Начертите пересекающиеся прямые а и в. обозначьте номера углов.

– Сумма, каких углов может быть равна 114°?

(вертикальных)

– Назовите вертикальные углы.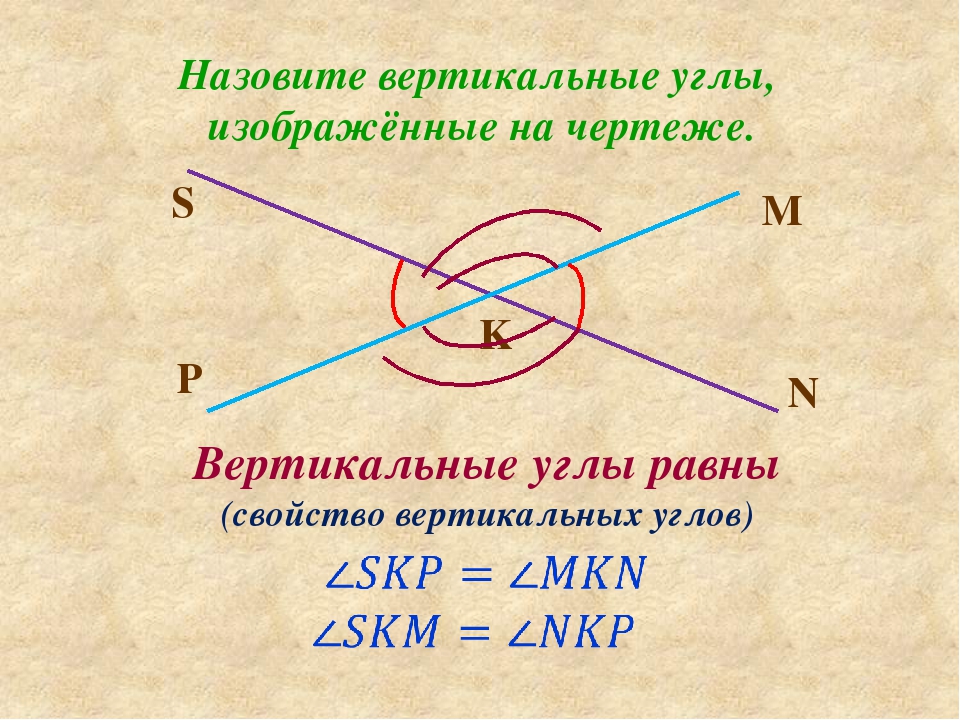

– Что мы знаем о вертикальных углах?

(они равны)

– Как найдём чему равен каждый из вертикальных углов?

(114°:2=57°)

– Углы 1 и 2 какие между собой?

(смежные)

– Как найдём 2?

(180°-1)

– Чему будет равна градусная мера 2?

(180°-57°=123°)

– Градусную меру, какого угла мы ещё не нашли?

(4)

– Чему она будет равна?

(градусной мере 2, так как они вертикальные)

– Читаем задание под буквой б.

б) сумма трёх углов равна 220°.

Дано: а пересекает в, 1+2+3=220°

Найти: 1, 2, 3, 4.

Решение.

1+2+3=220°

– Чему равна сумма углов 1 и 2?

(180°)

– Значит, 1+2=180° (как смежные)

– Заменим сумму 1 и 2 180°-ю градусами.

180°+3=220°

– Как найдём 3?

(220°-180°=40°)

– Угол 1 чему будет равен?

(1=3=40° – как вертикальные)

– Как найдём 2?

(2=180°-1 (так как они смежные), 2=180°-40°, 2=140°)

– Чему равен 4?

(4=2=140°)

Ответ:40°, 40°, 140°, 140°.

– Выполним № 66 устно.

– Читаем задание под буквой а.

На рисунке 41 найдите углы 1, 2, 3, 4 если:

а) 2+4=220°

– Какие это углы?

(вертикальные)

– Чему будет равна градусная мера каждого угла?

(110°)

– Как найдём градусные меры углов 1 и 3?

(1 и 2 – смежные, значит, 1+2=180° –> 1=180°-2)

1=180°-110°, 1=70°

1=3=70° (как вертикальные)

б) 3(1+3)= 2+4

– Решим эту задачу через уравнение.

– Пусть 1=х°, тогда 2=180°-х°, так как 3=1, то он тоже равен х°, а 4=2, то 4=180°-х°.

– Пусть 1=х°, тогда 2=180°-х°, так как 3=1, то он тоже равен х°, а 4=2, то 4=180°-х°.

– Подставим эти данные в равенство, которое нам дано:

3(х+х)=180-х+180-х;

6х=360-2х;

8х=360;

х=45.

– Итак, что мы обозначали за х?

(1 и 3)

– Значит, чему они будут равны?

(45°)

– Как найдём 2?

(180°-45°=135°)

4=2=135° (как вертикальные)

_Читаем задание под буквой в.

в) 2-1=30°

– Эту задачу также решим через уравнение.

– Пусть 1=х°, тогда 2=180°-х°, так как 3=1, то он тоже равен х°, а 4=2, то 4=180°-х°.

– Подставим эти данные в равенство, которое нам дано:

180-х-х=30;

180-2х=30;

2х=150;

х=75.

– Итак, что мы обозначали за х?

( 1 и 3)

– Значит, чему они будут равны?

(75°)

– А чему будут равны 2 и 4?

(180°-75°=105°)

– Сейчас выполним № 67. читаем задание.

На рисунке 47 изображены три прямые, пересекающиеся в точке О. найдите сумму углов: 1+2+3.

– 3 и 4 какие?

(вертикальные)

– Значит, какие они между собой?

(равны)

– Какой угол образуют углы: 2, 4 и 1?

(развёрнутый)

– Значит, сумма углов 2, 4 и 1 чему будет равна?

(180°)

– Значит и сумма 1,2,3 углов тоже равна 180°.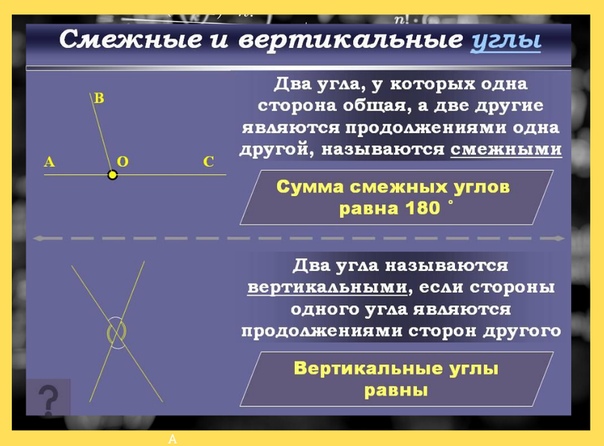

– Ответили на вопрос задачи?

(да)

– Теперь выполним № 80.

Известно, что АОВ=35°, ВОС=50°. Найдите АОС. Для каждого из возможных случаев сделайте чертёж.

– Чертим АОВ=35°. Теперь чертим ВОС=50°.

Дано: АОВ=35°, ВОС=50°.

Найти: АОС.

Решение.

– Как найдём АОС?

(ВОС – АОВ, 50°-35°=15°)

– Как ещё может располагаться луч ОС?

– Верно, по разные стороны от луча ОВ. Чертим.

– Как в этом случае найдём АОС?

(ВОС+АОВ, 50°+35°=85°)

– Выполняем № 83.

Найдите угол, образованный биссектрисами двух смежных углов.

– Чертим 2 смежных угла.

– Что такое биссектриса угла?

(Это луч, который выходит из вершины угла и делит и делит его пополам)

Проводим биссектрисы углов. Обозначаем буквами все углы.

Дано: АОВ и ВОС – смежные, DO и ОЕ – биссектрисы углов.

Найти: DOE.

Решение.

– Какой угол образуют все эти углы?

(развёрнутый)

АОВ+ВОС=180°

– Чему равен DOB?

(DOB=?АОВ)

– Чему равен LВOE?

(ВOE=?ВОС)

– А сумме каких углов равен DOE?

(DOE=(DOB+ ВOE=1/2АОВ+1/2ВОС= 1/2 (АОВ+ВОС)= 1/2 180°=90°)

– Следовательно, чему равен угол, образованный биссектрисами смежных углов?

(90°)

– Выполняем № 84.

Докажите, что биссектрисы вертикальных углов лежат на одной прямой.

– Чертим вертикальные углы.

– Возьмём вертикальные углы 3 и 4, проведём их биссектрисы.

– Чему равна сумма углов 1, 3 и 4?

(180°)

– Почему?

(так как образуют развёрнутый угол)

1+3+4=180°

– Теперь рассмотрим сумму углов 6, 1 и 3.

– 6 равен какому углу?

(углу 4)

– Можно в это равенство вместо 4 записать 6. Что получится?

1+3+6=180°

– Что из этого следует?

(углы 1, 3 и 6 образуют развёрнутый угол)

– А развёрнутый угол, что из себя представляет?

(прямую)

– Значит, биссектрисы лежат на одной прямой?

(да)

Урок «Смежные и вертикальные углы»

СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ Лиманская Инна Викторовна учитель математики специалист высшей категории учитель-методист МОУ «Амвросиевская школа №6» Амвросиевского района ДНР

Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать. Галилей

«ДА НЕ ВОЙДЁТ СЮДА НИ ОДИН ИЗ ТЕХ, КТО НЕ ОВЛАДЕЛ ГЕОМЕТРИЕЙ!»

Повторение Какие углы называются смежными? Ответ: Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми. ∠ АОВ и ∠СОВ — смежные ОВ — общая сторона АО и ОС дополнительные полупрямые. А В С О

Повторение Какими свойствами обладают смежные углы? Ответ: Сумма смежных углов равна 180° . Если два угла равны, то и смежные с ними углы равны. Если угол не развернутый, то его градусная мера меньше 180°. Угол, смежный с прямым, есть прямой угол.

Найдите пары смежных углов. Объясните, почему эти углы смежные. А В С М О а) б) К Р Н Е О в) Т А Р С г) А С К М В д) е) В С D А F D O A B

Какие углы называются вертикальными? Какие углы называются вертикальными? Ответ: Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. ∠ 1 и ∠ 3- вертикальные ∠ 2 и ∠ 4- вертикальные 1 2 3 4 а b Повторение

Каким свойством обладают вертикальные углы? Каким свойством обладают вертикальные углы? Ответ: Вертикальные углы равны. ∠ 1 = ∠ 3 ∠ 2 = ∠4 1 2 3 4 Повторение

Найдите пары вертикальных углов.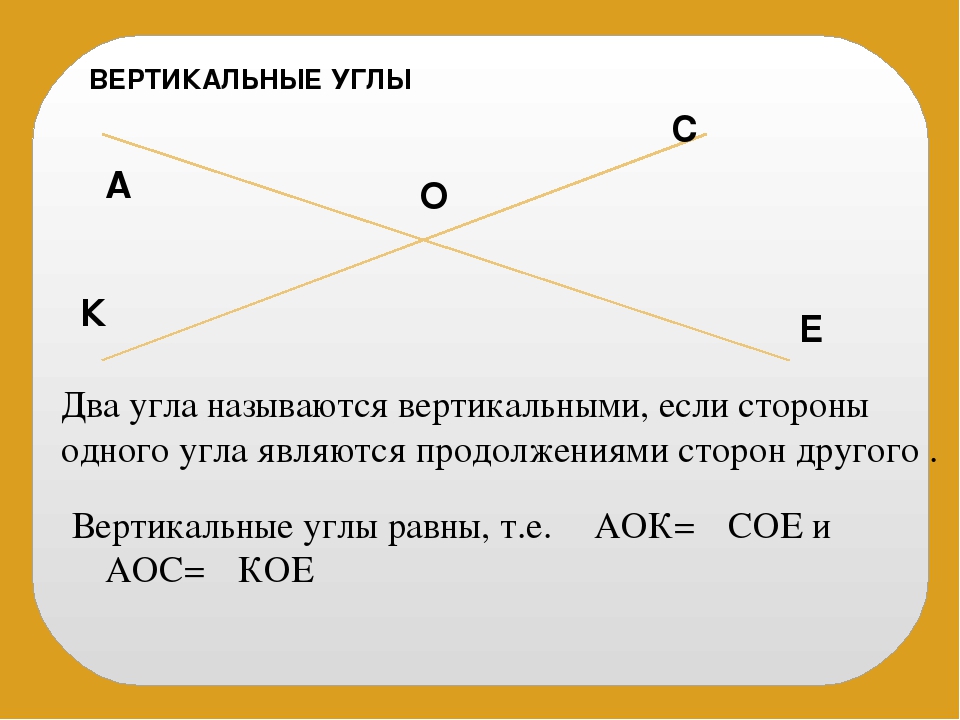 Объясните, почему эти углы являются вертикальными. а) А B C D O б) К Р Н Е О в) Т А Р О B C D г) С А д) В D О Е С А О B D

ТЕСТ ПО ТЕМЕ «ВЕРТИКАЛЬНЫЕ И СМЕЖНЫЕ УГЛЫ»

1. Сумма смежных углов равна… A. 3600 B. 900 C. 1800

2. Как называется угол меньше 1800, но больше 900? острый тупой прямой A B C

3. Чему равен угол, если смежный с ним равен 470? 1330 470 430 C B A

4. Какой угол образуют часовая и минутная стрелки часов, когда они показывают 6 часов? тупой развернутый прямой C B A

5. Найдите <AOC. А В С D О 1030 1030 770 30 C B A

6. Найдите <DOB. А В С D О 540 360 1260 540 B A C

7. Найдите смежные углы, если один из них в два раза больше другого. 600 и 1200 900 и 1800 1400 и 700 C B A

8. Дан угол 720. Чему равен вертикальный ему угол? 720 1080 180 C B A

9. Какой угол образуют часовая и минутная стрелки часов, когда они показывают три часа? острый тупой прямой C B A

Ответы 1. C 2. B 3. A 4. B 5. B 6. B 7. B 8. C 9. C

Умение решать задачи – практическое искусство, подобное катанию на лыжах, или игре на фортепиано: научиться этому можно лишь подражая избранным образцам и постоянно тренируясь. Джордж Пойа

А О В С Найти: № 1

О А D С В Найти: № 2

А В D С Найти: № 3

№ 4 А В С О Найти:

А В С О № 5 Найти:

А В С О № 6 Найти:

А С D В О Найти: № 7

А С D В О Найти: № 8

С А В D О Найти: № 9

С А В D Найти: О № 10

А В С D М О Найти: № 11

Найти: А В С D О Задача 12

С D К М А В О Найти: Задача 13

С D К М А В Найти: О Задача 14

О Равны ли и ? А В С D E Задача 15

А В С D О Найти: Задача 16

А В С D О Найти: Задача 17

А В С Сравните и Задача 18

А В С Докажите, что Задача 19

А В С Докажите, что Задача 20

О А В С D Найдите: К Р Задача 21

Самостоятельная работа А С В D 2. Начертите угол РОК. Постройте смежный с ним: а)  КОN; б)  РOR. 3. Запишите пары смежных углов, имеющиеся на рисунке: Е А D C В F 4. Запишите пары вертикальных углов, имеющиеся на рисунке: D В А М С N 1. На рисунке изображены прямые АС и ВD, пересекающиеся в точке О. Дополните записи: ВОС и  . . . — вертикальные, ВОС и  . . . — смежные, O СОD и  . . . — вертикальные, СОD и  . . . — смежные.

Повторили понятия смежных и вертикальных углов, их свойства Научились решать задачи Стали выше еще на одну ступеньку в изучении геометрии ПОДВЕДЕНИЕ ИТОГОВ

Рефлексия «ДЕРЕВО УСПЕХА» Я молодец! Мне все понятно Я старался, но получилось не все Мне есть над чем поработать

Домашнее задание § 6 пункт 11, №65(а), № 67 стр. 25. *Составить две задачи по готовым чертежам и их решить.

Измерение вертикальных углов

Вертикальный угол – это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние. Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν. Углы наклона бывают положительные и отрицательные.

Угол между вертикальным направлением и направлением линии местности называется зенитным расстоянием и обозначается буквой Z. Зенитные расстояния всегда положительные (рис.4.20).

Рис.4.20

Угол наклона и зенитное расстояние одного направления связаны соотношением:

Z + ν = 90 ,                 (4.22)

или

ν = 90 – Z ,                   (4.23)

или

Z = 90 – ν .                     (4.24)

Вертикальный круг теодолита. Вертикальный круг теодолита предназначен для измерения вертикальных углов, то-есть, углов наклона или зенитных расстояний.

Вертикальный круг большинства теодолитов устроен следующим образом: лимб вертикального круга жестко соединен с трубой (насажен на один из концов оси трубы), центр лимба совмещен с геометрической осью вращения трубы, а его плоскость перпендикулярна этой оси. Деления на лимбе наносят по разному: либо от 0 до 360, либо от 0 до 180 в обе стороны со знаками “плюс” и “минус” или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.

Пузырек уровня в момент отсчета приводится в нуль-пункт, то есть, ось уровня служит указателем горизонтального направления. Отсчетным индексом является нулевой штрих отсчетного приспособления. Ось уровня и линия отсчетного индекса (линия, соединяющая отсчетный индекс с центром лимба) должны быть параллельны; при выполнении этого условия линия отсчетного индекса будет горизонтальна в момент взятия отсчета по вертикальному кругу.

Взаимное положение лимба и зрительной трубы должно удовлетворять условию: визирная линия трубы и нулевой диаметр лимба должны быть параллельны.

Оба условия вместе составляют так называемое главное условие вертикального круга теодолита; оно читается так: визирная линия трубы должна занимать горизонтальное положение, когда отсчет по лимбу равен нулю и пузырек уровня находится в нульпункте.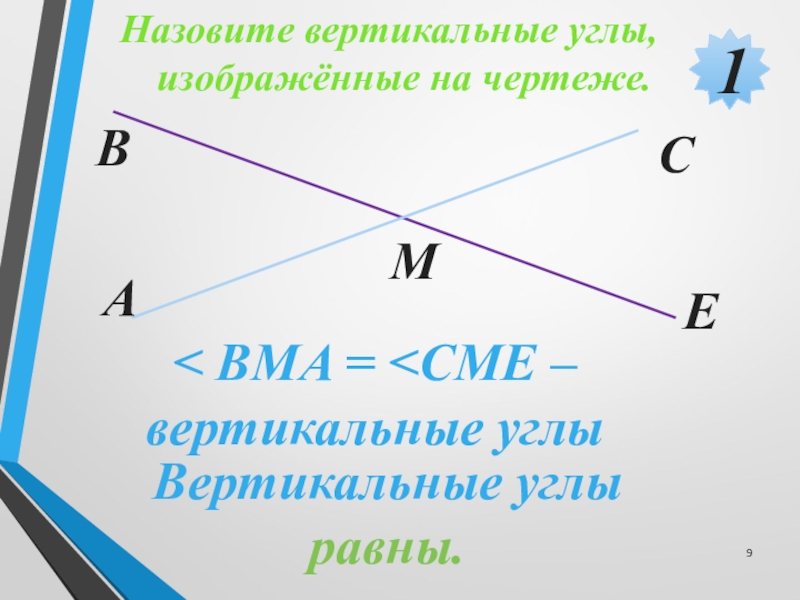 На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис.4.21-а.

Во-первых, при насаживании лимба на ось трубы между нулевым диаметром лимба и визирной линией трубы остается малый угол x. Во-вторых, линия отсчетного индекса может быть непараллельна оси уровня и между ними существует малый угол y. Таким образом, хотя отсчет по лимбу равен нулю, визирная линия трубы занимает наклонное положение, и угол наклона ее равен:

ν = x + y.

Рис.4.21

Если установить визирную линию горизонтально (рис.4.21-б), то отсчет по лимбу станет равным:

N = 360 – (x + y).                  (4.25)

Этот отсчет называется местом нуля вертикального круга и обозначается М0.

Таким образом, место нуля вертикального круга теодолита – это отсчет по лимбу вертикального круга при горизонтальном положении визирной линии трубы и оси уровня вертикального круга.

Для конкретного теодолита формулы для вычисления угла наклона и места нуля приводятся в паспорте. Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:

М0 = 0.5 . (NL + NR),                (4.26)

ν = 0.5 . (NL – NR),

ν = NL – M0,

ν = M0 – NR.

Положение вертикального круга, при котором отсчет по лимбу вертикального круга равен (с точностью до M0) углу наклона, считается основным; у большинства современных теодолитов основным положением является КЛ.

Для измерения углов наклона удобно иметь М0 близким к нулю, поэтому нужно регулярно выполнять поверку места нуля, которая предусматривает следующие действия:

наведение трубы на точку при КЛ, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
перевод трубы через зенит, наведение трубы на точку при КП, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
вычисление по соответствующим формулам места нуля М0 и угла наклона ν.

Если М0 получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нульпункта.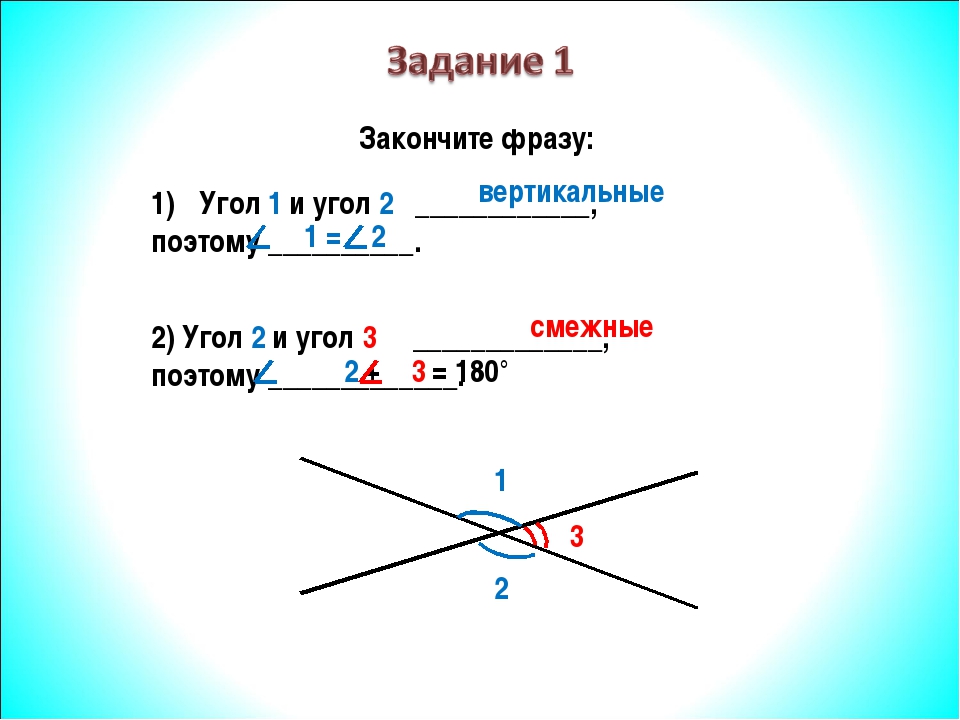 Исправительными винтами уровня привести пузырек в нульпункт.

Рекомендовать Google:

Вертикальные углы — объяснения и примеры

В этой статье мы узнаем , что такое вертикальные углы и , как их вычислить . Прежде чем мы начнем, давайте сначала познакомимся со следующими понятиями о линиях.

Что такое пересекающиеся и параллельные прямые?

Пересекающиеся линии — это прямые линии, которые пересекаются или пересекаются в определенной точке. На рисунке ниже показаны пересекающиеся линии.

Линия PQ и линия ST пересекаются в точке Q. Следовательно, эти две прямые пересекаются.

Параллельные прямые — это прямые, которые не пересекаются ни в одной точке на плоскости.

Линия AB и линия CD являются параллельными линиями, потому что они не пересекаются ни в одной точке.

Что такое вертикальные углы?

Вертикальные углы — это парные углы, образующиеся при пересечении двух прямых. Вертикальные углы иногда называют вертикально противоположными углами, потому что эти углы противоположны друг другу.

Реальные настройки, в которых используются вертикальные углы, включают: знак железнодорожного переезда, буква « X », открытые ножницы и т. д. Египтяне рисовали две пересекающиеся линии и всегда измеряли вертикальные углы, чтобы убедиться, что они равны.

Вертикальные углы всегда равны . В целом можно сказать, что при пересечении двух прямых образуются 2 пары вертикальных углов. См. Схему ниже.

На схеме выше:

  • ∠a и ∠b — вертикальные противоположные углы.Два угла также равны, т.е. ∠a = ∠
  • ∠c и ∠d составляют еще одну пару вертикальных углов, и они тоже равны.
  • Мы также можем сказать, что два вертикальных угла имеют общую вершину (общую конечную точку двух или более линий или лучей).

Доказательство теоремы о вертикальном угле

Мы можем доказать это на диаграмме выше.

Мы знаем, что угол b и угол d являются дополнительными углами, т.е.

Мы также знаем, что угол a и угол d являются дополнительными углами i.е.

Мы можем переставить приведенные выше уравнения:

Сравнивая два уравнения, имеем:

Значит, доказано.

Вертикальные углы — это дополнительные углы, когда линии пересекаются перпендикулярно.

Например, , ∠W и ∠ Y — это вертикальные углы, которые также являются дополнительными углами. Аналогично, ∠X и ∠Z — вертикальные углы, которые являются дополнительными.

Как найти вертикальные углы?

Не существует специальной формулы для вычисления вертикальных углов, но вы можете определить неизвестные углы, соотнося разные углы, как показано в примерах ниже.

Пример 1

Рассчитайте неизвестные углы на следующем рисунке.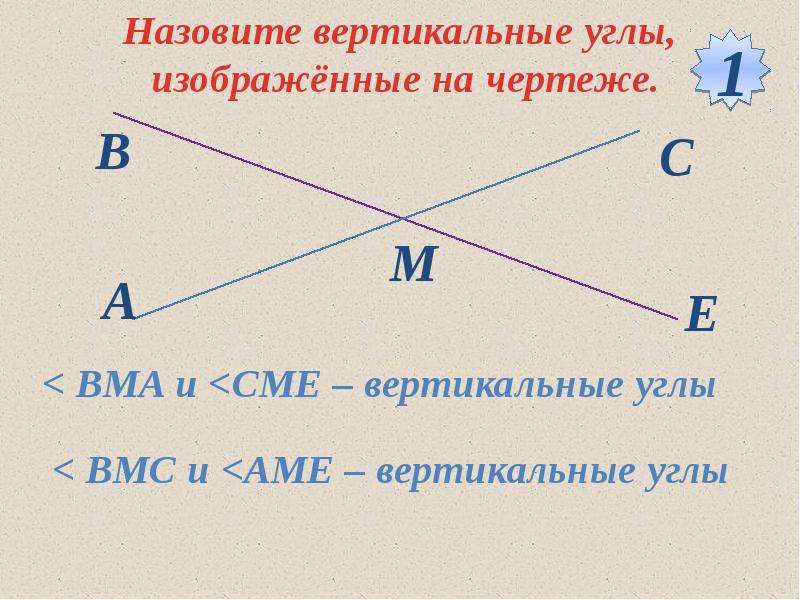

Решение

∠ 47 0 и ∠ b — вертикальные углы. Следовательно, ∠ b также равно 47 0 (вертикальные углы равны или равны).

∠47 0 и ∠ a — дополнительные углы. Следовательно, ∠a = 180 0 — 47 0

⇒∠a = 133 0

∠ a и ∠ c — вертикальные углы.Следовательно, ∠ c = 133 0

Пример 2

Определите значение θ на диаграмме, показанной ниже.

Решение

На диаграмме выше ∠ (θ + 20) 0 и ∠ x — вертикальные углы. Следовательно,

∠ (θ + 20) 0 = ∠ x

Но 110 0 + x = 180 0 (дополнительные углы)

х = (180 — 110) 0

= 70 0

Подставим x = 70 0 в уравнение;

⇒ ∠ (θ + 20) 0 = ∠ 70 0

⇒ θ = 70 0 -20 0 = 50 0

Следовательно, значение θ составляет 50 градусов.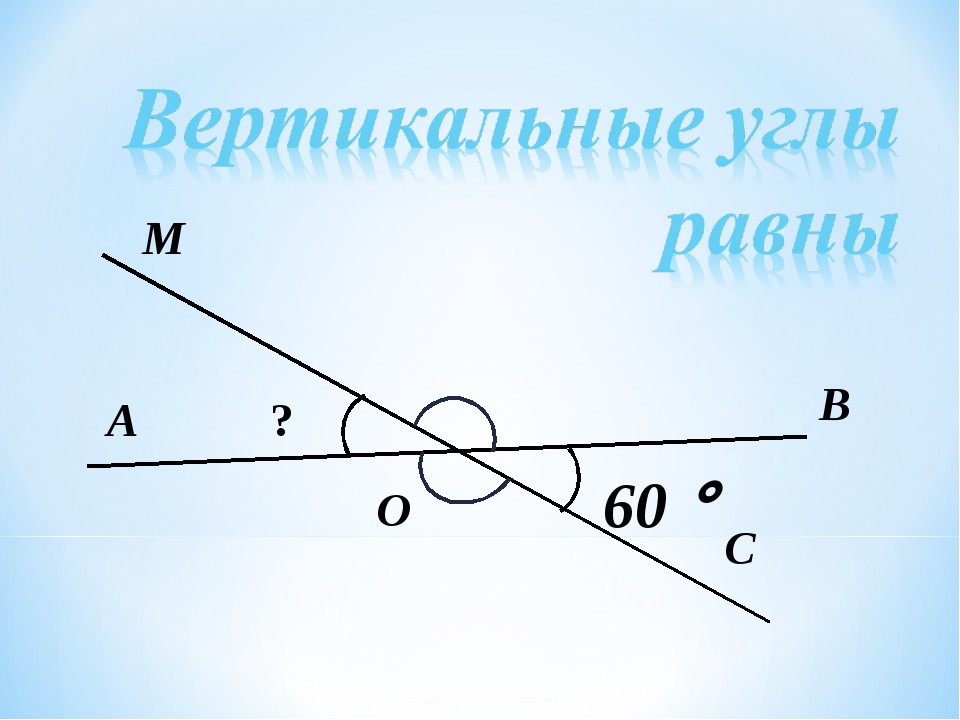

Пример 3

Рассчитайте значение угла y на рисунке, показанном ниже.

Решение

140 0 + z = 180 0

z = 180 0 — 140 0

г = 40 0

Но (x + y) + z = 180 0

(x + y) + 40 0 = 180 0

х + у = 140 0

90 0 + y = 140 0

y = 50 0

Пример 4

Если 100 0 и (3x + 7) ° — вертикальные углы, найдите значение x.

Решение

Следовательно, вертикальные углы равны;

(3x + 7) 0 = 100 0

3x = 100–7

3x = 93

х = 31 0

Следовательно, значение x равно 31 градусу.

Применение вертикальных углов (h4)

Вертикальные углы имеют множество применений, которые мы видим или испытываем в повседневной жизни.

  • Американские горки устанавливаются под определенным углом для правильной работы.Эти углы настолько важны, что если бы они сместились на градус выше или ниже, возникла бы вероятность аварии. Максимальный вертикальный угол, установленный для американских горок ( Mumbo Jumbo , Flamingo Land’s ), составляет 112 градусов.
  • На авиашоу мы видим два следа пара, которые пересекаются друг с другом и образуют вертикальные углы.
  • Знаки железнодорожных переездов (X), установленные на дорогах для обеспечения безопасности транспортных средств.
  • Воздушный змей, где две деревянные палки пересекаются и удерживают воздушный змей.
  • Доска для дротика имеет 10 пар вертикальных углов, где «яблочко» является виртуальной вершиной.

Предыдущий урок | Главная страница | Следующий урок

Вертикальные углы — Вертикальные углы в геометрии, теорема о вертикальных углах, решенные примеры.

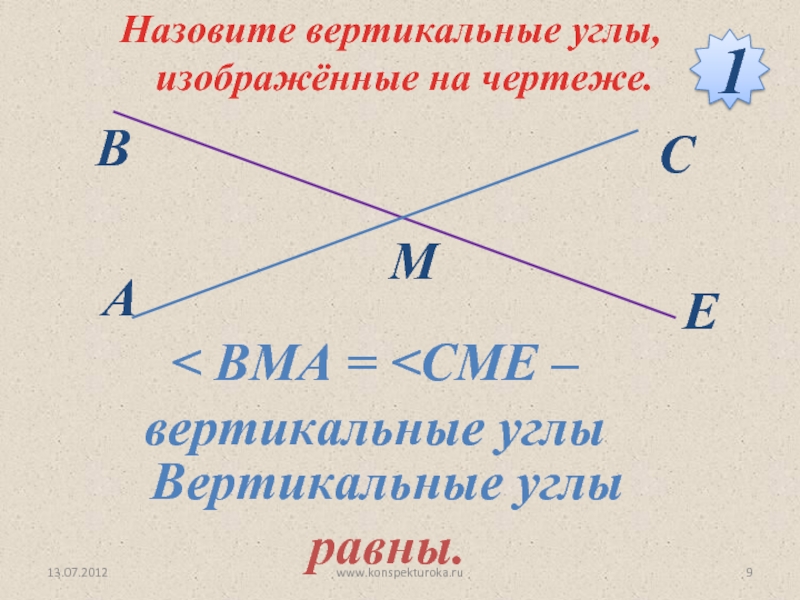
Вертикальные углы образуются, когда две прямые встречаются в одной точке. Они всегда равны друг другу. Другими словами, когда две линии пересекаются или пересекаются друг с другом, образуются 4 угла.Мы можем заметить, что два противоположных друг другу угла равны и называются вертикальными углами. Их также называют «вертикально противоположными углами», поскольку они лежат напротив друг друга.

Что такое вертикальные углы в геометрии?

При пересечении двух линий образуются четыре угла. Есть две пары несмежных углов. Эти пары называются вертикальными углами. На изображении, приведенном ниже, (∠1, ∠3) и (∠2, ∠4) представляют собой две пары вертикальных углов. Вертикальные углы — это пара несмежных углов, образованных пересечением двух прямых линий.Проще говоря, вертикальные углы расположены напротив друг друга в углах буквы «X», образованной двумя прямыми линиями. Их также называют вертикально противоположными углами, поскольку они расположены напротив друг друга.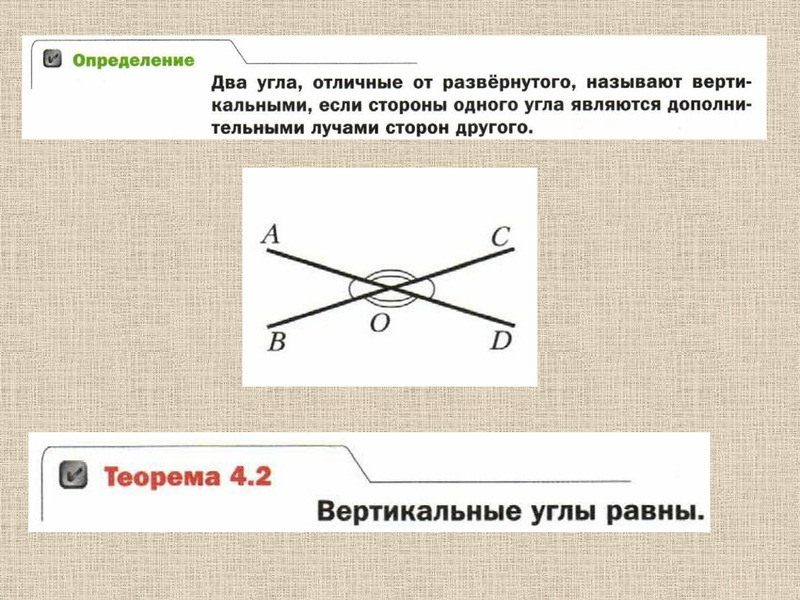

Теорема о вертикальных углах

Теорема о вертикальных углах или теорема о вертикально противоположных углах утверждает, что два вертикальных угла, образующиеся при пересечении двух прямых, всегда равны друг другу. Давайте узнаем об этой теореме и ее доказательстве подробно.

Заявление : Вертикальные углы (углы, которые образуются при пересечении двух линий) совпадают.

Доказательство : Доказательство простое и основано на прямых углах. Мы уже знаем, что углы на прямой в сумме составляют 180 °.


Итак, на приведенном выше рисунке
∠1 + ∠2 = 180 ° (поскольку они представляют собой линейную пару углов) ——— (1)
∠1 + ∠4 = 180 ° (поскольку они представляют собой линейную пару углов) — ——— (2)
Из уравнений (1) и (2), 1 + ∠2 = 180 ° = ∠1 + ∠4.
Согласно транзитивному свойству, если a = b и b = c, то a = c.
Следовательно, мы можем переписать утверждение в виде ∠1 + ∠2 = ∠1 + ∠4.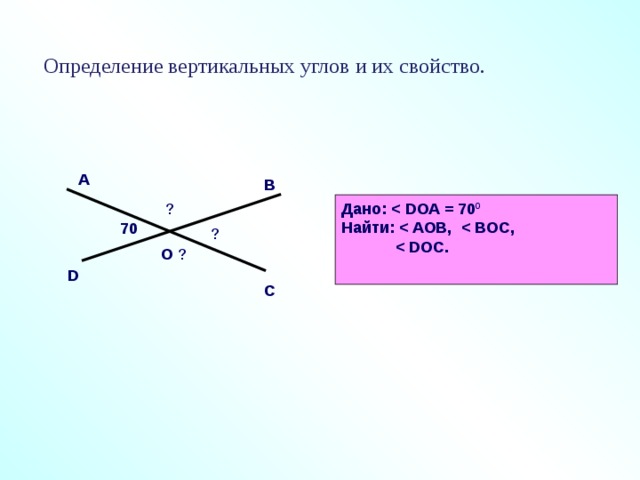 ——— (3)
Исключая 1 из обеих частей уравнения (3), получаем ∠2 = ∠4.
По аналогии. мы можем использовать тот же набор утверждений, чтобы доказать, что ∠1 = ∠3. Следовательно, мы заключаем, что вертикально противоположные углы всегда равны.

Чтобы найти меру углов на рисунке, мы одновременно используем свойство прямого угла и теорему о вертикальном угле.Давайте посмотрим на несколько решенных примеров, чтобы понять это.

Важные примечания

  • Вертикальные углы всегда равны.
  • Вертикальные углы могут быть как дополнительными, так и дополнительными.
  • Вертикальные углы всегда несмежны.

Темы, связанные с вертикальными углами

Ознакомьтесь с некоторыми интересными статьями о вертикальных углах.

Часто задаваемые вопросы о вертикальных углах

Что такое вертикальные углы?

Вертикальные углы образуются при пересечении двух линий.Из 4 образованных углов противоположные друг другу углы являются вертикальными. Их также называют «вертикально противоположными углами». Эти углы всегда равны.

Конгруэнтны ли вертикальные углы?

Когда две прямые линии пересекаются друг с другом, образуются вертикальные углы. Вертикальные углы всегда совпадают и равны. Вертикальные углы совпадают, поскольку две пары несмежных углов, образованных пересечением двух линий, накладываются друг на друга.

Вертикальные углы являются дополнительными?

Когда сумма любых двух углов составляет 180 °, мы называем их дополнительными углами. Если есть случай, когда вертикальные углы равны прямым углам или равны 90 °, то каждый вертикальный угол равен 90 °. Следовательно, сумма этих двух углов будет равна 180 °. Так что в таких случаях можно сказать, что вертикальные углы являются дополнительными. Следует отметить, что это особый случай, в котором вертикальные углы являются дополнительными. В противном случае во всех других случаях, когда значение каждого из вертикальных углов меньше или больше 90 градусов, они не являются дополнительными.

Что такое теорема о вертикальном угле?

Теорема о вертикальном угле утверждает, что углы, образованные двумя пересекающимися линиями, которые называются вертикальными углами, совпадают. Вертикальные углы имеют одинаковые размеры. Например, если ∠a, ∠b, ∠c, ∠d — это 4 угла, образованные двумя пересекающимися линиями, а ∠a вертикально противоположен ∠b, а ∠c вертикально противоположен ∠d, то ∠a конгруэнтно ∠ b и ∠c конгруэнтно ∠d.

Могут ли вертикальные углы быть прямыми?

Да, вертикальные углы могут быть прямыми.Когда два противоположных вертикальных угла составляют 90 ° каждый, тогда говорят, что вертикальные углы являются прямыми углами. Это можно наблюдать по линиям оси x и оси y декартовой диаграммы.

Всегда ли совпадают вертикальные углы?

Да, вертикальные углы всегда совпадают. Пересечение двух прямых составляет 4 угла. При этом образуются две пары вертикальных углов. Они равны по меру и конгруэнтны.

Вертикальных углов в геометрии: определение и примеры — видео и стенограмма урока

Вертикальные углы: другие примеры

Давайте рассмотрим еще несколько примеров вертикальных углов.

Линия c пересекает две прямые a и b . На каждом пересечении образуются вертикальные углы. Вертикальные пары углов следующие:

1 и 6
2 и 5
3 и 8
4 и 7

Вертикальные углы: свойство конгруэнтности

Основным свойством вертикальных углов является то, что они равны конгруэнтности . Другими словами, у них одинаковая угловая мера.Здесь, если мы добавим угловые меры, мы увидим, что вертикальные углы совпадают.

Доказательство

Давайте сделаем для этого простое доказательство. Прежде чем мы начнем, мы должны признать некоторые определения и теоремы в геометрии. Прежде всего, линейная пара углов — это пара смежных углов. Их необщие стороны всегда противоположные лучи. Кроме того, углы, образующие линейную пару, также равны дополнительным , поэтому их сумма всегда равна 180 градусам. Вот наше доказательство.

1. Прямые m и n пересекаются, образуя углы 1, 2, 3 и 4 (данные).
2. Углы 1 и 2 являются линейной парой, поэтому они являются дополнительными (определение линейной пары).
3. Угол 1 + угол 2 = 180 градусов (определение дополнительных углов).
4. Углы 2 и 3 являются линейной парой, поэтому они являются дополнительными (определение линейной пары).
5. Угол 2 + угол 3 = 180 градусов (определение дополнительных углов).
6. Угол 1 + угол 2 = угол 2 + угол 3 (замена; см. Утверждения 3 и 5).
7. Угол 1 = угол 3 (вычтите угол 2 из уравнения в утверждении 6).
QED (наше доказательство завершено)

Поиск угловых мер

Теперь решим задачу! Если угол 1 равен 115 градусам, каковы размеры других углов?

Угол 3 составляет 115 градусов, потому что углы 1 и 3 представляют собой пару вертикальных углов. Углы 1 и 2 представляют собой линейную пару, поэтому их сумма составляет 180 градусов; следовательно, угол 2 составляет 180 — 115 = 65 градусов. Угол 4 составляет 65 градусов, потому что углы 2 и 4 представляют собой пару вертикальных углов.

Чем не являются вертикальные углы

Давайте закончим этот урок, показав еще один не пример вертикальных углов. Здесь углы 1 и 3 не являются парой вертикальных углов. Несмотря на то, что они имеют общую вершину и не являются смежными, они не образованы одной и той же парой пересекающихся линий. Угол 1 образован линиями r и t , а угол 3 образован линиями s и t .

Резюме урока

Когда две линии пересекаются, они образуют две пары из вертикальных углов . Вертикальные углы имеют общую вершину, но никогда не являются смежными углами. Наконец, вертикальные углы всегда совпадают.

Ключевые термины

Углы в природе

Вертикальные углы — пара несмежных углов, образующихся при пересечении двух линий

Смежные углы — два угла с общей стороной

Конгруэнтные углы — углы с одинаковой величиной угла

Линейная пара — пара смежных углов

Дополнительные — углы, сумма которых составляет 180 градусов

Результаты обучения

После этого видео вы сможете:

  • Определить вертикальные углы
  • Различия между вертикальными и смежными углами
  • Опишите свойства вертикальных углов
  • Найдите величину угла на основе ваших знаний о вертикальных углах

Что такое вертикальный угол?

Овладейте семью столпами успеха в школе

Повысьте свои оценки и снизьте уровень стресса

Вертикальные углы — это углы, расположенные друг напротив друга.

  • У них одна и та же вершина. Вершина — это точка пересечения линий.
  • Кроме того, вертикальные углы совпадают. (равная мера)
  • Простой способ представить себе вертикальные углы — это визуализировать X. X будет иметь два набора вертикальных углов.

Расшифровка вертикальных углов

Привет, добро пожаловать в MooMooMath. Сегодня мы поговорим о вертикальных углах. Вертикальные углы — это углы, которые находятся через дорогу друг от друга, поэтому вы всегда смотрите на вертикальные углы по отношению друг к другу.Обратите внимание, у меня есть линия здесь, и у меня есть линия здесь, и одна здесь. У меня один, два, три, четыре угла, так что это те углы, на которые я смотрю, а соседями через улицу являются эти два и эти два. Если вы заметите, эти двое меньше по размеру и на самом деле совпадают друг с другом, что означает, что они равны. Я собираюсь отметить эти углы синим цветом с помощью одной маленькой дуги, которая показывает, что они совпадают друг с другом. Затем я отмечу эти другие углы, совпадающие зеленым цветом, с двумя дугами, и они расположены напротив друг друга.Вот что такое вертикальные углы. Эти два синих угла конгруэнтны, и эти два зеленых угла конгруэнтны. Теперь я добавлю туда несколько цифр. Что, если я сделаю этот угол равным ста двадцати градусам, как я могу вычислить остальное. Если этот угол составляет сто двадцать градусов. Мы знаем, что это должно быть сто двадцать, потому что это вертикальные углы. Теперь обратите внимание, что это прямая линия, и мы знаем, что линии составляют в сумме сто восемьдесят градусов. Итак, если у нас здесь один двадцать, у нас есть шестьдесят для другой стороны, поэтому этот вертикальный угол также равен шестидесяти градусам, так работают вертикальные углы.Они очень просты, если вы освоите их. Итак, давайте посмотрим на правила вертикальных углов. Правила гласят, что углы, пересекающие улицу друг от друга, совпадают, и это и есть вертикальный угол. Тогда углы, прилегающие друг к другу или рядом друг с другом, дополняют друг друга или составляют в сумме один восемьдесят. Давайте посмотрим на нашу диаграмму. Эти два угла в шестьдесят градусов — это вертикальные углы, эти два угла в двадцать градусов — это вертикальные углы, но эти два рядом друг с другом примыкают друг к другу и в сумме дают один восемьдесят.Надеюсь, это было полезно.

Углы A и B являются вертикальными углами, и они совпадают (равная угловая мера)

Если угол A равен 40 градусам, то угол B равен 40 градусам

9035 Вертикальные углы в реальной жизни.

Скрещивание лыж создает вертикальные углы.

Вертикальные углы встречаются повсюду. Вот лишь пара примеров.

Обратите внимание, как железнодорожный переезд и ножницы создают вертикальные углы.

Примеры задач вертикальных углов

Найдите угловую меру для углов 1,2 и 3.

∠2 = 40◦, потому что это вертикаль 40 °

40 + 40 = 80 Добавить два вертикальных угла вместе

360-80 = 280, потому что общая величина = 360 °

280 ÷ 2 = 140 °

Угол 1 и 3 измерения = 140 ° ∠1 и ∠3 — вертикальные углы

другой способ решить эту проблему:

∠2 = 40◦, потому что это вертикаль 40◦

∠3 и ∠1 — вертикальные углы, поэтому ∠1 = 70◦

Найдите значение X

5x + 182 = 7x + 194

Два уравнения равны, потому что они представляют собой вертикальные углы.

Стандарт Common Core 6.CO.9

К чему добавляются вертикальные углы?

Какие бывают 5 видов углов?

Типы углов острый угол — угол от 0 до 90 градусов. Прямой угол — угол 90 градусов. Угол наклона — угол между 90 и 180 градусами. Прямой угол — угол 180 градусов ..

Какие углы находятся в треугольник?

Треугольник имеет три угла. Сумма углов всегда равна 180 ° в треугольнике.У нас есть разные типы треугольников. Треугольник классифицируется по углам и количеству совпадающих сторон.

Суммируются ли вертикально противоположные углы в 180?

Углы a ° и c ° также являются вертикально противоположными углами, поэтому они должны быть равными, что означает, что они равны 140 ° каждый.

Равны ли вертикальные углы 90?

Вертикальные углы — это углы, которые противоположны друг другу, когда две прямые пересекаются друг с другом. Две пары противоположных углов равны друг другу.Две пары соседних углов являются дополнительными, то есть в сумме они составляют 180 градусов. … Дополнительные углы — это два угла, которые в сумме составляют 90 градусов.

Что такое вертикальные углы в треугольнике?

Вертикальные углы — это углы, противоположные друг другу при пересечении двух линий. «Вертикальный» в этом случае означает, что они имеют одну и ту же вершину (угловую точку), а не обычное значение «вверх-вниз».

Всегда ли вертикальные углы острые?

Пояснение: Два угла ∠A: вертикальный (образованный двумя пересекающимися линиями) и острый (меньше 90o).Углы ∠1 и ∠2 смежные (имеют одну сторону) и острые.

Каковы отношения углов в параллельных прямых?

Каждая из параллельных линий, пересекаемых трансверсалью, имеет 4 угла, окружающие точку пересечения.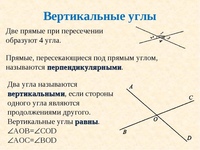 Они совпадают по размеру и положению с аналогом на другой параллельной линии. На каждой из параллельных линий есть две пары вертикальных углов. Каждый угол в паре соответствует другому углу в паре.

Как называются два равных угла?

равнобедренный треугольник Следовательно, равнобедренный треугольник имеет две равные стороны и два равных угла.Название происходит от греческих iso (то же самое) и скелос (нога). Треугольник со всеми равными сторонами называется равносторонним треугольником, а треугольник без равных сторон называется разносторонним треугольником.

Что такое пример вертикального угла?

Углы противоположны друг другу при пересечении двух линий. … В этом примере a ° и b ° — вертикальные углы. «Вертикаль» относится к вершине (где они пересекаются), а НЕ вверх / вниз. Их еще называют вертикально противоположными углами.

Как решить вертикальный угол?

Если углы вертикальные, то они равны или равны.Следовательно, если вертикаль равна 3x, а другая — 80-x, вы должны просто составить уравнение: 3x равняется 80-x. прибавив x к обеим сторонам, вы получите 4x, равное 80. Решите относительно x, и вы получите x, равный 20.

К чему складываются противоположные углы?

Вертикально противоположные углы равны. (b и c, e и h, f и g также противоположны по вертикали). g и c — соответствующие углы. … Смежные углы в сумме составляют 180 градусов.

Равны ли друг другу вертикальные углы?

Другой термин для обозначения противоположных углов — вертикальные углы.Вертикальные углы всегда совпадают, а это значит, что они равны. Смежные углы — это углы, выходящие из одной вершины. Соседние углы имеют общий луч и не перекрываются.

Раздел F. Вертикальные углы

Страница 1 из 3

1.

Определение; Типы

Вертикальный угол измеряется в направлении силы тяжести, рис. F-1

Рисунок F-1
Угловая ориентация

Есть два типа:

  • Традиционная вертикальная (или просто вертикальная)
  • Зенит

Традиционный угол по вертикали Угол измеряется вверх или вниз от горизонтали, рисунок F-2.Он колеблется от -90 ° ниже горизонтали (депрессия) до + 90 ° вверху (наклон). Это типично для угловых измерений с использованием традиционных американских транзитов с открытым стандартом.

Рисунок F-2
Вертикальный угол

Угол зенита измеряется от верхнего конца вертикальной линии непрерывно по всему периметру, рисунок F-3.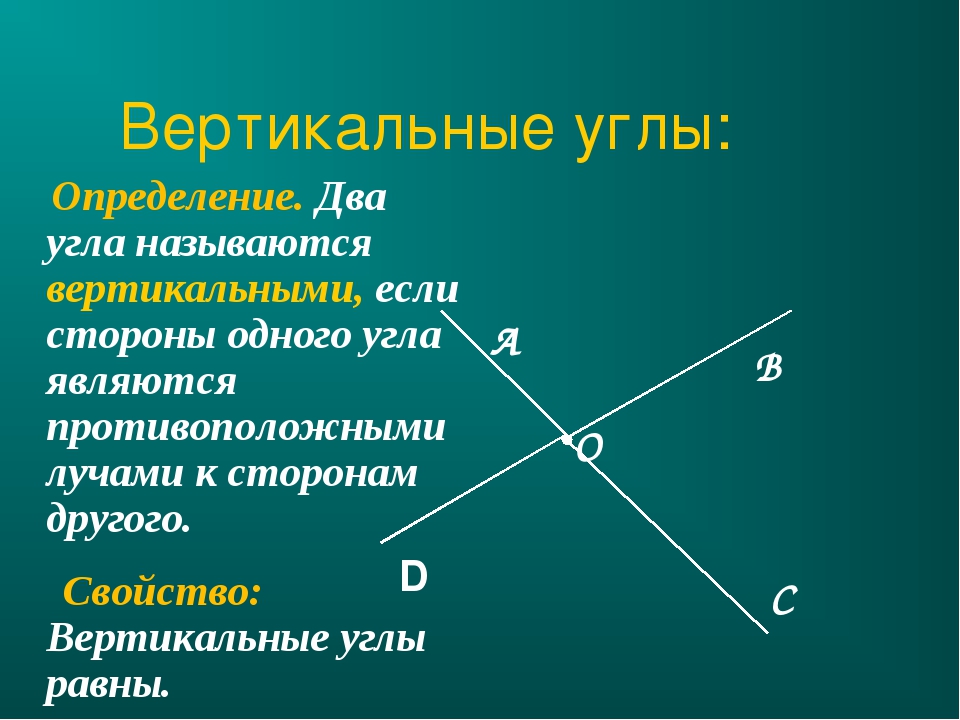 Он колеблется от 0 ° прямо вверх (в зените) до 90 ° по горизонтали, от 180 ° прямо вниз (надир), до 270 ° на противоположной горизонтали и до 360 ° назад в зените. Это типично для угловых измерений с использованием оптических транзитов с закрытым эталоном и теодолитов.

Рисунок F-3
Зенитный угол

На рисунке F-4 показаны совмещенные круги вертикального (красный) и зенитный (синий) углов с инструментом в их центре в качестве ориентира.Этот рисунок помогает понять, как два типа углов соотносятся друг с другом.

Рисунок F-4
Вертикальный и зенитный круги

Детали
Просмотров: 20279

евклидова геометрия — Объясните, почему вертикальные углы должны совпадать

евклидова геометрия — Объясните, почему вертикальные углы должны совпадать — Mathematics Stack Exchange
Сеть обмена стеков

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange
  2. 0
  3. +0
  6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил

Просмотрено 16к раз

$ \ begingroup $

Я знаю, почему вертикальные углы совпадают, но не знаю, почему они должны совпадать

Создан 24 янв.

Максимилиано

98533 золотых знака1515 серебряных знаков2828 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Две пересекающиеся прямые образуют две пары совпадающих вертикальных углов.Если вертикальные углы двух пересекающихся линий не совпадают с , тогда две пересекающиеся «прямые» должны фактически, не быть линиями … так что «вертикальные углы» на самом деле не будут « вертикальные углы «по определению.

Возможно, вам будет интересно посмотреть доказательство этого на видео Академии Хана:

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *