ГОСЫ / вопрос 5 / Лекция 9
Лекция №9
Эллипс. Каноническое уравнение. Исследование формы эллипса по его уравнению. Характеристические элементы эллипса. Параметрические уравнения эллипса. Способы построения эллипса. Эллипс как результат сжатия окружности к одному из ее диаметров
Пусть
на плоскости даны две точки  и
и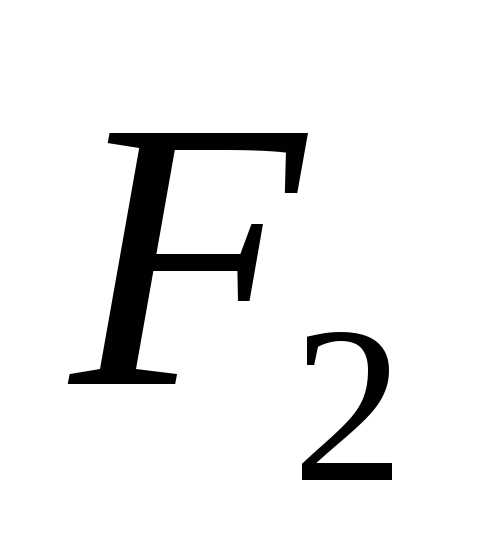 ,
расстояние между которыми равно,
и дано некоторое число
,
расстояние между которыми равно,
и дано некоторое число ,
которое удовлетворяет условиям:
,
которое удовлетворяет условиям: или
или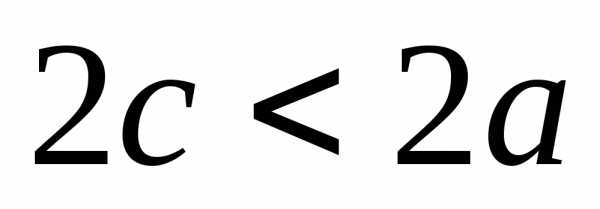
Определение
9.1. Эллипсом называется геометрическое
место точек плоскости, сумма расстояний
каждой из которых до двух данных точек  и
и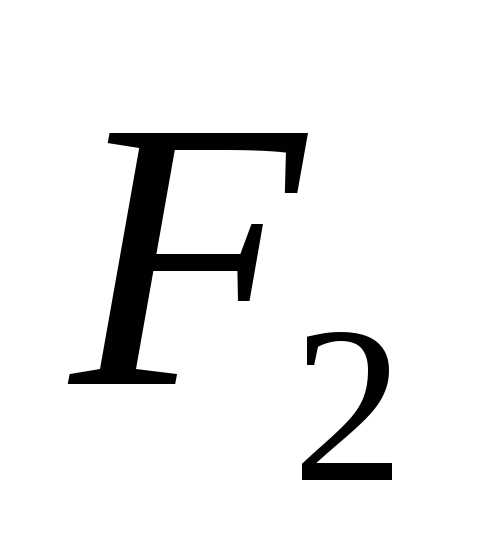 есть величина постоянная, равная
есть величина постоянная, равная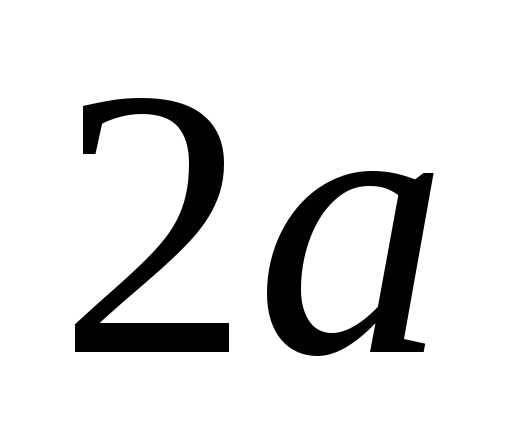
Точки  и
и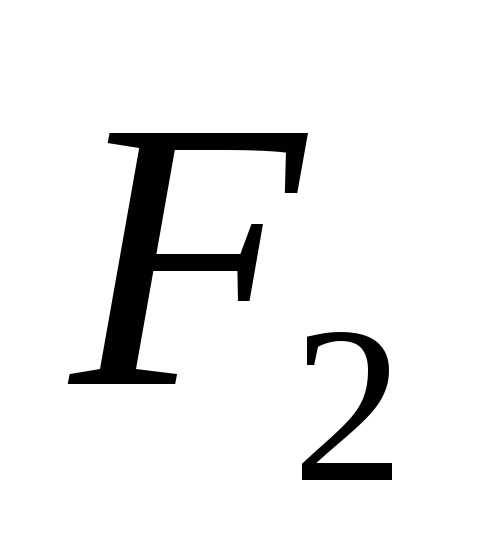 называются фокусами эллипса, расстояние
между ними обозначается через
называются фокусами эллипса, расстояние
между ними обозначается через 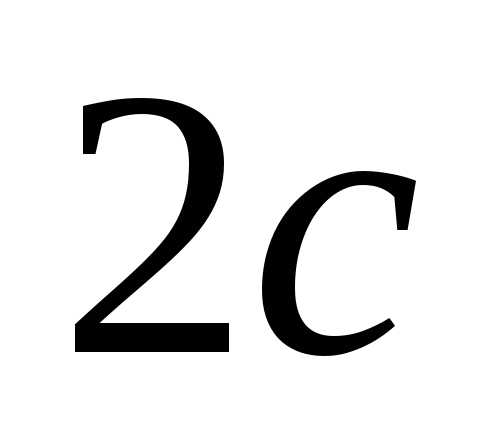 и называется фокусным расстоянием.
и называется фокусным расстоянием.
Введем
прямоугольную систему координат таким
образом, что ось 
 —
серединный перпендикуляр к отрезку
—
серединный перпендикуляр к отрезку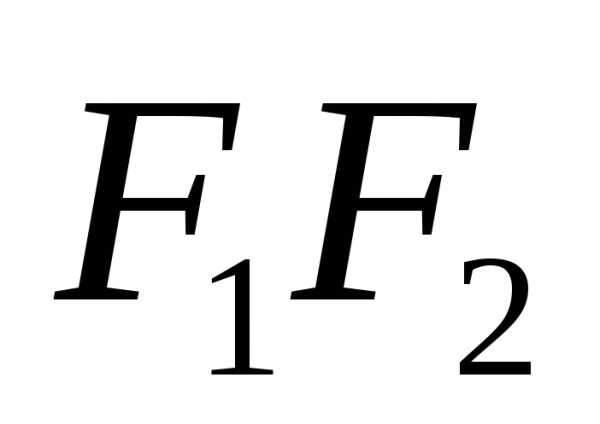 .
.1. Пусть
2. Точка 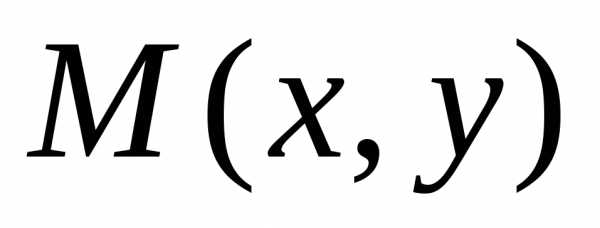 является
точкой эллипсатогда
и только тогда, когда
является
точкой эллипсатогда
и только тогда, когда
3. ;
(1)
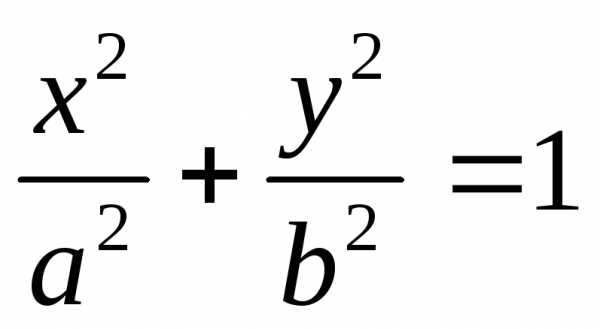 (2)
(2)
4. Покажем, что
данное уравнение действительно есть
уравнение эллипса – ведь пока мы доказали
только, что каждая точка 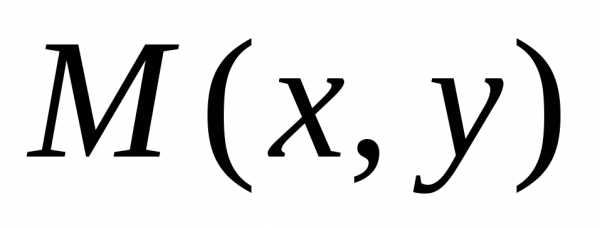
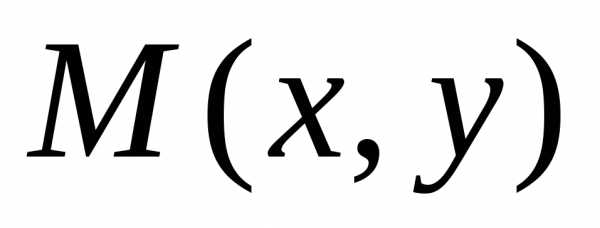 ,
удовлетворяющая уравнению (2), есть точка
эллипса, т.е. для нее выполняется условие
.
,
удовлетворяющая уравнению (2), есть точка
эллипса, т.е. для нее выполняется условие
.Найдем расстояния :
Выразим в координатах ;
Из уравнения (2) следует, что
 .
Так как,
имеем;
.
Так как,
имеем;Из (a) и (b) следует, что =

 .
Так как,
то
.
Так как,
то .
.Аналогичными рассуждениями приходим к выводу, что

Найдем
Таким образом, 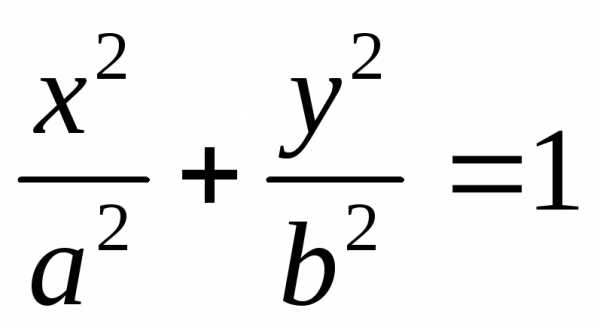 — каноническое уравнение эллипса
— каноническое уравнение эллипса
Исследование формы эллипса по каноническому уравнению
1. Эллипс
– фигура ограниченная. Координаты точек эллипса ограничены
неравенствами: 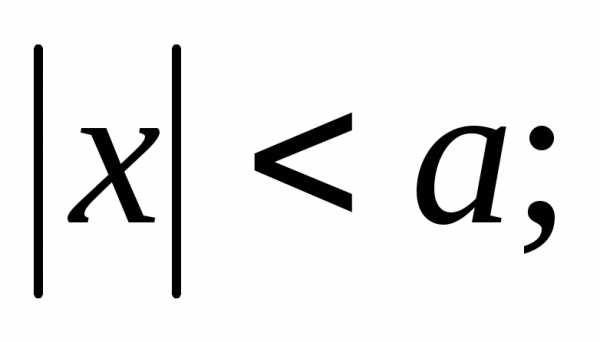
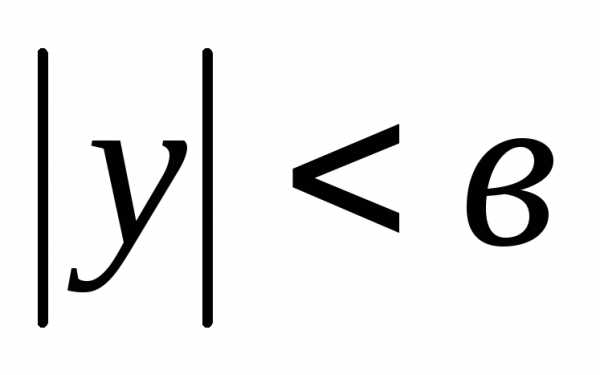 .
Это означает, что фигура эллипс есть
ограниченная фигура, не выходящая за
пределы прямоугольника со сторонами
.
Это означает, что фигура эллипс есть
ограниченная фигура, не выходящая за
пределы прямоугольника со сторонами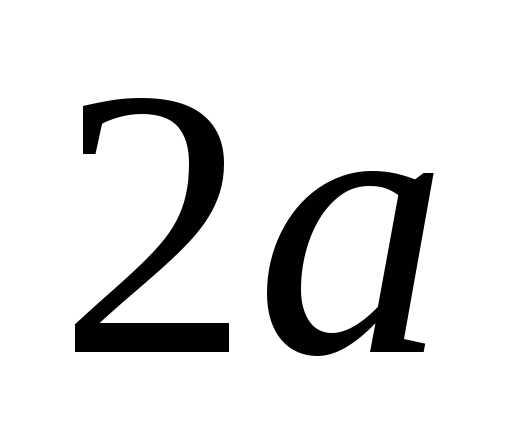 и
и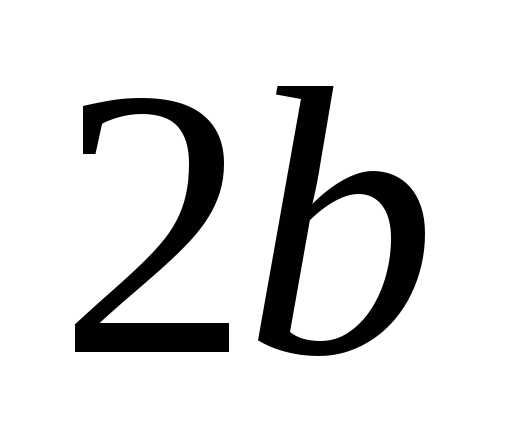 .
.
Если точка эллипса
принадлежит оси 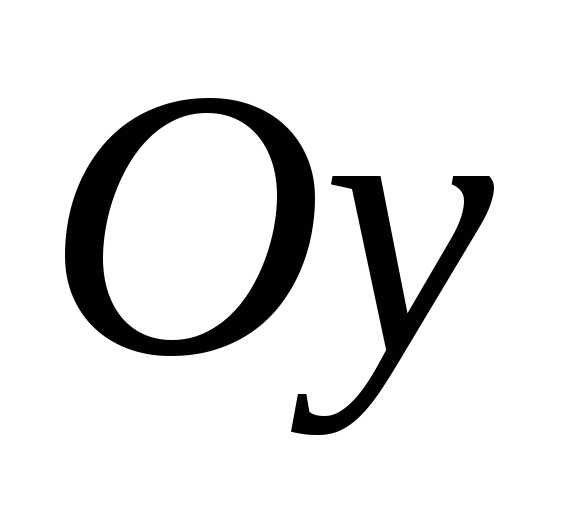
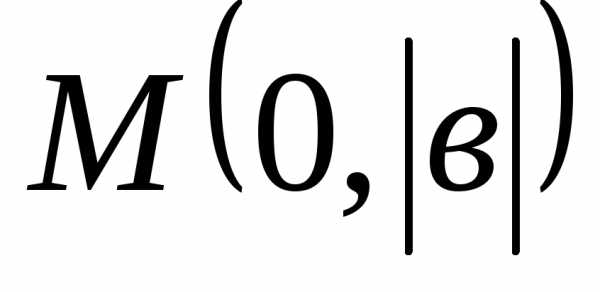 .
Если точка эллипса принадлежит оси
.
Если точка эллипса принадлежит оси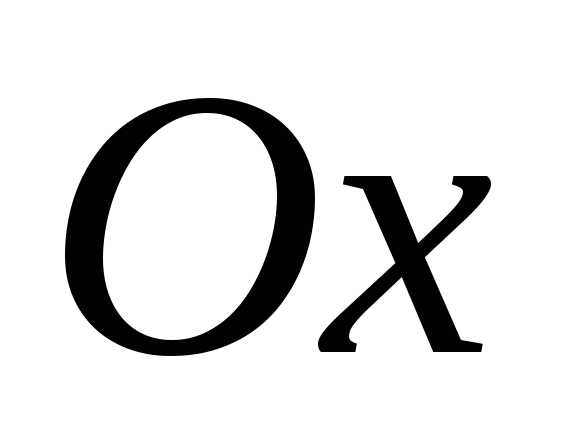 ,
то она имеет координаты
,
то она имеет координаты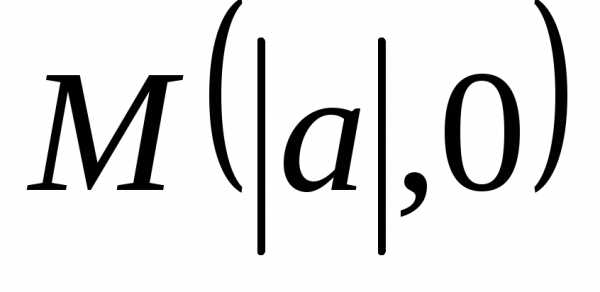 .
Значит, неравенства, определяющие
эллипс, имеют вид:
.
Значит, неравенства, определяющие
эллипс, имеют вид: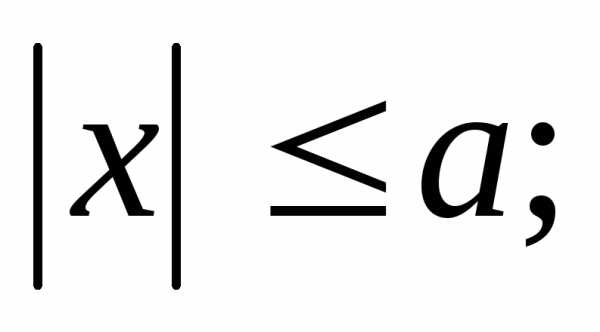
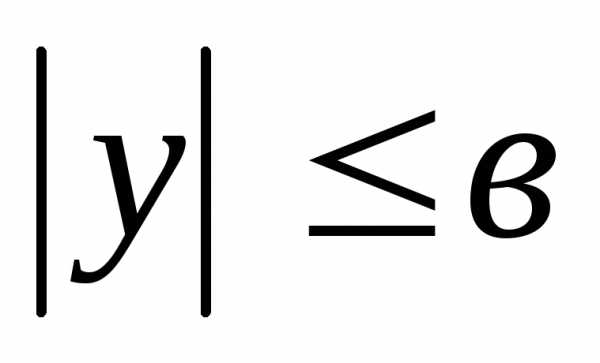 .
.Эллипс – фигура симметричная. В уравнение входят только чётные степени координат. Значит, эллипс есть линия, симметричная относительно осей координат и начала координат. Ось, проходящая через фокусы эллипса, называется первой или фокальной осью симметрии, а перпендикулярная к ней ось – второй осью симметрии.
Поэтому для исследования эллипса его достаточно рассмотреть в I четверти.
Для I
четверти получаем, что 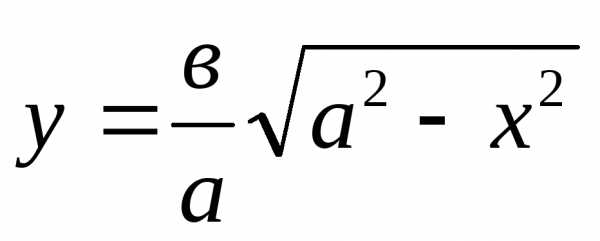 .
При возрастании
.
При возрастании от
от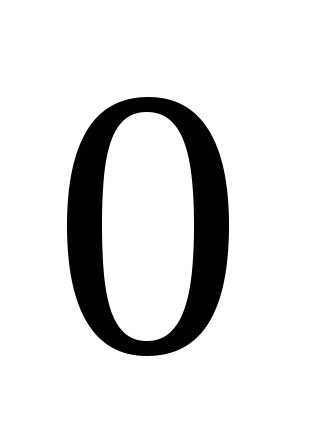 до
до ,
, монотонно убывает от
монотонно убывает от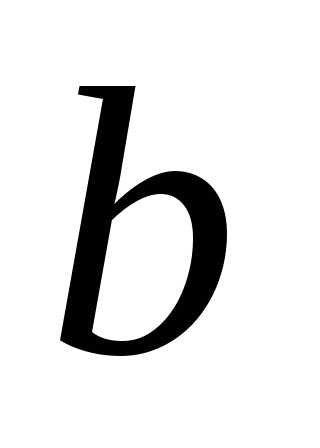 до
до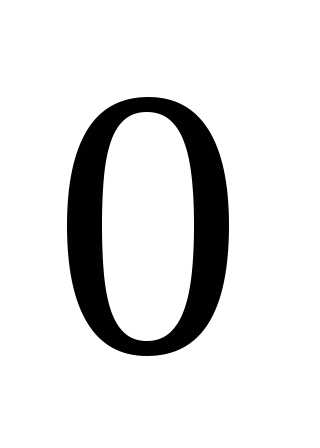 .
.
3. Каждая ось
симметрии пересекает эллипс в двух
точках: 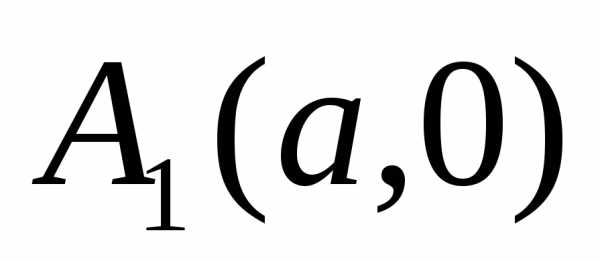
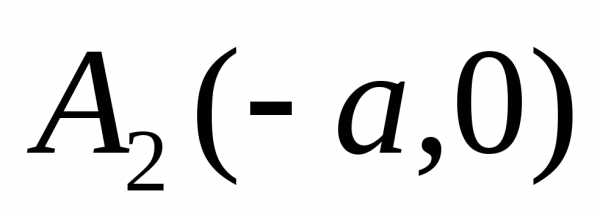 ,
,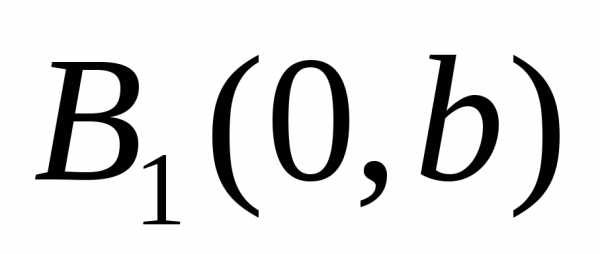 ,
,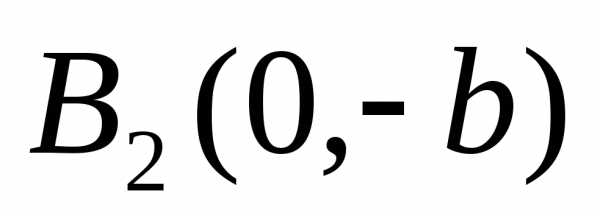 –вершины
эллипса.
Отрезки
–вершины
эллипса.
Отрезки 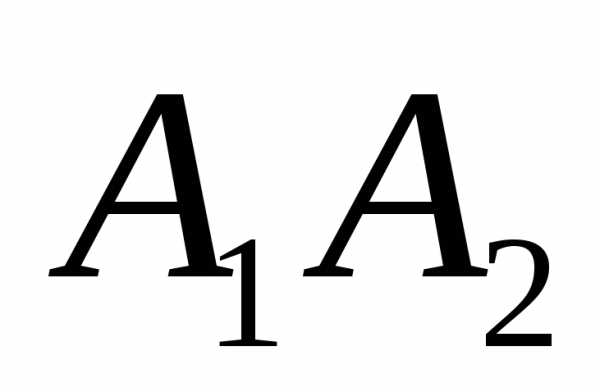 и
и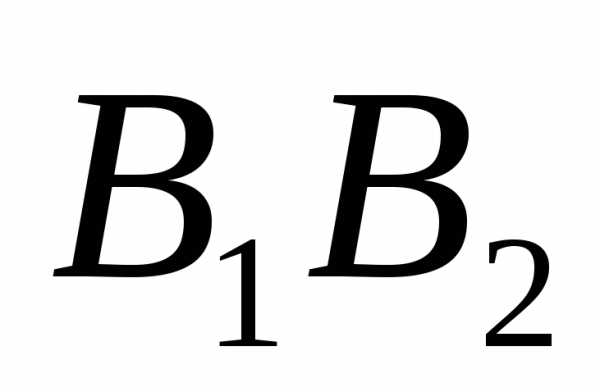 называютсяосями
эллипса.
— большая ось,-
малая ось. Начало координат
называютсяосями
эллипса.
— большая ось,-
малая ось. Начало координат –центр
эллипса. Отрезки
–центр
эллипса. Отрезки  ,
, ,
,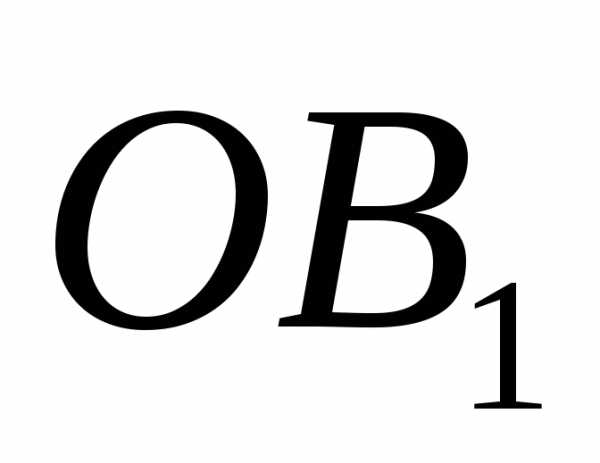 ,
,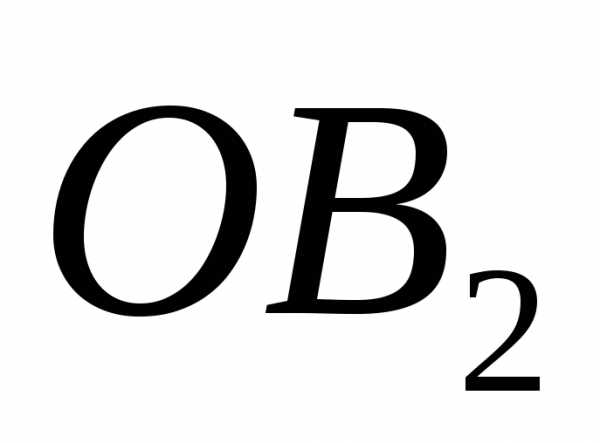 –полуоси
эллипса,
причём
–большие
полуоси;
–малые
полуоси.
–полуоси
эллипса,
причём
–большие
полуоси;
–малые
полуоси. 4. Когда фокусы
эллипса расположены на оси 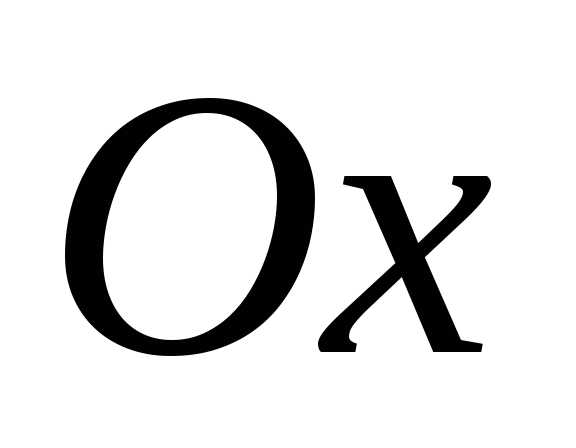 ,
имеем, что.
Когда фокусы располагаются на оси
,
имеем, что.
Когда фокусы располагаются на оси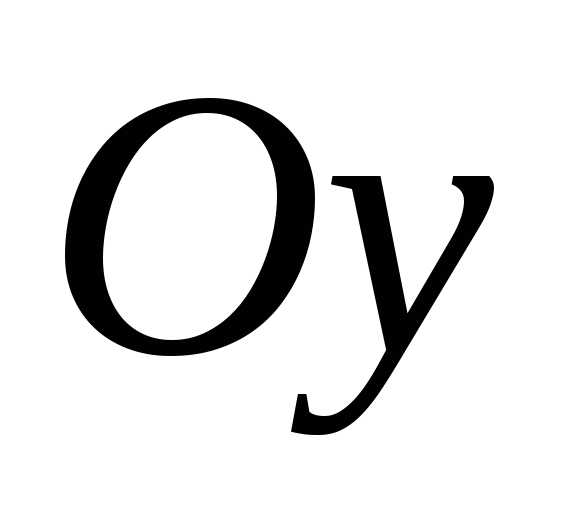 ,
, ,
тогда.
,
тогда.
Определение
9.2. Эксцентриситетом эллипса называется
число, равное отношению фокусного
расстояния к длине большей полуоси и
обозначается: 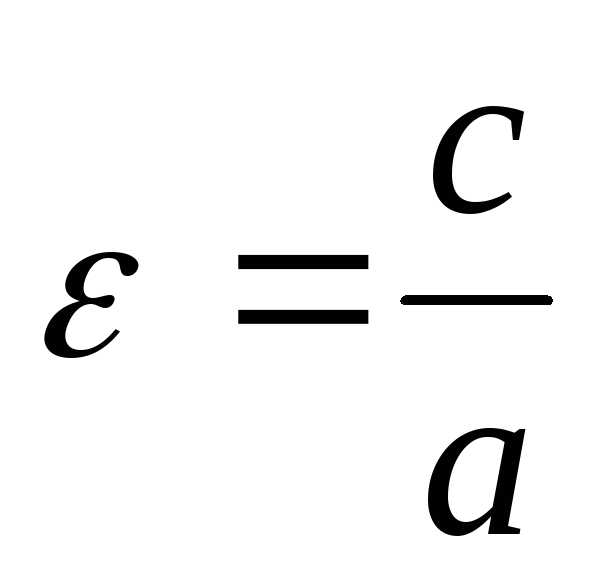 .
.
Так как .
От значения
эксцентриситета зависит форма эллипса.
Действительно, выразим отношение 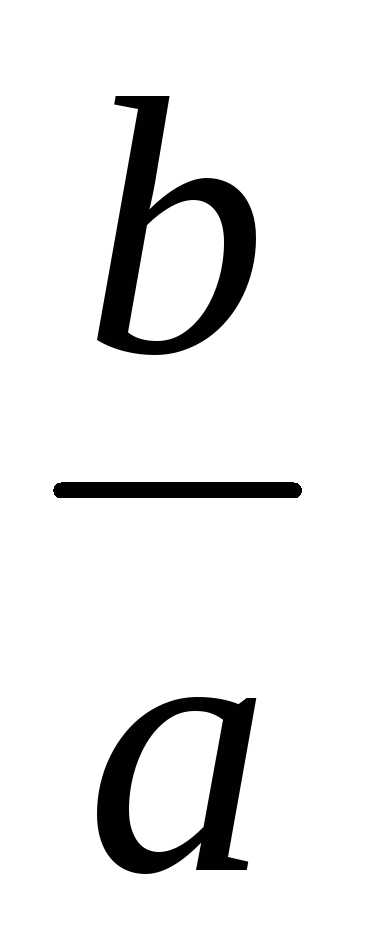
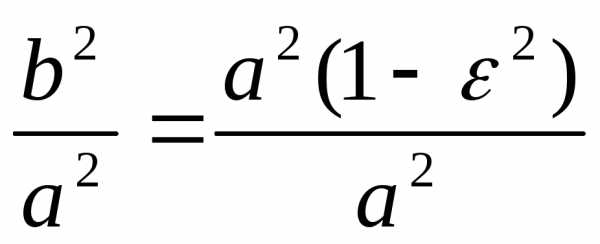

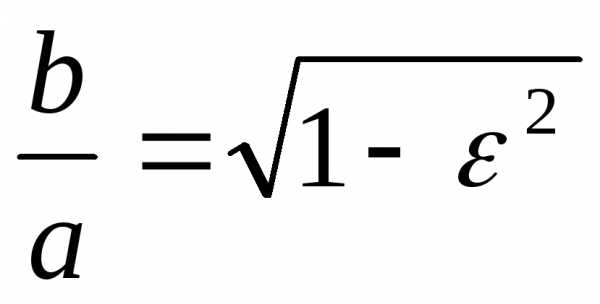 .
. Чем ближе
эксцентриситет к нулю, тем больше
и при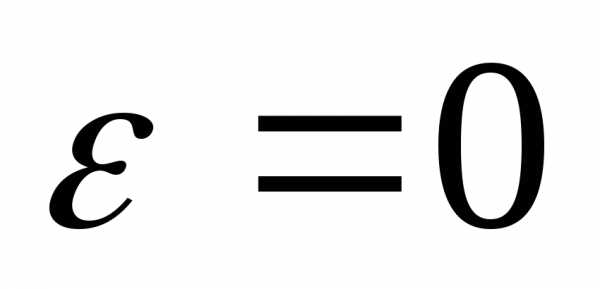
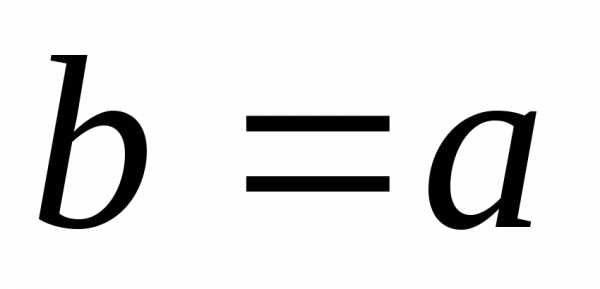 ,
эллипс похож на окружность. При увеличении
эксцентриситета эллипс вытягивается
вдоль оси
,
эллипс похож на окружность. При увеличении
эксцентриситета эллипс вытягивается
вдоль оси .
.
Определение
9.3. Фокальными
радиусами точки 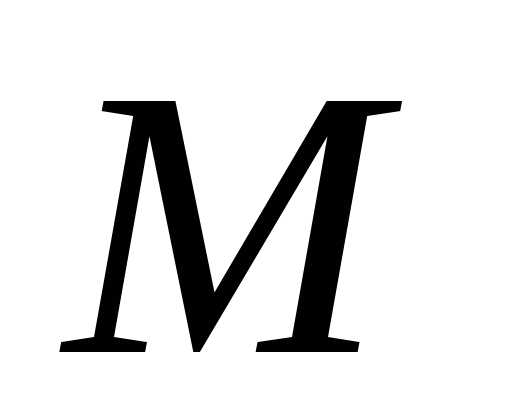 ,
принадлежащей эллипсу, называются
отрезки, соединяющие эту точку с фокусами
,
принадлежащей эллипсу, называются
отрезки, соединяющие эту точку с фокусами
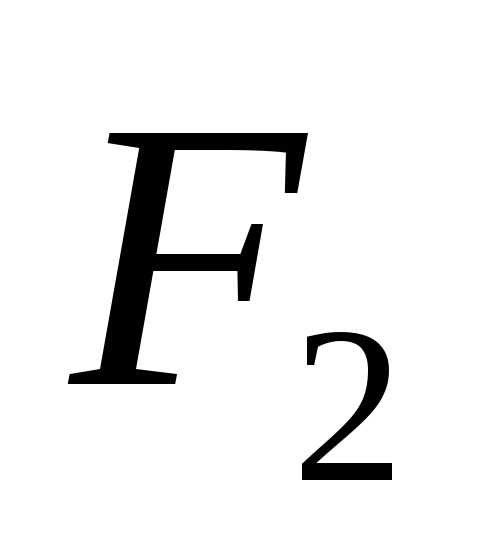 .
.Для каждой точки эллипса существует два фокальных радиуса.
Обозначаются: ,
.
Определение
9.4. Фокальным
параметром называется длина отрезка  ,
если он перпендикулярен оси
,
если он перпендикулярен оси и обозначается:
и обозначается:
Пусть
,
значит.
Т.к.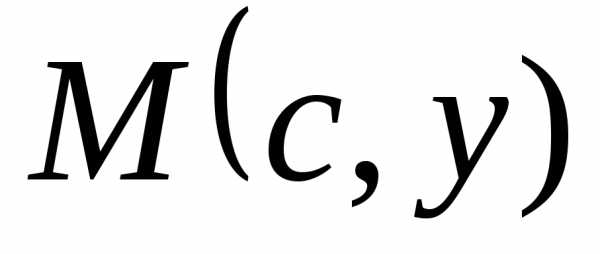 ,
то;
,
то;
Таким образом, фокальный параметр равен отношению квадрата малой полуоси эллипса к его большой полуоси.
Определение 9.5.
Так как эксцентриситет
эллипса меньше 1, то директрисы,
параллельные оси 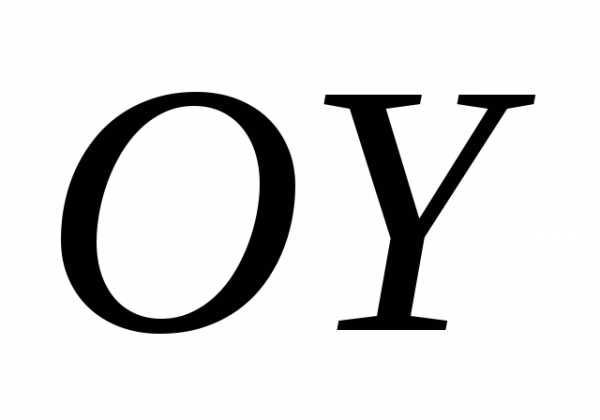 ,
находятся вне эллипса.
,
находятся вне эллипса.
Директриса и фокус считаются соответствующими, если они расположены по одну сторону от центра фигуры.
Геометрический смысл эксцентриситета эллипса
Теорема 9.6. Отношение расстояния от каждой точки 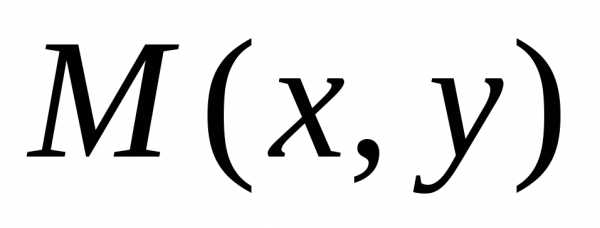 ,
принадлежащей эллипсу, до фокуса к
расстоянию от нее до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету.
,
принадлежащей эллипсу, до фокуса к
расстоянию от нее до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету.
Доказать:
Доказательство:
1. Выразим ;
2. Выразим
Найдем отношение:
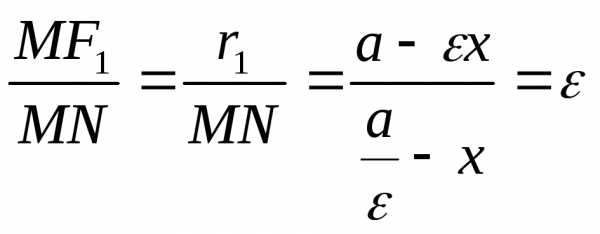
4. Аналогично
доказывается, что 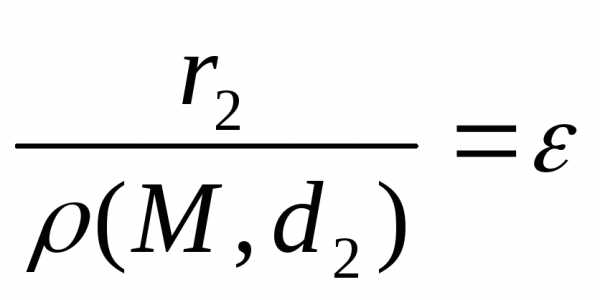
Параметрические уравнения эллипса.
1.
Пусть в прямоугольной системе координат
задан эллипс своим каноническим
уравнением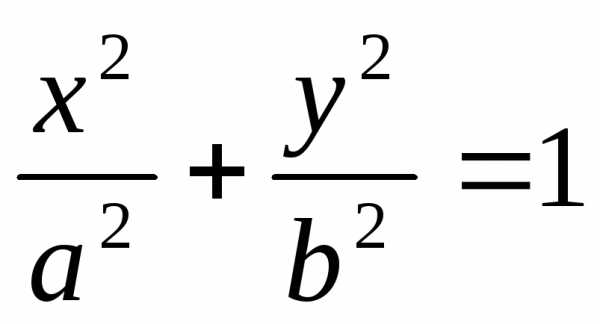 ,
причём
,
причём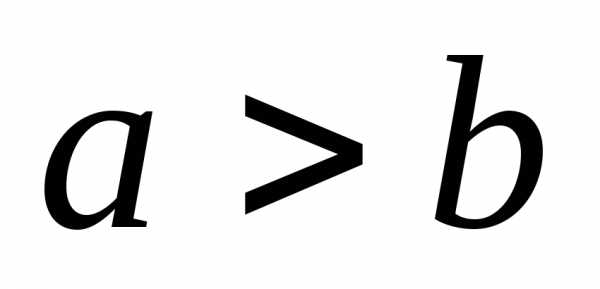 .
.
2. Начертим в этой системе координат
две окружности: и .
3. Рассмотрим — прямоугольные и
выразим координаты  ,
принадлежащей
,
принадлежащей
эллипсу:
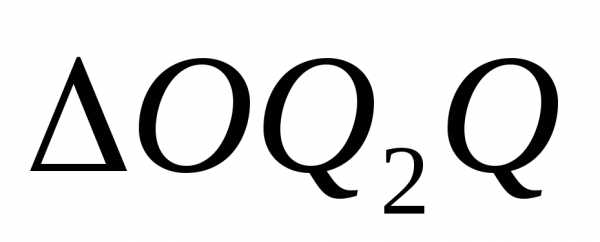 :
:
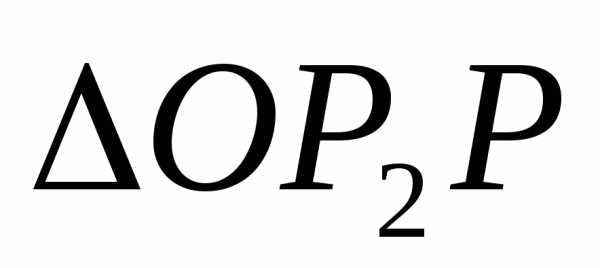 :
:
4. Подставим полученные выражения в уравнение эллипса:
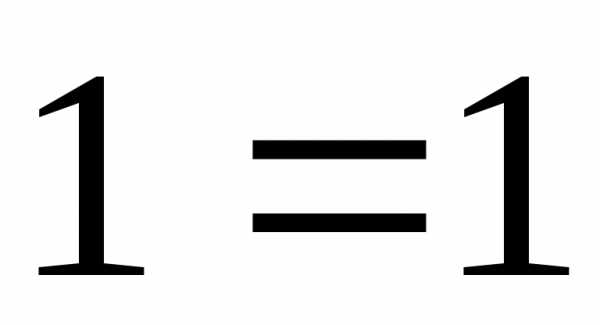 .
.
Таким образом, этот эллипс можно задать уравнениями вида:
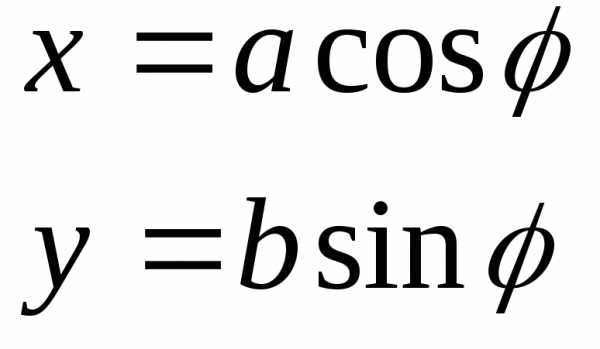 — параметрические
уравнения эллипса.
— параметрические
уравнения эллипса.
Способы построения эллипса
Способ №1 (в основу положено определение 9.1)
В чертежную доску
вбиваются два гвоздика  и
и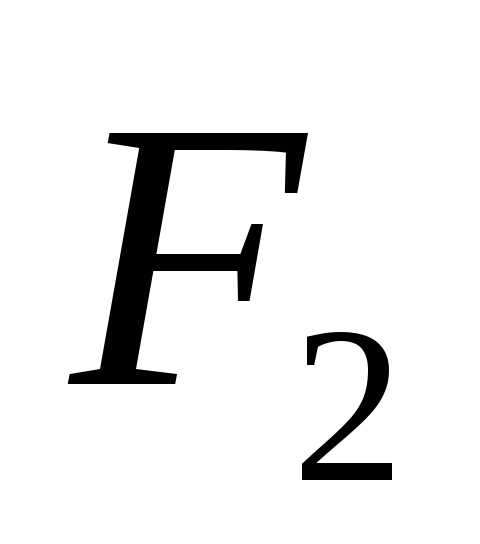 с расстоянием
с расстоянием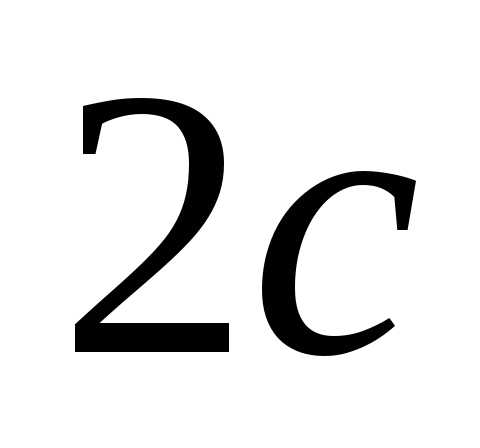 .
В них фиксируются концы нити длиной
.
В них фиксируются концы нити длиной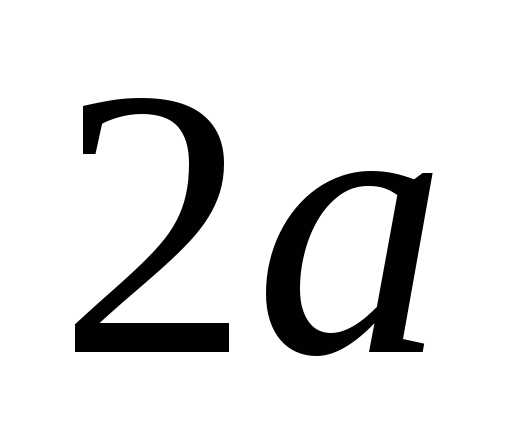 .
Натянув эту нить приложением к ней
острия карандаша, передвигают карандаш
так, чтобы нить все время была натянутой.
При этом карандаш вычертит эллипс, как
геометрическое место точек, сумма
расстояний каждой
из которых до двух данных
точек
.
Натянув эту нить приложением к ней
острия карандаша, передвигают карандаш
так, чтобы нить все время была натянутой.
При этом карандаш вычертит эллипс, как
геометрическое место точек, сумма
расстояний каждой
из которых до двух данных
точек  и
и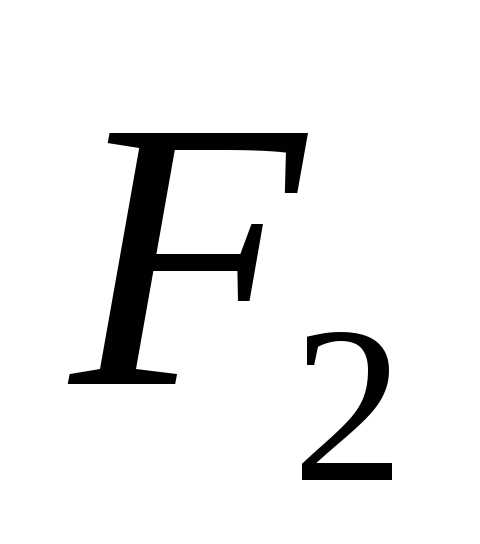 есть величина постоянная, равная
есть величина постоянная, равная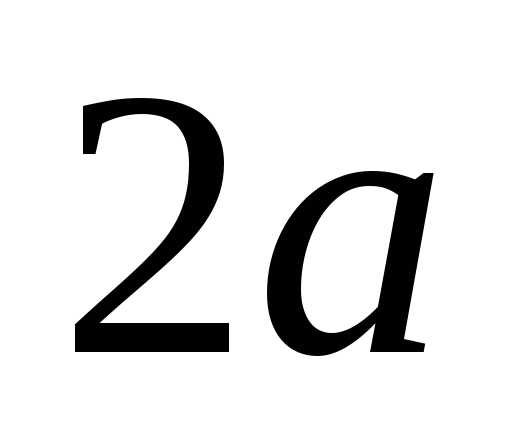
Способ №2 (в основу положено определение 9.1)
Так как эллипс
есть геометрическое место вершин
треугольников, имеющих общее основание 2с и данную сумму двух других сторон 2а, то необходимо
построить множество треугольников с
общей вершиной по стороне и сумме двух
других сторон, при этом всякий раз
задавая угол  .
.
Способ №3 (в
основу положено свойство симметричности
эллипса): построить
по точкам часть эллипса в первой четверти,
используя уравнение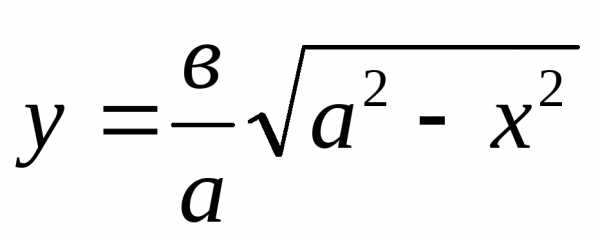 ,
а затем использовать симметричность
линии относительно осей координат и
начала координат.
,
а затем использовать симметричность
линии относительно осей координат и
начала координат.
Способ №4 (по заданным полуосям):
Построить две окружности с центром в начале координат и радиусами, равными полуосям эллипса: и ;
Проведем из начала координат луч, пересекающий каждую окружность соответственно в точках
 ,
, ;
;Через точку
 проведем прямую
проведем прямую ,
параллельно оси
,
параллельно оси ,
через точку
,
через точку — прямую
— прямую ,
параллельную оси
,
параллельную оси ;
;Точка пересечения прямых
 и
и –
точка эллипса
–
точка эллипса ;
;Аналогичные действия проводим при построении следующего луча, проходящего через начало координат.
Эллипс как результат сжатия окружности к одному из ее диаметров
Способ №3 построения
доказывает одно важное наглядное
свойство эллипса. Действительно,  — произвольная точка эллипса, а
— произвольная точка эллипса, а есть
точка большой окружности, имеющая ту
же абсциссу, т.е. лежащая на той же
вертикальной прямой, что и
есть
точка большой окружности, имеющая ту
же абсциссу, т.е. лежащая на той же
вертикальной прямой, что и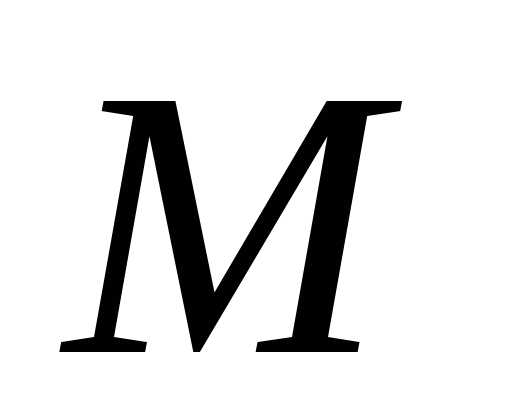 .
Тогда
.
Тогда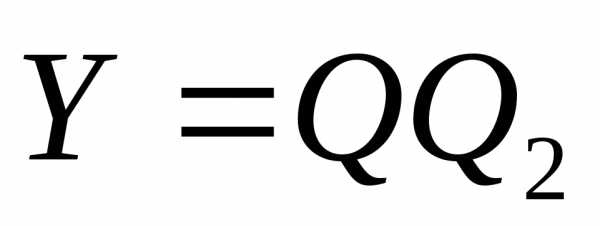 ,.
,.
Из подобия
:или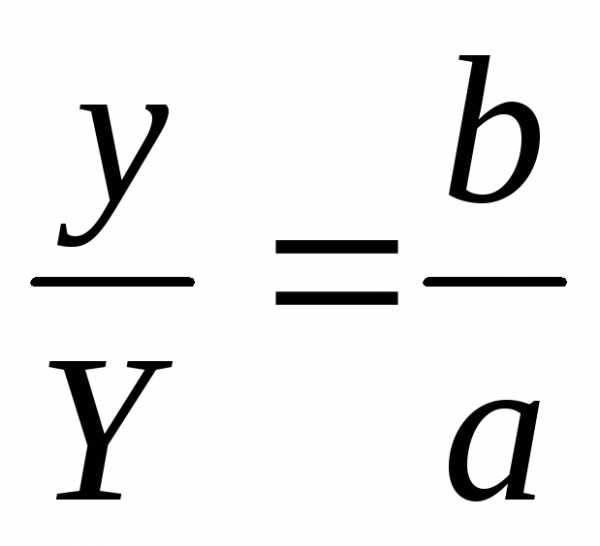
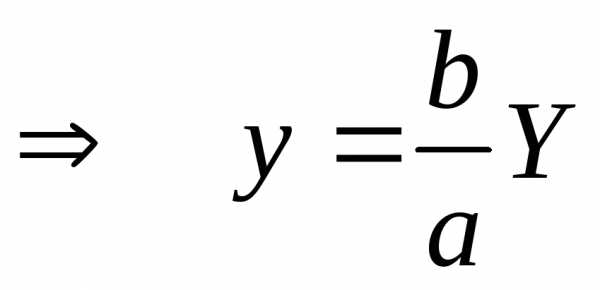
Таким образом,
эллипс получился из «большой» окружности
преобразованием плоскости: каждая
точка  большой окружности переходит в точку
большой окружности переходит в точку эллипса
с той же абсциссой, но с ординатой,
полученной из ординаты точки
эллипса
с той же абсциссой, но с ординатой,
полученной из ординаты точки умножением на число
умножением на число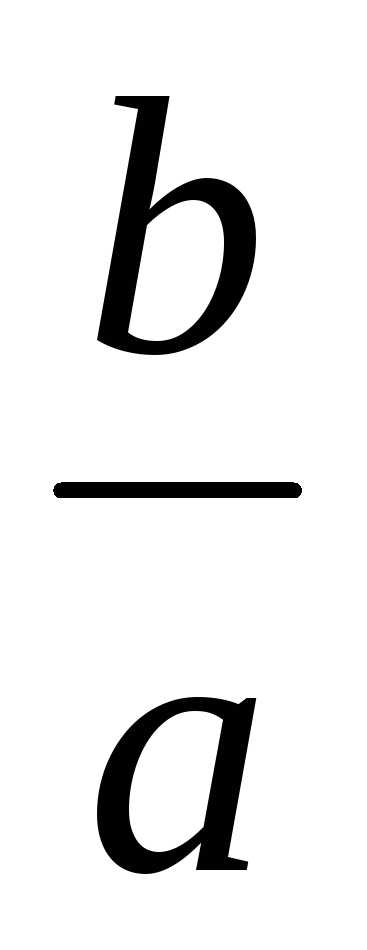 .
.
Такое преобразование
называется равномерным сжатием плоскости
к оси абсцисс в отношении 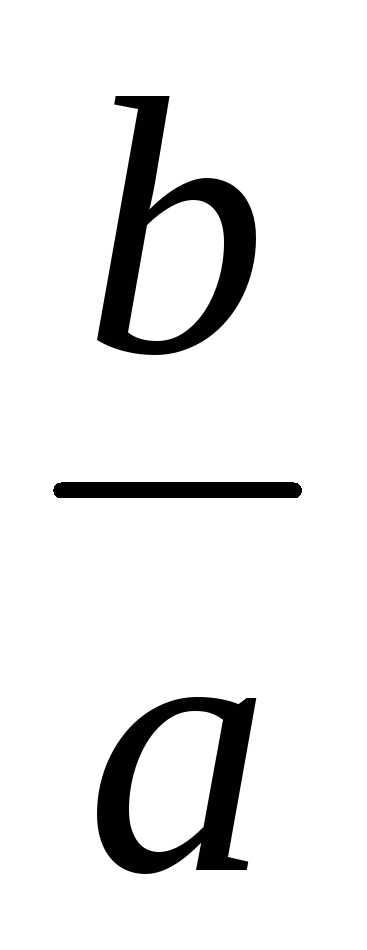 .
.
Таким образом, обосновывается следующее утверждение: всякий эллипс получается сжатием окружности к одному из ее диаметров.
studfiles.net
Конспект лекций по дисциплине «Высшая математика», страница 17
Отрезок B1B2 = 2b называется (при а > b) малой осью эллипса; – малая полуось эллипса.
3. ; ; и существует, если или , (от А1 до А2).
; и существует, если (от В1 до В2).
Кривая расположена в прямоугольнике А1В1А2В2.
4. Степень вытянутости эллипса определяет параметр – эксцентриситет:
или , .
Если a = b, то имеем окружность с центром в т.О(0;0) и радиуса а. В этом случае .
Если , то имеем отрезок А1А2 и . Эллипс (при ) получен равномерным сжатием окружности сверху – снизу.
Аналогично можно рассмотреть случай, когда фокусы F1F2 расположены на оси ОУ ().
Пример: построение эллипса по каноническому уравнению и отыскание его параметров…
б) Смещенный эллипс
– уравнение смещенного эллипса. Центр расположен в т. С(α;β).
При построении смещенного эллипса применяется преобразование системы координат – параллельный перенос.
ХОУ – старая система координат;
т.О(0;0) – начало координат;
Х’СУ’ – новая система координат; т.С(α,β) – ее начало координат.
, , масштабная единица одна и та же.
Возьмем на плоскости произвольно т.М. В системе ХОУ ее координаты х,у; в системе Х’СУ’ – х’,у’ , причем ; . Отсюда
Сделаем в уравнении смещенного эллипса замену переменной по формулам , получим каноническое уравнение эллипса .
Строим эллипс по его каноническому уравнению в системе Х’СУ’.
Пример: построение эллипса, заданного в смещенном виде: .
3.3 Гипербола – ГМТ плоскости, модуль разности расстояний которых до двух фиксированных точек плоскости – фокусов F1, F2 – постоянен и равен числу 2а.
а) Каноническое уравнение
Выбор системы координат: ось ОХ проходит через фокусы F1, F2; ось ОУ – срединный перпендикуляр к отрезку F1F2, называемому фокусным расстоянием F1F2 = 2с.
vunivere.ru
Лекция 15. Эллипс
Лекции по алгебре и геометрии. Семестр 1.
Лекция 15. Эллипс.
Краткое содержание: определение эллипса, основная терминология, каноническая для эллипса система координат и каноническое уравнение эллипса, параметрические уравнения эллипса, эллипс как результат сжатия окружности, касательная к эллипсу, зеркальное свойство эллипса, директрисы и фокальный параметр эллипса, второе определение эллипса.
Глава 15. Эллипс.
п.1. Основные определения.
Определение. Эллипсом называется ГМТ плоскости сумма расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.
рис.1.
Определение. Расстояние от произвольной точки М плоскости до фокуса эллипса называется фокальным радиусом точки М.
Обозначения: 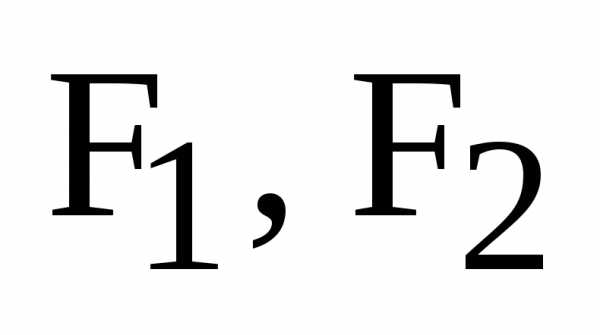 – фокусы эллипса,
– фокусы эллипса,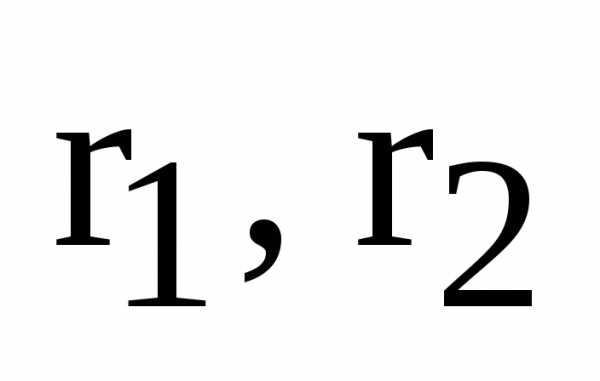 – фокальные радиусы точки М.
– фокальные радиусы точки М.
По
определению эллипса, точка М является
точкой эллипса тогда и только тогда,
когда 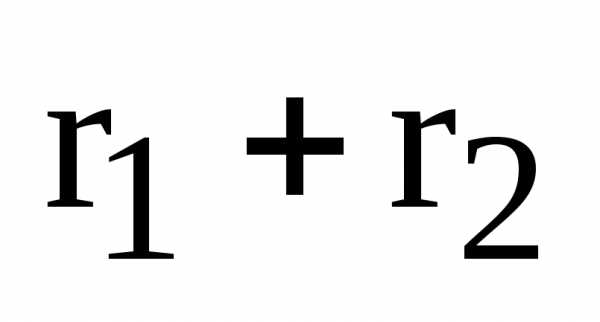 – постоянная величина. Эту постоянную
принято обозначать 2а:
– постоянная величина. Эту постоянную
принято обозначать 2а:
. (1)
Заметим,
что 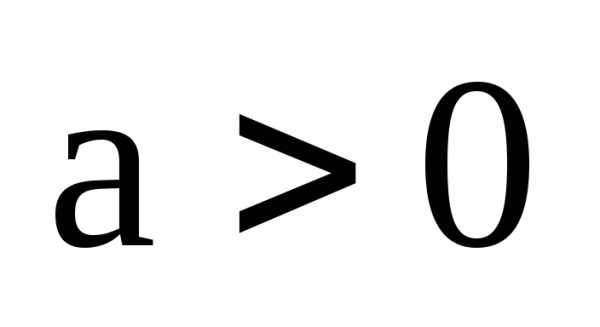 .
.
По определению эллипса, его фокусы есть фиксированные точки, поэтому расстояние между ними есть также величина постоянная для данного эллипса.
Определение. Расстояние между фокусами эллипса называется фокусным расстоянием.
Обозначение: 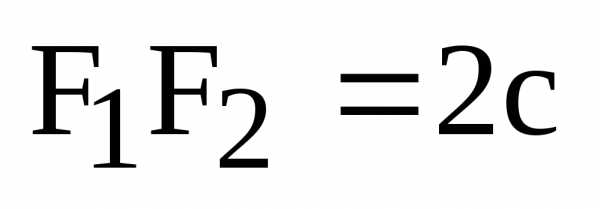 .
.
Из
треугольника  следует, что,
т.е.
следует, что,
т.е.
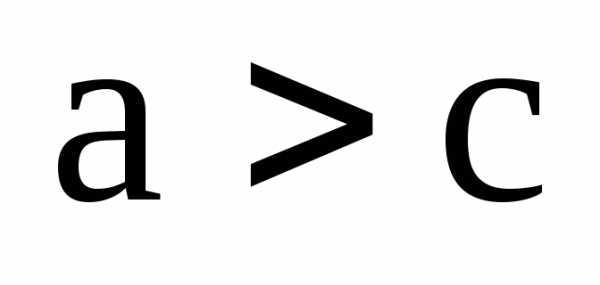 .
.
Обозначим
через bчисло равное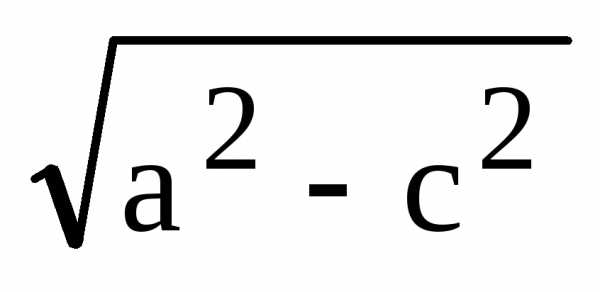 ,
т.е.
,
т.е.
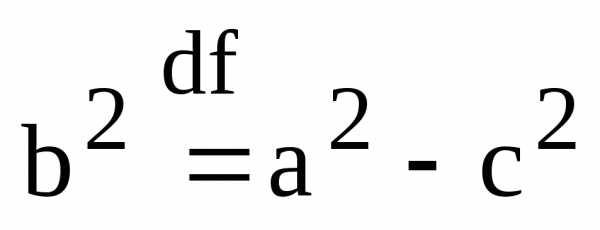 .
(2)
.
(2)
Определение. Отношение
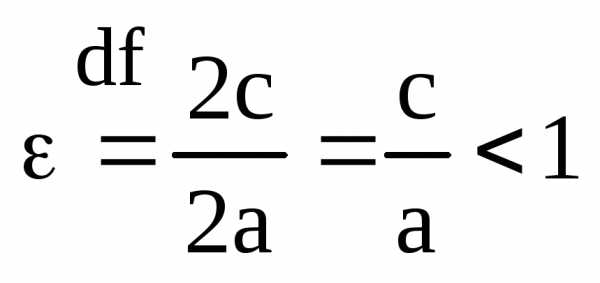 (3)
(3)
называется эксцентриситетом эллипса.
Введем на данной плоскости систему координат, которую мы будем называть канонической для эллипса.
Определение. Ось, на которой лежат фокусы эллипса, называется фокальной осью.
Построим каноническую для эллипса ПДСК, см. рис.2.
В
качестве оси абсцисс выбираем фокальную
ось, а ось ординат проводим через середину
отрезка  перпендикулярно фокальной оси.
перпендикулярно фокальной оси.
рис.2.
Тогда
фокусы имеют координаты 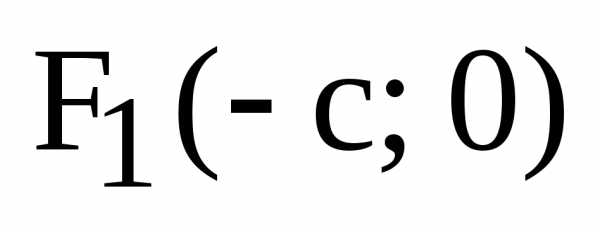 ,
,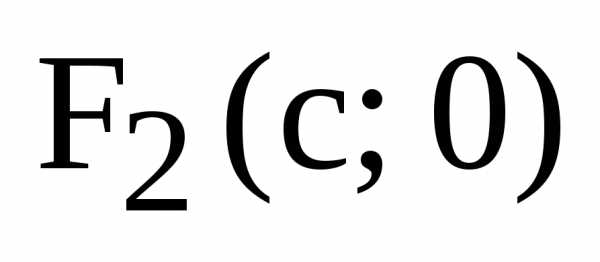 .
.
п.2. Каноническое уравнение эллипса.
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
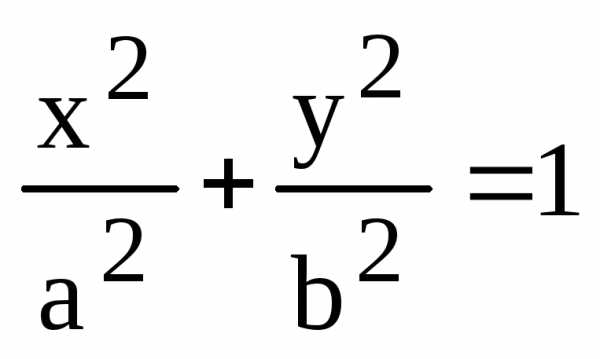 .
(4)
.
(4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
.
Воспользуемся формулой расстояния между двумя точками на координатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
, , откуда получаем:
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
.
Сокращая, получаем:
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
.
Возводим в квадрат
.
Раскрываем
скобки и сокращаем на 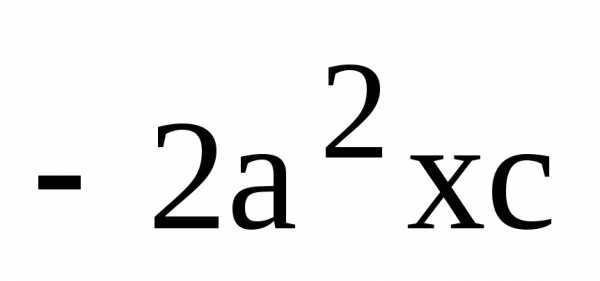 :
:
,
откуда получаем:
.
Используя равенство (2), получаем:
.
Разделив
последнее равенство на 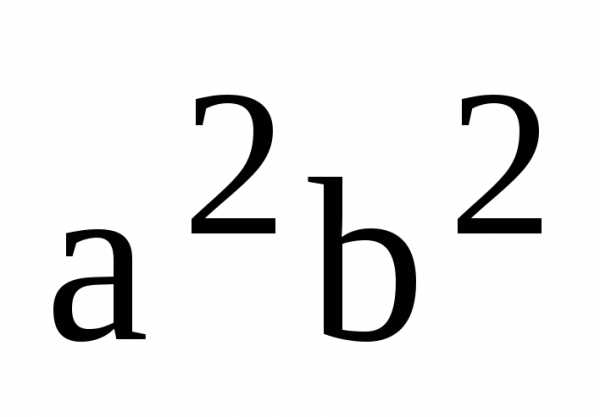 ,
получаем равенство (4), ч.т.д.
,
получаем равенство (4), ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
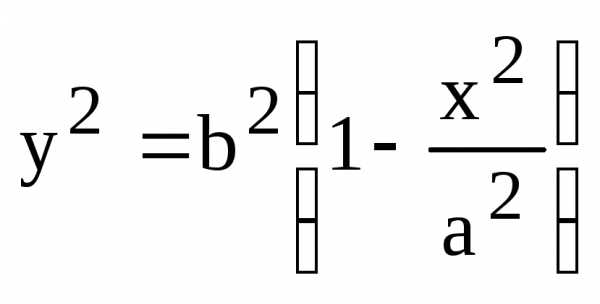 .
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
.
Здесь мы воспользовались равенством (2) и (3).
Таким образом, . Аналогично,.
Теперь заметим, что из равенства (4) следует, что
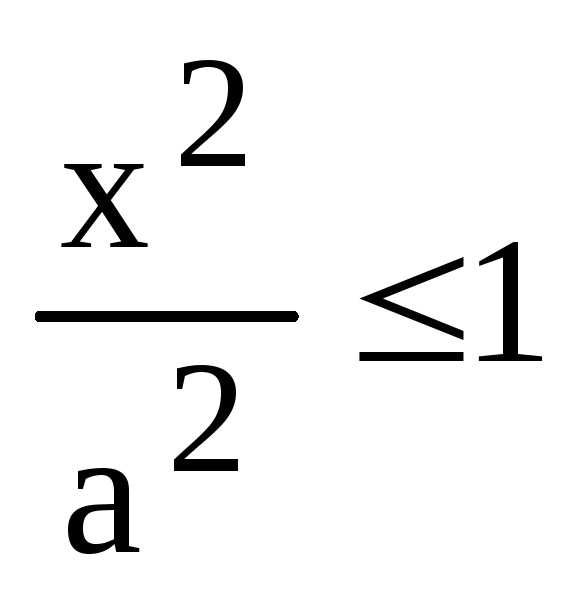 или
или 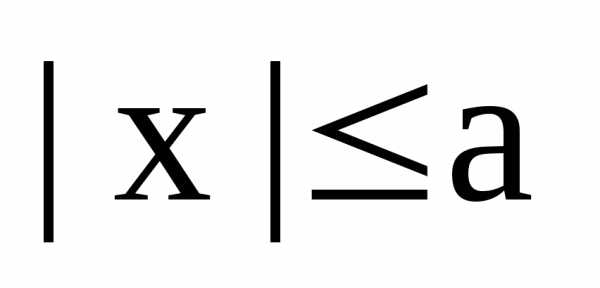 и т.к.
и т.к.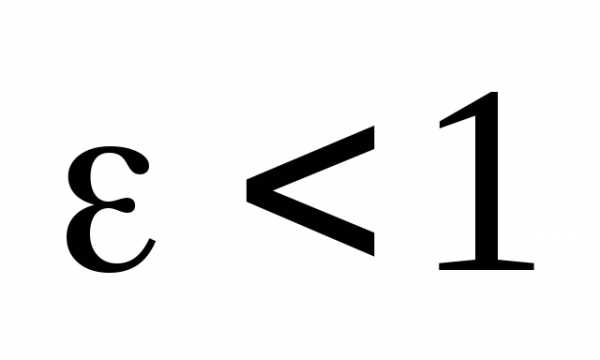 ,
то отсюда следует неравенство:
,
то отсюда следует неравенство:
.
Отсюда, в свою очередь, следует, что
или и
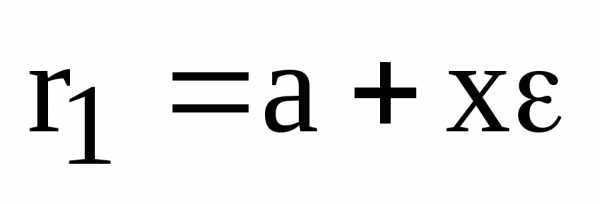 ,
.
(5)
,
.
(5)
Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.
Теорема доказана.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координат называется центром эллипса.
п.3. Свойства эллипса.
Теорема. (Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике
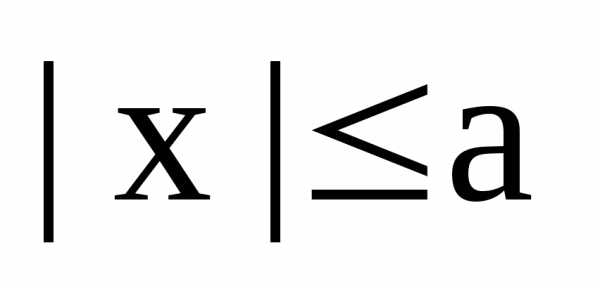 ,
, 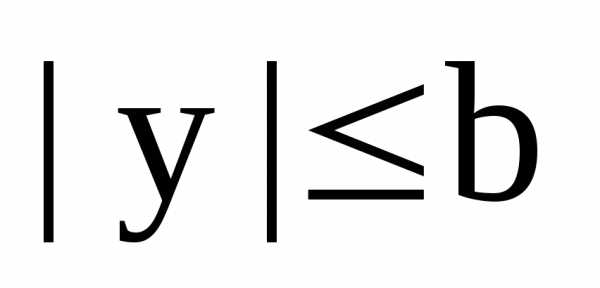 .
.
2. Точки лежат на
эллипсе.
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координаты удовлетворяют уравнению (4). Но тогда координаты точек также удовлетворяют уравнению (4), и, следовательно, являются точками эллипса, откуда и следуют утверждения теоремы.
Теорема доказана.
рис.3.
Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.
Определение. Величина 2bназывается малой осью эллипса, величинаbназывается малой полуосью эллипса.
Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.
Замечание.
Эллипс можно построить следующим
образом. На плоскости в фокусы «забиваем
по гвоздю» и закрепляем на них нить
длиной 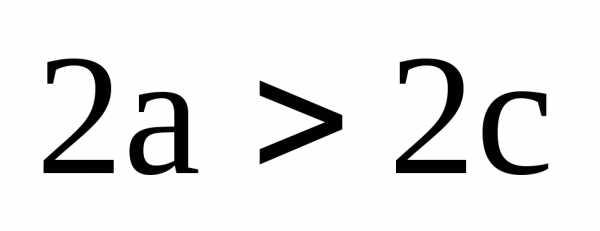 .
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
.
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
Из определения эксцентриситета следует, что
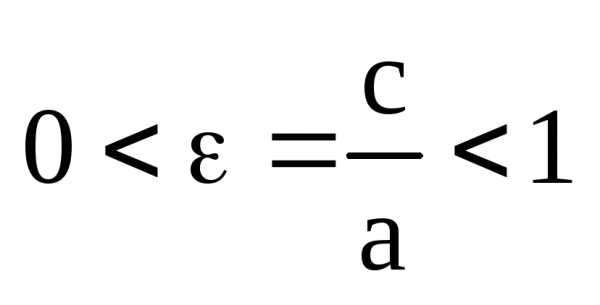
Зафиксируем число
а и устремим число с к нулю. Тогда при  ,
, и
и .
В пределе мы получаем
.
В пределе мы получаем
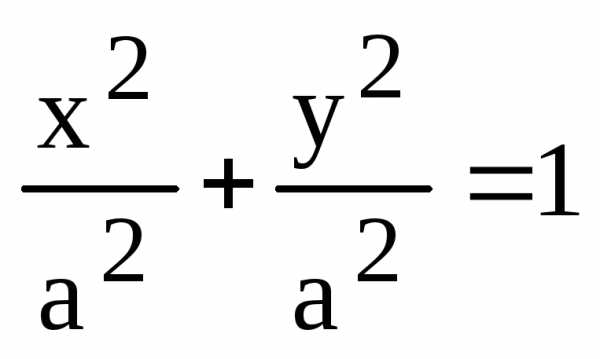 или
– уравнение окружности.
или
– уравнение окружности.
Таким образом, мы можем считать, что окружность есть эллипс с нулевым эксцентриситетом.
Устремим теперь 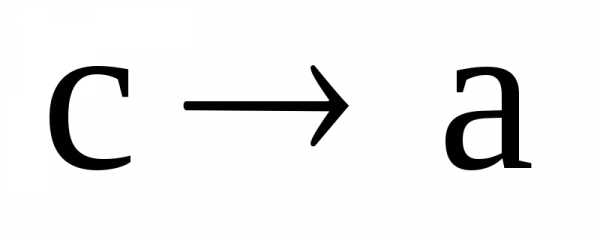 .
Тогда
.
Тогда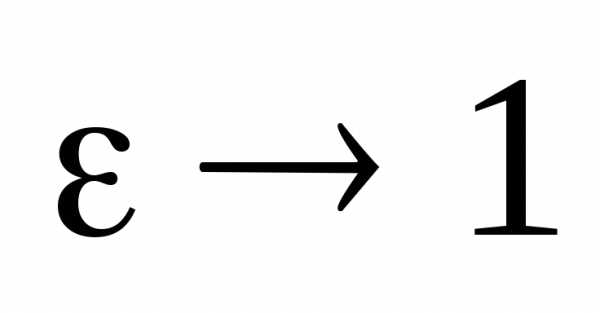 ,
, и мы видим, что в пределе эллипс вырождается
в отрезок прямой
и мы видим, что в пределе эллипс вырождается
в отрезок прямой в обозначениях рисунка 3.
в обозначениях рисунка 3.
п.4. Параметрические уравнения эллипса.
Теорема.
Пусть 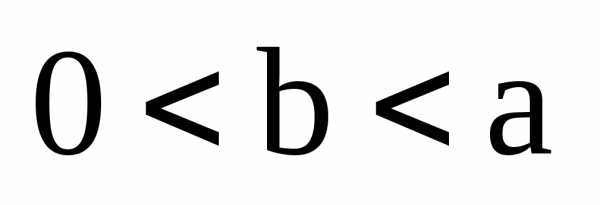 – произвольные действительные числа.
Тогда система уравнения
– произвольные действительные числа.
Тогда система уравнения
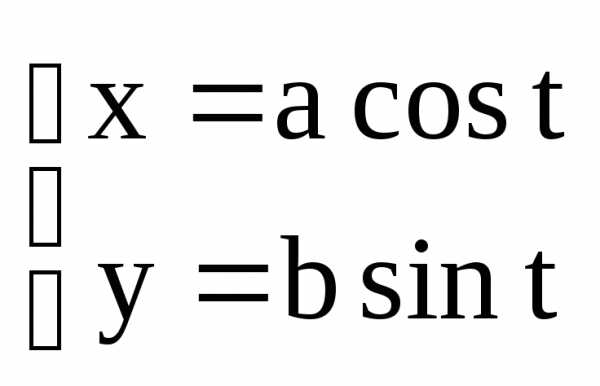 ,
, 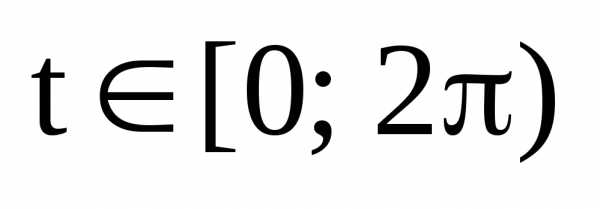 (6)
(6)
является параметрическими уравнениями эллипса в канонических для эллипса системе координат.
Доказательство. Достаточно доказать, что система уравнений (6) равносильна уравнению (4), т.е. они имеют одно и то же множество решений.
1) Пусть (х, у) – произвольное решение системы (6). Разделим первое уравнение на а, второе – на b, возводим оба уравнения в квадрат и складываем:
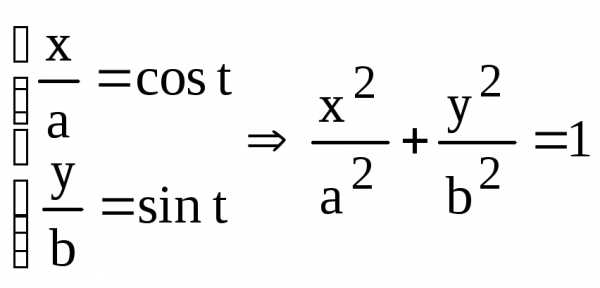 .
.
Т.е. любое решение (х, у) системы (6) удовлетворяет уравнению (4).
2) Обратно, пусть пара (х, у) является решением уравнения (4), т.е.
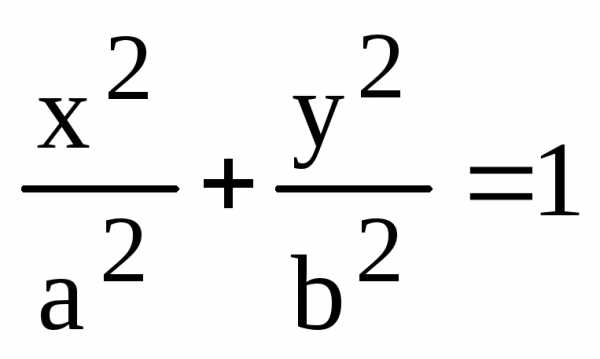 .
.
Из
этого равенства следует, что точка с
координатами 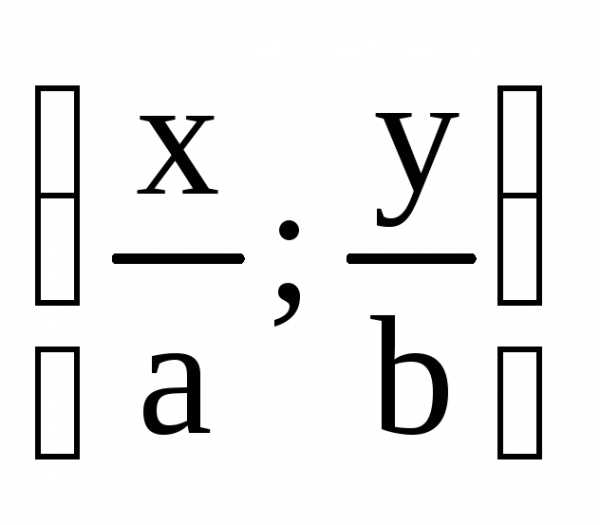 лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол
лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол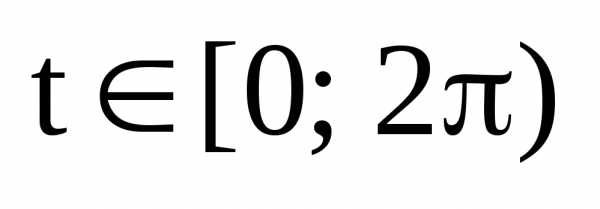 :
:
рис.4.
Из определения синуса и косинуса сразу же следует, что
 ,
, 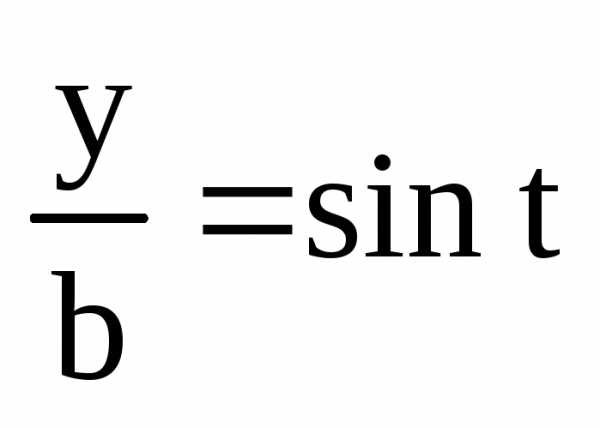 ,
где
,
где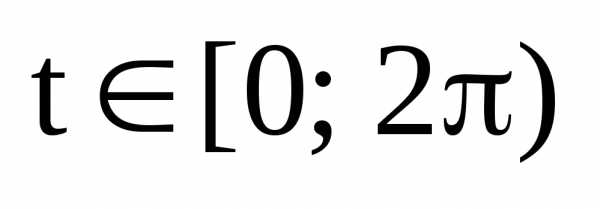 ,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.
,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.
Теорема доказана.
Замечание. Эллипс можно получить в результате равномерного «сжатия» окружности радиуса а к оси абсцисс.
Пусть
– уравнение окружности с центром в
начале координат. «Сжатие» окружности
к оси абсцисс есть ни что иное, как
преобразование координатной плоскости,
осуществляемое по следующему правилу.
Каждой точке М(х, у) поставим в соответствие
точку этой же плоскости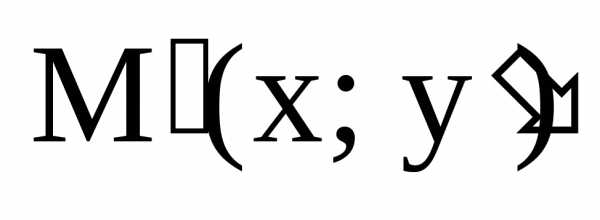 ,
где
,
где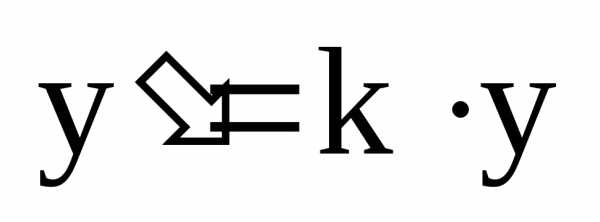 ,
,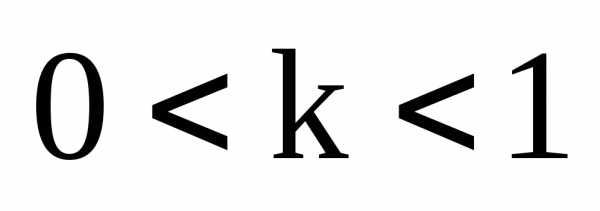 – коэффициент «сжатия».
– коэффициент «сжатия».
рис.5.
При этом преобразовании каждая точка окружности «переходит» в другую точку плоскости, имеющую ту же самую абсциссу, но меньшую ординату. Выразим старую ординату точки через новую:
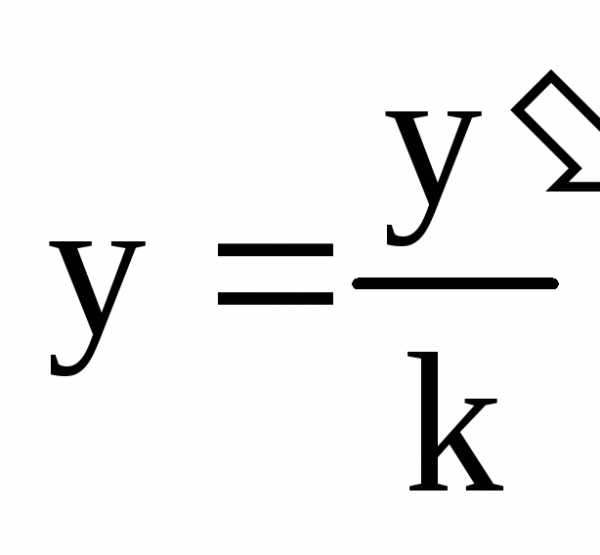
и подставим в уравнение окружности:
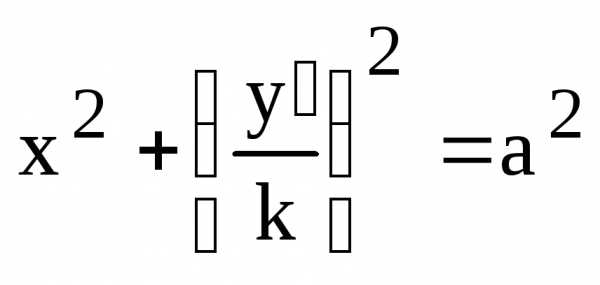 .
.
Отсюда получаем:
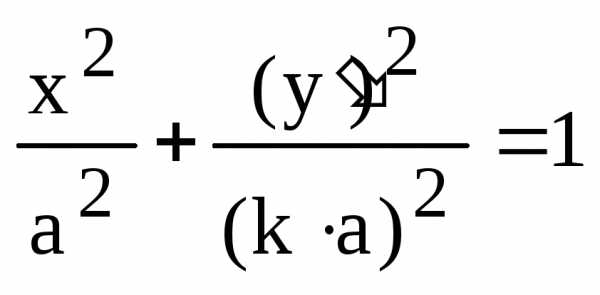 .
(7)
.
(7)
Отсюда
следует, что если до преобразования
«сжатия» точка М(х, у) лежала на
окружности, т.е. ее координаты удовлетворяли
уравнению окружности, то после
преображования «сжатия» эта точка
«перешла» в точку 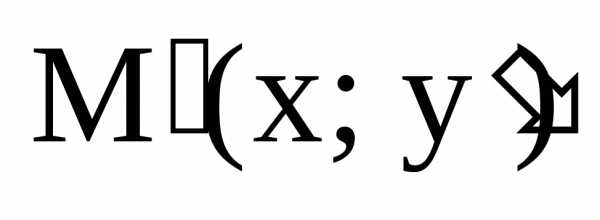 ,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосьюb, то нужно взять
коэффициент сжатия
,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосьюb, то нужно взять
коэффициент сжатия
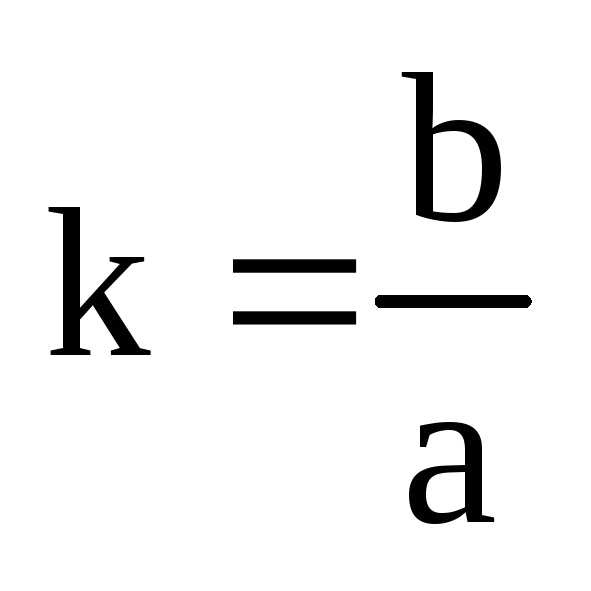 .
.
рис.6.
п.5. Касательная к эллипсу.
Теорема. Пусть – произвольная точка эллипса
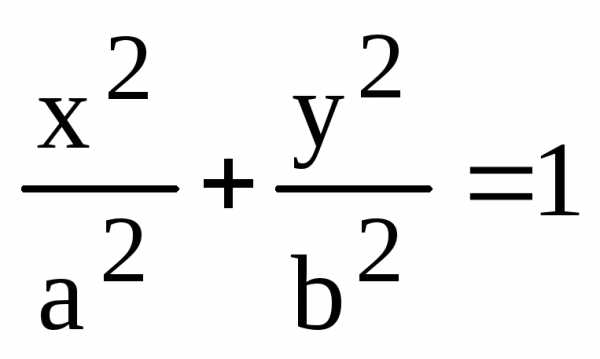 .
.
Тогда уравнение касательной к этому эллипсу в точке имеет вид:
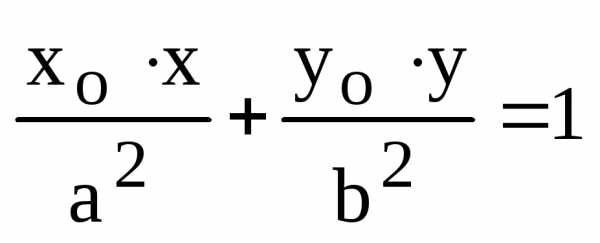 .
(8)
.
(8)
Доказательство. Достаточно рассмотреть случай, когда точка касания лежит в первой или второй четверти координатной плоскости: . Уравнение эллипса в верхней полуплоскости имеет вид:
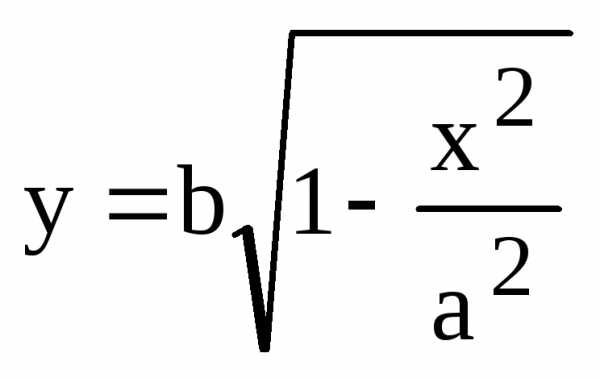 .
(9)
.
(9)
Воспользуемся
уравнением касательной к графику функции 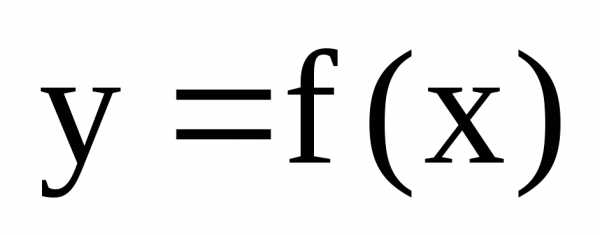 в точке:
в точке:
, (10)
где  – значение производной данной функции
в точке
– значение производной данной функции
в точке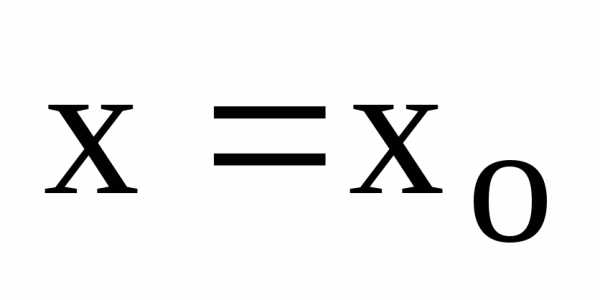 .
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания:
.
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания:
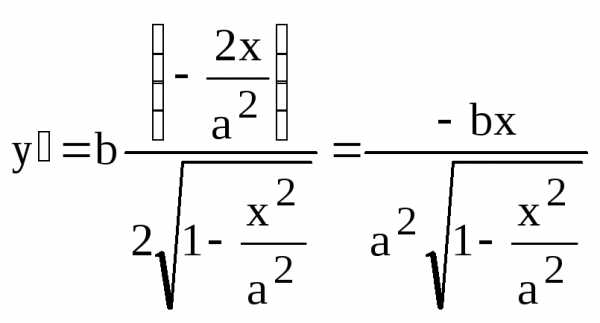 ,
,
. Здесь мы воспользовались тем, что точка касания является точкой эллипса и поэтому ее координаты удовлетворяют уравнению эллипса (9), т.е.
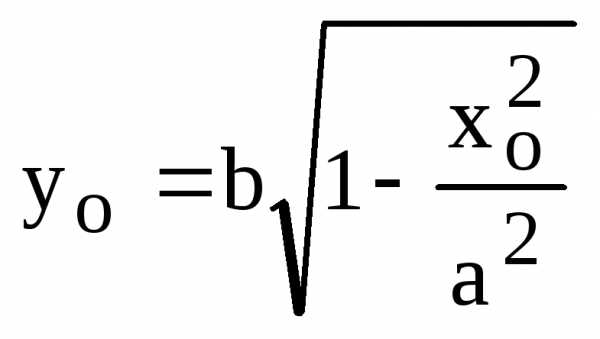 .
.
Подставляем найденное значение производной в уравнение касательной (10):
,
откуда получаем:
или
.
Отсюда следует:
.
Разделим
это равенство на 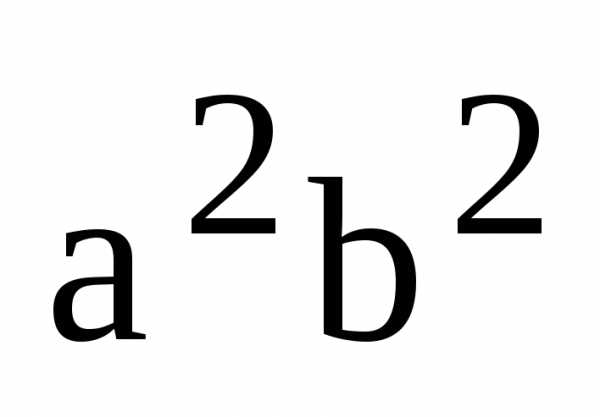 :
:
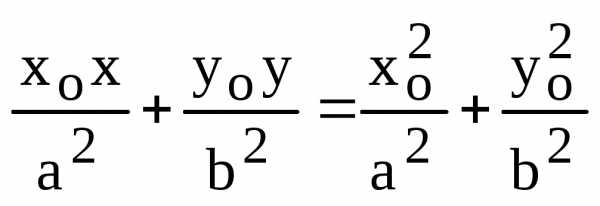 .
.
Осталось
заметить, что 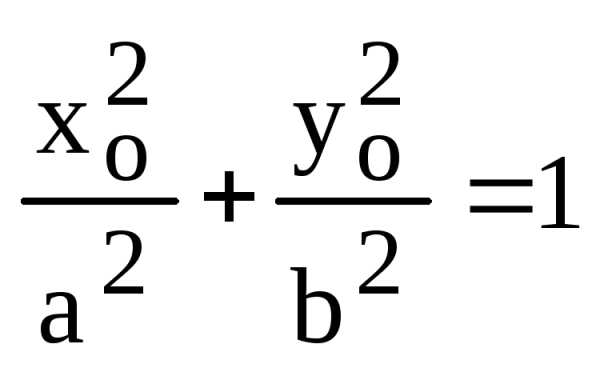 ,
т.к. точкапринадлежит эллипсу и ее координаты
удовлетворяют его уравнению.
,
т.к. точкапринадлежит эллипсу и ее координаты
удовлетворяют его уравнению.
Аналогично доказывается уравнение касательной (8) в точке касания, лежащей в третьей или четвертой четверти координатной плоскости.
И,
наконец, легко убеждаемся, что уравнение
(8) дает уравнение касательной в точках 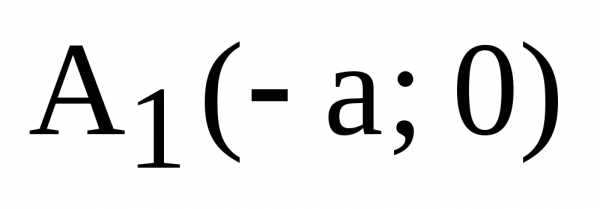 ,
,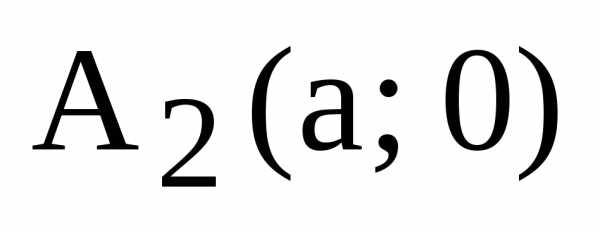 :
:
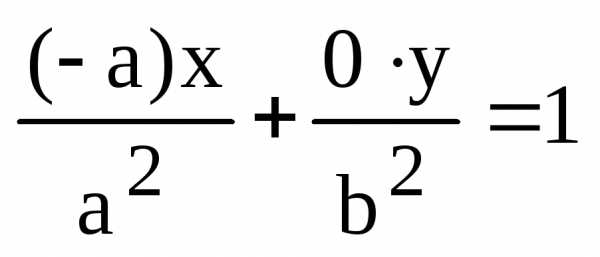 или
или 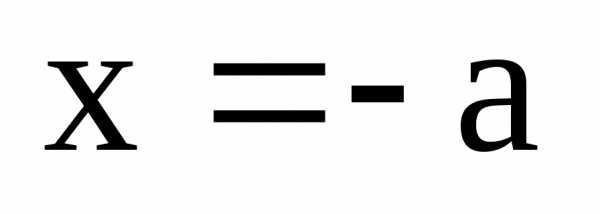 ,
и
,
и или
или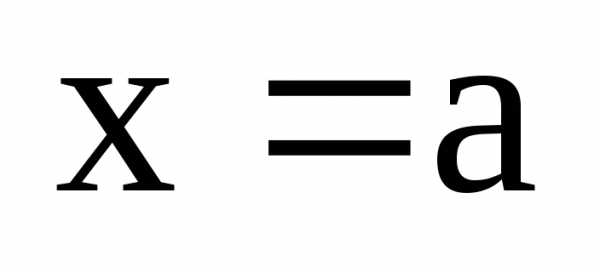 .
.
Теорема доказана.
п.6. Зеркальное свойство эллипса.
Теорема. Касательная к эллипсу имеет равные углы с фокальными радиусами точки касания.
рис.7.
Пусть
– точка касания,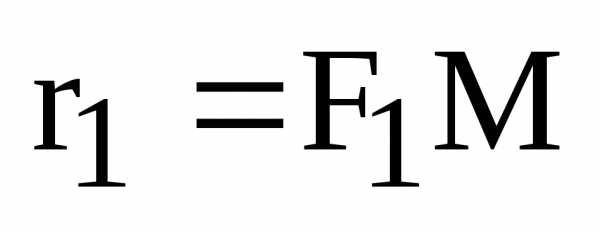 ,
,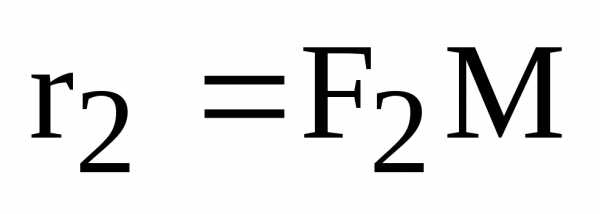 – фокальные радиусы точки касания, Р иQ– проекции фокусов на
касательную, проведенную к эллипсу в
точке.
– фокальные радиусы точки касания, Р иQ– проекции фокусов на
касательную, проведенную к эллипсу в
точке.
Теорема утверждает, что
. (11)
Это равенство можно интерпретировать как равенство углов падения и отражения луча света от эллипса, выпущенного из его фокуса. Это свойство получило название зеркального свойства эллипса:
Луч света, выпущенный из фокуса эллипса, после отражения от зеркала эллипса проходит через другой фокус эллипса.
Доказательство
теоремы. Для доказательства равенства
углов (11) мы докажем подобие треугольников 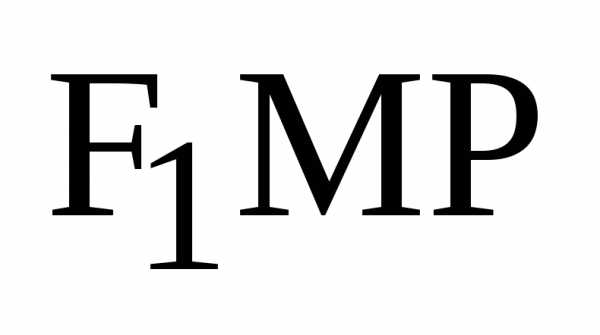 и
и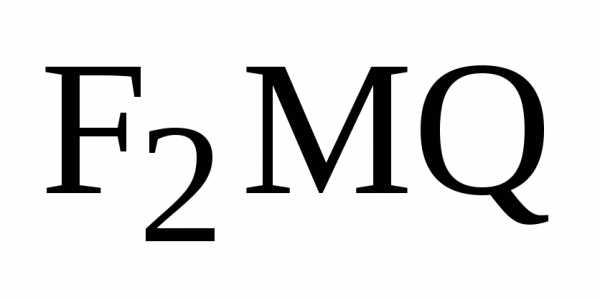 ,
в которых стороны
,
в которых стороны и
и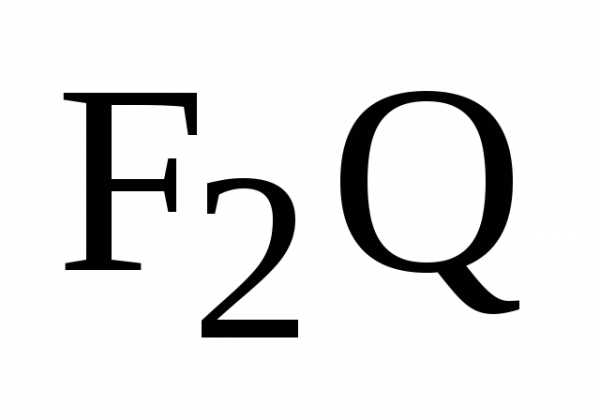 будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство
будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство
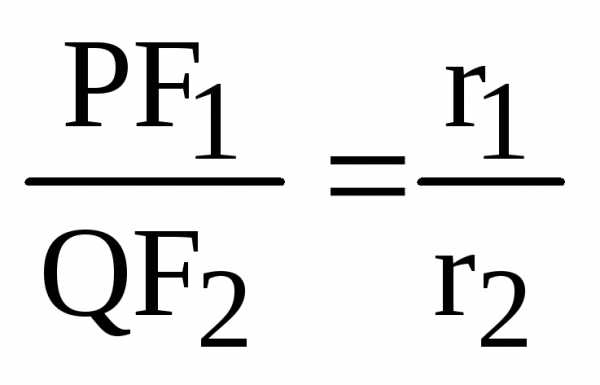 .
(12)
.
(12)
Так
как по построению
– расстояние от фокуса до касательнойL(см.
рис.7),.
Воспользуемся формулой расстояния от
точки до прямой на плоскости:
до касательнойL(см.
рис.7),.
Воспользуемся формулой расстояния от
точки до прямой на плоскости:
.
Так как уравнение касательной к эллипсу в точке имеет вид
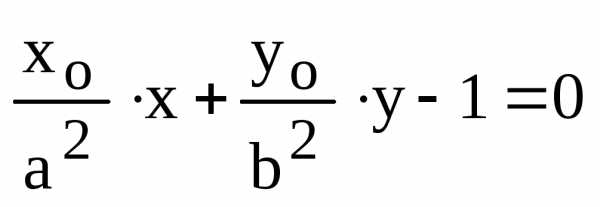 ,
,
то
,
и
.
Здесь мы воспользовались формулами (5) для фокальных радиусов точки эллипса.
Теорема доказана.
Второе доказательство теоремы:
,
,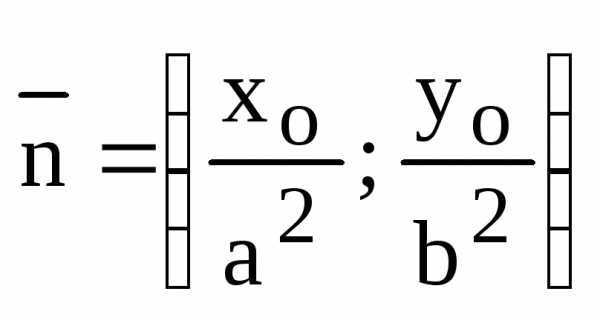 – нормальный вектор касательнойL.
– нормальный вектор касательнойL.
.
Отсюда, 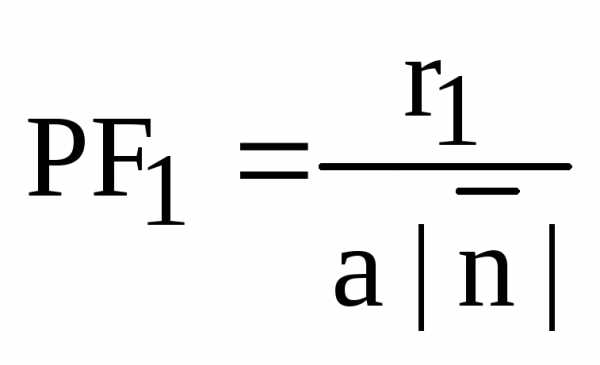 .
.
Аналогично
находим, 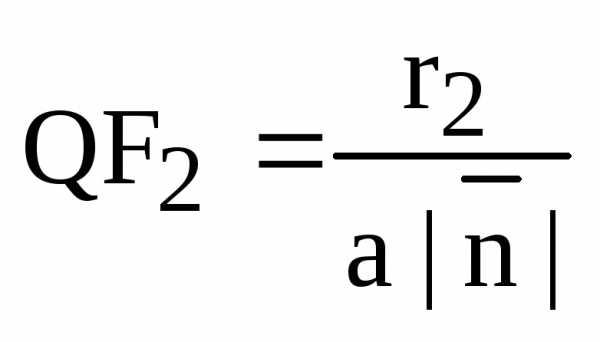 и
и ,
ч.т.д.
,
ч.т.д.
п.7. Директрисы эллипса.
Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
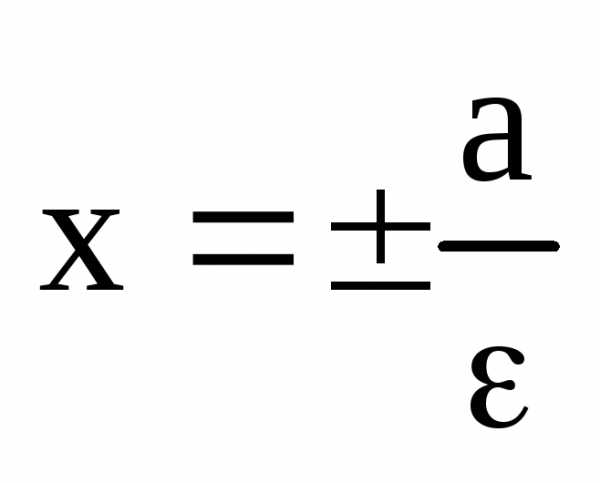 или
или 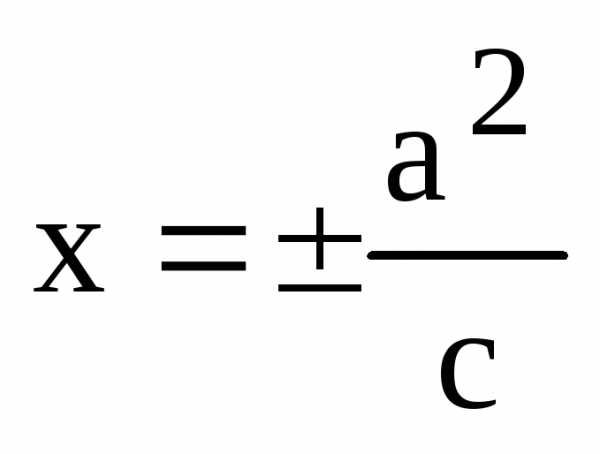 .
(13)
.
(13)
рис.8.
Теорема.
Пусть М – произвольная точка эллипса,  ,
,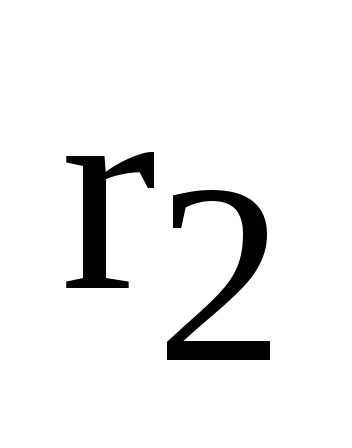 – ее фокальные радиусы,
– ее фокальные радиусы,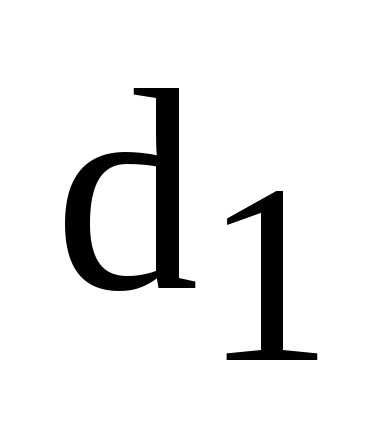 – расстояние от точки М до левой
директрисы,
– расстояние от точки М до левой
директрисы,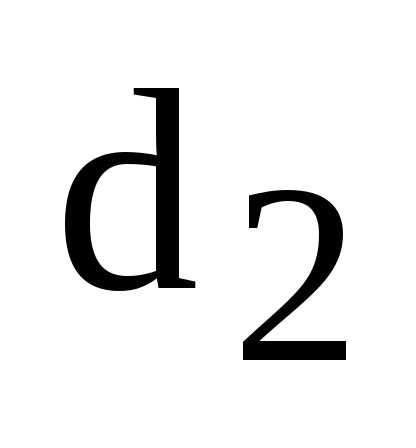 – до правой. Тогда
– до правой. Тогда
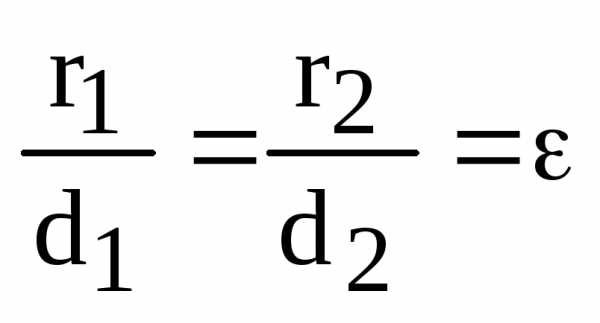 ,
(14)
,
(14)
где  – эксцентриситет эллипса.
– эксцентриситет эллипса.
Доказательство.
рис.9.
Пусть М(х, у) – координаты произвольной точки эллипса. Тогда
, ,
откуда и следуют равенства (14).
Теорема доказана.
п.8. Фокальный параметр эллипса.
Определение. Фокальным параметром эллипса называется длина перпендикуляра, восстановленного в его фокусе до пересечения с эллипсом.
Фокальный параметр принято обозначать буквой р.
рис.9.
Из определения следует, что фокальный параметр
 .
.
Теорема. Фокальный параметр эллипса равен
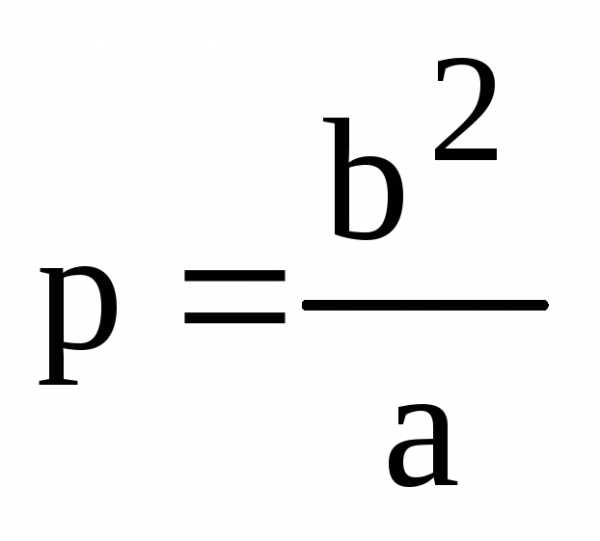 .
(15)
.
(15)
Доказательство.
Так как точка N(–с; р)
явяляется точкой эллипса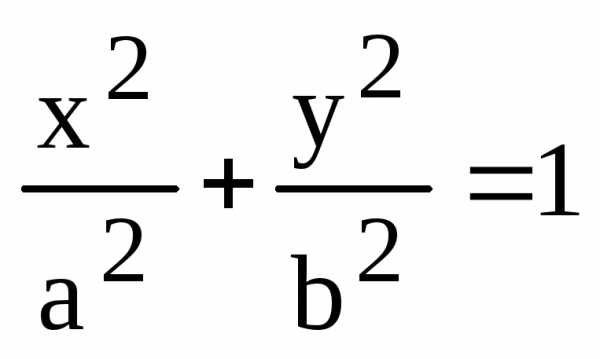 ,
то ее координаты удовлетворяют его
уравнению:
,
то ее координаты удовлетворяют его
уравнению:
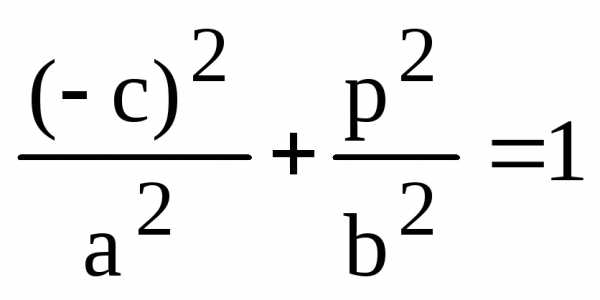 .
.
Отсюда находим
,
откуда и следует (15).
Теорема доказана.
п.9. Второе определение эллипса.
Теорема из п.7. может служить определением эллипса.
Определение. Эллипсом называется ГМТ для которых отношение расстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная меньше единицы и называемая его эксцентриситетом:
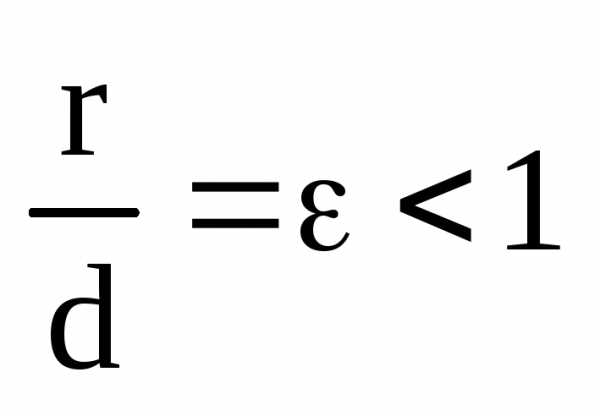 .
.
рис.10.
Разумеется, в этом случае, первое определение эооипса является теоремой, которую необходимо доказывать.
studfiles.net
Векторная алгебра. Элементы аналитической геометрии, страница 6
Определение 7.4. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний от двух заданных точек, называемых фокусами, есть величина постоянная, равная 2а, при условии, что 2а > 2с, где 2с – расстояние между фокусами.
Фокусы эллипса лежат на оси абсцисс, начало координат – в середине отрезка между фокусами, их координаты соответственно . Они располагаются внутри эллипса.
Уравнение эллипса:
, (7.12)
где (рис.7.9).
Если центр симметрии эллипса смещен в точку ), то уравнение эллипса будет записано так:
. (7.13)
Как видно из уравнений эллипса, его график симметричен относительно обеих осей координат и каждому значению х соответствует два значения у. Кроме того график пересекает оси координат в точках и . Эти точки называют вершинами эллипса. Для удобства его построения строят основной прямоугольник со сторонами, параллельными осям координат: х = а, х = –а, у = b, у = –b, и вписывают в него эллипс.
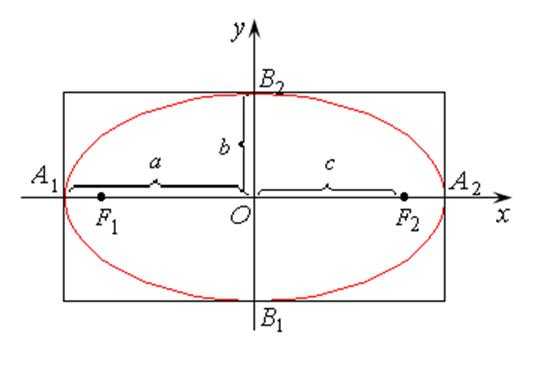
Рис. 7.9
7.7. Каноническое уравнение гиперболы
Определение 7.5. Гиперболой называется геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух заданных, называемых фокусами, есть величина постоянная, равная 2а, при условии, что , где 2с – расстояние между фокусами.
Фокусы гиперболы располагают на оси ОХ, которую называют фокальной и действительной осью, потому что только с ней пересекаются вершины гиперболы в точках . Фокусы гиперболы лежат на более удаленном расстоянии от начала координат, чем вершины, так как по условию . Пересечения с осью ОУ нет, поэтому ее называют еще мнимой осью гиперболы.
Уравнение гиперболы:
, (7.14)
где (рис. 7.10).
То же уравнение гиперболы со смещенным центром симметрии в точке ( запишется в виде:
. (7.15)
Гипербола также симметрична относительно обеих осей
координат. При построении ее графика также строится основной прямоугольник со
сторонами
и ,
затем проводят его диагонали. Они будут служить асимптотами – прямыми, к
которым стремятся точки графика гиперболы, но не достигают при неограниченном удалении x от начала координат. Если x неограниченно удаляется от начала координат, то y тоже будет
уходить в бесконечность. График гиперболы приведен на рис. 7.10. Если фокальной
и действительной осью будет служить ось ОY, то
уравнение такой гиперболы будет записано так:
На рис. 7.10 она изображена пунктирной линией.
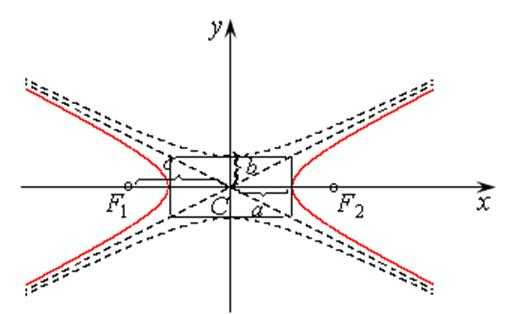
Рис. 7.10
7.8. Приведение уравнения кривой второго порядка
к каноническому виду
Все перечисленные уравнения носят название канонических уравнений, так как для их вывода использовался один и тот же прием.
Итак, мы рассмотрели четыре кривых второго порядка: окружность, параболу, эллипс и гиперболу. Возникает вопрос: существуют ли другие линии, определяемые уравнением второй степени ? Чтобы ответить на этот вопрос, приведем примеры.
1) . Этому уравнению удовлетворяет только одна точка на плоскости О(0,0), т.к. сумма квадратов двух чисел всегда больше нуля.
2) . Это уравнение можно переписать в виде (х – у)(х + у)=0, и приравнять каждый из сомножителей нулю. Получим две пересекающиеся прямые х = у и х = –у.
3) х – 2ху + у = 0. Оно равносильно уравнению = 0, которое представляет две слившиеся прямые х – у = 0.
4) , . Каждое из этих уравнений также представляет пары прямых х = , у = .
5) . Это уравнение не может определять никакую линию на плоскости, так как сумма положительных чисел не может быть равно нулю.
Приведенные примеры показывают, что нельзя однозначно ответить на поставленный вопрос. Необходимо подходить к каждому случаю отдельно.
Рассматривая уравнения второго порядка, не содержащие члена с произведением координат, можно привести его к одному из рассмотренных выше видов с помощью выделения полного квадрата по каждой из переменных. Покажем, как это делается, на примере.
Пример 7.7. Привести уравнение к каноническому виду, указать вид кривой.
.
Решение. Представим левую часть в виде суммы квадратов:
(х – 1 + (у – 9 – 7 = 0,
или
.
Это уравнение представляет окружность с центром в точке (–1,–3) и радиусом, равным .
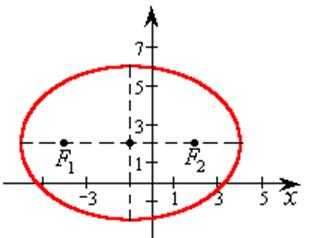
Пример 7.8. Показать, что данное уравнение
16x2 + 25y2 + 32x – 100y – 284 = 0
определяет эллипс, приведя его к каноническому виду. Найти центр эллипса, его полуоси и фокусы. Сделать чертеж
 Решение.
Сгруппируем слагаемые, содержащие x и y:
Решение.
Сгруппируем слагаемые, содержащие x и y:
16(x2 + 2x) + 25(y2– 4y) – 284 = 0
После этого выражения в скобках преобразуем таким образом, чтобы можно было воспользоваться формулой полного квадрата, т.е. в каждой скобке добавим и отнимем такое число, чтобы можно было воспользоваться формулой: a2 + 2ab + b2 = (a + b)2:
.
Отсюда получаем:
16(x2+1)2 – 16 + 25(y2–2)2 – 100 – 284 = 0,
или
16(x2+1)2 + 25(y2–2)2 = 400.
Разделив это уравнение на 400, получим
.
Это уравнение – каноническое уравнение эллипса, центр которого находится в точке С(–1,2). Большая полуось равна a=4, малая b=3, фокальное расстояние .
Пример 7.9. Показать, что уравнение
9x2 –16y2 + 18x + 64y – 199 = 0
определяет гиперболу, приведя его к каноническому виду. Найти центр гиперболы, ее полуоси, фокусы и уравнения асимптот. Сделать чертеж.
Решение. Дополняя члены, содержащие x и y, до полного квадрата:
9(x2 + 2x) – 16(y2 – 4y) – 199 = 0,
или
9(x + 1)2 – 9 – 16(y – 2)2 + 64 – 199 = 0.
Отсюда получаем каноническое уравнение гиперболы:
.
Следовательно, центр гиперболы находится в точке С(–1;2), действительная полуось a=4, мнимая b=3, фокальное расстояние . Уравнения асимптот имеют вид
,
или 3x–4y–10 = 0 и 3x+4y–2 = 0.
Построение гиперболы лучше начинать с построения асимптот, а затем уже отмечать вершины, фокусы и другие точки.
7.9. Заключение
На этом мы закончим знакомство с аналитической геометрии, и перейдем к новой теме, которая называется математический анализ. Основным понятием этого раздела высшей математики является понятие функции.
vunivere.ru
Каноническое уравнение эллипса. Полуоси эллипса. Построение эллипса, если известно его каноническое уравнение.
Каноническое уравнение эллипса имеет вид
где a – большая полуось; b – малая полуось. Точки F1(c,0) и F2(-c,0) − c называются
a, b — полуоси эллипса.
Нахождение фокусов, эксцентриситета, директрис эллипса, если известно его каноническое уравнение.
Определение гиперболы. Фокусы гиперболы.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
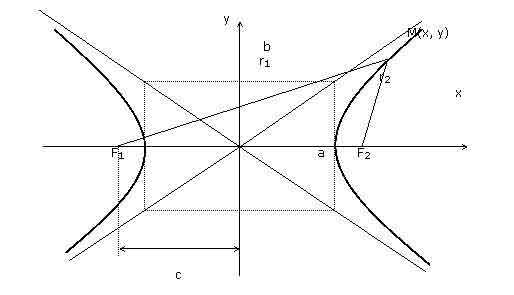
По определению |r1 – r2|= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
Каноническое уравнение гиперболы. Полуоси гиперболы. Построение гиперболы, если известно ее каноническое уравнение.
Каноническое уравнение:
Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:
Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:
Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.
Нахождение фокусов, эксцентриситета, директрис гиперболы, если известно ее каноническое уравнение.
Эксцентриситет гиперболы
Определение. Отношение называется эксцентриситетом гиперболы, где с –
половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а2 = b2:
Если а = b, e = , то гипербола называется равнобочной (равносторонней).
Директрисы гиперболы
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
Определение параболы. Фокус и директриса параболы.
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая — ее директрисой.
Каноническое уравнение параболы. Параметр параболы. Построение параболы.
Каноническое уравнение параболы в прямоугольной системе координат: (или , если поменять местами оси).
Построение параболы при заданной величине параметра p выполняется в следующей последовательности:
Проводят ось симметрии параболы и откладывают на ней отрезок KF=p;
Через точку K перпендикулярно оси симметрии проводят директрису DD1;
Отрезок KF делят пополам получают вершину 0 параболы;
От вершины отмеряют ряд произвольных точек 1, 2, 3, 5, 6 с постепенно увеличивающемся расстоянием между ними;
Через эти точки проводят вспомогательные прямые перпендикулярные оси параболы;
На вспомогательных прямых делают засечки радиусом равным расстоянию от прямой до директрисы;
Полученные точки соединяют плавной кривой.
studopedia.net
Эллипс. Формулы, признаки и свойства эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2. Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси: Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:
k = √1 — e2
где e — эксцентриситет. Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии ae от центра эллипса. Расстояние от фокуса до директрисы равно pe.
ru.onlinemschool.com
3.1. ЛИНИИ ВТОРОГО ПОРЯДКА. Каноническое уравнение эллипса
Определение. Эллипсом называется геометрическое место точек плоскости для которых сумма расстояний до двух фиксированных точек и , называемых фокусами, есть величина постоянная.
Выведем уравнение эллипса в соответствии с данным определением. Для этого зафиксируем декартову систему координат ХОу как показано на рисунке.
Согласно определению эллипса для точки М имеем , где А — некоторая постоянная. В координатах
.
Подставим эти значения в основное равенство, получим уравнение
.
После стандартного метода «уничтожения» радикалов (возведения обеих частей уравнения в квадрат (см. пример 1.)) получим каноническое уравнение эллипса
(1)
Где . Величины А и B, называются соответственно Большой и Малой Полуосями эллипса.
Замечание. В частности, при из (1) имеем уравнение окружности радиуса А с центром в начале координат
. (2)
Свойства эллипса:
1. Эллипс имеет две взаимно перпендикулярные оси симметрии Х и У (их называют главными осями эллипса) и центр симметрии О (его называют центром эллипса).
Утверждение следует из того, что замена координат на или или не изменяет вид уравнения (1). При этом, в первом случае, при преобразовании , имеем ось симметрии У, во втором — ось симметрии , а в третьем — центр симметрии О.
2. Эллипс полностью содержится в прямоугольнике
.
Из уравнения (1) имеем . Аналогично, .
3. Эллипс получается равномерным сжатием окружности.
Рассмотрим окружность . Произведем равно-мерное сжатие плоскости к оси Ох: . Подставим эти значения в уравнение окружности (2), имеем . После деления на получим уравнение (1).
Построим эллипс на основании его свойств и уравнения (1)
Пример 1. Написать уравнение кривой по которой движется точка M, если сумма расстояний от нее до точек и остается постоянной и равной .
Решение. Согласно условию задачи
.
Откуда
.
Возведем обе части уравнения в квадрат и приведем подобные члены, получим
Еще раз возводим в квадрат и приведем подобные члены
Пример 2. На эллипсе найти точку, расстояние от которой до фокуса в четыре раза больше расстояния чем до фокуса .
Решение. Запишем уравнение эллипса в каноническом виде:
.
Найдем координаты фокусов эллипса
.
Согласно условию задачи
Выразим Из уравнения эллипса , подставим в данное уравнение и приведем подобные члены, получим квадратное уравнение Его корни — лишний корень, т. к. . Тогда . Отв.
| < Предыдущая | Следующая > |
|---|
matica.org.ua

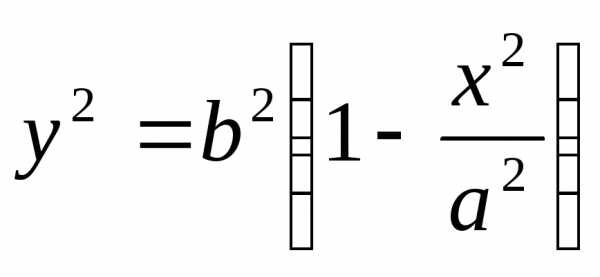 .
Так как,
имеем;
.
Так как,
имеем;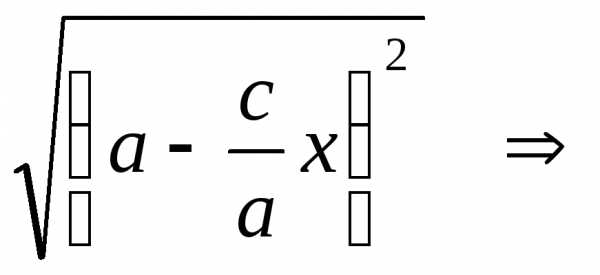
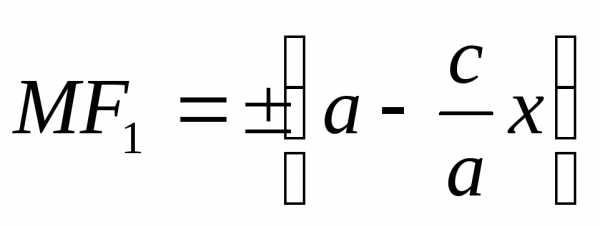 .
Так как,
то
.
Так как,
то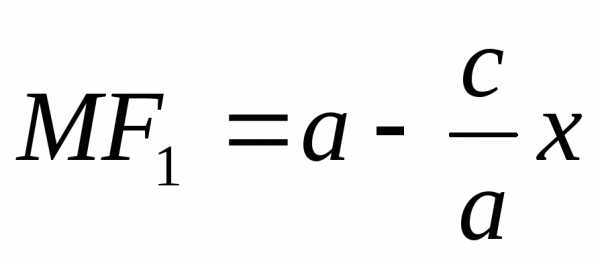 .
.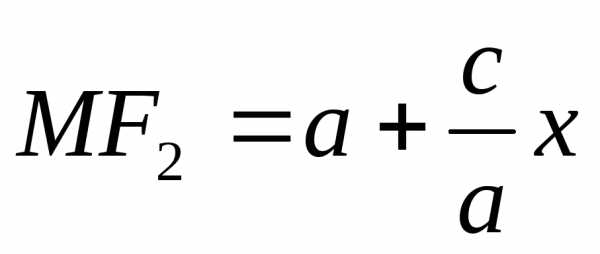
 ,
, ;
; проведем прямую
проведем прямую ,
параллельно оси
,
параллельно оси ,
через точку
,
через точку — прямую
— прямую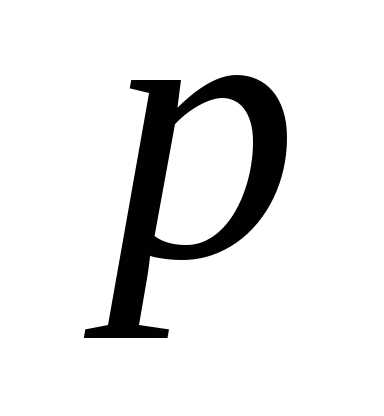 ,
параллельную оси
,
параллельную оси ;
; и
и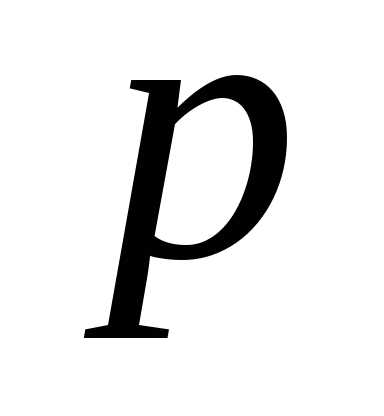 –
точка эллипса
–
точка эллипса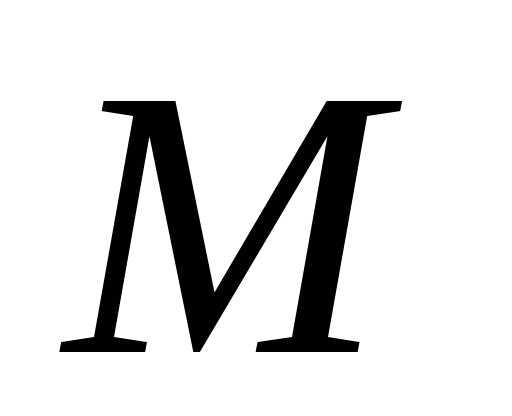 ;
;