Что такое предел функции как его найти
При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.
А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть .
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется «доопределить функцию», с этим определением вы можете ознакомиться в последующих частях главы «Предел»). Примем, что конечная величина, поделенная на бесконечность, равна нулю:
С рассмотренной последовательностью окружностей свяжем другую переменную величину — последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции при
Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Пример 1. Найти предел функции при .
Решение. Подставляем вместо x значение 0. Получаем:
Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Предел функции при , при и при
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение 2. Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: .
Определение 3. Число A называется пределом функции f(x)
при (),
если для любой бесконечно большой последовательности значений аргумента, элементы
которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: ().
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.
Пример 2. Найти предел функции при .
Решение. Подставляем вместо
.
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.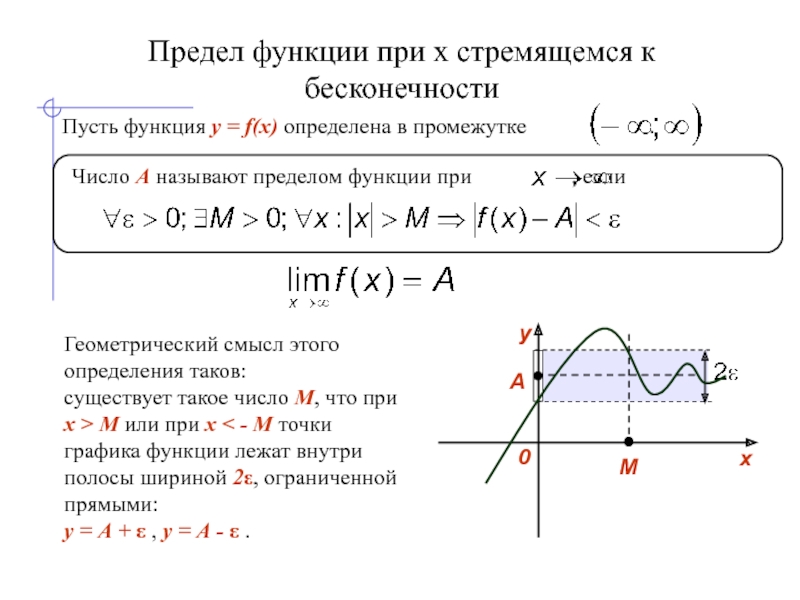
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(5)
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Теорема 3 (о пределе сложной функции).
 Если существует конечный предел
Если существует конечный предела функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида — самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 12. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки
вместо
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Проверить решение задачи на
пределы можно на калькуляторе пределов
онлайн.
Пример 13. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем «икс» под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо «икса».
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Неопределённость вида
Пример 14. Раскрыть неопределённость и найти предел .
Раскрыть неопределённость и найти предел .
Решение. В числителе — разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе — квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 15. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и
сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 16. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Продолжение темы «Предел»
Поделиться с друзьями
Предел функции. Примеры решения
Продолжаем разбирать ответы к пределам функций и последовательностей. Примеров накопилось настолько много, что можно написать отдельную книгу — методичку по их вычислению.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.
Пример 11. Вычислить предел последовательности:
Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.
На общий множитель упрощаем, а константы дают значение предела последовательности.
Пример 12. Найти предел последовательности:
Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности
Все что останется и будет пределом последовательности
Пример 13. Найти предел функции
Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки
Пример 14. Вычислить предел
Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.
Пример 15. Определить предел функции
Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.
Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.
Пример 16. Найти предел последовательности:
Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен
Пример 17. Вычислить предел последовательности:
Вычислить предел последовательности:
Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.
Пример 18. Определить лимит функции
Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.
Лимит функции, что осталась, вычисляем методом подстановки.
Пример 19. Найти предел функции
Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.
Пример 20. Найти лимит
Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.
Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2),
Урок 8.
 предел функции на бесконечности — Алгебра и начала математического анализа — 11 класс
предел функции на бесконечности — Алгебра и начала математического анализа — 11 классАлгебра и начала математического анализа, 11 класс
Урок №8. Предел функции на бесконечности.
Перечень вопросов, рассматриваемых в теме
1)понятие бесконечности;
2) определение предела функции на плюс бесконечности;
2) определение предела функции на минус бесконечности;
3) правила вычисления пределов функции на бесконечности;
4) формулы вычисления предела функции на бесконечности;
5) нахождение горизонтальные, вертикальные, наклонные асимптоты.
Глоссарий по теме
Бесконечность – сколь угодно большое(малое), безграничное число.
Дробно-рациональная функция – это такая алгебраическая дробь, у которой числитель и знаменатель представляют собой многочлены некоторой степени.
Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Понятие «бесконечность» используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел.
Бесконечность – сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость, то ось абсцисс(ординат) уходит на бесконечность, если ее безгранично продолжать влево или вправо (вниз или вверх).
Теперь давайте перейдем к пределу функции на плюс и минус бесконечности.
Предел функции на плюс бесконечности.
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:
Предел функции на минус бесконечности.
Посмотрим немного другой случай:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке:
Предел функции на бесконечности.
Так же наши соотношения могут выполняться одновременно:
Тогда принято записывать как:
Для вычисления предела на бесконечности пользуются несколькими утверждениями.
Основные свойства:
- Для любого натурально числа m справедливо следующее соотношение:
- Если и
а) Предел суммы равен сумме пределов:
б) Предел произведения равен произведению пределов:
в) Предел частного равен частному пределов:
г) Постоянный множитель можно вынести за знак предела:
А теперь давайте перейдем к дробно — рациональной функции.
Дробно-рациональная функция – это такая алгебраическая дробь, у которой числитель и знаменатель представляют собой многочлены некоторой степени.
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Перейдем к практической части.
Примеры и разбор решения заданий тренировочного модуля
Пример1. Вычислить пределы функций:
а)
б)
в)
г)
Пример 2. Построим график функции .
Преобразуем функцию с выделением целой части:
.
Дробно-линейная функция имеет две асимптоты: горизонтальную и вертикальную.
y=2 горизонтальная асимптота
x=1 вертикальная асимптота, т.к.
Точки пересечения графика с осями координат:
при x=0 y=3 , точка (0; 3)
при y=0 x=1,5 , точка (1,5; 0)
Пример 3
Построить график функции .
Преобразуем функцию с выделением целой части
- y=2x наклонная асимптота
X=0 вертикальная асимптота
функция ни четная, ни нечетная.
- точки пересечения графика с осями координат:
Приy=0
, точка
с осью ординат график функции не пересекается, т.к. эта ось есть асимптота.
y’=0
xкр=1
6) y(1)=3
7) Построим график
как понять, вычислить, подробное объяснение с решением
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина.
Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.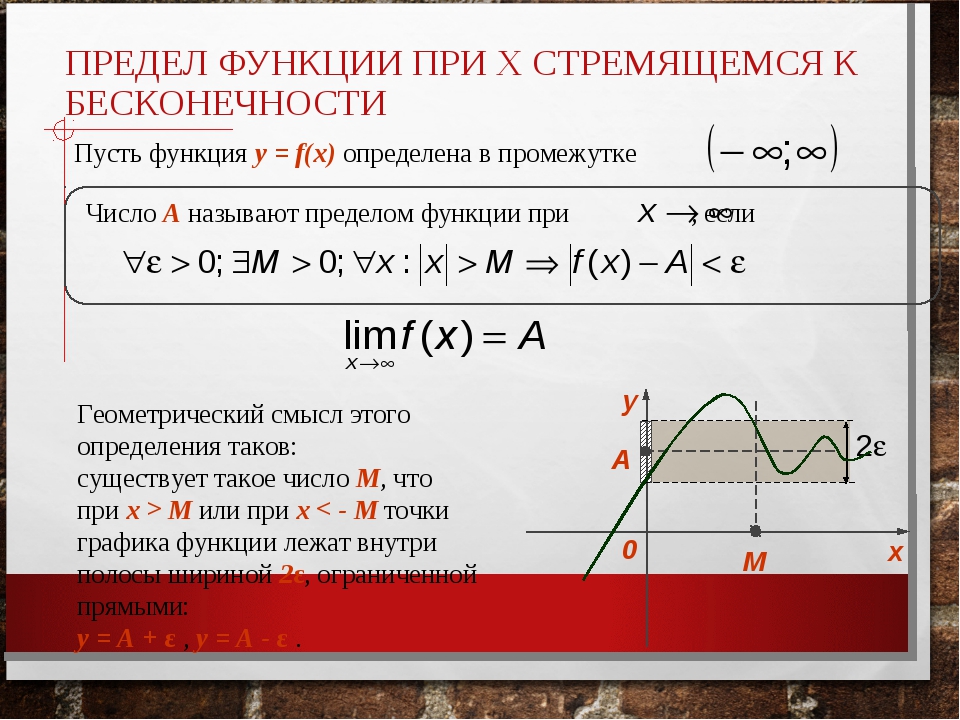
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Предел функции
В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.
Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.
| Название | Обозначение | Определение |
Предел функции f (x) при x, стремящемся к числу a, равен числу A | Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → a | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . | Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a – 0 | ||
Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. | Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a + 0 |
Название: Предел функции f (x) при x, стремящемся к числу a, равен числу A Обозначения: или f (x) → A при x → a Определение: Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при x → Определение: Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при x → Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . Обозначения: или f (x) → при x → a – 0 . Определение: Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . |
Название: Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. Обозначения: или f (x) → при x → a + 0 . Определение: Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . |
Свойства пределов функций
Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы
и ,
где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем
Если, кроме того, выполнено условие
то при x , стремящемся к a , существует предел дроби
причем
Для любой непрерывной функции F (x) справедливо равенство
Раскрытие неопределенностей типа
Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .
Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
Пример 1. Найти предел функции предел функции
Решение. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства пределов функций, получим
Ответ.
Пример 2. Найти предел функции предел функции
Решение. Преобразуем выражение, стоящее под знаком предела, к более удобному виду:
Далее, используя свойства пределов функций, находим
Ответ. 3 .
3 .
Раскрытие неопределенностей типа
Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .
В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .
Пример 3. Найти предел функции
Решение. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :
Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем
Ответ.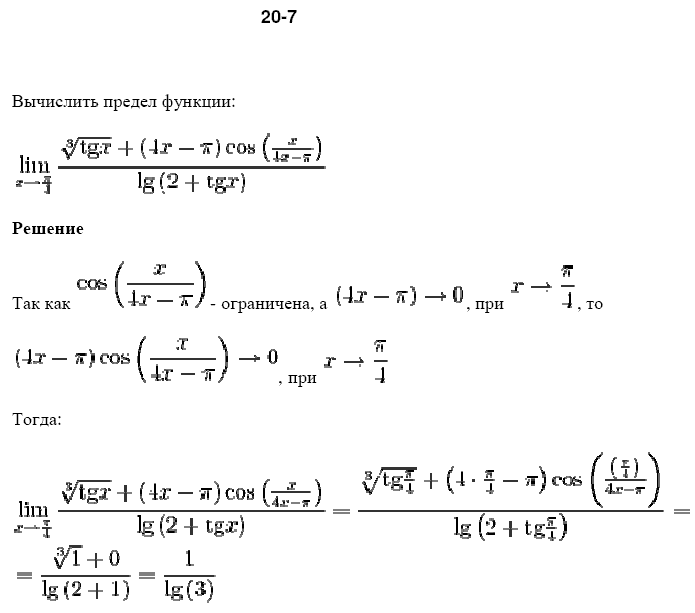
Пример 4. Найти предел функции
Решение. В этом примере также возникает неопределенность типа .
К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).
Указания к решению примера. Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то сначала необходимо домножить и числитель, и знаменатель дроби на сумму этих квадратных корней и применить формулу сокращенного уножения «разность квадратов». Затем, разложив квадратный трехчлен 4x2 – 9x – 55 на множители, сократить числитель и знаменатель на (x – 5) .
После этого, воспользовавшись свойствами пределов функций, получить ответ.
На Вашем мобильном устройстве отображается только результат описанных операций.
Ответ.
Первый замечательный предел
В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела
Пример 5. Найти предел функции
Решение. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x2, а в знаменателе воспользуемся формулой «разность косинусов»:
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Пример 6. Найти предел функции
Решение. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле
.
Поскольку
,
то предел можно преобразовать к виду
Применяя формулы приведения и формулу для косинуса двойного угла, получаем
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Раскрытие неопределенности типа . Второй замечательный предел
Определение 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .
Неопределенность раскрывается с помощью второго замечательного предела:
| (1) |
Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:
| (2) |
Пример 7. Найти предел функции предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x →. Применяя свойства логарифмов, получаем
Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,
и заметим, что
В пределе
и числитель, и знаменатель дроби стремятся к стремятся к, поэтому для раскрытия неопределенности вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим
Следовательно,
Таким образом,
Ответ.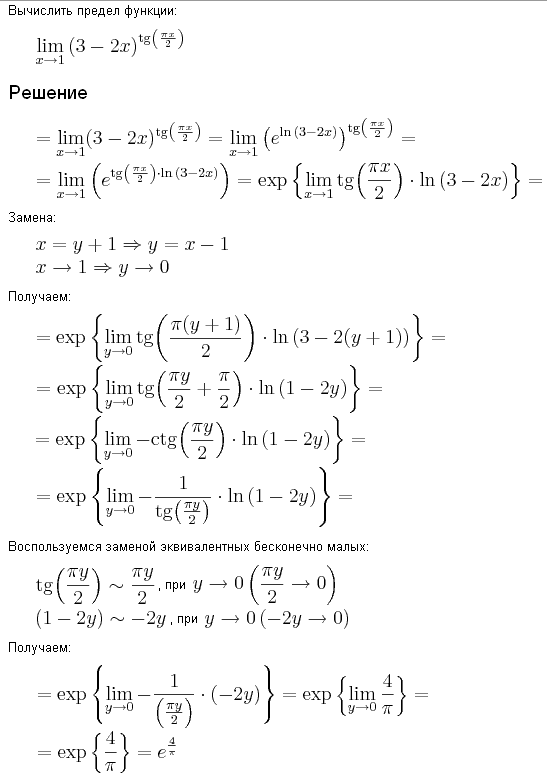
Пример 8. Найти предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем
Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле
x = – 6 + z .
Поскольку
то предел (3) можно преобразовать к виду, с помощью формулы (3), получаем
Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем
Следовательно,
Ответ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Алгебра – 10 класс. Предел функции в точке
Дата публикации: .
Что будем изучать:
1. Что такое предел функции в точке.
2. Определение непрерывной функции.
3. Обобщение знаний о непрерывных функциях.
4. Свойства предела.
5. Примеры.
1) Что такое предел функции в точке?
Ребята, давайте посмотрим на три графика функции, приведенные ниже:
На первый взгляд, графики выглядят совершенно одинаково, но давайте внимательнее посмотрим на наши графики. Посмотрим внимательно на значения функции y=f(x) в точке а.
На Рис1. изображен график непрерывной функции. Значение нашей функции в точке a f(a)=b.
На Рис2. изображен график с так называемой выколотой точкой, значения нашей функции в точке а не существует, посмотрите внимательно на график, наше значение как будто взяли и выкололи.
На Рис3. изображен график значение, которого в точке а существует, но где то отдельно от всего графика, f(a) – расположена выше нашего графика.
На наших рисунках изображены графики трех разных функций. Если мы не будем рассматривать точку а, то графики функций совпадают. При xа графики совершенно одинаковые.
Все случаи описанные для наших рисунков, на математическом языке записывается как:
Читается как: предел функции y=f(x) при x стремящимся к а равен b.
Теперь давайте постараемся понять, что же написано выше. Если значения аргумента функции y=f(x) подбирать все ближе к числу а (если из а вычитать подобранные значения аргумента, то результатом будет число практически равное нулю), то соответствующие значения функции будут все ближе и ближе к b (если из b вычитать полученные значения функции, то результатом будет число практически равное нулю). При этом стоит заметить, что саму точку а не учитываем.
Посмотрим опять на первый график: Можно заметить что:
График функции на нашем рисунке непрерывен. Тогда, давайте напишем определение непрерывной функции:
Определение непрерывной функции.

Определение. Функцию y=f(x) называют непрерывной в точке x=a, если выполняется тождество:
Функцию y=f(x) называют непрерывной в точке x=a, если предел функции при x стремящимся к а, равен значению функции в точке x=a.
Функция непрерывна на отрезке [a,b], если она непрерывна в каждой точке нашего отрезка.
Обобщение знаний о непрерывных функциях.
Полезно: В курсе высшей математики или математическом анализе, существует ряд теорем и утверждений которые доказывают, что все функции, которые мы с вами рассматривали в ранних курсах алгебры являются непрерывными, мы с вами интуитивно и с помощью графиков понимали, что функция непрерывна. Давайте обобщим изученное, важным утверждением:
Если выражение f(x) составлено из рациональных, иррациональных и тригонометрических выражений, то функция y=f(x) непрерывна в любой точке, в которой определенно выражение f(x).
Свойства функции
Если f(x)=b a g(x)=c то выполняются следующие свойства:
Примеры:
А) Найти предел функции:
Решение:
Наша функция непрерывна в точке x=2, тогда воспользуемся определением непрерывности функции в точке, которое говорит что если функция непрерывна в точке, то предел функции в этой точке равен значению функции в этой же точке.
Б) Найти предел функции:
Решение:
Давайте посмотрим не обращается ли знаменатель нашей функции при x=π/2 в нуль:
Знаменатель не равен нулю, тогда наша функция непрерывна в точке . Воспользуемся определением непрерывной функции и посчитаем предел нашей функции:
Ответ: -1/3
В) Найти предел функции:
Подставим x=2 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя. Давайте внимательно посмотрим на числитель нашей дроби.
x2 — 4 = (x — 2)(x + 2)
Сократим нашу дробь
Тогда получаем:
y= x+2 непрерывна точке x=2, тогда воспользуемся определением непрерывности
Ответ: 4
Г)Найти предел функции:
Решение:
Область определения функции
Наша точка x=2 не попадает в область определения, тогда предел функции не существует.
Ответ: Не существует.
Д) Найти предел функции:
Решение:
Подставим x=1 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя. Давайте найдем корни квадратного уравнения в числители и
воспользуемся теоремой Виета.
Давайте найдем корни квадратного уравнения в числители и
воспользуемся теоремой Виета.
Ответ: -1
Е) Построить график функции y=f(x), которая обладает следующими свойствами:
1)Область определения – множество действительных чисел.
2)lim f(x)=3
3) f(2)=4
4) f(x)
Решение:
Покажем один из возможных графиков.
Примеры для самостоятельного решения:
1) Найти предел функции:
2) Найти предел функции:
3) Найти предел функции:
4) Найти предел функции:
5)Построить график функции y=f(x), которая обладает следующими свойствами:
а)Область определения – множество действительных чисел.
б)
в) f(-2)=3
г) f(x)
д) f(x)>0 при x>-1
Правило Л’Опиталя
Правило L’Hôpital может помочь нам рассчитать лимит, который в противном случае может оказаться трудным или невозможным.
L’Hôpital произносится как «лопиталь». Он был французским математиком 1600-х годов.
Он говорит, что предел , когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции (с некоторыми специальными условиями, показанными позже).
В символах можно написать:
lim x → c f (x) g (x) = lim x → c f ’(x) g’ (x)
Предел, когда x приближается к c из «f-of-x over g-of-x» равен
пределу, когда x приближается к c «f-dash-of-x над g-dash-of-x»
Все, что мы сделали, это добавили маленькую черту ‘на каждой функции, что означает взятие производной.
Пример:
lim x → 2 x 2 + x − 6 x 2 −4
При x = 2 обычно получаем:
2 2 + 2−6 2 2 −4 = 0 0
Что неопределенно, так что мы застряли. Или мы?
Или мы?
Попробуем L’Hôpital!
Различия между верхом и низом (см. Производные правила):
lim x → 2 x 2 + x − 6 x 2 −4 = lim x → 2 2x + 1−0 2x − 0
Теперь мы просто подставляем x = 2 , чтобы получить ответ:
lim x → 2 2x + 1−0 2x − 0 = 5 4
Вот график, обратите внимание на «дыру» в точке x = 2:
Примечание: мы также можем получить этот ответ путем факторинга, см. Оценка пределов .
Пример:
lim x → ∞ e x x 2
Обычно это результат:
lim x → ∞ e x x 2 = ∞ ∞
Оба устремляются в бесконечность. Что неопределенно.
Что неопределенно.
Но давайте различим верх и низ (обратите внимание, что производная от e x равна e x ):
lim x → ∞ e x x 2 = lim x → ∞ e x 2x
Хммм, все еще не решено, оба стремятся к бесконечности.Но мы можем использовать его снова:
lim x → ∞ e x x 2 = lim x → ∞ e x 2x = lim x → ∞ e х 2
Теперь у нас:
lim x → ∞ e x 2 = ∞
Он показал нам, что e x растет намного быстрее, чем x 2 .
Ящики
Мы уже видели примеры 0 0 и ∞ ∞ . Вот все неопределенные формы, с которыми может помочь Правило Л’Опиталя:
Вот все неопределенные формы, с которыми может помочь Правило Л’Опиталя:
0 0 ∞ ∞ 0 × ∞ 1 ∞ 0 0 ∞ 0 ∞ − ∞
Условия
Дифференцируемая
Для предела, приближающегося к c, исходные функции должны быть дифференцируемыми по обе стороны от c, но не обязательно в c.
Точно так же g ’(x) не равно нулю по обе стороны от c.
Предел должен существовать
Этот предел должен существовать:lim x → c f ’(x) g’ (x)
Почему? Хороший пример — функции, которые никогда не устанавливают значение.
Пример:
lim x → ∞ x + cos (x) x
Это случай ∞ ∞ . Различаем верх и низ:
lim x → ∞ 1 − sin (x) 1
И поскольку он просто качается вверх и вниз, он никогда не приближается к какой-либо ценности.
Так что нового лимита не существует!
Итак, Правило L’Hôpital в этом случае неприменимо.
НО мы можем это сделать:
lim x → ∞ x + cos (x) x = lim x → ∞ (1 + cos (x) x )
По мере того, как x стремится к бесконечности, cos (x) x стремится к промежутку между −1 ∞ и +1 ∞ , и оба стремятся к нулю.
И у нас осталась только «1», поэтому:
lim x → ∞ x + cos (x) x = lim x → ∞ (1 + cos (x) x ) = 1
Пределы (формальное определение)
Приближается …
Иногда мы не можем что-то придумать напрямую … но мы можем видеть, что должно быть, когда мы приближаемся все ближе и ближе!
Пример:
(x 2 — 1) (x — 1)
Давайте разберемся с x = 1:
(1 2 — 1) (1 — 1) = (1 — 1) (1 — 1) = 0 0
Теперь 0/0 — это сложность! Мы действительно не знаем значение 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.
Итак, вместо того, чтобы пытаться вычислить это для x = 1, давайте попробуем , приближаясь к , это все ближе и ближе:
Продолжение примера:
| x | (x 2 — 1) (x — 1) | |
| 0,5 | 1,50000 | |
| 0,9 | 1, | |
| 0.99 | 1,99000 | |
| 0,999 | 1.99900 | |
| 0,9999 | 1.99990 | |
| 0,99999 | 1,99999 | |
| … | … |
Теперь мы видим, что когда x приближается к 1, тогда (x 2 −1) (x − 1) получает , близкое к 2
.Мы столкнулись с интересной ситуацией:
- Когда x = 1, мы не знаем ответа (это неопределенный )
- Но мы видим, что будет 2
Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»
Предел из (x 2 −1) (x − 1) , когда x приближается к 1, составляет 2
И записывается символами как:
lim x → 1 x 2 −1 x − 1 = 2
Таким образом, это особый способ сказать: «игнорировать то, что происходит, когда мы приближаемся к цели, но по мере того, как мы приближаемся все ближе и ближе, ответ становится все ближе и ближе к 2»
В виде графика это выглядит так: Итак, по правде говоря, мы не можем сказать, каково значение при x = 1. Но мы можем сказать, что по мере приближения к 1, предел равен 2. |
Более формальный
Но вместо того, чтобы говорить, что предел равен некоторому значению, потому что выглядел так, как будто он идет к , мы можем иметь более формальное определение.
Итак, начнем с общей идеи.
От английского языка к математике
Сначала скажем по-английски:
«f (x) приближается к некоторому пределу , поскольку x приближается к некоторому значению»
Когда мы называем предел «L» и значение, при котором x приближается к «a», мы можем сказать
«f (x) приближается к L, когда x приближается к»
Расчет «закрытия»
А теперь, как можно математически сказать «близко»… можем ли мы вычесть одно значение из другого?
Пример 1: 4,01 — 4 = 0,01 (выглядит хорошо)
Пример 2: 3,8 — 4 = -0,2 ( отрицательно, близко?)
Так что же делать с негативом? Нас не волнует положительное или отрицательное, мы просто хотим знать, как далеко . .. это абсолютное значение.
.. это абсолютное значение.
«Как близко» = | a − b |
Пример 1: | 4.01−4 | = 0,01
Пример 2: | 3.8−4 | = 0,2
А когда | a − b | маленький мы знаем, что близки, поэтому пишем:
«| f (x) −L | мало, когда | x − a | мало»
И эта анимация показывает, что происходит с функцией
f (x) = (x 2 −1) (x − 1)
f (x) приближается к L = 2, когда x приближается к a = 1,
, поэтому | f (x) −2 | мала, когда | x − 1 | маленький.
Дельта и Эпсилон
Но «small» по-прежнему английский, а не «математический».
Давайте выберем два значения меньше :
| δ | , что | x − a | должно быть меньше | |
| ε | , что | f (x) −L | должно быть меньше |
Примечание: эти две греческие буквы (δ — «дельта» и ε — «эпсилон») — это
, поэтому часто используется фраза « дельта-эпсилон »
А у нас:
| f (x) −L | <ε при | x − a | <δ
Вот и все! Итак, если вы понимаете, что вы понимаете пределы. ..
..
… но чтобы быть абсолютно точным, нам нужно добавить следующие условия:
- верно для любого ε> 0
- δ существует и> 0
- x равно и не равно a, что означает 0 <| x − a |
А вот что получаем:
Для любого ε> 0 существует δ> 0, так что | f (x) −L | <ε при 0 <| x − a | <δ
Это формальное определение. На самом деле это выглядит довольно устрашающе, не правда ли?
Но по сути он говорит что-то простое:
f (x) приближается к L , когда x приближается к
Как использовать это в доказательстве
Чтобы использовать это определение в доказательстве, мы хотим пойти
| из: | Кому: | |
| 0 <| x − a | <δ | | f (x) −L | <ε |
Обычно это означает поиск формулы для δ (в единицах ε), которая работает.
Как найти такую формулу?
Угадай и попробуй!
Верно, мы можем:
- Поиграйте, пока не найдете формулу, по которой может работать
- Проверьте , чтобы убедиться, что эта формула работает
Пример: попробуем показать, что
lim x → 3 2x + 4 = 10
Используя буквы, о которых мы говорили выше:
- Значение, к которому приближается x, «a», составляет 3
- Предел «L» равен 10
Итак, мы хотим знать, как мы перейдем от:
0 <| x − 3 | <δ от
до
| (2x + 4) −10 | <ε
Шаг 1. Поэкспериментируйте, пока не найдете формулу, по которой
может работатьНачнем с: | (2x + 4) −10 | <ε
Упрощать: | 2x − 6 | <ε
Переместите 2 наружу ||: 2 | x − 3 | <ε
Разделите обе стороны на 2: | x − 3 | <ε / 2
Итак, теперь мы можем предположить, что δ = ε / 2 может работать
Шаг 2:
Протестируйте , чтобы убедиться, что эта формула работает.
Итак, можем ли мы получить от 0 <| x − 3 | <δ до | (2x + 4) −10 | <ε …?
Посмотрим …
Начнем с: 0 <| x − 3 | <δ
Заменим δ на ε / 2: 0 <| x − 3 | <ε / 2
Умножьте все на 2: 0 <2 | x − 3 | <ε
Переместите 2 внутрь ||: 0 <| 2x − 6 | <ε
Заменить «−6» на «+ 4−10»: 0 <| (2x + 4) −10 | <ε
Да! Мы можем перейти от 0 <| x − 3 | <δ к | (2x + 4) −10 | <ε , выбрав δ = ε / 2
СДЕЛАНО!
Тогда мы увидели, что при заданном ε мы можем найти δ, поэтому верно, что:
Для любого ε существует такое δ, что | f (x) −L | <ε при 0 <| x − a | <δ
И мы доказали, что
lim x → 3 2x + 4 = 10
Заключение
Это было довольно простое доказательство, но, надеюсь, оно объясняет странное «существует… «формулировка, и это действительно показывает хороший подход к такого рода доказательств.
: Wolfram | Alpha
Что такое лимиты?
Пределы, основополагающий инструмент в исчислении, используются для определения того, приближается ли функция или последовательность к фиксированному значению, когда ее аргумент или индекс приближается к заданной точке.
Пределы могут быть определены для дискретных последовательностей, функций одного или нескольких действительных аргументов или комплексных функций. Для последовательности, индексированной по набору натуральных чисел, предел считается существующим, если, как, значение элементов произвольно близко к.
Говорят, что функция с действительным знаком имеет предел, если, поскольку ее аргумент взят произвольно близким к, ее значение можно сделать сколь угодно близким к. Формально определенная функция имеет конечный предел в точке, если для всех существует такой, что всякий раз. Это определение может быть расширено или доведено до бесконечности и до многомерных и сложных функций.
Для функций одной действительной переменной, к предельной точке можно приблизиться либо справа / сверху (обозначено), либо слева / снизу (обозначено).В принципе, это может привести к разным значениям, и считается, что предел существует тогда и только тогда, когда пределы как сверху, так и снизу равны:. Для многомерных или комплексных функций существует бесконечное количество способов приблизиться к предельной точке, и поэтому эти функции должны соответствовать более строгим критериям, чтобы существовало уникальное предельное значение.
В дополнение к формальному определению существуют другие методы, которые помогают в вычислении пределов. Например, алгебраическое упрощение может использоваться для устранения рациональных особенностей, которые появляются как в числителе, так и в знаменателе, а правило Лопиталя используется при обнаружении неопределенных пределов, которые появляются в форме неприводимого или.
Как Wolfram | Alpha решает проблемы с ограничениями
Wolfram | Alpha вызывает встроенную функцию Limit системы Mathematica для выполнения вычислений, которые не обязательно выполняют вычисления так же, как это делал бы человек. Обычно функция ограничения использует мощные общие алгоритмы, которые часто включают очень сложные математические операции.
Обычно функция ограничения использует мощные общие алгоритмы, которые часто включают очень сложные математические операции.
В дополнение к этому критически важно понимать, как человек будет принимать ограничения и воспроизводить понятные человеку шаги, и благодаря нашей пошаговой функциональности Wolfram | Alpha также может продемонстрировать методы, которые человек будет использовать для вычисления пределов .2−6x − 7} {x − 7} \ nonumber \]
Функцию можно разложить следующим образом:
\ [f (x) = \ dfrac {\ cancel {(x − 7)} (x + 1)} {\ cancel {x − 7}} \ nonumber \]
, что дает нам
\ [f (x) = x + 1, x ≠ 7. \ nonumber \]
Означает ли это, что функция \ (f (x) \) такая же, как функция \ (g (x) = x + 1? \)
Ответ — нет. Функция \ (f (x) \) не имеет \ (x = 7 \) в своей области определения, но \ (g (x) \) имеет. Графически мы видим, что в графике \ (f (x) \) есть дыра в точке \ (x = 7 \), как показано на рисунке, и нет такой дыры в графике \ (g (x) \), как показано на рисунке.
(слева) График функции \ (f \) содержит разрыв в точке \ (x = 7 \) и, следовательно, не является непрерывным в точке \ (x = 7 \). (Справа) График функции \ (g \) непрерывен.
Итак, эти две разные функции также имеют разные ограничения, поскольку \ (x \) приближается к 7? Не обязательно. Помните, что при определении предела функции, когда \ (x \) приближается к \ (a \), важно то, приближается ли результат к действительному числу, когда мы приближаемся к \ (x = a \). Существование предела не зависит от того, что происходит, когда \ (x \) равно \ (a \).
Посмотрите еще раз на рисунок и рисунок. Обратите внимание, что на обоих графиках, когда \ (x \) приближается к 7, выходные значения приближаются к 8. Это означает
.\ [\ lim \ limits_ {x \ to 7} f (x) = \ lim \ limits_ {x \ to 7} g (x). \ nonumber \]
Помните, что при определении предела важно то, что происходит рядом с \ (x = a \), а не с \ (x = a \). В этом разделе мы будем использовать различные методы, такие как переписывание функций на множители, чтобы оценить предел.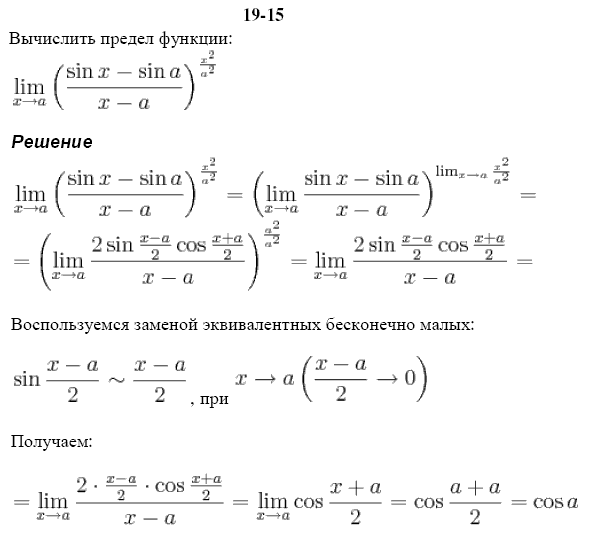 Эти методы дадут нам формальную проверку того, что мы раньше делали интуитивно.
Эти методы дадут нам формальную проверку того, что мы раньше делали интуитивно.
Определение предела суммы, разницы и произведения
Построение графика функции или изучение таблицы значений для определения предела может быть обременительным и трудоемким. По возможности более эффективно использовать свойства пределов , которые представляют собой набор теорем для нахождения пределов.
Знание свойств пределов позволяет нам вычислять пределы напрямую. Мы можем складывать, вычитать, умножать и делить пределы функций, как если бы мы выполняли операции над самими функциями, чтобы найти предел результата.Точно так же мы можем найти предел функции, возведенной в степень, подняв предел до этой степени. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых компонентных функций.
свойства лимитов
Пусть \ (a, k, A, \) и \ (B \) представляют действительные числа, а \ (f \) и \ (g \) будут функциями, такими, что \ (\ lim \ limits_ {x \ to a } f (x) = A \) и \ (\ lim \ limits_ {x \ to a} g (x) = B. \) Для существующих и конечных пределов свойства пределов сведены в Таблицу
\) Для существующих и конечных пределов свойства пределов сведены в Таблицу
| Константа, k | \ (\ lim \ limits_ {x \ to a} k = k \) |
| Постоянное время функции | \ (\ lim \ limits_ {x \ to a} [k⋅f (x)] = k \ lim \ limits_ {x \ to a} f (x) = kA \) |
| Сумма функций | \ (\ lim \ limits_ {x \ to a} [f (x) + g (x)] = \ lim \ limits_ {x \ to a} f (x) + \ lim \ limits_ {x to a} g (х) = А + В \) |
| Различие функций | \ (\ lim \ limits_ {x \ to a} [f (x) −g (x)] = \ lim \ limits_ {x \ to a} f (x) — \ lim \ limits_ {x \ to a} д (х) = А − В \) |
| Произведение функций | \ (\ lim \ limits _ {x \ to a} [f (x) ⋅g (x)] = \ lim \ limits _ {x \ to a} f (x) ⋅ \ lim \ limits_ {x \ to a} g (x) = A⋅B \) |
| Частное функций | \ (\ lim \ limits _ {x \ to a} \ frac {f (x)} {g (x)} = \ frac {\ lim \ limits _ {x \ to a} f (x)} {\ lim \ limits _ {x \ to a} g (x)} = \ frac {A} {B}, B ≠ 0 \) |
| Функция, возведенная в степень | \ (\ lim \ limits _ {x \ to a} [f (x)] ^ n = [\ lim \ limits _ {x \ to ∞} f (x)] ^ n = A ^ n \), где \ (n \) — натуральное число |
| n -й корень функции, где n — целое положительное число | \ (\ lim \ limits _ {x \ to a} f (x) \ sqrt [n] {f (x)} = \ sqrt [n] {\ lim \ limits _ {x \ to a} [f ( x)]} = \ sqrt [n] {A} \) |
| Полиномиальная функция | \ (\ lim \ limits _ {x \ to a} p (x) = p (a) \) |
Пример \ (\ PageIndex {1} \): алгебраическое вычисление предела функции
Вычислить \ [\ lim \ limits _ {x \ to 3} (2x + 5). \ nonumber \]
\ nonumber \]
Решение
\ [\ begin {align} \ lim \ limits _ {x \ to 3} (2x + 5) & = \ lim \ limits _ {x \ to 3} (2x) + \ lim \ limits _ {x \ to 3} (5) && \ text {Свойство суммы функций} \\ & = 2 \ lim \ limits_ {x \ to 3} (x) + \ lim \ limits _ {x \ to 3} (5) && \ text {Постоянное время свойство функции} \\ & = 2 (3) +5 && \ text {Evaluate} \\ & = 11 \ end {align} \ nonumber \]
Упражнение \ (\ PageIndex {1} \):
Оцените следующий предел: \ [\ lim \ limits_ {x \ to −12} (- 2x + 2).\ nonumber \]
Решение
26
Нахождение предела многочлена
Не все функции или их пределы включают простое сложение, вычитание или умножение. Некоторые могут включать многочлены. Напомним, что многочлен — это выражение, состоящее из суммы двух или более членов, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень. Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе. 5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)?
5.2 + 6x + 8} {x − 2}) \), можем ли мы определить предел функции, когда \ (x \) приближается к \ (a \)?
Да. Некоторые функции могут быть перегруппированы алгебраически, чтобы можно было оценить предел упрощенной эквивалентной формы функции.
Определение предела частного
Нахождение предела функции, выраженной как частное, может быть более сложным. Нам часто нужно переписать функцию алгебраически, прежде чем применять свойства предела. Если знаменатель равен 0, когда мы применяем свойства предела напрямую, мы должны переписать частное в другой форме.2−6x + 8} {x − 2}) & = \ lim \ limits_ {x \ to 2} (\ dfrac {(x − 2) (x − 4)} {x − 2}) && \ text {Фактор числитель.} \\ & = \ lim \ limits_ {x \ to 2} (\ dfrac {\ cancel {(x − 2)} (x − 4)} {\ cancel {x − 2}}) && \ text {Отмените общие множители.} \\ & = \ lim \ limits_ {x \ to 2} (x − 4) && \ text {Evaluate.} \\ & = 2−4 = −2 \ end {align} \ nonumber \]
Анализ
Когда предел рациональной функции не может быть вычислен напрямую, факторизованные формы числителя и знаменателя могут упроститься до результата, который может быть вычислен. 2−11x + 28} {7 − x} \ right). \ nonumber \]
2−11x + 28} {7 − x} \ right). \ nonumber \]
Решение
\ (- 3 \)
Пример \ (\ PageIndex {5} \): оценка предела коэффициента по ЖК-дисплею
Вычислить \ [\ lim \ limits_ {x \ to 5} \ left (\ dfrac {\ frac {1} {x} — \ frac {1} {5}} {x − 5} \ right). \ nonumber \]
Решение
Найдите ЖК-дисплей для знаменателей двух членов в числителе и преобразуйте обе дроби, чтобы ЖК-дисплей был их знаменателем.
Анализ
При определении предела рациональной функции, в которой добавлены или вычтены члены в числителе или знаменателе, первым шагом является поиск общего знаменателя добавленных или вычтенных членов; затем преобразуйте оба члена в этот знаменатель или упростите рациональную функцию, умножив числитель и знаменатель на наименьший общий знаменатель.Затем проверьте, есть ли у числителя и знаменателя общие множители.
Упражнение \ (\ PageIndex {5} \):
Вычислить \ [\ lim \ limits_ {x \ to −5} \ left (\ dfrac {\ frac {1} {5} + \ frac {1} {x}} {10 + 2x} \ right). \ nonumber \]
\ nonumber \]
Решение
\ (- \ frac {1} {50} \)
как: Учитывая предел функции, содержащей корень, используйте сопряжение для вычисления
- Если данное частное не имеет неопределенной формы \ ((\ frac {0} {0}) \), оцените напрямую.
- В противном случае перепишите сумму (или разность) двух частных как одинарное частное, используя наименьший общий знаменатель (ЖКД) .
- Если числитель включает корень, рационализируйте числитель; умножьте числитель и знаменатель на , сопряженное с числителя. Напомним, что \ (a ± \ sqrt {b} \) сопряжены.
- Упростить.
- Оцените полученный предел.
Пример \ (\ PageIndex {6} \): оценка предела, содержащего корень, с помощью конъюгата
Вычислить \ [\ lim \ limits_ {x \ to 0} \ left (\ dfrac {\ sqrt {25 − x} −5} {x} \ right).\ nonumber \]
Решение
\ [\ begin {align} \ lim \ limits_ {x \ to 0} \ left (\ dfrac {\ sqrt {25 − x} −5} {x} \ right) & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {(\ sqrt {25 − x} −5)} {x} ⋅ \ frac {(\ sqrt {25 − x} +5)} {(\ sqrt {25 − x} +5 )} \ right) && \ text {Умножьте числитель и знаменатель на сопряжение. } \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {(25 − x) −25} {x (\ sqrt {25 − x} +5)} \ right) && \ text {Умножить:} (\ sqrt {25 − x} −5) ⋅ (\ sqrt {25 − x} +5) = (25 − x) — 25. \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (25 − x + 5)} \ right) && \ text {Объединить как термины.} \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (\ sqrt {25 − x} +5)} \ right) && \ text {Упростить} \ dfrac {−x} {x} = — 1. \\ & = \ dfrac {−1} {\ sqrt {25−0} +5} && \ text {Оценить.} \\ & = \ dfrac {−1} {5 + 5} = — \ dfrac {1} {10} \ end {align} \ nonumber \]
} \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {(25 − x) −25} {x (\ sqrt {25 − x} +5)} \ right) && \ text {Умножить:} (\ sqrt {25 − x} −5) ⋅ (\ sqrt {25 − x} +5) = (25 − x) — 25. \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (25 − x + 5)} \ right) && \ text {Объединить как термины.} \\ & = \ lim \ limits_ {x \ to 0} \ left (\ dfrac {- \ cancel {x}} {\ cancel {x} (\ sqrt {25 − x} +5)} \ right) && \ text {Упростить} \ dfrac {−x} {x} = — 1. \\ & = \ dfrac {−1} {\ sqrt {25−0} +5} && \ text {Оценить.} \\ & = \ dfrac {−1} {5 + 5} = — \ dfrac {1} {10} \ end {align} \ nonumber \]
Анализ
При определении предела функции с корнем в качестве одного из двух членов, которые мы не можем вычислить напрямую, подумайте о умножении числителя и знаменателя на сопряжение членов.
Упражнение \ (\ PageIndex {6} \)
Оцените следующий предел: \ (\ lim \ limits_ {h \ to 0} \ left (\ dfrac {\ sqrt {16 − h} −4} {h} \ right) \).
Решение
\ (- \ frac {1} {8} \)
Пример \ (\ PageIndex {7} \): Оценка предела коэффициента функции путем факторинга
Вычислить \ [\ lim \ limits_ {x \ to 4} \ left (\ frac {4 − x} {\ sqrt {x − 2}}} \ right). \ nonumber \]
Решение
\ [\ begin {align} \ lim \ limits_ {x \ to 4} (\ dfrac {4 − x} {\ sqrt {x} −2}) & = \ lim \ limits_ {x \ to 4} (\ dfrac {(2+ \ sqrt {x}) (2 − x)} {\ sqrt {x} −2}) && \ text {Фактор.} \\ & = \ lim \ limits_ {x \ to 4} (\ dfrac {(2+ \ sqrt {x}) (\ cancel {2− \ sqrt {x}})} {- \ cancel {(2− \ sqrt {x})}}) && \ text {Выделяем -1 из знаменателя. Упростить.} \\ & = \ lim \ limits_ {x \ to 4} — (2 + x) && \ text {Evaluate.} \\ & = — (2+ \ sqrt {4}) \\ & = — 4 \ end {align} \ nonumber \]
Анализ
Умножение на конъюгат расширит числитель; вместо этого ищите множители в числителе. Четыре — это полный квадрат, поэтому числитель имеет вид
. 2 \ nonumber \]
2 \ nonumber \]и может быть разложен на
\ [(a + b) (a − b).\ nonumber \]
Упражнение \ (\ PageIndex {7} \)
Оцените следующий предел: \ [\ lim \ limits_ {x \ to 3} \ left (\ frac {x − 3} {\ sqrt {x} — \ sqrt {3}} \ right). \ nonumber \]
Решение
\ (2 \ sqrt {3} \)
как сделать: учитывая частное с абсолютными значениями, оцените его предел
- Попробуйте разложить на множители или найти ЖК-дисплей.
- Если предел не может быть найден, выберите несколько значений рядом и по обе стороны от входа, где функция не определена.
- Используйте числовое свидетельство, чтобы оценить пределы с обеих сторон.
Пример \ (\ PageIndex {8} \): оценка предела коэффициента с абсолютными значениями
Вычислить \ [\ lim \ limits_ {x \ to 7} \ frac {| x − 7 |} {x − 7}. \ nonumber \]
Решение
Функция не определена в \ (x = 7 \), поэтому мы попробуем значения, близкие к 7 слева и справа.
Предел слева: \ [\ frac {| 6.9-7 |} {6.9-7} = \ frac {| 6.99-7 |} {6.99-7} = \ frac {| 6.+} \ frac {6 − x} {| х − 6 |}. \ nonumber \]
Решение
Ключевые понятия
- Свойства ограничений могут использоваться для выполнения операций над пределами функций, а не с самими функциями. См. Пример.
- Предел полиномиальной функции можно найти, найдя сумму пределов отдельных членов. См. Пример и Пример.
- Предел функции, возведенный в степень, равен той же степени, что и предел функции.Другой метод — прямая подмена. См. Пример.
- Предел корня функции равен соответствующему корню предела функции.
- Один из способов найти предел функции, выраженной как частное, — это записать частное в факторизованной форме и упростить. См. Пример.
- Другой метод определения предела сложной дроби — найти ЖК-дисплей. См. Пример.
- Предел, содержащий функцию, содержащую корень, может быть вычислен с использованием конъюгата.
 См. Пример.
См. Пример. - Пределы некоторых функций, выраженные в виде частных, можно найти с помощью факторизации. См. Пример.
- Один из способов оценить предел частного, содержащего абсолютные значения, — использовать числовое свидетельство. Также может быть полезна его настройка по частям. См. Пример.
Глоссарий
- свойства лимитов
- Сборник теорем для нахождения пределов функций путем выполнения математических операций над пределами
Исчисление I — Предел
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-2: Предел
В предыдущем разделе мы рассмотрели несколько проблем, и в обеих задачах у нас была функция (наклон в случае касательной задачи и средняя скорость изменения в задаче скорости изменения), и мы хотели знать, как эта функция ведет себя в некоторая точка \ (x = a \).На этом этапе игры нас больше не волнует, откуда взялись функции, и нас больше не волнует, увидим мы их в будущем или нет. Все, что нам нужно знать или о чем беспокоиться, — это то, что у нас есть эти функции, и мы хотим что-то о них знать.
Чтобы ответить на вопросы в последнем разделе, мы выбираем значения \ (x \), которые все ближе и ближе к \ (x = a \), и вставляем их в функцию. Мы также убедились, что мы посмотрели на значения \ (x \), которые были как слева, так и справа от \ (x = a \).2} + 25}} {{t — 5}} = 15 \]
В этих обозначениях мы заметим, что мы всегда указываем функцию, с которой работаем, а также указываем значение \ (x \) (или \ (t \)), к которому мы движемся.
В этом разделе мы собираемся применить интуитивный подход к ограничениям и постараемся понять, что они собой представляют и что они могут рассказать нам о функции. Помня об этой цели, мы пока не будем вдаваться в подробности того, как на самом деле вычислять пределы. Вместо этого мы будем полагаться на то, что мы сделали в предыдущем разделе, а также на другой подход, чтобы угадать значение пределов.
Оба подхода, которые мы собираемся использовать в этом разделе, призваны помочь нам понять, что такое ограничения. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления пределов, и во многих случаях их может быть очень сложно использовать даже для оценки значения предела и / или иногда мы даем неправильное значение. Мы рассмотрим фактически вычисляемые пределы в нескольких разделах.
Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления пределов, и во многих случаях их может быть очень сложно использовать даже для оценки значения предела и / или иногда мы даем неправильное значение. Мы рассмотрим фактически вычисляемые пределы в нескольких разделах.
Давайте сначала начнем со следующего «определения» лимита.
Определение
Мы говорим, что предел \ (f (x) \) равен \ (L \), когда \ (x \) приближается к \ (a \), и записываем это как
\ [\ mathop {\ lim} \ limits_ {x \ to a} f \ left (x \ right) = L \]при условии, что мы можем сделать \ (f (x) \) настолько близким к \ (L \), насколько мы хотим, для всех \ (x \), достаточно близких к \ (a \), с обеих сторон, фактически не позволяя \ (x \) быть \ (а \).
Это не точное определение предела. Если вы хотите увидеть более точное и математическое определение лимита, вам следует ознакомиться с разделом «Определение лимита» в конце этой главы. Приведенное выше определение является скорее «рабочим» определением. Это определение помогает нам понять, что такое ограничения и что они могут сказать нам о функциях.
Приведенное выше определение является скорее «рабочим» определением. Это определение помогает нам понять, что такое ограничения и что они могут сказать нам о функциях.
Так что же означает это определение? Что ж, предположим, что мы знаем, что предел действительно существует.Согласно нашему «рабочему» определению, мы можем решить, насколько близко к \ (L \) мы хотим сделать \ (f (x) \). В качестве аргумента предположим, что мы хотим сделать \ (f (x) \) не более чем на 0,001 от \ (L \). Это означает, что нам нужен один из следующих
\ [\ begin {array} {lcl} f \ left (x \ right) — L Теперь, согласно «рабочему» определению, это означает, что если мы получим \ (x \) достаточно близко к \ (a \), мы можем сделайте одно из вышеперечисленных истинным. Однако на самом деле это говорит немного больше.Он говорит, что где-то в мире есть значение \ (x \), скажем \ (X \), так что для всех \ (x \), которые ближе к \ (a \), чем \ (X \), то одно из приведенных выше утверждений будет верным.
Это довольно важная идея. В мире существует множество функций, которые мы можем сделать как можно ближе к \ (L \) для определенных значений \ (x \), которые близки к \ (a \), но будут и другие значения \ (x \) ближе к \ (a \), которые дают значения функций, далеко не близкие к \ (L \).Чтобы предел существовал, как только мы получим \ (f (x) \) настолько близко к \ (L \), насколько мы хотим для некоторого \ (x \), тогда ему нужно будет оставаться в таком близком к \ (L \) ) (или приблизиться) для всех значений \ (x \), которые ближе к \ (a \). Мы увидим пример этого позже в этом разделе.
В несколько более простых терминах определение говорит, что по мере того, как \ (x \) становится все ближе и ближе к \ (x = a \) (с обеих сторон, конечно …), то \ (f (x) \) должен приближаться. и ближе к \ (L \). Или, когда мы приближаемся к \ (x = a \), тогда \ (f (x) \) должно быть двигаться к \ (L \).
Важно еще раз отметить, что мы должны смотреть на значения \ (x \), которые находятся по обе стороны от \ (x = a \). Мы также должны отметить, что нам не разрешено использовать \ (x = a \) в определении. Мы часто будем использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в \ (x = a \), но само ограничение не связано с тем, что на самом деле происходит в \ (x = a \) . Предел касается только того, что происходит вокруг точки \ (x = a \). Это важное понятие об ограничениях, которое нам нужно иметь в виду.
Мы также должны отметить, что нам не разрешено использовать \ (x = a \) в определении. Мы часто будем использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в \ (x = a \), но само ограничение не связано с тем, что на самом деле происходит в \ (x = a \) . Предел касается только того, что происходит вокруг точки \ (x = a \). Это важное понятие об ограничениях, которое нам нужно иметь в виду.
Альтернативное обозначение, которое мы иногда будем использовать для обозначения пределов, —
. \ [f (x) \ to L \ hspace {0,25 дюйма} {\ rm {as}} \ hspace {0,25in} x \ to a \] Как мы можем использовать это определение, чтобы помочь нам оценить пределы? Мы делаем именно то, что делали в предыдущем разделе. Мы берем \ (x \) по обе стороны от \ (x = a \), которые перемещаются все ближе и ближе к \ (a \), и вставляем их в нашу функцию. Затем мы смотрим, можем ли мы определить, к какому числу движутся значения функции, и используем это в качестве нашей оценки. 2} — 2x}} \]
Показать решение
2} — 2x}} \]
Показать решение
Обратите внимание, что мы сказали «оценка значения лимита». Опять же, в этом разделе мы не собираемся напрямую вычислять пределы. Цель этого раздела — дать нам лучшее представление о том, как работают ограничения и что они могут рассказать нам о функции.
Итак, имея это в виду, мы будем работать с этим почти так же, как в предыдущем разделе. Мы выберем значения \ (x \), которые становятся все ближе и ближе к \ (x = 2 \), и подставим эти значения в функцию.Это дает следующую таблицу значений.
| \ (х \) | \ (е (х) \) | \ (х \) | \ (е (х) \) |
|---|---|---|---|
| 2,5 | 3,4 | 1,5 | 5,0 |
| 2,1 | 3.857142857 | 1. 9 9 | 4,157894737 |
| 2,01 | 3.985074627 | 1,99 | 4.015075377 |
| 2,001 | 3.998500750 | 1,999 | 4,001500750 |
| 2.0001 | 3.999850007 | 1,9999 | 4.000150008 |
| 2,00001 | 3.999985000 | 1,99999 | 4,000015000 |
Обратите внимание, что мы убедились и выбрали значения \ (x \), которые были по обе стороны от \ (x = 2 \), и что мы переместились очень близко к \ (x = 2 \), чтобы убедиться, что любые тенденции, которые мы можем наблюдать, на самом деле верны.2} — 2x}} = 4 \]
Давайте еще немного подумаем о том, что здесь происходит. Давайте изобразим график функции из последнего примера. График функции в интересующем диапазоне значений \ (x \) показан ниже.
Давайте изобразим график функции из последнего примера. График функции в интересующем диапазоне значений \ (x \) показан ниже.
Во-первых, обратите внимание на довольно большую открытую точку в точке \ (x = 2 \). Это нужно для того, чтобы напомнить нам, что функции (и, следовательно, графика) не существует в \ (x = 2 \).
Когда мы вставляли значения \ (x \) в функцию, мы фактически перемещаемся по графику в направлении точки как \ (x = 2 \).Это показано на графике двумя стрелками на графике, которые перемещаются к точке.
Когда мы вычисляем ограничения, мы действительно задаемся вопросом, к какому значению \ (y \) приближается наш график, когда мы приближаемся к \ (x = a \) на нашем графике. Мы НЕ спрашиваем, какое значение \ (y \) принимает график в рассматриваемой точке. Другими словами, мы спрашиваем, что делает график вокруг точки \ (x = a \). В нашем случае мы можем видеть, что по мере того, как \ (x \) приближается к 2 (с обеих сторон), функция приближается к \ (y = 4 \), хотя сама функция даже не существует в \ (x = 2 \ ). Таким образом, можно сказать, что ограничение на самом деле составляет 4.
Таким образом, можно сказать, что ограничение на самом деле составляет 4.
Итак, что мы узнали об ограничениях? Пределы спрашивают, что делает функция вокруг \ (x = a \), и не связаны с тем, что функция на самом деле делает в \ (x = a \). Это хорошо, поскольку многие функции, которые мы рассмотрим, даже не будут существовать в \ (x = a \), как мы видели в нашем последнем примере.
Давайте рассмотрим еще один пример, чтобы доказать это.
Пример 2 Оцените значение следующего предела.2} — 2x}} & {\ mbox {if}} x \ ne 2 \\ 6 & {\ mbox {if}} x = 2 \ end {array} \ right. \] Показать решениеПрежде всего, следует отметить, что это точно такая же функция, как и в первом примере, за исключением того, что мы присвоили ей значение для \ (x = 2 \). Итак, сначала отметим, что
\ [g \ left (2 \ right) = 6 \] Что касается оценки значения этого лимита, то по сравнению с первым примером ничего не изменилось. Мы могли бы составить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение лимита.
Мы могли бы составить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение лимита.
Давайте сначала взглянем на таблицу значений и посмотрим, что она нам говорит. Обратите внимание, что наличие значения функции в \ (x = 2 \) не изменит наш выбор для \ (x \). Мы выбираем только значения \ (x \), которые приближаются к \ (x = 2 \), но никогда не берем \ (x = 2 \). Другими словами, таблица значений, которую мы использовали в первом примере, будет точно такой же, как и здесь.Итак, поскольку мы уже сделали это один раз, нет причин переделывать его здесь.
Из этой таблицы снова ясно, что предел равен
. \ [\ mathop {\ lim} \ limits_ {x \ to 2} g \ left (x \ right) = 4 \] Предел НЕ 6! Помните из обсуждения после первого примера, что ограничения не заботятся о том, что функция на самом деле делает в рассматриваемой точке. Пределы касаются только того, что происходит на около точки.Поскольку единственное, что мы изменили в функции, — это ее поведение при \ (x = 2 \), это не изменит предел.
Пределы касаются только того, что происходит на около точки.Поскольку единственное, что мы изменили в функции, — это ее поведение при \ (x = 2 \), это не изменит предел.
Давайте также быстро взглянем на график этой функции, чтобы убедиться, что это то же самое.
Опять же, мы можем видеть, что по мере того, как мы приближаемся к \ (x = 2 \) на нашем графике, функция все еще приближается к значению \ (y \), равному 4. Помните, что мы только спрашиваем, что функция делает вокруг \ (x = 2 \), и нам все равно, что функция на самом деле делает в \ (x = 2 \).График также подтверждает вывод о том, что предел составляет
. \ [\ mathop {\ lim} \ limits_ {x \ to 2} g \ left (x \ right) = 4 \] Давайте еще раз поговорим об этом, чтобы убедиться, что мы его поняли. Пределы , а не , связанные с тем, что происходит в \ (x = a \). Ограничения касаются только того, что происходит на около \ (x = a \). Мы постоянно говорим об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить.Итак, мы воспользуемся любой возможностью, чтобы напомнить себе об этой идее.
Ограничения касаются только того, что происходит на около \ (x = a \). Мы постоянно говорим об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить.Итак, мы воспользуемся любой возможностью, чтобы напомнить себе об этой идее.
Поскольку ограничения не связаны с тем, что на самом деле происходит в \ (x = a \), мы иногда будем видеть ситуации, подобные предыдущему примеру, где предел в точке и значение функции в точке различаются. Конечно, это не всегда будет происходить. Бывают случаи, когда значение функции и предел в точке совпадают, и в конечном итоге мы увидим несколько таких примеров. Однако важно не волноваться из-за того, что функция и предел не принимают одно и то же значение в одной точке.Иногда такое случается, поэтому нам нужно иметь возможность разбираться в тех случаях, когда они возникают.
Давайте взглянем на другой пример, чтобы попытаться опровергнуть эту идею.
Пример 3 Оцените значение следующего предела. \ [\ mathop {\ lim} \ limits _ {\ theta \ to 0} \, \ frac {{1 — \ cos \ left (\ theta \ right)}} {\ theta} \]
Показать решение
\ [\ mathop {\ lim} \ limits _ {\ theta \ to 0} \, \ frac {{1 — \ cos \ left (\ theta \ right)}} {\ theta} \]
Показать решениеВо-первых, не волнуйтесь о функции \ (\ theta \) in. Это просто буква, как \ (x \) буква! Это греческая буква, но это буква, и иногда вам будет предложено работать с греческими буквами, так что на этом этапе неплохо было бы начать к ним привыкать.
Теперь также обратите внимание, что если мы подключим \ (\ theta = 0 \), мы получим деление на ноль, и поэтому функция в данный момент не существует. На самом деле, в этот момент мы получаем 0/0, но из-за деления на ноль этой функции не существует в \ (\ theta = 0 \).
Итак, как мы это сделали в первом примере, давайте возьмем таблицу значений и посмотрим, что, если мы сможем угадать, к какому значению движется функция.
| \ (\ theta \) | \ (е \ влево (\ тета \ вправо) \) | \ (\ theta \) | \ (е \ влево (\ тета \ вправо) \) |
|---|---|---|---|
| 1 | 0. 45969769 45969769 | –1 | -0,45969769 |
| 0,1 | 0,04995835 | -0,1 | -0,04995835 |
| 0,01 | 0,00499996 | -0,01 | -0,00499996 |
| 0,001 | 0.00049999 | -0,001 | -0,00049999 |
Хорошо, похоже, что функция приближается к нулю, поскольку \ (\ theta \) приближается к 0, конечно с обеих сторон.
Следовательно, предположим, что предел имеет значение
\ [\ mathop {\ lim} \ limits _ {\ theta \ to 0} \, \ frac {{1 — \ cos \ left (\ theta \ right)}} {\ theta} = 0 \]Итак, еще раз, предел имел значение, даже если функция не существовала в интересующей нас точке.
Пришло время поработать еще пару примеров, которые приведут нас к следующему представлению об ограничениях, которое мы собираемся обсудить.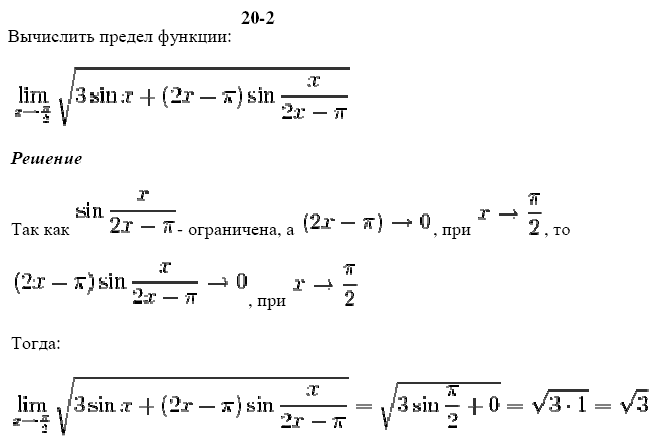
Давайте составим таблицу значений и посмотрим, что в этом случае происходит с нашей функцией.
| \ (т \) | \ (f (t) \) | \ (т \) | \ (f (t) \) |
|---|---|---|---|
| 1 | –1 | –1 | –1 |
| 0.1 | 1 | -0,1 | 1 |
| 0,01 | 1 | -0,01 | 1 |
| 0,001 | 1 | -0,001 | 1 |
Теперь, если бы мы угадали предел из этой таблицы, мы бы предположили, что предел равен 1. Однако, если бы мы сделали это предположение, мы ошиблись бы. Рассмотрим любую из следующих оценок функций.
Однако, если бы мы сделали это предположение, мы ошиблись бы. Рассмотрим любую из следующих оценок функций.
Во всех трех оценках функции мы оценили функцию с числом меньше 0,001 и получили три совершенно разных числа. Напомним, что определение предела, с которым мы работаем, требует, чтобы функция приближалась к единственному значению (наше предположение) по мере приближения \ (t \) к рассматриваемой точке.Это не говорит о том, что только некоторые значения функции должны приближаться к предположению. Он говорит, что все значения функций должны приближаться к нашему предположению.
Было бы удобно увидеть, что здесь происходит, на графике функции.
Из этого графика мы можем видеть, что по мере того, как мы приближаемся к \ (t = 0 \), функция начинает дико колебаться, и на самом деле колебания увеличиваются по скорости по мере приближения к \ (t = 0 \), которое мы получаем. Вспомните из нашего определения предела, что для существования предела функция должна устанавливаться в сторону одного значения по мере того, как мы приближаемся к рассматриваемой точке.
Вспомните из нашего определения предела, что для существования предела функция должна устанавливаться в сторону одного значения по мере того, как мы приближаемся к рассматриваемой точке.
Очевидно, что эта функция не сводится к одному номеру, поэтому этот предел не существует !
Этот последний пример указывает на недостаток простого выбора значений переменной и использования таблицы значений функций для оценки значения предела.Значения переменной, которые мы выбрали в предыдущем примере, были действительными и на самом деле, вероятно, были значениями, которые многие выбрали бы. Фактически, это были точно такие же значения, которые мы использовали в задаче до этой, и они работали в этой задаче!
При использовании таблицы значений всегда будет вероятность того, что мы не выберем правильные значения и что мы будем неправильно угадывать наш предел. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение лимитов. Фактически, это такая проблема, что после этого раздела мы никогда не будем использовать таблицу значений, чтобы снова угадать значение лимита.
Фактически, это такая проблема, что после этого раздела мы никогда не будем использовать таблицу значений, чтобы снова угадать значение лимита.
Этот последний пример также показал нам, что ограничения не должны существовать. До этого момента мы видели только существующие ограничения, но это не всегда так.
Давайте взглянем на еще один пример в этом разделе.
Пример 5 Оцените значение следующего предела. \ [\ mathop {\ lim} \ limits_ {t \ to 0} H \ left (t \ right) \ hspace {0.25 дюймов} {\ mbox {где,}} \ hspace {0,25 дюйма} H \ left (t \ right) = \ left \ {\ begin {array} {ll} 0 & {\ mbox {if}} t Показать решениеЭта функция часто называется функцией Heaviside или step . Мы могли бы использовать таблицу значений для оценки предела, но в этом случае, вероятно, так же быстро можно использовать график, так что давайте сделаем это. Ниже представлен график этой функции.
Из графика видно, что если мы приближаемся к \ (t = 0 \) с правой стороны, функция приближается к значению \ (y \), равному 1. На самом деле он просто остается на уровне 1, но в терминологии, которую мы использовали в этом разделе, он приближается к 1…
На самом деле он просто остается на уровне 1, но в терминологии, которую мы использовали в этом разделе, он приближается к 1…
Кроме того, если мы переместимся в сторону \ (t = 0 \) слева, функция будет двигаться в направлении значения \ (y \), равного 0.
Согласно нашему определению предела, функция должна приближаться к одному значению, когда мы приближаемся к \ (t = a \) (с обеих сторон). В данном случае этого не происходит, поэтому в этом примере мы также скажем, что ограничения не существует.
Обратите внимание, что ограничение в этом примере немного отличается от предыдущего. В предыдущем примере функция не сводилась к одному числу, когда мы приближались к \ (t = 0 \). Однако в этом примере функция сводится к одному числу как \ (t = 0 \) с обеих сторон. Проблема в том, что число разное с каждой стороны от \ (t = 0 \). Это идея, которую мы рассмотрим более подробно в следующем разделе.
Давайте подведем итог тому, что мы (надеюсь) узнали в этом разделе.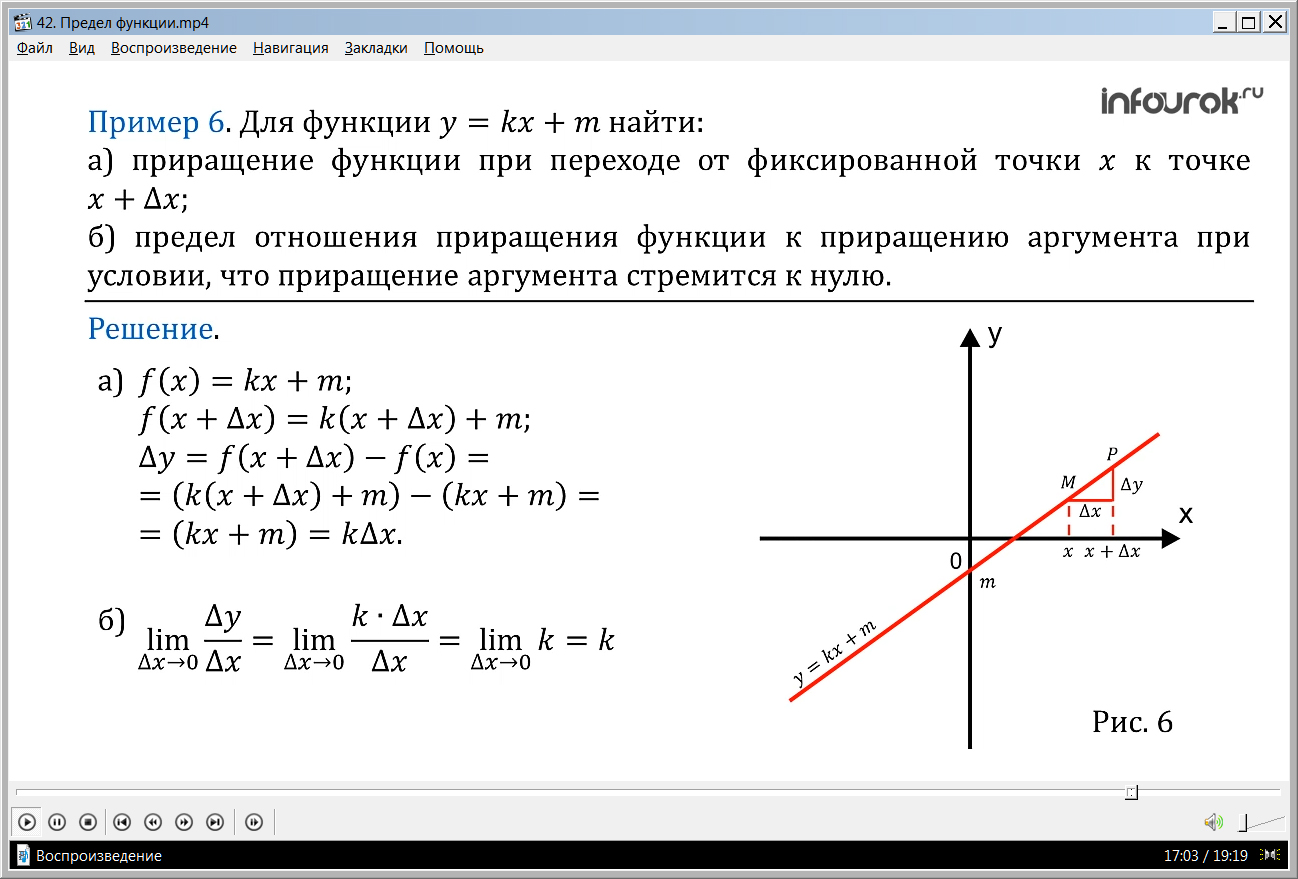 В первых трех примерах мы видели, что ограничения не заботятся о том, что функция на самом деле делает в рассматриваемой точке. Их беспокоит только то, что происходит вокруг точки. Фактически, у нас могут быть пределы в \ (x = a \), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет причин (на этом этапе) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в одной точке, а в других случаях — разные значения.
В первых трех примерах мы видели, что ограничения не заботятся о том, что функция на самом деле делает в рассматриваемой точке. Их беспокоит только то, что происходит вокруг точки. Фактически, у нас могут быть пределы в \ (x = a \), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет причин (на этом этапе) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в одной точке, а в других случаях — разные значения.
Далее, в третьем и четвертом примерах мы увидели основную причину отказа от использования таблицы значений для определения значения лимита. В этих примерах мы использовали точно такой же набор значений, однако они работали только в одном из примеров. Использование таблиц значений для угадывания значения лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы это сделаем. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.
Последние два примера показали нам, что на самом деле не все ограничения существуют.Мы не должны зацикливаться на идее, что ограничения будут существовать всегда. В большинстве курсов по математике мы работаем с ограничениями, которые существуют почти всегда, поэтому легко начать думать, что пределы существуют всегда. Ограничения существуют не всегда, поэтому не привыкайте предполагать, что они будут.
Наконец, в четвертом примере мы увидели, что единственный способ справиться с ограничением — это построить график функции. Иногда это единственный способ, однако этот пример также проиллюстрировал недостаток использования графиков.Чтобы использовать график, чтобы угадать значение предела, вам нужно иметь возможность на самом деле нарисовать график. Для многих функций это сделать не так просто.
Есть еще один недостаток в использовании графиков. Даже если у вас есть график, он будет полезен, только если значение \ (y \) приближается к целому числу. Если значение \ (y \) приближается, скажем, \ (\ frac {{- 15}} {{123}} \), вы никак не сможете угадать это значение по графику, а мы обычно требуются точные значения для наших пределов.
Если значение \ (y \) приближается, скажем, \ (\ frac {{- 15}} {{123}} \), вы никак не сможете угадать это значение по графику, а мы обычно требуются точные значения для наших пределов.
Итак, хотя графики функций могут иногда облегчить вам жизнь при угадывании значений пределов, они снова, вероятно, не лучший способ получить значения пределов. Они будут полезны только в том случае, если вы сможете их достать, а значение лимита — «хорошее» число.
Возникает естественный вопрос, почему мы вообще говорили об использовании таблиц и / или графиков для оценки пределов, если они не являются лучшим способом. На то было несколько причин.
Во-первых, они могут помочь нам лучше понять, что такое ограничения и что они могут нам сказать.Если мы не сделаем хотя бы пару ограничений таким образом, мы не сможем получить все хорошее представление о том, что это за пределы.
Вторая причина использования ограничений таким образом — указать на их недостатки, чтобы у нас не возникало соблазна использовать их все время!
В конце концов мы поговорим о том, как мы действительно устанавливаем лимиты. Однако есть еще одна тема, которую мы должны обсудить, прежде чем делать это. Поскольку этот раздел уже существует некоторое время, мы поговорим об этом в следующем разделе.
Однако есть еще одна тема, которую мы должны обсудить, прежде чем делать это. Поскольку этот раздел уже существует некоторое время, мы поговорим об этом в следующем разделе.
Исчисление III — Пределы
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Пределы
В этом разделе мы рассмотрим ограничения, связанные с функциями более чем одной переменной. Фактически, мы сконцентрируемся в основном на пределах функций от двух переменных, но идеи могут быть распространены на функции с более чем двумя переменными.-}} е \ влево (х \ вправо) \]
является левым пределом и требует, чтобы мы смотрели только на значения \ (x \), которые меньше \ (a \).
Другими словами, у нас будет \ (\ mathop {\ lim} \ limits_ {x \ to a} f \ left (x \ right) = L \) при условии \ (f \ left (x \ right) \) подходов \ (L \) по мере продвижения к \ (x = a \) (не допуская \ (x = a \)) с обеих сторон.
Теперь обратите внимание, что в этом случае есть только два пути, по которым мы можем идти по направлению к \ (x = a \). Мы можем войти либо слева, либо справа.Затем, чтобы существовал предел функции одной переменной, функция должна приближаться к тому же значению, что и каждый из этих путей в направлении \ (x = a \).
С функциями двух переменных нам придется проделать нечто подобное, за исключением того, что на этот раз (потенциально) потребуется гораздо больше работы. Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в такого рода ограничениях.
Мы будем просить принять предел функции \ (f \ left ({x, y} \ right) \), когда \ (x \) приближается к \ (a \) и когда \ (y \) приближается к \ ( б \).Это можно записать несколькими способами. Вот пара наиболее стандартных обозначений.
\ [\ mathop {\ lim} \ limits_ {x \ to a \ atop y \ to b} f \ left ({x, y} \ right) \ hspace {0.5in} \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) \] В этом курсе мы будем чаще использовать второе обозначение. Второе обозначение также немного более полезно для иллюстрации того, что мы на самом деле делаем здесь, когда принимаем предел.Принимая предел функции двух переменных, мы действительно спрашиваем, что делает значение \ (f \ left ({x, y} \ right) \), когда мы перемещаем точку \ (\ left ({x, y } \ right) \) все ближе и ближе к точке \ (\ left ({a, b} \ right) \), фактически не позволяя ей быть \ (\ left ({a, b} \ right) \).
Как и в случае с ограничениями функций одной переменной, для существования этого ограничения функция должна приближаться к одному и тому же значению независимо от пути, который мы выбираем, когда приближаемся к \ (\ left ({a, b} \ верно)\).Проблема, с которой мы сразу же сталкиваемся, заключается в том, что существует буквально бесконечное количество путей, по которым мы можем идти по направлению к \ (\ left ({a, b} \ right) \). Вот несколько примеров путей, по которым мы могли бы пойти.
Мы добавили пару прямых путей, а также пару «незнакомых» путей, которые не являются прямыми путями. Кроме того, мы включили сюда только 6 путей, и, как вы можете видеть, просто варьируя наклон прямых путей, их бесконечное количество, и тогда нам нужно будет рассмотреть пути, которые не являются прямыми путями.
Другими словами, чтобы показать, что ограничение существует, нам технически необходимо проверить бесконечное количество путей и убедиться, что функция приближается к одному и тому же значению, независимо от пути, который мы используем для приближения к точке.
К счастью для нас, мы можем использовать одну из основных идей из пределов Calculus I, чтобы помочь нам установить пределы здесь.
Определение
Функция \ (f \ left ({x, y} \ right) \) является непрерывной в точке \ (\ left ({a, b} \ right) \) если,
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) = f \ left ({a, b} \ right) \]С графической точки зрения это определение означает то же самое, что и тогда, когда мы впервые увидели непрерывность в исчислении I.Функция будет непрерывной в точке, если на графике нет дыр или разрывов в этой точке.
Как это может помочь нам установить ограничения? Как и в исчислении I, если вы знаете, что функция непрерывна в \ (\ left ({a, b} \ right) \), то вы также знаете, что
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({a, b} \ right)} f \ left ({x, y} \ right) = f \ left ({a, b} \ right) \] должно быть правдой. Итак, если мы знаем, что функция непрерывна в точке, все, что нам нужно сделать, чтобы взять предел функции в этой точке, — это вставить точку в функцию.
Итак, если мы знаем, что функция непрерывна в точке, все, что нам нужно сделать, чтобы взять предел функции в этой точке, — это вставить точку в функцию.
Все стандартные функции, которые, как нам известно, являются непрерывными, остаются непрерывными, даже если мы сейчас подключаем более одной переменной. Нам просто нужно следить за делением на ноль, квадратными корнями из отрицательных чисел, логарифмами нуля или отрицательных чисел, и т. Д.
Обратите внимание, что идея путей — это то, о чем мы не должны забывать, поскольку это хороший способ определить, не существует ли ограничения. Если мы сможем найти два пути, по которым функция приближается к разным значениям, когда мы приближаемся к точке, мы будем знать, что предела не существует.2} \ left ({- 1} \ right) + \ left (1 \ right) \ left (2 \ right) \ cos \ left ({2 \ pi + \ pi} \ right) = — 14 \]
б \ (\ displaystyle \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({5,1} \ right)} \ frac {{xy}} {{x + y}} \) Показать решение
В этом случае функция не будет непрерывной вдоль линии \ (y = — x \), поскольку мы получим деление на ноль, когда это верно. Однако для этой проблемы нам не стоит беспокоиться об этом, поскольку точка, в которой мы принимаем предел, находится не на этой линии.
Однако для этой проблемы нам не стоит беспокоиться об этом, поскольку точка, в которой мы принимаем предел, находится не на этой линии.
Следовательно, все, что нам нужно сделать, это подключить точку, поскольку функция в этой точке является непрерывной.
\ [\ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({5,1} \ right)} \ frac {{xy}} {{x + y}} = \ frac {5} {6} \]В предыдущем примере не было никаких ограничений. Функции были непрерывными в рассматриваемой точке, поэтому все, что нам нужно было сделать, это подключить точку. Это, конечно, не всегда так, поэтому давайте рассмотрим несколько примеров, которые более типичны из тех, что вы здесь увидите.2}}} \] Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке (явно деление на ноль). Однако это не означает, что ограничение невозможно. Мы видели много примеров этого в исчислении I, где функция не была непрерывной в рассматриваемой точке, но предел все же существовал. 2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1, 1} \ right)} \ frac {{\ left ({2x + y} \ right) \ left ({x — y} \ right)}} {{\ left ({x — y} \ right) \ left ( {x + y} \ right)}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{x + y}} \]
2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1, 1} \ right)} \ frac {{\ left ({2x + y} \ right) \ left ({x — y} \ right)}} {{\ left ({x — y} \ right) \ left ( {x + y} \ right)}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{x + y}} \]
Итак, как мы видели во многих примерах в исчислении I, после разложения на множители и отмены общих множителей мы приходим к функции, которая на самом деле может принимать предел.2}}} = \ mathop {\ lim} \ limits _ {\ left ({x, y} \ right) \ to \ left ({1,1} \ right)} \ frac {{2x + y}} {{ х + у}} = \ гидроразрыва {3} {2} \]
Прежде чем мы перейдем к следующему набору примеров, мы должны отметить, что ситуация в предыдущем примере — это то, что обычно происходило во многих предельных примерах / задачах в исчислении I. Однако в исчислении III это, как правило, исключение в примерах / проблемы, как покажет следующий набор примеров. Другими словами, не следует ожидать, что большинство из этих типов ограничений будут просто множителями, а затем будут существовать, как в Исчислении I.4}}} \) Показать решение
Другими словами, не следует ожидать, что большинство из этих типов ограничений будут просто множителями, а затем будут существовать, как в Исчислении I.4}}} \) Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке, и поэтому мы не можем просто вставить точку. Также обратите внимание, что, в отличие от предыдущего примера, мы не можем факторизовать эту функцию и выполнить некоторую отмену, чтобы можно было взять лимит.
Следовательно, поскольку функция не является непрерывной в данной точке и поскольку мы не можем выполнить факторинг, существует, по крайней мере, шанс, что предел не существует. Если бы мы могли найти два разных пути для приближения к точке, которая дает разные значения для предела, мы бы знали, что предела не существует.Два наиболее распространенных пути для проверки — это оси \ (x \) и \ (y \), поэтому давайте попробуем их.
Перед тем, как это сделать, нам нужно выяснить, что именно мы имеем в виду, когда говорим, что собираемся приблизиться к точке на пути. Когда мы приближаемся к точке на пути, мы сделаем это, зафиксировав \ (x \) или \ (y \), или связав \ (x \) и \ (y \) с помощью некоторой функции. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из Исчисления I.4}}} = \ mathop {\ lim} \ limits _ {\ left ({0, y} \ right) \ to \ left ({0,0} \ right)} 0 = 0 \]
Когда мы приближаемся к точке на пути, мы сделаем это, зафиксировав \ (x \) или \ (y \), или связав \ (x \) и \ (y \) с помощью некоторой функции. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из Исчисления I.4}}} = \ mathop {\ lim} \ limits _ {\ left ({0, y} \ right) \ to \ left ({0,0} \ right)} 0 = 0 \]
Итак, один и тот же предел по двум путям. Не поймите это неправильно. Это НЕ означает, что предел существует и имеет нулевое значение. Это означает только то, что предел имеет одно и то же значение на двух путях.
Давайте взглянем на третий довольно распространенный путь. В этом случае мы будем двигаться к началу координат по пути \ (y = x \). Это то, что мы имели в виду ранее, говоря о соотношении \ (x \) и \ (y \) через функцию.4}}} = \ mathop {\ lim} \ limits _ {\ left ({x, x} \ right) \ to \ left ({0,0} \ right)} \ frac {1} {4} = \ frac {1} {4} \]
Значит, значение отличается от двух предыдущих путей, и это означает, что ограничение не может существовать. 2}}} \) Показать решение
2}}} \) Показать решение
Хорошо, с этим последним у нас снова есть проблемы с непрерывностью в источнике, и снова нет факторинга, который мы можем сделать, который позволил бы взять предел.3}} \ right) \ to \ left ({0,0} \ right)} \ frac {1} {2} = \ frac {1} {2} \]
Теперь у нас есть два пути, которые дают разные значения предела, поэтому предела не существует.
Как показал этот предел, мы можем и часто должны использовать пути, отличные от строк, как мы это делали в первой части этого примера.
Итак, как мы видели в предыдущем примере, ограничения здесь немного отличаются от тех, которые мы видели в исчислении I. Пределы нескольких переменных может быть довольно сложно оценить, и мы показали несколько примеров, где потребовалась небольшая работа. чтобы показать, что предела не существует.
В поисках предела — Бесплатная справка по математике
Что такое предел?
Предел — это определенное значение, к которому приближается функция. Поиск предела обычно означает определение значения y, когда x приближается к определенному числу. Вы обычно можете сформулировать это как что-то вроде «предел функции f (x) равен 7, когда x приближается к бесконечности. Например, представьте себе такую кривую, когда x приближается к бесконечности, эта кривая приближается к y = 0, в то время как никогда действительно добираюсь туда.Итак, как нам алгебраически найти этот предел? Один из способов найти предел — использовать метод подстановки .
Поиск предела обычно означает определение значения y, когда x приближается к определенному числу. Вы обычно можете сформулировать это как что-то вроде «предел функции f (x) равен 7, когда x приближается к бесконечности. Например, представьте себе такую кривую, когда x приближается к бесконечности, эта кривая приближается к y = 0, в то время как никогда действительно добираюсь туда.Итак, как нам алгебраически найти этот предел? Один из способов найти предел — использовать метод подстановки .
Например, предел следующего графика равен 0, когда x приближается к бесконечности, что хорошо видно, когда график приближается к 0, вот так:
Теперь давайте рассмотрим несколько примеров, где мы можем найти предел реальных функций:
Пример A
Найдите предел \ (f (x) = 4x \), когда x стремится к 3.
Шагов:
1) Заменить x на 3.
2) Упростить.2-7x} {x} = \ frac {x (6x-7)} {x} = 6x-7 $$
Мы отменили множитель x в числителе и знаменателе, оставив нам простой предел:
$$ \ lim_ {x \ to0} (6x-7) $$Теперь мы можем заменить x на 0, чтобы найти предел -7:
$$ \ lim_ {x \ to0} (6x-7) = -7 $$ Примечание. Несмотря на то, что мы смогли упростить функцию в примере C с помощью факторинга, мы не можем делать вид, что этого не произошло. Помните, что мы находили предел, когда x приближался к 0, а не пытались оценить функцию AT x = 0.Функция все еще не определена при x = 0. Однако у него есть предел. Только упрощенная версия имеет решение при x = 0. Только после факторинга, в некоторых случаях, мы можем применить замену, чтобы найти предел.
Несмотря на то, что мы смогли упростить функцию в примере C с помощью факторинга, мы не можем делать вид, что этого не произошло. Помните, что мы находили предел, когда x приближался к 0, а не пытались оценить функцию AT x = 0.Функция все еще не определена при x = 0. Однако у него есть предел. Только упрощенная версия имеет решение при x = 0. Только после факторинга, в некоторых случаях, мы можем применить замену, чтобы найти предел.
Предоставлено г-ном Feliz
.

 Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
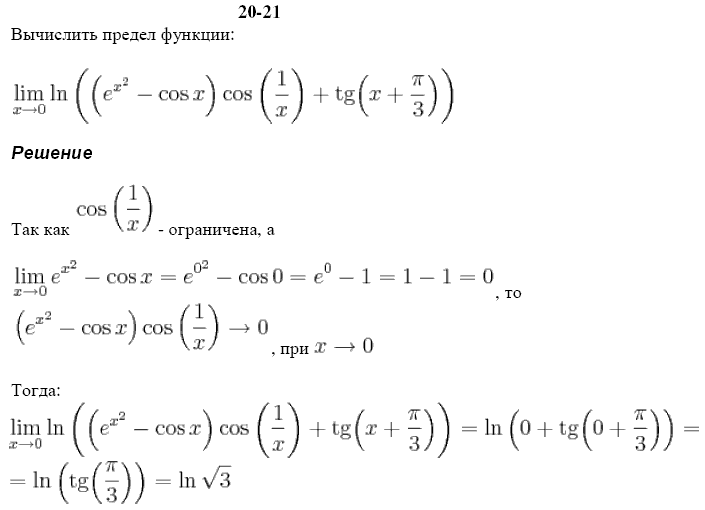


 Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .
Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .
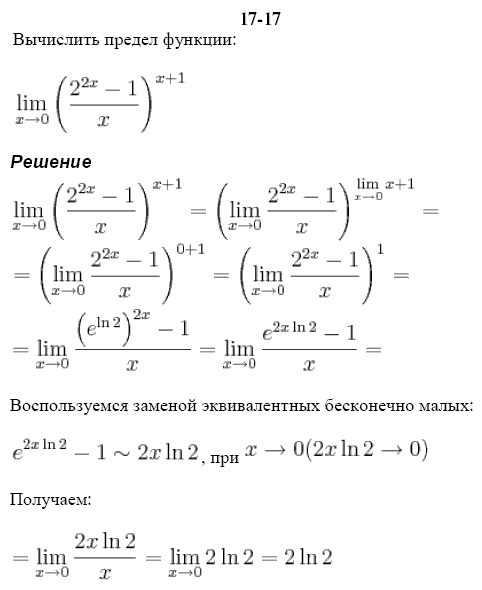


 Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .
Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .
 См. Пример.
См. Пример.