Операции над множествами — Мегаобучалка
Федеральное агентство по образованию
Тверской колледж имени А.Н. Коняева
«Множества»
Учебно-методическое пособие по предмету «Математика»
для студентов первого курса
Тверь,
Одобрено предметной (цикловой) Заместитель директора
комиссией по учебной работе
Председатель Дац В.А. Виноградов Н.Е.
____________________ _____________________
Составил: Бодров Е.Н.
__________________
Учебное пособие содержит теоретический и практический материал по теме «Множества». Пособие предназначено для студентов, изучающих дисциплины «Математика», «Дискретная математика», а также может быть полезно преподавателям математики.
Оглавление
ВВЕДЕНИЕ……………………………………………………………………………………….. 4
1. Основные понятия теории множеств…………………………………………………. 5
2. Изображение множеств……………………………………………………………………. 6
3. Операции над множествами……………………………………………………………… 7
4. Основные свойства операций над множествами…………………………………. 9
5. Примеры решения задач……………………………………………………………….. 10
6. Задачи для самостоятельного решения……………………………………………. 12
Приложение А………………………………………………………………………………….. 15
Список литературы…………………………………………………………………………… 22
ВВЕДЕНИЕ
Теоретико-множественные понятия встречаются практически во всех разделах современной математики и составляют ее фундамент. Теоретико-множественный подход способствует развитию общей культуры студентов, помогает видеть связи между явлениями. Таким образом, теоретико-множественный подход при изучении курса математики создает благоприятные условия для целенаправленного изучения языка математики, способствует повышению научности и четкости в изложении материала, содействует выявлению связей между различными разделами математики, помогает развитию математической культуры студентов.
Основным средством формирования теоретико-множественных понятий и их применения при изучении программного материала является специальный подбор системы упражнений и задач. Предлагаемое пособие по теме «Множества» содержит как теоретический, так и практический материал. Рассматриваемая система упражнений рассчитана на овладение студентами общими методами рассуждений, активизацию их мыслительной деятельности, выработку творческого подхода к решению задач, установление связи теоретико-множественных понятий с окружающей действительностью.
Основные понятия теории множеств
Понятия множество, элементы множества – одни из основных неопределяемых понятий современной математики.
Под множеством (семейством, набором, ансамблем) понимается совокупность объектов, объединенных некоторым признаком, свойством. Объекты, из которых состоит множество, называются элементами.
Пример 1.1. — множество натуральных чисел, — множество целых чисел,
— множество рациональных чисел, — множество действительных чисел.
Запись означает, что элемент принадлежит множеству .
Запись означает, что элемент не принадлежит множеству .
Для обозначения множеств будем применять прописные буквы латинского алфавита, а элементов – строчные буквы латинского алфавита.
Способы задания множества:
1. Перечислением, то есть
2. Указанием свойства, которым обладают элементы, принадлежащие этому множеству. Данное свойство называется характеристическим. Множество записывается следующим образом:
, — характеристическое свойство.
Пример 1.2. — множество цифр, .
Определение 1.1. Множество называется пустым, если оно не содержит ни одного элемента. Обозначение — Ø.
Определение 1.2. Множество называется подмножеством множества , если всякий элемент множества является элементом множества . Обозначение — .
Определение 1.3. Универсальным называют множество , состоящее из всех возможных элементов, обладающих данным признаком.
Определение 1.4. Множества и называются равными, если они состоят из одних и тех же элементов.
Определение 1.5. Мощность множества — это число элементов множества . Обозначение — .
Множества принято изображать с помощью кругов Эйлера-Венна. Элементы множества изображаются точками внутри круга, если они принадлежат множеству, и точками вне круга, если они не принадлежат множеству. Тот факт, что является подмножеством , с помощью кругов Эйлера-Венна изображается следующим образом (рисунок 2.1).
Рисунок 2.1. Иллюстрация кругами Эйлера-Венна
Операции над множествами
1. Под объединением двух множеств и (обозначение ) понимается множество тех и только тех элементов, которые принадлежат хотя бы одному из множеств и (рисунок 3.1).
Рисунок 3.1. Объединение множеств
Пример 3.1.Даны множества и . Тогда объединение этих множеств: .
2. Под пересечением двух множеств и (обозначение ) понимается множество тех и только тех элементов, которые принадлежат одновременно множествам и (рисунок 3.2.).
Рисунок 3.2. Пересечение множеств
Пример 3.2.Даны множества и . Тогда пересечение этих множеств:
3. Разностью множеств и (обозначение ) называется множество тех и только тех элементов , которые не принадлежат множеству (рисунок 3.3.).
Рисунок 3.3. Разность множеств
Пример 3.3.Даны множества и . Тогда разность этих множеств: .
4. Симметрической разностью множеств и (обозначения или ) называется множество тех и только тех элементов, которые принадлежат одному из множеств, но не являются общими элементами (рисунок 3.4.).
Рисунок 3.4. Симметрическая разность множеств
Пример 3.4.Даны множества и . Тогда симметрическая разность этих множеств: .
5. Дополнением к множеству (обозначение ) называется множество тех и только тех элементов, которые не принадлежат множеству , то есть дополняют его до универсального множества (рисунок 3.5.).
Рисунок 3.5. Дополнение к множеству
megaobuchalka.ru
Множества Операции над множествами
РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2 -5х+6=0;
6) множество действительных корней уравнения х2 +9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а
А, а если а не принадлежит А, то пишут: а А.В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+ , Q+ , R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ , QЇ , RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d ,обозначают с помощью фигурных скобок: А={a; b; c; …;d} . Множество корней уравнения х2 -5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х
Другой пример: Х={х | -1 ≤ х < 4, х
Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ хРассмотрим и такой пример: F={f | │fґ(x)│≤ 1 , 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А — пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А={х | хІ+9=0, х
R} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х
У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и . Если, например, А — множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В А. Пустое множество считают подмножеством любого множества Х, т.е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.Если для двух множеств Х и У одновременно имеют место два включения Х
У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.Если Х
У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если А
В, а В С, то АС.Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х
А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому А С.mirznanii.com
Операции над множествами
К переменным типа set применимы следующие операции: =, <>, >=, <=, in, +, -, *.
Операции = и <> используются для проверки эквивалентности: два значения переменной типа set считаются равными, если они состоят из одних и тех же элементов.
Пример.
[1, 3] = [3, 1] возвращает true, [1..3] = [1, 2, 3] возвращает true, [1] <> [2] возвращает true, [1, 2, 3] = [1, 4, 3] возвращает false, [red, blue] = [red, yellow] возвращает false.
Операции >= и <= используются для проверки принадлежности одного множества другому: так, если множество a содержится во множестве b, то a <= b дает true.
Пример.
[1, 2] <= [1, 2, 3] дает <span>true</span>
Пустое множество [ ] содержится во всех множествах, т.е. всегда [ ] <= [b] дает true.
Операция in используется для установления наличия определенного элемента в величине типа set. Так, если x есть элемент множества b, то (x in b) дает true. Общий вид:
здесь x – величина базового типа, a – величина типа set.
Пример.
red in [red, yellow] возвращает true; red in [blue, green] возвращает false.
Замечание 1. Чтобы проверить, является ли значение n цифрой, удобно использовать операцию in следующим образом:
Замечание 2. Результат операции in может быть неопределенным в некоторых случаях.
Пример. Пусть
a: set of 1..50; x: integer.
Если заслать в x число, большее максимального значения 50 (например, x := 55), то в этом случае результат операции x in a не всегда false.
К переменным типа set, относящимся к одному и тому же конкретному типу, применимы операции:
+ объединение;
* пересечение;
— дополнение.
Пусть a и b – операнды, имеющие один и тот же конкретный тип. Тогда
a + b представляет собой объединение множества элементов, входящих в a и b (одинаковые элементы не повторяются).
a * b – пересечение множества элементов a и b (только те, которые есть в обоих множествах).
a – b – множество элементов, которые есть в a, но отсутствуют в b.
Пример.
[1, 3] + [1, 4] = [1, 3, 4]; [1, 3] * [1, 4] = [1]; [1, 3] - [1, 4] = [3].
Операция a := a + x добавляет элемент x к множеству a. Если x уже имелся в a, то множество a не меняется. a := a – x исключает x из a. Если x отсутствовал в a, то множество a не меняется.

Операции над множествами:
- присвоение
- объединение
- пересечение
- дополнение
- тождественность
- нетождественность
- содержится во множестве
- содержит множество
- принадлежность элемента множеству
pas1.ru
Пример1. Найдем пересечение множеств А = {а, b, с, d, е} и В = {b, d, e, g, к}.
Пояснение. Пересечением множеств A и B называется множество A ∩ B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B. Пример 2. Найдем объединение и разность множеств А и В, если
Пояснение. Объединением двух множеств A и B называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B. Разностью множеств A и B называется множество A \ B, которое состоит из тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B. Разность между основным множеством E и множеством A называется дополнением множества A в E и обозначается A’ Пример 3. Известно, что А – множество учащихся, увлекающихся историей, В –
|
www.reshim.su
Операции над множествами и их свойства
Шпаргалка: Множества Операции над множествами
РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2 -5х+6=0;
6) множество действительных корней уравнения х2 +9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А.
Например, пусть N–множество натуральных чисел. Тогда 5N, но N, N. Если А — множество корней уравнения х2 -5х+6=0, то 3 А, а 4А.
В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+, Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d, обозначают с помощью фигурных скобок: А={a; b; c; …;d}. Множество корней уравнения х2 -5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2 -5х+6=0}. Решив уравнение х2 -5х+6=0, мы можем записать множество А первым способом: А={2; 3}.
Другой пример: Х={х | -1 ≤ х < 4, х Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такой пример: F={f | │fґ(x)│≤ 1, 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А — пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А={х | хІ+9=0, хR} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и . Если, например, А — множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В А. Пустое множество считают подмножеством любого множества Х, т.е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.
Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.
Если Х У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если АВ, а В С, то АС.
Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому А С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств
Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А В={х | хА или хВ}.
Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
На диаграмме объединение множеств А и В выделено штриховкой.
Если множество А определяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х), то А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k Z}, B={x | x=8n-4, n Z}. Тогда A B ={x | 4m, mZ}.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {Аα } называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются.
Таким образом, элемент хтогда и только тогда, когда найдется такой индекс α0 М, что х A α0.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись Если M=N, то имеем объединение последовательности множеств .
Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда = [0;2).
Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1A2 = A2 А1, и ассоциативна, т.е. (А1A2 ) А3 = А1(A2 А3 ).
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | хА и х В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7}.Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m Z}.
4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов.
Операцию пересечения можно определить и для произвольной системы множеств {Аα }, где α М. Пересечением системы множеств {Аα }, называется множество , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α М, т.е. = {x | xАα для каждого α М}.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись . Если M=N, то имеем пересечение последовательности множеств .
В рассмотренном выше примере системы множеств Аα =[0; α], αМ =(1; 2) получим:=[0;1].
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1 ∩A2 = A2 ∩А1 и (А1 ∩A2 )∩ А3 = А1 ∩(A2 ∩ А3 ).
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
А\В={х | х А и хВ},
что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность А\В выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А — множество всех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогда А\В — множество всех четных целых чисел, которые не делятся на 3, а В\А –множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество А и В таковы, что АВ. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СB А=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СU А=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.
На диаграммах Эйлера-Венна можно так пояснить определения СВ А и СА:
laservirta.ru
Операция над множествами — это… Что такое Операция над множествами?
- Операция над множествами
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые.
Сравнение множеств
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:
В этом случае A называется подмножеством B, B — надмножеством A. Если и , то A называется собственным подмножеством B. Заметим, что . По определению .
Два множества называются равными, если они являются подмножествами друг друга:
Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:
Операции над множествами
Бинарные операции
Ниже перечислены основные операции над множествами:
- Если множества A и B не пересекаются: , то их объединение обозначают также: .
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Унарные операции
- Операция дополнения подразумевает некоторый универсум (множество U, которое содержит A):
Результатом является кардинальное число (для конечных множеств — натуральное).
Обозначение происходит из того, что
Приоритет выполнения операций
Сначала выполняются операции дополнения, затем объединения, пересечения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.
Wikimedia Foundation. 2010.
- Операция на Плайя-Хирон
- Операция присваивания в С++
Смотреть что такое «Операция над множествами» в других словарях:
Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Операции над нечёткими множествами — обобщают операции над обыкновенными множествами. Эти операции обычно определяются поэлементно над значениями функции принадлежности. Наиболее популярны операции пересечения и объединения нечётких множеств, определяемые, соответственно, операциями … Википедия
Операции над нечеткими множествами — Операции над нечёткими множествами обобщают операции над обыкновенными множествами. Эти операции обычно определяются поэлементно над значениями функции принадлежности. Наиболее популярны операции пересечения и объединения нечетких множеств,… … Википедия
Теория топосов — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Теория топосов раздел теории категорий, изучающий топосы категор … Википедия
Объединение (значения) — Объединение многозначный термин, входит в состав сложных терминов. В Викисловаре есть статья «объединение» Объединение разновидность организаций. Объединение общее название крупных воинских формирований … Википедия
ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел теории множеств, изучающий внутреннее строение множеств в зависимости ют тех операций, при помощи к рых эти множества могут быть построены из множеств сравнительно простой природы (напр., замкнутых или открытых подмножеств данного… … Математическая энциклопедия
Множеств теория — учение об общих свойствах множеств, преимущественно бесконечных. Понятие множества, или совокупности, принадлежит к числу простейших математических понятий; оно не определяется, но может быть пояснено при помощи примеров. Так, можно… … Большая советская энциклопедия
МНОЖЕСТВ ТЕОРИЯ — наивная учение о свойствах множеств, преимущественно бесконечных, элиминирующее свойства элементов, составляющих эти множества. . Понятие множества принадлежит к числу первоначальных математич. понятий и может быть пояснено только при помощи… … Математическая энциклопедия
ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ — точно определенное указание действий над данными, позволяющее с помощью цифровой вычислительной машины дискретного действия преобразовать за конечное количество операций нек рый массив данных (входные данные) в другой массив данных (выходные… … Математическая энциклопедия
Прямое произведение — Прямое или декартово произведение множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих… … Википедия
dic.academic.ru
2.2.4 Операции над множествами
Объединением множествА и В (обозначается ) называется множество, состоящее из
всех тех элементов, которые принадлежат
хотя бы одному из множествA,B(рис. 2.2):
) называется множество, состоящее из
всех тех элементов, которые принадлежат
хотя бы одному из множествA,B(рис. 2.2):
 = {x:
= {x: или
или }.
}.
Пересечением множествAиВ (обозначается ) называется множество, состоящее из
всех тех и только тех элементов, которые
принадлежат иА, иВ (рис.
2.3):
) называется множество, состоящее из
всех тех и только тех элементов, которые
принадлежат иА, иВ (рис.
2.3):
 = {x:
= {x: и
и }.
}.
Если общих элементов в множествах AиBнет, то =
=
Пусть U–универсальное множество такое, что все рассматриваемые множества являются его подмножествами.
Дополнением (доU) множестваА (обозначается )
называется множество всех элементов,
не принадлежащихA, но принадлежащихU (рис. 2.4):
)
называется множество всех элементов,
не принадлежащихA, но принадлежащихU (рис. 2.4):
 = U \ A.
= U \ A.
Операции объединения, пересечения и дополнения {} часто называютбулевыми операциями над множествами, а алгебру множеств, в которой используются только эти операции, – булевой алгеброй множеств.
Рисунок 2.2 – Диаграмма объединения множеств АиВ
Рисунок 2.3 – Диаграмма пересечения множеств АиВ
Рисунок 2.4 – Диаграмма дополнения множества А
В алгебре множеств, кроме рассмотренных операций, определены также операции разности, симметрической разности и прямого (декартова) произведения множеств.
Разностью множествА иВ (обозначаетсяА\В) называется множество всех тех и только тех элементовА, которые не содержатся вВ (рис. 2.5):
А\В= {x: и
и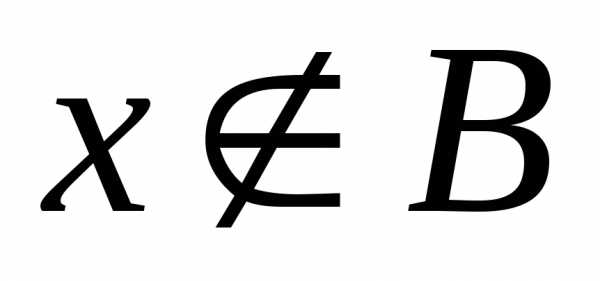 }.
}.
Разность множеств – операция строго двуместная и некоммутативная: в общем случае
А\В 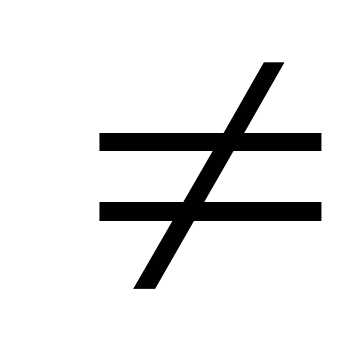 В\А.
В\А.
Разность множеств можно представить через пересечение и дополнение
A\B =  .
.
Рисунок 2.5 – Диаграмма разности множеств А и В
Симметрической
разностью множествА иВ (обозначаетсяА B) называется множество всех тех элементовА или B, которые не содержатся вAиВ одновременно (рис. 2.6):
B) называется множество всех тех элементовА или B, которые не содержатся вAиВ одновременно (рис. 2.6):
А В= {x:
В= {x: или
или ,
но}.
,
но}.
Рисунок 2.6 – Диаграмма симметрической разности множеств АиВ
Прямое (декартово) произведение множеств Aи B – это множество элементов в виде упорядоченных пар (a,b), где
Для этой операции можно записать
{(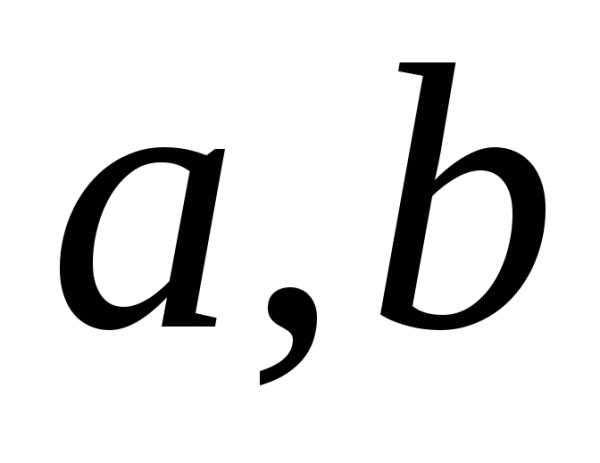 )|}.
)|}.
Элементы
(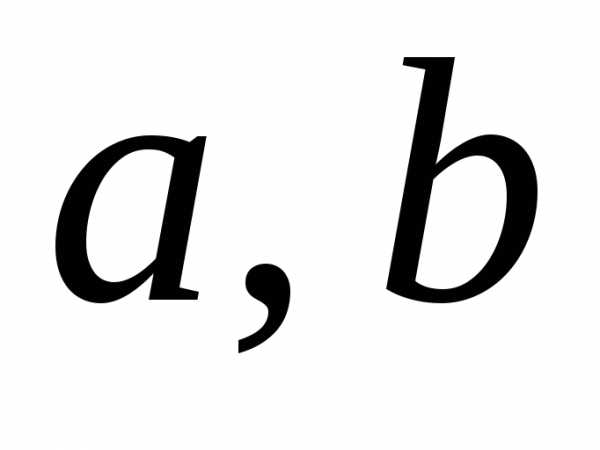 )
называются кортежами (векторами,
наборами, словами). В произведении могут
участвовать более двух множеств.
Количество множеств, участвующих в
произведении, определяет длину кортежей.
)
называются кортежами (векторами,
наборами, словами). В произведении могут
участвовать более двух множеств.
Количество множеств, участвующих в
произведении, определяет длину кортежей.
Произведение множеств – операция некоммутативная
,
поэтому элементы кортежей нельзя переставлять.
В множествах АиВмогут быть одинаковые элементы, поэтому и в кортеже могут оказаться одинаковые элементы, например как буквы в словах.
Если множество А умножается на себя, то можно записать
,и т.д.
где А2, А3 – степени множества А.
Произведение двух множеств A= {a1,a2,a3} иB= {b1,b2} можно представить в виде графика, показанного на рис. 2.7, где каждая вертикальная линия обозначена элементом изА, каждая горизонтальная линия элементом изВ, а каждая жирная точка представляет пару (ai,bi).
Рисунок 2.7 – График произведения множеств А и В
Пример 1. Пусть универсальное множествоU – множество всех сотрудников некоторой фирмы;А – множество всех сотрудников данной организации старше 35 лет;В – множество сотрудников, имеющих стаж работы более 10 лет; С – множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следующих множеств:
а) 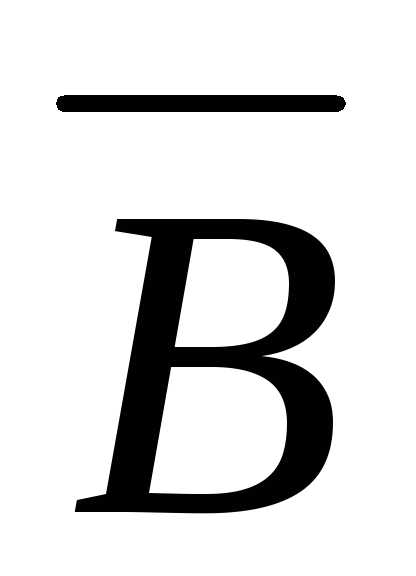 ; б); в); г)В \ С; д)С\B?
; б); в); г)В \ С; д)С\B?
а)  – множество сотрудников организации,
стаж работы которых не превышает 10 лет.
– множество сотрудников организации,
стаж работы которых не превышает 10 лет.
б) – множество менеджеров фирмы не старше 35 лет, имеющих стаж работы более 10 лет.
в) – множество всех сотрудников фирмы старше 35 лет, а также сотрудников, не менеджеров, стаж работы которых более 10 лет.
г) В\С – множество сотрудников организации со стажем работы более 10 лет, не работающих менеджерами.
д) С\В – множество менеджеров со стажем работы не более 10 лет.
Пример
2. Задать множества ,
, ,
если:
,
если:
М – множество всех натуральных чисел, не превосходящих 100;
N – множество натуральных чисел.
 – множество всех натуральных чисел,
больших 100.
– множество всех натуральных чисел,
больших 100.
Запись  без указания универсального множестваU не ясна:
без указания универсального множестваU не ясна:
– то ли это множество всех отрицательных целых чисел;
– то ли это множество положительных дробных чисел;
– то ли это пустое множество натуральных чисел.
Пример 3. Осуществить операции объединения, пересечения, дополнения, разности и симметрической разности над множествами
А = {a, b, c, d} и B = {с, d, e, f, g, h}.
 = {a, b, c,d,e, f, g, h};
= {a, b, c,d,e, f, g, h};
 = {c, d}.
= {c, d}.
A \ B = {a, b};
B \ A = {e, f, g, h};
{a, b,e, f, g, h}.
Универсальное множество U не определено, поэтому, строго говоря, операции дополнения над множествамиAиВне могут быть выполнены. Если принять в качестве универсального множества объединение множествA и B
U= {а,b,с,d,e,f,g,h}, тогда
 =U\А = {е, f, g,h},
=U\А = {е, f, g,h},  = U\B = {а, b}.
= U\B = {а, b}.
Пример 4. ПустьU = {1, 2, 3, 4},А = {1, 3, 4},В = {2, 3}, С ={1, 4}.
Найти:
a) 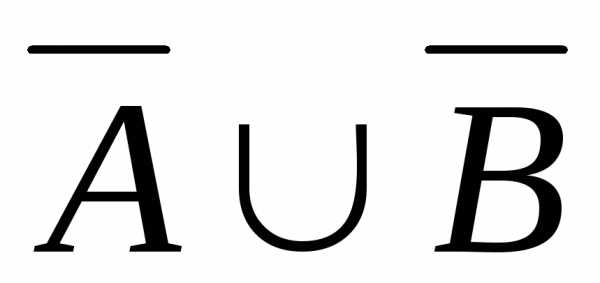 ; б)
; б)  ; в)
; в) ; г).
; г).
a)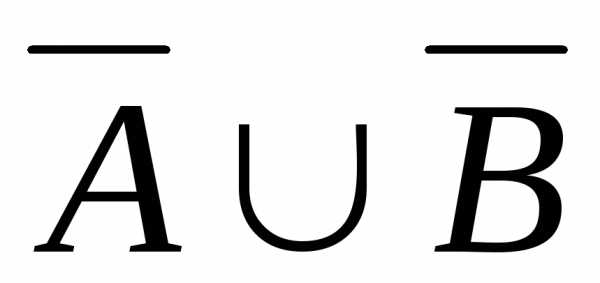 == ({1, 2, 3, 4} \ {1, 3, 4})
== ({1, 2, 3, 4} \ {1, 3, 4}) ({1,
2, 3, 4}\{2, 3}) =
({1,
2, 3, 4}\{2, 3}) =
{2} {1,
4} = {1, 2, 4}.
{1,
4} = {1, 2, 4}.
б)  = = {1, 2, 3, 4}\ ({1, 3, 4}
= = {1, 2, 3, 4}\ ({1, 3, 4} {2,
3}) = {1, 2, 3, 4}\{3} =
{2,
3}) = {1, 2, 3, 4}\{3} =
= {1, 2, 4}.
в)  =={l, 3, 4}
=={l, 3, 4} ({l,
2, 3, 4}\{2, 3}) ={1, 3, 4}
({l,
2, 3, 4}\{2, 3}) ={1, 3, 4} {1,
4} =
{1,
4} =
= {1, 4}.
г) = ({2, 3}\{1, 3, 4}) ({1,
2, 3, 4}\{1, 4}) ={2}
({1,
2, 3, 4}\{1, 4}) ={2} {2,
3} =
{2,
3} =
= {2, 3}.
Пример 5. Получить прямое произведение множеств
А = {a, b} и В = {p, q, r}.
А В = {(a, p),(a, q),(a, r),(b, p),(b, q),(b, r)}.
В = {(a, p),(a, q),(a, r),(b, p),(b, q),(b, r)}.
studfiles.net
