Длина вектора калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор вычисления длины вектора, даст подробное решение и вычислит модуль вектора плоскости, а так же вектора пространства.
Укажите размерность пространства 23
Укажите форму представления вектора
Координаты точек начала и конца вектораКоординаты вектора
Задайте координаты вектора ā
ā =
{
;
}
Как найти модуль вектора
Модулем вектора |AB| называется число, равное расстоянию между начальной и конечной точками вектора.
Для того чтобы найти модуль (длину) вектора, если известны координаты его начальной и конечной точек необходимо воспользоваться одной из формул:
|AB| = √(Bx — Ax)2 + (By — Ay)2 — для вычисления длины вектора плоскости
|AB| = √(Bx — Ax)2 + (By — Ay)2 + (Bz — Az)2 — для вычисления длины вектора пространства
Для того чтобы найти модуль (длину) вектора, если известны его координаты необходимо воспользоваться одной из формул:
|a| = √ax2 + ay2 — для вычисления длины вектора плоскости
|a| = √ax2 + ay2 + az2 — для вычисления длины вектора пространства
Пример 1.
Найдем длину вектора плоскости с координатами начальной и конечной точек A(x;y) и точки B(x;y), где A(1;9) и B(4;7).
Тогда согласно формуле:
Bx = 4;
Ax = 1;
By = 7;
Ay = 9;
Подставим значения в формулу и найдем модуль вектора |AB|:
|AB| = √(Bx — Ax)2 + (By — Ay)2
=
√(4 — 1)2 + (7 — 9)2
√32 + (-2)2 =
√9 + 4 =
√13 = 3.60555127546399
Пример 2. Найдем длину вектора пространства с координатами начальной и конечной точек A(x;y;z) и точки B(x;y;z), где A(5;2;9) и B(3;6;7).
Тогда согласно формуле
Bx = 3;
Ax = 5;
By = 6;
Ay = 2;
Bz = 7;
Az = 9;
Подставим значения в формулу и найдем длину вектора |AB|
|AB| = √(Bx — Ax)2 + (By — Ay)2 + (Bz — Az)2
=
√(3 — 5)2 + (6 — 2)2 + (7 — 9)2
=
√(-2)2 + 42 + (-2)2
=
√4 + 16 + 4
=
√24
= 2
√6
= 4.89897948556636
Пример 3. Найдем длину вектора a плоскости с координатами a(x; y), где a(3; 8).
Тогда согласно формуле:
ax = 3;
ay = 8;
Подставим значения в формулу и найдем модуль вектора |a|
|a| = √ax2 + ay2 =
√32 + 82 =
√9 + 64 =
Пример 4. Найдем длину вектора a пространства с координатами a(x;y;z), где a(4;2;7).
Тогда согласно формуле:
ax = 4;
ay = 2;
ay = 7;
Подставим значения в формулу и найдем модуль вектора |a|
|a| = √ax2 + ay2 + az2 =
√42 + 22 + 72 =
√16 + 4 + 49 =
√69 = 8.30662386291807
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Сумма векторов, длина вектора
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-09-29
Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения.
Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Понятие вектора
Вектор — это направленный отрезок.
Все векторы, имеющие одинаковое направление и равные по длине являются равными.
*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Обозначение векторов
Вектор может быть обозначен латинскими заглавными буквами, например:
При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):
Возможно также обозначение без стрелок:
Сумма векторов
Суммой двух векторов АВ и ВС будет являться вектор АС.
Записывается как АВ+ВС=АС.
Это правило называется – правилом треугольника.
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:
Перенесём вектор b, или по-другому – построим равный ему:
Как находится сумма нескольких векторов? По тому же принципу:
* * *
Правило параллелограмма
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:
Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:
Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:
Мы построили вектор противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:
То есть, координаты вектора представляют собой пару чисел.
Если
И координаты векторов имеют вид:
То c1= a1+ b1 c2= a2+ b2
Если
То c1= a1– b1 c2= a2– b2
Модуль вектора
Модулем вектора называется его длина, определяется по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Рассмотрим задачи:
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.
Найдём вектор, который будет являться результатом АО–ВО:
АО–ВО=АО+(–ВО)=АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Ответ: 8
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ+AD.
Найдём вектор, который будет являться суммой векторов AD и AB.
Вектор BC равен вектору AD. Значит AB+AD=AB+BC=AC
Длина вектора AC это длина диагонали ромба АС, она равна 16.
Ответ: 16
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО+ВО.
Найдём вектор, который будет являться суммой векторов АО и ВО. Вектор ВО равен вектору OD, значит
Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:
По теореме Пифагора:
Ответ: 10
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО–ВО.
Найдём вектор, который будет являться результатом АО–ВО:
Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:
По теореме Пифагора:
Ответ: 10
Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ–АС.
Найдём результат разности векторов:
Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.
Ответ: 3
27663. Найдите длину вектора а(6;8).
Посмотреть решение
27664. Найдите квадрат длины вектора АВ.
Посмотреть решение
27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС.
Посмотреть решение
27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD.
Посмотреть решение
27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD.
Посмотреть решение
27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО.
Посмотреть решение
27713. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ.
Посмотреть решение
27715. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ–AD.
Посмотреть решение
27716. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ–АС.
Посмотреть решение
Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ+АС.
Посмотреть решение
В будущем мы продолжим рассматривать задачи с векторами, не пропустите! Задания будут связаны с координатами векторов, скалярным произведением.
На этом всё. Успеха вам!
С уважением, Александр
Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный.Но мест уже нет!
Но мест уже нет!P.S: Буду благодарен, если расскажете о статье в социальных сетях.
Категория: Векторы | ЕГЭ-№1
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 27.
Связь между координатами вектора и координатами его начала и конца.
Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.
Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как M1 и M2.
Абсциссой точки М является число x, которое является длиной отрезка OM1. А ординатой — число y, которое является длиной отрезка OM2.
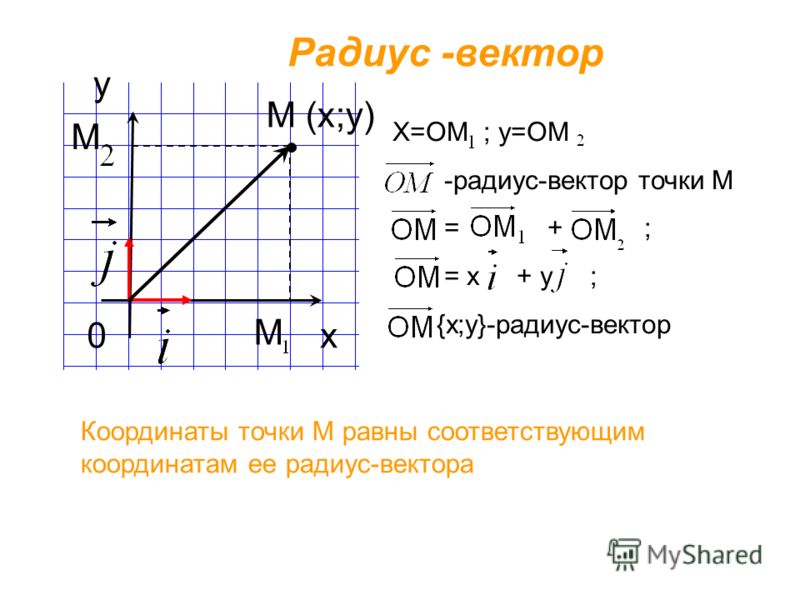
M(x; y) x = OM1, y = OM2
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.
Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.
Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.
Доказать: M(x;y)=OM⃗x;y
Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.
Теперь необходимо доказать, что вектор
OM1⃗=xi⃗, а вектор OM2⃗=yj⃗
Тем самым мы докажем, что вектор OM⃗x;y.
Если x > 0, то x = OM1, а векторы OM1⃗ и i⃗ сонаправлены, поэтому
OM1⃗=OM1∙i⃗=xi⃗
Если x x = OM1, а векторы OM1⃗ и i⃗ противоположно направлены. Поэтому OM1⃗=-OM1∙i⃗=xi⃗.
Наконец, если x = 0
OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.
Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗
Отсюда следует, что координаты радиус-вектора OM равны (x; y), то есть равны соответствующим координатам точки M.
Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.
Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.
Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
Рассмотрим три вспомогательные задачи:
-
Как найти координаты середины отрезка.
Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2. Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
OC⃗=12OA⃗+OB⃗.
x=x1+x22; y=y1+y22
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
-
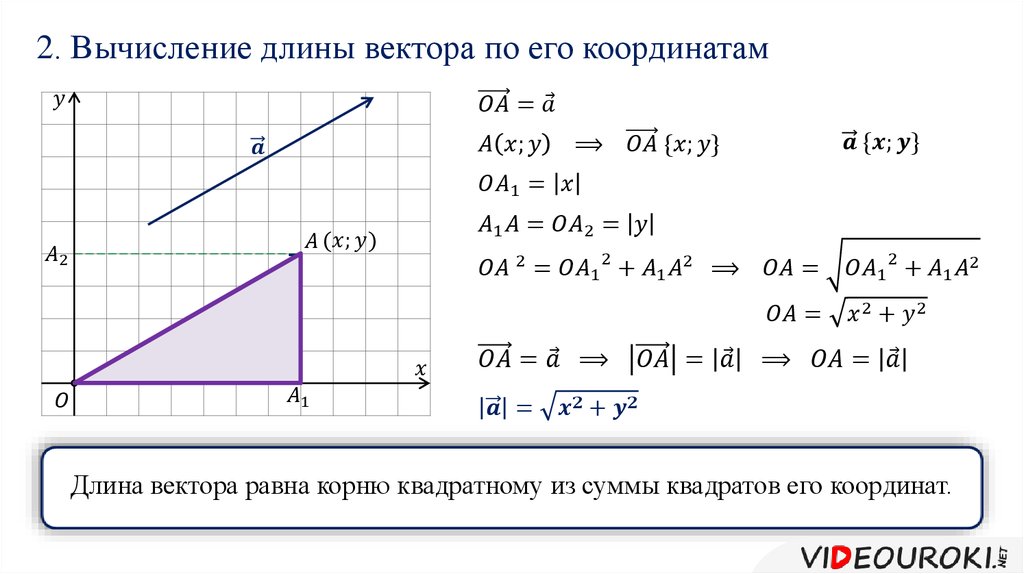
Вычисление длины вектора по его координатам.
Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:
a⃗=x2+y2
-
Вычисление расстояния между двумя точками. Пусть точка M1 имеет координаты (x1; y1), точка M2 – координаты (x2; y2).
Выразим расстояние d между точками M1 и M2 через их координаты.
Выразим расстояние d между точками M1 и M2 через их координаты.
Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
M1M2⃗=x2-x12+y2-y12
Пример:
-
Найти длину вектора a⃗-3;4
a⃗=x2+y2=-32+42=25=5
Ответ: 5
-
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)
d=-2-22+7-72=16=4
Ответ: 4
Единичный вектор — формула, определение, расчет, обозначение
Векторы — это геометрические объекты, имеющие величину и направление. Векторы имеют начальную точку и конечную точку, которая представляет конечное положение точки. К векторам можно применять различные арифметические операции, такие как сложение, вычитание и умножение.
Вектор, величина которого равна 1, называется единичным вектором. Например, вектор v = (1, 3) не является единичным, поскольку его модуль не равен 1, т. е. |v| = √(1 2 +3 2 ) ≠ 1.
Любой вектор может стать единичным вектором, если мы разделим его на величину того же заданного вектора. Единичный вектор также иногда называют вектором направления. Давайте узнаем больше об единичном векторе, его формуле вместе с несколькими решенными примерами.
| 1. | Что такое единичный вектор? |
| 2. | Обозначение единичного вектора |
| 3. | Формула единичного вектора |
| 4. | Как рассчитать единичный вектор? |
| 5. | Применение единичного вектора |
| 6. | Свойства векторов |
| 7. | Решенные примеры |
8. | Практические вопросы по единичному вектору |
‘, который называется кепкой или шляпой, например \(\hat{a}\). Это определяется как \(\шляпа{а}\) = и /| и | Где | и | для нормы или величины вектора a . Его можно рассчитать с помощью формулы единичного вектора или с помощью калькулятора.
Его также называют «нормальным» к поверхности, содержащей вектор. Единичный вектор, полученный после нормализации вектора нормали, является единичным вектором нормали, также известным как «единичная нормаль». Для этого разделим ненулевой вектор нормали на его векторную норму.
Например, рассмотрим вектор v = (3, 4), величина которого равна | против |. Если мы разделим каждый компонент вектора v на | против | чтобы получить единичный вектор \(\hat{v}\), который имеет то же направление, что и v.
2 + z 2 ). i + у/ √ (x 2 + у 2 + z 2 ) . j + z/ √ (x 2 + y 2 + z 2 ). к 
В математических обозначениях единичный вектор вдоль оси x представлен как i . Единичный вектор вдоль оси Y представлен как j , а единичный вектор вдоль оси Z представлен как k .
А 
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Итак, для заданных двух векторов x и y мы знаем, что x × y будет вектором, перпендикулярным как x , так и y . Далее, чтобы найти единичный вектор этого результирующего вектора, мы делим его на его величину. т. е. ( x × г ) / | x × y |, это дало бы единичный вектор, который перпендикулярен заданным двум векторам.
Величина вектора является аналогом абсолютного
значение для действительных чисел; следовательно, обозначение величины наследует использование абсолютного
ценность.
Найдите значение ‖‖⃑𝑣‖‖.
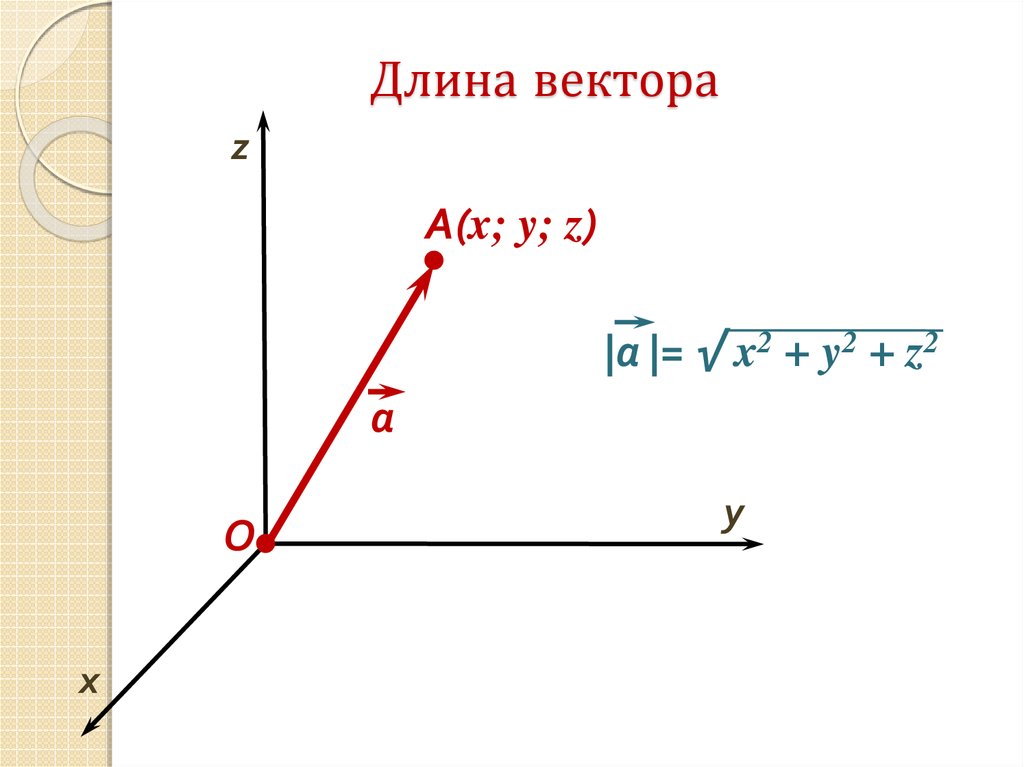Затем
величина этого вектора определяется выражением
‖‖⃑𝑣‖‖=√𝑎+𝑏.
Это означает, что величины этих векторов равны
задано |𝑎| или же
|𝑏|. Поскольку либо 𝑦-
или 𝑥-координата этих векторов равна нулю, это согласуется с формулой для
величина двумерных векторов, указанных выше.
Другой способ определения вектора — это
указание двух конечных точек. Напомним, что вектор, начинающийся в точке 𝐴 и
заканчивающийся в точке 𝐵 обозначается 𝐴𝐵. Если мы
имеют координаты точек 𝐴=(𝑥,𝑦) и 𝐵=(𝑥,𝑦), то этот вектор задается формулой
𝐴𝐵=(𝑥−𝑥,𝑦−𝑦).
Затем
величина этого вектора определяется выражением
‖‖⃑𝑣‖‖=√𝑎+𝑏.