Формулы для нахождения площади треугольника 9 класс
ТЕОРИЯ. ПЛОЩАДЬ ТРЕУГОЛЬНИКА
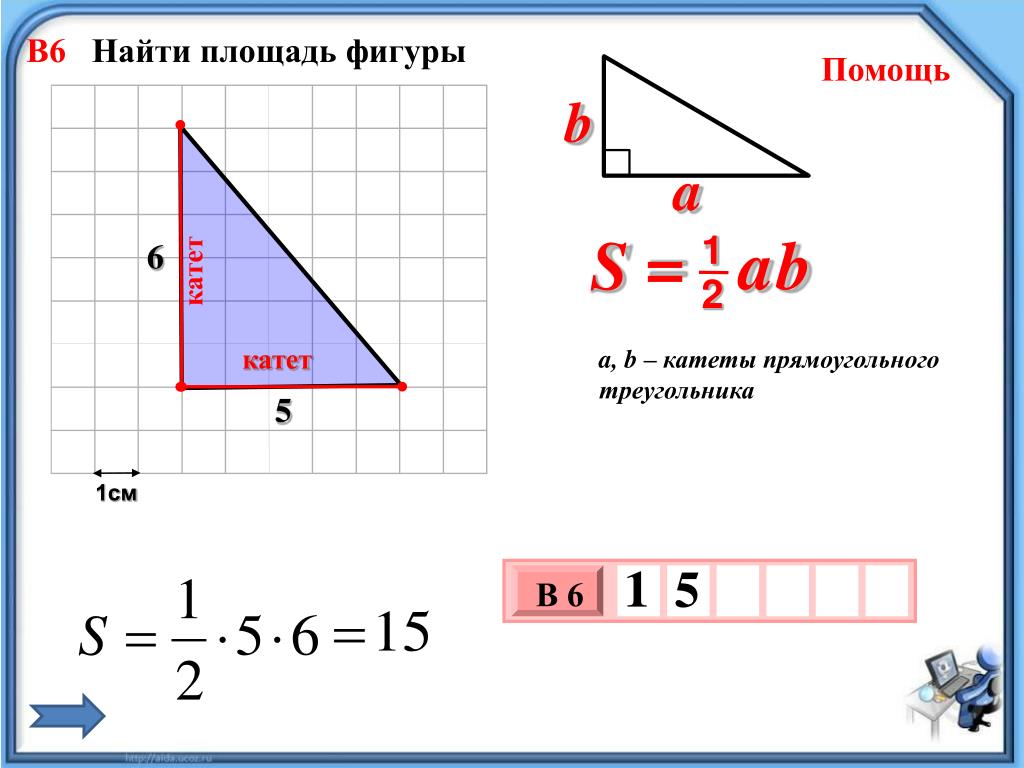
Прямоугольный треугольник
Разносторонний треугольник (по высоте)
Формула Герона
По двум сторонам и углу между ними
По радиусу описанной окружности
По радиусу вписанной окружности
Лайд выбора последующих действий
ЗАДАЧИ
6
5
4
3
2
1
7
8
9
10
11
12
Прямоугольный треугольник
В
с
а
С
А
b
a, b – катеты
с – гипотенуза
Разносторонний треугольник (по высоте)
В
h
С
А
h
а
H
a
H
С
А
a – основание
h – высота
Формула Герона
В
с
а
А
С
b
a, b, c – стороны тр-ка
p – полупериметр
По двум сторонам и углу между ними
В
а
γ
С
А
b
a, b – cтороны тр-ка
γ – угол между a и b
По радиусу описанной окружности
В
R
с
а
О
С
А
b
a, b, c – cтороны тр-ка
R – радиус описанной
около треугольника окружности
По радиусу вписанной окружности
В
а
K
r
с
О
С
А
b
a, b, c – cтороны тр-ка
p – полупериметр
r – радиус вписанной
в треугольник окружности
Найдите площадь треугольника, если:
1
а = 4см;
1)
а = 4см; b = 7см; γ = 120º
2)
а = 9см; b = 4см; γ = 45º
3)
1. Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.
Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.
а = 9см; b = 4см; γ = 150º
4)
Найдите площадь параллелограмма,
если:
2
1)
2)
3)
1. Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.
4)
Найдите площадь ромба, если:
3
1)
2)
3)
1. Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.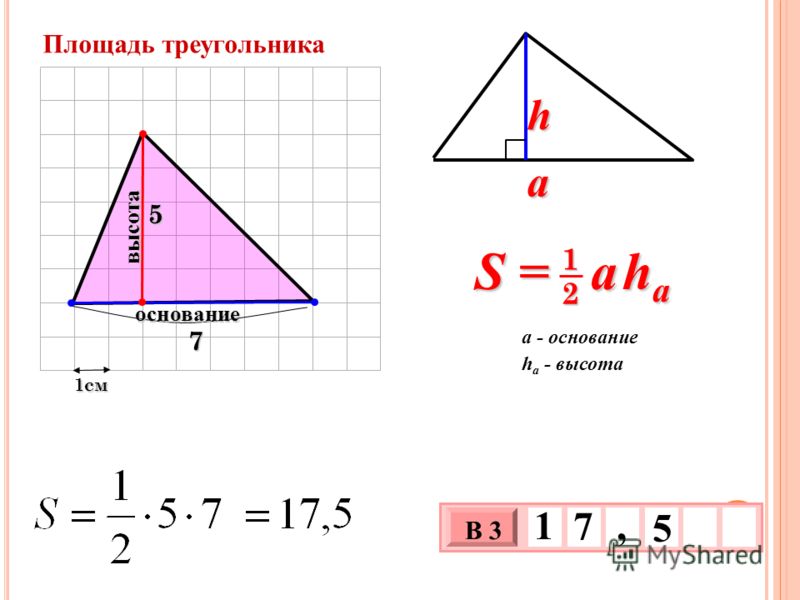
4)
Ромб – параллелограмм у которого все стороны равны
Найдите боковую сторону
равнобедренного треугольника, если:
4
В
1)
2)
γ
а
а
3)
1. Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.
С
А
В равнобедренном треугольнике боковые стороны равны
Отрезки АВ и CD пересекаются
в точке О. Найдите отношение
площадей треугольников АОD и СОВ (по рис.)
5
2)
1)
А
D
С
9
А
5
5
О
О
3
С
В
4
6
D
В
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2.На слайде выполнены настройки анимированной ДВОЙНОЙ сорбонки: 1 нажатие – решение, 2 нажатие – ответ. При последующем нажатии – исходная позиция и повтор действий. 3. При завершении решений на слайде нажимаем на мини-изображение в правом нижнем углу.
Нажимаем на мини-изображение девочки в правом нижнем углу. 2.На слайде выполнены настройки анимированной ДВОЙНОЙ сорбонки: 1 нажатие – решение, 2 нажатие – ответ. При последующем нажатии – исходная позиция и повтор действий. 3. При завершении решений на слайде нажимаем на мини-изображение в правом нижнем углу.
На сторонах угла отложены отрезки.
Найдите отношение площадей
треугольника и четырёхугольника(по рис.)
6
2)
1)
C
С
5
9
B
K
4
3
А
А
M
4
2
6
6
B
E
D
В
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2.На слайде выполнены настройки анимированной ДВОЙНОЙ сорбонки: 1 нажатие – решение, 2 нажатие – ответ. При последующем нажатии – исходная позиция и повтор действий. 3. При завершении решений на слайде нажимаем на мини-изображение в правом нижнем углу.
При последующем нажатии – исходная позиция и повтор действий. 3. При завершении решений на слайде нажимаем на мини-изображение в правом нижнем углу.
Найдите площадь Δ ABC, если:
7
a = 4см; b = 13см; c = 15см
1)
а = 3см; b = 25см; c = 26cм
2)
а = 7см; b = 15см; с = 20см
3)
1. Нажать на мини-изображение мальчика в правом нижнем углу. 2 Для визуализации ответа – нажать на прямоугольник с примером 3. При завершении работы со слайдом нажимаем на мини-изображение в правом нижнем углу.
а = 5см; b = 12см; с = 15см
4)
Три окружности, радиусы которых равны
12 см, 14 см и 16 см, попарно касаются
друг друга внешним образом.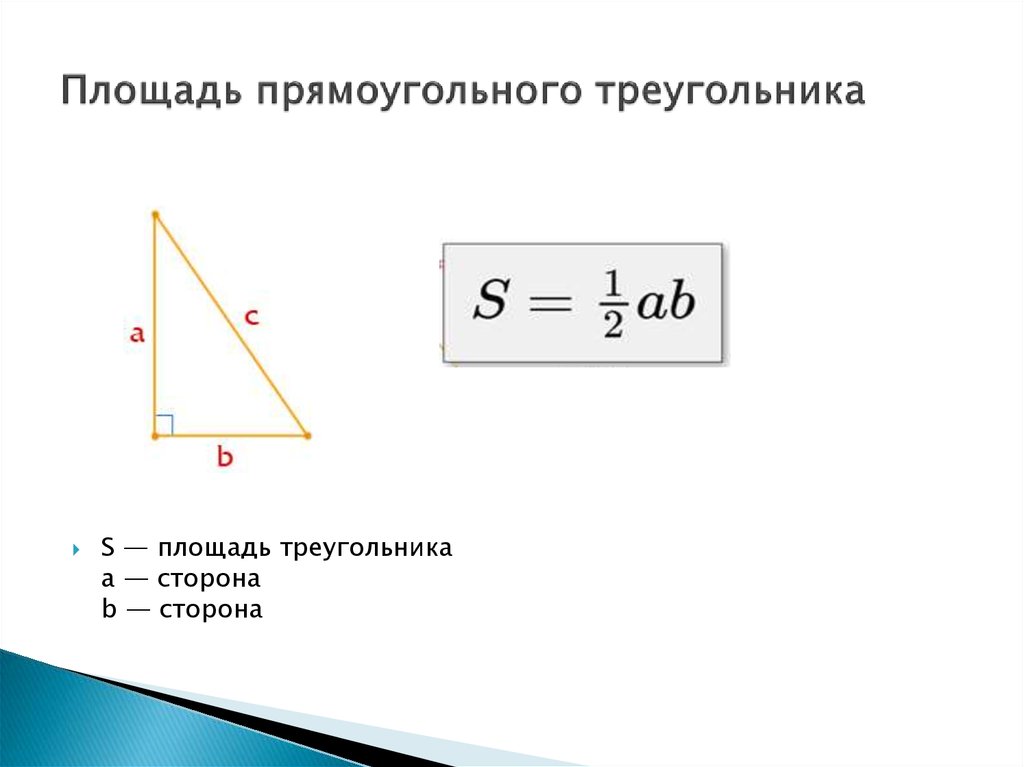 Найдите S/////
Найдите S/////
8
Рисунок
Ответ
14
12
O 2
O 1
12
14
Проверка
16
16
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку. 4. Кнопка со знаком вопроса – переход на слайд теории.
O 3
9
10
Стороны тр-ка равны 9см, 10см и 17см.
Найдите наименьшую высоту, радиусы
вписанной в него и описанной около него окр.
9
В
Рисунок
Ответ
Проверка
H
А
С
17
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку. 4. Кнопка со знаком вопроса – переход на слайд теории.
Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку. 4. Кнопка со знаком вопроса – переход на слайд теории.
Один из углов ромба на 120º больше
другого, а его сторона равна 6√3 см.
Найдите площадь ромба.
10
А
Рисунок
Ответ
В
D
Проверка
С
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку.
Ромб – параллелограмм у которого все стороны равны
Углы ромба относятся как 1 : 3, а его
сторона равна 3 см. Найдите площадь ромба.
11
А
Рисунок
Ответ
В
D
Проверка
С
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку.
Ромб – параллелограмм у которого все стороны равны
15
26
37
В треугольник со сторонами 26см, 15см
и 37см вписана окр-ть, центр которой
соединён с вершинами тр-ка. Найдите площади
трёх образовавшихся треугольников.
12
В
Рисунок
Ответ
r
r
Проверка
О
r
С
А
1. Нажимаем на мини-изображение девочки в правом нижнем углу. 2. нажимаем на прямоугольник «Рисунок». 3. Задачу учащиеся решают на доске. Кнопка «Ответ» – проверяем ответ, который получился у ребёнка. Кнопка «Проверка» – проверяем алгоритм решения задачи. Каждый последующий пункт появляется после нажатия на кнопку. 4. Кнопка со знаком вопроса – переход на слайд теории.
ИСТОЧНИКИ
Теорема о площади треугольника
Урок 22. Геометрия 9 класс ФГОС
В начале урока мы повторим известные нам формулы для вычисления площади треугольника, а затем выведем еще одну формулу, которая позволяет найти площадь треугольника, зная две стороны и синус угла между ними.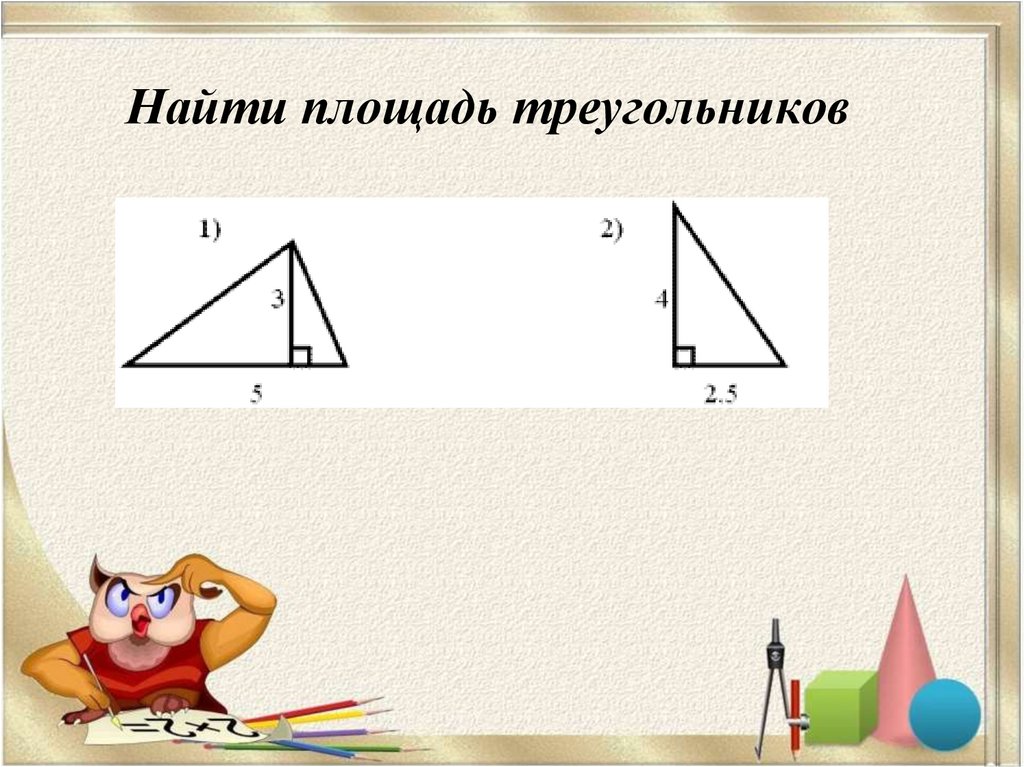 Также получим формулу для вычисления площади параллелограмма. Рассмотрим примеры применения этих формул.
Также получим формулу для вычисления площади параллелограмма. Рассмотрим примеры применения этих формул.
Конспект урока «Теорема о площади треугольника»
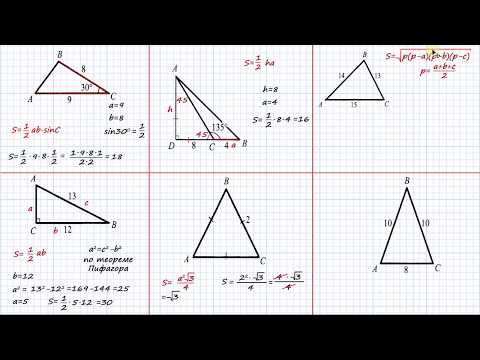
Мы с вами уже знаем несколько формул для вычисления площади треугольника. Давайте вспомним их. Если мы знаем длину одной из сторон треугольника и длину высоты, проведенной к этой стороне, то площадь треугольника можно найти как половина произведения этих длин .
Например, найдем площадь треугольника, показанного на рисунке при h= 6, а a=5. Площадь этого треугольника .
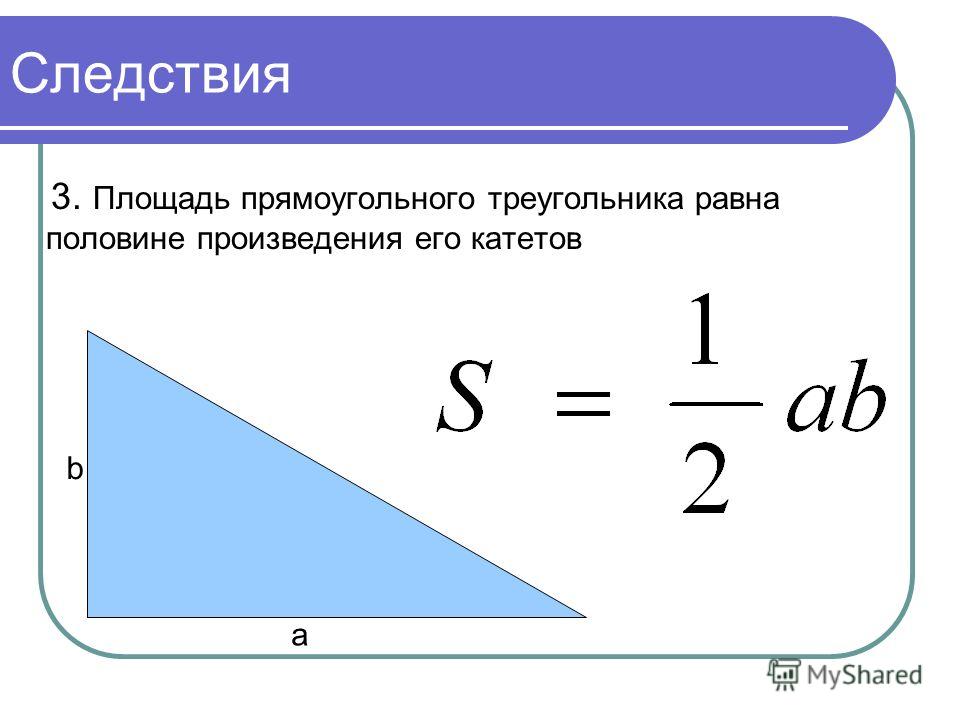
Если треугольник прямоугольный, то его площадь находится как половина произведения катетов
Например, найдем площадь прямоугольного треугольника с катетами равными 4 и 9. Площадь .
Если нам известны длины всех сторон треугольника, то площадь можно вычислить по формуле Герона, где p – полупериметр треугольника.
.
Найдем, например,
площадь треугольника со сторонами 13, 14 и 15 сантиметров. Полупериметр этого
треугольника .
Тогда площадь этого треугольника по формуле Герона
.
Сегодня на уроке мы с вами познакомимся еще с одной формулой, но сначала давайте вспомним формулу для координат произвольной точки А, расположенной в верхней полуплоскости.
Рассмотрим произвольный треугольник ABC со сторонами a, b, c и углами α, β, γ.
Докажем, что площадь треугольника вычисляется по формуле .
Расположим треугольник ABC в координатной плоскости так, чтобы точка C совпадала с началом координат, а точка B лежала на положительной полуоси Cx, а точка А имела положительную ординату, то есть располагалась в верхней полуплоскости.
Опустим из точки А высоту h. Площадь этого треугольника равна половине произведения
стороны a на h. Координаты
точки А равны
.
Высота h
будет равна ординате точки А, то есть равна произведению длины стороны АC на синус угла γ, или .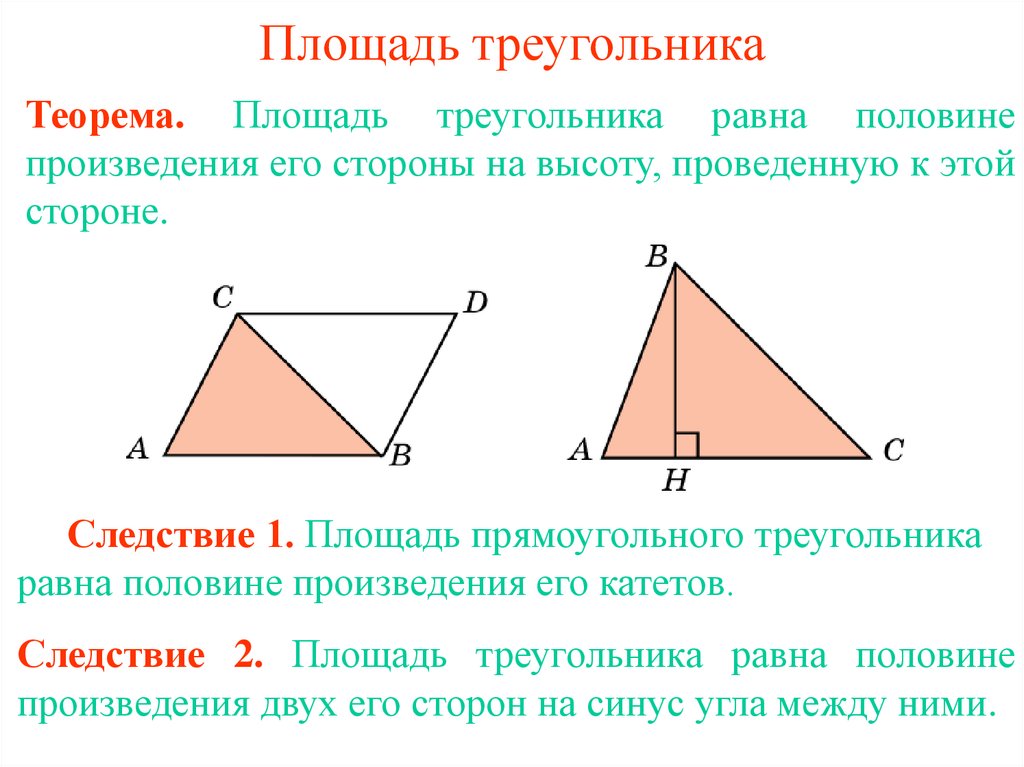
Таким образом, мы доказали теорему. Сформулируем ее.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Нетрудно убедиться, что если с началом координат совместить точку А, точку C расположить на положительном полуоси Ax, а точку B расположить в верхней полуплоскости, то можно записать, что площадь треугольника .
Если же с началом координат совместить точку B, точку А расположить на положительной полуоси Bx, а точку C расположить в верхней полуплоскости, тогда площадь треугольника .
Нетрудно заметить, что формула для
вычисления площади прямоугольного треугольника является частным случаем этой
формулы. Рассмотрим прямоугольный треугольник. Применяя общую формулу для
вычисления площади треугольника, получим, что площадь этого . Угол
C – прямой, его синус равен 1, то есть площадь
прямоугольного треугольника равна половине произведения катетов .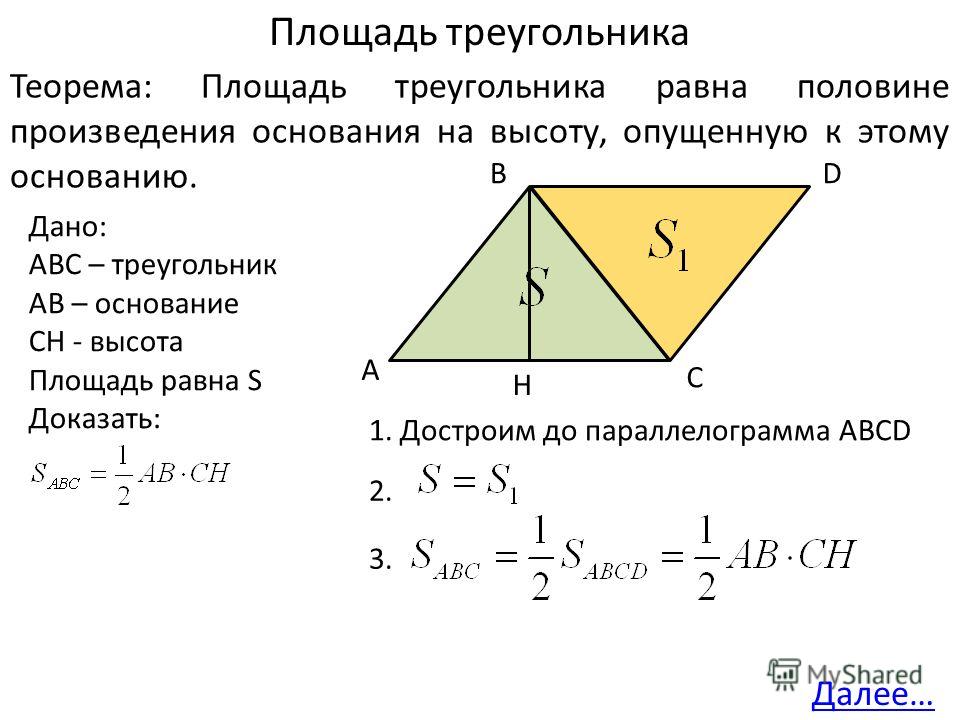 Мы
получили, уже известную нам формулу.
Мы
получили, уже известную нам формулу.
Решим несколько задач.
Задача. Найти площадь треугольника если:
а) , ; б) , ;
в) , .
Решение.
Запишем формулу для вычисления площади треугольника.
а)
б)
в)
Поскольку 46 – не табличное значение, то можно оставить в таком виде. Или с помощью калькулятора найти приближенное значение синуса 46°. Тогда получим, площадь треугольника приблизительно равна 40,28 сантиметрам квадратным.
Задача. . Найти , если , .
Решение.
Теперь давайте рассмотрим параллелограмм ABCD.
Проведем диагональ АC. Эта диагональ делит параллелограмм на два треугольника.
Легко увидеть, что эти треугольники равны по третьему признаку (стороны AB и CD, АD и
BC равны по свойству сторон параллелограмма, АC – общая).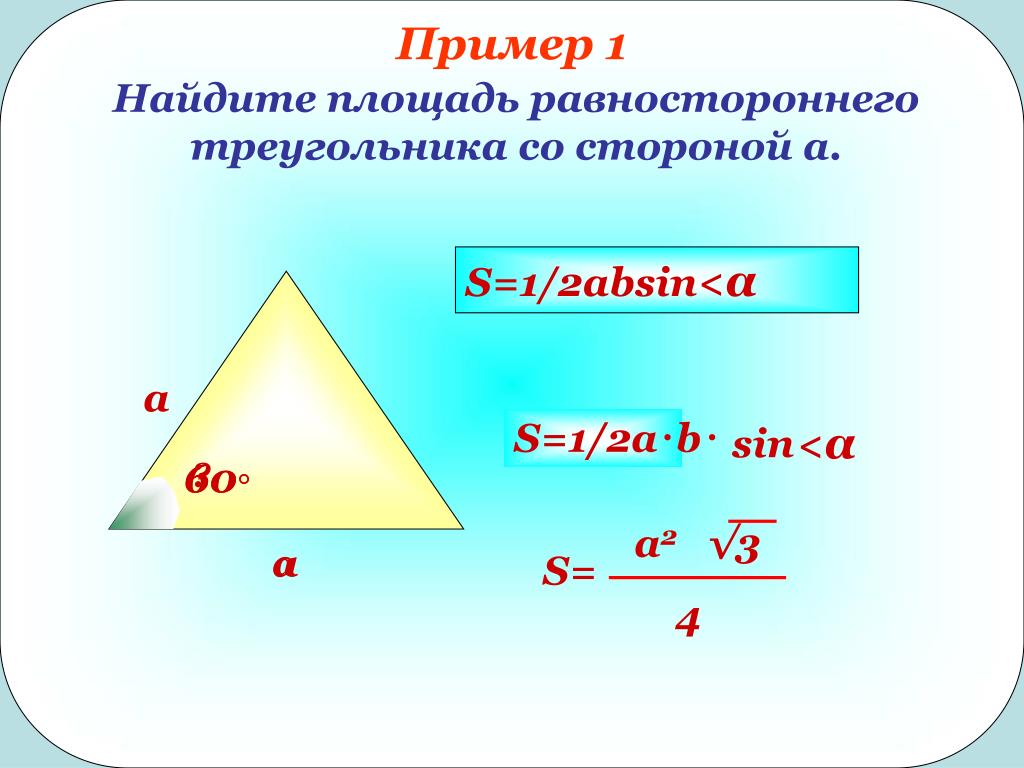 Площадь треугольника ABC
можно найти по формуле: .
Площадь треугольника ACD можно найти по формуле: .
Тогда площадь параллелограмма равна сумме площадей этих треугольников .
Площадь треугольника ABC
можно найти по формуле: .
Площадь треугольника ACD можно найти по формуле: .
Тогда площадь параллелограмма равна сумме площадей этих треугольников .
, .
То есть, другими словами, площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
И опять, как в случае с треугольником, формула для вычисления площади прямоугольника является частным случаем формулы для вычисления площади параллелограмма. Прямоугольник – параллелограмм, углы которого равны 90°.
Обратите внимание, что угол между сторонами параллелограмма можно записать так.
Задача. Найти площадь параллелограмма если:
, .
Решение.
Задача. Соседние стороны параллелограмма равны , . Какой угол должен быть между ними, чтобы площадь параллелограмма была наибольшей?
Решение.
Таким образом мы
получили, что наибольшей будет площадь прямоугольника со сторонами a и b.
Задача. Найти площадь ромба, если его стороны равны , а один из углов равен .
Решение.
Ромб – параллелограмм, значит, для вычисления площади ромба мы можем использовать формулу для вычисления площади параллелограмма.
Задача. Площадь треугольника равна . Сторона в 2 раза больше стороны . Найти .
Решение.
Подведем итоги урока:
Сегодня на уроке, мы вспомнили формулы для вычисления площади треугольника, а также познакомились с новой. Мы познакомились с формулой вычисления площади параллелограмма. Рассмотрели примеры применения этих формул.
Предыдущий урок 21 Формулы для вычисления координат точки
Следующий урок 23 Теорема синусов
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Площадь треугольника / Площадь / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь треугольника
Одну из сторон треугольника часто называют основанием.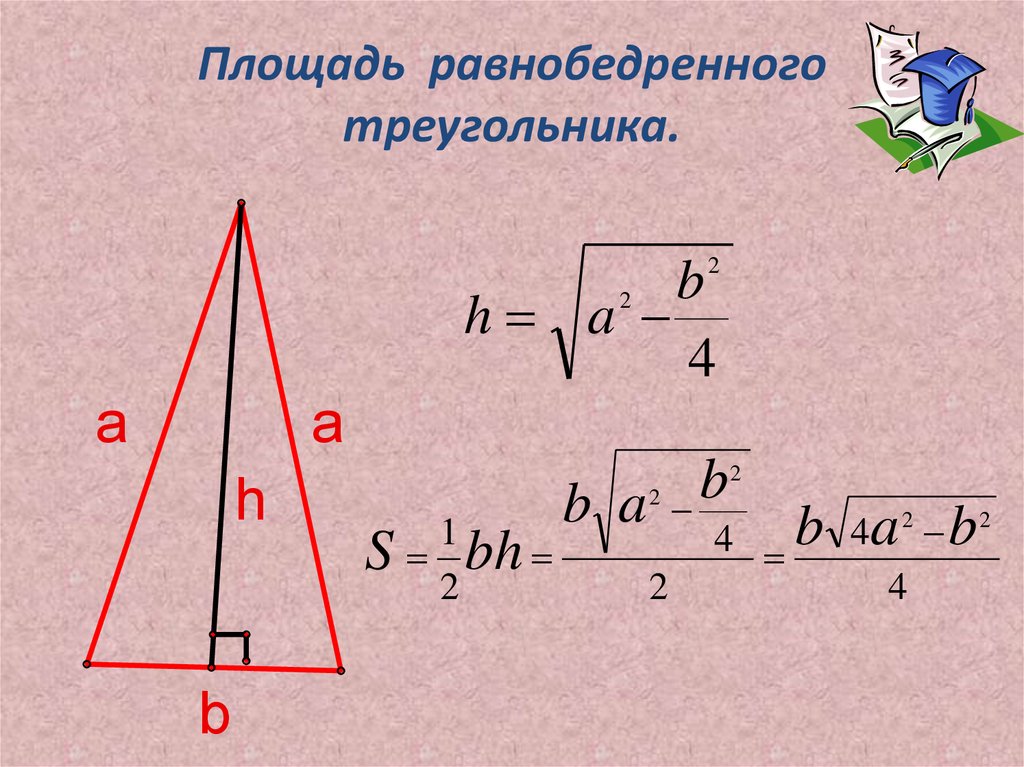 Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Теорема
| Площадь треугольника равна половине произведения его основания на высоту |
Доказательство
Дано: АВС, СН — высота, S — площадь АВС
Доказать: S = АВ СН
Доказательство:
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке. АВС = DCB (по трем сторонам (ВС — общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S — площадь АВС равна половине площади параллелограмма ABCD, т.е. S = АВ СН. Теорема доказана.
Следовательно, площадь S — площадь АВС равна половине площади параллелограмма ABCD, т.е. S = АВ СН. Теорема доказана.
Следствие 1
| Площадь прямоугольного треугольника равна половине произведения его катетов |
Следствие 2
| Если высоты двух треугольников равны, то их площади относятся как основания |
Теорема
| Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы |
Доказательство
Дано: АВС, СН — высота, S — площадь АВС, А1В1С1, В1Н1 — высота, S1— площадь А1В1С1, А = А1
Доказать:
Доказательство:
Наложим треугольник А1В1С1на треугольник АВС так, чтобы вершина А1совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.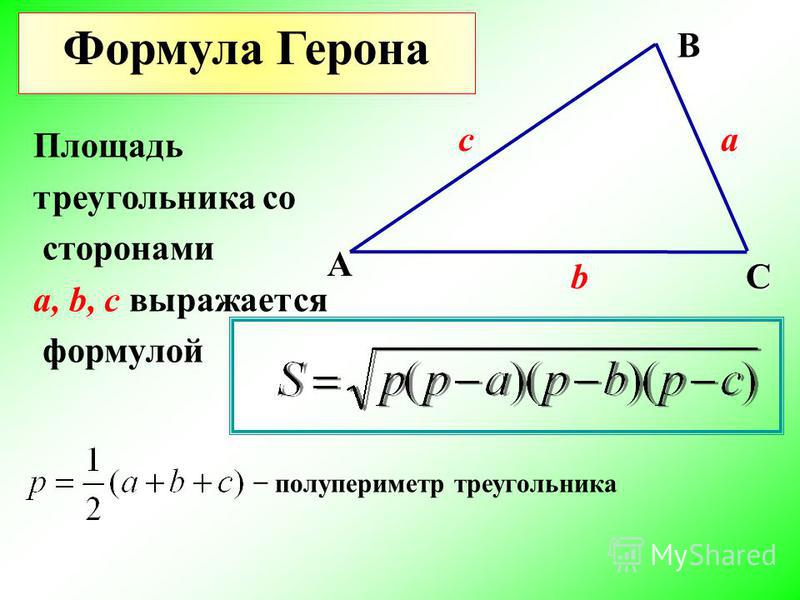
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому
Перемножая полученные равенства, находим:
или
Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 492, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 499, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 517, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 522, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 530, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 832, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 846, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1208, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Нахождение площади треугольника с помощью синуса
Горячая математика Вы знакомы с формулой
р
знак равно
1
2
б
час
найти
площадь треугольника
куда
б
длина основания треугольника и
час
высота или длина перпендикуляра к основанию из противоположной вершины.
Предполагать Δ А Б С имеет длины сторон а , б , а также с . Позволять час быть длиной перпендикуляра к стороне длины б от вершины Б что встречается со стороной А С ¯ в Д .
Затем площадь р треугольника А Б С является р знак равно 1 2 б час .
Теперь посмотри на Δ А Д Б . Это прямоугольный треугольник с гипотенуза А Б ¯ который имеет длину с единицы.
Рассмотрим синус ∠ А .
грех ( А ) знак равно Обратная сторона Гипотенуза знак равно час с грех ( А ) знак равно час с ⇒ час знак равно с грех ( А )
Подставляя значение час по формуле площади треугольника получается
р знак равно 1 2 б ( с грех ( А ) ) знак равно 1 2 б с грех ( А )
Точно так же вы можете написать формулы для площади в терминах
грех
(
Б
)
или же
грех
(
С
)
.
р знак равно 1 2 а б грех ( С ) р знак равно 1 2 а с грех ( Б )
Пример 1:
Найдите площадь Δ п Вопрос р .
У вас есть длины двух сторон и мера угла между ними. Таким образом, вы можете использовать формулу р знак равно 1 2 п р грех ( Вопрос ) куда п а также р длины сторон, противоположных вершинам п а также р соответственно.
Используя формулу площади,
р
знак равно
1
2
(
3
)
(
4
)
грех
(
145
°
)
.
Упрощать.
р знак равно 6 грех ( 145 ° ) ≈ 6 ( 0,5736 ) ≈ 3,44
Следовательно, площадь Δ п Вопрос р около 3,44 кв.см
Пример 2:
Площадь справа
Δ
Икс
Д
Z
с прямым углом при вершине
Д
является
39
кв.ед.
Если
Д
Z
знак равно
12
а также
Икс
Z
знак равно
13
, решить треугольник.
Сначала нарисуйте фигуру с заданными размерами.
Использовать Теорема Пифагора найти длину третьей стороны треугольника.
Икс Д знак равно ( Икс Z ) 2 − ( Д Z ) 2 знак равно 13 2 − 12 2 знак равно 169− 144 знак равно 25 знак равно 5
Теперь у вас есть длины трех сторон и площадь треугольника.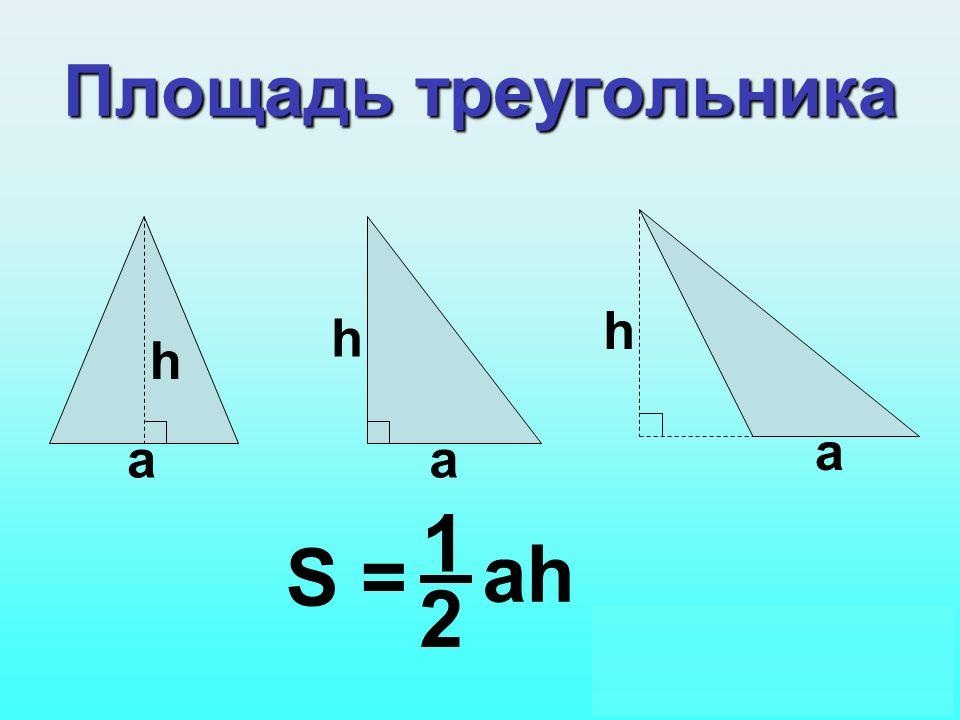
Подставить в формулу площади.
Область знак равно 1 2 × ( Д Z ) × ( Икс Z ) × грех ( Z ) 39знак равно 1 2 ( 12 ) ( 13 ) грех ( Z )
Решить для Z .
грех ( Z ) знак равно ( 39 ) ( 2 ) ( 12 ) ( 13 ) знак равно 0,5
Взяв обратное,
Z знак равно грех − 1 ( 0,5 ) знак равно 30 °
То есть,
м
∠
Z
знак равно
30
°
.
Учитывая, что угол при вершине Д является прямым углом. Следовательно, м ∠ Д знак равно 90 ° .
С использованием Теорема суммы углов треугольника , мера третьего угла,
м ∠ Икс знак равно 180 − ( м ∠ Д + м ∠ Z ) знак равно 180 − ( 90 + 30 ) знак равно 60
Следовательно, мера
∠
Икс
является
60
°
.
Формула площади треугольника и примеры
Площадь треугольника A равна половине произведения его основания b на высоту h. Высота треугольника также известна как высота. Эта формула работает, только если основание перпендикулярно высоте. Это означает, что основание и высота образуют прямой угол.
Пример 1: Найдите площадь треугольника с основанием 5 и высотой 3.
У нас есть \color{blue}b=5 и \color{red}h=3. Подставьте значения в формулу, затем упростите.
Поскольку единица измерения не указана, мы можем записать окончательный ответ как A = 7,5 квадратных единиц.
Пример 2: Найдите площадь треугольника ABC.
Очевидно, что основание равно \color{синему}9 футам, а высота \color{красному}4 футам. Обратите внимание, что основание и высота встречаются под углом 90 градусов. Чтобы найти площадь данного треугольника, мы умножаем основание и высоту, а затем делим произведение на 2.
Обратите внимание, что высота треугольника находится внутри треугольника. 9\цирк}. Более того, ноги также служат высотой и основанием треугольника. Если мы позволим базе быть более короткой ногой, это заставит более длинную ветвь быть высотой. Таким образом, у нас есть \color{blue}b=5 и \color{red}h=7.
Обратите внимание, что высота является частью самого треугольника, который является одной из двух сторон. На самом деле любой из катетов можно обозначить как высоту, так как они пересекаются под углом 90 градусов.
Вычисляя площадь прямоугольного треугольника, мы имеем
Окончательный ответ: 17,5 квадратных дюймов.
Пример 4: Нарисуйте тупоугольный треугольник с основанием 4 сантиметра и внешней высотой 4,5 сантиметра. Затем найдите его площадь.
Тупоугольный треугольник — это тип треугольника, в котором один из его внутренних углов имеет градусную меру больше 90 градусов, но меньше 180 градусов.
В этом случае высота треугольника образована снаружи, а точнее напротив одного из острых углов. Высота перпендикулярна расширенному основанию. 92.
Высота перпендикулярна расширенному основанию. 92.
Чтобы выразить площадь в квадратных футов , мы сохраним основание 2,5 фута, но преобразуем высоту 12 дюймов в футы. Путем преобразования 12 дюймов равны 1 футу. Теперь у нас есть \color{blue}b=2,5 фута и \color{red}h=1 фут.
Таким же образом, чтобы выразить площадь в квадратных дюймов , мы сохранили бы высоту 12 дюймов, но перевести 2,5 фута в дюймы. Поскольку 1 фут равен 12 дюймам, это означает, что 2,5 фута равны 30 дюймам, 2,5 х 12 = 30. Наконец, мы имеем \color{blue}b=30 дюймов и \color{red}h=12 дюймов 92}.
Пример 6: Основание треугольника 17 метров. Его площадь составляет 204 квадратных метра. Найдите высоту треугольника.
Это очень простая задача. Мы подставляем известные значения в формулу, а затем находим оставшуюся переменную.
В этом случае мы знаем основание b и площадь A треугольника. Это означает, что мы можем найти высоту h.
Это означает, что мы можем найти высоту h.
Следовательно, высота треугольника 24 метра.
Пример 7: Площадь треугольника равна 162,56 квадратных сантиметра. Чему равно основание треугольника в дюймов , если высота равна 16 сантиметрам?
Эта задача представляет собой комбинацию примеров №5 и №6. После того, как мы найдем основание в сантиметрах, мы переведем его в дюймы, используя коэффициент преобразования 1 дюйм = 2,54 см.
Так как площадь треугольника 162,56 см , а его высота 16 см , мы имеем
Основание равно 20,32 сантиметра. Однако нам все еще нужно преобразовать сантиметры в дюймы, чтобы получить окончательный ответ.
Так как 1 дюйм = 2,54 см, мы делим 20,32 на 2,54, чтобы получить дюймы.
{\Large{{{20,32\,}\более {2,54}}}} = 8
Следовательно, длина основания 8 дюймов.
Пример 8: Основание треугольника вдвое больше его высоты. Найдите площадь основания, если площадь равна 289 квадратных километров.
Найдите площадь основания, если площадь равна 289 квадратных километров.
Дано, что основание в два раза больше его удвоенного, {\color{blue}b}=2{\color{red}h}. Итак, если высота равна h, то основание равно 2h.
высота = \color{red}h
основание = 2 {\ color {красный} h}
Площадь также равна 289 квадратных километров.
Площадь = 289
Подставляем эти значения в формулу и находим \color{red}h.
Поскольку основание равно 2\color{red}h, то
Следовательно, основание равно 34 км.
Давайте проверим правильность нашей базы и высоты. Для треугольника с основанием 34 км и высотой 17 км площадь должна быть 289 кв.
Да, проверяет. Это основание и высота дают нам площадь 2892.
Пример 9: Основание треугольника на 5 единиц больше его высоты. Если площадь треугольника равна 117 квадратных единиц, какова мера высоты?
Пусть h высота треугольника. Говорят, что основание на 5 единиц длиннее высоты, которая может быть выражена как b=h+5.
Поскольку b=h+5, а площадь треугольника равна 117 квадратных единиц, мы можем подставить эту информацию в формулу, чтобы получить квадратное уравнение, решаемое с помощью метода факторинга.
Мы проигнорируем отрицательное решение, потому что отрицательной высоты не существует.
Следовательно, высота составляет 13 единиц.
Мы можем выполнить быструю проверку правильности нашего ответа.
Если h=13, основание равно 13+5=18. Вычисляя площадь треугольника получаем
Да, получаем ту же площадь 117 квадратных единиц. Это означает, что наши значения для основания и высоты верны!
Вам может быть интересно:
Высота треугольника
Площадь круга
Площадь треугольника – определение, формула, примеры, часто задаваемые вопросы как пространство, занимаемое границами треугольника. Мы можем вычислить площадь треугольника, если известны основание и высота треугольника. Следовательно, площадь треугольника можно вычислить по формуле половины произведения основания и высоты.
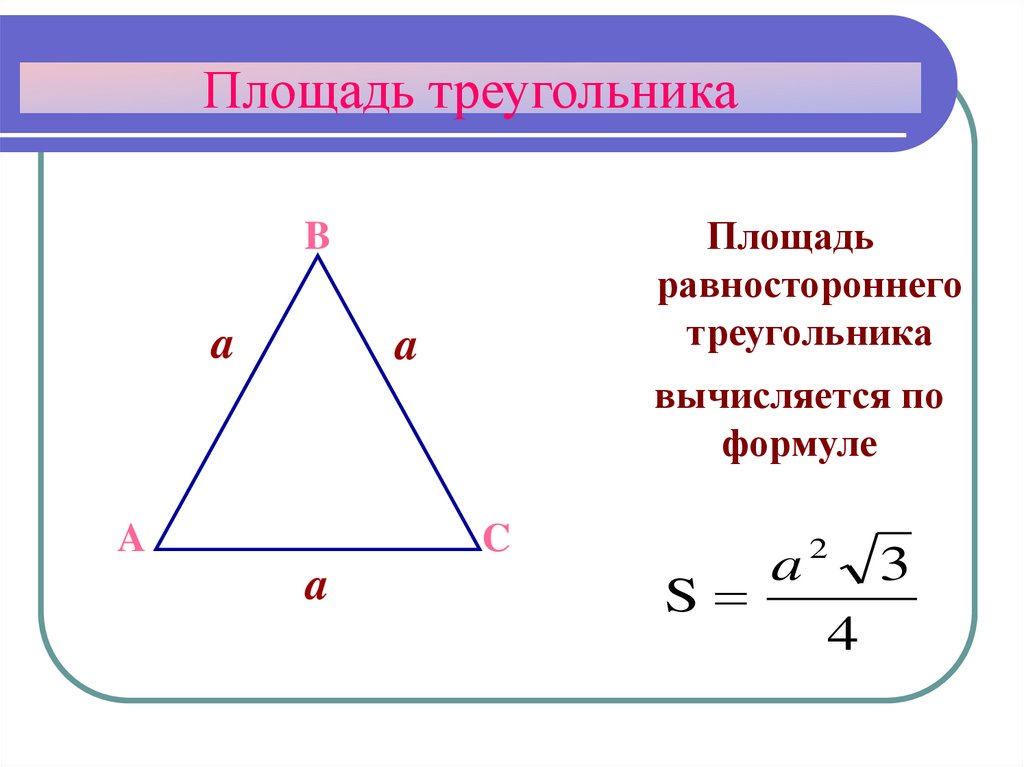
Как правило, область можно рассматривать как область пространства, занятую двухмерным объектом внутри его границ. Площадь измеряется в квадратных единицах, а единицей площади в системе СИ является кв. м или м 2 . Его можно измерять и в других единицах. Различные формулы используются для нахождения площадей различных типов многоугольников, включая треугольники, квадраты, прямоугольники, пятиугольники и т. д.
Трехсторонний фигурный треугольник можно разделить на различные категории на основе его сторон и углов. Существуют различные методы нахождения площади треугольников, которые обсуждаются ниже в этой статье.
Какова площадь треугольника?
Площадь треугольника определяется как общая поверхность, занятая или окруженная границами треугольника на плоской поверхности. И формула для вычисления площади треугольника дается половиной произведения основания и высоты данного треугольника.
Примечание. Основание и высота треугольника всегда перпендикулярны друг другу, образуя прямой угол (90 градусов).

Определение треугольника
Треугольник — простейший многоугольник, имеющий только три стороны. Это замкнутая фигура, которая может быть правильной или неправильной. Правильный треугольник называется равносторонним треугольником. В зависимости от сторон и углов треугольники можно разделить на несколько категорий.
Площадь треугольника Формула
Площадь треугольника зависит от размеров треугольника, как правило, площадь зависит от основания и высоты фигуры. Для треугольника площадь вычисляется путем умножения половины основания на его высоту. Площадь треугольника измеряется в квадратных единицах, то есть м 2 , CM 2 и т. Д.
Математически Формула дается
Площадь треугольника (A) = 1/2 × B × H
, где
B 6
. основание треугольника
h высота треугольника
Пример: Какова площадь треугольника с основанием b = 5 м и высотой h = 6 м?
Решение:
Используя общую формулу, Площадь треугольника, A = 1/2 × b × h
Площадь = 1/2 × 5 (м) × 6 (м)
= 5 (м) × 6 )
= 15 м 2
Площадь треугольника по формуле Герона
Площадь треугольника со всеми тремя заданными сторонами можно найти по формуле Герона. Применение формулы Герона включает два шага, которые обсуждаются ниже:
Применение формулы Герона включает два шага, которые обсуждаются ниже:
Пусть дан треугольник со сторонами a, b и c, тогда для нахождения его площади
Шаг 1: Вычислить полупериметр(ы) заданного треугольника по
s = (a+b+c)/2
Шаг 2: найти формулу Герона 90 необходимая площадь.
Площадь = √ {S (S-A) (S-B) (S-C)}
, где,
S -полуэлементный
A, B и C -это стороны.
Если в треугольнике даны все три стороны, применить общую формулу очень сложно, так как найти высоту в таком случае очень сложно. Поэтому мы полагаемся на формулу Герона в таких случаях, чтобы найти искомую площадь.
Пример: Какова площадь треугольника со сторонами 3 см, 4 см и 5 см?
Решение:
Используя формулу Герона,
s = (a+b+c)/2
= (3+4+5)/2
= 6 12/20 Площадь = √{ s(s-a)(s-b)(s-c)}
= √{ 6(6-3)(6-4)(6-5)}
= √(6×3×2×1) = √(36)
= 6 см 2
Площадь различных типов треугольников обсуждается далее в этой статье.
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, у которого все три стороны равны и все три угла равны 60 градусов. Предположим, что задан равносторонний треугольник со сторонами, равными единице, тогда площадь равностороннего треугольника определяется как
Площадь равностороннего треугольника (A) = (√3)/4 × сторона 2
= (√3)/4 × a 2
Пример: Найдите площадь треугольника со стороной a = 8 см
Решение:
Сторона треугольника A) = 8 см
Область (A) = (√3)/4 × A 2
= (√3)/4 × 8 2
= 16√3 СМ 2
равнобедренного треугольника
Равнобедренный треугольник — это треугольник, имеющий две равные стороны и углы, противолежащие этим равным сторонам, также равны. Предположим, что у равнобедренного треугольника общая сторона b и другая сторона a, тогда его площадь равна
Предположим, что у равнобедренного треугольника общая сторона b и другая сторона a, тогда его площадь равна
Площадь равнобедренного треугольника = ¼×b√(4a 2 – b 2 )
см сторона b = 8 см
Решение:
Дано,
общая сторона треугольника (a) = 5 см
другая сторона треугольника (b) = 8 см
Площадь(A) = ¼×b (4a 2 – b 2 )
= ¼×8√(4×5 2 – 8 2 )
= 2 × 6 = 12 см 2
Площадь прямоугольного треугольника
Прямоугольным треугольником считается треугольник, содержащий прямоугольный треугольник. Если известны все три стороны прямоугольного треугольника, то, применяя общую формулу, формула Герона очень проста. Так как в прямоугольном треугольнике одна из сторон ведет себя как основание, а другая как высота.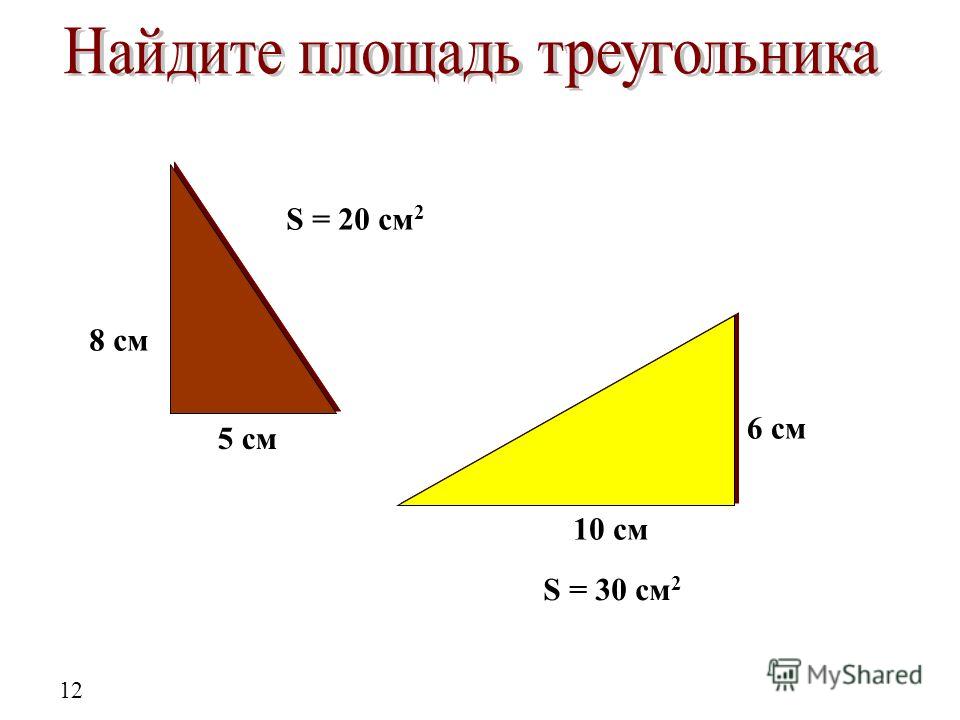 На приведенном ниже рисунке а — основание треугольника, а с — его высота. Таким образом, применить общую формулу здесь легко,
На приведенном ниже рисунке а — основание треугольника, а с — его высота. Таким образом, применить общую формулу здесь легко,
Площадь треугольника (A) = 1/2 × A × C
, где
A является основанием треугольника
C — высота Triangle
925 C Пример: Найдите площадь треугольника с основанием а = 8 см и высотой с = 5 см.
Решение:
Дано
Основание треугольника (а) = 8 см
Высота треугольника (с) = 5 см
Имеем,
Площадь(A) = 1/2 × a × c
= 1/2 × 8 × 5
)
Для нахождения площади треугольника, если известны две стороны треугольника и угол между ними, используйте формулу, обсуждаемую ниже.
Возьмем треугольник PQR, углы при вершинах которого равны ∠P, ∠Q и ∠R, а стороны равны p,q и r.
Теперь, когда даны две стороны треугольника и угол между ними, формула для вычисления площади треугольника равна
- Площадь (∆PQR) = ½ qr sin P
- Площадь (∆PQR) = ½ pq sin R
- Площадь (∆PQR) = ½ rp sin Q
Пример: найти площадь треугольника ∆PQR , если P = 60° и q = 3, r = 2 в единицах.

Решение:
, P = 60 ° и Q = 3, R = 2
Площадь (∆PQR) = ½ QR SIN A
= ½ (3) (2) SIN 30 (SIN 60° = √3/2 )
= 3 × √3/2
= (3√3) /2 кв.ед.
Как найти площадь треугольника?
Площадь треугольника рассчитывается с использованием следующих шагов:
Шаг 1: Отметьте размеры (основание и высота) данного изделия.
Шаг 2: Используйте формулу для нахождения площади треугольника. Площадь = 1/2 × (основание × высота)
Шаг 3: Площадь, полученная на шаге 2, является необходимой площадью, она измеряется в единицах 2 .
Таким образом, площадь треугольника находится с помощью описанных выше шагов.
Решенные примеры на площадь треугольника
Пример 1: Найдите площадь треугольника с основанием 12 см и высотой 4 см.

Решение:
Дано
Основание треугольника = 12 см ‘
Высота треугольника = 4 см
,
Область (A) = 1/2 × B
=. 1/2 × 12 × 4
= 24 см 2
Пример 2. Какова площадь треугольника со сторонами 8 см, 6 см и 10 см (по формуле Герона)?
Решение:
Используя формулу Герона,
s = (a+b+c)/2
= (8+6+10)/2
= 0 3 Площадь 2 24/20 = √{ s(s-a)(s-b)(s-c)}= √{ 12(12-8)(12-6)(12-10)}
= √(12×4×6×2) = √(576)
= 24 см 2
Пример 3. Найдите площадь прямоугольного треугольника с основанием a = 5 см и высотой c = 3 см.
Решение:
Дано
Основание треугольника (а) = 5 см
Высота треугольника (с) = 3 см = 1/2 × 5 × 3
= 7,5 см 2
Пример 4: Найдите площадь равностороннего треугольника, имеющего сторону A = 6 см
Решение:
.
сторона треугольника (a) = 6 см
Площадь (A) = (√3)/4 × a 2
= (√3)/4 × 6 2
= 9√3 см 2
Пример 5: Найдите область треугольника, имеющего основание 15 см и высоты 5cm. .
Решение:
Основание треугольника=15 см
Высота треугольника=5 см /2 × 15 × 5
= 37,5 см 2
Часто задаваемые вопросы о площади треугольника
Вопрос 1: Какова площадь треугольника?
Ответ:
Область, ограниченная границей треугольника, т. е. площадь, занимаемая периметром треугольника, называется площадью треугольника.
Вопрос 2: Какова площадь треугольника, если известны все его три стороны a, b и c?
Ответ:
Если известны все три стороны треугольника, то его площадь рассчитывается по формуле Герона.




 сторона треугольника (a) = 6 см
сторона треугольника (a) = 6 см