Мнимая единица — это… Что такое Мнимая единица?
Мнимая единица — обычно комплексное число, квадрат которого равен отрицательной единице. Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксона или в рамках алгебр по Клиффорду.
Для комплексных чисел
В математике, физике мнимая единица обозначается как латинская или . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами, имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «-i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» и на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для через радикал (как ).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. — это одно из решений уравнения
- или
И тогда его вторым решением уравнения будет , что проверяется подстановкой.
Степени мнимой единицы
Степени i повторяются в цикле:
Что может быть записано для любой степени в виде:
где n — любое целое число.
Отсюда: где mod 4 это остаток от деления на 4.
Число является вещественным :
- [1]
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
Также,
- [2]
Корни из мнимой единицы
В поле комплексных чисел корень n-ой степени имеет n решений. На комплексной плоскости эти корни находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
В частности, и
Также корни мнимой единицы могут быть представлены в показательном виде:
Иные мнимые единицы
В конструкции Кэли — Диксона (или в алгебрах Клиффорда) «мнимых единиц расширения» может быть несколько, и/или их квадрат может быть =«+1» или даже =«0». Но в этом случае могут возникать делители нуля, имеются и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения «».
См.также
Ссылки
Мнимая единица — Википедия
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин употребляется также в обобщённом смысле в конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду.
Для комплексных чисел

В математике, физике мнимая единица обозначается как латинская i {\displaystyle i} или j {\displaystyle j} . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 {\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 {\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} через радикал (как − 1 {\displaystyle {\sqrt {-1}}} ).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i {\displaystyle i} — это одно из решений уравнения
- x 2 + 1 = 0 , {\displaystyle x^{2}+1=0,} или x 2 = − 1. {\displaystyle x^{2}=-1.}
И тогда его вторым решением уравнения будет − i {\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Степени i {\displaystyle i} повторяются в цикле:
- … {\displaystyle \ldots }
- i − 3 = i {\displaystyle i^{-3}=i}
- i − 2 = − 1 {\displaystyle i^{-2}=-1}
- i − 1 = − i {\displaystyle i^{-1}=-i}
- i 0 = 1 {\displaystyle i^{0}=1}
- i 1 = i {\displaystyle i^{1}=i}
- i 2 = − 1 {\displaystyle i^{2}=-1}
- i 3 = − i {\displaystyle i^{3}=-i}
- i 4 = 1 {\displaystyle i^{4}=1}
- … {\displaystyle \ldots }
Что может быть записано для любой степени в виде:
- i 4 n = 1 {\displaystyle i^{4n}=1}
- i 4 n + 1 = i {\displaystyle i^{4n+1}=i}
- i 4 n + 2 = − 1 {\displaystyle i^{4n+2}=-1}
- i 4 n + 3 = − i . {\displaystyle i^{4n+3}=-i.}
где n — любое целое число.
Отсюда: i n = i n mod 4 {\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.
Из тождества Эйлера следует, что число i i {\displaystyle i^{i}} является вещественным:
- i i = e ( i π / 2 ) i = e i 2 π / 2 = e − π / 2 = 0,207 87957635 … {\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots } .
Точнее, в комплексном анализе возведение в степень: x y = exp ( y ⋅ Ln x ) {\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому
- i i = e − π ( 1 + 4 n ) 2 {\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}} , где n ∈ Z {\displaystyle n\in \mathbb {Z} } .
Также верно, что ( − i ) ( − i ) = i i {\displaystyle (-i)^{(-i)}=i^{i}} .
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i ! = Γ ( 1 + i ) ≈ 0.4980 − 0.1549 i . {\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- | i ! | = π sinh ( π ) ≈ 0.521564…. {\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
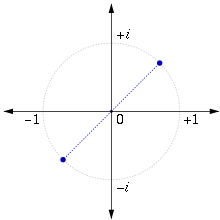 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- u k = cos π 2 + 2 π k n + i sin π 2 + 2 π k n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
- i = cos π 2 + i sin π 2 {\displaystyle i=\cos \ {\frac {\pi }{2}}+i\ \sin \ {\frac {\pi }{2}}}
В частности, i = { 1 + i 2 ; − 1 − i 2 } {\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i 3 = { − i ; i + 3 2 ; i − 3 2 } {\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- u k = e ( π 2 + 2 π k ) i n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
В конструкции Кэли — Диксона (или в алгебрах Клиффорда) «мнимых единиц расширения» может быть несколько, и/или их квадрат может быть = «+1» или даже = «0». Но в этом случае могут возникать делители нуля, имеются и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения « x 2 = − 1 {\displaystyle x^{2}=-1} ».
К вопросу об интерпретации и названии
 | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |  |
Обозначения
Обычное обозначение i {\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j {\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i = i ( t ) {\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
См.также
Примечания
Ссылки
Мнимая единица — Википедия
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин употребляется также в обобщённом смысле в конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду.
Для комплексных чисел

В математике, физике мнимая единица обозначается как латинская i {\displaystyle i} или j {\displaystyle j} . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 {\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 {\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} через радикал (как − 1 {\displaystyle {\sqrt {-1}}} ).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i {\displaystyle i} — это одно из решений уравнения
- x 2 + 1 = 0 , {\displaystyle x^{2}+1=0,} или x 2 = − 1. {\displaystyle x^{2}=-1.}
И тогда его вторым решением уравнения будет − i {\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Степени i {\displaystyle i} повторяются в цикле:
- … {\displaystyle \ldots }
- i − 3 = i {\displaystyle i^{-3}=i}
- i − 2 = − 1 {\displaystyle i^{-2}=-1}
- i − 1 = − i {\displaystyle i^{-1}=-i}
- i 0 = 1 {\displaystyle i^{0}=1}
- i 1 = i {\displaystyle i^{1}=i}
- i 2 = − 1 {\displaystyle i^{2}=-1}
- i 3 = − i {\displaystyle i^{3}=-i}
- i 4 = 1 {\displaystyle i^{4}=1}
- … {\displaystyle \ldots }
Что может быть записано для любой степени в виде:
- i 4 n = 1 {\displaystyle i^{4n}=1}
- i 4 n + 1 = i {\displaystyle i^{4n+1}=i}
- i 4 n + 2 = − 1 {\displaystyle i^{4n+2}=-1}
- i 4 n + 3 = − i . {\displaystyle i^{4n+3}=-i.}
где n — любое целое число.
Отсюда: i n = i n mod 4 {\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.
Из тождества Эйлера следует, что число i i {\displaystyle i^{i}} является вещественным:
- i i = e ( i π / 2 ) i = e i 2 π / 2 = e − π / 2 = 0,207 87957635 … {\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots } .
Точнее, в комплексном анализе возведение в степень: x y = exp ( y ⋅ Ln x ) {\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому
- i i = e − π ( 1 + 4 n ) 2 {\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}} , где n ∈ Z {\displaystyle n\in \mathbb {Z} } .
Также верно, что ( − i ) ( − i ) = i i {\displaystyle (-i)^{(-i)}=i^{i}} .
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i ! = Γ ( 1 + i ) ≈ 0.4980 − 0.1549 i . {\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- | i ! | = π sinh ( π ) ≈ 0.521564…. {\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- u k = cos π 2 + 2 π k n + i sin π 2 + 2 π k n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
- i = cos π 2 + i sin π 2 {\displaystyle i=\cos \ {\frac {\pi }{2}}+i\ \sin \ {\frac {\pi }{2}}}
В частности, i = { 1 + i 2 ; − 1 − i 2 } {\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i 3 = { − i ; i + 3 2 ; i − 3 2 } {\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- u k = e ( π 2 + 2 π k ) i n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
В конструкции Кэли — Диксона (или в алгебрах Клиффорда) «мнимых единиц расширения» может быть несколько, и/или их квадрат может быть = «+1» или даже = «0». Но в этом случае могут возникать делители нуля, имеются и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения « x 2 = − 1 {\displaystyle x^{2}=-1} ».
К вопросу об интерпретации и названии
 | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |  |
Обозначения
Обычное обозначение i {\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j {\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i = i ( t ) {\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
См.также
Примечания
Ссылки
Мнимая единица — Википедия. Что такое Мнимая единица
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин употребляется также в обобщённом смысле в конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду.
Для комплексных чисел

В математике, физике мнимая единица обозначается как латинская i {\displaystyle i} или j {\displaystyle j} . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 {\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 {\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} через радикал (как − 1 {\displaystyle {\sqrt {-1}}} ).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i {\displaystyle i} — это одно из решений уравнения
- x 2 + 1 = 0 , {\displaystyle x^{2}+1=0,} или x 2 = − 1. {\displaystyle x^{2}=-1.}
И тогда его вторым решением уравнения будет − i {\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Степени i {\displaystyle i} повторяются в цикле:
- … {\displaystyle \ldots }
- i − 3 = i {\displaystyle i^{-3}=i}
- i − 2 = − 1 {\displaystyle i^{-2}=-1}
- i − 1 = − i {\displaystyle i^{-1}=-i}
- i 0 = 1 {\displaystyle i^{0}=1}
- i 1 = i {\displaystyle i^{1}=i}
- i 2 = − 1 {\displaystyle i^{2}=-1}
- i 3 = − i {\displaystyle i^{3}=-i}
- i 4 = 1 {\displaystyle i^{4}=1}
- … {\displaystyle \ldots }
Что может быть записано для любой степени в виде:
- i 4 n = 1 {\displaystyle i^{4n}=1}
- i 4 n + 1 = i {\displaystyle i^{4n+1}=i}
- i 4 n + 2 = − 1 {\displaystyle i^{4n+2}=-1}
- i 4 n + 3 = − i . {\displaystyle i^{4n+3}=-i.}
где n — любое целое число.
Отсюда: i n = i n mod 4 {\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.
Из тождества Эйлера следует, что число i i {\displaystyle i^{i}} является вещественным:
- i i = e ( i π / 2 ) i = e i 2 π / 2 = e − π / 2 = 0,207 87957635 … {\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots } .
Точнее, в комплексном анализе возведение в степень: x y = exp ( y ⋅ Ln x ) {\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому
- i i = e − π ( 1 + 4 n ) 2 {\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}} , где n ∈ Z {\displaystyle n\in \mathbb {Z} } .
Также верно, что ( − i ) ( − i ) = i i {\displaystyle (-i)^{(-i)}=i^{i}} .
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i ! = Γ ( 1 + i ) ≈ 0.4980 − 0.1549 i . {\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- | i ! | = π sinh ( π ) ≈ 0.521564…. {\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- u k = cos π 2 + 2 π k n + i sin π 2 + 2 π k n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
- i = cos π 2 + i sin π 2 {\displaystyle i=\cos \ {\frac {\pi }{2}}+i\ \sin \ {\frac {\pi }{2}}}
В частности, i = { 1 + i 2 ; − 1 − i 2 } {\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i 3 = { − i ; i + 3 2 ; i − 3 2 } {\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- u k = e ( π 2 + 2 π k ) i n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
В конструкции Кэли — Диксона (или в алгебрах Клиффорда) «мнимых единиц расширения» может быть несколько, и/или их квадрат может быть = «+1» или даже = «0». Но в этом случае могут возникать делители нуля, имеются и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения « x 2 = − 1 {\displaystyle x^{2}=-1} ».
К вопросу об интерпретации и названии
 | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |  |
Обозначения
Обычное обозначение i {\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j {\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i = i ( t ) {\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
См.также
Примечания
Ссылки
Мнимая единица Википедия

Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не только для комплексных чисел[⇨].
В математике, физике мнимая единица обозначается как латинская i {\displaystyle i} или j {\displaystyle j} . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 {\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 {\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «−i» и «−i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} через радикал (как − 1 {\displaystyle {\sqrt {-1}}} ).
Определение[
Мнимая единица — Абсурдопедия
Единица — вздор! Единица — ноль!
- ~ Маяковский про мнимую единицу
Мнимая единица (讠, один с точечкой) — это:
- … мнимое число, которое определяется так: мнимая единица, умноженная на мнимую единицу, умноженная на мнимую единицу ещё раз, и ещё умноженная два раза на мнимую единицу, умноженная на мнимую единицу равна −1. Если то, что говорится в предыдущем предложении истинно, то оно ложно, если ложно — то истинно.
- выше была приведёна упрощённая формулировка для двоечников. Крайне сложная формулировка такова: i 2 = − 1 {\displaystyle i^{2}=-1} .
Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.
История открытия[править]
История мнимой единицы такова. Математик, напившись, сел за компьютер. Там он открыл блокнот, чтобы напечатать чистый лист из принтера и высморкаться в него. Но из-за пьянки он нечаянно нажал знак i. Шрифт был большим, потому что вчера он учил ребёнка примеру 3 − 4 {\displaystyle 3-4} . Вот он и напечатал этот лист. И высморкался в него. Поэтому лист стал мятым. Он сказал: «Мятая единица с точечкой». А его друг не расслышал и сказал: «Мнимая единица… Эээ… Эх, какая водочка! Козявочкин, к доске! Вот тебе, двоечник, ещё пример. Вот это число в квадрате равно…». А наш математик ответил: «О, да, давай ещё стопочку! Ааа… Ты что, не знаешь отрицательных чисел? Нужно слушать, что говорят на уроке. Ответ равен минус одному». И они стали продолжать пить. Открытие осталось бы незапомненным, если бы не вор, который пробрался украсть компьютер. Он нёс с собой диктофон. И записывал всё, что говорили пьяные учёные. Зачем — неизвестно. Вор украл компьютер. Он хотел включить его, подключив к молниеотводу один провод, а другой — засунув себе в рот. Ударила молния… Дальше понятно. А диктофон нашёл пьяница и бросил его в окно дома учёных с целью разбить его. Он добился своего, но в то же время оказал невообразимое содействие науке. Учёные-математики после отрезвления прочитали запись в диктофоне и поняли, что они совершили открытие! Записав, что они сказали тогда, в математической форме, они получили выражение: i 2 = − 1 {\displaystyle i^{2}=-1} Но оно было очень сложное, и понять его не удалось даже этим двум математикам. Математик, который напечатал мнимую единицу и высморкался в лист, поблагодарил своего друга за исправление. Вскоре, проанализировав осколки разбитого окна, математики решили, что данных для того, чтобы понять их слова, недостаточно. Поэтому они стали думать. Но вдруг один из них понял, что надо делать. И разбил головой другое окно. Сделав записи состояний окон, головы и крыши, он, проведя сложнейшие расчёты, решил, что крыша у него съехала и что мнимая единица, умноженная на мнимую единицу, умноженная на мнимую единицу ещё раз, и ещё умноженная два раза на мнимую единицу, умноженная на мнимую единицу равна − 1 {\displaystyle -1} .
Основные свойства[править]
После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:
i 2 + 1 = 0 {\displaystyle i^{2}+1=0}
i 3 = − i {\displaystyle i^{3}=-i}
( − i ) 2 = − 1 = i 2 {\displaystyle (-i)^{2}=-1=i^{2}} , поэтому − i = i {\displaystyle -i=i} , далее: ( − i ) / i = − 1 {\displaystyle (-i)/i=-1} , ( − i ) / i = i / i = 1 {\displaystyle (-i)/i=i/i=1}
В итоге доказано, что 1 = − 1 {\displaystyle 1=-1} , т.е отрицательные и положительные числа неотличимы.
Теперь докажем одно из самых важных свойств мнимой единицы — то, что в любом выражении её можно заменить на 1 ⋅ {\displaystyle 1\cdot } . Точку можно поставить и справа, содержание от этого не изменится. Действительно, ведь мнимая единица — это единица с точечкой, то есть со знаком умножения, что и требовалось доказать.
Далее:
2 i = 2 i e e = 21 ⋅ e e = 21 {\displaystyle 2i={\frac {2ie}{e}}={\frac {21\cdot e}{e}}=21}
В итоге мы получили e-нное представление числа 2 i {\displaystyle 2i} — это 2 i = 21 {\displaystyle 2i=21}
Тождество Эйлера[править]
Существует следующее тождество:
e i π + 1 = 0 {\displaystyle e^{i\pi }+1=0}
Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.
Доказательство[править]
Т.к i = − i {\displaystyle i=-i} , данную формулу можно переписать в виде: e − i π = − 1 {\displaystyle e^{-i\pi }=-1} . Первую формулу также перепишем: e i π = − 1 {\displaystyle e^{i\pi }=-1} . Перемножим эти формулы:
e − i π ∗ e i π = ( − 1 ) ∗ ( − 1 ) {\displaystyle e^{-i\pi }*e^{i\pi }=(-1)*(-1)}
e i π − i π = 1 {\displaystyle e^{i\pi -i\pi }=1}
1 = 1 {\displaystyle 1=1}
В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!
Опровержение[править]
Т.к мнимая единица — это 1 с точечкой, или проще говоря, i = 1 ⋅ {\displaystyle i=1\cdot } . Поэтому:
e i π + 1 = e 1 ⋅ π + 1 = e π + 1 ≠ 0 {\displaystyle e^{i\pi }+1=e^{1\cdot \pi }+1=e^{\pi }+1\neq 0}
Тождество опровергнуто.
Опровержение опровержения[править]
Не верьте этому опровержению, Эйлер говорил правду!!! (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)
Следствие 1[править]
Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:
e i π = − 1 {\displaystyle e^{i\pi }=-1}
Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:
e 2 i π = 1 {\displaystyle e^{2i\pi }=1}
Отсюда неминуемо следует, что 2 i π = 0 {\displaystyle 2i\pi =0} , а значит, i = 0 {\displaystyle i=0} . Говорят, когда Эйлер это обнаружил, он свернулся в ленту Мёбиуса и укатился в Соловецкий монастырь, где и закончил свои дни в полном безумии. Тем не менее, официальная наука доказала, что Эйлер заразился безумием от Фридриха Ницше, к тому времени ещё бывшего одним из носителей бесов безумия.
Следствие 2[править]
Еще раз рассмотрим вышеприведённое тождество Эйлера:
e i π = − 1 {\displaystyle e^{i\pi }=-1}
А теперь возведем обе его части в любую целую нечётную степень n:
e n i π = − 1 {\displaystyle e^{ni\pi }=-1}
А значит, при любом нечётном n,
e n i π = e i π {\displaystyle e^{ni\pi }=e^{i\pi }} . Логарифмируя по основанию е, получаем n i π = i π {\displaystyle ni\pi =i\pi }
Сокращая на i π {\displaystyle i\pi } , получаем n=1, то есть каждое нечётное целое число равно единице. Отсюда со всей очевидностью следует божественность мироздания, множественность параллельных миров и реальность существования чебурашек в дикой природе.
Интересные факты[править]
- Если пользоваться мнимой единицей, то существует вероятность 65 % сдать ЕГЭ по математике на 95 баллов путем выноса мозга проверяющим.
- Вполне возможно, что успех компании Apple принесла именно мнимая единица, подсознательно влияющая на моск и вызывающая мнимое представление о реальных вещах.
- Поделить мнимую единицу на ноль можно: получается Мнимая бесконечность.
- Кроме мнимой единицы существуют и мнимая двойка, тройка, четверка и т. д. Однако ими не пользуются, ибо нефиг!
- Британские ученые доказали, что если выйти в плоскость комплексных чисел, то по замкнутому контуру можно проходить сквозь двери. Однако всех, кто пытался доказать это на практике, засосало в нуль-телепорт.
- Исходя из вышеописаного явления, можно предположить, что черная дыра может существовать только в плоскости комплексных чисел.
- Существует мнение, что изображение мнимой единицы получилось путем банального переворачивания знака !. Возможно это сделали для того, чтобы показать, насколько это число опасно и таинственно, и лучше глубоко не лезть в эти дебри. Скорее всего так и есть: в последнее время почти никто не занимается изучением мнимой единицы, особенно после экспериментов британских ученых. И только безумные ученые изредка решаются рискнуть своими задницами ради очередного, никому не нужного, мнимого открытия.
Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует. i 2 = − 1 {\displaystyle i^{2}=-1} далее
i 2 + 1 = 0 {\displaystyle i^{2}+1=0} в нормальном виде ( − 1 ) 2 + 1 = 0 {\displaystyle (-1)^{2}+1=0}
i 3 = − i {\displaystyle i^{3}=-i} приведем в нормальный вид ( ( − 1 ) 2 + 1 ) ∗ ( − 1 ) = 0 {\displaystyle ((-1)^{2}+1)*(-1)=0} , раскроем скобки и получим ( − 1 ) 3 + ( − 1 ) = 0 {\displaystyle (-1)^{3}+(-1)=0} , именно так должна выглядеть формула,МЫ ЖЕ ЗНАЕМ со школы «При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом!»(кстати, никто не может объяснить этого правила в физическом смысле!) отсюда следует вывод в физическом смысле ВСЕ ОТРИЦАТЕЛЬНЫЕ ЧИСЛА = 0 Их не существует!
В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы!!!
Мнимая единица Википедия
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не только для комплексных чисел[⇨].
В математике, физике мнимая единица обозначается как латинская i {\displaystyle i} или j {\displaystyle j} . Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f ( x ) = 0 {\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x 2 + 1 = 0 {\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «−i» и «−i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} через радикал (как − 1 {\displaystyle {\sqrt {-1}}} ).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i {\displaystyle i} — это одно из решений уравнения
- x 2 + 1 = 0 , {\displaystyle x^{2}+1=0,} или x 2 = − 1. {\displaystyle x^{2}=-1.}
И тогда его вторым решением будет − i {\displaystyle -i} , что проверяется подстановкой.
Степени мнимой единицы
Степени i {\displaystyle i} повторяются в цикле:
- … {\displaystyle \ldots }
- i − 3 = i {\displaystyle i^{-3}=i}
- i − 2 = − 1 {\displaystyle i^{-2}=-1}
- i − 1 = − i {\displaystyle i^{-1}=-i}
- i 0 = 1 {\displaystyle i^{0}=1}
- i 1 = i {\displaystyle i^{1}=i}
- i 2 = − 1 {\displaystyle i^{2}=-1}
- i 3 = − i {\displaystyle i^{3}=-i}
- i 4 = 1 {\displaystyle i^{4}=1}
- … {\displaystyle \ldots }
Что может быть записано для любой степени в виде:
- i 4 n = 1 {\displaystyle i^{4n}=1}
- i 4 n + 1 = i {\displaystyle i^{4n+1}=i}
- i 4 n + 2 = − 1 {\displaystyle i^{4n+2}=-1}
- i 4 n + 3 = − i . {\displaystyle i^{4n+3}=-i.}
где n — любое целое число.
Отсюда: i n = i n mod 4 {\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.
Из тождества Эйлера следует, что число i i {\displaystyle i^{i}} является вещественным:
- i i = e ( i π / 2 ) i = e i 2 π / 2 = e − π / 2 = 0,207 87957635 … {\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots } .
Точнее, в комплексном анализе возведение в степень: x y = exp ( y ⋅ Ln x ) {\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому
- i i = e − π ( 1 + 4 n ) 2 {\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}} , где n ∈ Z {\displaystyle n\in \mathbb {Z} } .
Также верно, что ( − i ) ( − i ) = i i {\displaystyle (-i)^{(-i)}=i^{i}} .
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i ! = Γ ( 1 + i ) ≈ 0.4980 − 0.1549 i . {\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- | i ! | = π sinh ( π ) ≈ 0.521564…. {\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….} [1]
Корни из мнимой единицы
В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- u k = cos π 2 + 2 π k n + i sin π 2 + 2 π k n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
В частности, i = { 1 + i 2 ; − 1 − i 2 } {\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i 3 = { − i ; i + 3 2 ; i − 3 2 } {\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- u k = e ( π 2 + 2 π k ) i n , k = 0 , 1 , . . . , n − 1 {\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
Иные мнимые единицы
В конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду «мнимых единиц расширения» может быть несколько. Но в этом случае могут возникать делители нуля и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения x 2 = − 1 {\displaystyle x^{2}=-1} .
К вопросу об интерпретации и названии
| Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i.Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |
Обозначения
Обычное обозначение i {\displaystyle i} , но в электро- и радиотехнике мнимую единицу принято обозначать j {\displaystyle j} , чтобы не путать с обозначением мгновенной силы тока: i = i ( t ) {\displaystyle i=i(t)} .
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как I.
См.также
Примечания
Ссылки
Мнимая единица — Простая английская Википедия, бесплатная энциклопедия
В математике мнимая единица или я {\ displaystyle i} — это число, которое может быть представлено уравнениями, но относится к значению, которое может существовать только вне действительных чисел. Математическое определение мнимой единицы: я знак равно — 1 {\ displaystyle i = {\ sqrt {-1}}} (я.{2}} должен был бы равняться — 1 {\ displaystyle -1} ). Хотя проблема разрешима, квадратный корень из — 1 {\ displaystyle -1} вряд ли может быть представлено физическим количеством объектов в реальной жизни.
Иногда предполагается, что нужно создать другое число, чтобы показать квадратные корни из . я {\ displaystyle i} , но это не нужно.Квадратные корни из я {\ displaystyle i} можно записать как: ± я знак равно ± 2 2 ( 1 + я ) {\ displaystyle \ pm {\ sqrt {i}} = \ pm {\ frac {\ sqrt {2}} {2}} (1 + i)} , результат, который можно показать следующим образом:
Силы я {\ displaystyle i} следуют предсказуемой схеме:
- я — 3 знак равно я {\ Displaystyle я ^ {- 3} = я}
- я — 2 знак равно — 1 {\ Displaystyle я ^ {- 2} = — 1}
- я — 1 знак равно — я {\ Displaystyle я ^ {- 1} = — я}
- я 0 знак равно 1 {\ displaystyle i ^ {0} = 1}
- я 1 знак равно я {\ Displaystyle я ^ {1} = я}
- я 2 знак равно — 1 {\ displaystyle i ^ {2} = — 1}
- я 3 знак равно — я {\ displaystyle i ^ {3} = — i}
- я 4 знак равно 1 {\ displaystyle i ^ {4} = 1}
- я 5 знак равно я {\ displaystyle i ^ {5} = i}
- я 6 знак равно — 1 {\ displaystyle i ^ {6} = — 1}
Это может быть показано с помощью следующего шаблона (где N {\ displaystyle n} — любое целое число):
- я 4 N знак равно 1 {\ displaystyle i ^ {4n} = 1}
- я 4 N + 1 знак равно я {\ Displaystyle я ^ {4n + 1} = я}
- я 4 N + 2 знак равно — 1 {\ displaystyle i ^ {4n + 2} = — 1}
- я 4 N + 3 знак равно — я {\ displaystyle i ^ {4n + 3} = — i}
- ↑ «Сборник математических символов». Математическое хранилище . 2020-03-01. Проверено 10 августа 2020.
- ↑ Weisstein, Eric W. «Imaginary Unit». mathworld.wolfram.com . Проверено 10 августа 2020.
Мнимые числа
| Мнимое число, возведенное в квадрат, дает отрицательный результат . |
Попробуйте
Давайте попробуем возвести в квадрат некоторые числа, чтобы увидеть, можем ли мы получить отрицательный результат:
Не повезло! Всегда положительный или ноль.
Похоже, что мы не можем умножить число на себя, чтобы получить отрицательный ответ…
… но представьте себе , что существует такое число (назовите его i для воображаемого), которое могло бы сделать это: Будет ли это полезно и что мы можем с этим сделать? |
Итак, извлекая квадратный корень из обеих частей, мы получаем:
| Это означает, что i — это ответ на квадратный корень из −1. |
Что на самом деле очень полезно , потому что …
… просто принимая , что i существует, мы можем решить задачи
, которые требуют квадратного корня из отрицательного числа.
Поехали:
Пример: Что такое квадратный корень из −9?
√ (−9) = √ (9 × −1)
= √ (9) × √ (−1)
= 3 × √ (-1)
= 3 и
(посмотрите, как упростить квадратные корни)
Эй! это было интересно! Квадратный корень из −9 — это просто квадратный корень из +9, умноженный на i .
Всего:
Пока мы сохраняем там маленькое «i», чтобы напоминать нам, что нам все еще нужно умножить
на √ − 1, мы можем безопасно продолжить наше решение!
Используя i
Пример: Что такое (5 i ) 2 ?
(5 i ) 2 = 5 i × 5 i
= 5 × 5 × i × i
= 25 × i 2
= 25 × −1
= −25
Интересно! Мы использовали мнимое число (5 i ) и получили реальное решение (−25).
Мнимые числа могут помочь нам решить некоторые уравнения:
Пример: Решить x 2 + 1 = 0
Используя вещественные числа нет решения, но теперь мы можем решить его!
Вычтем 1 с обеих сторон:
х 2 = -1
Извлеките квадратный корень из обеих частей:
х = ± √ (-1)
х = ± я
Ответ: x = −i или + i
Чек:
- (−i) 2 + 1 = (−i) (- i) + 1 = + i 2 + 1 = −1 + 1 = 0
- (+ i) 2 +1 = (+ i) (+ i) +1 = + i 2 +1 = −1 + 1 = 0
Мнимый номер единицы
Квадратный корень из минус единицы √ (−1) — это «единичное» мнимое число, эквивалентное 1 для действительных чисел.
В математике символ √ (−1) равен i для мнимого.
Можно ли из извлечь квадратный корень из −1?
Ну и можно!
Примеры мнимых чисел
| и | 12,38i | −i | 3i / 4 | 0.01i | πi |
Мнимые числа не являются «Мнимые»
Мнимые числа когда-то считались невозможными , и поэтому их назвали «Мнимыми» (чтобы посмеяться над ними).
Но затем люди исследовали их больше и обнаружили, что они на самом деле были полезными и важными , потому что они заполнили пробел в математике … но «воображаемое» название прижилось.
Так и произошло название «Реальные числа» (реальные не мнимые).
Мнимые числа полезны
Комплексные числа
Мнимые числа становятся наиболее полезными в сочетании с действительными числами для получения комплексных чисел, например 3 + 5i или 6−4i
Анализатор спектра
Те крутые дисплеи, которые вы видите, когда играет музыка? Да, для их вычисления используются комплексные числа! С помощью так называемого «преобразования Фурье».
На самом деле, многие умные вещи можно сделать со звуком, используя комплексные числа, например, отфильтровать звуки, услышать шепот в толпе и так далее.
Это часть предмета «Обработка сигналов».
Электричество
AC (переменный ток) Электричество изменяется с положительного на отрицательное в виде синусоиды.
Когда мы объединяем два переменного тока, они могут не совпадать должным образом, и может быть очень сложно вычислить новый ток.
Но использование комплексных чисел значительно упрощает вычисления.
И результат может иметь «Мнимый» ток, но он все равно может вам навредить!
Набор Мандельброта
Прекрасный набор Мандельброта (часть его изображена здесь) основан на комплексных числах.
Квадратное уравнение
Квадратное уравнение, которое имеет множество применений,
может давать результаты, которые включают мнимые числа
Также в науке, квантовой механике и теории относительности используются комплексные числа.
Интересная недвижимость
Мнимое число i обладает интересным свойством. Каждый раз при умножении он «циклически» проходит через 4 различных значения:
| |||||||||||||||||
Итак, у нас есть это:
| i = √ − 1 | i 2 = −1 | i 3 = −√ − 1 | и 4 = +1 |
| i 5 = √ − 1 | i 6 = −1 | …etc |
Пример Что такое i 10 ?
i 10 = i 4 × i
= 1 × 1 × -1
= -1
Заключение
Единичное мнимое число i равно квадратному корню из минус 1
Воображаемые числа не «воображаемые», они действительно существуют и имеют множество применений.
,{2} = — 1} , Они определены отдельно от отрицательных действительных чисел, поскольку представляют собой квадратный корень из отрицательного действительного числа (вместо положительного действительного числа). Это невозможно с действительными числами, поскольку нет действительного числа, которое умножается само на себя, чтобы получить отрицательное число (например, 3 × 3 знак равно 9 {\ displaystyle 3 \ times 3 = 9} и — 3 × — 3 знак равно 9 {\ displaystyle -3 \ times -3 = 9} ).Набор мнимых чисел иногда обозначают буквой я {\ displaystyle \ mathbb {I}} , [1] [2]Один из способов подумать о мнимых числах — сказать, что они относятся к отрицательным числам, как отрицательные числа к положительным числам. Если мы говорим «иди на восток на 1 милю», это то же самое, как если бы мы сказали «иди на запад на 1 милю». Если мы говорим «пройдите на восток на 1 милю», это будет означать то же самое, как если бы мы сказали «пройдите на север на 1 милю».Точно так же, если мы говорим «иди на восток на 1 милю», это означает то же самое, как если бы мы сказали «иди на юг на 1 милю».
Добавить тоже легко. Если мы говорим «иди на восток на 1 + 1 милю», это означает то же самое, как если бы мы сказали «иди на восток на одну милю и на север на одну милю».
Умножение двух мнимых чисел во многом похоже на умножение положительного числа на отрицательное. Если мы говорим «иди на восток на 2 × -3 мили», это означает «повернуть до конца (так, чтобы теперь вы смотрели на запад) и проехать 2 × 3 = 6 миль». Мнимые числа работают так же, за исключением того, что вы можете вращаться частично.Если мы говорим «идти на восток на 2 × 3i мили», это означает то же самое, как если бы мы сказали «поверните, пока не окажетесь лицом к северу, а затем пройдите 2 × 3 = 6 миль».
Вычитания, такие как 5–9, были невозможны, пока не были изобретены отрицательные числа, точно так же, как извлечение квадратного корня из отрицательного числа раньше было невозможным, пока не были изобретены мнимые числа. Квадратный корень из 9 равен 3, но квадратный корень из −9 не равен −3. Это потому, что −3 x −3 = +9, а не −9. Долгое время казалось, что нет ответа на квадратный корень из −9.
Вот почему математики изобрели мнимое число i и сказали, что это главный квадратный корень из −1. Квадратный корень из -1 не является действительным числом, поэтому это определение создает новый тип числа, точно так же, как дроби создают числа вроде 2/3, которые не считают числа, такие как 4 или 10, а отрицательные числа создают числа, которые меньше 0. Иногда математикам кажется довольно удобным использовать столь необычное число, но имя воображаемый не должно вводить вас в заблуждение, потому что i так же верно, как 3 или 145 379.
Этот номер нашел применение во многих областях науки и техники. Например. инженерам-электрикам необходимо i , чтобы понять, как будет работать электрическая цепь, при ее проектировании (инженеры-электрики используют
Мнимые числа можно смешивать с числами, с которыми мы более знакомы. Например, действительное число, такое как 2 , можно добавить к мнимому числу, например 3i , чтобы получить 2 + 3i . Такие смешанные числа известны как комплексные числа.
- ↑ «Исчерпывающий список символов алгебры». Математическое хранилище . 2020-03-25. Проверено 10 августа 2020.
- ↑ Вайсштейн, Эрик В. «Воображаемое число». mathworld.wolfram.com . Проверено 10 августа 2020.
Что такое мнимая единица i? Что такое комплексное число? Определите мнимую и действительную части комплексного числа. Практика — см. Учебник стр.103 №7 —
Презентация на тему: «Что такое мнимая единица i? Что такое комплексное число? Определите мнимую и действительную части комплексного числа. Практика — см. Учебник стр.103 № 7 -» — стенограмма презентации:
1
Что такое мнимая единица i? Что такое комплексное число? Определите мнимую и действительную части комплексного числа.Практика — см. Учебник стр. 103 № 7 — 42 1.3 Комплексные числа http://www.youtube.com/watch?v=NeTRNpBI17I 
2
Практика сложения и вычитания комплексных чисел — см. Учебник на стр.103 №43 — 50. Сложите действительные и мнимые части, как при объединении одинаковых терминов. Обязательно распределите отрицательный знак при вычитании! http://www.youtube.com/watch?v=eyy_SR1JfyQ&feature=youtu.be 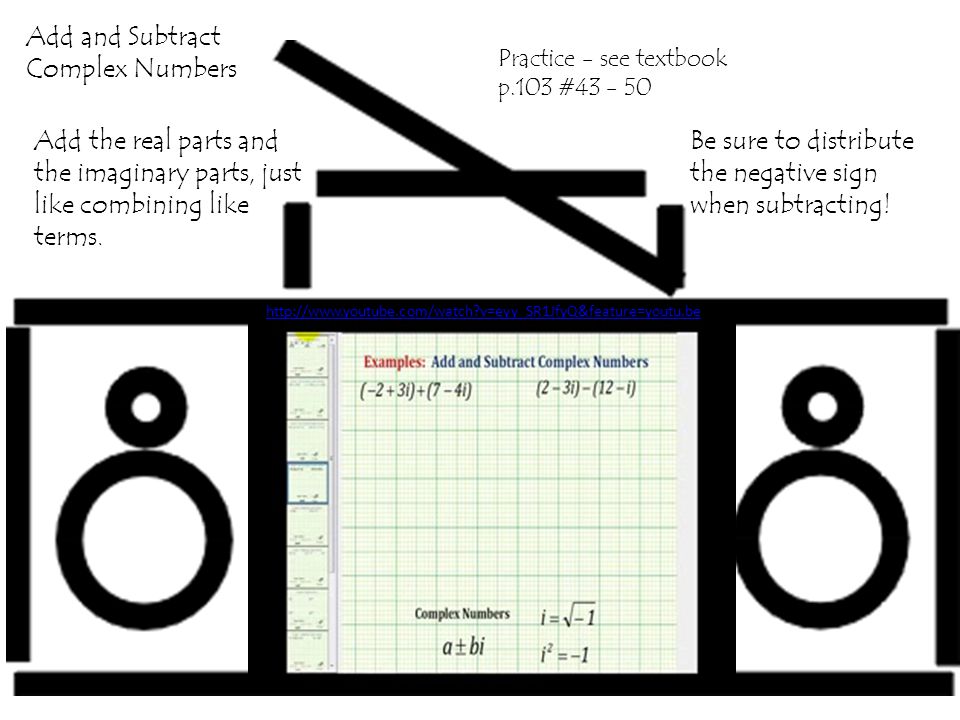
3
HTTP: // WWW.youtube.com/watch?v=O9xQaIi0NX0 Умножение простых комплексных чисел * Помните, что i 2 = -1 
4
Умножение комплексных чисел Практика — см. Учебник на стр.103 №51-68 http://www.youtube.com/watch?v=Fmr3o2zkwLM&feature=youtu.be 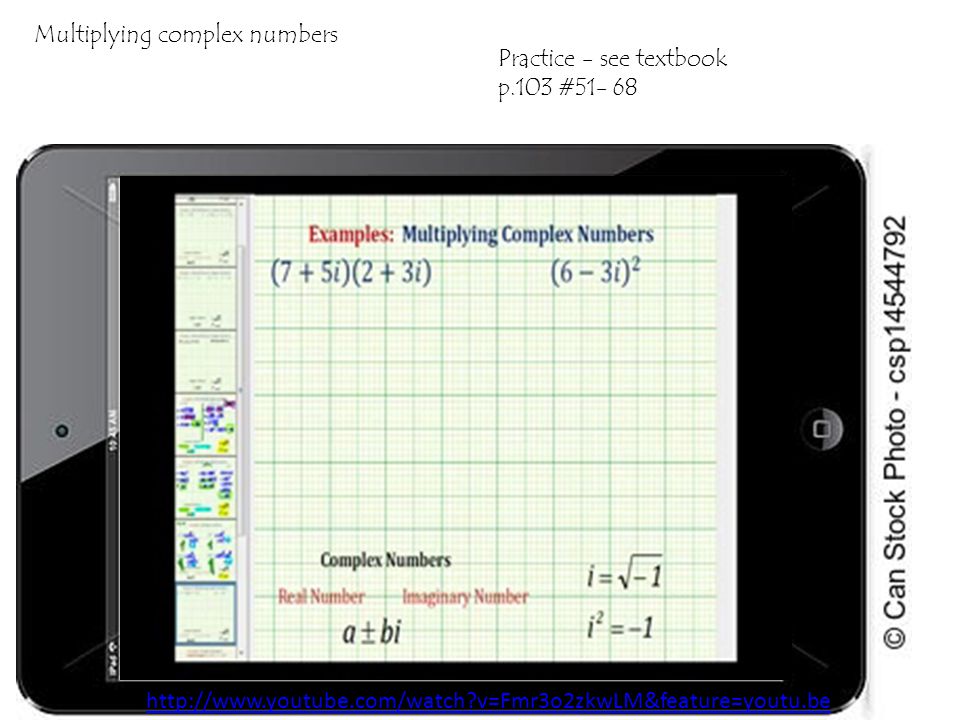
5
Комплексные числа и их сопряжение Сопряжение комплексного числа — это просто такое же комплексное число с измененным знаком в мнимой части.Когда вы умножаете комплексное число на сопряжение, произведение упрощается до действительного числа без мнимой части. Комплексные сопряжения необходимы для деления комплексных чисел. http://www.youtube.com/watch?v=VbOzEkvMb_A&feature=youtu.be 
6
Деление комплексных чисел Чтобы разделить комплексные числа, умножьте числитель и знаменатель на сопряжение знаменателя и упростите.Практика — см. Учебник на стр. 103 № 69 — 80 http://www.youtube.com/watch?v=XBJjbJAwM1c 
7
Практика — см. Учебник на стр. 103 № 85 — 96 Упрощающие возможности i http://www.youtube.com/watch?v=sfP6SmEYHRw 
8
Что вы должны знать: сложение и вычитание комплексных чисел Мнимая часть Действительная часть Комплексное число Мнимая единица Деление комплексных чисел Умножение комплексных чисел Упрощение радикалов с отрицательными подкоренными числами Стандартная форма Фактор Комплексное сопряжение числитель Знаменатель Степень произведения i 1.3 комплексных числа 
