Чему равна площадь боковой поверхности конуса: Площадь поверхности и объём конуса — урок. Геометрия, 11 класс.

Площадь поверхности конуса — онлайн калькулятор

Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Площадь боковой поверхности конуса

Образующая lВысота h= ммсмдмм
Радиус основания rДиаметр основания d = ммсмдмм

S_б.пов =

мм²см²дм²м²

Округление числа π: 3.143,1415915 знаков Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Площадь полной поверхности конуса

Образующая lВысота h= ммсмдмм
Радиус основания rДиаметр основания d = ммсмдмм

S_п.пов =

мм²см²дм²м²

Округление числа π: 3.143,1415915 знаков Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*

Просто введите данные, и получите ответ.

Теория

Площадь

боковой поверхности конуса через образующую

Чему равна площадь боковой поверхности конуса S_б.пов, если образующая l, а радиус основания r:

Формула

S_б.пов = π ⋅ r ⋅ l

через диаметр:

S_б.пов = π ⋅ l ⋅ ^d⁄₂

Пример

Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:

S_б.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²

Площадь боковой поверхности конуса через высоту

Чему равна площадь боковой поверхности конуса S_б.пов, если высота h, а радиус основания r:

Формула

S_б.пов = π ⋅ r ⋅ √r² + h²

через диаметр:

S_б.пов = π ⋅ ^d⁄₂ ⋅ √(d/2)² + h²

Пример

Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:

S_{б. пов} ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²

Площадь полной поверхности конуса через образующую

Чему равна площадь полной поверхности конуса S_п.пов, если образующая l, а радиус основания r:

Формула

S_п.пов = π ⋅ r ⋅ (r + l)

через диаметр:

S_п.пов = π ⋅ ^d⁄₂ ⋅ (^d⁄₂ + l)

Пример

Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:

S_п.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²

Площадь полной поверхности конуса через высоту

Чему равна площадь полной поверхности конуса S_п.пов, если высота h, а радиус основания r:

Формула

S_п.пов = π ⋅ r ⋅ (r + √r² + h²)

через диаметр:

S_п.пов = π ⋅ ^d⁄₂ ⋅ (^d⁄₂ + √(d/2)² + h²)

Пример

Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:

S_{п.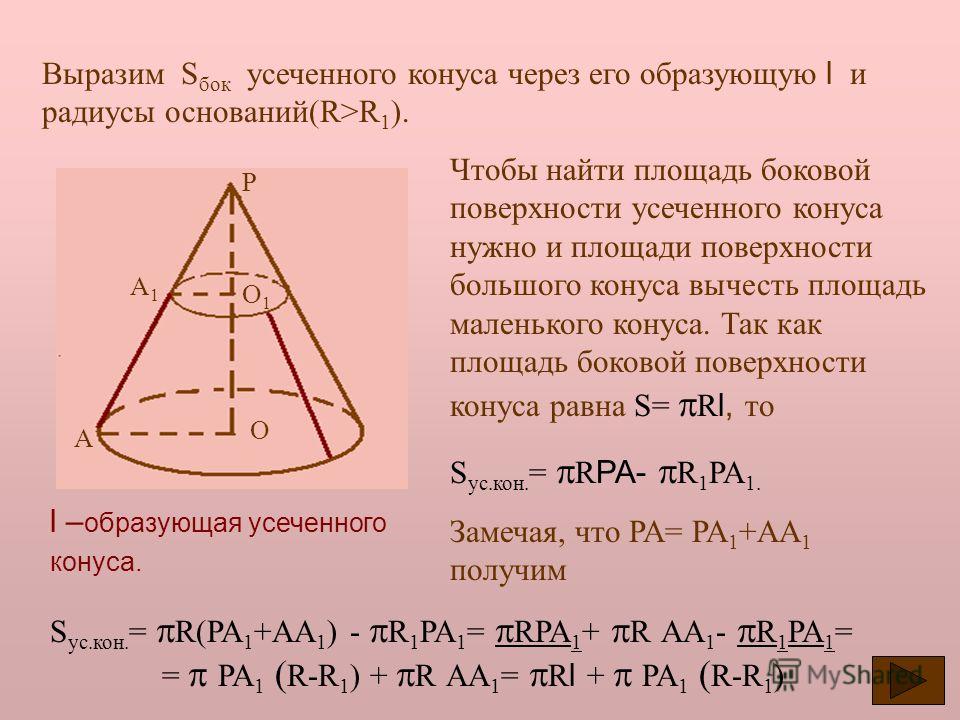 пов} ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²

См. также

Площадь поверхности конуса

На этом уроке мы выведем и научимся применять формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса.

Для начала давайте вспомним, что же это за геометрическое тело – конус.

Итак, тело, ограниченное конической поверхностью и кругом с границей , называется конусом.

Напомним, что боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.

На экране изображён конус, у которого радиус равен , а образующая равна . Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих.

Давайте представим, что боковую поверхность конуса разрезали по образующей  и развернули таким образом, что получился круговой сектор .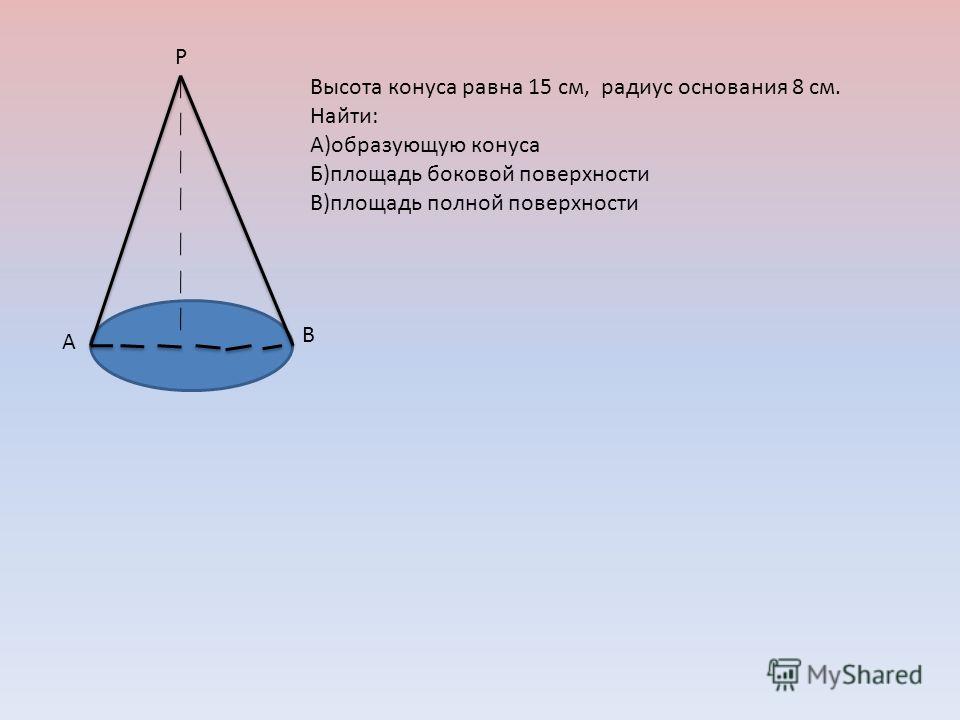

Стороны  и  которого являются двумя краями разреза боковой поверхности конуса.

Развёрткой боковой поверхности конуса является круговой сектор. Обратите внимание, радиус сектора равен образующей конуса, т.е. . А длина дуги сектора равна длине окружности основания конуса, т.е. равна .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через его образующую  и радиус основания .

Площадь кругового сектора – развёртки боковой поверхности конуса – равна , где  – градусная мера дуги .

Выразим  через длину дуги и радиус окружности. Длина дуги окружности с градусной мерой  и радиусом  равна . С другой стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто восемьдесят равно . Отсюда, . Подставим это выражение в формулу площади боковой поверхности конуса. Тогда площадь боковой поверхности конуса равна .

Т.е. площадь боковой поверхности конуса с образующей  и радиусом основания  выражается следующей формулой:  .

Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Теперь выведем формулу для вычисления площади полной поверхности конуса.

Вообще, площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Формулу для вычисления площади боковой поверхности конуса  мы с вами выразили выше, а площадь круга равна . Подставим все данные в формулу.

Упростим. Отсюда, получаем, что площадь полной поверхности конуса равна .

А сейчас давайте решим несколько задач на применение выведенных формул.

Задача: образующая  конуса равна  см, а его высота –  см. Вычислите площадь боковой поверхности конуса.

Решение: запишем формулу для вычисления площади боковой поверхности конуса.

Теперь внимательно рассмотрим рисунок.

Напомним, что высота конуса перпендикулярна его основанию. А, значит, она перпендикулярна любой прямой, лежащей в плоскости основания конуса. Следовательно, высота конуса .

Рассмотрим . Он прямоугольный. Применяя теорему Пифагора, найдём длину стороны , которая и является радиусом основания конуса. Получаем, что ОА равно  . 

Подставим длину образующей конуса и его радиус в формулу для вычисления площади боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности конуса равна .

Запишем ответ.

Задача: радиус основания конуса равен  дм, а площадь его осевого сечения –  дм². Вычислите площадь боковой поверхности конуса.

Решение: запишем формулу для вычисления площади боковой поверхности конуса.

Теперь рассмотрим рисунок.

Напомним, что осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось, и представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Значит,  – равнобедренный.

Так как по условию задачи радиус основания конуса равен 9 дм, то основание осевого сечения равно  .

Напомним, что площадь треугольника равна половине произведения длины основания на высоту . Выразим из формулы высоту . Получаем, что высота треугольника, а она является и высотой конуса, равна  .

Рассмотрим . Он прямоугольный, так как . Применяя теорему Пифагора, найдём длину . Получаем, что  . Обратите внимание, гипотенуза  есть образующая нашего конуса.

Подставим найденную длину образующей конуса и его радиус в формулу для вычисления площади боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности конуса равна  .

Не забудем записать ответ.

Задача: прямоугольный треугольник, длины катетов которого равны  см и  см, вращается вокруг меньшего катета. Вычислите площадь полной поверхности конуса, образованного при этом вращении.

Решение: запишем формулу для вычисления площади полной поверхности конуса.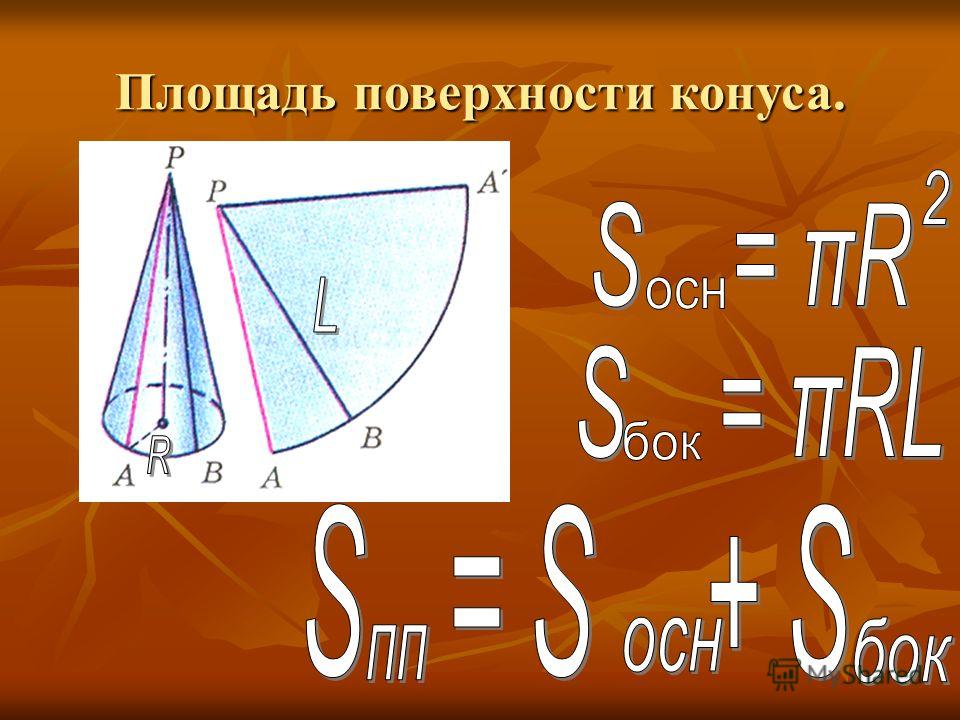

Рассмотрим . Он прямоугольный по условию.

Воспользуемся теоремой Пифагора и найдём длину гипотенузы , которая и является образующей конуса. Имеем, .

Так как по условию задачи треугольник вращается вокруг меньшего катета, то радиус основания конуса, образованного при этом вращении, равен .

Подставим длину образующей конуса и его радиус в формулу для вычисления площади полной поверхности конуса. Посчитаем. Получим, что площадь полной поверхности нашего конуса равна .

Запишем ответ.

Итоги:

На этом уроке мы вывели формулы для вычисления площади боковой поверхности конуса и площади полной поверхности конуса. А также научились их применять при решении задач.

 

 

Объяснение урока: Площади поверхности конусов

В этом объяснении мы научимся вычислять боковую и общую площади поверхности конусы по их формулам.

Мы начнем с обзора языка, связанного с конусами и их площадями. Есть три ключевых измерения, которые описывают конус:

• радиус 𝑟 круглого основания конуса, также называемый радиусом основания;
• высота по перпендикуляру, ℎ, то есть расстояние по перпендикуляру между центром основание и вершина конуса;
• наклонная высота, 𝑙, то есть расстояние от вершины до точки на окружности основания, вдоль стороны конуса.

Эти три длины представлены на рисунке ниже. Мы увидим, как эти три длины связаны друг с другом позже.

Площадь поверхности конуса состоит из двух различных частей: площадь изогнутой поверхность, которая называется боковой площадью или площадью боковой поверхности, и площадь круглая основа.

Формулы: площадь поверхности конуса

Формула площади боковой поверхности конуса 𝐴L: 𝐴=𝜋𝑟𝑙,L где 𝑟 представляет радиус основания конуса и 𝑙 обозначает наклонную высоту.

Формула общей площади поверхности конуса 𝐴T: 𝐴=𝜋𝑟𝑙+𝜋𝑟. T

Мы должны тщательно различать эти две области поверхности, чтобы определить, должна ли область основания быть включена в какую-либо конкретную задачу.

Теперь продемонстрируем, как применить формулу для расчета боковой поверхности площадь конуса при заданном диаметре основания и наклонной высоте.

Пример 1. Нахождение площади боковой поверхности конуса по диаметру основания и высоте наклона

Найдите с точностью до десятых площадь боковой поверхности конуса с диаметр 40 сантиметров и наклонная высота 29 сантиметров.

Ответ

Во-первых, отметим, что вопрос касается только боковой области конуса, а не его общая площадь. Требуемая формула латеральная область = 𝜋𝑟𝑙 поэтому нам нужно знать наклонную высоту конуса и его радиус. Наклонная высота из 29см дан в вопросе, и мы можем рассчитать радиус, разделив его вдвое диаметр: 𝑟=402=20 см

Наконец, подставляем эти значения в формулу для площади боковой поверхности и оценить: латеральная площадь=𝜋𝑟𝑙=𝜋×20×29=580𝜋=1822,123….

Округляя наш ответ до ближайшей десятой, как того требует вопрос, боковой площадь конуса 1‎ ‎822,1 см ² .

Ключевым моментом из предыдущего примера было то, что нам дали диаметр, а не радиус основания конуса. Это не представляло серьезной проблемы, поскольку два легко связаны, но это еще одна деталь, на которую следует обратить внимание при подходе к проблема.

Было также важно, чтобы мы определили, рассчитываем ли мы боковой или общая площадь поверхности конуса. Поскольку мы вычисляли боковую площадь, мы не необходимо включить площадь круглого основания. Теперь рассмотрим пример применяя формулу для расчета общей площади поверхности, учитывая наклонную высоту и радиус основания конуса.

Пример 2. Определение общей площади поверхности конуса по его наклонной высоте и радиусу основания

Определите с точностью до сотых общую площадь поверхности показанного конуса.

Ответ

Из рисунка видно, что нам дан радиус основания конуса, что составляет 19 см, а его наклонная высота, которая составляет 40 см. Чтобы рассчитать общую площадь поверхности, подставляем обе эти величины в соответствующую формулу и упрощать: totalsurfaceareacm=𝜋𝑟+𝜋𝑟𝑙=𝜋×19+(𝜋×19×40)=361𝜋+760𝜋=1121𝜋.

В некоторых случаях от нас может потребоваться дать точный ответ, и в этом случае мы оставил бы наш ответ с точки зрения 𝜋. Однако в этой задаче нас просят даем наш ответ с точностью до сотых, поэтому оцениваем дальше: общая площадь=3521,725…≈3521,73.

Общая площадь поверхности конуса с точностью до сотых составляет 3‎ ‎521,73 см ² .

Теперь мы видели примеры того, как рассчитать как боковую, так и общую поверхность. площади конуса с заданными радиусом основания (или диаметром) и наклонной высотой. Однако, нам может потребоваться вычислить площадь поверхности конуса, когда вместо этого нам дано его перпендикулярная высота. Нам не нужна отдельная формула, а вместо этого мы рассмотрим соотношение между радиусом основания, высотой перпендикуляра и высотой наклона.

Из рисунка выше видно, что радиус основания, высота перпендикуляра и наклонная высота образует прямоугольный треугольник. Соотношение между этими тремя длинами может, следовательно, описывается применением теоремы Пифагора: 𝑙=𝑟+ℎ.

Следовательно, если мы знаем две из этих длин, мы можем вычислить третью, составив и решение уравнения. Давайте рассмотрим пример этого.

Пример 3. Определение общей площади поверхности конуса по его наклонной высоте и высоте перпендикуляра

Найдите полную площадь поверхности правильного конуса, округленную до двух знаков после запятой. места.

Ответ

Из рисунка видно, что две указанные длины — это наклонная высота и перпендикулярная высота конуса. Формула полной площади поверхности конус общая площадь поверхности = 𝜋𝑟𝑙+𝜋𝑟, и поэтому нам нужно определить радиус его основания 𝑟.

Мы можем составить уравнение, связывающее радиус основания, высоту перпендикуляра, и наклонную высоту, применяя теорему Пифагора: 𝑟+ℎ=𝑙. 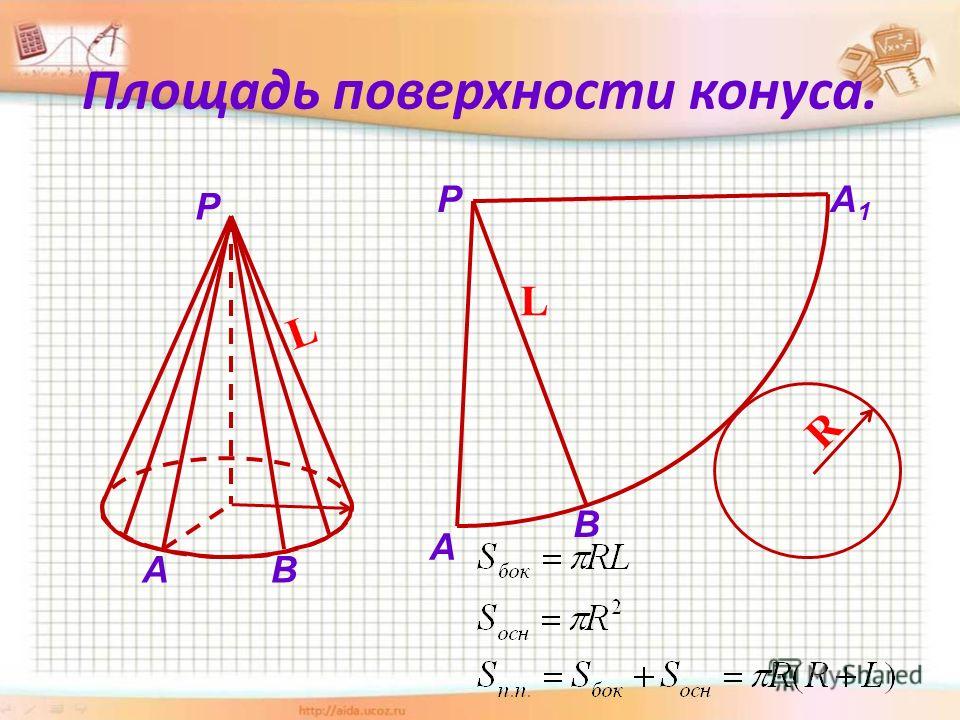

Замена ℎ=14,5 и 𝑙=16,5 и упрощение дает 𝑟+14,5=16,5𝑟+210,25=272,25𝑟=62,

Находим 𝑟 методом извлечения квадратного корня, принимая только положительное значение поскольку 𝑟 — это длина: 𝑟=√62=7,874….cmcm

Наконец, мы подставляем радиус и наклонную высоту конуса в Формула полной площади поверхности. Предпочтительно использовать точное значение для 𝑟, и действительно 𝑟, чтобы предотвратить введение любых ошибок округления: общая площадь поверхности = 𝜋𝑟𝑙+𝜋𝑟=𝜋×√62×16,5+(𝜋×62)=602,938…≈602,94.

Общая площадь поверхности конуса с точностью до двух знаков после запятой равна 602,94 см ² .

Теперь мы видели примеры того, как рассчитать боковую и общую площадь поверхности конус, заданный двумя из трех его ключевых измерений. Мы можем обобщить эти процессы в следующие шаги.

Как: Расчет площади поверхности конуса

1. Определите, требуется ли боковая площадь или общая площадь поверхности.
2. Определите радиус основания и наклонную высоту конуса.
3. Если одна из этих длин не указана, но есть перпендикулярная высота, вычислите недостающую длину, применив теорему Пифагора.
4. Подставьте длину радиуса и высоту наклона в соответствующую формулу и оцените.

Как и во всех областях математики, навыки, с которыми мы здесь столкнулись, также могут быть применены к проблемам в реальном контексте. Всякий раз, когда объект реального мира может разумно смоделировать конусом, мы можем применить введенные нами формулы к вычислить его боковую или общую площадь поверхности, как мы увидим в следующих двух примерах.

Пример 4. Определение площади боковой поверхности конуса в реальном контексте

Коническая гора имеет радиус 1,5 км и перпендикуляр высота 0,5 км. Определить боковую площадь горы с точностью до десятых. место.

Ответ

Вопрос говорит нам, что эта гора коническая, поэтому задача по существу геометрический. Чтобы применить формулу боковой поверхности, нам нужно знать как радиус основания, так и наклонную высоту горы. Мы не учитывая наклонную высоту, но поскольку мы знаем как радиус основания, так и перпендикулярной высоте, мы можем применить теорему Пифагора: 𝑙=𝑟+ℎ.

Замена 𝑟=1,5 и ℎ=0,5 и упрощение дает 𝑙=1,5+0,5=2,25+0,25=2,5.

Чтобы найти 𝑙, найдем квадратный корень, взяв только положительный значение, поскольку 𝑙 является длиной: 𝑙=√2.5=1.581….cmcm

Теперь подставим значения радиуса и наклонной высоты конуса в формулу боковой площади: латеральная площадь=𝜋𝑟𝑙=𝜋×1,5×(1,581…)=7,450…≈7,5.

Боковая площадь горы с точностью до одного десятичного знака составляет 7,5 км ² .

Мы всегда должны следить за тем, чтобы в нашем ответе использовались правильные единицы измерения. Поскольку мы вычисляем площади, единицами для нашего ответа должны быть квадратные единицы. В предыдущем примере длины были измерены в километрах, поэтому единицами для нашего ответа были квадратные километры. Мы также должны убедиться, что мы проверяем вопрос требует, чтобы ответ был дан в единицах, отличных от те, которые были даны изначально, например, если единицами длины были метры, а площадь требуется в квадратных километрах.

Пример 5. Нахождение площади боковой поверхности конуса в реальном контексте

Конический абажур имеет высоту 31 см и основание по окружности. 145,2 см. Найдите площадь криволинейной поверхности внешней стороны абажура. Дайте ответ ближайшему квадратный сантиметр.

Ответ

Криволинейная поверхность абажура – ​​это его боковая площадь, которая рассчитывается используя формулу латеральная область=𝜋𝑟𝑙.

Следовательно, нам нужно знать как радиус основания конуса, так и его наклонную высоту, ни один из них не указан в вопросе. Вместо этого рассмотрим другой информацию, которую нам дают, и определить, как мы можем использовать ее для расчета длин нам нужно.

Круглое основание конуса имеет окружность 145,2 см. Мы знаем формула длины окружности 𝐶=2𝜋𝑟 и поэтому мы можем вычислить радиус, составив и решив уравнение: 2𝜋𝑟=145,2𝑟=145,22𝜋=23,109….cm

Теперь мы знаем радиус основания и высоту перпендикуляра конуса. Для расчета наклонной высоты применим теорему Пифагора: 𝑙=𝑟+ℎ=(23,109…)+31=1495,039….

Находим 𝑙 методом извлечения квадратного корня: 𝑙=√1495,039…=38,665….cmcm

Наконец, мы подставляем значения, которые мы вычислили для радиуса и наклонной высоты в формулу площади боковой поверхности: латеральная площадь=𝜋𝑟𝑙=𝜋×(23,109…)×(38,665…)=2807,132…≈2807.

Изогнутая поверхность внешней стороны абажура с точностью до квадратный сантиметр, это 2‎ ‎807 см ² .

В других задачах нам может быть задана площадь поверхности конуса и еще одна часть информации и попросили определить одну из других длин ключей. Это по существу «работая в обратном направлении», как мы увидим в нашем последнем примере.

Пример 6. Определение высоты конуса по площади его поверхности и радиусу основания

Площадь поверхности конуса 364𝜋 квадратные дюймы, и радиус база 13 дюймов. Определить наклонную высоту конуса.

Ответ

В этой задаче нам даны радиус и площадь поверхности конуса и попросили определить его наклонную высоту. Напомним формулу для (суммы) площадь поверхности конуса: surfacearea=𝜋𝑟𝑙+𝜋𝑟.

Подставив известную площадь поверхности и известный радиус, мы можем сформировать уравнение: (𝜋×13×𝑙)+𝜋×13=364𝜋.

Теперь мы можем решить это уравнение, чтобы определить значение 𝑙. Фактор 𝜋 может быть сначала отменено от каждого термина, чтобы дать 13𝑙+169=364.

Затем мы вычитаем по 169 с каждой стороны и делим на 13: 13𝑙=195𝑙=15.

Наклонная высота конуса составляет 15 дюймов.

Давайте закончим, повторив некоторые ключевые моменты.

Ключевые точки

• Тремя ключевыми длинами, описывающими конус, являются радиус его основания 𝑟, его перпендикулярная высота ℎ и наклонная высота 𝑙.
• Эти три длины связаны теоремой Пифагора: 𝑟+ℎ=𝑙.
• Площадь криволинейной поверхности конуса называется его боковой площадью и равна рассчитывается по формуле латеральная область=𝜋𝑟𝑙.
• Чтобы найти полную площадь поверхности конуса, нам также нужно включить площадь круглое основание: общая площадь поверхности=𝜋𝑟𝑙+𝜋𝑟.

Площадь поверхности и объем

Площадь поверхности и объем Вернуться к оглавлению

Обзор урока

• Боковая поверхность: призма/цилиндр, пирамида/конус
• Площадь поверхности: призма/цилиндр, пирамида/конус, сфера
• Объем: призма/цилиндр, пирамида/конус, сфера
• Принцип Кавальери
• Домашнее задание

Боковая зона

Боковая площадь — это площадь поверхности трехмерной фигуры, но без учета площади любых баз. L ateral A rea часто обозначается аббревиатурой L.A. Представьте банку с супом. Теперь обрежьте боковую часть банки и раскатайте ее. То, что было окружностью основания, теперь является длиной прямоугольника. Чтобы найти площадь этого прямоугольника, которая равна боковой площади, умножьте эту длину на ширину, которая была высотой банки.

Боковая площадь призмы: периметр × высота

Боковая площадь цилиндра: длина окружности × высота.

Боковая часть правильной пирамиды: ½ периметра × высота наклона.

Боковая площадь правого конуса: ½ периметра × высота наклона.

Боковая площадь правильной пирамиды или прямого конуса аналогична призмы, но поскольку каждая грань представляет собой треугольник (или подобный треугольнику), есть коэффициент в половину. Таким образом, боковая площадь равна половине высоты наклона, умноженной на периметр. высота наклона — это расстояние от вершины до края основания, где он находится на полпути между вершинами основания. Если пирамида неправильная и конечно если конус наклонен, площадь поверхности не может быть рассчитана с использованием элементарных методов (что является причудливым способом сказать, что вам может понадобиться исчисление). Это зависит от того, сможете ли вы получить высоту (наклонную высоту) каждой треугольной грани.

Площадь поверхности

Площадь поверхности фигуры равна сумме площадей всех поверхностей фигуры. S urface A rea часто обозначается аббревиатурой S.A. Площадь поверхности призмы или цилиндра равна боковой площади плюс площадь каждой базы. Так как основания призмы или цилиндра конгруэнтны, это часто выражается как удвоенная площадь основания.

Площадь поверхности = Боковая площадь + n × основания n = 2 для призм/цилиндров; n = 1 для пирамид/конусов; n = 0 для сфер.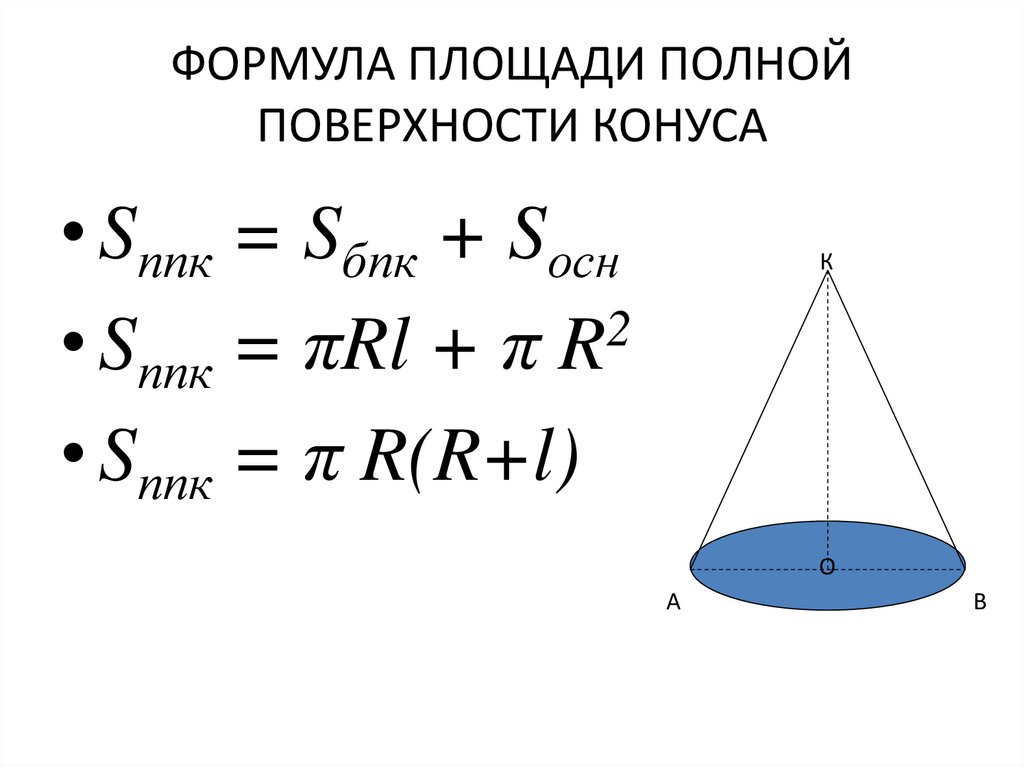

Площадь поверхности пирамиды или конуса равна боковой площади плюс площадь одной базы.

Площадь поверхности шара равна 4 r ² . Аналогом единичного круга является единичная сфера. Точно так же, как есть 2 радиана угла за один оборот, есть 4 стерадиана телесного угла во всех направлениях.

Пример: Рассмотрим правильную пирамиду A-BCDE с вершиной А и квадратное основание BCDE длиной 20 дюймов на с каждой стороны и наклонной высотой 26 дюймов. Каковы его боковые поверхности и площади?

Ответ: Нам не нужна высота для этого расчета, но мы все равно рассчитаем его, чтобы подчеркнуть разницу между наклонной высотой и высота. Наклонная высота – это гипотенуза прямоугольного треугольника, где высота — это одна нога, а 20 дюймов / 2 = 10 дюймов — другая нога. Таким образом, 10 ² + ч ² = 26 ² или 100 + ч ² = 676. Таким образом, ч ² = 576 или h = 24″. Боковые поверхности — все треугольники с основанием 20″. и высота (наклонная высота) 26 дюймов. Их четыре. Таким образом, боковая площадь равна 4×½×20″×26″ = 1040 в ² . Основание квадратное 20 дюймов или 400 дюймов ² . Таким образом, [общая] площадь поверхности равна 1440 в ² .

Понимание площади поверхности может быть более ясным, если вы вернетесь к сети. связанные с объектом. Слева — сетка для куба, а справа — часть сетки для сферы. Каждая из этих частей сферы называется кровью .

Сейчас самое время повторить то, что вы узнали из алгебры, а именно ( х + у ) ² = х ² + ху + ху + у ² = x ² + 2 xy + y ² . Диаграмма справа должна прояснить это дальше, помочь вам вспомнить FOIL метод , а также дать физическую основу для этой связи. (Помните также, что квадратный корень из ( x ² + y ² ) НЕ равно x + y .) Рассмотрим сначала расширение метода FOIL на трехчлены: ( a + b + c )( d + e + f ) = ad + ae + af + bd + be + bf + cd + ce + cf . Распределяемое свойство — это еще один способ рассмотрения этой ситуации. Здесь полезен метод коробки .

	д	е	е
а	объявление		аф
б	бд	до	бф
к	кд	CE	ср.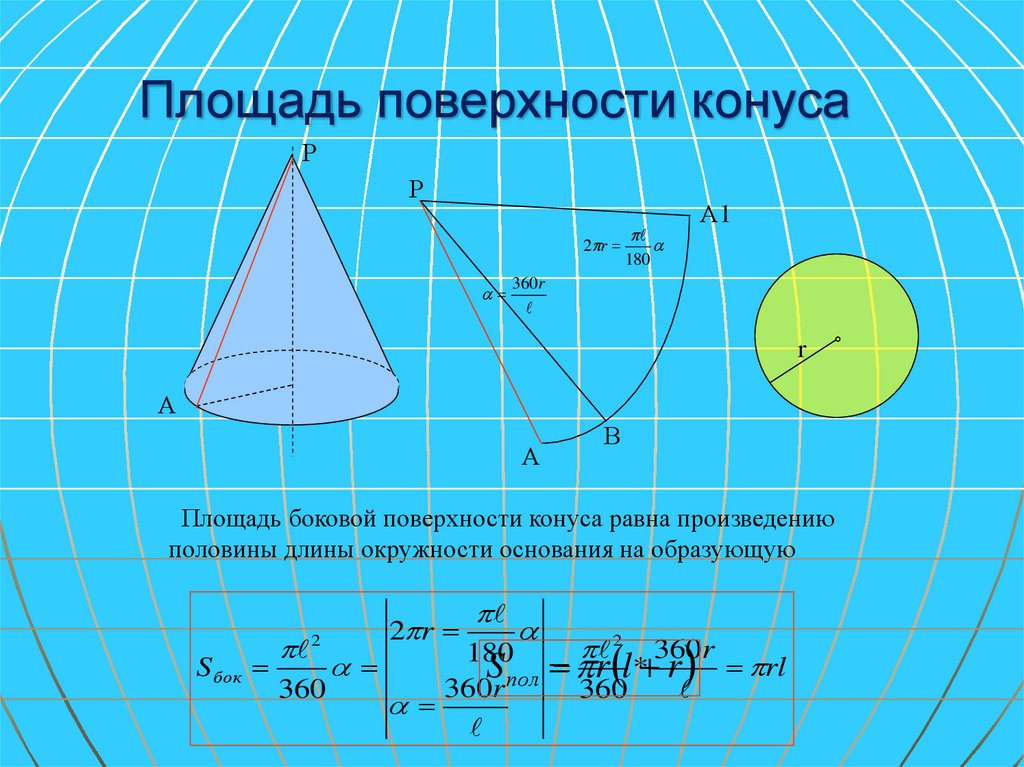

Теперь расширьте метод на три измерения, чтобы найти: V = ( a + b )( c + d )( e + f ) = туз + акф + аде + адф + bce + bcf + bde + bdf . Это было бы полезно для нахождения объема, вот почему его трудно отобразить в двух измерениях.

Том

Объем объекта имеет основные свойства, перечисленные ниже. Обратите внимание, что они аналогичны приведенным ранее для области.

• Каждая полиэдральная область имеет уникальный объем , зависит только от вашего блока куба .
• Коробка имеет объем длины × ширины × высоты ( V = lwh ).
• Конгруэнтные фигуры имеют эквивалентный объем.
• Общий объем представляет собой сумму всех непересекающихся областей.

Зная объем, можно определить размеры многогранника. В частности, для куба с ребром s и объемом s ³ , дан куб объемом 1000 кубических сантиметров (1 литр), Вы можете извлечь кубический корень, чтобы определить, что каждая сторона имеет длину 10 сантиметров. или около 3,937 дюйма. Поскольку один галлон равен 231 кубическому дюйму, 3,785 литра. Можно ожидать и другие преобразования единиц измерения, которые суммируются. в числах урок 9. Кубические корни и объем лежат в основе древнего невозможного геометрического сооружение из древности, Проблема удвоения делианского куба. Другая важная концепция заключается в том, что если вы удвоите размеры куба, объем увеличивается в 8 раз = 2 ³ , точно так же, как площадь увеличилась в 4 раза = 2 ² . Это проблема, обычно возникающая при преобразовании из кубических футов. в кубических метрах!

Пример: Предположим, вы хотите залить бетоном 4-дюймовую глубину подъездной дорожки. что 90 футов в длину и 9 футов в ширину.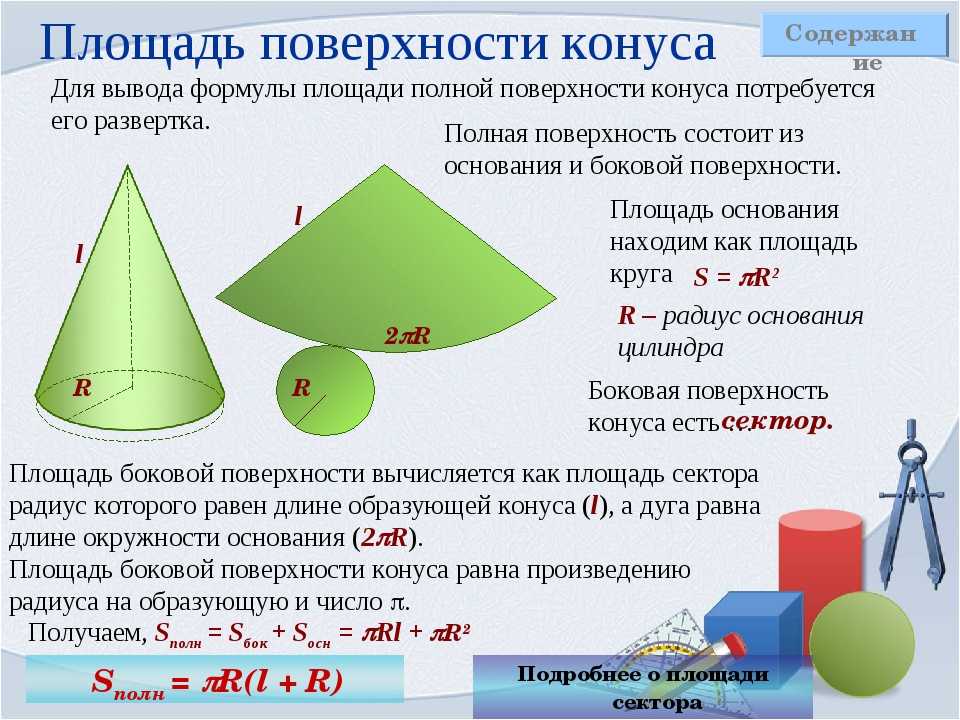

Ответ: Вы быстро обнаружите, что есть 90×9÷3=270 футов ³ . Однако есть только 10 ярдов ³ , так как каждый ярд равен 3 футам и 3 ³ = 27.

Расчет в «родной единице» ярдов: 30×3÷9 кан. помогите предотвратить такую ​​ошибку. Под «родным» мы подразумеваем здесь то, что окончательные результаты ожидаются в кубических ярдах. Если исходные единицы конвертируются в ярды, будет сделано меньше ошибок. это ЧРЕЗВЫЧАЙНО распространено ошибочное деление на 3 или 9а не 27 при переводе кубических футов в кубические ярды.

Пример: Предположим, вы хотите найти объем правильная пирамида с квадратным основанием A-BCDE , приведенная в предыдущем примере с наклонная высота 26 дюймов и основание 20 дюймов с каждой стороны.

Ответ: Высота 24 дюйма, рассчитанная в предыдущем примере. Таким образом, объем равен (1/3) × B × ч = (1/3) × 20 дюймов × 20 дюймов × 24 дюйма = 3200 дюймов ³ .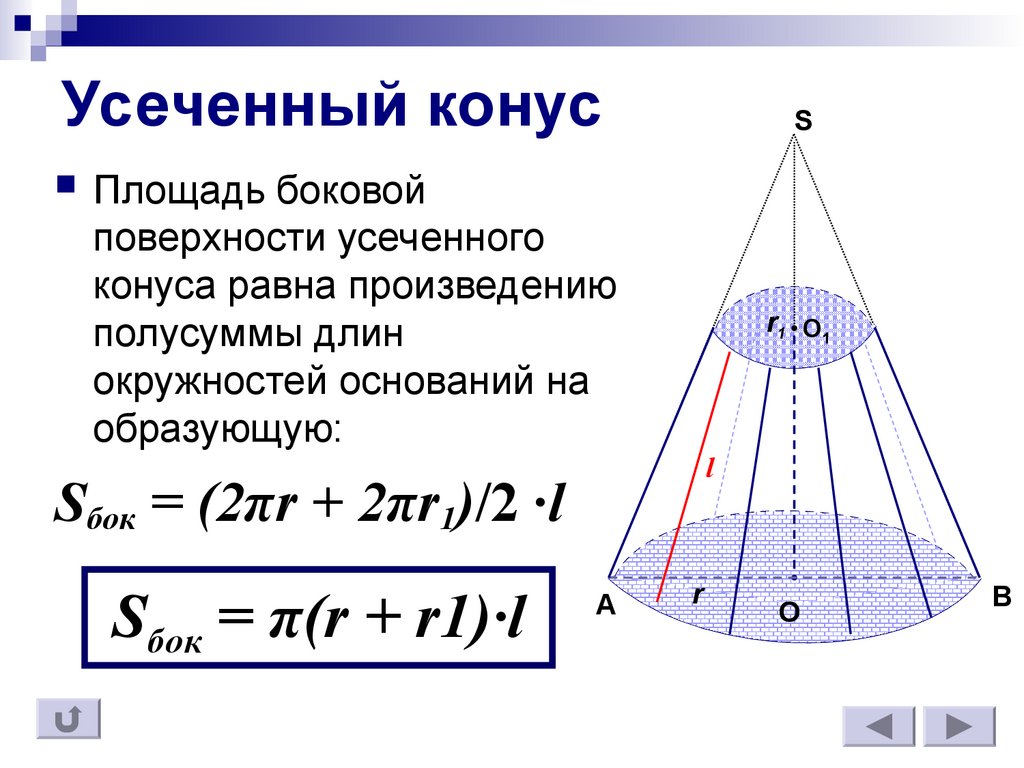

Объемные формулы

Призма или цилиндр: V = площадь основания × высота

Пирамида или конус: V = (1/3) × площадь основания × высота

Сфера: В = (4/3) × (радиус) 3

Обычно эти формулы записываются как V = Bh (призма или цилиндр), V = (1/3) Bh (пирамида или конус), или V =(4/3) r ³ (сфера). Обратите внимание, как большой B используется для обозначения того, что это двухмерный основание или площадь и не одинаковые (линейные) б используем в треугольниках.

Наклонные призмы и цилиндры имеют тот же объем, что и прямая призма. или цилиндр той же высоты и площади основания. Представьте себе стопку бумаги, верхняя часть которой отодвинута в сторону. Стек больше не является вертикальным. Однако объем бумаги не изменился. В формуле нахождения объема косой призмы учтите, что высота — это перпендикулярный отрезок между верхним и нижним основаниями. Когда вы изучите исчисление, вы обнаружите площадь поверхности сферы. быть производной по r формулы объема шара. То же самое происходит между площадью круга и его окружностью. Это может быть случайность или может быть глубокая причина что я хотел бы знать.

Пример: Любимая задача на объем/площадь выглядит следующим образом. Бассейн имеет длину 24 фута, ширину 20 футов, глубину 3 фута в мелкой части, и 10 футов глубиной в глубоком конце. Пол имеет ровный уклон. Что это внутренняя поверхность бассейна и каков его объем (в галлонах)?

Ответ: Бассейн представляет собой трапециевидную призму. Пол имеет длину 25 футов, так как 10 футов — 3 фута = 7 футов и 7 ² +24 ² = 49 + 576 = 625 = 25 ² . Площадь поверхности представляет собой сумму 5 поверхностей: 2 конгруэнтных трапециевидных стороны (½(3+10)24), 2 прямоугольных конца (320 + 1020) и нижний (2025). Это 2156 + 60 + 200 + 500 = 1072 фута ² . Объем — это основание × высота, где основание — это площадь одной стороны. (½(3+10)24), а высота – это ширина бассейна (20). Таким образом, объем составляет 3120 футов ³ или 23339 галлонов (умножить на 12 ³ кубических дюймов на кубический фут и разделить на 231 кубический дюйм на галлон).

мысленный эксперимент (мысленный эксперимент), используемый для обоснования Формула объема шара выглядит следующим образом. Во-первых, помните о деятельность в области круга, где мы разрезаем круг на 16 клиньев, а затем переставляем клиньев в параллелограмм r × r . По тем же линиям разрежьте сферу на пирамиды. Суммарная площадь оснований этих пирамид равна 4 р ² . Высота каждого r . Отсюда выводится формула. В том же духе некоторые предлагали вспомнить 1/3 в формулах конического объема, сопоставив его с аналогичным двумерная треугольная формула площади, в которой есть 1/2.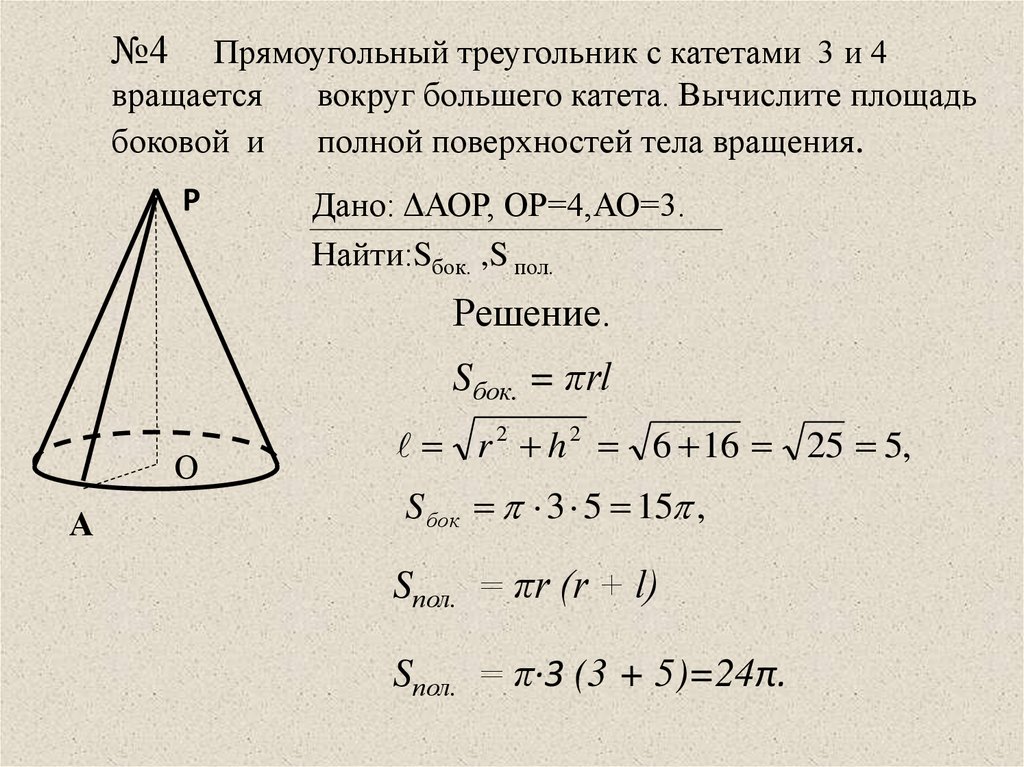

Принцип Кавальери

Следующая идея была развита намного раньше несколькими группами людей, но итальянский математик 17 века сделал его популярным в как раз в нужное время, и его имя было прикреплено к нему.

Даны два тела, заключенные между параллельными плоскостями. Если каждое плоское сечение параллельно заданным плоскостям имеет одинаковую площадь в обоих телах, тогда объемы твердых тел равны. Это известно как Принцип Кавальери .

Греческий Архимед входит в тройку величайших математиков всех времен. Среди его важных открытий — взаимосвязь между объемами конус, шар и цилиндр. На самом деле, это открытие было настолько его фаворита, что он просил, чтобы это было вписано в его надгробие. В частности, рассмотрим сферу радиусом р , два конуса одинакового радиуса и высоты ( r ), и цилиндр такого же радиуса и высоты (2 r ). Цилиндр будет содержать либо два конуса, либо сферу. Легко видеть, что их объемы равны (4/3) r ³ , 2(1/3) r ³ , и 2 р ³ . Таким образом, конусы плюс сфера в точности равняются цилиндру. (На самом деле Архимеду чаще приписывают демонстрацию объем шара должен составлять 2/3 объема цилиндра.) См. соответствующие схемы в учебнике, относящиеся к доказательству. Принцип Кавальери.

Пример: Вопрос 10.2#24 в нашем тексте задавался учащимся. о конусах из кругов (радиус 4″) с центральными углами 45 °, 60 ° и 120 ° удалены (которые были заклеены лентой к доске под шутки Мадонны). Выполните следующее. Найдите объем каждого конуса. Найдите центральный угол, который максимизирует объем. Найдите центральный угол, при котором отношение объема к поверхности максимально.

Ответ: Для получения бонусных баллов сдайте свое решение к тому времени, когда должны быть рассмотрены главы.

НАЗАД	ДОМАШНЕЕ ЗАДАНИЕ	ДЕЯТЕЛЬНОСТЬ	ПРОДОЛЖИТЬ

---

• электронная почта: calkins@andrews.

  No related posts.