Как найти площадь геометрических фигур?boeffblog.ru

Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
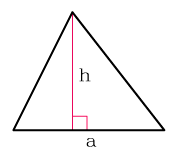
1. Самая известная формула площади треугольника по стороне и высоте:
S =
a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.

Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. 
Если треугольник тупоугольный, то высота опускается на продолжение основания:

Если треугольник прямоугольный, то основанием и высотой являются его катеты:

2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S =
a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.


Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.

4. Формула площади треугольника через радиус описанной окружности:
S =

где a, b и с – стороны треугольника, а R – радиус описанной окружности.

5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.

Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
2. Также площадь квадрата можно найти через его диагональ:
S =
d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:

2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα

Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα

3. Площадь ромба через диагонали:
S =
d1 · d2

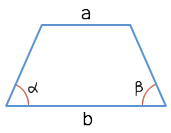
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S =
· h

Как найти площадь круга?
1. Площадь круга можно найти через радиус:
S = π
r2

2. Площадь круга можно найти через диаметр:
S = πd2/4

Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

Площади фигур — Математические этюды
Площадь квадрата равна квадрату длины его стороны. Легко посчитать площадь фигуры, разбивающейся на несколько квадратов. А чему равна площадь фигуры, ограниченной произвольной кривой?
Наложим на изучаемую фигуру квадратную сетку.
Покрасим в жёлтый цвет квадраты, которые хотя бы частично пересекаются с фигурой. Чтобы зрительно увидеть и подсчитать площадь, занимаемую жёлтыми квадратами, сложим из них прямоугольник. Очевидно, что величина, которую мы хотим назвать площадью изучаемой фигуры, меньше площади этого жёлтого прямоугольника.
В синий цвет покрасим те квадраты, которые полностью лежат внутри нашей фигуры. Таких квадратов набралось, конечно, меньше, чем жёлтых. Выложим и из них прямоугольник. Площадь нашей фигуры больше площади этого синего прямоугольника.
Итак, то, что мы хотим назвать площадью изучаемой фигуры, больше площади синего прямоугольника и меньше площади жёлтого. Но площади этих двух прямоугольников сильно различаются, и пока мы плохо представляем, какова же искомая площадь.
Для того чтобы получить более точные нижнюю и верхнюю границы искомой величины, рассмотрим сеточку из более маленьких квадратов. Повторим предыдущие действия. В жёлтый покрасим те квадраты, которые хотя бы частью пересекаются с фигурой. В синий — те, которые полностью лежат внутри фигуры. Снова площадь фигуры больше площади синего прямоугольника и меньше площади жёлтого. Но в этот раз, взяв более мелкую сетку, мы получили более точные границы.
Рассматривая ещё более мелкую сетку, мы получим еще более точные верхнюю и нижнюю границы площади изучаемой фигуры.
Будем продолжать уменьшать ячейки сетки, делая их всё мельче и мельче так, чтобы сторона квадратиков, из которых она составлена, стремилась к нулю. Абстрагировавшись от реальности, в математической модели считается, что делать квадратики можно сколь угодно маленького размера. Тогда, как говорят, в пределе, жёлтый и синий многоугольники окажутся равными. Рассмотрим прямоугольник, составленный из половинок синего и желтого прямоугольников (можно было рассмотреть и любой из них).
Площадью изучаемой фигуры по определению называется площадь двуцветного прямоугольника.
В жизни бывают случаи, когда необходимо приближённо определить площадь фигуры. При этом посчитанная площадь должна отличаться от настоящей не больше чем на некоторую заданную величину. Для решения этой задачи необходимо взять сетку из таких квадратиков, чтобы разница между площадями жёлтого и синего прямоугольников не превосходила удвоенной заданной величины погрешности. Тогда за площадь изучаемой фигуры нужно взять число, равное сумме площадей жёлтого и синего прямоугольников, поделённой пополам.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Урок 3: Площадь — 100urokov.ru
План урока:
Понятие площади многоугольника
Свойство аддитивности площади
Площадь квадрата
Соотношение между единицами измерения площадей
Площадь прямоугольника
Понятие площади многоугольника
Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.
Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м2):

Аналогично можно определить такие величины, как квадратный сантиметр (см2), квадратный километр (км2), квадратный миллиметр (мм2) и т.д.:

Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.

Общепринято, что площадь фигуры обозначается буквой S.
Свойство аддитивности площади
Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:
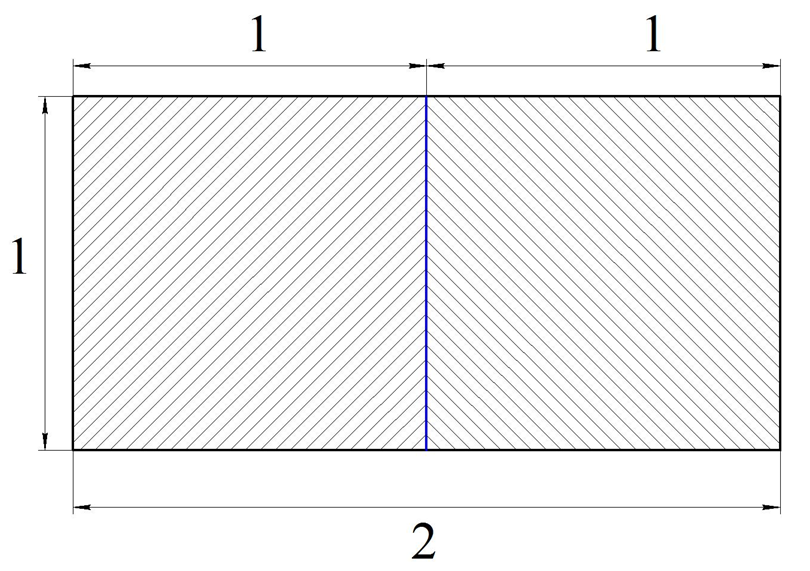
Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.
В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.
Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.
Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:
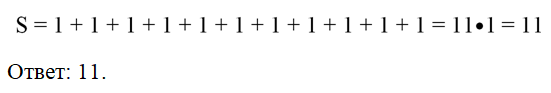
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:
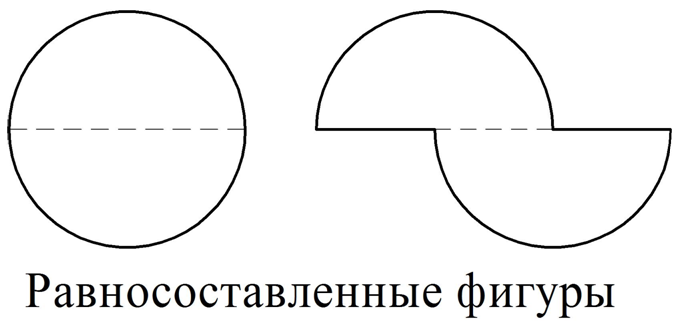
Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.
Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.
Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.
Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:
- площадь квадрата со стороной 1 равна единице:
- равносоставленные фигуры имеют равную площадь.
Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.
Площадь квадрата
Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.
Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.
Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.
Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».
Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2<S (случай, когда I2>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.
Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.
Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.
Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.
Ответ: 16 см2.
Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2. Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.
Соотношение между единицами измерения площадей
Площадь измеряется в «квадратных» величинах: м2, см2, км2 и т.д. Как связаны эти единицы измерения? Для ответа на этот вопрос построим квадрат со стороной 1 см и разобьем каждую его сторону на отрезки длиной 1 мм. Естественно, что таких отрезков будет 10, ведь, в 1 см равен 10 мм. Далее разобьем большой квадрат на маленькие, их число будет равно 102 = 100:

Площадь большого квадрата равна 1 см2, а площадь маленьких составляет 1 мм2. Так как большой квадрат состоит из 100 маленьких, мы можем записать:

Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:

В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:

Задание. Площадь окружности равна 24 см2. Выразите эту величину в мм2 и м2.
Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см2 равен 100 мм2:

Площадь прямоугольника
Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.
Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):

С одной стороны, площадь большого квадрата (со стороной а + b) равна величине (а + b)2. С другой стороны, он состоит из 4 фигур, а потому его площадь равна сумме

Итак, мы доказали следующее утверждение:

Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?
Решение. Просто перемножаем эти числа:

Задание. Найдите площадь фигуры, изображенной на рисунке:

Решение. Необходимо разбить фигуры на несколько прямоугольников:

Далее считаем площадь каждого отдельного прямоугольника:

Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?
Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:

Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:

Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно

Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.
Решение. Запишем формулу площади прямоугольника:

Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.
Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел

Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна

Задание. Одна сторона прямоугольника длиннее другой на 5 см, а площадь прямоугольника равна 150 см2. Вычислите обе стороны прямоугольника.
Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:
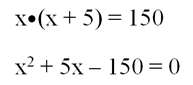
Это обычное квадратное уравнение, решаемое с помощью:

Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна

Задание. Периметр прямоугольника равен 16 см, а площадь составляет 15 см2. Каковы стороны этого прямоугольника?
Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:

Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:

Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:
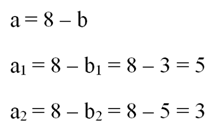
В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.
Ответ: 5 см; 3 см.
Формулы площадей 📐 всех фигур
Площадь треугольника
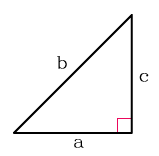
Прямоугольного
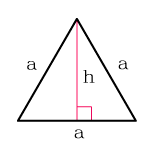
Равностороннего треугольника
Площадь равнобедренного прямоугольного треугольника
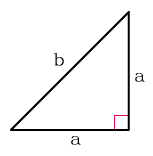
S = a2/2
Площадь треугольника через синус
Площадь треугольника через косинус
 Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен:
Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен: Следовательно:
Далее используем формулу Герона:
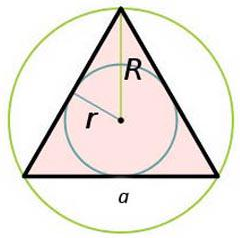
Площадь треугольника через радиус описанной окружности
Произвольного треугольника
 Формула Герона
Формула Герона Площадь треугольника через высоту
Площадь треугольника через полупериметр
 Формула Герона
Формула Герона является полупериметром.
Площадь тупоугольного треугольника
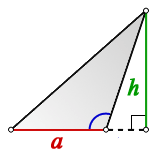
S = ah/2
Площадь треугольника через радиус вписанной окружности

S = p×r
где p — полупериметр:Площадь параллелограмма
Через синус
Через стороны и углы
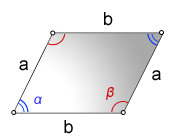
S = a×b×sin(α) = a×b×sin(β)
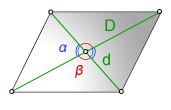
Через диагонали и угол между ними
Формула площади прямоугольника
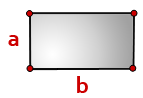
S = a×b
Площадь квадрата
S = a2
Площадь четырехугольника
Выпуклого четырехугольника
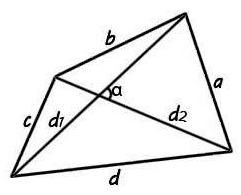
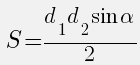
где
Площадь многоугольника
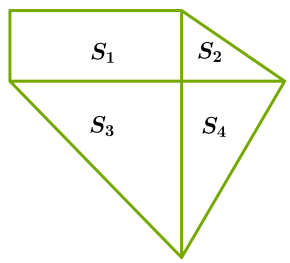
S = S1 + S2 + S3 + S4
Правильного многоугольника
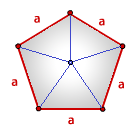
где n — количество сторон многоугольника.
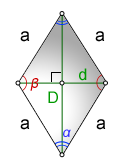
Площадь ромба
Площадь многогранника
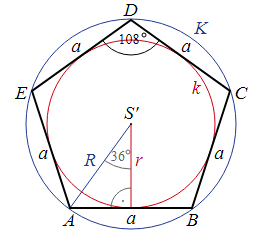
Площадь пятиугольника
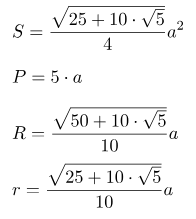
Площадь закрашенного сектора
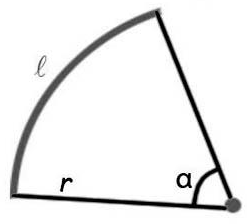
Площадь круга

S = πr2
Площадь трапеции
Через основания и высоту
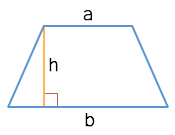
Через высоту и среднюю линию
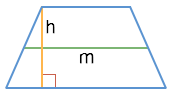
S = hm
Через четыре стороны
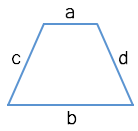
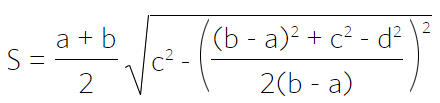
Через диагонали и угол между ними
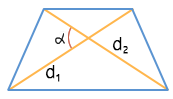

Через основания и два угла
Стандартное обозначение площади — S
Площадь
Пусть длина стороны квадрата равна a, тогда формул квадрата:
S = a ⋅ a = a2
Прямоугльник
Пусть длины сторон прямоугольника равны a и b
S = a ⋅ b
Параллелограмм
Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
S = a ⋅ ha = b ⋅ hb
Трапеция
Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). Тогда формула площади:
$S = \frac{(a + b)\cdot h}{2}$
Площадь круга
$P = \pi\cdot r^2$
$\pi=3,14$
Площадь прямоугольного треугольника
$S=\frac{a \cdot b}{2}$
$S=\frac{c \cdot h_c}{2}$
Площадь треугольника — калькулятор
Стороны треугольника:Треугольник
ABC — треугольник
длина его сторон: a, b, c и длина его высот: ha, hb и hc.
S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)
p = ½(a + b + c)
S = √p(p — a)(p — b)(p — c) — формула Герона
$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$
где R — радиус описанной окружностиПлощадь параллелограмма(ромба)
$S = AB\cdot DE = BC \cdot DF$
$S = AB \cdot AD \sin \alpha$
$S = \frac12 AC \cdot BD \sin \gamma$
Площадь выпуклого четырехугольника
$S = \frac12 AC \cdot BD \sin \varphi $
Площадь правильного многоугольника
$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$
n — число ребер(вершин).
$\pi=3,14159265359$

 a · h
a · h a · b · sinα
a · b · sinα 






 · h
· h