Введение в планиметрию
На этой странице вы узнаете:- Какими бывают углы?
- По каким признакам можно сказать, что треугольники равны?
- Что такое коэффициент подобия?
- Какие бывают многоугольники?
- Какими формулами пользоваться, чтобы найти площадь фигуры?
- Что такое окружность и из чего она состоит?
- Когда можно вписать окружность в многоугольник, а когда около него можно её описать?
Квадрат, круг, треугольник. Несомненно, вы знаете о таких геометрических фигурах, эти фигуры относятся к разделу геометрии, который называется планиметрия. Планиметрия – это наука о изучении геометрических фигур на плоскости. Точки, прямые, отрезки, лучи и углы являются основой этого раздела геометрии. Давайте их и рассмотрим.
Прямая – это линия, не имеющая ни начала, ни конца, такая линия может быть бесконечной.
Отрезок – это часть прямой, ограниченная с обеих сторон.
Луч – это отрезок, ограниченный только с одной стороны.
Угол – это фигура, образованная двумя лучами, исходящими из одной точки, измеряется в градусах.
Рассмотрим части угла:
Углы бывают четырёх видов:
Смежные и вертикальные углы
Смежные углы – это углы, имеющие одну общую сторону, а две другие стороны этих углов лежат на одной прямой.
Смежные углы в сумме дают 1800.
Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого угла.
Рассмотрим углы при параллельных прямых
Накрест лежащие углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по разные стороны от секущей между параллельным прямыми. Такие углы всегда равны.
Внутренние односторонние углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей между параллельным прямыми. Сумма этих углов 1800.
Сумма этих углов 1800.
Соответственные углы — это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей так, что один угол находится между двумя прямыми относительно одной прямой, а другой угол прилегает к другой прямой с внешней стороны. Эти углы равны.
Пусть a || b, а с – секущая
Тогда 3 и 6, 4 и 5 накрест лежащие; 3 и 5, 4 и 6 внутренние односторонние; 1 и 5, 2 и 6, 3 и 7, 4 и 8 соответственные
Треугольники, их виды и признаки их равенстваСумма углов любого треугольника равна 1800
Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон
Элементы треугольника:Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)
Биссектриса – это отрезок, делящий угол на два равных угла.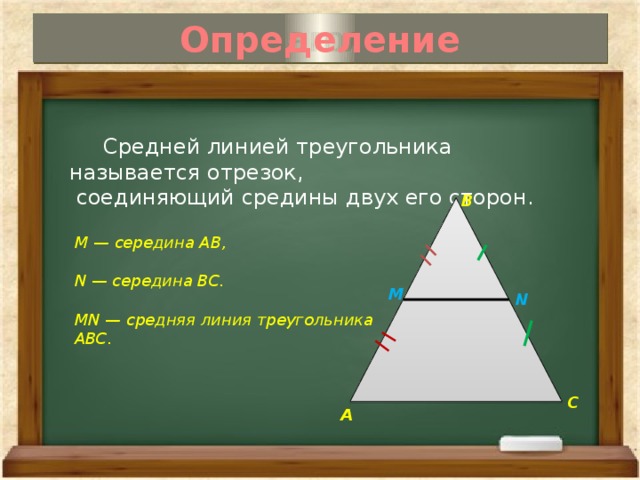 Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)
Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)
Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)
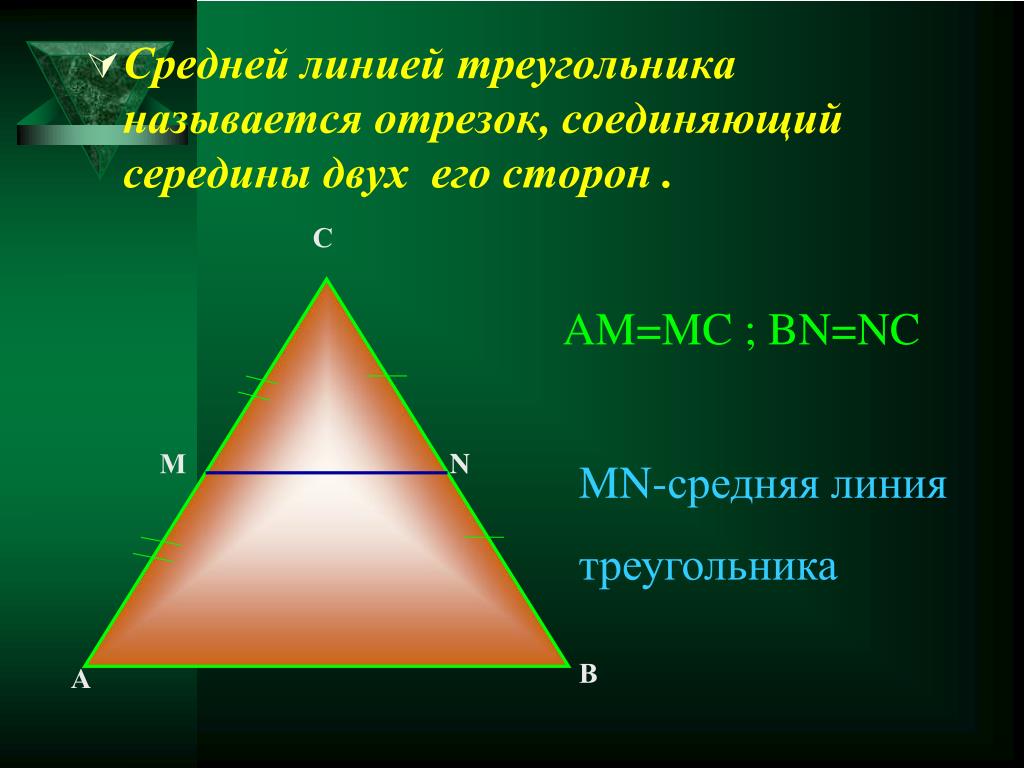
Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.
Виды треугольников:У равностороннего треугольника все стороны равны и углы по 600.
У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой.
У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы
Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы
- Треугольники равны по двум сторонам и углу между ними
АВ = А1В1
АС = А1С1
Угол ВАС = угол В1А1С1
- Треугольники равны по стороне и двум прилежащим к ней углам
АВ = А1В1
Угол ВАС = угол В1А1С1
Угол АВС = угол А1В1С1
- Треугольники равны по трём сторонам
АВ = А1В1
АС = А1С1
ВС = В1С1
Давайте теперь разберёмся, что значит подобие:
Если треугольники похожие, но отличаются только размером, тогда поможет подобие треугольников
Коэффициент подобия – это число, в которое отличаются стороны треугольников
Если АВС подобен А1В1С1, тогда верно равенство, где к – коэффициент подобия
Если треугольники подобны, тогда отношение их площадей равно квадрату коэффициента подобия
Признаки подобия треугольников:- По двум сторонам и углу между ними
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны
- По двум углам
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны
- По трём сторонам
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
Площадь треугольникаПлощадь треугольника, если известна высота и основание, к которому она проведена
Площадь треугольника с двумя известными сторонами и углом между ними
Площадь прямоугольного треугольника с известными катетами
Площадь правильного треугольника, если известна только сторона
Формула Герона позволяет вычислить площадь треугольника, если известны его стороны
Площадь треугольника, когда известен полупериметр и радиус вписанной окружности
Площадь треугольника, когда известны стороны и радиус описанной окружности
МногоугольникМногоугольник – это часть плоскости, ограниченная замкнутой ломаной линией
Многоугольники бывают выпуклые и невыпуклые
Многоугольник является выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону
Для нахождения площади любого выпуклого четырёхугольника существует формула:
Виды многоугольников:- Параллелограмм – это четырёхугольник, у которого стороны попарно параллельны
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся точкой пересечения пополам
- Прямоугольник – это четырехугольник, у которого все углы прямые
- Диагонали равны
- Противоположные стороны параллельны и равны
- Угол между сторонами прямой
- Сумма углов 360 градусов
Квадрат – это частный случай прямоугольника
Свойства квадрата:- Диагонали взаимно перпендикулярны и равны
- Диагонали делят углы квадрата пополам
- Все стороны равны
- Угол между сторонами прямой
- Сумма углов 360 градусов
- Трапеция – это четырёхугольник с двумя параллельными сторонами (основаниями), а две другие стороны у него не параллельны
Трапеция может быть произвольной, равнобедренной или прямоугольной.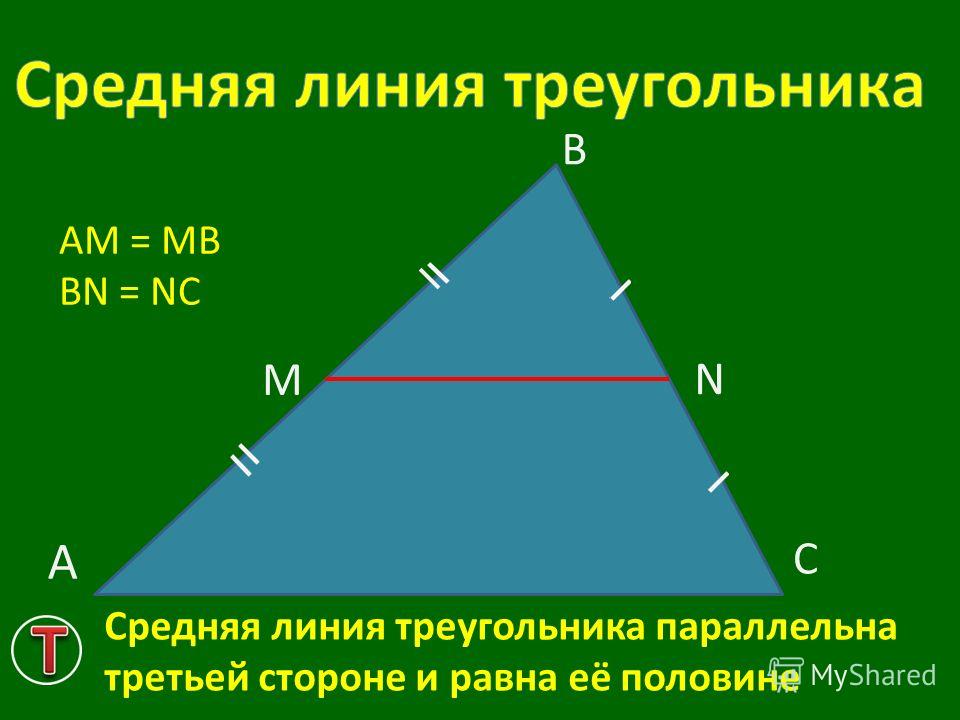
- Сумма углов, прилежащих к боковой стороне, равна 180 градусов
- Средняя линия равна полусумме оснований
- Отрезок, соединяющий середины диагоналей, равен полуразности её оснований
- Углы при основании равны
- Диагонали равны
- Ромб – это параллелограмм, у которого все стороны равны
- Противоположные углы равны
- Все стороны равны
- Диагонали делятся точкой пересечения пополам
- Диагонали перпендикулярны друг другу
- Диагонали являются биссектрисами углов
Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)
Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности
В окружности можно провести радиус, диаметр и хорду
Радиус – расстояние от центра до окружности
Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности
Хорда – прямая, соединяющая две любых точки окружности
Также в окружности есть два вида углов
Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается
Такой угол равен половине дуги, на которую опирается
Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается
Окружность, вписанная в четырёхугольникЧтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны
a + c = b + d
Окружность, вписанная в прямоугольный треугольникУ вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r
Окружность, описанная около четырёхугольникаЧтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:
- Сумма противоположных углов треугольника равна 180 градусов
- Вписанные углы, опирающиеся на одну хорду, равны
- Диаметр окружности равен гипотенузе вписанного треугольника
- Радиус описанной окружности равен половине гипотенузы
R=c/2, где c-диаметр
Теорема синусов:Отношения длин сторон треугольника к синусам противолежащих углов равны между собой, а также равны двум радиусам описанной окружности
ФактчекРавенство треугольников можно определить по одному из трёх признаков равенства треугольников (по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам).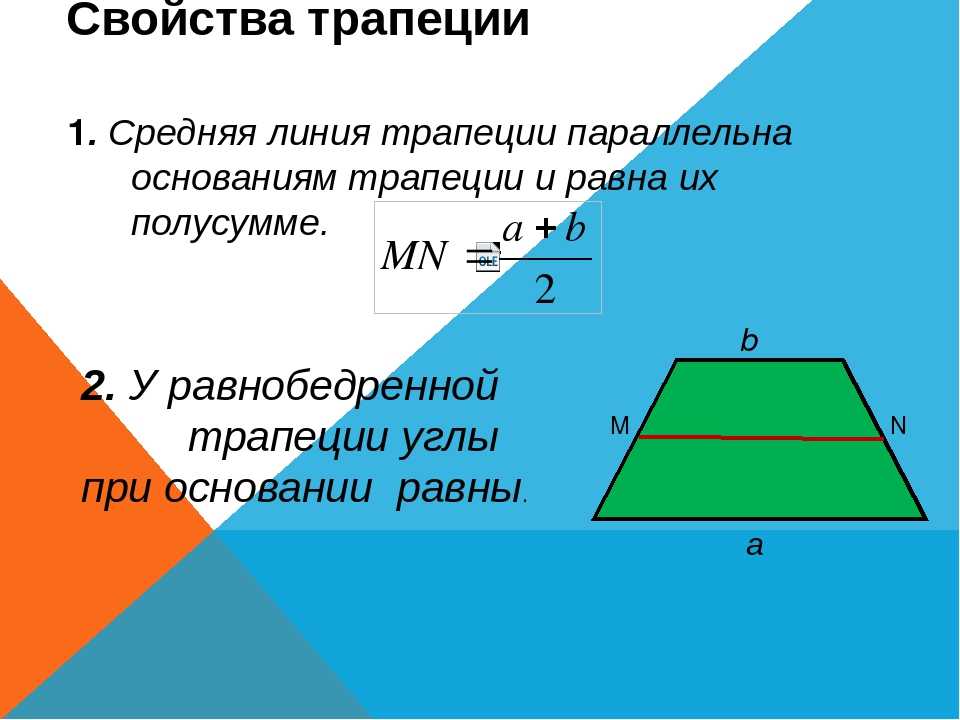
- Признаки подобия немного отличаются от признаков равенства треугольников (по двум сторонам и углу между ними, по двум углам, по трём сторонам), по ним определяется отношение соответственных сторон одного треугольника к сторонам другого.
- Для нахождения площади выпуклого четырёхугольника есть универсальная формула
S = ½* d1* d2 *sin α , где d 1, d 2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.
- Окружность можно вписать в четырёхугольник, если суммы его противоположных сторон равны, а описать окружность около четырёхугольника можно, если пара противоположных углов в сумме даёт 180 градусов.
- Так же стоит помнить, что в теореме синусов равны не только отношения противолежащих сторон к синусам углов, но и каждое такое отношение равно двум радиусам описанной окружности.
Задание 1.
Чему равен отрезок соединяющий середины диагоналей в трапеции с основаниями а и b?
1. (a + b) / 2
(a + b) / 2
2. (a — b) / 2
3. a-b
4. a+b
Задание 2.
В прямоугольном треугольнике один из катетов равен половине гипотенузы, чему равен угол напротив этого катета?
1. 90
2. 60
3. 30
4. 20
Задание 3.
Чему равен вписанный угол, опирающийся на хорду равную 84 градусам?
1. 42
2. 21
3. 84
4. 90
Задание 4.
Чему равен радиус описанного прямоугольного треугольника с катетами 3 и 4?
1. 5
2. 1,5
3. 2,5
4. 2
Задание 5.
Из каких длин сторон треугольника нельзя получить треугольник?
1. 4 16 12
2. 5 6 9
3. 3. 41 18 24
4. 17 14 28
Ответы: 1. — 2; 2. — 2; 3. — 1; 4. — 3; 5. — 1.
Сайт:
Сайт:
перейти в каталог файлов |
Что такое линия симметрии? Определение, типы, формы, примеры
Что такое линия симметрии?
В математике говорят, что объект обладает симметрией, если его можно разделить на две одинаковые половины. Линия, которая делит предмет на одинаковые половины, называется линией симметрии. Например, на данном изображении линия, проходящая через середину цветка, является его линией симметрии.
Линия, которая делит предмет на одинаковые половины, называется линией симметрии. Например, на данном изображении линия, проходящая через середину цветка, является его линией симметрии.
Определение линии симметрии
Линия симметрии — это линия, которая делит фигуру или объект на две равные и симметричные части. Мы также называем эту линию осью симметрии или зеркальной линией, потому что она симметрично делит фигуру, а разделенные части выглядят как зеркальные отражения друг друга. Дополнительные примеры линий симметрии показаны на рисунке ниже.
Симметричные и асимметричные фигуры
Фигура или форма, которую можно разделить на две равные части линией, называется СИММЕТРИЧНОЙ фигурой. Формы и объекты, которые имеют неправильную форму и не похожи друг на друга при разделении на две части, называются АСИММЕТРИЧНЫМИ.
Типы линий симметрии
Линия симметрии может быть классифицирована на основе ее ориентации.
Горизонтальная линия симметрии: Если горизонтальная линия делит объект на две одинаковые половины, она называется горизонтальной линией симметрии.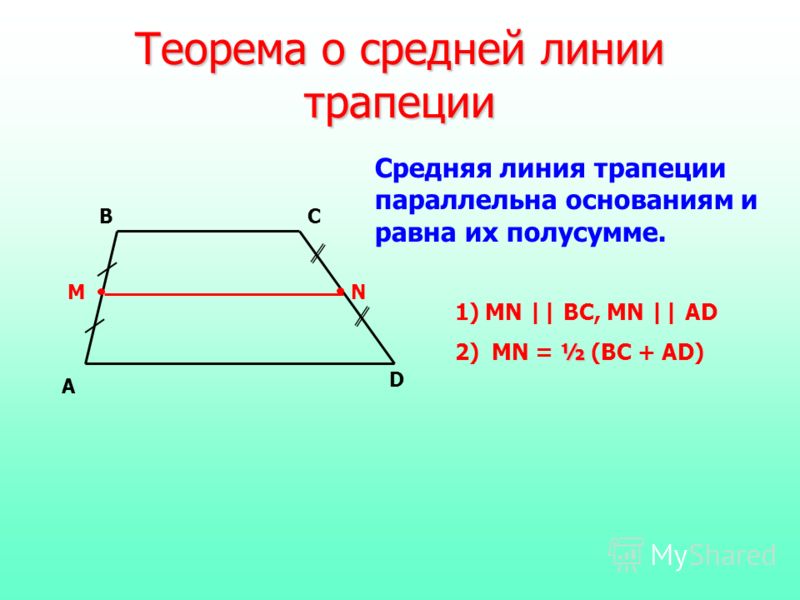 Это означает, что горизонтальная линия симметрии проходит слева направо (или наоборот) в объекте.
Это означает, что горизонтальная линия симметрии проходит слева направо (или наоборот) в объекте.
Вертикальная линия симметрии: Если вертикальная линия делит объект на две одинаковые половины, она называется вертикальной линией симметрии. Это означает, что вертикальная линия идет сверху вниз (или наоборот) в объекте и делит его на зеркальные половины.
Диагональная линия симметрии: Если диагональная линия делит объект на две одинаковые половины, она называется диагональной линией симметрии. Это означает, что диагональная линия симметрии идет вбок или под наклоном в объекте.
Количество линий симметрии в фигуре
Линия симметрии дает совпадающие отражения. Форма или объект могут иметь несколько линий симметрии в соответствии со своей структурой. Фигуры с одной линией симметрии имеют только одну линию, которая делит их на одинаковые части. Формы с несколькими линиями симметрии имеют более одной линии, которая разделяет их поровну.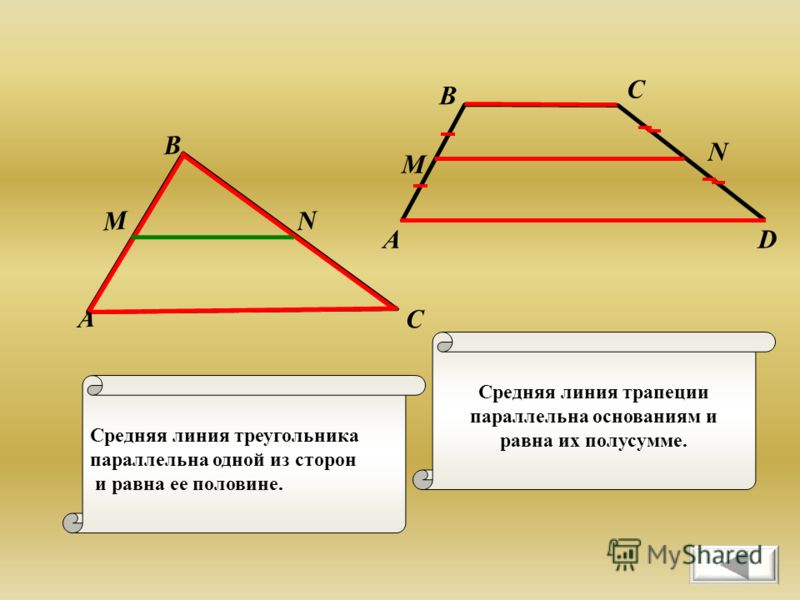 Ось симметрии может быть горизонтальной, вертикальной или диагональной. Например,
Ось симметрии может быть горизонтальной, вертикальной или диагональной. Например,
Линия симметрии в геометрии
Ось симметрии в обычных двумерных геометрических фигурах приведены ниже:
Геометрические фигуры могут иметь более одной линии симметрии. Изучим некоторые геометрические фигуры с одной и несколькими осями симметрии.
Решенные примеры
Пример 1: Сколько осей симметрии имеет данная фигура?
Решение : Данная фигура имеет только одну линию симметрии.
Пример 2: Определите, является ли данная линия симметрии вертикальной, горизонтальной или диагональной линией симметрии.
Решение: Данная прямая является вертикальной линией симметрии.
Пример 3: Напишите три заглавные буквы английского алфавита не имеют линий симметрии?
Решение: Три буквы английского алфавита, не имеющие линий симметрии, это P, G и J.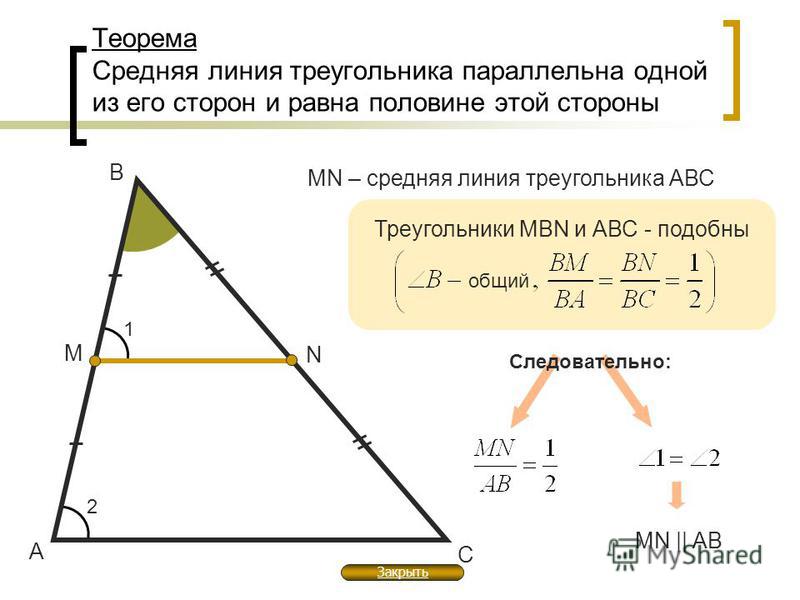
Пример 4. Напишите три заглавные буквы английского алфавита с горизонтальными и вертикальными линиями симметрии.
Решение: Английский алфавит с горизонтальными и вертикальными линиями симметрии равен H, I и O.
Практические задачи
1
Сколько осей симметрии имеет равнобедренный прямоугольный треугольник?
1
2
3
Правильный ответ: 1
Все равнобедренные треугольники имеют одну линию симметрии.
2
Какой из следующих алфавитов является асимметричным?
A
D
R
U
Правильный ответ: R
Алфавит «R» асимметричен, потому что он не может быть разделен поровну и симметрично по какой-либо оси.
3
Какая из следующих фигур имеет ровно две оси симметрии?
Квадрат
Воздушный змей
Ромб
Параллелограмм
Правильный ответ: Ромб
Когда ромб сложен по диагоналям, две половинки идентичны.
4
Какая из следующих пунктирных линий не является линией симметрии?
A
B
C
D
Правильный ответ: A
Пунктирная линия во всех вариантах (b), (c) и (d) делит фигуру симметрично. Горизонтальная линия, нарисованная на (а), не делит форму воздушного змея на две равные или зеркально отраженные половины. Нижняя часть больше верхней половины.
Заключение
Линии симметрии могут помочь детям понять и создать узоры. Он учит чувству баланса и порядка и открывает им мир природы, где изобилует симметрия — насекомые, морские ракушки и листья, и это лишь некоторые из них.
Узнайте больше о математических понятиях на SplashLearn, игровой платформе для обучения, оснащенной интерактивными играми и забавными рабочими листами.
Часто задаваемые вопросы
Каково максимальное количество линий симметрии в объекте?
Количество линий симметрии зависит от формы или фигуры.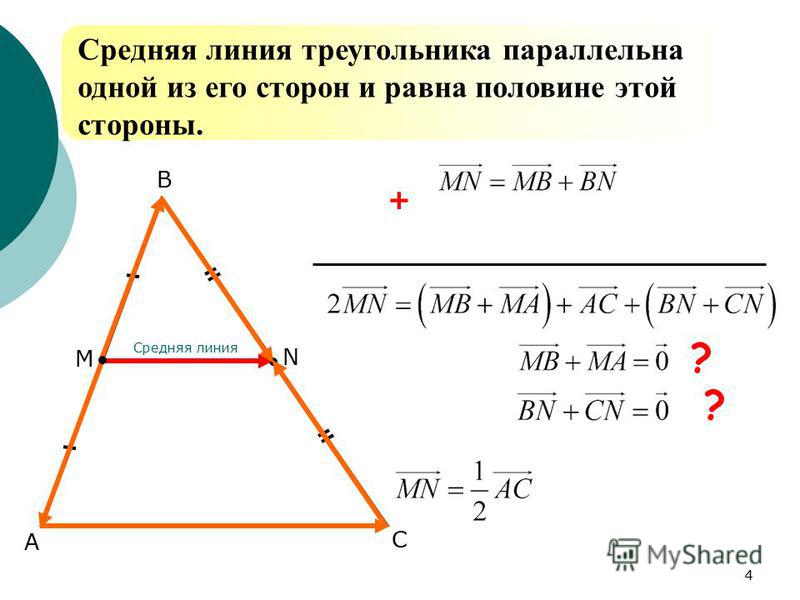 Например, у равнобедренного треугольника одна линия симметрии, у прямоугольника две оси симметрии, а у окружности бесконечная линия симметрии.
Например, у равнобедренного треугольника одна линия симметрии, у прямоугольника две оси симметрии, а у окружности бесконечная линия симметрии.
Существуют ли фигуры, у которых нет линий симметрии?
Формы или объекты, которые имеют неправильную форму и не похожи друг на друга при разделении на две части, называются АСИММЕТРИЧНЫМИ. Такие фигуры не имеют линии симметрии. Разносторонний треугольник, параллелограмм и трапеция являются примерами фигур, не имеющих линий симметрии.
Как найти линию симметрии фигуры?
Сложите фигуру так, чтобы одна половина была идентична другой половине. Линия, по которой вы сложили, можно назвать линией симметрии. Таких линий или линий симметрии может быть более одной.
Сколько осей симметрии имеет правильный многоугольник?
В правильном многоугольнике все стороны и углы равны. Если у него «n» сторон, то у него будет «n» и линий симметрии. Например, квадрат с четырьмя равными сторонами имеет четыре линии симметрии, а правильный пятиугольник — пять линий симметрии.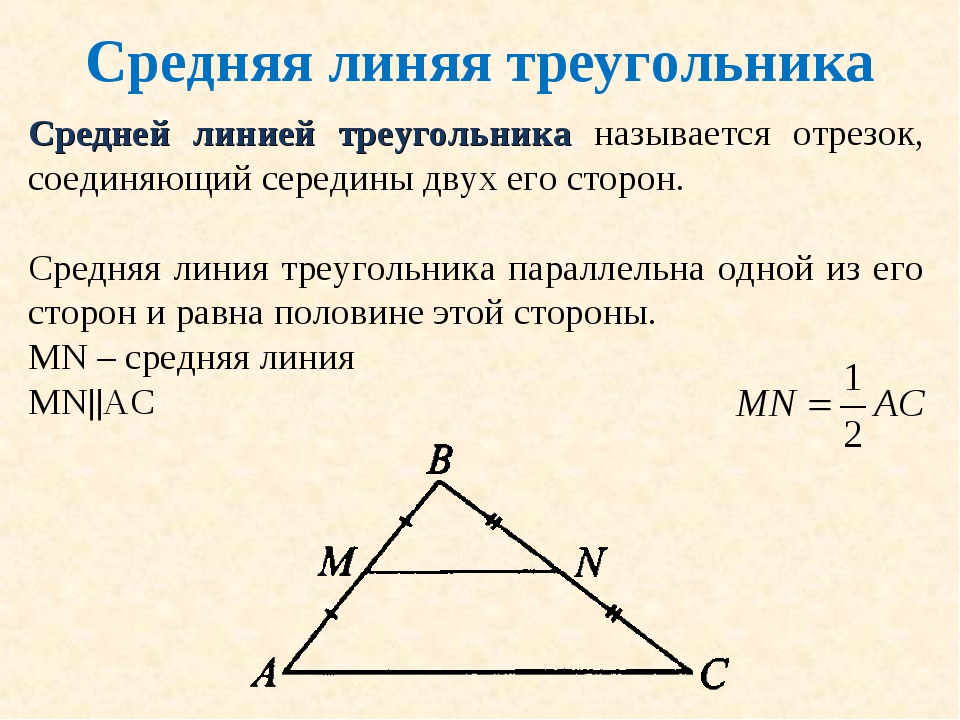
Линия Эйлера — открытая ссылка по математике
Линия Эйлера — открытая ссылка по математикеОткрытый математический справочник
Главная Контакт О Тематический указатель
В любом треугольнике центроид, центр окружности а также ортоцентр всегда лежат на прямой линии, называемой линией Эйлера.
Попробуйте это Перетащите любую оранжевую точку на вершину треугольника. Три точки, представляющие три центра, всегда будут лежать на зеленой линии Эйлера.
В 18 веке швейцарский математик Леонард Эйлер заметил, что три из многих центры треугольника всегда коллинеарный, то есть они всегда лежат на прямой линии. Эта линия получила название в его честь — линия Эйлера. (Его имя произносится на немецкий лад — «маслёнок»). Три центра, обладающие этим удивительным свойством, — это центры треугольника. центр тяжести , центр окружности а также ортоцентр.
На рисунке выше (сначала нажмите «сброс», если необходимо) центроид представляет собой черную среднюю точку на линии.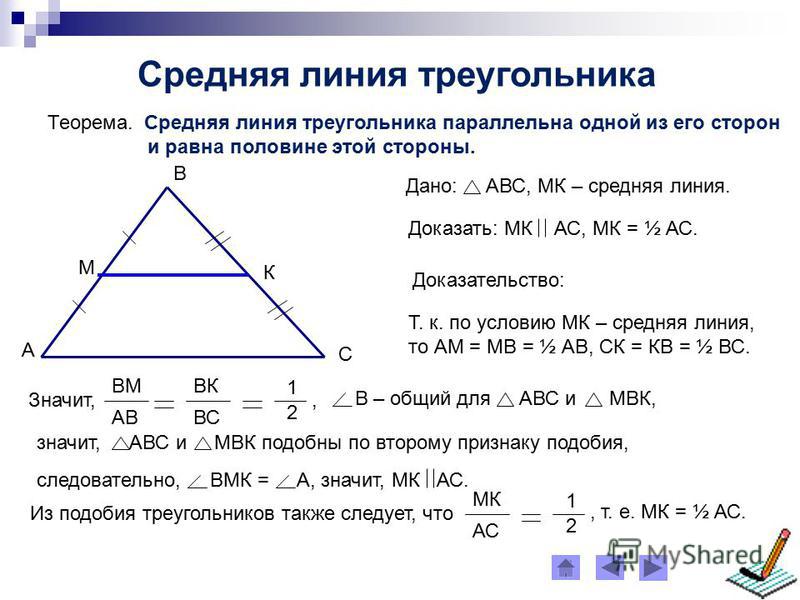
У каждого из трех задействованных центров есть собственная страница с их описанием, но вот краткий обзор:
Центроид
Центроид – это точка, где три медианы сходятся. На рисунке выше нажмите «показать детали Centroid». Медианы (здесь окрашены в черный цвет) — это линии, соединяющие вершину с серединой противоположной стороны. См. Центроид треугольника для получения дополнительной информации.Циркумцентр
Центр окружности – это точка, в которой серединные перпендикуляры стороны треугольника сходятся. На рисунке выше нажмите «Показать детали Circumcenter». Три перпендикулярные биссектрисы (здесь окрашены в пурпурный цвет) — это линии, которые пересекают каждую сторону треугольник под прямым углом точно в их середине.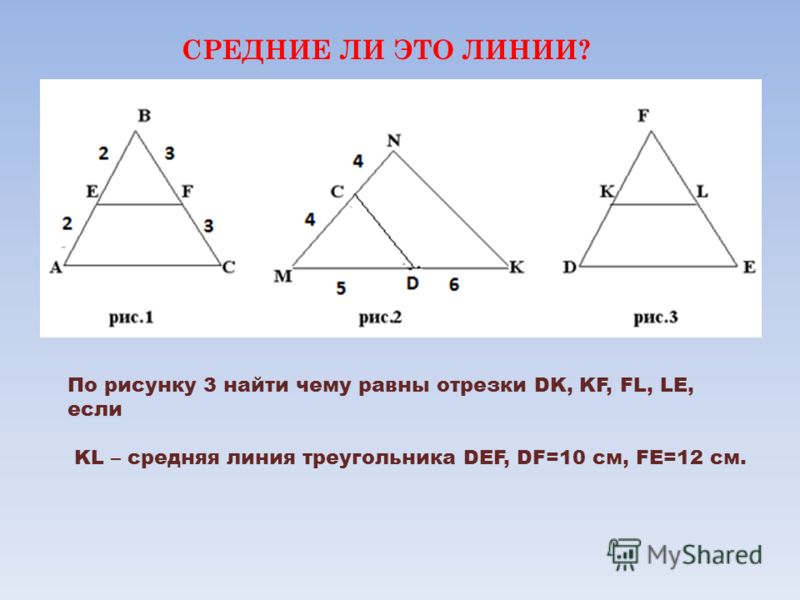

 Средняя линия Треугольники
Средняя линия Треугольники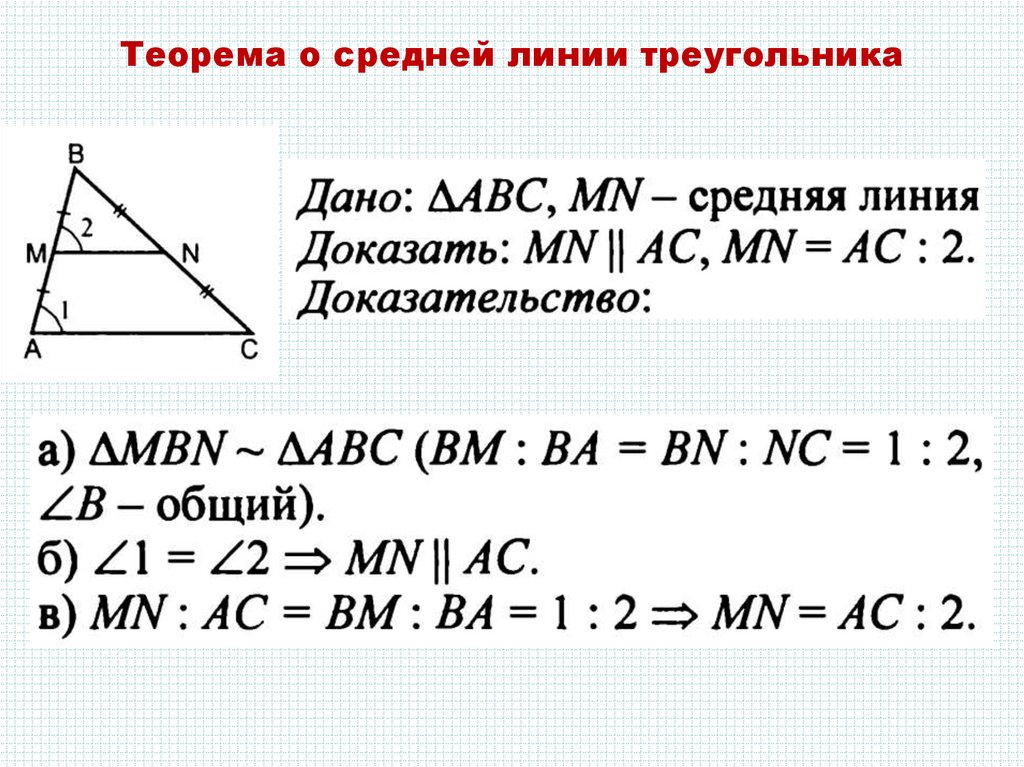

 6
6 