Чему равны углы: Чему равны углы равнобедренного прямоугольного треугольника ?

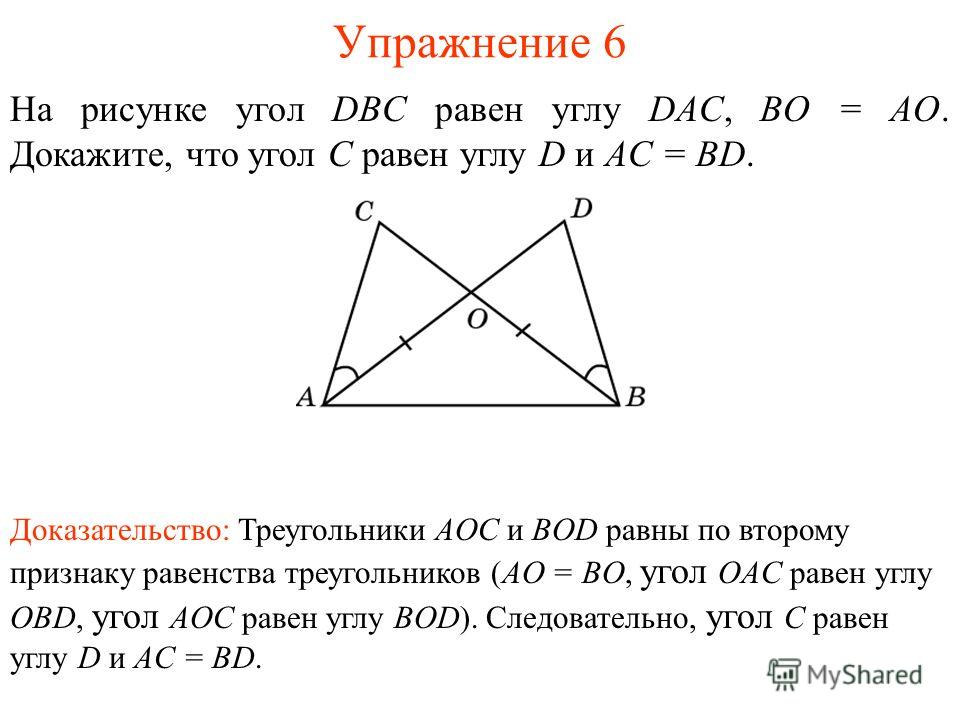
Сумма углов прямоугольного треугольника – чему равна

4.5

Средняя оценка: 4.5

Всего получено оценок: 244.

Обновлено 9 Июля, 2021

4.5

Средняя оценка: 4.5

Всего получено оценок: 244.

Обновлено 9 Июля, 2021

Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Треугольник

Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.

Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.

Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.

Рис. 1. Фигура, разбитая на треугольники

Сумма углов треугольника

Есть два варианта нахождения общей суммы углов треугольника:

• Математический анализ. За столь страшными словами кроется обычная простая формула:

180*(n-2)- где n – количество сторон многоугольника.

• Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равна 180 градусам.
  Рассмотрим его подробнее.

Рис. 2. Рисунок к задаче

Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.

Рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.

Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.

Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.

Прямоугольный треугольник

Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же,как и в любом другом треугольнике – 180 градусам. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:

180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равна 90 градусам.

Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:

90-90=0 – и третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.

Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равна 90 градусам.

Рис. 3. Острые углы прямоугольного треугольника

Что мы узнали?

Мы поговорили о формуле суммы углов прямоугольного треугольника. Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 244.

---

А какая ваша оценка?

Теорема об углах с соответственно перпендикулярными сторонами / Параллельные прямые / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Параллельные прямые
5. Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 1800.

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ =

А₁О₁В₁или АОВ + А₁О₁В₁ = 180⁰.

Доказательство:

1 случай

Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА  и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁  и О₁В₁  также будут лежать на одной прямой, следовательно, А

1О₁В₁  — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

Пусть угол АОВ — прямой, т.е. равен 90⁰ (Рис.2). 

АОВ = 90⁰, то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО

1А₁, тогда по теореме об односторонних углах их сумма равна 180⁰, т.е. 1 + А₁О₁В₁= 180⁰, откуда А₁О₁В₁= 180⁰ —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т. е. 1 = 90⁰, следовательно, А₁О₁В₁ = 180⁰ — 90⁰ = 90⁰. Из равенств АОВ = 90⁰ и А₁О₁В₁ = 90⁰ следует, что АОВ = А₁О₁В₁   и АОВ + А₁О₁В₁ = 90⁰ + 90⁰ = 180⁰.

3 случай

Пусть ОО₁А₁(Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В.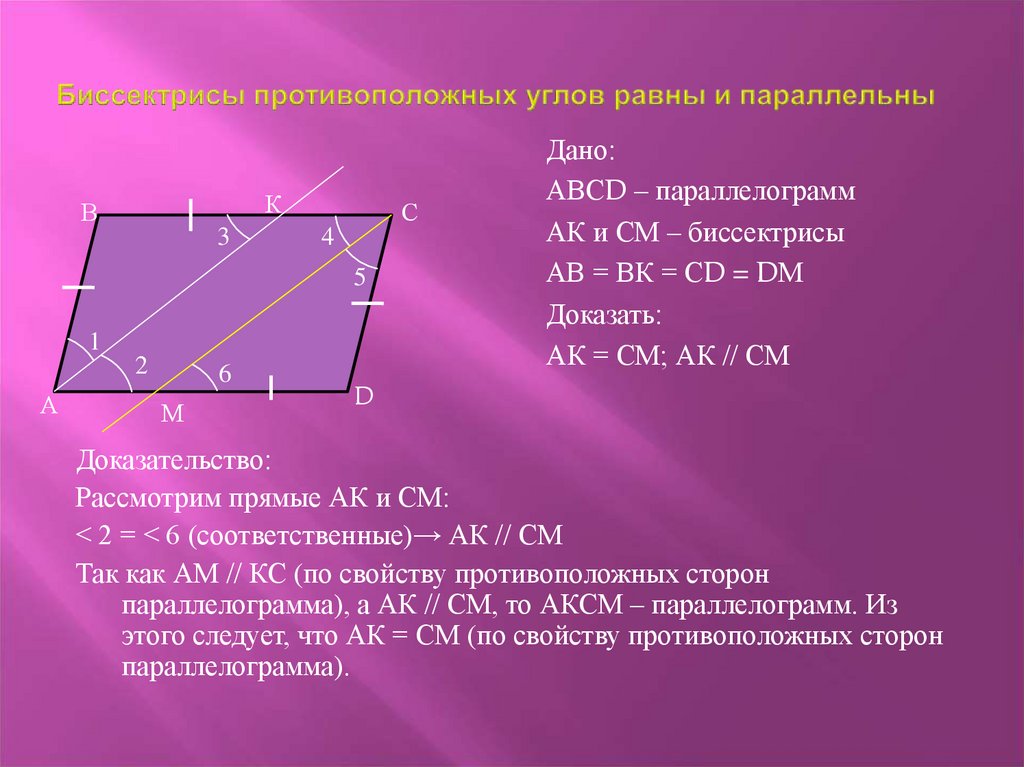

По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А ₁, ОВО₁В₁ эти углы будут прямые, т. е. АОВ = А₁О₁В₁ = 90⁰, тогда АОВ + А₁О₁В₁ = 90⁰ + 90⁰= 180⁰.

4 случай

Пусть ОО₁В₁(Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁.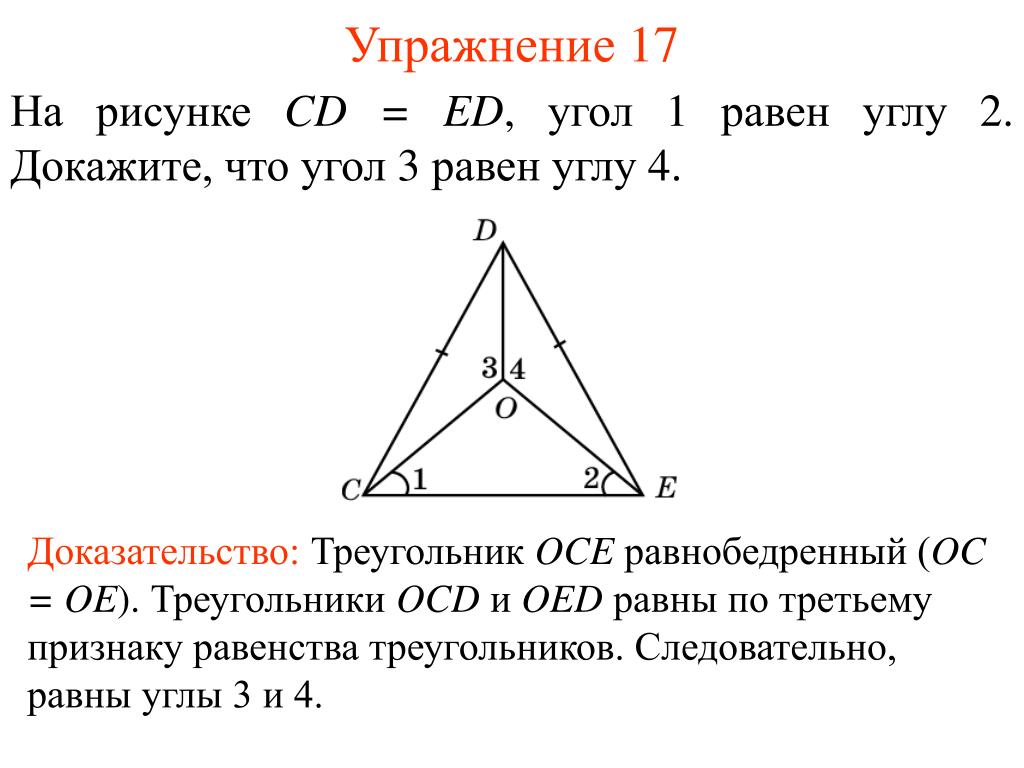 Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90⁰, тогда АОВ + А₁О₁В₁ = 90⁰ + 90⁰= 180⁰.

5 случай

Пусть угол АОВ — острый, т.е. меньше 90⁰, при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис. 6).

Получим, что АОВ = 90⁰ — АОD, а СОD = 90⁰ — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180⁰. Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180⁰.

6 случай

Пусть угол АОВ — тупой, т.е. меньше 180⁰, но больше 90⁰, при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.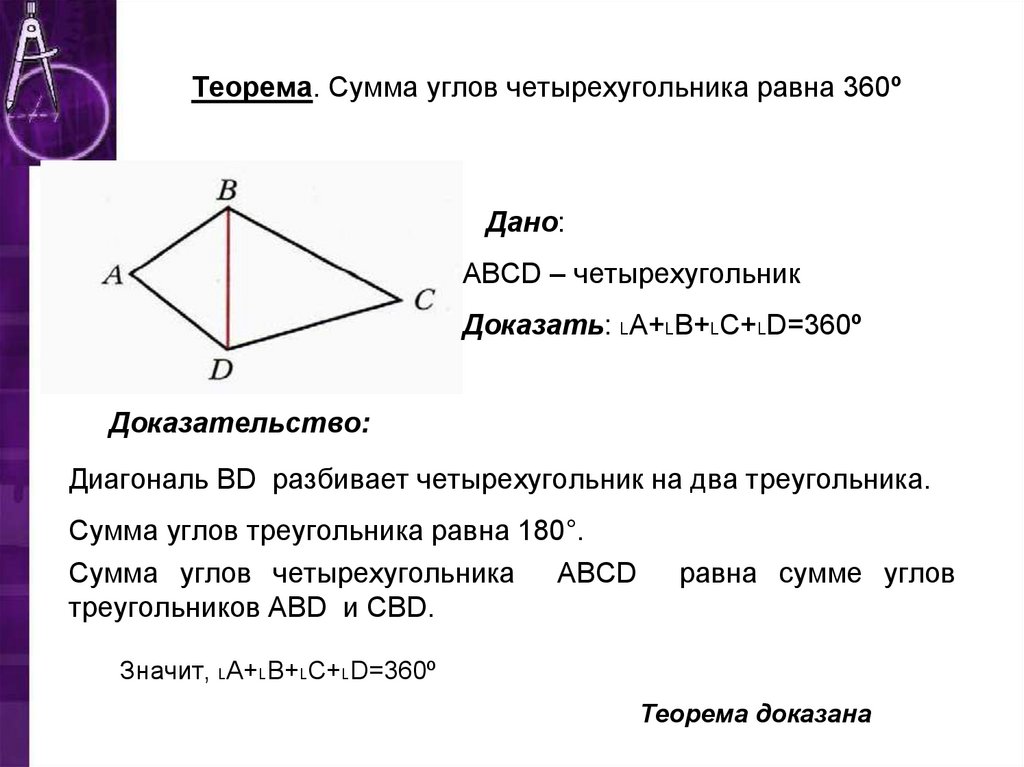 8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180⁰, либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180⁰, значит АОС = 180⁰ — АОВ, следовательно, в первом случае 180⁰ — АОВ + А₁О₁В₁ = 180⁰, откуда АОВ = А₁О₁В₁, а во втором случае 180⁰ — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180⁰. Что и требовалось доказать.

Советуем посмотреть:

Параллельные прямые

Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об односторонних углах

Теорема об углах с соответственно параллельными сторонами

Параллельные прямые

Правило встречается в следующих упражнениях:

7 класс

Задание 212, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1278, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Какие бывают виды углов?

Геометрия сыграла важную роль в развитии современного мира. В свое время геометрия использовалась при проектировании, строительных работах, в архитектуре при выборе материала для строительства и во многом другом. Это также жизненно важная часть технической основы для расчета различных конструкций, производства, создания чертежей, программирования и т. д.

Геометрия — это раздел математики, который занимается изучением форм и их свойств.

Подход к геометрии прослеживается с древних времен в их конструкциях благодаря использованию различных форм очень специфическим образом. Термин первоначально произошел от греческих слов «ге» и «материя», что означает землю и измерение соответственно.

Данная статья представляет собой исследование углов и их различных видов на основе их измерения.

Углы

Углы можно просто определить как пространство между двумя пересекающимися линиями, встречающимися в определенной точке. Они состоят из двух ветвей, известных как стороны угла, и точки встречи, где образуется угол, называемой вершиной. Углы измеряются в градусах от 0° до 360°.

  Угол — это форма или пространство, образованное в точке встречи двух пересекающихся лучей.

Слово «угол» происходит от латинского слова «angulus», что означает «угол». Первый угол предположил Карп Антиохийский.

Углы делятся на различные типы на основе измерения и поворота.

Типы углов

Углы делятся на несколько типов, т.е. на основе измерения и на основе вращения, то есть:

Углы на основе измерения:

Острый угол: Угол, величина которого меньше 90°, является острым углом. Градус всегда измеряется между 0 и 90. Острые углы измеряются положительно, когда вращение происходит против часовой стрелки, и отрицательно, когда вращение угла происходит по часовой стрелке.
 

На рисунке О — вершина угла, а ОА и ОВ — два пересекающихся луча, которые пересекаются в точке О, образуя угол меньше 90°. Следовательно, ∠AOB — острый угол.

Прямой угол: Угол, равный 90°, является прямым. Он также считается половиной прямого угла, так как половина 180° образует прямой угол. Значение угла может быть положительным или отрицательным в зависимости от поворота угла.

На рисунке О — вершина угла, а ОА и ОВ — два пересекающихся луча, которые пересекаются в точке О, образуя угол ровно 90°. Следовательно, угол ∠AOB прямой.

Тупой угол: Угол, размер которого больше 90° и меньше 180°, является тупым углом. Градус всегда лежит между 90° и 180°. Значение тупого угла будет положительным, если вращение против часовой стрелки, и отрицательным, если вращение по часовой стрелке.

На рисунке О — вершина угла, а ОА и ОВ — два пересекающихся луча, которые пересекаются в точке О, образуя угол более 90°. Следовательно, ∠AOB — тупой угол.

Прямой угол: Угол, равный точно 180°, является прямым углом. Прямые углы образуют прямые линии. Мера прямого угла может быть положительной или отрицательной. Если мы будем двигаться против часовой стрелки, прямой угол будет равен 180°, а если мы будем двигаться по часовой стрелке, угол будет равен -180°

На рисунке прямого угла видно, что O — это точка встречи двух плеч, называемая вершиной, а OA и OB — две стороны угла.

Угол рефлекса: Угол, который больше 180° и меньше 360°, является углом рефлекса. Градус всегда лежит между 180° и 360°.

На рисунке О — вершина угла, а ОА и ОВ — два пересекающихся луча, которые пересекаются в точке О, образуя угол более 180°. Следовательно, ∠AOB является рефлекторным углом.

Углы на основе вращения:

• Положительные углы: Угол, который движется против часовой стрелки от своего основания и проводится из точки (x, y), являющейся его началом, является положительным углом.
• Отрицательные углы: Угол, который движется по часовой стрелке от своего основания и проводится из точки (-x, -y), которая является его началом, является отрицательным углом.

Дополнительные углы

Если сумма двух углов равна 90°, то угол называется дополнительным. Два угла, соединяющиеся вместе, не обязательно должны быть смежными или подобными. Это могут быть любые два типа углов, равных 9. 0° после добавления.

На данном рисунке (i) ∠AOC и ∠COB — два соседних острых угла с мерой 45°. И их сумма равна 90 °, что означает, что это дополнительный угол.

На рисунке (ii) ∠AOC и ∠COB представляют собой два угла, равные 70° и 20° соответственно. Два угла не смежны друг с другом, но их сумма равна 90 °, следовательно, это также дополнительный угол.

Дополнительные углы

Если сумма двух углов равна 180°, то угол называется дополнительным углом. Дополнительные углы подразделяются на четыре типа, которые кратко обсуждаются ниже:

Вертикальный угол: Когда два угла, объединенные вместе, имеют одну и ту же вершину и равны друг другу, тогда это вертикальный угол.

На приведенном выше рисунке ∠AOD и ∠COB представляют собой вертикальные углы. Точно так же ∠AOC и ∠BOD также являются вертикальными углами, расположенными друг напротив друга.

Альтернативный внутренний угол: Углы, находящиеся на противоположных сторонах поперечной, являются альтернативным внутренним углом.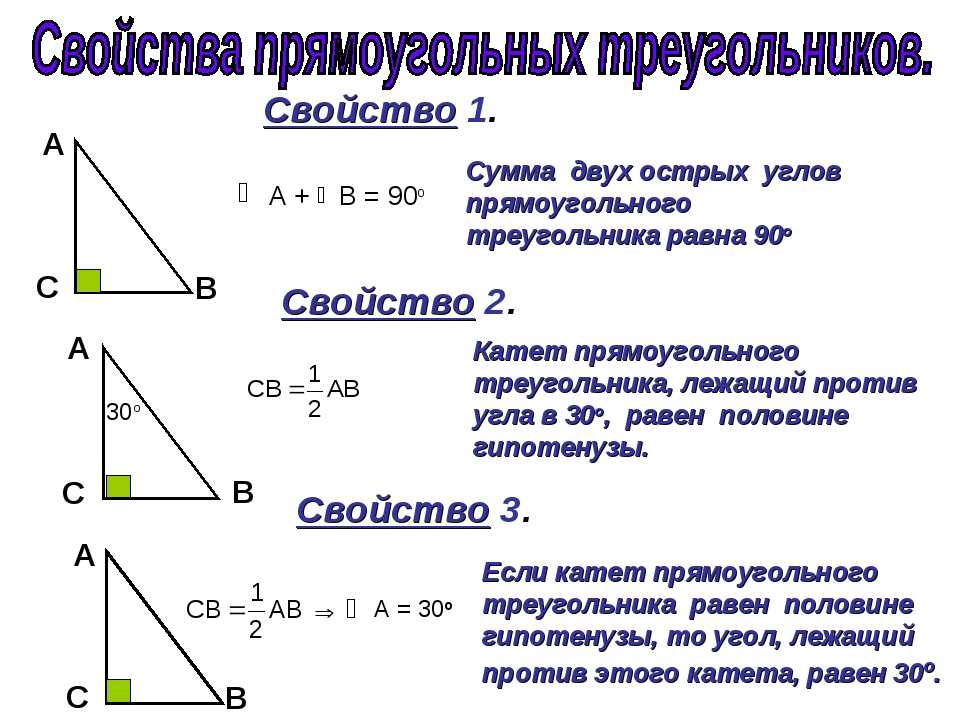 Они присутствуют на внутренней стороне буквы Z, образованной на рисунке. Оба угла равны между собой.

Фигура, которую мы привели ниже, представляет собой комбинацию разных углов. На рисунке ∠AOT и ∠OTR представляют собой чередующиеся внутренние углы, расположенные внутри, чередующиеся друг с другом. Точно так же ∠BOT и ∠OTQ также являются внутренними углами.

Альтернативный внешний угол: Углы, находящиеся на противоположных сторонах поперечной, но находящиеся снаружи, являются альтернативным внешним углом. Они отмечены на внешней части, и оба угла имеют одинаковые размеры.

На рисунке ∠SOB и ∠QTP, ∠SOA и ∠RTP представляют собой пару альтернативных внешних углов.

Соответствующий угол: Углы, находящиеся в одинаковых положениях, являются соответствующими углами. Оба угла измеряются одинаково.

На рисунке ∠SOB и ∠OTR представляют собой соответствующие углы, расположенные в одинаковых положениях один снаружи, а другой во внутренней части.

Примеры вопросов

Вопрос 1: Какие из углов образуют прямую?

Ответ:

Прямой угол величиной 180 градусов образует прямую с двумя концами.

Вопрос 2: Какой из углов также известен как половина оборота?

Ответ:

Прямой угол называется половиной оборота, так как сумма двух прямых углов составляет 360°, то есть полный угол поворота.

Вопрос 3: Перечислите размеры всех углов.

Ответ:

Острый угол: меньше 90°

Прямой угол: ровно 90°

Тупой угол: больше 90° и меньше 180°

Прямой угол: точно 180°

Угол рефлектора: больше 180° и меньше 360°

90 Вопросов 4:00029 90 Вопросы быть отрицательным?

Ответ:  

Да, углы могут быть положительными или отрицательными в зависимости от поворота угла. Если вращение против часовой стрелки, угол будет положительным, а если вращение по часовой стрелке, то он будет отрицательным.

Какие бывают типы углов

Какие бывают разные типы углов

Угол:
Два луча с общим концом образуют угол.
OA, OB — лучи, O — конечная точка.

Типы углов

В геометрии углы можно классифицировать по размеру (или величине) угла.

• Прямой угол: Угол, градусная мера которого равна 90°, называется прямым углом. Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.
• Острый угол: Угол, градусная мера которого меньше 90°, называется острым углом.
• Тупой угол: Угол, градусная мера которого больше 90° и меньше 180°, называется тупым углом.
• Прямой угол: Угол, градусная мера которого равна 180°, называется прямым углом.
• Угол рефлекса: Угол, величина которого больше 180°, но меньше 360°, называется углом рефлекса.
• Полный угол: Угол, градусная мера которого равна 360°, называется полным углом.
• Нулевой угол: Угол, градусная мера которого равна 0°, называется нулевым углом.

Мера угла:
Величина поворота от OA к OB называется мерой ∠AOB и записывается как m ∠AOB. Угол измеряется в градусах, обозначаемых знаком «°».

• Угол 360°:
  Если луч OA, начиная с исходного положения OA, вращается вокруг точки O против часовой стрелки и, совершив полный оборот, возвращается в исходное положение, говорят, что он повернулся на 360 градусов, записывается как 360°.
  
  Полный оборот делится на 360 равных частей. Каждая часть имеет размер 1°.
  1° = 60 минут, записывается как 60′.
  1′ = 60 секунд, записывается как 60”.
  Мы используем транспортир для измерения угла.
• Биссектриса угла:  
  Луч ОС называется биссектрисой ∠AOB, если m∠AOC = m∠BOC.
  
  В этом случае ∠AOC = ∠BOC = 1/2 ∠AOB.
• Дополнительные углы:
  Два угла называются дополнительными, если сумма их мер равна 90°, и говорят, что каждый угол дополняет друг друга.
  Например, (45°, 45°), (10°, 80°), (20°, 70°), (30°, 60°).
  Примечание:
  (a) Если два угла дополняют друг друга, то каждый угол является острым, но любые два острых угла могут не дополнять друг друга, например, 20° и 60° являются острыми углами, но не дополняют друг друга друг друга.
  (b) Два тупых угла и два прямых угла не могут дополнять друг друга.
• Дополнительные уголки:
  Два угла называются дополнительными, если сумма их мер равна 180°.
  Два дополнительных угла называются дополнением друг друга.
  Например, (10°, 170°), (20°, 160°), (30°, 150°), (40°, 140°), (50°, 130°) и т. д. — все пары дополнительных углы.
  Примечание:
  (a) Два острых угла не могут дополнять друг друга.
  (b) Два прямых угла всегда являются дополнительными.
  (c) Два тупых угла не могут дополнять друг друга.
• Смежные углы:
  Два угла называются смежными, если
  (i) имеют одну и ту же вершину,
  (ii) имеют общее плечо и
  (iii) их необщие стороны по обе стороны от общего рукава.
  
  На данном рисунке ∠AOC и ∠BOC — смежные углы с одной вершиной O, общим плечом OC и их не общими плечами OA и OB по обе стороны от OC.
• Линейная пара углов
  Говорят, что два смежных угла образуют линейную пару, если их необщие стороны являются двумя противоположными лучами.
  На рисунке ∠POQ и ∠QOR образуют линейную пару, так как их необщие плечи OP и OR представляют собой два противоположных луча, т. е. POR представляет собой прямую.
  
  Примечание:
  (a) Два линейных парных угла также могут быть смежными углами, но нет необходимости, чтобы два смежных угла были линейными парными углами.
  (b) Пара дополнительных углов образует линейную пару, когда они расположены рядом друг с другом.
• Вертикально противоположные углы
  Два угла, образованные двумя пересекающимися прямыми, не имеющими общего плеча, называются вертикально противоположными углами.
  На рисунке две линии PQ и RS пересекаются в точке О. Заметим, что при пересечении этих линий образовалось четыре угла.
  
  ∠POR и ∠SOQ образуют пару вертикально противоположных углов, а ∠POS и ∠ROQ образуют другую пару вертикально противоположных углов.
  Примечание:
  Вертикально противоположные углы всегда равны.
  Важные факты:
  (1) Сумма всех углов, образованных по одну сторону от прямой в данной точке прямой, равна 180°.
  (2) Сумма всех углов вокруг точки равна 360°.

Типы углов Пример Задачи с решениями

Пример 1:     Найдите угол, который на 20° больше своего дополнения.
Решение:     Пусть искомый угол равен x°.
Тогда мера его дополнения = (90 – x)°.
∴  x – (90 – x) = 20  ⇔  2x = 110  ⇔  x = 55
Следовательно, мера искомого угла равна 55°.

Пример 2:     Найдите градусную меру угла, который на 40° меньше своего дополнения.
Решение:     Пусть искомый угол равен x°.
Тогда мера его дополнения = (180 – x)°.
∴  (180 – x) – x = 40  ⇔  2x = 140  ⇔  x = 70
Следовательно, мера искомого угла равна 70°.

Пример 3:     Найдите градусную меру угла, если его дополнение, умноженное на шесть, на 12° меньше, чем удвоенное его дополнение.
Решение:     Пусть искомый угол равен x°.
Тогда мера его дополнения = (90 – x)°.
Мера его дополнения = (180 – x)°.
∴ 6(90 – х) = 2(180 – х) – 12
⇔  540 – 6х = 360 – 2х – 12
⇔ 4х = 192 ⇔ х = 48.
Следовательно, мера искомого угла равна 48°.

Пример 4:     Преобразование 180° в градусы, минуты и секунды.
Решение:     180° = 179° 59′ 60”.

Пример 5:     Найдите величину сложения угла 87°28’43”.
Решение:     Мы можем написать: 180° = 179°59’60”.
∴дополнение к углу (87°28’43»)
= угол [180° — (87°28’43»)]
= угол [179°59’60» — 87°28′ 43”]
= угол (92°31’17”).
Отсюда мера искомого угла
= (92°31’17”).

Пример 6:     Если ∠A = 36°27’46” и ∠B = 28°43’39”,
найти ∠A + ∠B.
Солутон:     ∠A + ∠B = 36°27’46» + 28°43’39»
= 64°70’85»
= 64°71’25»
= 65°11’25»

Пример 7:       Найдите дополнение каждого из следующих углов:
(i) 58°       (ii) 16°
(iii) 2/3 прямого угла       (iv) 46° 30′
Решение:     ( i) 90° – 58° = 32°
(ii) 90° – 16° = 74°
(iii) 90° – 2/3 (90°)
= 90° – 60° = 30°
(iv) 90° – 46° 30′
= 89° 60′ – 46° 30′
= 43° 30′

Пример 8:     Найдите меру угла, который является дополнительным к самому себе.
Решение:     Пусть угол равен xº, Тогда
Тогда мера его дополнения равна xº.
Поскольку сумма мер угла и его дополнения равна 90º
xº + xº = 90º
⇒ 2xº = 90º
⇒ xº = 45º

Пример 9:     Найдите угол, который образует пару дополнительные углы сами с собой.
Решение:     Пусть угол равен xº. Тогда
xº + xº = 180º
⇒ 2xº = 180º
⇒ xº = 90º

Пример 10:     Угол в пять раз больше своего дополнения. Определите его меру.
Решение:     Пусть мера заданного угла равна x градусов. Тогда его дополнение равно (90 – x)º.
Дано, что:
Угол = 5 × Его дополнение
⇒ x = 5(90 – x)
⇒ x = 450 – 5x
⇒ 6x = 450
⇒ x = 75
Таким образом, мера данных углов равна 75º.

Пример 11:     Угол равен одной трети своего дополнения. Найдите его меру.
Решение:     Пусть искомый угол равен x градусов.