НАНЕСЕНИЕ РАЗМЕРОВ НА ЧЕРТЕЖЕ. (Размеры; Методы нанесения размеров ; Правила нанесения размеров; ГОСТ 2.307-68.)
ГБПОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»
ПРОМЫШЛЕННОЕ ОТДЕЛЕНИЕ
Инженерная графика
Практическая работа №2
НАНЕСЕНИЕ РАЗМЕРОВ
Размеры;
Методы нанесения размеров ;
Правила нанесения размеров;
ГОСТ 2.307-68.
Воронеж 2018
СОДЕРЖАНИЕ
1. НАЗНАЧЕНИЕ РАЗМЕРОВ…………….….…………………….3
НАЗНАЧЕНИЕ РАЗМЕРОВ…………….….…………………….3
2. МЕТОДЫ НАНЕСЕНИЯ РАЗМЕРОВ…………………………..3
3. ПРАВИЛА НАНЕСЕНИЯ РАЗМЕРОВ…………………………5
4. ПОЛОЖЕНИЯ ГОСТА 2.307-68 ……………………………….8
5. ЗАДАНИЕ К ПРАКТИЧЕСКОЙ РАБОТЕ………………….…..11
6. КОНТРОЛЬНЫЕ ВОПРОСЫ……………………………………18
7. УПРАЖНЕНИЯ…………………………………………………..17
8. СПИСОК ЛИТЕРАТУРЫ…………………………………………16
ПРАКТИЧЕСКАЯ РАБОТА №2
Тема: Нанесение размеров на деталях простой
конфигурации по ГОСТ 2. 307-68.
307-68.
Цель: Приобретение навыков быстрого и правильного выполнения размерных линий и определения линейных размеров.
НАЗНАЧЕНИЕ РАЗМЕРОВ
Для определения величины изображенного изделия или какой-либо его части но чертежу на нем наносят размеры.
Размеры разделяют на линейные и угловые. Линейные размеры характеризуют длину, ширину, толщину, высоту, диаметр или радиус измеряемой части изделия. Угловые размеры характеризуют величину углов.
Линейные размеры на чертежах указывают в миллиметрах, но обозначение единицы измерения не выносят. Угловые размеры указывают в градусах, минутах и секундах.
Общее количество размеров на чертеже должно быть наименьшим, но достаточным для изготовления и контроля изделия.
МЕТОДЫ НАНЕСЕНИЯ РАЗМЕРОВ
Способы нанесения размеров на чертеже зависят от
последовательности обработки поверхностей детали. В практической работе
конструкторы применяют три метода нанесения размеров – цепной, координатный и
комбинированный.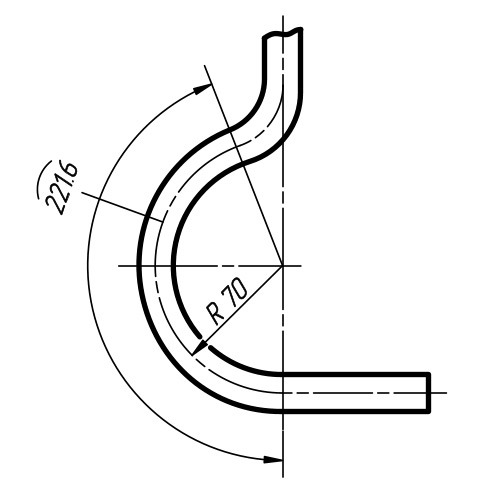
Цепной метод – размеры наносят по одной линии, цепочкой, один за другим (рис. 5) размеры А, А1, А2, А3, А4. За технологическую базу принята торцовая поверхность вала. Метод характеризуется постепенным накоплением суммарной погрешности при изготовлении элементов детали. Значительная суммарная погрешность может привести к непригодности изготовлен- ной детали (А*- размер для справки).
Координатный метод – все размеры Б1, Б2, Б3, Б4, Б5 наносят от одной и той же базовой поверхности (см. рис. 3). Этот метод отличается значительной точностью изготовления детали. При нанесении размеров этим методом необходимо учитывать повышение стоимости изготовления детали.
Рис.3
Комбинированный метод – простановка размеров осуществляется цепным и координатным методами
одновременно (рис. 4). Этот метод наиболее оптимален. Он позволяет
изготавливать более точно те элементы детали, которые этого требуют.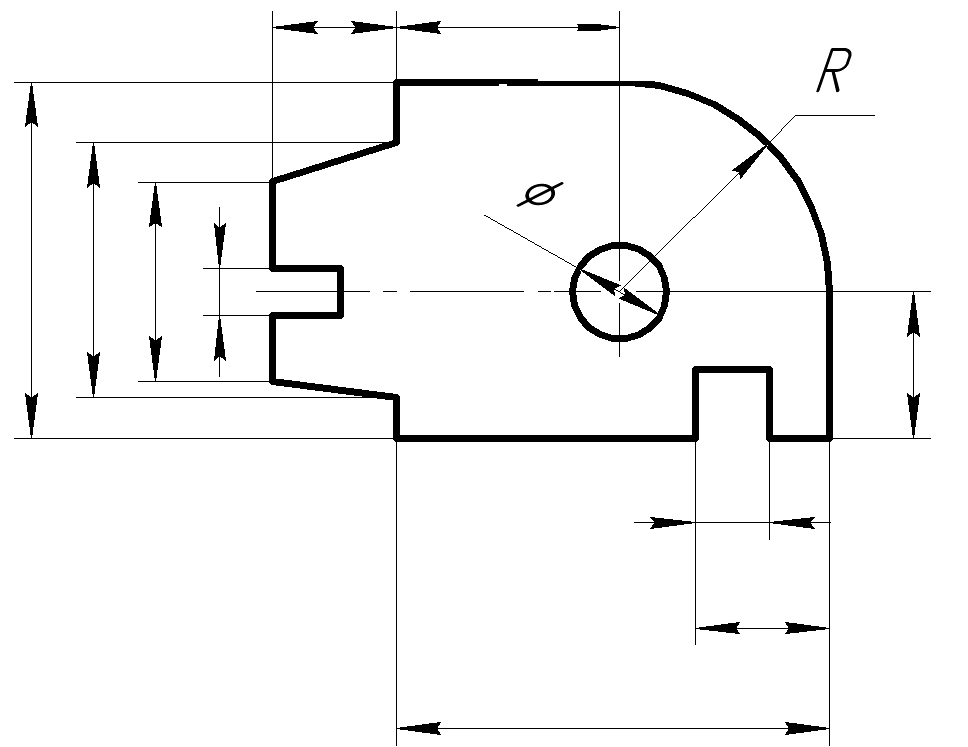
Рис.4
Размерные линии предпочтительно наносить вне контура изображения, располагая по возможности внутренние и наружные размеры деталей по разные стороны изображения.
При неполном изображении симметричного контура, а также при соединении вида и разреза размерные числа ставят со стороны вида для наружных и со стороны разреза для внутренних элементов изделия.
При этом размерную линию обрывают дальше линии разграничения вида и разреза (рис.5,а) или за осью симметрии (рис. 5,б).
Рис. 5
ПРАВИЛА НАНЕСЕНИЯ РАЗМЕРОВ
Размеры на чертежах указывают размерными числами и
размерными линиями. Для этого сначала проводят выносные линии перпендикулярно
отрезку, размер которого указывают (рис. 6, а). Затем на расстоянии не менее 10
мм от контура детали проводят параллельную ему размерную линию. Размерная линия
ограничивается с двух сторон стрелками.
Рис. 6. Нанесение линейных размеров
Если на чертеже несколько размерных линий, параллельных друг другу, то ближе к изображению наносят меньший размер. Так, на рисунке 6, в сначала нанесен размер 5, а затем 26, чтобы выносные и размерные линии на чертеже не пересекались. Расстояние между параллельными размерными линиями должно быть не менее 7 мм.
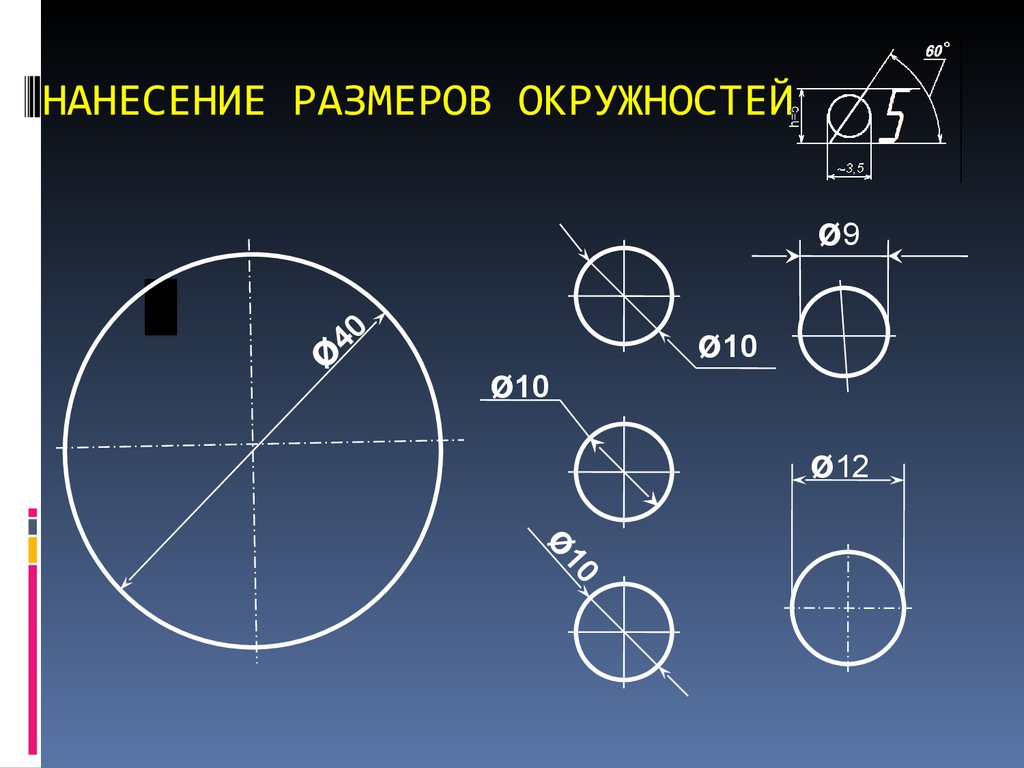
Для обозначения диаметра перед размерным числом наносят специальный знак — кружок, перечеркнутый линией (рис. 7). Если размерное число внутри окружности не помещается, его выносят за пределы окружности, как показано на рисунке 7, в и г. Аналогично поступают при нанесении размера прямолинейного отрезка (см. рис. 6, в).
Рис. 7. Нанесение размера окружностей
7. Нанесение размера окружностей
Для обозначения радиуса перед размерным числом пишут прописную латинскую букву R (рис. 8, а). Размерную линию для указания радиуса проводят, как правило, из центра дуги и оканчивают стрелкой с одной стороны, упирающейся в точку дуги окружности.
Рис. 8. Нанесение размеров дуг и угла
При указании размера угла размерную линию проводят в виде дуги окружности с центром в вершине угла (рис. 8, б).
Перед размерным числом, указывающим сторону квадратного элемента, наносят знак «квадрата» (рис. 9). При этом высота знака равна высоте цифр.
Рис. 9. Нанесение размера квадрата
Если размерная линия расположена вертикально или наклонно, то размерные числа располагают, как показано на рисунках 6, в; 7; 8.
Если деталь имеет несколько одинаковых элементов, то
на чертеже рекомендуется наносить размер лишь одного из них с указанием
количества.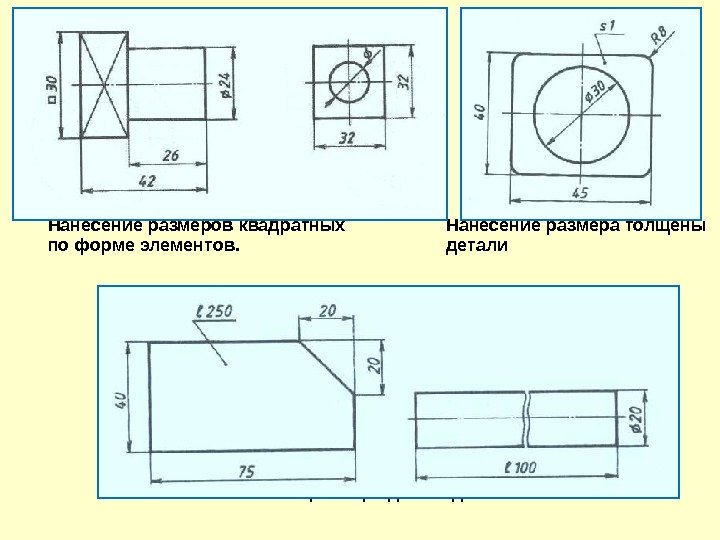 Например, запись на чертеже «3 отв. 0 10» означает, что в детали
имеются три одинаковых отверстия диаметром 10 мм.
Например, запись на чертеже «3 отв. 0 10» означает, что в детали
имеются три одинаковых отверстия диаметром 10 мм.
При изображении плоских деталей в одной проекции толщина детали указывается, как показано на рисунке 6, в. Обратите внимание, что перед размерным числом, указывающим толщину детали, стоит латинская строчная буква 5.
Допускается подобным образом указывать и длину детали (рис. 10), но перед размерным числом в этом случае пишут латинскую букву
Рис. 10. Нанесение размера длины детали
ПОЛОЖЕНИЯ ГОСТА 2.307-68
При нанесении размера радиуса перед размерным числом
помещают прописную букву R.
Если при нанесении размера радиуса дуги окружности необходимо указать размер,
определяющий положение ее центра, то последний изображают в виде пересечения
центровых или выносных линий.
При большой величине радиуса центр допускается приближать к дуге, в этом случае размерную линию радиуса показывают с изломом под углом 90° (рис.11).
Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра (рис. 12).
Рис.11,12.
При проведении нескольких радиусов из одного центра размерные линии любых двух радиусов не располагают на одной прямой (рис. 13а). При совпадении центров нескольких радиусов их размерные линии допускается не доводить до центра, кроме крайних (рис. 13б).
Рисунок 13. Нанесение нескольких радиусов из одного центра.
Задание №1
Выполнить чертеж плоской детали в указанном масштабе,
определяя размеры по клеткам.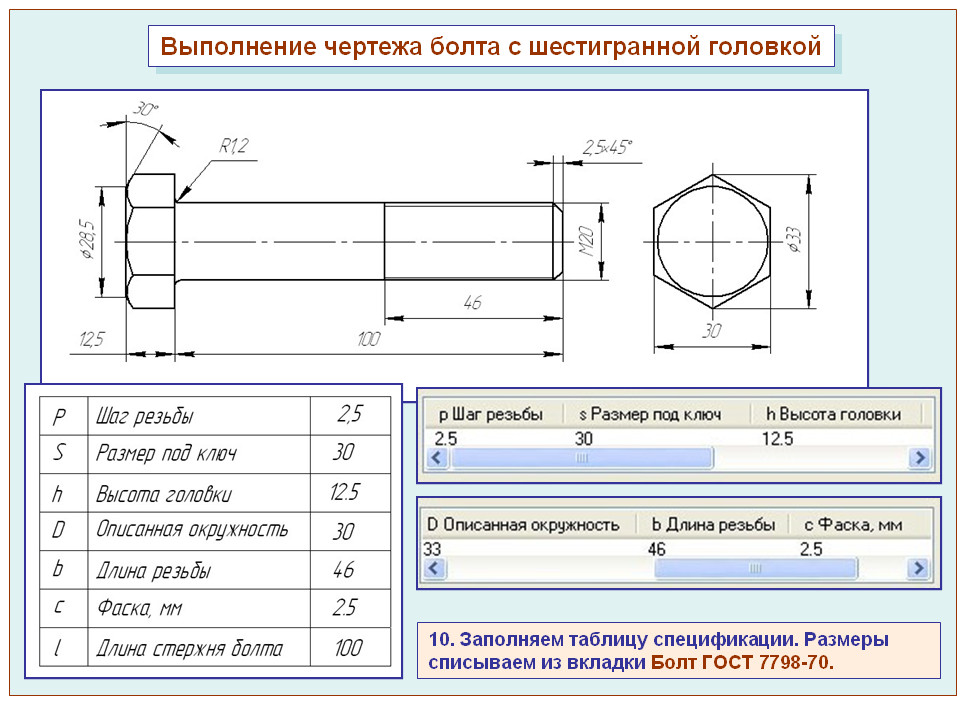 Сторона клетки равна 5 мм. Проставить размеры.
Работа выполняется на листе формата А4
Сторона клетки равна 5 мм. Проставить размеры.
Работа выполняется на листе формата А4
Вариант задания получить у преподавателя.
Пример выполнения
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Приведите пример условных обозначений
применяемых на чертеже.
Приведите пример условных обозначений
применяемых на чертеже.
2. Назовите и охарактеризуйте методы нанесения размеров.
3. В каких случаях на чертежах при нанесении размеров ставят знак Ø и знак. R?
4. Что называют масштабом чертежа?
5. Как наносится размерное число на заштрихованном поле?
6. Как проставляют размеры углов?
7. В каких единицах выражают линейные размеры на машиностроительных чертежах?
8. Какой толщины должны быть выносные и размерные линии?
9. Какое расстояние оставляют между контуром изображения и размерными линиями? между размерными линиями?
10. Как наносят размерные числа на наклонных размерных линиях?
11. Какие знаки и буквы наносят перед размерным числом при указании величины диаметров и радиусов?
Упражнение №1
Перечертите в рабочую тетрадь,
сохраняя пропорции, изображение детали, данное на рисунке 14, увеличив его в 2
раза. Нанесите необходимые размеры, укажите толщину детали (она равна 4 мм).
Нанесите необходимые размеры, укажите толщину детали (она равна 4 мм).
Рис. 14
Упражнение №2
Начертите в рабочей тетради окружности, диаметры которых равны 40, 30, 20 и 10 мм. Нанесите их размеры. Начертите дуги окружности с радиусами 40, 30, 20 и 10 мм и нанесите размеры.
СПИСОК ЛИТЕРАТУРЫ
1. Аристов, В.М. Инженерная графика: Уч. пос. для вузов / В.М. Аристов, Е.П. Аристова. — М.: Альянс, 2016. — 256 c.
2. Белякова, Е.И. Инженерная графика. Практикум по чертежам сборочных единиц: Учебное пособие / П.В. Зеленый, Е.И. Белякова, О.Н. Кучура . — М.: НИЦ ИНФРА-М, Нов. знание, 2013. — 128 c.
3. Боголюбов,
С.К. Инженерная графика: учебник для средних специальных учебных заведений. /
С.К. Боголюбов. — М.: Альянс, 2016. — 390 c.
/
С.К. Боголюбов. — М.: Альянс, 2016. — 390 c.
4. Большаков, В.П. Инженерная и компьютерная графика: Учебное пособие / В.П. Большаков. — СПб.: BHV, 2014. — 288 c.
5. Емельянов, С.Г. Начертательная геометрия. Инженерная и компьютерная графика в задачах и примерах: Учебное пособие / П.Н. Учаев, С.Г. Емельянов, К.П. Учаева; Под общ. ред. проф. П.Н. Учаева. — Ст. Оскол: ТНТ, 2013. — 288 c.
6. Кочиш, И., И. Начертательная геометрия. Инженерная графика. Уч. пособие, 3-е изд., стер. / И. И. Кочиш, Н. С. Калюжный, Л. А. Волчкова и др.. — СПб.: Лань, 2016. — 308 c.
7. Крундышев, Б.Л. Инженерная графика: Учебник. 6-е изд., стер. / Б.Л. Крундышев. — СПб.: Лань, 2016. — 392 c.
8. Куликов, В.П. Инженерная графика: Учебник / В.П. Куликов, А.В. Кузин.. — М.: Форум, НИЦ ИНФРА-М, 2013. — 368 c.
9. Пуйческу,
Ф.И. Инженерная графика: Учебник для студентов учреждений среднего
профессионального образования / Ф.И. Пуйческу, С.Н. Муравьев, Н.А. Чванова.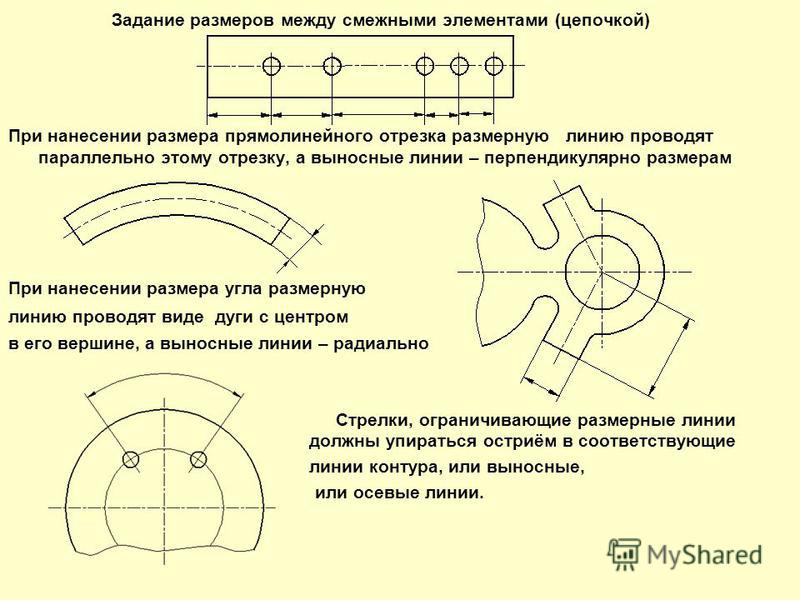 —
М.: ИЦ Академия, 2013. — 320 c.
—
М.: ИЦ Академия, 2013. — 320 c.
10. Сорокин, Н.П. Инженерная графика: Учебник. 6-е изд., стер / Н.П. Сорокин, Е.Д. Ольшевский, А.Н. Заикина, Е.И. Шибанова. — СПб.: Лань, 2016. — 392 c.
11. Учаев, П.Н. Инженерная графика в учебных дисциплинах: Учебное пособие / П.Н. Учаев, С.Г. Емельянов. — Ст. Оскол: ТНТ, 2013. — 352 c.
12. Чекмарев, А.А. Инженерная графика 12-е изд., испр. и доп. учебник для прикладного бакалавриата / А.А. Чекмарев. — Люберцы: Юрайт, 2016. — 381 c.
13. Чекмарев, А.А. Инженерная графика. Машиностроительное черчение: Учебник / А.А. Чекмарев. — М.: НИЦ ИНФРА-М, 2013. — 396 c.
Построение третьего вида по двум данным. Часть 4.
Рассмотрим пример к графической работе №5. Дается задание: «Постройте третий вид детали по двум данным. На чертеже проставьте размеры. УГОЛЬНИК. СТАЛЬ».
Следующий этап – это нанесение размеров на чертеже детали.
КОМПАС-3D позволяет создать в графическом
документе любой из предусмотренных стандартом вариантов размеров.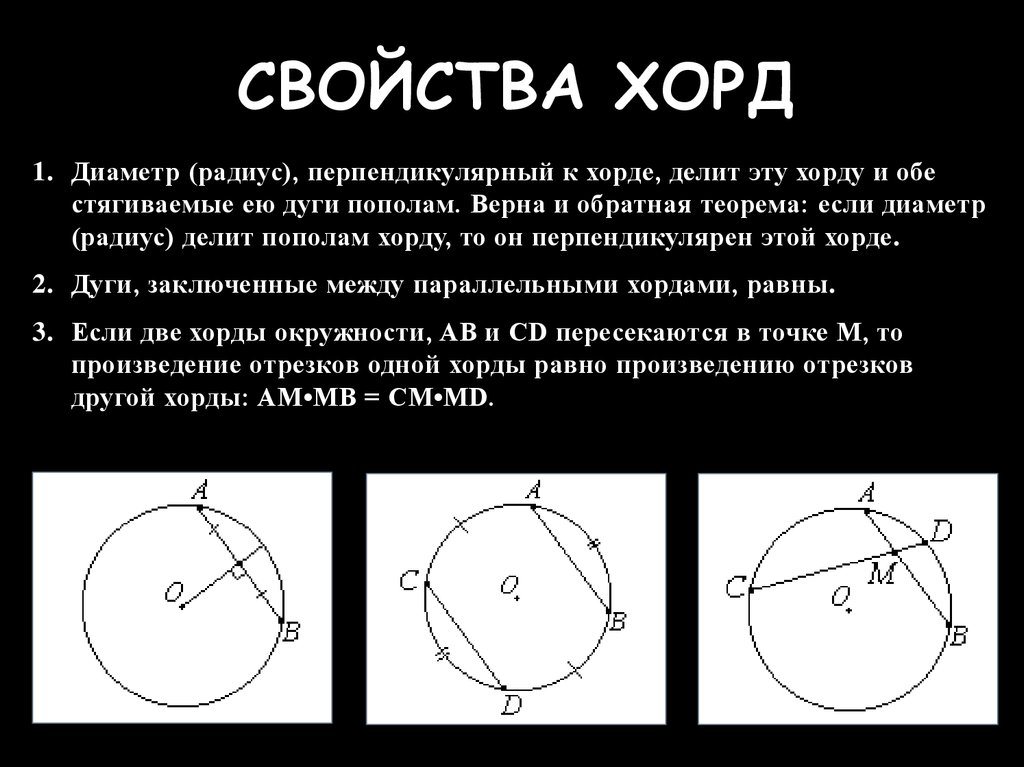 Возможна
простановка нескольких типов линейных, угловых, радиальных размеров,
диаметрального размера, размеров высоты и дуги. Кроме того, доступен
специальный способ простановки размеров, при котором тип размера автоматически
определяется системой.
Возможна
простановка нескольких типов линейных, угловых, радиальных размеров,
диаметрального размера, размеров высоты и дуги. Кроме того, доступен
специальный способ простановки размеров, при котором тип размера автоматически
определяется системой.
Команды простановки размеров сгруппированы в меню Инструменты — Размеры, а кнопки для вызова команд — на панели Размеры.
Общая последовательность действий при простановке большинства размеров следующая:
1. Вызов команды простановки размера нужного типа или команды автоматической простановки размеров.
2. Указание объектов (объекта), к которым требуется проставить размер.
3. Настройка начертания размера с помощью вкладок Панели свойств.
4. Редактирование (при необходимости) размерной надписи и задание ее положения.
Для определения величины изображенного
изделия или какой-либо его части по чертежу на нем наносят размеры. Размеры
разделяют на линейные и угловые. Линейные размеры характеризуют длину, ширину,
толщину, высоту, диаметр или радиус измеряемой части изделия.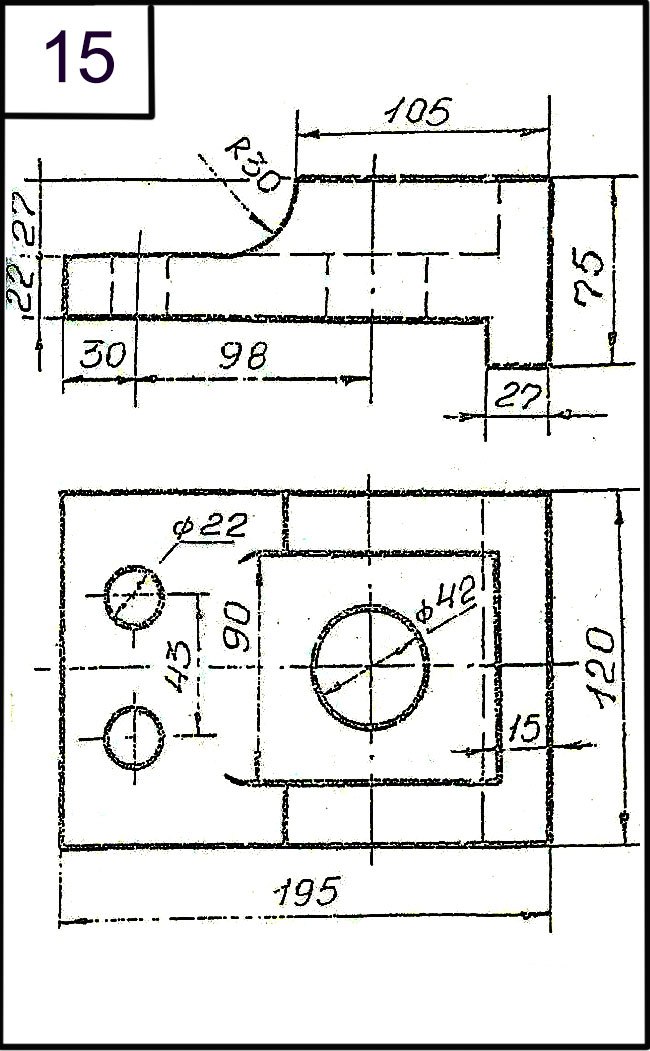 Угловой размер
характеризует величину угла.
Угловой размер
характеризует величину угла.
Линейные размеры на чертежах указывают в миллиметрах, но обозначение единицы измерения не наносят. Угловые размеры указывают в градусах, минутах и секундах с обозначением единицы измерения.
Общее количество размеров на чертеже должно быть наименьшим, но достаточным для изготовления и контроля изделия.
Правила нанесения размеров установлены стандартом. ГОСТ 2.307-68. ЕСКД.
1. Размеры на чертежах указывают размерными числами и размерными линиями. Для этого сначала проводят выносные линии перпендикулярно отрезку, размер которого указывают. Затем на расстоянии не менее 10 мм от контура детали проводят параллельную ему размерную линию. Размерная линия ограничивается с двух сторон стрелками. Выносные линии выходят за концы стрелок размерной линии на 1…5 мм. Выносные и размерные линии проводят сплошной тонкой линией. Над размерной линией, ближе к ее середине, наносят размерное число.
2. Если на чертеже несколько
размерных линий, параллельных друг другу, то ближе к изображению наносят
меньший размер.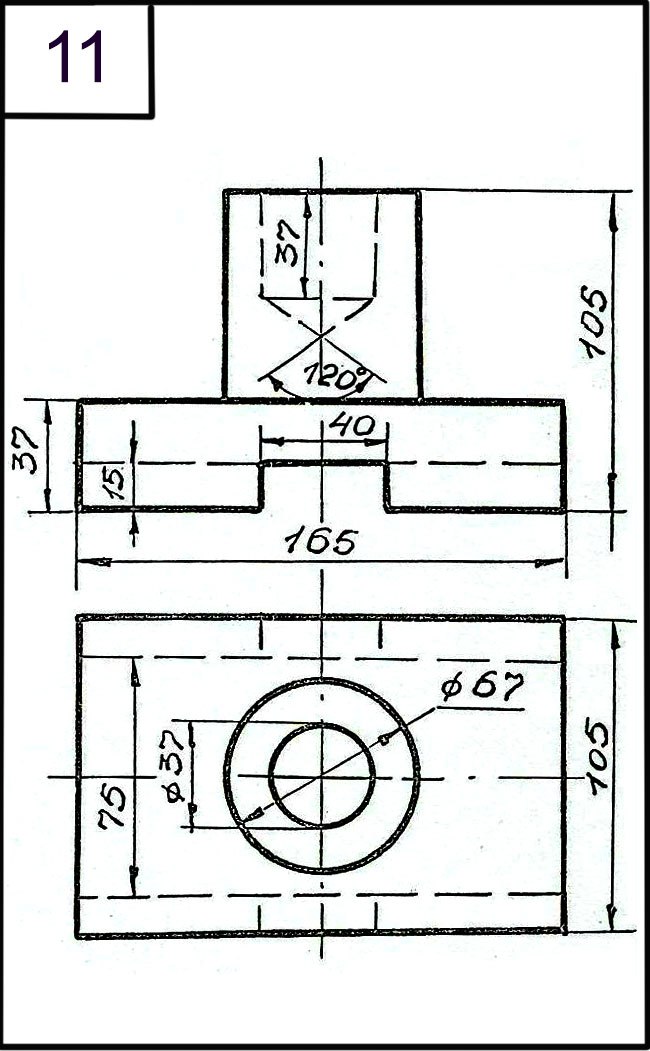 Расстояние между параллельными размерными линиями должно быть
не менее 7 мм.
(см. п. 1).
Расстояние между параллельными размерными линиями должно быть
не менее 7 мм.
(см. п. 1).
3. Для обозначения диаметра перед размерным числом наносят специальный знак — кружок, перечеркнутый линией. Если размерное число внутри окружности не помещается, его выносят за пределы окружности. Аналогично поступают при нанесении размера прямолинейного отрезка.
4. Для обозначения радиуса перед размерным числом пишут прописную латинскую букву R. Размерную линию для указания радиуса проводят, как правило, из центра дуги и оканчивают стрелкой с одной стороны, упирающейся в точку дуги окружности.
5. При указании размера угла размерную линию проводят в виде дуги окружности с центром в вершине угла.
6. Перед размерным числом, указывающим сторону квадратного элемента, наносят знак ò. При этом высота знака равна высоте цифр.
7. Если размерная линия
расположена вертикально или наклонно, то размерные числа располагают над
размерной линией или с левой стороны размерной линии.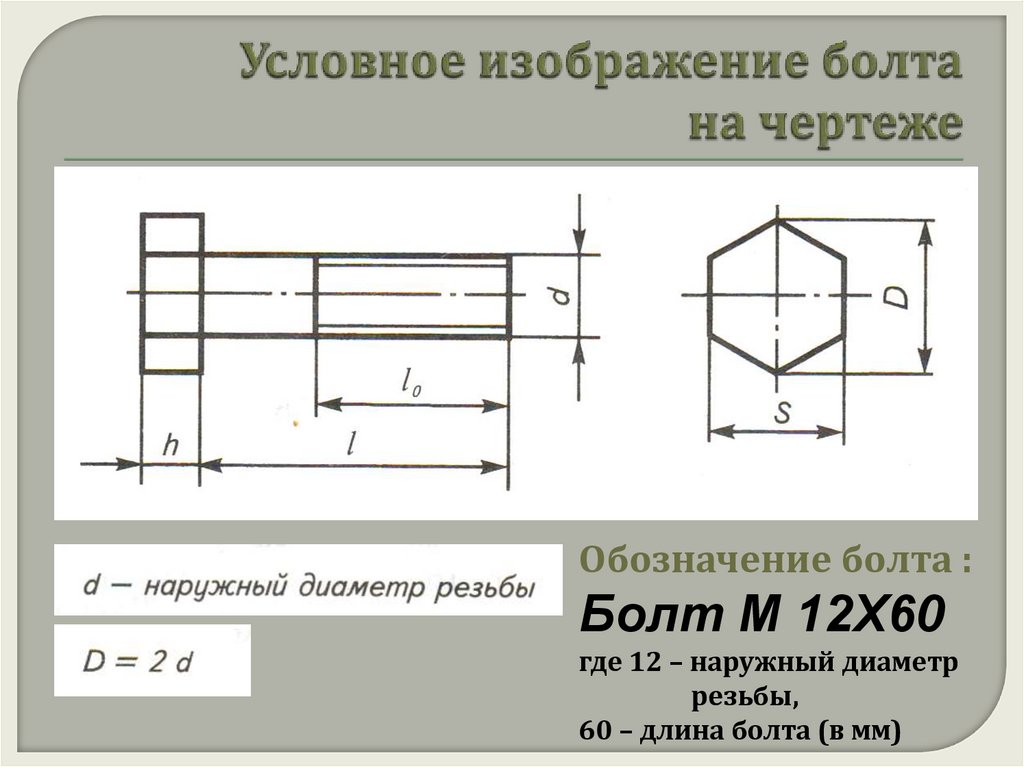 (см. п: 1, 2, 3, 4, 5,
6).
(см. п: 1, 2, 3, 4, 5,
6).
8. Если деталь имеет несколько одинаковых элементов, то на чертеже рекомендуется наносить размер, лишь одного из них с указанием количества. Например, запись на чертеже «6 отв. Ø10» означает, что в детали имеются шесть одинаковых отверстия диаметром 10 мм.
9. При изображении плоских деталей в одной проекции толщина детали указывается латинской буквой s и рядом пишется размерное число, указывающим толщину детали. (см. п. 8).
10. Допускается подобным образом указывать и длину детали, но перед размерным числом в этом случае пишут латинскую букву l.
Каждый размер на чертеже указывают только один раз. В то же время чертеж должен содержать все размеры, необходимые для изготовления предметов.
На чертежах обязательно наносят
габаритные размеры. Габаритными называют размеры, определяющие предельные
(наибольшие и наименьшие) величины вершин (и внутренних) очертаний изделий. Без
габаритных размеров чертеж не закончен.
При нанесении размеров меньшие размеры располагают ближе к изображению, а большие – дальше.
Размеры надо наносить так, чтобы удобно было читать чертеж и при изготовлении детали не выяснять что-либо путем подсчетов.
Размеры наносят, как правило, вне контура изображения и так, чтобы размерные линии по возможности не пересекались между собой.
Осевая (штрихпунктирная) линия должна выходить за контур изображения примерно на 3 мм и не пересекать размерное число.
По возможности, при нанесении размеров, равномерно распределить их на видах чертежа.
Чертежно-конструкторская система КОМПАС-График поддерживает все предусмотренные ЕСКД типы размеров и позволяет значительно сократить время на простановку размеров за счет автоматического измерения их значений.
Принципы ввода простановки размеров в КОМПАС-График
едины для всех типов. Если при построении размера его значение не соответствует
заданному, то вы ошиблись при построении. Текст размерной надписи может быть отредактирован
с помощью диалогового окна Задание размерной надписи.
Текст размерной надписи может быть отредактирован
с помощью диалогового окна Задание размерной надписи.
Размеры выражают основные геометрические характеристики объектов и наносятся в соответствии с общими правилами нанесения размеров по ГОСТу 3.307-68 Нанесение размеров и предельных отклонений.
Имеются три режима нанесения размеров: автоматический, полуавтоматический и ручной.
В автоматическом режиме процесс простановки достаточно прост. После вызова команды конструктор указывает нужный элемент объекта, и система автоматически вписывает в размерную надпись номинальное значение. Это применяется в том случае, когда не нужно вписывать значение квалитета и предельных отклонений, или они все одинаковые.
В основном применяется
полуавтоматический режим простановки размеров. В этом случае система
автоматически вписывает номинальное значение размера, а конструктор настраивает
параметры размера с помощью вкладок Панели
свойств и устанавливает размерное число в нужную точку.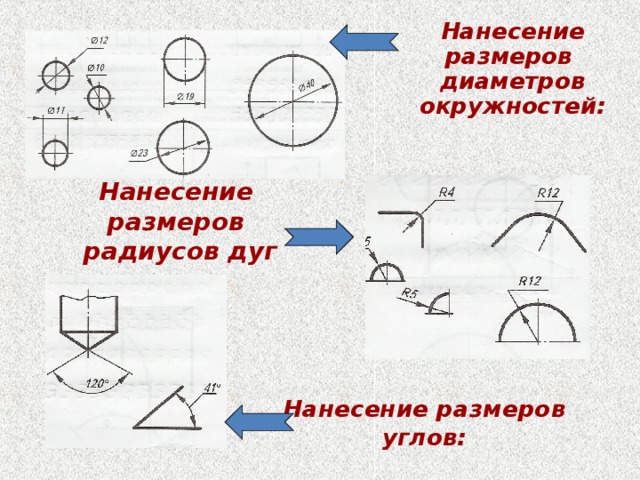
При ручном вводе отключается автоматическое создание объектов, и конструктор самостоятельно вводит номинальное значение с допусками.
Команды простановки размеров сгруппированы в Строке меню в пункте Инструменты — Размеры, а кнопки для вызова команд — на инструментальной панели инструментов Размеры.
Линейные размеры
В большинстве случаев измерения производится параллельно осям X, Y. То есть объекты на чертеже измеряются вдоль этих осей. И, хотя сами объекты могут быть наклонными, размеры все равно определяются по вертикали (ось X) или горизонтали (ось Y). В КОМПАС-График такие размеры называются линейными.
Для простановки линейных размеров на инструментальной панели инструментов имеется выпадающая панель расширенных команд с кнопкой Линейный размер.
Линейные размеры делятся на
горизонтальные, вертикальные, параллельные и повернутые, в зависимости от их
ориентации. Точки т1 и т2—точки привязки (точки выхода основных линий). Система
автоматически располагает выносные линии параллельно друг другу, а размерную
линию перпендикулярно им. Если длина размерной линии меньше суммарной длины
двух стрелок, стрелки автоматически будут сформированы снаружи выносных линий.
На расстоянии от 6 — 10 мм
от контура детали проводят параллельную ему размерную линию.
Точки т1 и т2—точки привязки (точки выхода основных линий). Система
автоматически располагает выносные линии параллельно друг другу, а размерную
линию перпендикулярно им. Если длина размерной линии меньше суммарной длины
двух стрелок, стрелки автоматически будут сформированы снаружи выносных линий.
На расстоянии от 6 — 10 мм
от контура детали проводят параллельную ему размерную линию.
На Панели свойств по умолчанию на вкладке Размер в группе переключателей Тип всегда активна кнопка Параллельно объекту.
Параллельные размеры измеряются и вычерчиваются вдоль стороны выбранного объекта или вдоль расстояния между указанными точками. При этом размерная линия всегда параллельна стороне объекта. Чтобы построить вертикальный или горизонтальный размер, необходимо активизировать соответствующий переключатель в разделе Тип;
Проставляем остальные размеры. Общее
количество размеров на чертеже должно быть наименьшим, но достаточным для
изготовления и контроля изделия.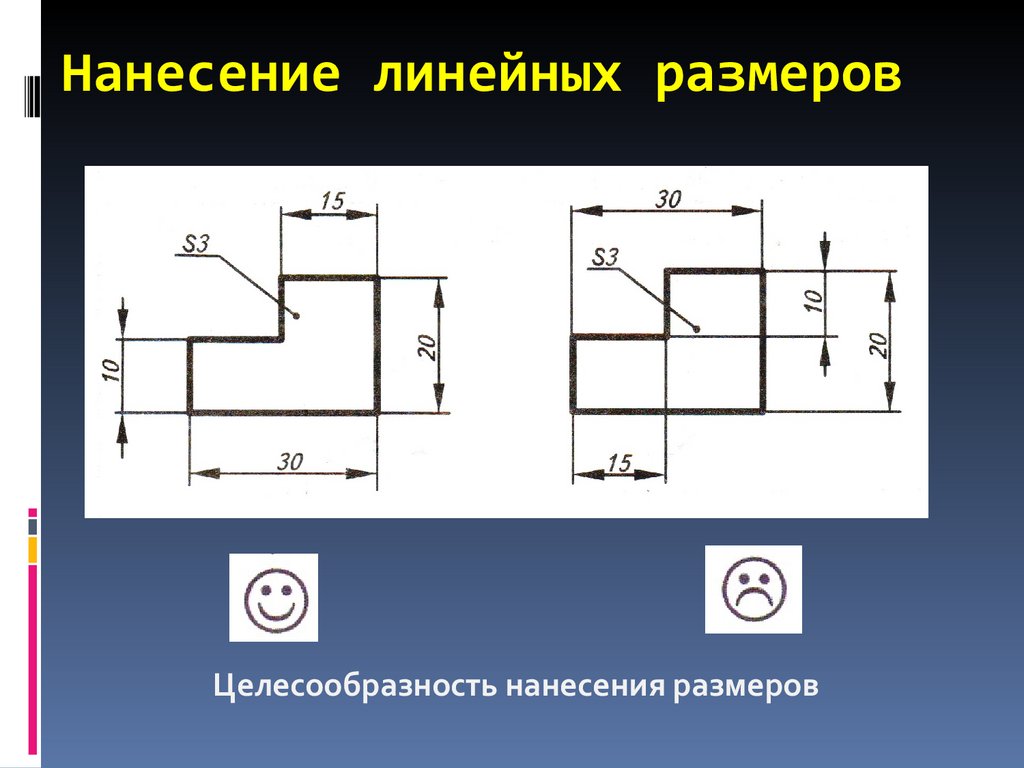 Равномерно распределяем размеры на все виды.
Осталось проставить размер окружности.
Равномерно распределяем размеры на все виды.
Осталось проставить размер окружности.
На всех разрабатываемых чертежах есть окружности и дуги, значит, необходимо поставить значение диаметра или радиуса. В КОМПАС-График проставить диаметральные размеры достаточно просто. Для ввода диаметрального размера необходимо указать ловушкой объект. Размерная линия строится через центр окружности или дуги и точку положения размерной линии. Последовательность выбора параметров размера такая же, как при простановке линейных размеров. Знак диаметра проставляется автоматически. Способ нанесения размера при различных положениях размерных линий определяется наибольшим удобством чтения.
На панели инструментов Геометрия щелкните левой кнопки мыши по
кнопке Диаметральный размер. По умолчанию на Панели свойств открыта вкладка Размер, на которой в группе
переключателей Тип имеется две кнопки: Полная размерная линия, Размерная
линия с обрывом. Выберите кнопку Полная размерная линия.
Выберите кнопку Полная размерная линия.
Подведите курсор мышки окружности (она становится красной) и щелкните левой кнопки мыши. Появился фантом диаметрального размера, который плавно перемещается при движении мыши. Обратите внимание на положение размерного числа: то в центре размерной линии, то сдвигается вправо или влево. В данный момент система, как в случае линейного размера, ожидает указания точки положения размерной надписи. Нельзя фиксировать текст внутри окружности, тогда он належится на осевые линии окружности, что противоречит требованиям ГОСТ ЕСКД.
Если необходимо, щелкните в окне Текст или просто нажмите любую клавишу и отредактируйте размерную надпись в диалоговом окне Задание размерной надписи;
На вкладке Параметры (элементы ее управления точно такие же, как при установке начертания линейного
размера) установите местоположение текста: На полке, вправо. В большинстве
случаев диаметральные и радиусные размеры ставятся на полках и выносятся за
пределы контура детали, чтобы не перекрывать основной контур детали.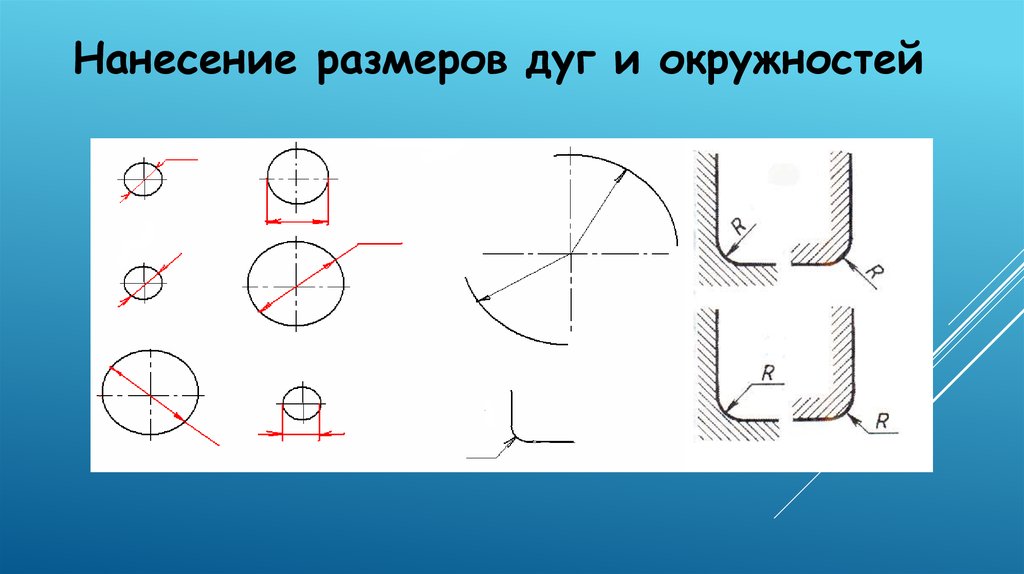 Местоположение
размера определяется наличием свободного места.
Местоположение
размера определяется наличием свободного места.
Щелкните левой стороной мыши в точке, где будет положения размерной линии и надписи. Размер построен. Обратите внимание, что знак диаметра система установила автоматически.
Заполняем основную надпись чертежа. Название детали Угольник, изготовлен из Стали, масштаб изображения 1:1, № работы 5. Чертеж построен.
Урок черчения по теме «Нанесение размеров. Масштабы». 8-й класс
Цель урока: Познакомить с правилами нанесения размеров на чертеже ГОСТ 2.307-68, с выполнением размерных стрелок, выносных линий, размерных чисел и знаков, с масштабами увеличения и уменьшения ГОСТ 2.302-68
Оборудование: чертежные инструменты, учебник, мультимедиа.
Ход урока
I. Организационный момент
Приветствие, проверка готовности к уроку.
II.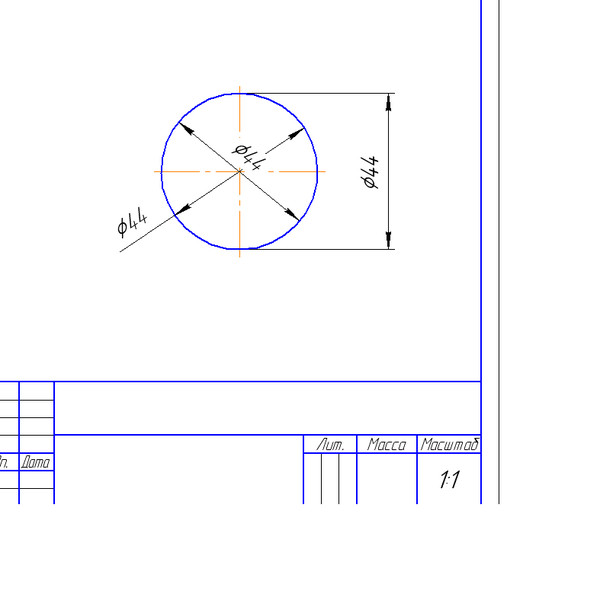 Повторение изученного материала.
Повторение изученного материала.
Можно вызвать учащегося к доске и попросить начертить линии чертежа, назвать их назначение и размеры.
III. Знакомство с новым материалом
1. Вводная беседа.
(Учитель показывает чертеж детали без размеров)
— Можем ли мы определить величину изображенного изделия по данному чертежу?
Для определения величины изображенного изделия и его элементов служат размерные числа, нанесенные на чертеже.
Исключение составляют случаи, когда величину изделия или его элементов определяют по изображениям, выполненным с достаточной степенью точности.
2. Объяснение нового материала.
Слайд 1 Записываем в тетрадке шрифтом 5 тему урока: “ Нанесение размеров”
Правила нанесения размеров установлено стандартом ГОСТ 2.307 – 68.
Слайд 2 Размеры изделия разделяются на линейные и угловые.
— Как вы думаете, что характеризуют линейные размеры детали? (ответы учеников)
Линейные размеры характеризуют длину, ширину,
высоту, толщину, диаметр или радиус детали.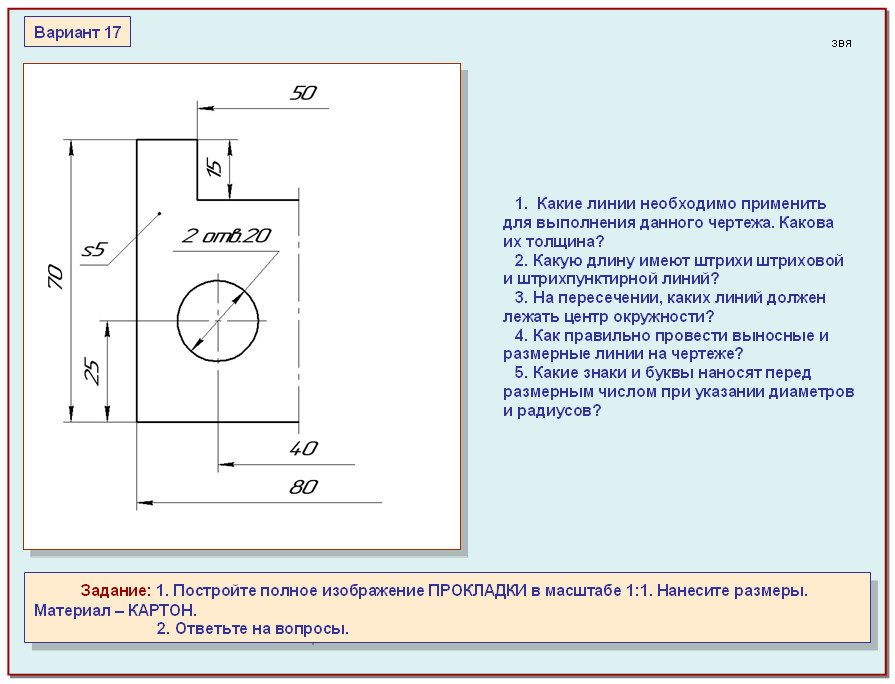 Линейные размеры на чертежах указывают в
миллиметрах, без обозначения единицы измерения.
Линейные размеры на чертежах указывают в
миллиметрах, без обозначения единицы измерения.
— А что характеризуют угловые размеры? (ответы учеников)
Угловые размеры характеризуют величину угла и указывают в градусах, минутах и секундах с обозначением единицы измерения.
Общее количество размеров должно быть минимальное, но достаточное для изготовления и контроля изделия.
Слайд 3 Размеры на чертежах указывают размерными числами и размерными линиями.
При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии — перпендикулярно размерным. Размерную линию с обоих концов ограничивают стрелками, упирающимися в выносные линии.
Размерные линии предпочтительно наносить вне контура изображения.
Выносные линии должны выходить за концы стрелок размерной линии на 1 . . 5 мм.
Минимальное расстояние между размерной линией
и линией контура — 10 мм.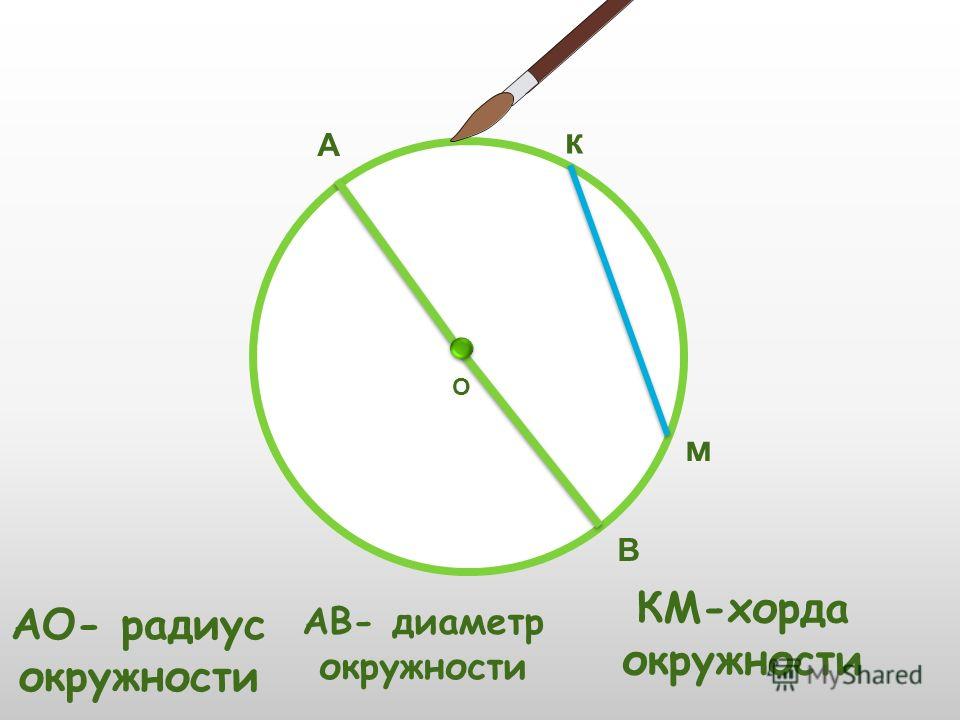
Необходимо избегать пересечения размерных и выносных линий.
Не допускается использовать линии контура, осевые, центровые и выносные линии в качестве размерных.
Величины элементов стрелок размерных линий выбирают в зависимости от толщины линий видимого контура и вычерчивают их приблизительно одинаковыми на всем чертеже.
Размерные числа наносят над размерной линией возможно ближе к ее середине. Предложить детям перечертить изображение в тетрадь, измерить размерную линию и записать размерное число в мм.
Слайд 4 Минимальные расстояния между параллельными размерными линиями должны быть 7 мм.
При нанесении нескольких параллельных размерных линий размерные числа над ними рекомендуется располагать в шахматном порядке.
Слайд 5 При нанесении размера диаметра перед
размерным числом помещают специальный знак –
кружок, перечеркнутый линией под углом 60 град.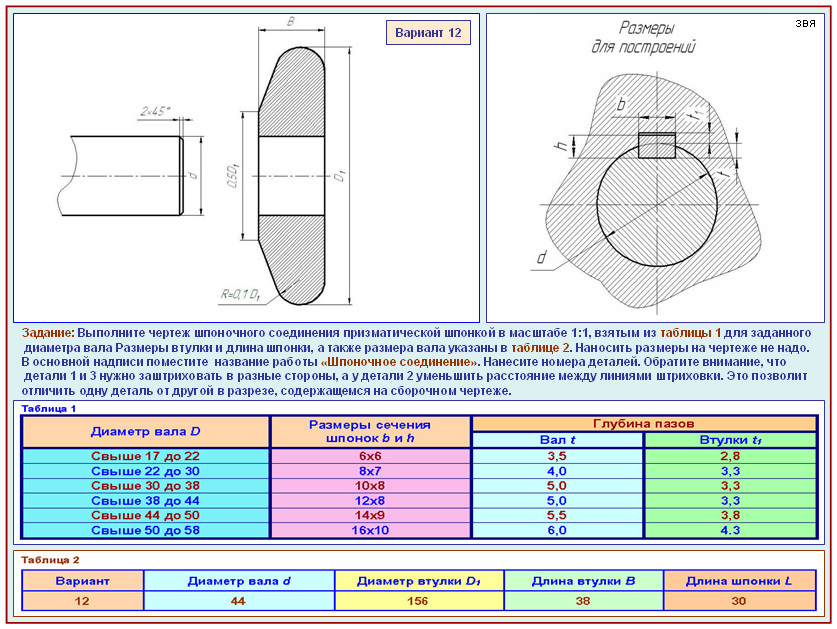
Если для написания размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на чертеже на продолжении размерных линий или на полке выноске. Если недостаточно места для нанесения стрелок, то их наносят с наружной стороны окружности.
Слайд 6 При нанесении размера радиуса перед размерным числом помещают прописную букву R . Размерную линию для обозначения радиуса проводят из центра дуги и оканчивают стрелкой с одной стороны. Такое обозначение используют когда на чертеже дона только часть окружности, а не целая окружность.
Запишите обозначение: радиус 15. (R15)
Слайд 7 Размерные числа линейных размеров при различных наклонах размерных линий располагают над размерной линией.
Слайд 8 Угловые размеры наносят так: В зоне,
расположенной выше горизонтальной осевой линии,
размерные числа помещают над размерными линиями
со стороны их выпуклости; в зоне, расположенной
ниже горизонтальной осевой линии — со стороны
вогнутости размерных линий.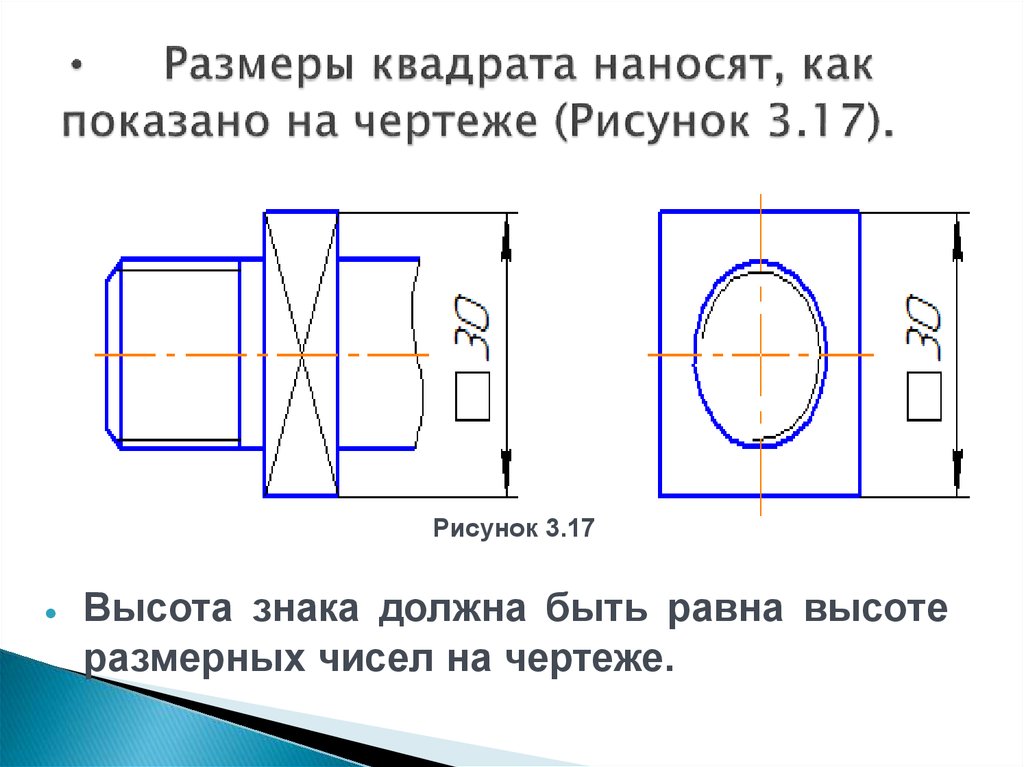 В заштрихованной
зоне наносить размерные числа не рекомендуется.
В этом случае размерные числа указывают на
горизонтально нанесенных полках.
В заштрихованной
зоне наносить размерные числа не рекомендуется.
В этом случае размерные числа указывают на
горизонтально нанесенных полках.
Слайд 9 Если в детали присутствует квадратный элемент, то перед размерным числом, указывающим размер этого элемента наносят знак ?, причем высота этого знака равна высоте цифры. Запишите обозначение стороны квадрата 45. (?45)
Слайд 10 Допускается подобным образом указывать длину детали, но перед размерным числом пишут латинскую букву ?. Запишите обозначение длина 80. (?80)
Слайд 11 Выполнить упражнение в тетрадке с последующей проверкой.
Слайд 12. Записать в тетрадях заголовок “Масштабы” и предложить вспомнить определение изученное на уроках географии.
Слайд 13. Стандарт устанавливает следующие
масштабы: уменьшения, натуральная величина и
масштаб увеличения.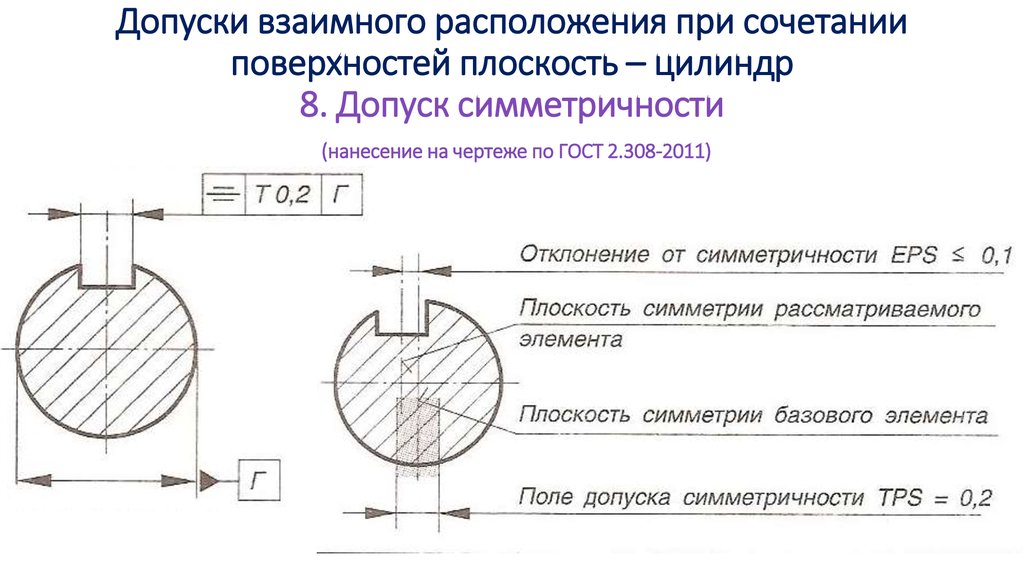
Слайд 14. Следует помнить, что, в каком бы масштабе ни выполнялось изображение, размеры на чертеже наносят действительные.
Масштаб указывают прописной буквой М, если масштаб указывают в основной надписи, то букву М не пишут.
IV. Подведение итога урока.
Запишите в тетрадях, упражнение стр.28 п.1
Слайд 15. По центру тетрадного листа выполняем чертеж плоской детали в М 2:1, работу выполняем карандашом средней твердости, заточенным под конус.
- По центру листа провести, горизонтально, тонкую штрихпунктирную линию.
- Начертить в М 2:1 прямоугольник, предварительно измерив его на рис. 34
- С правой стороны делаем вырез половины окружности, в масштабе, предварительно измерив, радиус дуги на рисунке.
- С левой стороны вырезаем прямоугольник, в
масштабе, предварительно измерив, прямоугольник
на рисунке 34.

- Размеры наносим в обратном порядке, как строили геометрические фигуры.
- (дуга, прямоугольник, прямоугольник, толщина детали.)
- При нанесении размеров не забывайте правила, и проверяйте правильность выполнения с доской.
- Обвести видимые контуры детали мягким карандашом заточенным лопаткой.
Домашнее задание.
Параграф 2, стр.28 п.2 (письменно)
На следующем уроке графическая работа, подготовьте формат А4.
Нанесение размеров — Всё для чайников
- Подробности
- Категория: Инженерная графика
Содержание материала
- Нанесение размеров
- НАНЕСЕНИЕ РАЗМЕРОВ НА ЧЕРТЕЖАХ ДЕТАЛЕЙ
- Все страницы
Страница 1 из 2
Автор видеоурока: к.пед.н., доцент кафедры ИГиСАПР Кайгородцева Н.В.
ПРАВИЛА НАНЕСЕНИЯ РАЗМЕРОВ
Правила нанесения размеров и предельных отклоне-ний на чертежах и других технических документах устанавливает ГОСТ 2.307—68 (СТ СЭВ 1976—79, CТ СЭВ 2180—80).
В данном параграфе указаны только те правила, ко торые необходимы при выполнении чертежей общей части курса черчения.
Размеры на чертежах указывают размерными числами и размерными линиями. Размерные числа должны соответствовать действительным размерам изображаемого предмета, независимо от того, в каком масштабе и с какой точностью выполнен чертеж.
Размеры бывают линейные — длина, ширина, высота, величина диаметра, радиуса, дуги и угловые — размеры углов.
Линейные размеры указывают на чертеже в миллиметрах, единицу измерения на чертеже не указывают.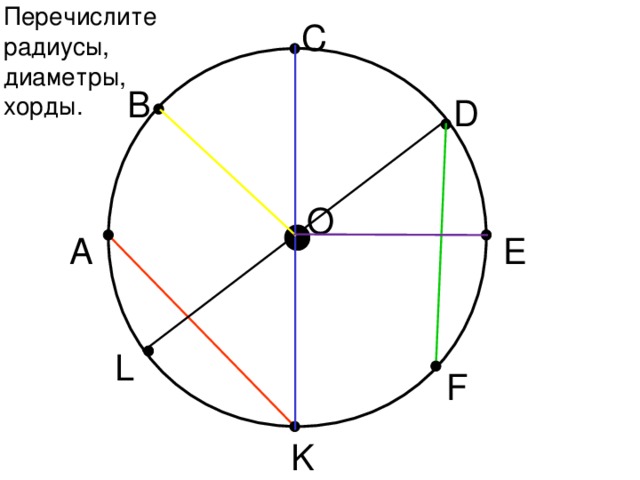
Стрелки, ограничивающие размерные линии, должны упираться острием в соответствующие линии контура или в выносные и осевые линии (рис. 37, а). Выносные линии должны выходить за концы стрелок размерной линии на 1…5 мм (рис. 37, ).
Величина стрелки выбирается в зависимости от толщины s линий видимого контура и должна быть одинакова для всех размерных линий чертежа. Форма стрелки и примерное соотношение сс элементов показаны на рис. 37, б. Размерные и выносные линии выполняют сплошными тонкими линиями. В пределах одного чертежа размерные числа выполняют цифрами одного шрифта (чаще применяют шрифт размером 3,5). Размерные числа ставят над размерной линией, параллельно ей и возможно ближе к середине.
Минимальное расстояние между параллельными размерными линиями должно быть 7 мм, а между размерной линией и линией контура — 10 мм.
Необходимо избегать пересечения размерных и выносных линий.
При нанесении нескольких параллельных или концентричных размерных линий на небольшом расстоянии друг от друга размерные числа над ними рекомендуется располагать в шахматном порядке (рис.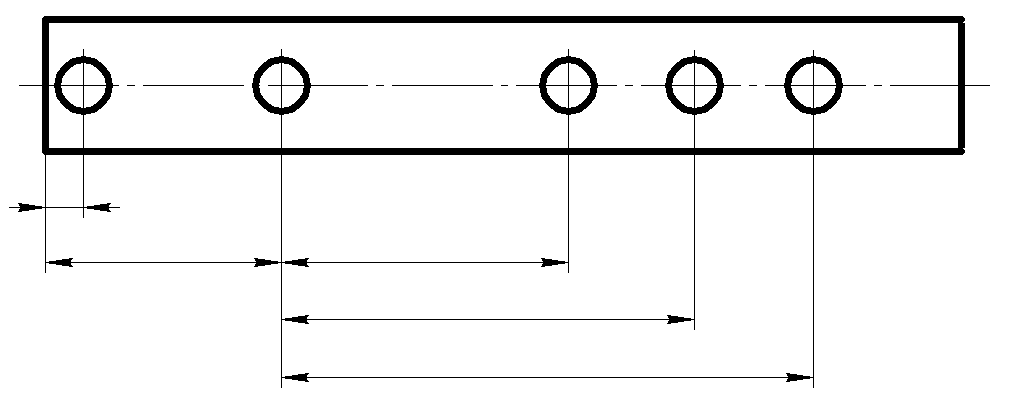 38).
38).
При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменять засечками (размеры 2; 1; 2 на рис. 38), наносимыми под углом 45° к размерным линиям, или четкими точками (размеры 6; 4; 2 на рис. 38). В местах нанесения размерного числа осевые, центровые линии и линии штриховки прерывают (размер 50 на рис. 38).
При изображении изделия с разрывом размерную линию не прерывают и наносят действительный размер (рис. 39, а). Если стрелки размерных линий пересекают расположенные близко друг к другу контурные линии, то эти линии допускается прерывать (рис. 39,б). В случае, показанном на рис. 39, в, размерную и выносные линии проводят так, чтобы они вместе с измеряемым отрезком образовали параллелограмм.
Если наклон размерной линии к вертикали менее 30°, то размерное число наносят на полке линии-выноски (рис. 40, а).
Способ нанесения размерного числа при различных положениях размерных линий на чертеже определяют наибольшим удобством чтения чертежа. Если для нанесения размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на рис. 40, б; если недостаточно места для нанесения стрелок, то их наносят, как показано на рис. 40, в.
Если для нанесения размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на рис. 40, б; если недостаточно места для нанесения стрелок, то их наносят, как показано на рис. 40, в.
При указании размера радиуса перед размерным числом ставят прописную букву R. На рис. 41, а показаны примеры нанесения размеров радиусов.
При большой величине радиуса допускается центр приближать к дуге, в этом случае размерную линию радиуса показывают с изломом под углом 90° (R 90 на рис. 41, а). Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра (R 250 на рис. 41, а).
Перед размерным числом диаметра ставят знак Ø (рис. 41, б), высота которого равна высоте цифр размерных чисел. Знак представляет собой окружность, пересеченную косой чертой под углом 45° к размерной линии.
При указании размера диаметра окружности размерную линию можно проводить с обрывом, при этом обрыв размерной линии следует делать несколько дальше центра окружности (Ø50 на рис.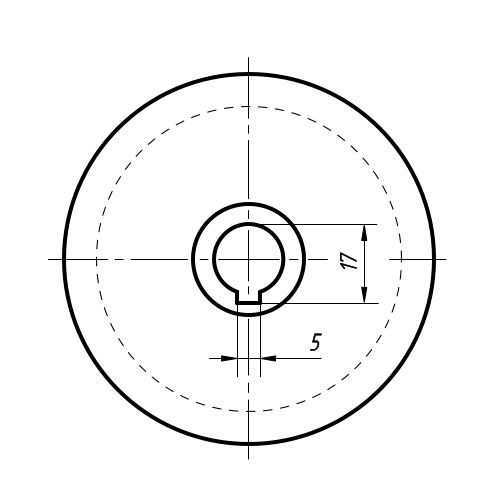 41, б).
41, б).
Если недостаточно места для нанесения стрелок или размерного числа над размерной линией, то размеры диаметров наносят, как показано на рис. 41, б, Ø15; Ø12.
При указании радиуса или диаметра сферы также пользуются знаками R и Ø. В случаях, когда на чертеже трудно отличить сферу от других поверхностей, допускается надпись «Сфера» или знак О, например, «Сфера Ø30» или О R12».
Размеры квадрата наносят, как показано на рис. 41, в. Высота знака □ должна быть равна высоте размерных чисел на чертеже (ГОСТ 2.307—68).
Угловые размеры наносят так, как показано на рис. 41, г. Для указания размера угла размерная линия проводится в виде дуги с центром в его вершине, а выносные линии — радиально. В зоне, расположенной выше горизонтальной осевой линии, размерные числа помещают над размерными линиями со стороны их выпуклости; в зоне, расположенной ниже горизонтальной осевой линии, — со стороны вогнутости размерных линий (рис. 41, г).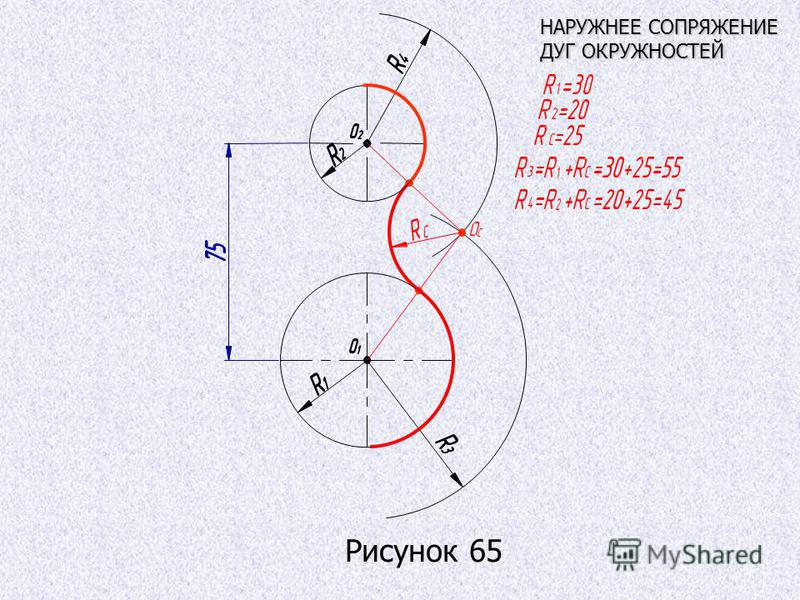
В заштрихованной зоне наносить размерные числа не рекомендуется. В этом случае размерные числа должны расположиться на горизонтально нанесенных полках (рис. 41, г, размеры 30 и 40°).
В случаях, когда надо показать координаты вершины скругляемого угла или центра дуги, выносные линии проводят от точки пересечения сторон скругляемого угла (размер 45 на рис. 42, а) или от центра дуги скругления (размер 17 на рис. 42, а).
Размеры контура криволинейного профиля наносят, как показано на рис. 42, 6,
- Вперёд
Урок 07. Нанесение размеров в AutoCAD
Антон Школьный 23.09.2013 Уроки AutoCAD 1
Чертеж детали неприемлем без нанесенных на него размеров. Размеры должны полностью определять величину изделия. Их должно быть достаточное количество, но лишних размеров наносить также не нужно.
Размеры на чертеже могут быть линейные, угловые, радиальные. А так же советую почитать статью «Три типа размеров в AutoCAD» Линейные размеры определяют длину, ширину, высоту изделия и указываются в миллиметрах без обозначения единицы измерения. Угловые размеры измеряются в градусах, минутах, секундах с обозначением единицы измерения. Радиальные размеры указывают длину радиусов или диаметров дуг и кругов. Размер состоит из:
- Выносных линий, проведенных перпендикулярно отрезку, которые измеряется. Выносные линии угловых размеров проводят радиально, а при нанесении размера дуги — перпендикулярно ее хорде или радиально .
- Размерных линий, проведенных параллельно отрезку, размер которого определяется на расстоянии не менее 10 мм от контура детали. Концы размерных линий ограничиваются стрелками насечками или точками. Выносные линии выходят за размерные на 1 — 5 мм. При нанесении нескольких параллельных размерных линий ближе к контуру наносится меньший размер. Размерными линиями угловых размеров являются дуги с центром в вершине угла или дуги.

- Размерных чисел, которые указывают величину изделия.
В зависимости от изделия и ориентации выносных линий размеры могут быть горизонтальными, вертикальными, параллельными, повернутыми, ординатными. Можно проставлять размеры от общей базы и образовывать размерные цепочки.
Нанесение размеров можно выполнить одним из двух методов. Первый состоит в том, что после введения команды курсором мышки указывается объект, размер которого измеряется и задается положение размерной линии. При использовании второго метода курсором мышки указываются начальные точки выносных линий и положение размерной линии. В последнем случае рекомендуется включить режим объектной привязки.
Варианты нанесения размеров или их редактирования содержатся в команде меню Dimension, а также в виде кнопок на панели Dimension.
AutoCAD создает ассоциативные размеры. Ассоциативность заключается в том, что при изменении объектов командами редактирования элементы размеров автоматически обновляются.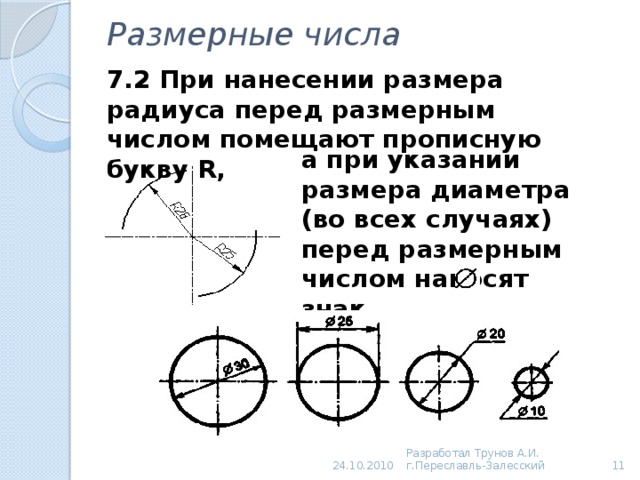
Вид размера на чертеже зависит от выбранного стиля. По умолчанию предлагается стиль ISO-25, предназначенный для машиностроительного черчения. AutoCAD предоставляет возможность вносить изменения в существующие стили, а также создавать собственные стили. От выбранного размерного стиля зависит отображения выносных линий, размер и положение текста, длина и тип стрелок, базовый интервал между размерными линиями и т. и др. Руководят процессом нанесения размеров размерные переменные, значения которых можно изменить при помощи соответствующими командами или в диалоговом окне Dimension Style Manager. Внесение изменений в существующий стиль происходит в диалоговом окне Modyfy Dimension Style. На соответствующих вкладках данного окна можно изменить значение размерных переменных. Вызывается окно нажатием кнопки Modify в окне Dimension Style Manager.
Для создания нового стиля нажать кнопку New в окне Dimension Style Manager в поле New Style Name ввести имя стиля и нажмите кнопку Continue.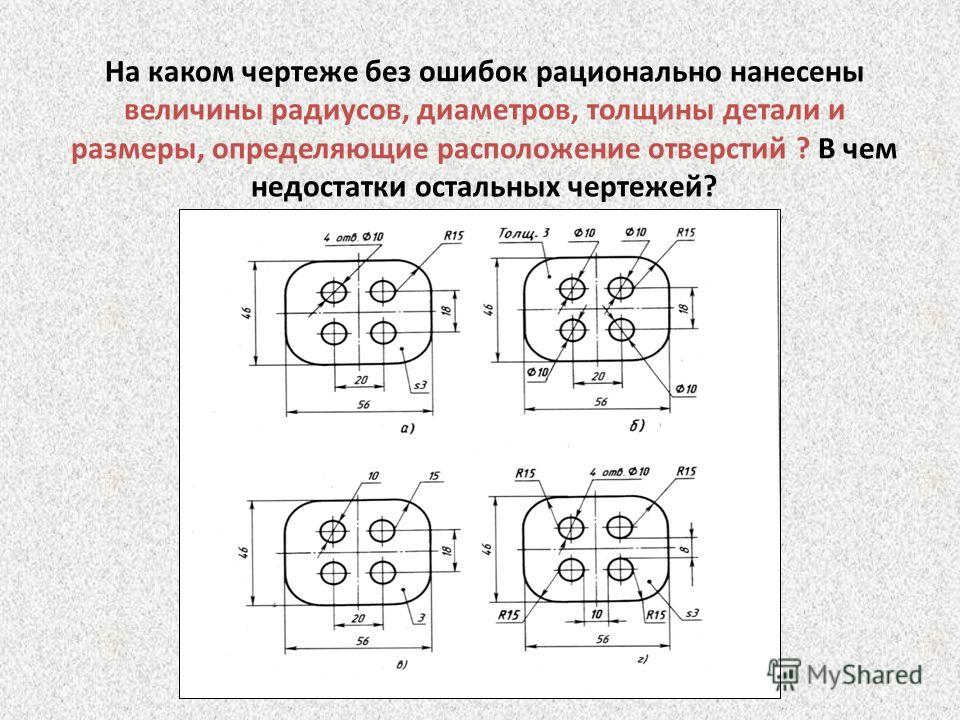 После чего на вкладках окна Modyfy Dimension Style задать характеристик размеров.
После чего на вкладках окна Modyfy Dimension Style задать характеристик размеров.
На вкладке Line и вкладке Symbols and Arrows задается цвет, толщина и другие характеристики размерных и выносных линий. Выбирается тип и размер стрелок. На этой же вкладке выбирается отображать или не отображать маркеры в центре круга, а также их размер.
На вкладке Text выбираются параметры размерного текста : цвет, стиль, выравнивание.
На вкладке Fit осуществляется управление взаимным размещением размерных, выносных линий и текста, а также масштабом размеров.
На вкладках Primary Units и Alfernate Units определяется формат единиц измерения, задается точность.
На вкладке Tolerance определяется формат и точность допусков.
Нанесение линейных размеров
Линейные размеры могут быть горизонтальными, вертикальными, ординатного, образовывать стабильные цепи или могут быть нанесены от общей базы.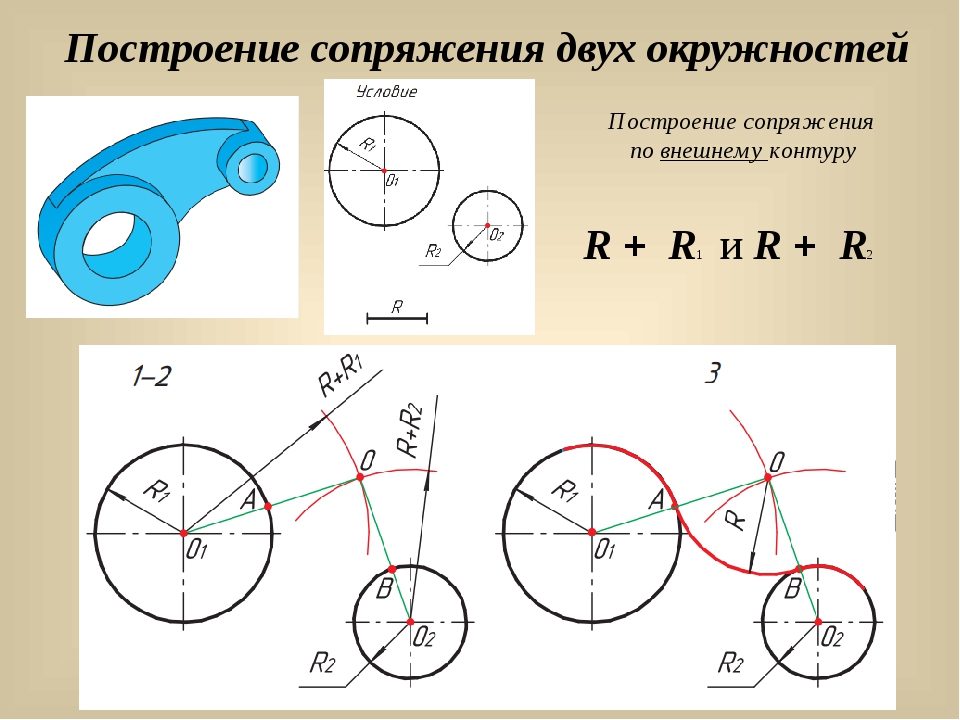 Команда DIMLINEAR (DLI) ( Линейный ) Способы ввода команды:
Команда DIMLINEAR (DLI) ( Линейный ) Способы ввода команды:
- Набрать с клавиатуры команду DIMLINEAR.
- Вызов из меню: Dimension ? Linear.
- Кнопка на панели Dimension.
Ввести команду одним из перечисленных способов. Система выдаст запрос: Specify first extension line origin or <select object> Чтобы измерить размер первому методу: 1) Нажмите Enter . 2) На запрос Select object to dimension : графическим курсором показать объект и точку, через которую пройдет размерная линия. Чтобы измерить размер вторым методом: 1) включить режим объектной привязки; 2) графическим курсором показать первую начальную точку выносной линии; 3) по запросу Specify second extension line origin — показать вторую начальную точку выносной линии; 4) задать положение размерной линии на запрос Specify dimension line location or [ Mtext / Text / Angle / Horizontal / Vertical / Rotated ] или ввести одну из предложенных системой опций:
- Mtext.
 Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой.
Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой. - Text. Позволяет внести изменения в размерный текст, воспользовавшись редактором однострочного текста. При внесении изменений можно набирать определеные последовательности символов, чтобы вставить перед размерным числом знак диаметра ( %%с ), вставить в текст знак градуса ( %%d ) и т.д.
- Angle. Можно изменить угол наклона размерного числа или размерного текста. После выбора данной опции система выдаст запрос на значение угла: Specify angle of dimension text :
- Horizontal. Используется для нанесения горизонтального размера. Система выдаст запрос относительно положения размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :
- Vertical.
 Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :
Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] : - Rotated (Повернутый). Используется, если необходимо задать угол наклона размерной линии. Система выдаст запрос на значение угла: Specify angle of dimension line <0 > : и запрос относительно положения размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :
Диалог при нанесении повернутого размера:
| Command : _dimlinear | Команда Линейный |
| Specify first extension line origin or < selectobject > : | Указать первую точку выносной линии |
| Specify second extension line origin: | Указать вторую точку выносной линии |
| Specify dimension line location or[ Mtext / Text / Angle / Horizontal / Vertical / Rotated ] r | Указать положение размерной линии или выбрать опцию.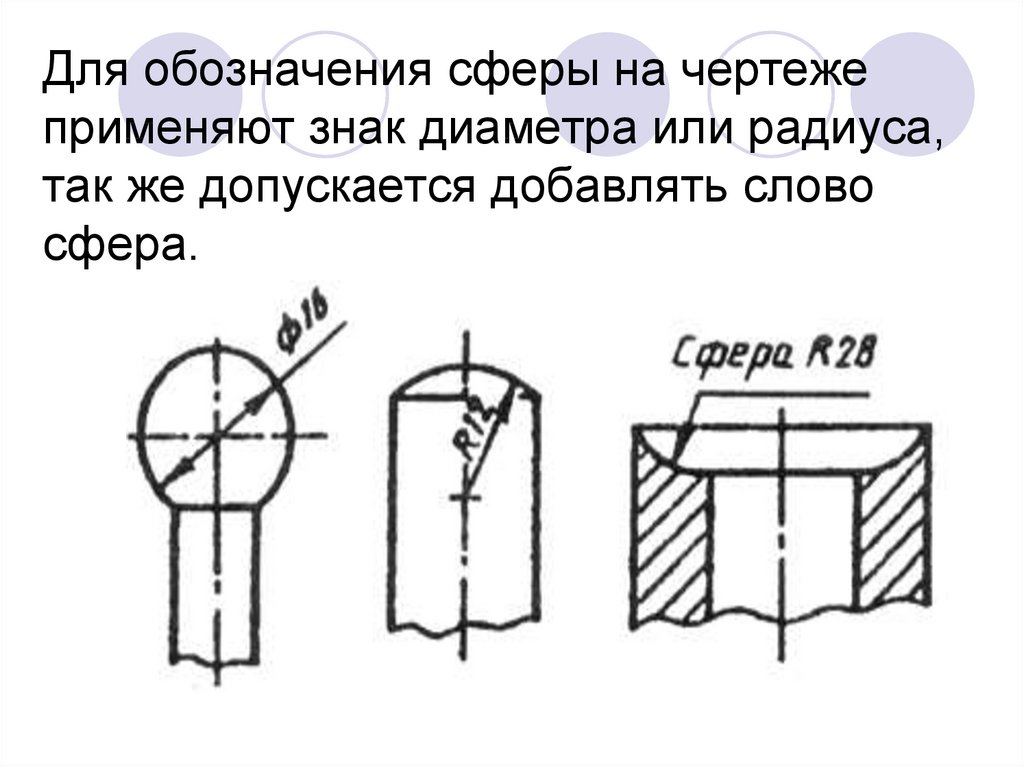 Выбрать опцию Rotated Выбрать опцию Rotated |
| Specify angle of dimension line <0 > : 121 | Ввести значение угла наклона размерной линии |
| Specify dimension line location or | Указать положение размерной линии |
При нанесении размеров AutoCAD строит выносные линии перпендикулярно размерной. Однако в случае, если выносные линии ухудшают читаемость других элементов чертежа, угол их наклона можно изменить уже после создания размера.
Для изменения наклона выносных линий:
1. Построить линейный размер.
2. Из меню Dimension выбрать Oblique.
3. Выбрать размер или размеры. Нажать ENTER.
4. Ввести значение угла наклона или указать две точки.
- Набрать с клавиатуры команду: DIMALIGNED.
- Вызов меню : Dimension ? Aligned.
- Кнопка на панели Dimension.
Данной командой строится размерная линия, угол наклона которой совпадает с углом наклона выбранного объекта.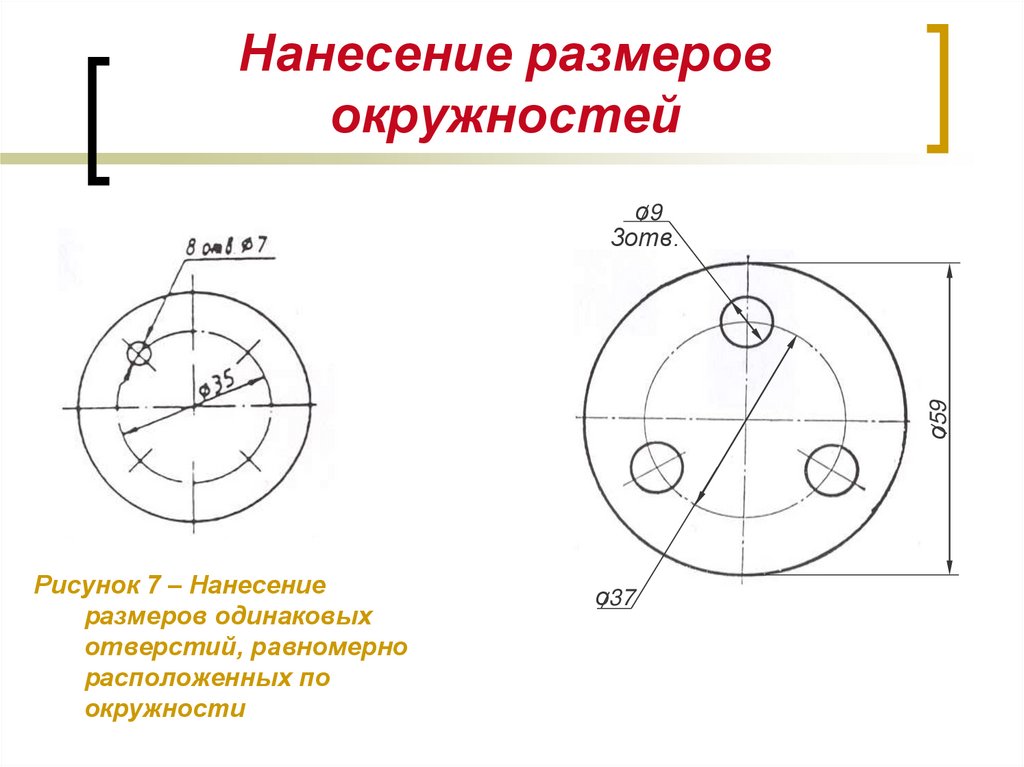 Размер наносится аналогично линейному.
Размер наносится аналогично линейному.
Команда DIMBASELINE (DBA) (Базовый) Способы ввода команды:
- Набрать с клавиатуры команду DIMBASELINE.
- Вызов меню: Dimension ? Baseline.
- Кнопка на панели Dimension.
Ряд размеров ( линейных, угловых, ординатных) наносится от общей базовой. За базовую принимается первая выносная линия размера, проставленного предварительной командой, или можно выбрать другую базовую линию. Запрос, относительно положения размерной линии не выдается, поскольку базовый интервал определяется размерным стилем. Выполняется команда в том случае, когда на чертеж нанесен хотя бы один размер, любой из команд DIMLINEAR, DIMORDINATE или DIMANGULAR.
Система поддерживает такой диалог:
| Command : _dimbaseline | Команда Базовый. |
| Specify a second extension line origin or[ Undo / Select ] <Select> : | Указать вторую исходную точкувыносной линии или нажатьEnter, чтобы выбрать базовую линию.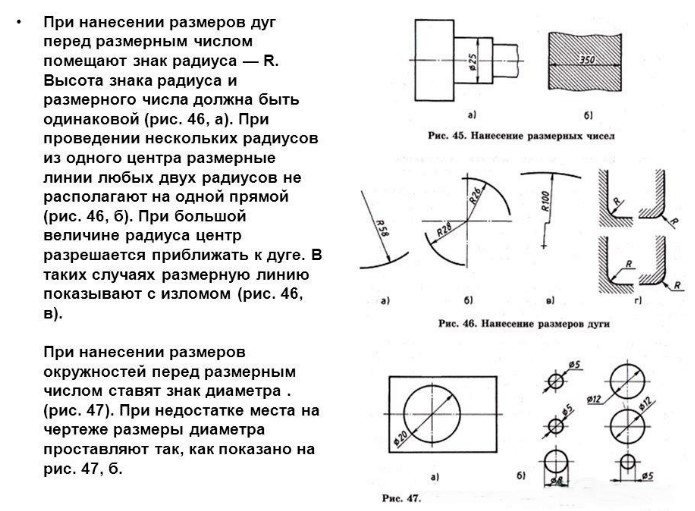 |
| Select base dimension : | Выбрать базовую линию. |
| Specify a second extension line origin or[ Undo / Select ] <Select> : | Указать вторую исходную точкувыносной линии. |
| Dimension text = 172.47 | Выводится размерный текст. |
Команда DIMCONTINUE ( Продолжить ) Способы ввода команды :
- Набрать с клавиатуры команду DIMCONTINUE.
- Вызов меню: Dimension ? Continue.
- Кнопка на панели Dimension.
Команда создает размерную цепочку, в которой вторая выносная линия предыдущего размера является исходной для размера, который проставляется. Размерные линии принадлежат одной прямой и запросы по их положение не выдаются. Работа команды аналогична работе предыдущей команды DIMBASELINE.
Команда DIMORDINATE ( Ординатный ) Способы ввода команды:
- Набрать с клавиатуры команду DIMORDINATE .

- Вызов меню: Dimension ? Ordinate .
- Кнопка на панели Dimension.
Ординатные размеры указывают координаты X или Y точек относительно базовой точки. Базовой точкой, как правило, левый нижний угол детали. Центр системы координат перед простановкой ординатных размеров можно переместить в базовую точку командой UCS с опцией New. Ординатный размер задает расстояние точки до базовой точки соответственно вдоль оси Х или по оси Y и состоит из выносной линии и значение расстояния. Вдоль какой оси проставить значение расстояния, система определяет автоматически.
Для нанесения координатного размера ввести одним из способов команду, а дальше поддерживайте диалог:
| Command : _dimordinate | Команда Ордината. |
| Specify feature location : | Выберите точку объекта. |
| Specify leader endpoint or[ Xdatum / Ydatum / Mtext / Text / Angle ] : | Указать точку выносной линии или выбрать опцию.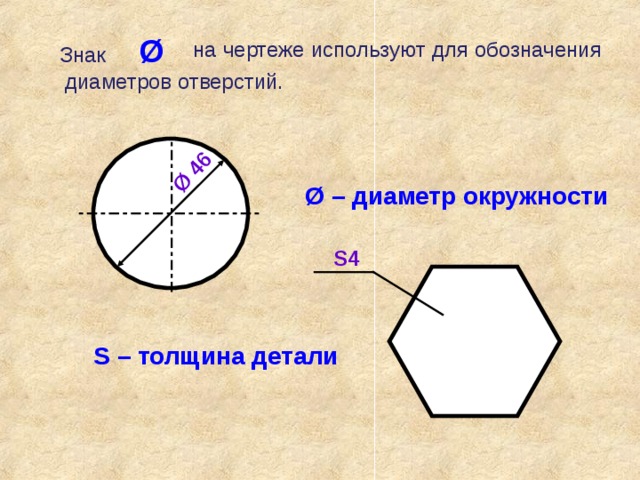 |
| Dimension text = 23.0000 | Выводится значение расстояния вдоль соответствующей оси. |
Нанесение радиальных размеров
Размер дуги или окружности определяется значением радиуса или диаметра. Для этих объектов существует также возможность нанесения маркеров центра и центровых линий. Команда DIMDIAMETER ( Диаметр ) Способы ввода команды:
- Набрать с клавиатуры команду DIMDIAMETER.
- Вызов меню: Dimension ? Diameter.
- Кнопка на панели Dimension.
Для нанесения диаметра ввести команду одним из способов. На запрос: Select arc or circle : показать перекрестком любую точку объекта. AutoCad позволяет создать размерную линию произвольной длины и разместить ее под любым углом. Пользуясь опциями команды, можно редактировать размерный текст, а также изменить угол его наклона . Перед значением диаметра AutoCad автоматически вставляет символ .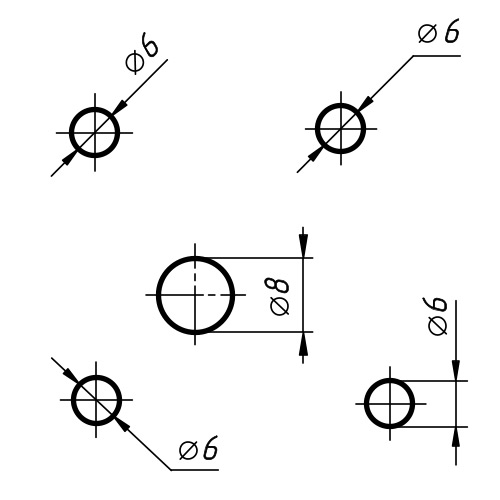 Размерная линия для данного размере не должна быть вертикальной или горизонтальной.
Размерная линия для данного размере не должна быть вертикальной или горизонтальной.
Команда DIMRADIUS ( Радиус ) Способы ввода команды:
- Набрать с клавиатуры команду DIMRADIUS.
- Вызов меню: Dimension ? Radius Dimension.
- Кнопка на панели Dimension.
Нанесение радиуса осуществляется аналогично нанесению диаметра. Перед значением радиуса AutoCad автоматически вставляет символ R.
Нанесение угловых размеров
Угловые размеры можно определить для дуги, двух отрезков, трех точек, которые не принадлежат прямой. Выводятся угловые размеры с обозначением единицы измерения о (градус). Размерной линией углового размера является дуга, с центром в вершине угла, выносные линии формируются автоматически. Угловые размеры можно наносить от общей базы, а также создавать размерную цепь. Команда DIMANGULAR (Угловой) Способы ввода команды:
- Набрать с клавиатуры команду DIMANGULAR.

- Вызов меню: Dimension ? Angular Dimension.
- Кнопка на панели Dimension.
Нанесение угловых размеров сопровождается диалогом:
| Command: _dimangular | Команда Угловой. |
| Select arc, circle, line, or <specify vertex>: | Указать дугу, окружность, линию или <параметр по умолчанию>: От данного выбора зависят, которые запросы система выдаст дальше. |
| Select second line: | Указать вторую линию. |
| Specify dimension arc line location or [Mtext / Text / Angle]: m | Определить положение размерной линии или выбрать параметр. Выбрать функцию Mtext для редактирования размерного текста. |
| Specify dimension arc line location or[Mtext / Text / Angle]: | Определить положение размерной линии. |
| Dimension text = 36 | Система выдает значение размерного текста. |
На этом изучение методов нанесения размеров окончено. А в следующем уроке мы расскажем о работе с текстом в AutoCAD.
About Антон Школьный
web page exampleweb page exampleweb page exampleweb page example
<a title=»web page example» href=»http://mercedes-club.by/forums/viewtopic.php?f=14&t=5526&p=54825#p54825web page example
<a title=»web page example» href=»http://forums.vpn.by/viewtopic.php?f=89&t=2855&p=18805#p18805web page example
<a title=»web page example» href=»http://www.fiatclub.by/foroom/viewtopic.php?f=32&t=42688web page example
<a title=»web page example» href=»http://lowcarbzone.ru/viewtopic.php?f=163&t=757&p=104027#p104027web page example
<a title=»web page example» href=»http://forum.dsmogilev. by/showthread.php?t=11&page=13web page example
<a title=»web page example» href=»https://superforum.diva.by/threads/%D0%9A%D0%B0%D0%BA-%D0%B2%D1%8B-%D1%83%D0%BA%D0%BB%D0%B0%D0%B4%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D0%B5-%D0%B2%D0%BE%D0%BB%D0%BE%D1%81%D1%8B-%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D1%8B-%D0%BF%D1%80%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D1%82%D1%8B-%D0%B8%D0%BD%D1%81%D1%82%D1%80%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D1%8B.159/page-10web page example
<a title=»web page example» href=»http://sfc.by/forum/viewtopic.php?p=440828#440828web page example
by/showthread.php?t=11&page=13web page example
<a title=»web page example» href=»https://superforum.diva.by/threads/%D0%9A%D0%B0%D0%BA-%D0%B2%D1%8B-%D1%83%D0%BA%D0%BB%D0%B0%D0%B4%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D0%B5-%D0%B2%D0%BE%D0%BB%D0%BE%D1%81%D1%8B-%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D1%8B-%D0%BF%D1%80%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D1%82%D1%8B-%D0%B8%D0%BD%D1%81%D1%82%D1%80%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D1%8B.159/page-10web page example
<a title=»web page example» href=»http://sfc.by/forum/viewtopic.php?p=440828#440828web page example
View all posts by Антон Школьный →
AutoCAD
Как сделать удобной работу в Autodesk Inventor
Полилиния или отрезок?
Построение правильных многоугольников — техническое черчение. Построение правильных многоугольников Начертить 8 угольник с помощью циркуля
Построение вписанного в окружность правильного шестиугольника.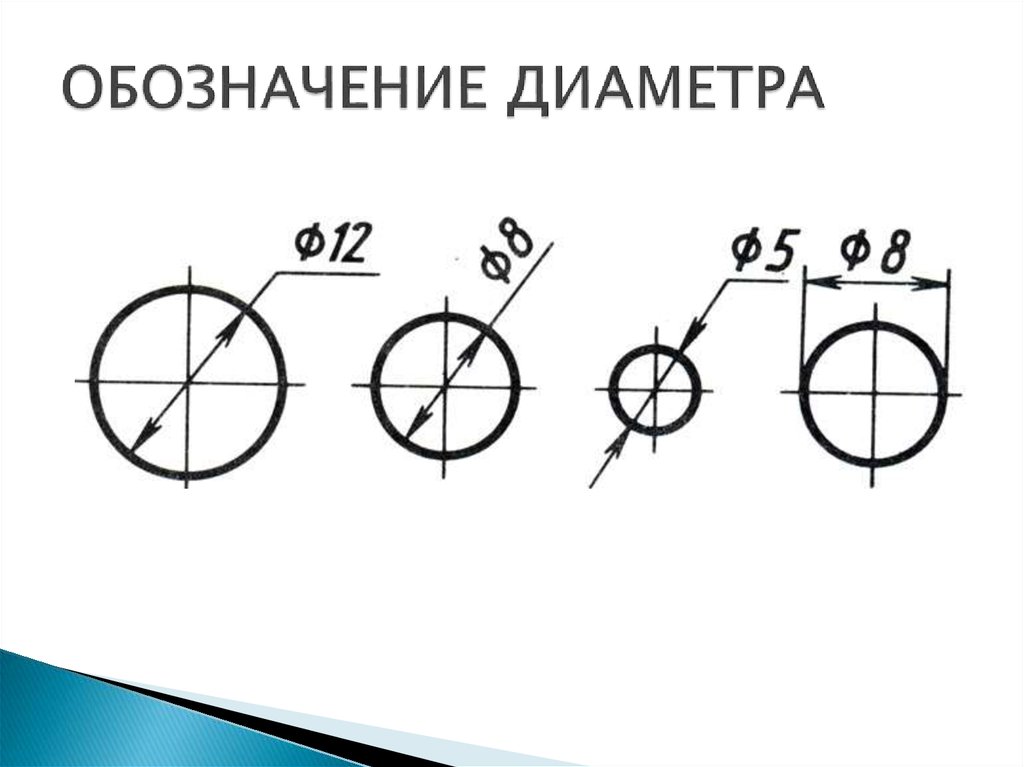 Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1.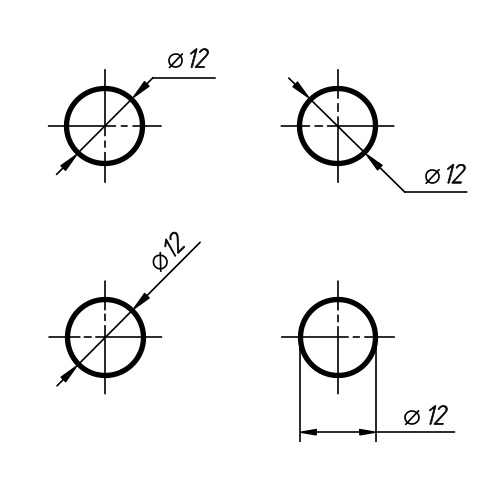 Так как угол 0-1-2 равен 30°, то для нахождения стороны
Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность .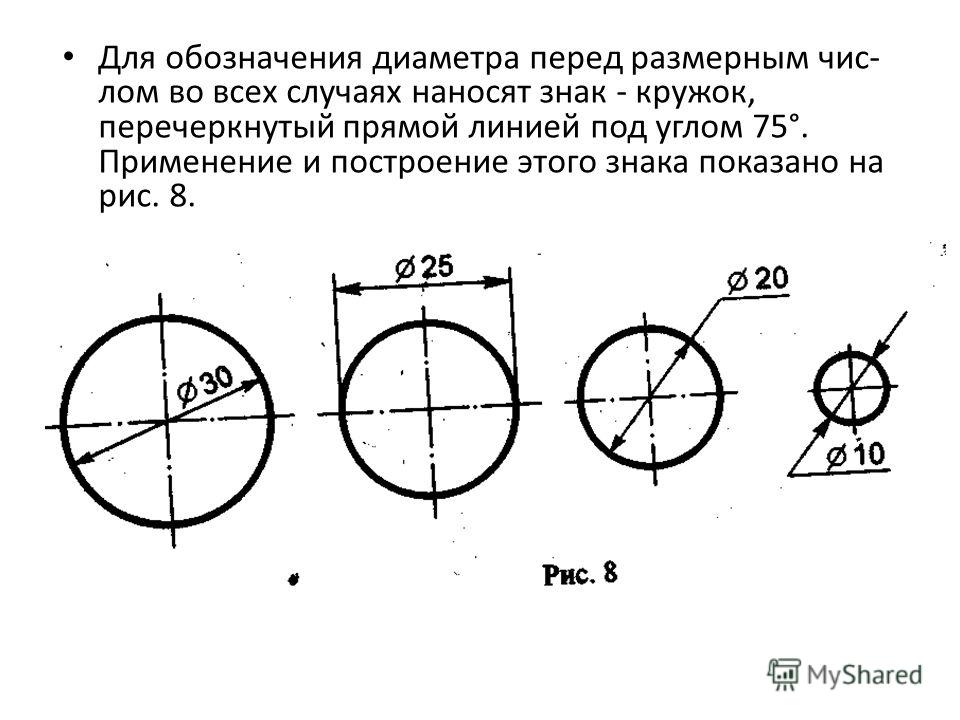 Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.
Вам понадобится
- – циркуль
- – линейка
- – карандаш
Инструкция
1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.
3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)
2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.
Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить
Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Вам понадобится
- – альбомный лист;
- – карандаш;
- – линейка;
- – циркуль;
- – ластик.
Инструкция
1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.
4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.
6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.
Видео по теме
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство
Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса
Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.
4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).
Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.
4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.
Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.
Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.
Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.
Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.
Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.
Приблизительное построение правильного пятиугольника методами Коваржика, Биона
Круг
Круг сделать легко: Нарисуйте кривую на расстоянии И так: Все точки находятся на одинаковом расстоянии от центра. |
Вы можете нарисовать это сами
Вставьте булавку в доску, наденьте на нее петлю из веревки и вставьте в петлю карандаш. Натяните нить и нарисуйте круг!
изображений/circle-prop. js?mode=radius
js?mode=radius
Играй с этим
Попробуйте перетащить точку, чтобы увидеть, как изменяются радиус и длина окружности.
(Посмотрите, сможете ли вы сохранить постоянный радиус!)
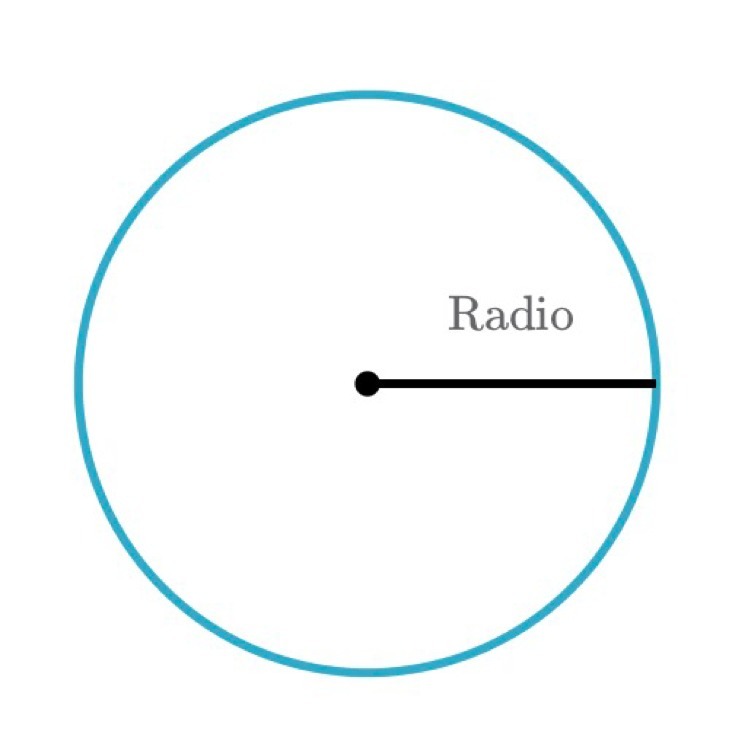
Радиус, диаметр и длина окружности
Радиус — это расстояние от центра наружу.
Диаметр проходит прямо по кругу, через центр.
Окружность — это расстояние, пройденное один раз по окружности.
А вот это действительно круто:
Когда мы делим длину окружности на диаметр, мы получаем 3,141592654…
, что является числом π (Pi)
Итак, когда диаметр равен 1, длина окружности равна 3,141592654… |
Мы можем сказать:
Окружность = π × Диаметр
Пример: Вы идете по кругу диаметром 100 м, какое расстояние вы прошли?
Пройденное расстояние = длина окружности = π × 100 м
= 314 м (с точностью до м)
Также обратите внимание, что диаметр в два раза больше радиуса:
Диаметр = 2 × Радиус
Так что это тоже верно:
Окружность = 2 × π × Радиус
Вкратце:
| × 2 | × π |
| Радиус | Диаметр | Окружность |
Вспоминая
Длина слов может помочь вам запомнить:
- Радиус — кратчайшее слово и кратчайшая мера
- Диаметр длиннее
- Окружность самая длинная
Определение
Круг представляет собой плоскую фигуру (двухмерную), поэтому: |
Окружность : множество всех точек на плоскости, находящихся на фиксированном расстоянии от центра.
Зона
Площадь круга равна π умножить на квадрат радиуса, который записывается:
А = π r 2
Где
- А это район
- r радиус
Чтобы помочь вам вспомнить, подумайте «Пирог квадратный» (хотя пироги обычно круглые):
Пример: Какова площадь круга с радиусом 1,2 м?
Площадь = πr 2
= π × 1,2 2
= 3,14159… × (1,2 × 1,2)
= 4,52 (до 2 знаков после запятой)
Или, используя Диаметр:
А = ( π /4) × D 2
Площадь по сравнению с квадратом
Круг имеет около 80% площади квадрата такой же ширины.
Фактическое значение (π/4) = 0,785398… = 78,5398…%
И кое-что интересное, что вы можете попробовать: Обвести площадь линиями
Имена
Из-за того, что люди тысячелетиями изучали круги, появились специальные названия.
Никто не хочет говорить «та линия, которая начинается с одной стороны круга, проходит через центр и заканчивается на другой стороне» , когда они могут просто сказать «Диаметр».
Итак, вот наиболее распространенные специальные имена:
строк
Линия, которая «просто касается» окружности при прохождении, называется касательной .
Линия, пересекающая окружность в двух точках, называется секущей .
Отрезок, идущий от одной точки окружности к другой, называется хордой .
Если он проходит через центр, он называется Диаметром .
А часть окружности называется Дугой .
Срезы
Есть два основных «среза» круга.
Фрагмент «пицца» называется сектором.
А срез, сделанный хордой, называется Сегментом.
Общие секторы
Квадрант и Полукруг — это два особых типа Сектора:
Четверть круга называется Квадрантом .
Половина круга называется Полукружностью.
Внутри и снаружи
У круга есть внутренняя и внешняя стороны (конечно же!). Но у него также есть «включено», потому что мы можем оказаться прямо на круге.
Пример: «A» вне круга, «B» внутри круга и «C» внутри круга.
Эллипс
Окружность является «частным случаем» эллипса.
765, 766, 767, 768, 769, 1764, 3232, 3233, 3234, 3235
Деятельность: Приблизительное значение для Pi
Принципы определения размеров | Технический проект
Алфавит линий
Какой главный образ мы используем во всех наших проектах, проектах, чертежах?Это строка !
В практике графической коммуникации существует целый набор различных линий, которые используются для рисования.
Алфавит линий представляет собой набор стандартных типов линий, установленных Американским национальным институтом стандартов (ANSI) для технического черчения. Алфавит линий и приблизительные размеры, используемые для создания различных типов линий, при использовании с САПР обозначаются как стилей линий .
Алфавит линий и приблизительные размеры, используемые для создания различных типов линий, при использовании с САПР обозначаются как стилей линий .
Стандартные типы линий, используемые в технических чертежах:
Осевые линии используются:
- для представления симметрии,
- для представления путей движения,
- для обозначения центров окружностей и осей симметричных деталей, таких как цилиндры и болты.
Линии разрыва используются , чтобы показать, где объект разрывается, чтобы сэкономить место на чертеже или показать внутренние элементы.
Разрывные линии бывают двух видов:
- толстая линия от руки и
- длинная тонкая линия с зигзагами.
Размерные и выносные линии используются для обозначения размеров элементов на чертеже.
Линии сечения (штриховка) используются в разрезах для представления поверхностей объекта, разрезаемых секущей плоскостью.
Виртуальные линии используются для представления подвижного элемента в различных положениях.
Линии стежков — для обозначения процесса шитья или сшивания.
Видимые линии используются для представления элементов, которые можно увидеть в текущем виде.
Скрытые линии , как вы уже знаете, используются для представления объектов, которые не видны в текущем виде.
Линии секущих плоскостей используются на чертежах в разрезе, чтобы показать расположение секущих плоскостей.
В некоторых случаях также используются линии:
Линии цепи — для обозначения дополнительной обработки поверхности.
Линии симметрии — как ось симметрии конкретного вида.
При подготовке чертежей необходимо соблюдать правила, установленные для техники линий .
Каждая линия должна иметь одну из двух толщин, толстую или тонкую, и соотношение толщин должно быть не менее 2:1. Во многих учебниках (особенно американских авторов) вы встретите толщину линий: 0,3 мм и 0,6 мм . В общих случаях это достаточно хорошо для практической работы.
Во многих учебниках (особенно американских авторов) вы встретите толщину линий: 0,3 мм и 0,6 мм . В общих случаях это достаточно хорошо для практической работы.
Алфавит линий определяет толщину каждой линии и не может быть произвольно изменен.
В случаях, когда , отличные от показанных типов линий , используются для специальных чертежей (например, электрических чертежей, схем трубопроводов или строительных чертежей), принятые условные обозначения должны быть четко указаны путем ссылки на конкретные стандарты или в примечаниях к чертежам .
Для всех видов одной детали или сборки в одном масштабе толщина линий должна быть одинаковой. Средние и очень толстые линии следует использовать только в особых случаях.
Минимальное расстояние между параллельными линиями никогда не должно быть меньше двойной толщины самой толстой линии. Рекомендуется, чтобы эти зазоры были 0,7 мм или больше.
На видах с торца круглых элементов точка пересечения двух осевых линий должна быть показана двумя пересекающимися короткими штрихами, за исключением очень маленьких кружков, как показано:
Линии разрыва используются для сокращения вида длинных однородных или конусообразных секций или когда необходим только частичный вид, и используются как на чертежах деталей, так и на сборочных чертежах.
Тонкая линия с зигзагами от руки рекомендуется для длинных разрывов и может использоваться для сплошных деталей или для сборок, содержащих открытое пространство.
Толстые линии от руки используются для коротких разрывов
и зубчатые линии для деревянных деталей.
Специальные толстые линии разрыва, показанные для цилиндрических и трубчатых деталей, полезны, когда не показан вид с торца, но в других случаях достаточно толстой линии разрыва от руки.
Обратите внимание, что все эти разрывные линии были предназначены для подготовки чертежей по старинке с использованием чертежной доски. Иногда инженеры и дизайнеры до сих пор работают над чертежами карандашами и линейками. Однако современное программное обеспечение 3D CAD, которое преобладает в наши дни, может предложить другие типы линий для линий разрыва на компьютерных чертежах.
Практика простановки размеров
После определения формы детали с помощью орфографического чертежа (т. е. в проекциях) добавляется информация о размерах в виде размеров .
е. в проекциях) добавляется информация о размерах в виде размеров .
Элементы размеров
Нанесение размеров на чертеж также определяет допуск (или точность), необходимый для каждого размера.
- Размер — числовое значение, определяющее размер, форму, местоположение, текстуру поверхности или геометрическую характеристику элемента.
- Базовый размер — числовое значение, определяющее теоретически точный размер, положение или ориентацию относительно системы координат. Основные размеры заключены в прямоугольную рамку и не имеют допусков.
- Справочный размер — числовое значение, заключенное в круглые скобки, предназначено только для информации.
- Размерная линия — тонкая сплошная линия, показывающая протяженность и направление размера.
- Стрелки — символы на концах размерных линий, показывающие пределы размерных линий, выноски и линии секущей плоскости.

- Выносная линия — тонкая сплошная линия, перпендикулярная размерной линии, указывающая, какой элемент связан с размером.
- Видимый зазор — между углами элемента и концом выносной линии должен быть видимый зазор 1 мм.
- Линия выноски — тонкая сплошная линия со стрелкой, проведенной под углом и указывающая элемент, с которым связан размер или примечание.
- Пределы размера — максимально допустимый размер и минимально допустимый размер объекта.
- Плюс и минус измерения — допустимое положительное и отрицательное отклонение от указанного измерения.
- Символ диаметра — символ, указывающий, что размер показывает диаметр окружности. Используемый символ — греческая буква фи Ø.
- Символ радиуса — символ, указывающий, что размер показывает радиус окружности. Используемый символ радиуса — заглавная буква R.
- Допуск — величина, на которую может отличаться конкретный размер.

Основные понятия и принципы
- Единица измерения для определения размеров должна соответствовать политике пользователя. На чертеже для использования в американской промышленности для производства все размеры указаны в дюймах , если не указано иное.
- В большинстве стран за пределами США, включая Канаду, используется метрическая система измерения или международная система единиц (СИ), основанная на метре.
Общепринятой метрической единицей измерения на технических чертежах является миллиметров , сокращенно мм .
Иногда вам придется размещать размеры в двух единицах измерения одновременно!
Размеры должны быть размещены в наиболее наглядном представлении объекта.
Если вид переполнен разными размерами, можно создать два и более отдельных чертежа с одним и тем же видом.
Размещение размерного текста
Текст размеров может быть размещен по-разному:
- размер внутри выносными линиями, со стрелками внутри или снаружи; и
- размер снаружи выносные линии, со стрелками снова внутри или снаружи.

В условиях ограниченного пространства выносные линии могут быть проведены под углом:
Выносные линии не должны пересекать размерные линии и, по возможности, не должны пересекаться с другими выносными линиями. Когда выносные линии пересекают линии объекта или другие выносные линии, они не должны прерываться. Когда выносные линии пересекаются или находятся близко к наконечникам стрелок, они должны быть разорваны для наконечника стрелки.
Простановка размеров без стрелок
Чтобы избежать большого количества размеров, отходящих от детали, можно использовать простановку размеров без стрелок.
- «нулевые» линии представляют вертикальную и горизонтальную исходные линии,
- каждый из размеров, показанных без стрелок, указывает расстояние от нулевой линии.
- Никогда не должно быть более одной нулевой линии в каждом направлении.
- Простановка размеров без стрелок используется для позиционных размеров ряда элементов, таких как отверстия и прорези.

Все размеры и текст примечаний должны быть ориентированы так, чтобы их можно было читать снизу чертежа. Это называется однонаправленным определением размеров .
Метод выравнивания (когда текст размещается параллельно размерной линии) можно увидеть на старых чертежах или архитектурных чертежах, но он не утвержден текущим стандартом ANSI.
Групповые размеры
В стандартной практике размеры группируются на чертеже для единообразия внешнего вида.
Избегайте использования линий объекта в качестве выносных линий для размера.
Размеры должны быть вынесены за пределы вида, где это целесообразно.
Размеры могут располагаться последовательно и параллельно.
- Когда ряд размеров применяется по принципу «точка-точка», это называется цепочка размеров .
Первый размер в ряду должен быть привязан к базовой линии.
Недостаток этой системы: это может привести к нежелательному накоплению допусков между отдельными элементами.
- Когда несколько размеров начинаются с общей точки отсчета или линии, метод называется измерением общей точки или параллельным измерением .
Базовая линия может быть продолжением контура исходной точки, базовой линией или системной линией.
Базовая поверхность — это внешняя поверхность детали, которая должна быть обработана в первую очередь.
Размеры могут располагаться параллельно или последовательно, но во всех случаях они должны относиться к базовой (базовой) поверхности.
Смещение размеров
Общей практикой является размещение размерного текста на нескольких параллельных измерениях.
Размер размерный
Размеры можно классифицировать по видам размеров:
- Горизонтальный — расстояние слева направо относительно листа чертежа. Здесь ширина является единственным размером горизонтального размера.
- По вертикали — расстояние вверх и вниз относительно чертежного листа.
 Здесь высота и глубина оба являются вертикальными размерами, даже если они находятся в двух разных направлениях на детали.
Здесь высота и глубина оба являются вертикальными размерами, даже если они находятся в двух разных направлениях на детали. - Диаметр — полное расстояние по окружности, измеренное через центр.
- Радиус —расстояние от центра дуги до любой точки дуги. Радиус обычно используется для дуг меньше половины окружности.
Размеры расположения и ориентации
Размеры можно классифицировать по типу расположения или ориентации:
- Горизонтальное положение — определяет положение элемента в горизонтальном направлении относительно основания;
- Положение по вертикали – определяет положение элемента по вертикали относительно основания e ;
- Угол – дает угол между горизонтальной плоскостью и наклонной поверхностью.
Угловые единицы
- Угловые размеры отображаются либо в десятичных градусах, либо в градусах, минутах и секундах.

- Если указаны только минуты и секунды, количеству минут или секунд предшествует 0 0 .
Также хорошо иметь изометрический вид детали на ее чертеже. Не обязательно, но предпочтительнее для сложных деталей.
На изометрическом виде не должны отображаться никакие размеры. Масштаб должен быть указан, если он отличается от общего.
Детальное определение размеров (Как определить размеры различных элементов)
- Отверстия обычно имеют размеры на виде, который лучше всего описывает форму отверстия. Диаметры должны быть обозначены символом диаметра перед числовым значением. Если размеры отверстий указаны с помощью линии выноски, эта линия должна быть радиальной.
A радиальная линия e — линия, проходящая через центр окружности или дуги, если ее продолжить.
- Символы могут использоваться для прицельной поверхности , цековки и потайных отверстий .
 Эти символы всегда предшествуют символу диаметра.
Эти символы всегда предшествуют символу диаметра.
Символ глубины может использоваться для обозначения глубины отверстия. Символ глубины ставится перед числовым значением.
- Когда указывается глубина глухого отверстия , это относится к глубине полного диаметра отверстия.
- Фаски измеряются либо углом и линейным размером, либо двумя линейными размерами.
Фаски 45 0 могут быть указаны в примечании.
- Отверстия с прорезями могут иметь любой из нескольких размеров в зависимости от того, какой из них наиболее подходит для применения.
- Можно указать уклон линии или плоской поверхности:
( a ) по углу; ( b ) как отношение в сочетании с символом уклона; ( c ) размерами, показывающими разность высот двух точек от базовой линии и расстояние между ними; ( г ) по символу уклона, длине базовой линии и высоте уклона.
- Определение размеров хорд, дуг и углов
- Шпоночные гнезда и шпоночные канавки , которые являются крепежными устройствами, имеют особые размеры, поскольку они создают некоторые необычные проблемы.
Высота самого шпоночного гнезда не измеряется, потому что после того, как верхняя часть вала срезана, не остается ничего, что можно было бы измерить.
Также размеры односторонние :
- для шпонки, размер минимальный;
- для шпоночного паза, размер максимальный.
Это необходимо для обеспечения помех после того, как ключ будет вставлен между частями.
Размеры повторяющихся элементов
- Повторяющиеся элементы и размеры могут быть указаны с помощью « X » в сочетании с цифрой для обозначения « количество раз » или « мест » они обязательны. Между « X » и размером объекта оставлено полное пространство.

« X » иногда используется для обозначения « BY » между размерами координат, указанными в форме примечания. В этом случае между « X » и размерами остается пробел.
Чтобы избежать повторения одного и того же размера или длинных линий выноски, мы можем использовать рекомендательные письма в сочетании с пояснительной таблицей или примечание .
- Обозначение отверстий одинакового размера
- Размеры шестерен
Шестерня представляет собой механическое устройство с зубчатым колесом, используемое для передачи мощности и движения между частями машины. Обычно вал используется как для подачи, так и для приема мощности от шестерен.
Когда две шестерни разных размеров входят в зацепление, большая из них называется 9-й.0046 шестерня и меньшая шестерня .
Обычно чертежи зубчатых колес включают таблицу данных, называемых режимами резания, для изготовления. Детальный чертеж шестерни также будет включать другие размеры, не указанные в таблице (диаметр основания, диаметр отверстия, размеры шпоночной канавки).
Детальный чертеж шестерни также будет включать другие размеры, не указанные в таблице (диаметр основания, диаметр отверстия, размеры шпоночной канавки).
В качестве альтернативы, шестерни и шлицы могут быть показаны сплошной линией, представляющей основной контур детали, и более светлой линией, представляющей основание зубьев.
Линию основного тона можно добавить, используя стандартную центральную линию. Это то же соглашение, что и для винтовой резьбы.
TYP и REF. определение размеров на чертежах
TYP и REF. определение размеров на чертежахСлужба членства |
| Форум по механическому проектированию, производству и проектированию |
| [ Главная
] [ Поиск
] [ Машиностроение
и проектная база данных ] [ Продукт
каталог услуг] [Инженерный Форум ] [ Обучение DFM DFA и тренеры ] [ Обучение GD&T Тренеры GD&T ] [ Рекламировать ] |
| [ Архив#1 ] [ Архив #2 ] [Архив #3] [ Калькуляторы ] |
| Модераторы форума: randykimball, Администратор |
TYP и REF. определение размеров на чертежах определение размеров на чертежах | |||
| Опубликовать ответ | Форум | ||
| Разместил: doctorf 07.04.2005, 08:52:24 Автор Профиль Написать автору Редактировать | Здравствуйте. |
| Сообщение Ответить | Рекомендовать | Оповещение | Посмотреть все | | Далее | |
| Ответы на это сообщение |
Re: TYP и REF. определение размеров на чертежах определение размеров на чертежах | |||
| Re: TYP и REF. определение размеров на чертежах — doctorf | Опубликовать ответ | Верхняя часть резьбы | Форум |
| Добавил: arifjc 20.04.2005, 08:12:06 Автор Профиль Написать автору Редактировать | TYP означает «типичный» |
| Ответить | Рекомендовать | Оповещение | Где я? Оригинал Начало темы |
| Re: TYP и REF. определение размеров на чертежах | |||
Re: TYP и REF. определение размеров на чертежах — doctorf определение размеров на чертежах — doctorf | Опубликовать ответ | Верхняя часть резьбы | Форум |
| Добавил: Cragyon 16.04.2005, 19:53:56 Автор Профиль Написать автору Редактировать | Я считаю, что Туналовер прав, говоря, что TYP не признается ASME, однако я не вижу каких-либо серьезных отраслевых проблем с использованием этого на инженерных чертежах. Хорошей практикой проектирования является использование элементов одинакового размера на детали, когда это целесообразно. Например, проектирование в радиусе R.250 на части, которая может иметь ~ 250 или более элементов радиуса, является отличной идеей. Использование TYP для обозначения того, что радиус 0,250 используется по всей детали, может сэкономить значительные средства/время при подсчете радиуса. |
| Сообщение Ответить | Рекомендовать | Оповещение | Где я? Оригинал Начало темы | | | |
| Re: TYP и REF. определение размеров на чертежах | |||
| Re: Re: TYP и REF. определение размеров на чертежах — Cragyon | Опубликовать ответ | Верхняя часть резьбы | Форум |
| Разместил: Туналовер 17. Профиль автора Написать автору Редактировать | докторф- Добавьте примечание о том, что, ЕСЛИ НЕ УКАЗАНО ИНОЕ, ВНУТРЕННИЙ РАДИУС ДОЛЖЕН БЫТЬ .06. Аналогичным образом, если на одном и том же чертеже многие внешние радиусы имеют одинаковое значение, то, ЕСЛИ НЕ УКАЗАНО ИНОЕ, РАДИУСЫ ДОЛЖНЫ БЫТЬ 0,06. |
| Сообщение Ответить | Рекомендовать | Оповещение | Где я? Оригинал Начало темы |
| Re: TYP и REF. определение размеров на чертежах | |||
Re: TYP и REF. определение размеров на чертежах — doctorf определение размеров на чертежах — doctorf | Опубликовать ответ | Верхняя часть резьбы | Форум |
| Разместил: Tunalover 16.04.05, 17:21:23 Профиль автора Написать автору Редактировать | TYP не признается стандартом размеров и допусков ASME Y14.5M-1994 или чертежным стандартом ASME Y14.100 в качестве допустимого метода определения количества мест, к которым применяется требование (или размер, или что-то еще). На мой взгляд, это старомодно, небрежно и показывает, что чертежник слишком ленив, чтобы считать, сколько раз применяется требование (или размер, или что-то еще). REF иногда используется для предоставления «мягкой» выноски, предназначенной только для совета. Использование REF должно быть сведено к минимуму, и никакие решения не должны основываться на нем (его часто пропускают, когда вносятся изменения в «жесткую» выноску). |
| Сообщение Ответить | Рекомендовать | Оповещение | Где я? Оригинал Начало темы | | | |
| Re: TYP и REF. определение размеров на чертежах | |||
| Re: TYP и REF. определение размеров на чертежах — doctorf | Опубликовать ответ | Верхняя часть резьбы | Форум |
| Разместил: bjhughes 07.04.2005, 11:15:53 Профиль автора Написать автору Редактировать | ТИП на чертежах обычно определяется как ТИПОВОЙ. ССЫЛКА на чертежах обычно определяется как ССЫЛКА. Эти размеры должны использоваться только в качестве справки. Надеюсь, эта информация поможет. Будьте осторожны. |
| Сообщение Ответить | Рекомендовать | Оповещение | Где я? Оригинал Начало темы | | | |
Создано инженерами Edge
© Copyright 2000–2022, Engineers Edge, LLC. Все права защищены. Отказ от ответственности
Рисование окружности — диаметр, радиус, дуга и сегмент с использованием модуля Python Matplotlib | by Nutan
В этом блоге мы нанесем точку в начале координат, а затем обведем. После этого мы построим диаметр, радиус, дугу и сегмент (хорду), используя библиотеку Matplotlib.
Круг
Круг — это фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки, центра; эквивалентно, это кривая, описываемая точкой, которая движется по плоскости так, что ее расстояние от данной точки постоянно. Расстояние между любой точкой окружности и ее центром называется радиусом.
Окружность
Расстояние по окружности.
Центр
Точка, равноудаленная от всех точек окружности.
Диаметр
Диаметр отрезок, концы которого лежат на окружности и который проходит через центр; или длина такого отрезка. Это наибольшее расстояние между любыми двумя точками на окружности.
Радиус
Расстояние между любой точкой окружности и центром называется радиусом.
Дуга
любая соединенная часть окружности. Указание двух конечных точек дуги и центра позволяет использовать две дуги, которые вместе составляют полный круг.
Хорда
Отрезок, концы которого лежат на окружности, таким образом, делит окружность на два сегмента.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
из numpy import sin, cos, pi, linspace
#draw point at origin (0, 0)
plt.plot(0,0, color = 'красный', маркер = 'o')
plt.show()
Вывод :
Точка начала координат (0, 0)Добавить аннотацию и установить xlim и ylim
#draw point at origin (0, 0) 0)
plt.plot(0,0, цвет = 'красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1 ), xycoords='data', fontsize=10) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt. show()
Вывод :
Точка с аннотацией# точка рисования в начале координат (0, 0)
plt.plot(0,0, цвет = 'красный', маркер = 'o')
plt.gca( ).annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=10) #нарисовать круг
angles = linspace(0 * pi, 2 * pi, 100 ) xs = cos(angles)
ys = sin(angles) plt.plot(xs, ys, color = 'green') plt.xlim (-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Выход :
Циклplt.plot(0, 0, цвет = 'красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='данные', fontsize=10)#нарисовать круг
angles = linspace(0 * pi, 2 * pi, 100)
r = 1,5
xs = r * cos(углы)
ys = r * sin(углы) plt.plot(xs, ys, color = 'green')plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Вывод :
Круг с радиусом 1,5#точка рисования в начале координат
plt.plot(0,0, color = ' красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=10)# нарисовать круг
углов = linspace(0 * pi, 2 * pi, 100 )
r = 1,5
xs = r * cos(углы)
ys = r * sin(angles)plt.plot(xs, ys, color = 'green') #draw daimeter
plt.plot(1.5, 0, marker = 'o', color = 'blue')
plt .plot(-1.5, 0, маркер = 'o', цвет = 'синий')
plt.plot([1.5, -1.5], [0, 0])
plt.gca().annotate('Диаметр' , xy=(-0,5, -0,25), xycoords='data', fontsize=10) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect( 'равно')
plt.show()
Вывод :
ДиаметрДиаметр вытягивания от 90 градусов
#точка вытягивания в начале
plt.plot(0,0, цвет = 'красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1) , xycoords='data', fontsize=10)#draw circle
angles = linspace(0 * pi, 2 * pi, 100 )
r = 1.5
xs = r * cos(angles)
ys = r * sin(angles )plt.plot(xs, ys, цвет = 'зеленый')#draw daimeter
plt.plot(0, 1.5, маркер = 'o', цвет = 'синий')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt.plot([0, 0], [1.5, -1.5])
plt.gca().annotate('Диаметр', xy=(-0.25, - 0,25), xycoords='data', размер шрифта=10, поворот = 90) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Выход :
Диаметр# точка рисования в начале
plt.plot(0,0, цвет = 'красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1 , 0 + 0.1), xycoords='data', fontsize=10)#draw circle
r = 1.5
angles = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)plt.plot(xs, ys, color = 'green')#draw daimeter
plt.plot(0, 1.5, marker = 'o', color = 'blue')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt.plot([0, 0], [1.5, -1.5])
plt.gca().annotate(' Диаметр', xy=(-0.25, -0.25), xycoords='data', fontsize=10, вращение = 90) #draw radius
plt.plot(0, 0, marker = 'o', color = 'purple ')
plt.plot(1.5, 0, маркер = 'o', цвет = "фиолетовый")
plt.plot([0, 1.5], [0, 0], цвет = "фиолетовый")
plt.gca ().annotate('Радиус', xy=(0.5, -0.2), xycoords='data', fontsize=10) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt .gca().set_aspect('равно')
plt.show()
Вывод :
Радиус# Точка рисования в начале координат
plt.plot(0,0, color = 'red', marker = 'o')
plt.gca().annotate( 'O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=10)#draw circle
r = 1.5
angles = linspace(0 * pi, 2 * pi , 100 )
xs = r * cos(углы)
ys = r * sin(углы)plt.plot(xs, ys, color = 'green')#draw daimeter
plt.plot(0, 1.5, marker = ' o', цвет = 'синий')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt.plot([0, 0], [1.5, -1.5])
plt.gca().annotate('Диаметр', xy=(-0.25, -0.25), xycoords='data', размер шрифта=10 , вращение = 90) # радиус рисования
plt.plot (0, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot (1.5, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot([0, 1.5], [0, 0], color = 'фиолетовый')
plt.gca().annotate('Радиус', xy=(0.5, -0.2), xycoords='данные' , fontsize=10) #draw arc
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'red', lw = 3)
plt.gca().annotate('Arc', xy=(1.5, 0.4), xycoords='data', fontsize=10, вращение = 120) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Выход :
ДугаНарисуйте радиус от 0 до pi/4 и завершите дугу
plt.figure(figsize = (18, 7))#draw point at orgin
plt.plot(0,0, color = 'red', marker = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=10)#draw circle
r = 1,5
углов = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)plt.plot(xs, ys, color = 'green' )#draw daimeter
plt.plot(0, 1.5, маркер = 'o', цвет = 'синий')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt. plot([0, 0], [1.5, -1.5])
plt.gca().annotate('Диаметр', xy=(-0.25, -0.25), xycoords='data', размер шрифта=10, вращение = 90)#draw radius
#plt.plot(0, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot(1.5, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot([0, 1.5], [0, 0], color = 'фиолетовый')
plt.gca().annotate('Радиус', xy=(0.5, -0.2), xycoords='данные' , fontsize=10)#draw arc
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'red', lw = 3)
plt.gca().annotate('Arc', xy=(1.5, 0.4), xycoords='data', fontsize=10, rotate = 120) #нарисовать другой радиус
plt.plot(r * cos(pi/4), r * sin(pi/4), маркер = 'o', цвет = 'красный')
plt.plot([0, r * cos(pi/4)], [0, r * sin(pi/4)], color = "фиолетовый") plt.xlim(-2, 2)
plt. ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Вывод :
ДугаЗапись аннотации дуги
plt.figure(figsize = (18, 7))#точка рисования в начале
plt.plot(0,0, цвет = 'красный', маркер = 'o')
plt.gca().annotate('O (0, 0)', xy=( 0 - 0,1, 0 + 0,1), xycoords='data', fontsize=10)#draw circle
r = 1,5
angles = linspace(0 * pi, 2 * pi, 100)
xs = r * cos(углы)
ys = r * sin(углы)plt.plot(xs, ys, color = 'green')#draw daimeter
plt.plot(0, 1.5, marker = 'o', цвет = 'синий')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt.plot([0, 0], [1.5, -1.5])
plt.gca ().annotate('Диаметр', xy=(-0.25, -0.25), xycoords='data', fontsize=10, rotate = 90)#draw radius
#plt.plot(0, 0, marker = 'o ', color = 'фиолетовый')
plt.plot(1.5, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot([0, 1.5], [0, 0], color = 'фиолетовый ')
plt.gca().annotate('Радиус', xy=(0.5, -0.2), xycoords='data', fontsize=10)#draw arc
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'red', lw = 3)
#plt.gca().annotate('Arc ', xy=(1.5, 0.4), xycoords='data', fontsize=10, вращение = 120)
plt.gca().annotate(r'Arc = r * $\theta$', xy=(1.3, 0.4), xycoords='data', fontsize=10, rotate = 120) #нарисовать другой радиус
plt.plot(r * cos(pi/4), r * sin(pi/4), marker = 'o' , цвет = 'красный')
plt.plot([0, r * cos(pi/4)], [0, r * sin(pi/4)], color = "purple") # рисуем тета-угол и аннотацию
r1 = 0,5
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r1 * cos(arc_angles)
arc_ys = r1 * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'green', lw = 3)
plt.gca().annotate(r'$\theta$', xy=(0,5, 0,2), xycoords='data', размер шрифта=15, вращение = 90)
plt.gca().annotate('< ----- r = 1,5 ---->', xy=(0 - 0,2, 0 + 0,2), xycoords='data', размер шрифта=15, поворот = 45) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Выход :
Дуга с аннотациейplt.figure(figsize = (18, 7))#точка рисования в начале координат
plt.plot(0,0, color = 'red', marker = 'o')
plt.gca().annotate('O ( 0, 0)', xy=(0 - 0.1, 0 + 0.1), xycoords='data', fontsize=10)#draw circle
r = 1.5
angles = linspace(0 * pi, 2 * pi, 100)
xs = r * cos(angles)
ys = r * sin(angles)plt.plot(xs, ys, color = 'green')#draw daimeter
plt.plot(0, 1.5, маркер = 'o', цвет = 'синий')
plt.plot(0, -1.5, маркер = 'o', цвет = 'синий')
plt.plot([0 , 0], [1.5, -1.5])
plt.gca().annotate('Диаметр', xy=(-0.25, -0.25), xycoords='data', fontsize=10, вращение = 90)#draw радиус
#plt.plot(0, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot(1.5, 0, маркер = 'o', цвет = 'фиолетовый')
plt.plot([ 0, 1.5], [0, 0], color = 'фиолетовый')
plt.gca().annotate('Радиус', xy=(0.5, -0.2), xycoords='data', fontsize=10)# нарисовать дугу
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'red', lw = 3)
#plt.gca().annotate('Дуга', xy=(1.5, 0.4), xycoords='data', размер шрифта=10, вращение = 120)
plt.gca().annotate(r'Дуга = r * $\theta$', xy=(1.3, 0.4), xycoords='data', fontsize=10, rotate = 120)#нарисовать другой радиус
plt.plot(r * cos(pi/4), r * sin(pi/4), маркер = 'o', цвет = 'красный')
plt.plot([0, r * cos(pi/4)], [0, r * sin(pi/4)] , color = "purple")# нарисуйте тета-угол и аннотацию
r1 = 0,5
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r1 * cos(arc_angles)
arc_ys = r1 * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'green ', lw = 3)
plt.gca().annotate(r'$\theta$', xy=(0,5, 0,2), xycoords='data', размер шрифта=15, вращение = 90)
plt.gca( ).annotate('<----- r = 1.5 ---->', xy=(0 - 0.2, 0 + 0.2), xycoords='data', размер шрифта=15, вращение = 45) #draw сегмент
r2 = 1,5
segment_angles = линейное пространство (3/4 * 2 * пи, 2 * пи, 100)
segment_xs = r2 * cos(segment_angles)
segment_ys = r2 * sin(segment_angles) plt.plot(segment_xs, segment_ys, color = 'yellow') plt.plot([1.5, 0], [0, - 1.5], color = 'желтый')
plt.gca().annotate('Сегмент', xy=(0.5, -1.2), xycoords='data', размер шрифта=15, вращение = 45)
seg_x_p1 = r2 * cos(2 * pi) plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.show()
Выход :
Сегмент(аккорд)Вот и все. Спасибо за чтение.
Простановка размеров на инженерном чертеже — № 1 Подробное руководство
Содержание
Что такое проставление размеров на инженерном чертеже?
Размеры на инженерных чертежах представляют собой числовые значения, указанные графически в соответствующих единицах измерения на инженерном чертеже с помощью линий, символов и примечаний.
Они указываются на техническом чертеже для определения размерных характеристик, таких как длина, высота, ширина, диаметр, радиус, угол и т. д.
Бюро индийских стандартов (BIS) рекомендует общий принцип определения размеров в инженерных чертежах в своем бюллетене IS 11669:1986 (подтверждено в 1999 г.).
Важность размеров в инженерных чертежах
Чтобы обеспечить четкое и полное описание особенностей объекта, необходимы правильные размеры в технических чертежах.
Типы размеров на технических чертежах:
Размеры подразделяются на следующие типы:
- Функциональные размеры.
- Нефункциональные размеры.
- Дополнительные размеры.
Функциональные размеры (F)
Это размеры в инженерном чертеже, которые важны для функции детали или пространства.
Нефункциональные размеры (NF)
Это размеры в техническом чертеже, которые не важны для функции детали или пространства.
Дополнительные размеры (AUX)
Размеры на техническом чертеже, которые даны только в информационных целях. Он выводится из других значений, показанных на чертеже или в соответствующих документах.
Вспомогательный размер дан в безродительском формате, и к нему не применяются допуски.
Терминология простановки размеров
Различные термины, связанные с простановкой размеров в технических чертежах, следующие:
Размерное значение
размерный. Размеры выражены в конкретных единицах на чертеже с соответствующей информацией.
Размеры выражены в конкретных единицах на чертеже с соответствующей информацией.
Размерные линии
Размерные линии представляют собой тонкие непрерывные линии, показывающие протяженность и направление размера. Эти линии должны располагаться на расстоянии от 8 до 10 мм от контура чертежа и должны располагаться равномерно на расстоянии от 6 до 8 мм друг от друга. Значения размеров предпочтительно размещать рядом с серединой размерных линий.
Линии проекций
Линии проекций представляют собой тонкие непрерывные линии, вытянутые из контуров для определения размеров и выступающие на 2–3 мм за пределы размерных линий. Они должны быть нарисованы в направлении, перпендикулярном элементу, размер которого необходимо измерить. Линии размеров и линии проекций не должны пересекаться с другими линиями, за исключением случаев, когда это неизбежно.
Но в случае особых обстоятельств линии проекций могут быть проведены косо, но параллельно друг другу.
Выноски
Выноски представляют собой тонкие непрерывные линии, оканчивающиеся стрелкой или точкой, обозначающей элемент и примечание. Рисунок и примечания пишутся над расширенной размерной линией.
Во избежание путаницы выноски не должны быть –
- наклонены под углом менее 30°
- параллельно соседним линиям проекций.
- параллельные или смежные размеры.
Выноски никогда не рисуются горизонтально, вертикально, изогнуто или от руки. Обычно их рисуют под любым удобным углом 30°, 45° и 60°. Обычно избегают длинных лидеров.
Стрелки
Окончание размерных линий указано стрелками. Наконечники стрелок могут быть открыты под удобным углом от 30° до 90°, закрыты заполненными или закрытыми пустыми. Закрытые заполненные наконечники стрел имеют длину, примерно в три раза превышающую ширину/глубину, и обычно предпочтительны на инженерных чертежах.
Обычно длина наконечника стрелки для мелкого рисунка составляет 3 мм, а для большого рисунка длина наконечника стрелки составляет 5 мм.
Если места для окончания наконечников стрелок недостаточно, можно использовать косую черту и точки.
Способы нанесения размеров на инженерном чертеже:
Размеры наносятся на чертеже одним из следующих способов, рекомендованных СП 46-2003.
SP 46 (2003): Практика инженерного черчения для школ и колледжей.
Ниже приведены две рекомендуемые системы нанесения размеров:
Выровненная система размеров на инженерном чертеже:
При этом способе нанесения размеров размерный текст размещается параллельно размерной линии и желательно над ней в середине.
Тексты размеров размещены таким образом, чтобы их можно было прочитать либо снизу, либо с правой стороны чертежа.
Линейные размеры
Угловые размеры
Однонаправленная система размеров на техническом чертеже:
При однонаправленном методе размеров размеры указаны таким образом, что их можно нанести только в горизонтальном направлении.
Линейные размеры
Угловые размеры
Расположение размеров
Если на инженерном чертеже необходимо разместить несколько размеров, эти размеры должны быть расположены таким образом, чтобы они давали однозначное объяснение.
Классификация размеров на основе расположения следующая.
Цепное или непрерывное определение размеров
В этом методе последовательные размеры располагаются в виде непрерывной прямой линии.
Параллельное нанесение размеров или последовательное нанесение размеров
В этом методе ряд отдельных размеров, параллельных друг другу, размещаются из общего начала. Этот метод применяется, когда ряд измерений имеют общее происхождение. Накопленной ошибки можно избежать, следуя этому методу.
Текущие размеры или наложенные размеры
В этом методе размеров все размеры начинаются от общего начала, которое обозначено маленьким кругом диаметром 3 мм, и заканчиваются стрелками, где заканчивается отдельный размер.
Тексты размеров повернуты на 90° и размещены на одной линии с линией разложения или над линией размера рядом со стрелкой.
Комбинированное нанесение размеров
При таком расположении размеров на одном чертеже одновременно используются параллельные, цепные и непрерывные размеры.
Простановка размеров в координатах
Всякий раз, когда деталь имеет слишком много размеров, легче читать чертеж с помощью метода простановки размеров в координатах.
Пример : Пластина с большим количеством отверстий может быть легко прочитана с помощью метода измерения координат. Другие стили определения размеров в этом случае дадут чрезмерно загроможденный результат.
В этой системе происхождение и другие особенности должны быть численно нивелированы. Координатная таблица содержит все размерные детали, которые должны быть размещены рядом с чертежом.
Правила нанесения размеров в инженерном чертеже
Соблюдение набора стандартных правил определения размеров очень важно, поскольку размеры используются для определения характеристик размера нарисованного объекта, таких как длина, высота, ширина, радиус, диаметр, угол и т. д. с линиями, примечаниями и символами.
д. с линиями, примечаниями и символами.
Бюро индийских стандартов (BIS) предлагает правила определения размеров в инженерных чертежах в своем бюллетене IS 11669:1986 (подтверждено в 1999 г.).
ИС 11669: 1986 (подтверждено в 1999 г.): Общие принципы нанесения размеров на технические чертежи
Правила нанесения размеров:
При нанесении размеров необходимо соблюдать следующие правила размеров:
- Однако в случае простановки радиуса дуги или окружности он может быть показан внутри.
2. Правила определения размеров для круга: Размер круга должен быть обозначен символом диаметра Ø. Символ Ø должен располагаться перед значением размера.
Размер дуги должен быть обозначен символом радиуса R .
3. Правила определения размеров осевой линии:
i. Ось или осевая линия не должны использоваться в качестве размерной линии со стрелками на концах.
ii. Оси или осевые линии должны выходить примерно на 3 мм за границу детали, детали которой они обозначают.
III. Отметка размера от осевой линии неверна , за исключением случаев, когда осевая линия проходит через центр отверстия.
Кроме того, удлиненная осевая линия может использоваться в качестве удлинительной линии.
4. Правила простановки размеров отверстий:
Расстояние между центрами отверстий должно быть равно размеру на виде, на котором отверстия видны.
5. Размеры должны быть сделаны по видимым линиям , а не по невидимым или скрытым линиям.
6. Значение размера должно располагаться примерно на 2 мм выше размерной линии.
7. Выносная линия должна выходить за размерную линию на 2 мм.
8. Правила определения размеров конической секции:
Размер конической сужения по диаметру должен быть указан, как показано на рисунке.
Коническая конусность = (D-d)/L= 1 дюйм n
9. Правила нанесения размеров для заштрихованной части:
При проставлении размеров в заштрихованной части чертежа линия штриховки не должна пересекать размерный текст.
10. Правила определения размеров повторяющихся элементов:
Насколько это возможно, избегают измерения повторяющихся элементов одного размера.
Заметки должны быть написаны горизонтально. Линии выноски должны быть наклонены под углом 30°, 45° и 60° к горизонтали.
11. Общие правила определения размеров:
Габаритные размеры должны располагаться вне промежуточных размеров.
Меньшие размеры должны располагаться ближе к виду, а большие — дальше, чтобы выносные линии или линии проекций не пересекали размерные линии.
12. Правила нанесения размеров ломаного элемента:
Размерная линия должна быть показана сплошной там, где фигура, которую она представляет, показана ломаной.
13. Если размерную линию невозможно полностью провести до ее нормальной точки окончания, свободный конец должен заканчиваться двойной стрелкой.
14. Насколько это возможно, все размеры на конкретном чертеже должны быть указаны только в одной единице.
15. Размеры, указанные на одном виде, не обязательно повторять на другом виде, за исключением случаев ясности и идентификации.
16. Размеры должны быть размещены на том виде, который наиболее четко показывает соответствующие элементы.
17. Линия чертежа никогда не должна использоваться в качестве размерной линии или не должна совпадать с размерной линией. Размерная линия должна располагаться равномерно по всему чертежу. Размерные линии должны быть на расстоянии 8–10 мм от контура чертежа и на расстоянии 6–8 мм друг от друга.
18. Размерный текст желательно располагать ближе к середине. Если это неизбежно из-за нехватки места, размерный текст может быть размещен над расширенной частью размерной линии за пределами стрелок, предпочтительно с правой стороны.
Определение размеров – Базовое чтение чертежей
- Цифры
- Размеры
- Удлинительные линии
- Наконечники стрел
- Фигуры с размерами
- Изометрические размеры
- Орфографические размеры
Если рисунок должен быть завершен, чтобы объект, представленный на рисунке, мог быть выполнен так, как задумал дизайнер, он должен рассказывать две полные истории. Об этом говорит просмотров , которые описывают форму объекта, а также с размерами и примечаниями , в которых указаны размеры и другая информация, необходимая для изготовления объекта.
Таким образом, ваш следующий шаг — изучить основы простановки размеров. Таким образом, вы поймете не только, как интерпретировать рисунок, чтобы получить необходимую информацию, но и как определить размеры ваших эскизов, чтобы их можно было использовать для передачи информации о размерах другим.
Цифры Это может показаться немного простым, но перед определением размеров следует выполнить несколько упражнений с фигурами чисел. Причина такого пересмотра просто в том, что неправильно или небрежно нанесенные цифры на чертеже или эскизе могут быть легко неверно истолкованы кем-то на работе. Это может дорого обойтись.
Причина такого пересмотра просто в том, что неправильно или небрежно нанесенные цифры на чертеже или эскизе могут быть легко неверно истолкованы кем-то на работе. Это может дорого обойтись.
Таким образом, изучение форм чисел оправдано.
Представленные здесь числовые формы признаны наиболее разборчивыми и используются в промышленности по всей стране. Стандартизированные в США вертикальные числа 1/8” правильно формируются следующим образом:
Размерные линииРазмерная линия представляет собой тонкую темную сплошную линию со стрелками на каждом конце. Указывает направление и протяженность измерения. В машинных эскизах и чертежах, в которых дроби и десятичные знаки используются для размеров, размерная линия обычно прерывается около середины, чтобы освободить место для цифр размера. На архитектурных и конструктивных эскизах и чертежах цифры обычно располагают над сплошной размерной линией.
В любом случае ближайшая к объекту размерная линия должна располагаться примерно на расстоянии
1/2″. Другие размеры за пределами первого измерения (если есть) должны быть разделены примерно на 3/8″. Вам не обязательно помнить об этом, но вы должны помнить, что размерные линии не должны сгущаться, а расстояние между ними должно быть одинаковым.
Другие размеры за пределами первого измерения (если есть) должны быть разделены примерно на 3/8″. Вам не обязательно помнить об этом, но вы должны помнить, что размерные линии не должны сгущаться, а расстояние между ними должно быть одинаковым.
Самое главное, чтобы чертеж был «чистым», а размеры располагались в пространстве, где их нельзя было бы спутать с поверхностью, для которой они не предназначены.
Вот как должны быть нарисованы размерные линии:
Примечание. Размеры менее шести футов (72 дюймов) указаны в дюймах. Размеры свыше шести футов обычно указываются в футах и дюймах. Убедитесь, что понятно, как вызываются размеры. При вызове размеров, которые превышают 12 дюймов, убедитесь, что ВСЕ размеры указаны в дюймах или футах в дюймах по всему чертежу. Либо 4 фута-5 дюймов, либо 53 дюйма, они оба означают одно и то же, но если есть сочетание размеров, может быть легко посмотреть на 4 фута-8 дюймов и увидеть 48 дюймов.
Выносные линии Выносные линии на чертеже — это тонкие, темные, сплошные линии, которые выходят наружу из точки на чертеже, к которой относится размер. Обычно размерная линия пересекается с выносной линией под прямым углом. Должен быть зазор около 1/16″ там, где выносная линия будет встречаться с контуром объекта, а выносная линия должна выходить за крайний наконечник стрелки примерно на 1/8″. Также не должно быть пробелов в местах пересечения выносных линий. Обратите внимание, что в этом примере большие размеры правильно размещены снаружи или за пределами более коротких размеров, и что размеры желательно не наносить на сам объект. Однако иногда необходимо нанести размер на объект.
Обычно размерная линия пересекается с выносной линией под прямым углом. Должен быть зазор около 1/16″ там, где выносная линия будет встречаться с контуром объекта, а выносная линия должна выходить за крайний наконечник стрелки примерно на 1/8″. Также не должно быть пробелов в местах пересечения выносных линий. Обратите внимание, что в этом примере большие размеры правильно размещены снаружи или за пределами более коротких размеров, и что размеры желательно не наносить на сам объект. Однако иногда необходимо нанести размер на объект.
Важно не забывать размещать размеры на видах в двух- или трехвидовом чертеже, где их будет легче всего понять. Избегайте нанесения размеров по скрытой линии и избегайте дублирования размеров. Используй здравый смысл; размеры должны быть максимально четкими и простыми. Помните, что человек, читающий ваш рисунок, должен четко понимать, что делать дальше. В противном случае дорогостоящее время и материалы будут потрачены впустую.
Существует два основных метода нанесения размеров на эскиз. Их можно разместить так, чтобы они читались снизу эскиза (однонаправленные размеры) или снизу и справа (выровненные размеры). Однонаправленная система обычно лучше, потому что она легче читается рабочими.
Когда размеры не помещаются в пространстве обычным способом, используются другие методы для четкого определения размеров, когда существуют условия тесноты.
Наконечники стрелок
Наконечники стрелок размещаются на каждом конце размерных линий, на направляющих линиях и т. д. пока они широкие. Обычно у них есть небольшая зазубрина, очень похожая на рыболовный крючок.
Чтобы ваш рисунок выглядел четким, используйте один и тот же стиль во всем рисунке или наброске.
Цифры размеров
Цифры, используемые для обозначения размеров объекта, обычно имеют высоту около 1/8 дюйма.
Когда размер включает дробную часть, дробная часть имеет высоту примерно 1/4″, что делает дробные числа немного меньше, чтобы обеспечить пространство над и под дробной линией.
Опять же, особенно важно, чтобы числа и дроби, которые вы можете нанести на эскиз или рисунок, были разборчивыми. Неаккуратные числа могут привести к дорогостоящим ошибкам.
Примечания
Примечания используются на чертежах для предоставления дополнительной информации. Они должны быть краткими и тщательно сформулированными, чтобы избежать неправильного толкования, и располагаться на эскизе в малолюдном месте. Линии выноски, идущие к ноте, должны быть короткими. Примечания обычно добавляются после того, как на эскизе были нанесены размеры, чтобы избежать помех с размерами.
Викторина
Указания: Измерьте примеры, как указано.
Измерьте этот прямоугольник 3 ¼ x 6 15/32 в одном направлении сверху и справа.
С примечанием покажите просверленное отверстие 5/16.
Измерьте этот объект. Более короткие линии имеют длину 3 дюйма.
Более короткие линии имеют длину 3 дюйма.
Измерьте этот объект. Используйте линейку или шкалу, чтобы определить длину линий.
Наклонное определение размеров
Косое определение размеров в основном связано с тем, чтобы не наносить размеры на сам объект (когда это возможно) и использовать принципы определения размеров, основанные на здравом смысле. Также обычно лучше всего считывать размеры снизу (в одном направлении), как показано здесь.
Хотя лучше не наносить размеры на сам вид, обычно принято размещать размеры диаметра и радиуса на видах, если позволяет место.
Иногда пространство и время ограничены, и вам, возможно, придется изменить типичные правила рисования и определения размеров. Самое главное, чтобы рисунок был чистым, лаконичным, старайтесь не повторять размеры, а давать все необходимые.
Направления: Заполните, как указано.
Измерьте этот трехдюймовый куб.
Более короткая часть этого стержня имеет диаметр 5/8 дюйма и длину 2 1/8 дюйма. Более длинная секция имеет диаметр 7/8 дюйма и длину 3 ½ дюйма. Размер чертежа.
Изометрические размеры
При нанесении размеров в изометрическом эскизе важно, чтобы размеры не касались самого объекта, а размер располагался в той же плоскости, что и поверхность измеряемого объекта. Вы, вероятно, обнаружите, что для правильного измерения в изометрии потребуется некоторая практика.
Размещайте заметки на изометрическом чертеже без оглядки на размещение их на той же плоскости, что и с размерами. Это легче сделать, и легче читать.
Изометрические заметки не обязательно должны быть в одной плоскости.
Обратите внимание, что в приведенном выше примере часть каждой линии выноски к примечаниям нарисована приблизительно под углом 15, 30, 45, 60 или 75 градусов. Это сделано для того, чтобы избежать путаницы с другими линиями. Никогда не рисуйте линии выноски полностью горизонтально или вертикально .
Это сделано для того, чтобы избежать путаницы с другими линиями. Никогда не рисуйте линии выноски полностью горизонтально или вертикально .
Викторина
Направления: выполните, как указано.
Измерьте этот чертеж. Размеры: 3 дюйма в длину, 2 1/8 дюйма в ширину, 1 5/8 дюйма в высоту и угол 45◦ ½ дюйма в глубину. Угол начинается как середина размера длиной 3 дюйма.
Измерьте этот чертеж. Основание квадратное ½” x 1 ½”. Цилиндр имеет диаметр 1 дюйм. x 1-1/8”
длин. Просверленное сквозное отверстие ∅5/8”.
Викторина
Указания: Вам дадут объект для эскиза и измерения.
Орфографические размеры Когда вы смотрите на объект в виде ласточкиного хвоста несколько страниц назад, легко заметить, что изометрический эскиз может быстро загромождаться размерами. Из-за этого более сложные наброски и рисунки имеют размерность в орфографии. Этот метод обеспечивает наилучший способ четкого и подробного определения размеров.
Из-за этого более сложные наброски и рисунки имеют размерность в орфографии. Этот метод обеспечивает наилучший способ четкого и подробного определения размеров.
Вот семь общих правил, которым необходимо следовать при определении размеров.
- Покажите достаточное количество размеров, чтобы предполагаемые размеры можно было определить, не заставляя рабочего рассчитывать или принимать какие-либо расстояния.
- Четко укажите каждое измерение, чтобы оно понималось только одним способом.
- Покажите размеры между точками, линиями или поверхностями, которые имеют необходимую взаимосвязь друг с другом или которые определяют расположение других компонентов или сопряженных частей.
- Выберите или расположите размеры, чтобы избежать накопления размеров, которые могут привести к неудовлетворительному сопряжению деталей. (Другими словами, предусмотрите наращивание допусков, как в примере ниже.
- Показать каждое измерение только один раз.


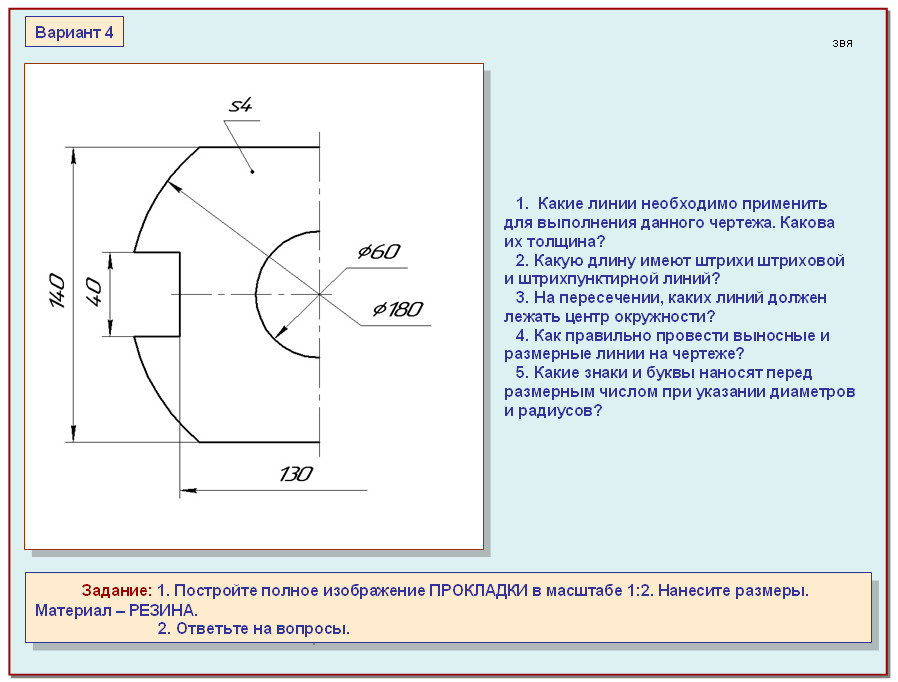
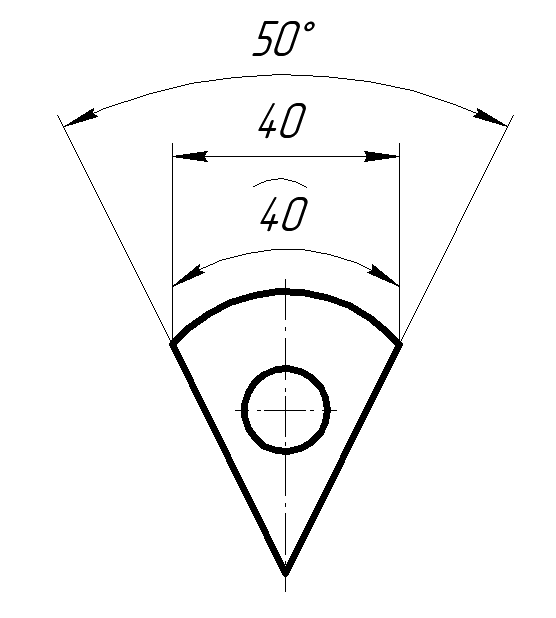
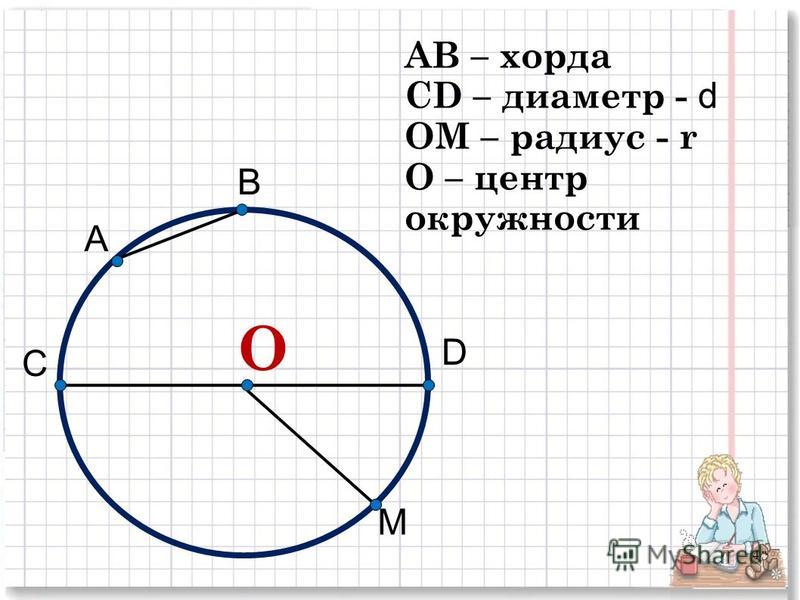 Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой.
Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой.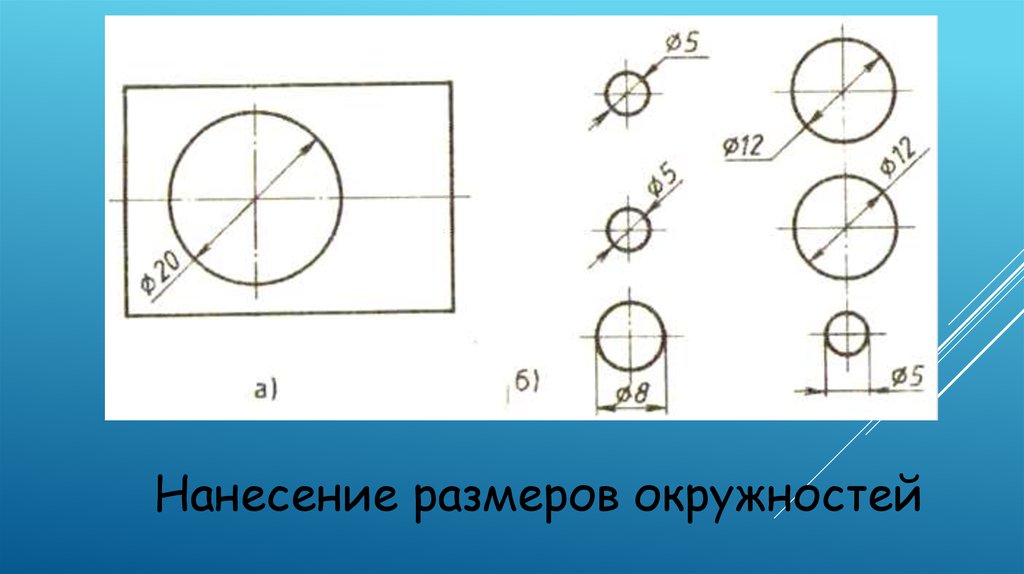 Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :
Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :