Графы. Применение графов к решению задач
1. Методические рекомендации к теме “Графы”.
Понятие графа целесообразно вводить после
того, как разобрано несколько задач, подобных
задаче 1, решающее соображение в которых –
графическое представление. Важно, чтобы ученики
сразу осознали, что один и тот же граф может быть
нарисован разными способами. Строгое
определение графа, на мой взгляд, давать не нужно,
т.к. оно слишком громоздко и это только затруднит
обсуждение. На первых порах хватит и
интуитивного понятия. При обсуждении понятия
изоморфизма можно решить несколько упражнений
на определение изоморфных и неизоморфных графов.
Одно из центральных мест темы – теорема о
четности числа нечетных вершин. Важно, чтобы
ученики до конца разобрались в ее доказательстве
и научились применять к решению задач. При
разборе нескольких задач рекомендую не
ссылаться на теорему, а фактически повторять ее
доказательство. Чрезвычайно важно также понятие
связности графа. Содержательным соображением
здесь является рассмотрение компоненты
связности, на это необходимо обратить особое
внимание.
Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).
2. Теоретический материал к теме “Графы”.
Введение
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1. Между девятью планетами
солнечной системы установлено космическое
сообщение.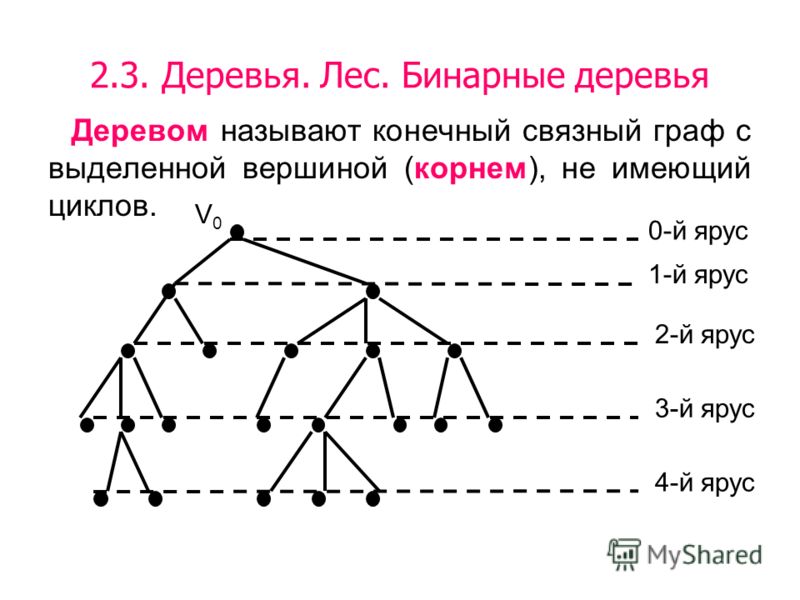 Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако
решения этих двух задач объединяет общая идея –
графическое представление решения. При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные
графы, называются изоморфными.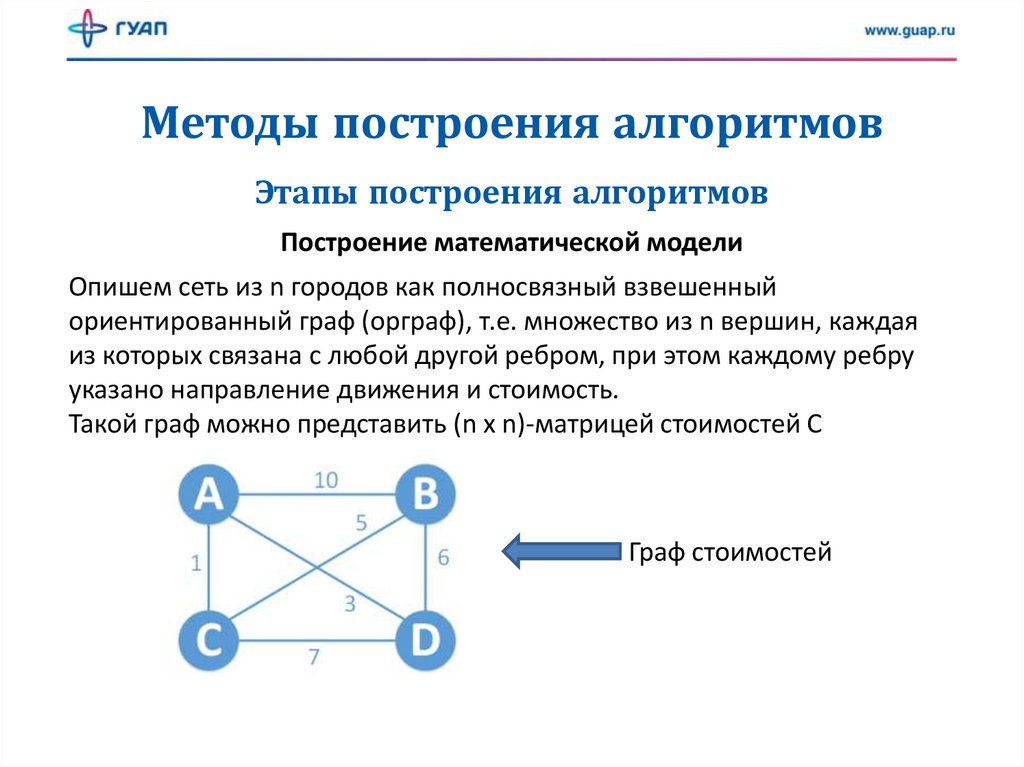
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение
телефонов возможно. Тогда представим себе граф, в
котором вершины обозначают телефоны, а ребра –
провода, их соединяющие. Подсчитаем, сколько
всего получится проводов. К каждому телефону
подключено ровно 5 проводов, т.е. степень каждой
вершины нашего графа – 5.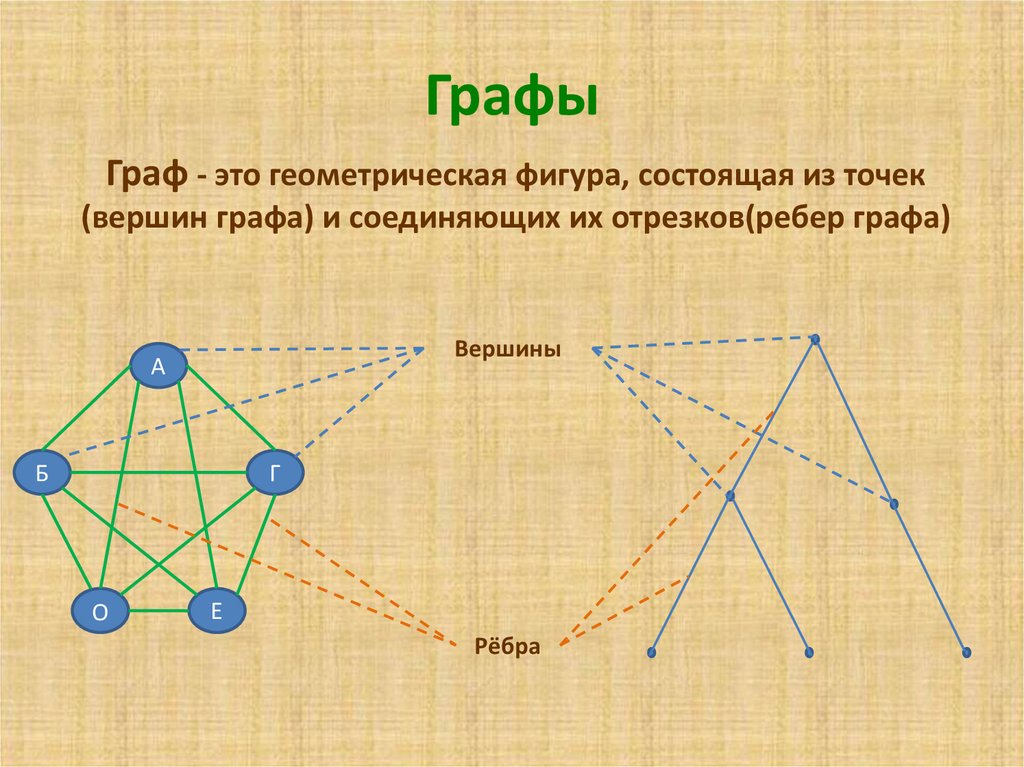 Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если из любые две
его вершины можно соединить путем, т. е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее
определение, то утверждение задачи можно
переформулировать и по-другому: “Доказать, что
граф дорог страны Семерка связен.
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если
нарисовать граф ковролиний Царства, то он может
быть несвязным. Рассмотрим компоненту связности,
которая включает в себя столицу Царства. Из
столицы выходит 21 ковролиния, а из любых других
городов, кроме города Дальний – по 20, поэтому,
чтобы выполнялся закон о четном числе нечетных
вершин необходимо, чтобы и город Дальний входил в
эту же самую компоненту связности.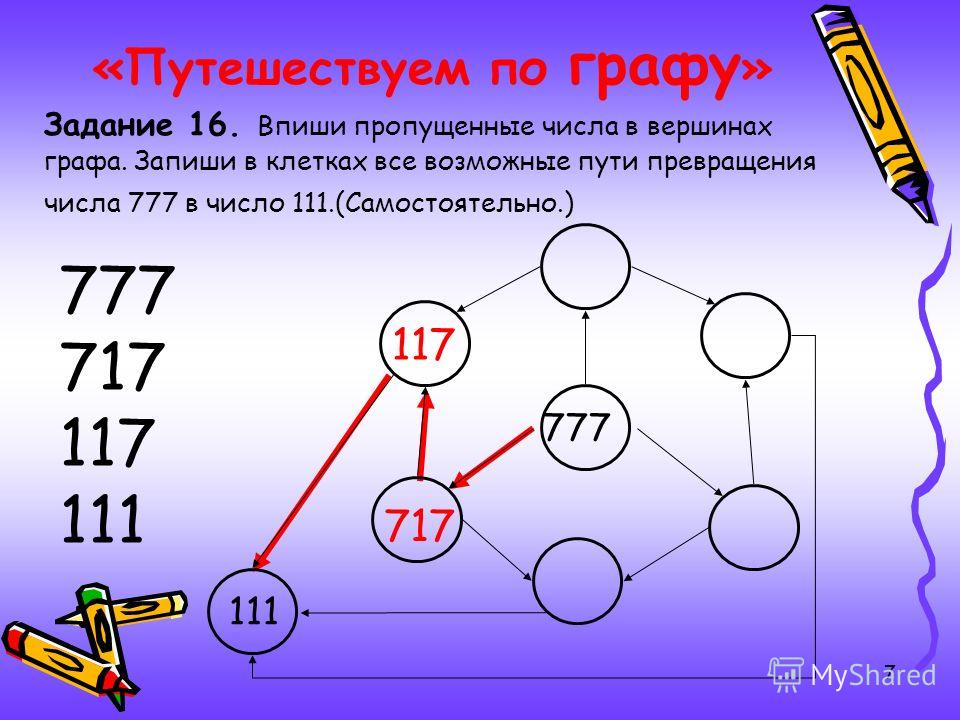
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так,
как сказано в условии, то в каждую вершину, кроме
начальной и конечной, мы войдем столько же раз,
сколько выйдем из нее. То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
Рис. 1 | Рис. 2 |
Решение.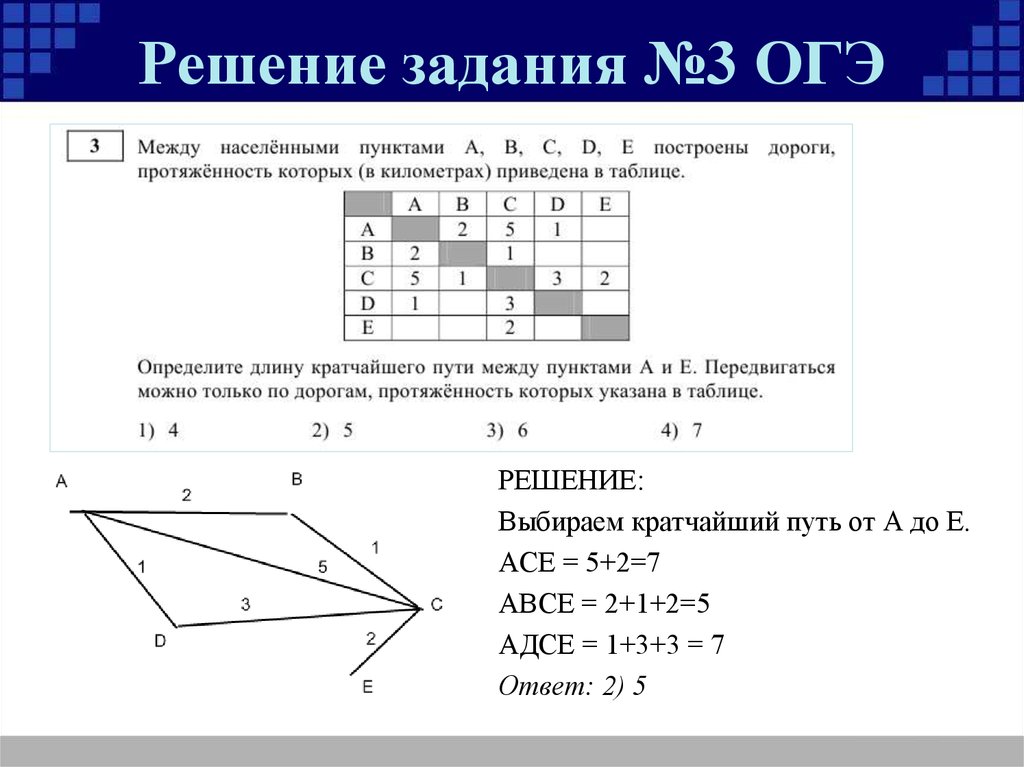 Занумеруем клетки доски, как
показано на рисунке:
Занумеруем клетки доски, как
показано на рисунке:
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому
городу точку и соединив точки линией, если сумма
цифр делится на 3, получим граф, в котором цифры 3,
5, 9 связаны между собой, но не связаны с
остальными. Значит долететь из города 1 в город 9
нельзя.
Значит долететь из города 1 в город 9
нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?
Ответ. Нет (теорема о четности числа нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число
дорог равно числу городов х, умноженному на 3
(число выходящих из каждого города дорог) и
разделенному на 2 (см.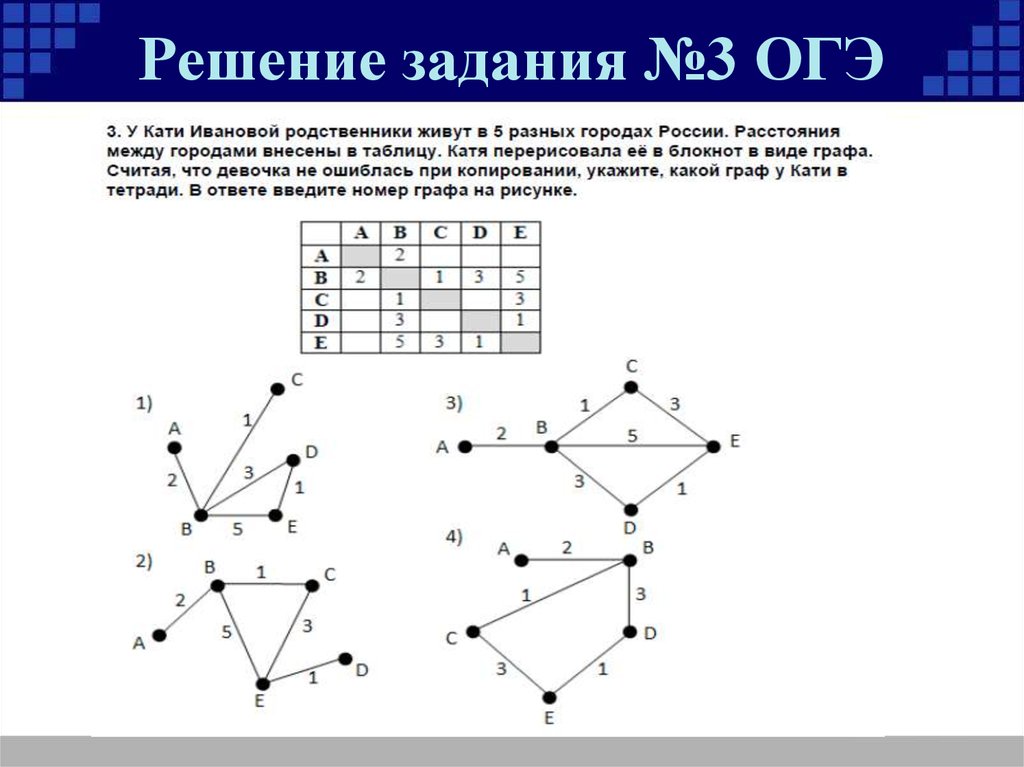 задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами
так, что от каждого острова можно добраться до
любого другого. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?
Применение графов при решении задач
Задачи на вычерчивание фигур одним росчерком
Задача 1. О Кенигсбергских мостах. Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города были соединены семью мостами. По воскресеньям горожане совершали прогулки по городу.
Вопрос: можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту. Благодаря этой задаче была создана теория графов.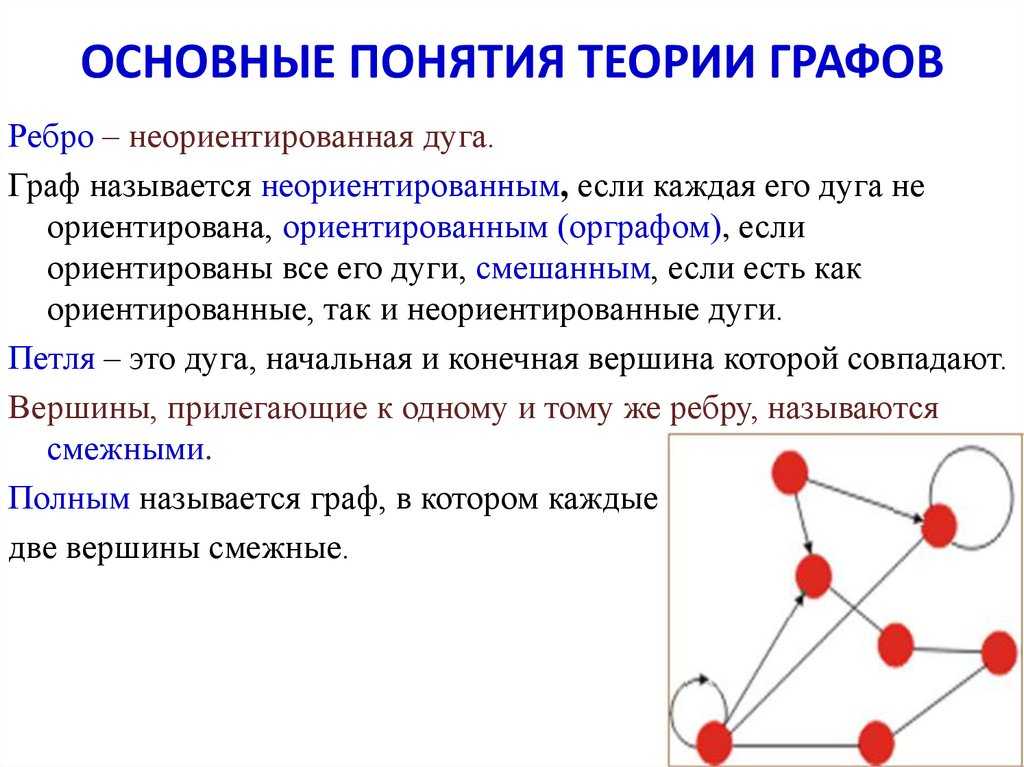
Мосты через реку Прегель расположены как на рисунке.
(приложение 2 рис.1).
Рассмотрим граф, соответствующий схеме мостов
Проблема семи мостов Кёнигсберга.
Суть: можно ли пройти по 7 мостам города Кёнигсберга, не ступив на каждый более одного раза.
Решение: было найдено русско-немецким математиком Леонардом Эйлером(1736 год).
Его рассуждения заключались в следующем:
1) Число нечётных вершин графа должно быть чётно (теорема 2).
2) Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
3) Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
4) Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Задача 2. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса?
Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса?
Решение: Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршруты – не пересекающиеся между собой линии.
Ответ: с Земли до Марса добраться нельзя.
Логические задачи.
Задача 3. В соревнованиях по борьбе, проходящих по олимпийской системе, участвуют 20 борцов. За какое минимальное время можно провести соревнование, если в спортивном зале есть только три борцовских ковра, и на каждую схватку, включая разминку и отдых, отводится час? Изобразите схему соревнований с помощью корневого дерева.
Решение: одна из возможных схем приведена на рисунке.
(приложение 2 рис.2)
Ответ: На соревнование уйдет 7 часов.
Задача 4. Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах.
Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах.
Решение: Разобьем монеты на три группы по три монеты. Положим монеты двух групп на разные чашки весов.
Если чашки придут в равновесие, то фальшивая монета — в третьей группе. Если чашки не придут в равновесии, то фальшивая — в более легкой группе. Поиск фальшивой монеты среди троих: положим две монеты на разные чашки весов.
Если чашки придут в равновесие, то фальшивая — третья монета. Если чашки не придут в равновесии, то фальшивая — более легкая монета.
Решение этой задачи легко изобразить в виде графа-дерева, похожего на алгоритм. (приложение 2, рис.3)
Задачи на группу знакомств
Задача 5. Однажды Андрей, Борис, Володя, Даша и Галя договорились вечером пойти в кино. Выбор кинотеатра и сеанса они решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?
Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?
Решение:
Нарисуем пять точек и обозначим их буквами А, Б, В, Г, Д.
Это первые буквы имён.
Соединим те точки, которые соответствуют именам созвонившихся ребят.
(приложение 2, рис.4)
Задача 6. В первенстве класса по настольному теннису 6 участников: Андрей, Борис Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?
Сколько игр проведено к настоящему моменту и сколько еще осталось?
Решение: Получим, что сыграно 7 игр, а осталось – 8. Можно проверить: в графе 6 вершин тогда всего ребер 6*5/2=15 (7+8).
Логическая задача на переливание. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. Требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю.
Решение:
Ситуацию в каждый момент можно описать тремя числами (приложение рис.16).
В результате получаем два решения:
одно в 7 ходов, другое в 8 ходов.
(приложение 2, рис.5)
Задача 7. Имеется шахматная доска 3×3, в верхних двух углах стоят два чёрных коня, в нижних – два белых (рисунок ниже). За 16 ходов поставьте белых коней на место чёрных, а чёрных на место белых и докажите, что за меньшее число ходов это сделать невозможно.
Решение: Развернув граф возможных ходов коней в круг, получим, что в начале кони стояли так, как на рисунке ниже. А в конце кони должны поменяться местами, при этом каждый конь должен сделать 4 хода, а меньшим числом ходов обойтись не удастся, т. к. кони не могут перепрыгивать через друг друга.
Тогда, передвигая коней в графе, каждый раз перемещая всех коней, как показано на рисунках 1-4, мы получим за 16 ходов белых коней на месте чёрных, а чёрных на месте белых (рис.5). (приложение 2, рис.6)
Примеры задач, решаемых методом графов в приложении 3.
Перейти к разделу 2.3. Генеалогическое древо – один из способов применения теории графов
4. Решение задач с помощью графов. Мерзляк (угл.)
Онлайн. Глава 1. Линейное уравнение с одной переменной. § 4. Решение задач с помощью графов. Упражнения №№ 4.1 — 4.14. Итоги главы 1. Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Алгебра 7 класс Мерзляк, Поляков (угл.изуч.)
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
§ 4. Решение задач с помощью графов.
Вы хорошо знаете, что составление уравнений — это не единственный способ решения текстовых задач. Также эффективным приёмом является «решение задач по действиям», т. е. арифметическим способом, когда в определённой последовательности находят значения числовых выражений и в конечном итоге получают ответ. Здесь переводом задачи из реальной жизни на математический язык является запись одного или нескольких числовых выражений.
Заметим, что в начальной школе именно с этого способа вы начали знакомство с методами решения текстовых задач.
Методы решения задач, представляющие реальные ситуации, разнообразны и далеко не исчерпываются моделями в виде числовых выражений или уравнений. Изучая математику, вы будете расширять список соответствующих моделей. Сейчас познакомимся с методом, применение которого основано на построении математической модели в виде геометрической фигуры. Заметим, что вы уже использовали элементы этого приёма, когда в задачах на движение строили различные схемы: движения в одном направлении, в противоположных направлениях, навстречу друг другу и т. п.
Изучая математику, вы будете расширять список соответствующих моделей. Сейчас познакомимся с методом, применение которого основано на построении математической модели в виде геометрической фигуры. Заметим, что вы уже использовали элементы этого приёма, когда в задачах на движение строили различные схемы: движения в одном направлении, в противоположных направлениях, навстречу друг другу и т. п.
ПРИМЕР 1. В регионе есть пять городов. Можно ли эти города связать дорогами так, чтобы из каждого города выходили: 1) четыре дороги; 2) три дороги?
Решение. Построим схему, на которой города будут изображены точками А, В, С, D и Е. Дорогу, соединяющую два города, будем изображать в виде отрезка. Например, на рисунке 4.1 показана кольцевая схема дорог.
1) Задача сводится к тому, чтобы выяснить, можно ли пять точек плоскости соединить отрезками так, чтобы из каждой точки выходили четыре отрезка. На рисунке 4.2 показано, как это сделать.
2) Предположим, что такая схема возможна. Подсчитаем, сколько отрезков будет на этой схеме. Имеем: 5*3 = 15 (отрезков). Однако при таком подсчёте каждый отрезок был учтён дважды. Получается, что количество отрезков равно 15/2. Это число не является целым. Получили противоречие.
Подсчитаем, сколько отрезков будет на этой схеме. Имеем: 5*3 = 15 (отрезков). Однако при таком подсчёте каждый отрезок был учтён дважды. Получается, что количество отрезков равно 15/2. Это число не является целым. Получили противоречие.
Ответ: 1) да; 2) нет. ■
В повседневной жизни нам нередко приходится пользоваться рисунками, состоящими из точек, некоторые из которых соединены линиями. Например, на рисунке 4.3 изображена схема метрополитена Санкт–Петербурга.
Такие рисунки называют графами. Точки на рисунке называют вершинами графа, а соединяющие их линии — рёбрами графа.
На рисунке 4.4 приведены ещё несколько примеров графов.
Вооружившись фантазией, можно представить, что эти рисунки иллюстрируют схемы автомобильных дорог, план городка аттракционов и даже отношения между людьми, например такие как дружба.
Любопытно, что рисунки такого вида и дворянский титул имеют одинаковое название — граф. Это слово произошло от латинского grafito — пишу.
Это слово произошло от латинского grafito — пишу.
Графами удобно пользоваться тогда, когда хотят описать связь между объектами, событиями или процессами. Проиллюстрируем сказанное на примере решения следующей задачи.
ПРИМЕР 2. Существует ли компания из 16 человек, в которой каждый дружит ровно с 6 другими людьми из этой компании?
Решение. Нарисуем 16 точек так, как показано на рисунке 4.5. Эти точки изображают 16 человек данной компании. Возьмём произвольную точку и соединим её со всеми точками, находящимися с ней на одной горизонтали или вертикали. Получили 6 рёбер графа, которые соответствуют дружеским связям. Так можно поступить с каждой из 16 точек.
Ответ: существует. ■
Количество рёбер, выходящих из вершины графа, называют степенью этой вершины. Например, степень каждой вершины, изображённой на рисунке 4.1, равна 2.
Заметим, что решение задачи 2 из примера 1 свелось к выяснению вопроса: существует ли пятивершинный граф, степень каждой вершины которого равна 3? Ответ на этот вопрос оказался отрицательным. На самом деле имеет место более общий факт: в любом графе количество вершин, степень которых нечётная, является чётным числом. Он следует из того, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер, а следовательно, является чётным числом.
На самом деле имеет место более общий факт: в любом графе количество вершин, степень которых нечётная, является чётным числом. Он следует из того, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер, а следовательно, является чётным числом.
При проектировании системы транспортных маршрутов важнейшим требованием является возможность попасть из любого населённого пункта в любой другой. На языке теории графов это означает, что соответствующий граф должен обладать таким свойством: любые две вершины графа соединены некоторым путём, т. е. последовательностью рёбер, каждое следующее из которых начинается в конце предыдущего. Граф, обладающий описанным свойством, называют связным.
На рисунке 4.6 изображён связный граф, а граф, изображённый на рисунке 4.7, связным не является.
ПРИМЕР 3. В некотором регионе 9 городов. Из каждого города выходят 4 дороги, связывающие его с четырьмя городами этого региона. Докажите, что из любого города можно проехать в любой другой город.
Решение. Предположим, что не существует пути, соединяющего города А и В. Каждый их этих двух городов соединён с четырьмя другими (отличными от А и В).
Если город А и город В соединены с одним и тем же городом, это означает, что существует путь, соединяющий города А и В. Следовательно, чтобы такого пути не существовало, все 8 городов, с которыми соединены города А и В, должны быть различными. Добавив к ним города А и В, получаем, что количество городов в данном регионе не меньше 10, что противоречит условию задачи. Следовательно, наше предположение неверно. ■
Рассмотренный пример иллюстрирует следующий общий факт: если граф имеет n вершин и степень каждой вершины не меньше, чем (n — 1)/2, то такой граф является связным.
Воспользовавшись идеей решения задачи из примера 3, докажите этот факт самостоятельно.
ИТОГИ ГЛАВЫ 1.
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 4. Решение задач с помощью графов.
Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 4. Решение задач с помощью графов.
Ученик знает назначение графов | |||
Понимание | Умеет приводить примеры использования графов в различных учебных предметах (химия, информатика, биология, геометрия и др. | ||
Применение | Умеет записывать арифметические выражения в виде графов, отражать информацию в виде семантической сети, изображать классификации различных объектов в виде дерева | ||
Анализ | Умеет из множества предметов вычленить объекты, обозначить связи между ними. | Айдар | Тима | Саша |
№1 | — | — | + |
№2 | — | + | — |
№3 | + | — | — |
Тема: «Графы и решение логических задач».

Тема: «Графы и решение логических задач».
Посельский Борис учеником 8 «в» класса МБОУ «Нижнесаянтуйская СОШ»
Научный руководитель:
Кожемякина Ирина Семеновна
учитель математики
МБОУ «Нижнесаянтуйская СОШ»
2018г
Оглавление.
1. Введение
2. Глава 1.Теория графов
2.1. История возникновения графов
2.2. Задача о кёнигсбергских мостах
2.3.Граф и его элементы
2.4. Степени вершин и подсчет числа ребер
2.4. Эйлеровы графы
3. Глава 2. Решение задач с помощью графов
4. Заключение
5. Список литературы
Введение.
На занятиях математического кружка в 5 классе при решении логических задач, мне понравился метод решения задач с помощью построения графов, и захотелось как можно больше узнать о графах, поэтому я и начал заниматься исследовательской работой по данной теме. Графы заинтересовали меня своей возможностью помогать в решении различных головоломок, математических и логических задач.
Предмет моего исследования: графы
Объект исследования: логические задачи, решаемые с помощью построения графов
Актуальность исследования: актуальность моей работы обусловлена большим интересом к теме данного исследования по математике. Кроме этого, выбранная мною тема актуальна, так как в последнее время теория графов стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем.
Цели моего исследования:
Выяснить особенности применения теории графов при решении логических задач и в практической деятельности.
Задачи исследования:
- познакомиться с историей возникновения графов;
- познакомиться с основными понятиями графа, видами, элементами;
- рассмотреть решение логических задач с помощью графов;
Гипотеза:
Можно предположить, что решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту.
Представление данных в виде графа придает им наглядность и простоту.
Глава 1. ТЕОРИЯ ГРАФОВ
1.История возникновения теории графов.
Начало теории графов все единодушно относят к 1736 г., когда Леонард Эйлер — один из крупнейших математиков XVIII, члена Петербургской академии наук, не только решил популярную в то время задачу о кёнигсбергских мостах, но и
нашел критерий существования в графе специального маршрута, который сегодня называют эйлеровым циклом.
Однако эти результаты Эйлера более ста лет являлись, по сути, единственным достижением математической дисциплины, которую позднее назовут теорией графов. Лишь в середине XIX века инженер-электрик Г. Кирхгоф разработал
теорию графов, называемых деревьями, для исследования
Рис. 4 Портрет Леонарда Эйлера. электрических цепей, а математик А. Кэли в связи с
описанием строения углеводородов решил перечислительные задачи для трех видов
деревьев.
Термин «Графы» ввёл в язык немецкий математик Д. Кёниг. Он первым предложил называть такие схемы «графами». Термин «граф» (от латинского слова «графио» — пишу) приобрел права гражданства и вошел в математический язык в 1936 году, после выхода в свет монографии Кёнига, в которой впервые графы рассматриваются как самостоятельные математические объекты независимо от их конкретного содержания.
2. Задача о кёнигсбергских мостах.
Проблема семи мостов Кёнигсберга или Задача о кёнигсбергских мостах — старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Издавна жители Кёнигсберга пытались пройти по всем мостам через реку Преголя, не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок.
Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.
Задача о семи мостах заинтересовала Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем кёнигсбергским мостам, не проходя дважды ни по одному из них. Его ответ был — «нельзя».
Читая письмо Эйлера выясним, какое же правило он нашел:
«Вопрос состоит, писал Эйлер, в том, чтобы определить, можно ли обойти все эти семь мостов, проходя через каждый только однажды, или нельзя. Мое правило приводит к следующему решению этого вопроса. Прежде всего, нужно смотреть, сколько есть участков, разделенных водой, — таких, у которых нет другого перехода с одного на другой, кроме как через мост. В данном примере таких участков четыре — A, B, C, D.»
Эйлеровский ход решения задачи я представлю в виде графа, где вершины — острова и берега, а ребра — мосты. Рис. 1
Построим граф без посторонних линий. Рис. 2
Рис. 2
Читаем письмо Эйлера дальше: «Далее нужно различать, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным. Так, в нашем случае к участку A ведут пять мостов, а к остальным — по три моста. То есть нам нужно определить степень каждой вершины, и узнать какие вершины четные, а какие нечетные. Подпишем степени вершин в кружочках. И посчитаем количество нечетных вершин. Нечетные вершины: А, B, C, D.
Покажу это на графе — Рис. 3.
Читаем письмо: «Когда это определено, применяем следующее правило: если все вершины имеют четную степень, то тогда обход, о котором идет речь, возможен, и начать этот обход можно с любого участка. Если же из этих вершин две нечетные, то и тогда можно совершить переход, как это предписано, но только начало обхода непременно должно быть взято в одной из этих двух вершин, а конец обхода непременно должен быть во второй нечетной вершине. Если, наконец, больше двух нечетных вершин, то тогда такое движение вообще невозможно. ..».
..».
Итак, используя правило Леонардо Эйлера мы можем сделать вывод: так как количество нечетных вершин в графе равно 4, а это > 2, то обойти все кенигсбергские мосты, проходя только один раз через каждый из этих мостов нельзя.
В своей работе Эйлер доказал общее утверждение, для решения каждой подобной задачи о мостах — для того, чтобы можно было обойти все рёбра графа по одному разу и вернуться в исходную вершину, необходимо и достаточно выполнение двух условий:
- Из любой вершины графа должен существовать путь по его рёбрам в любую другую вершину.
- Из каждой вершины должно выходить чётное количество рёбер.
3. Граф и его элементы.
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» — пишу.
В математике определение графа дается так:
Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Абсолютно неважно, какой вид имеют эти линии, и как точки расположены в пространстве. Идея графа — это набор каких-то объектов, с описанными связями между ними. В самом простом случае связь может быть, а может не быть. Приведу пример. Допустим, мы имеем группу людей. Это будут точки в графе. Мы можем описать связи между этими людьми. Например, связь — «знакомства». Если два человека знают друг друга, то между ними есть связь. На рисунке такого графа связь между ними будет обозначена линией от одного человека к другому. Вот как выглядит такой рисунок (граф):
По рисунку (графу) видно, что с Мариной никто не знаком, а Саша знаком с Олегом, Катей и Леной.
В графе точки называются вершинами графа, а соединяющие их линии (дуги) – рёбрами. Смотрим Рис. 1.
Схема графа, состоящая из «изолированных» вершин, называется нулевым графом. (рис.2)
Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.3)
(рис.3)
Графы, в которых построены все возможные ребра, называются полными графами. (рис.4)
Если на ребрах графа нанесены стрелочки, указывающие направление ребер, то такой граф называют направленным.
4. Степени вершин и подсчет числа ребер.
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.
рис.5
На рисунке 5 изображен граф с пятью вершинами. Степень вершины А обозначим Ст.А.
На рисунке: Ст.А = 1, Ст.Б = 2, Ст.В = 3, Ст. Г= 2, Ст. Д= 0.
Сформулируем некоторые закономерности, присущие определенным графам.
Закономерность 1.
Степени вершин полного графа одинаковы, и каждая из них на 1 меньше числа вершин этого графа.
Закономерность 2.
Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа.
Эта закономерность справедлива не только для полного, но и для любого графа.
Теорема .
Число нечетных вершин любого графа четно.
Если полный граф имеет n вершин, то количество ребер будет равно .
Действительно, количество ребер в полном графе с n-вершинами определяется как число неупорядоченных пар, составленных из всех n-точек-ребер графа, т. е. как число
сочетаний из n по 2. Граф, не являющийся полным, можно дополнить до полного с теми же вершинами, добавив недостающие ребра. Так, например, на рисунке 3 изображен неполный граф с пятью вершинами. На рисунке 4 ребра превращающие граф в полный граф изображены другим цветом, совокупность вершин графа с этими ребрами называется дополнением графа.
5. Эйлеровы графы.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. (рис.6) Такими графы названы в честь учёного Леонарда Эйлера.
Закономерность 3 (вытекает из рассмотренной нами теоремы).
Невозможно начертить граф с нечетным числом нечетных вершин.
Закономерность 4.
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
Закономерность 5.
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Закономерность 6.
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
Фигура (граф), которую можно начертить, не отрывая карандаш от бумаги, называется уникурсальной.
рис.6 (Эйлеровы графы)
Глава 2. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ГРАФОВ.
Графы часто используют для решения логических проблем, связанных с перебором вариантов.
Задача 1. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?
Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?
Молоко | Лимонад | Квас | Вода | |
Бутылка | — | + | — | — |
Стакан | — | — | — | + |
Кувшин | + | — | — | — |
Банка | — | — | + | — |
Ответ: в кувшине-молоко, в банке-квас, в стакане-вода, в бутылке-лимонад
Эту же задачу можно решить с помощью графов.
Соединим пунктирными ребрами те вершины, которые не могут быть связаны друг с другом.
Тогда получаем:
В бутылке – квас или лимонад, так как в банке только квас, значит в бутылке – лимонад;
В кувшине – молоко или вода, так как в стакане не молоко, значит – вода, а кувшине тогда молоко.
Ответ: в кувшине-молоко, в банке-квас, в стакане-вода, в бутылке-лимонад
Решение задачи в графах.
Задача 2. На международном конгрессе встретились четверо ученых: физик, историк, биолог и математик. Национальности их различны и, хотя каждый из ученых владеет двумя языками их четырех (русский, английский, французский и итальянский), нет такого языка, на котором они могут разговаривать вчетвером. Есть язык, на котором они могут разговаривать сразу трое, – итальянский. Никто из ученых не владеет французским и русским языками одновременно. Хотя физик не говорит по-английски, но может быть переводчиком, если биолог и историк захотят поговорить друг с другом. Историк может говорить с математиком по-французски. Физик, биолог и математик не могут беседовать втроем на одном языке. Какими двумя языками владеет биолог (укажите названия языков в именительном падеже через пробел).
Историк может говорить с математиком по-французски. Физик, биолог и математик не могут беседовать втроем на одном языке. Какими двумя языками владеет биолог (укажите названия языков в именительном падеже через пробел).
Решение: Соединим пунктирными ребрами те вершины, которые не могут быть связаны друг с другом.
Ответ: русский английский
Задача 3. Однажды мама, в магазине купила разную приправу: красный перец, коричневый имбирь, зелёную петрушку и белую горчицу. Придя домой, она разложила всё это в баночки для специй. Я знаю, что у нас дома каждая специя лежит в своей баночке и цвет банки не соответствует свету специй. Так же известно, что зеленая петрушка лежит в коричневой банке, а красный перец не лежит в белой баночке. Мне для приготовления плова нужно узнать: «В какой банке лежит каждая специя?»
Решение: Обозначим точками специи и баночки. Сплошная линия будет обозначать, что специя лежит в соответствующей баночке, а пунктирная, что не лежит. Тогда с учетом задачи имеем граф G1,
Далее достраиваем граф по следующему правилу: поскольку в баночке может лежать только одна специя, то из каждой точки должны выходить одна сплошная линия и три пунктирные.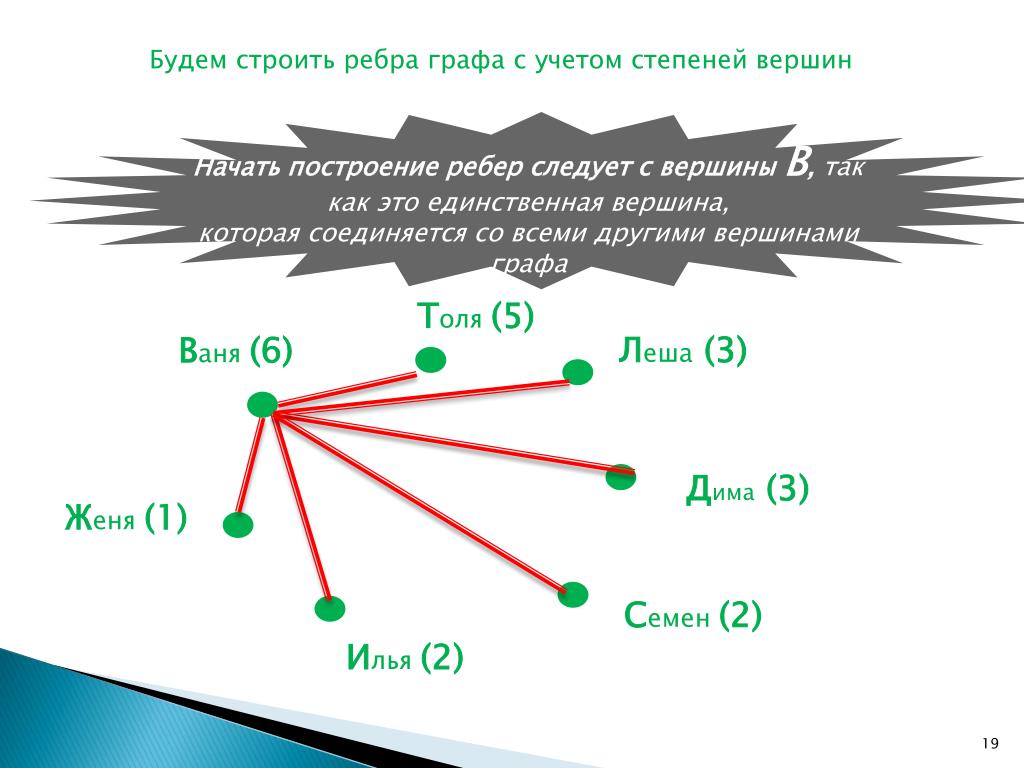 Получается граф G2 — решение задачи.
Получается граф G2 — решение задачи.
Ответ: Красный перец лежит в зелёной банке, имбирь лежит в белой банке, зелёная петрушка – в коричневой, а белая горчица лежит в красной баночке.
Задача 4. Запишите все трехзначные числа, для записи которых употребляются только цифры 1 и 2.
Ответ: 111, 112, 121, 122, 211, 212, 221, 222.
Задача 4. Сколько трехзначных чисел можно составить из цифр 2,4,6,8, если цифры в записи числа не повторяются?
Решение: первой цифрой может быть одна из четырех данных цифр, вторая любая из трех, а третья – любая из двух оставшихся, получается:
Всего можно составить 4*3*2= 24 трехзначных числа.
К топологическим относятся и задачи на вычерчивание фигур одним росчерком. В данных задачах требуется начертить какую-либо фигуру, не отрывая карандаша от бумаги и не проводя два раза по одной и той же линии.
Задача 5.
Рис.1 Рис. 2
На рисунке 1 пять вершин, причем три из них – четные ( 1,2 и 3), а два нечетных (4 и 5). Эту фигуру можно начертить одним росчерком. Основываемся при решении на
Эту фигуру можно начертить одним росчерком. Основываемся при решении на
Закономерность 5.
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
А вот домик с дверью рис.2 – это уже другая фигура, содержит 9 вершин, 5 из которых четные, а 4 – нечетные. Если в фигуре на графе больше двух нечетных вершин, то ее нельзя начертить одним росчерком!
Задача 6. Можно ли нарисовать графы изображенные на рисунках, не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?
Решение:
- Можно, т. к. только 2 нечетные вершины.
- Нельзя, т. к. 4 нечетные вершины.
Задача 7. Мальчики 10 б класса Андрей, Витя, Сережа, Валера, Дима при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
Решение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена.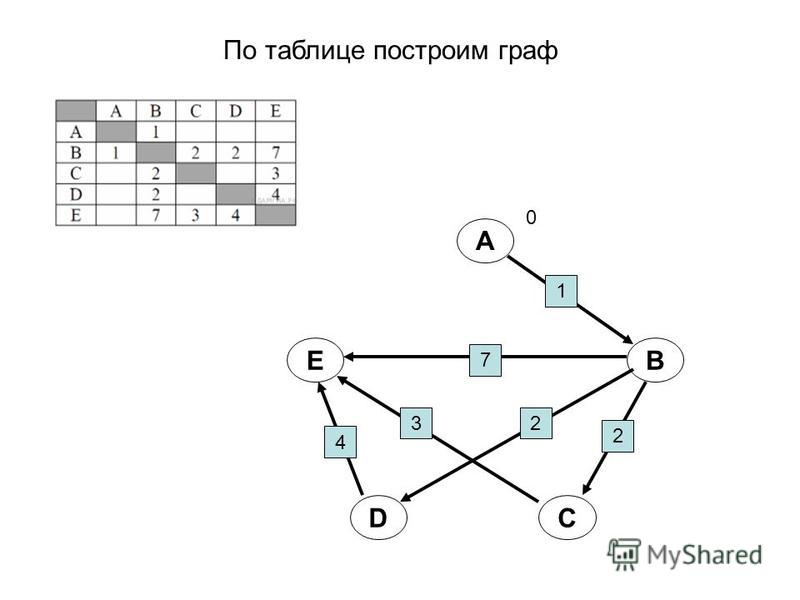
Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми.
Их 10. Ответ: 10.
Задача 8. В трех различных домах живут три поссорившиеся между собой соседа. Недалеко от их домов имеются три колодца. Можно ли от каждого дома проложить к каждому из колодцев тропинку так, чтобы никакие две из них не пересекались?
Решение:
Построим граф, вершины которого,
А, Б, В, 1, 2, 3
соответствуют домам и колодцам условия задачи, и попробуем доказать, что девятую тропинку — ребро графа, не пересекающее остальные ребра, провести нельзя.
Проведенные в графе на рисунке ребра А1, А2, A3 и В1,В2, ВЗ (соответствующие тропинкам от домов А и В ко всем колодцам). Построенный граф разбил плоскость на три области: X, У, Z. Вершина Б, в зависимости от ее расположения на плоскости, попадает в одну из этих трех областей. Если вы рассмотрите каждый из трех случаев «попадания» вершины Б в одну из областей X, Y или Z, то убедитесь, что всякий раз одна из вершин графа 1, 2 или 3 (один из колодцев) будет «недоступной» для вершины Б (т. е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер).
е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер).
Задача 9. Дан кусок проволоки, длиной 120 см. Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см?
Решение:
Если куб – граф, тогда он имеет более двух нечетных вершин (8). Значит, невозможно изготовить такой каркас, не ломая проволоки.
Задача 10. Можно ли обвести карандашом, не отрывая его от бумаги и не проходя по одной линии дважды, правильный пятиугольник с диагоналями?
Решение:
Если пятиугольник – граф и все вершины его четные – то это выполнить
ЗАКЛЮЧЕНИЕ:
Выделяя из словесных рассуждений главное — объекты и отношения между ними, графы представляют изучаемые факты в наглядной форме. Приёмы решения логических задач с использованием графов подкупают своей естественностью и простотой, избавляют от лишних рассуждений, во многих случаях сокращающих нагрузку на память.
С одной стороны, графы помогают проследить все логические возможности изучаемой ситуации, с другой, благодаря своей обозримости, помогают тут же, в ходе решения задачи, классифицировать логические возможности, отбрасывать неподходящие случаи, не доводя до полного перебора всех случаев. Что подтверждает нашу гипотезу.
Что подтверждает нашу гипотезу.
Теория графов в настоящее время является интенсивно развивающимся разделом дискретной математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношения между людьми и многое другое. В последнее время теория графов находит всё больше применений и в прикладных вопросах.
Графы используются при составлении карт и генеалогических древ. С помощью графов удобно и наглядно изображается информация о разных объектах и отношениях между ними. В дальнейшем хочу составить генеалогическое древо своей семьи.
Графовые задачи обладают рядом достоинств, позволяющих их использовать для развития воображения и улучшения логического мышления, применимы в решении многих геометрических задач. Графовые задачи допускают изложение в занимательной, игровой форме.
СПИСОК ЛИТЕРАТУРЫ:
1. Весёлые задачи, Я. И. Перельман, Москва, 2003г
Весёлые задачи, Я. И. Перельман, Москва, 2003г
2. Графы и их применение, О. Оре, Москва, 1979г
3. Ленинградские математические кружки: пособие для внеклассной работы, С. А. Генкин, И. В. Итенберг, Киров, 1994г
4. Математика (Дополнительные главы). Е. В. Смыкалова Санкт-Петербург СМИО Пресс 2006
5 Математическая смекалка, Е. И. Игнатьев, Москва 1994г.
6. Сборник олимпиадных задач по математике, В. Г. Горбачев, 2004г.
7. Физико-математический журнал «Квант», А. Савин, №6 1994г.
8. Наглядная геометрия И.Ф.Шарыгин, Л.Н. Ерганжиева М, дрофа, 2000г.
Построение графов. Решение задач c использованием графов — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Цели: в результате выполнения практической работы, обучающиеся должны уметь строить графы, записывать матрицы, решать задачи.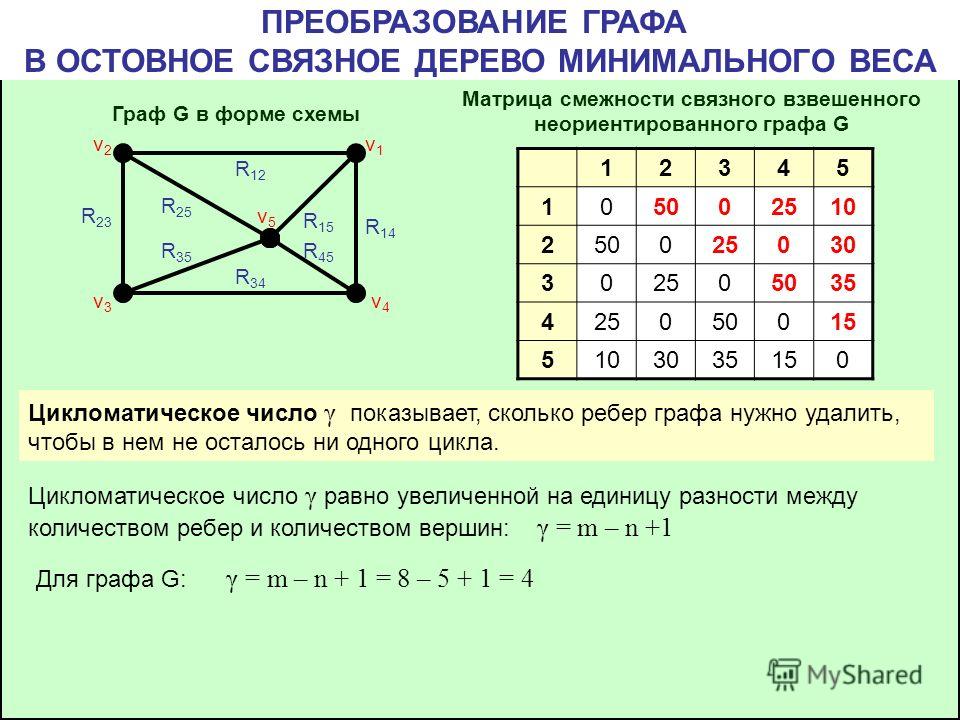
Пояснения к работе
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий Х, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом.
При этом элементы множества V называются вершинами графа, а элементы множества Х – ребрами.
В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями. Одинаковые пары в множестве Х называются кратными (или параллельными) ребрами. Количество одинаковых пар
(v, w) в Х называется кратностью ребра (v, w).
Множество V и набор Х определяют граф с кратными ребрами – псевдограф.
G = ( V, X)
Псевдограф без петель называется мультиграфом.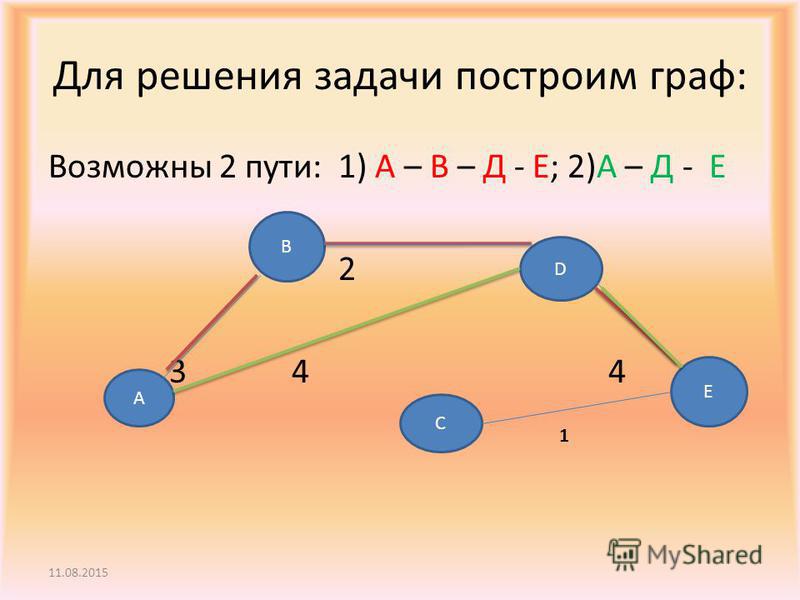
Если в наборе Х ни одна пара не встречается более одного раза, то мультиграф называется графом.
Если пары в наборе Х являются упорядочными, то граф называется ориентированным или орграфом.
Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины.
Определение. Если х = {v, w} – ребро графа, то вершины v, w называются концами ребра х.
Если х = ( v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
Определение. Вершины v, w графа G = (V, X) называются смежными, если {v, w}ÎX. Два ребра называются смежными, если они имеют общюю вершину.
Определение.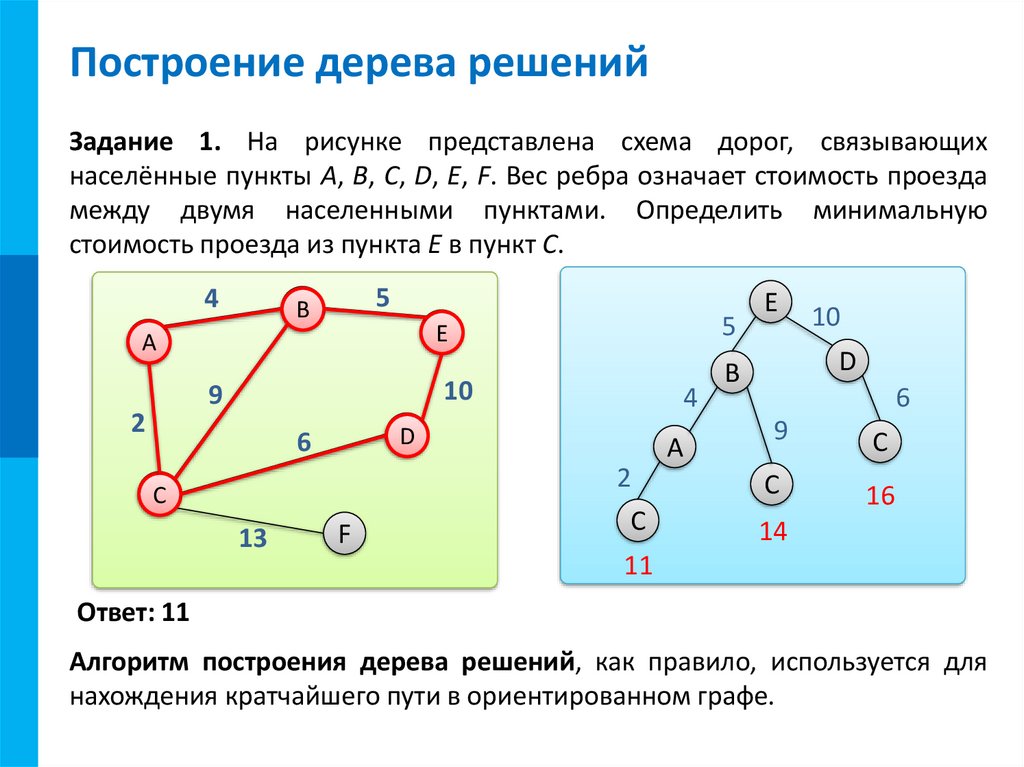 Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.
Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.
Определение. Графы G1(V1, X1) и G2(V2, X2) называются изоморфмными, если существует взаимно однозначное отображение j: V1 ® V2, сохраняющее смежность.
Определение. Маршрутом (путем) для графа G(V, X) называется последовательность v1x1v2x2v3…xkvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиной маршрута (пути).
Определение.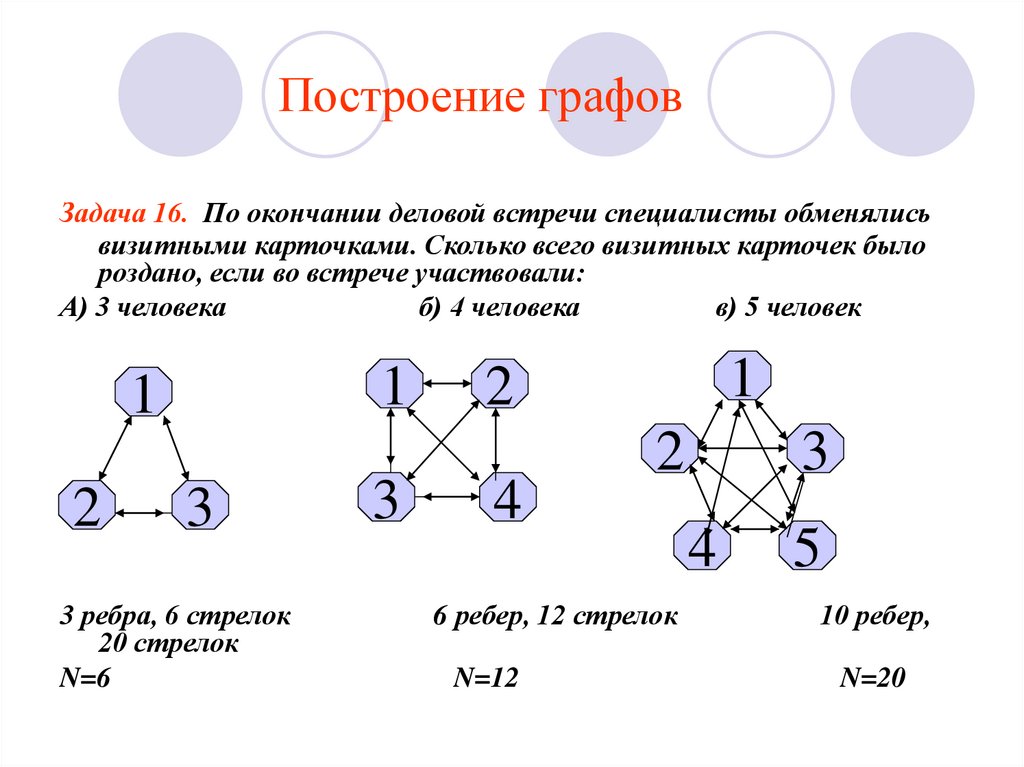 Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Определение. Замкнутый маршрут (путь) называется циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Матрицы графов.
Пусть D = (V, X) – орграф, где V = {v1, …, vn}, X = {x1, … , xm}.
Определение. Матрицей смежности орграфа D называется квадратичная матрица A(D) = [aij] порядка п, у которой
Определение. Если вершина v является концом ребра х, то говорят, что v и х – инциндентны.
Определение. Матрицей инциндентности оргафа D называется матрица размерности п´т B(D) = [bij], у которой
Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
x1
v1 x4 v2
x2
x3
v3
Составим матрицу смежности:
| v1 | v2 | v3 | |
| v1 | 0 | 1 | 0 |
| v2 | 1 | 0 | 1 |
| v3 | 1 | 0 | 0 |
Т.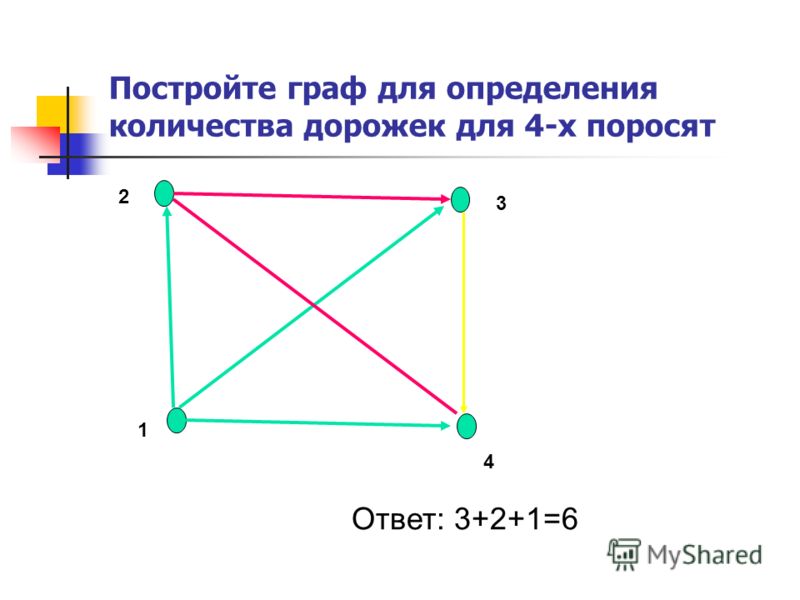 е. — матрица смежности.
е. — матрица смежности.
Матрица инциндентности:
| x1 | x2 | x3 | x4 | |
| v1 | -1 | 0 | 1 | 1 |
| v2 | 1 | -1 | 0 | -1 |
| v3 | 0 | 1 | -1 | 0 |
Т.е.
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij= k, где k – кратность дуги (ребра).
С помощью матриц смежности и инциндентности всегда можно полностью определить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.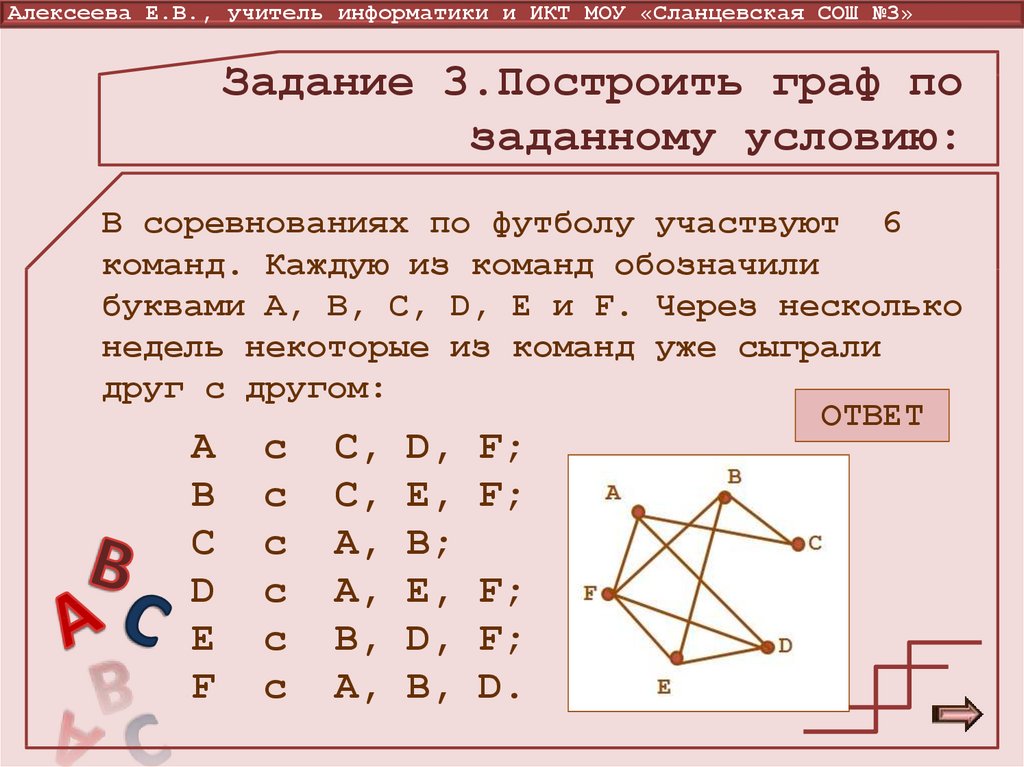
Пример. Задана симметрическая матрица Q неотрицательных чисел. Нарисовать на плоскости граф G(V, X), имеющий заданную матицу Q своей матрицей смежности. Найти матрицу инциндентности R графа G. Нарисовать также орграф , имеющий матрицу смежности Q, определить его матрицу инциндентности С.
x4
x3
v2
x2 x5
x6
x1 v1 v3 x7 x8
x10
x11 x9
v4
Составим матрицу инциндентности:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | |
| v1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| v2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| v3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| v4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Итого:
Построим теперь ориентированный граф с заданной матрицей смежности.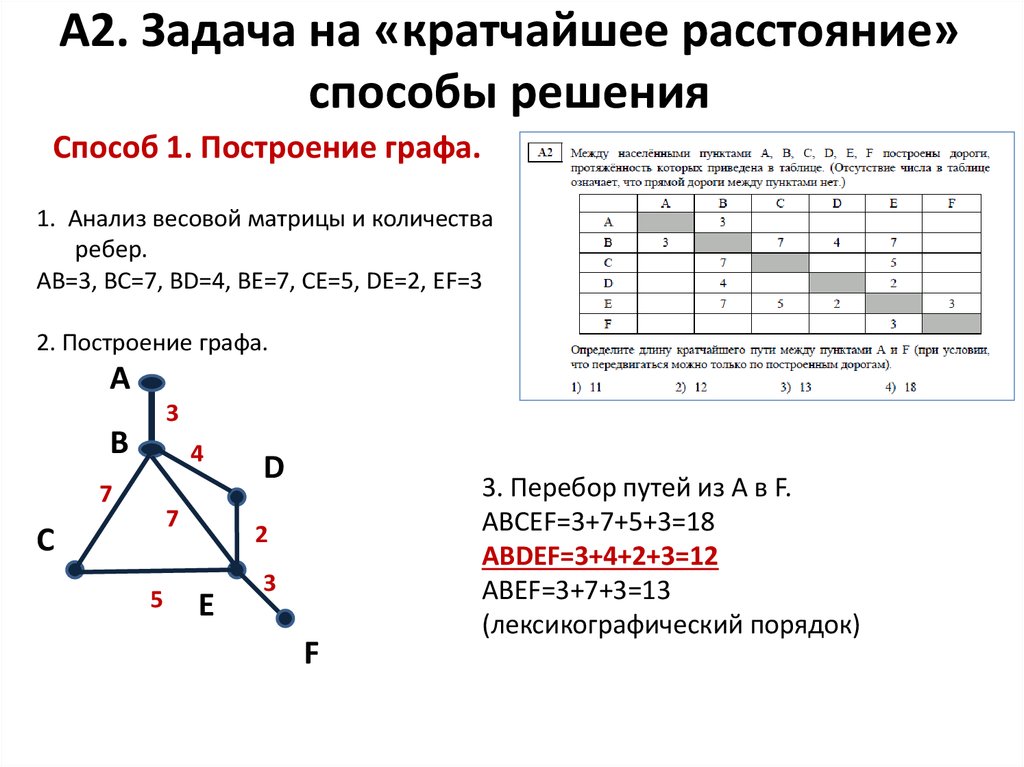
x4
x5
v2
x2 x7
х3 x6
x1 v1 х8 v3 x10 x11
х9
х17 х15 x14
x16 х13 x12
v4
Составим матрицу инциндентности для ориетированного графа.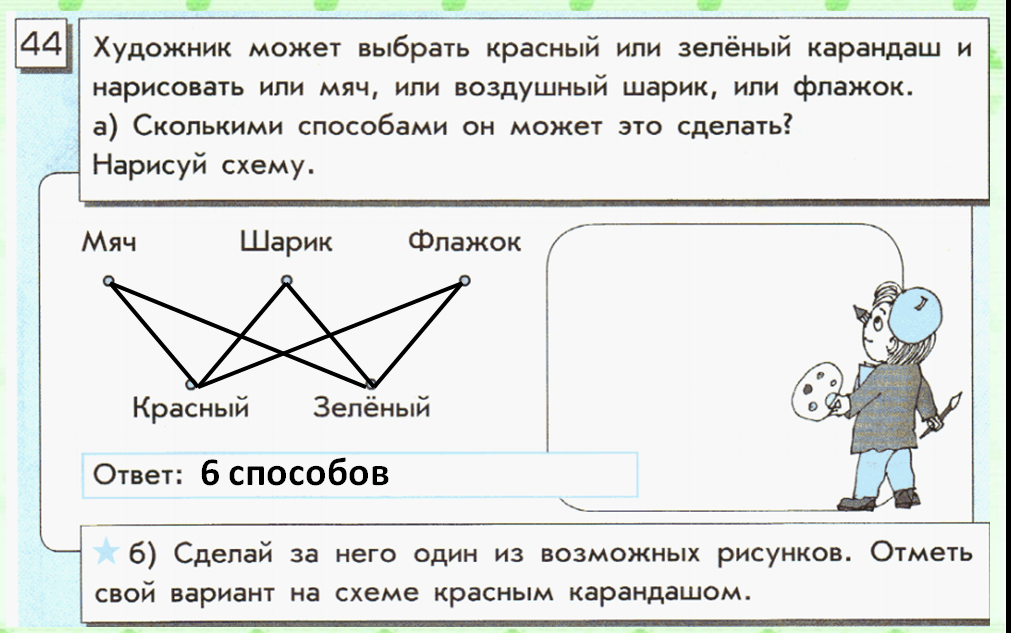
Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как ±1.
Таким образом, операции с графами можно свести к операциям с их матрицами.
Задание
Вариант 1.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 9 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 2.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача2. Решите задачу, решение представьте в виде графа: из 27 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 3.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача 3. Решите задачу, решение представьте в виде графа: из 18 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 4.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 12 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 5.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 15 монет одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Вариант 6.
Задача1.Ориентированный граф с множеством вершин задан списком дуг .
Построить реализацию графа . Построить матрицу смежности и матрицу инцидентности графа . Укажите степени вершин графа.
Задача 2. Решите задачу, решение представьте в виде графа: из 21 монеты одна фальшивая (более легкая). Как двумя взвешиваниями на чашечных весах определить фальшивую монету?
Содержание отчёта
Отчёт о проделанной работе должен содержать:
— название темы практического занятия;
— цели практического занятия;
— условие задачи;
— подробное решение задачи;
— ответ.
Контрольные вопросы
1. Графы являются «топологическими» или «геометрическими» объектом.
2. Каково соотношение между количествами вершин, рёбер и граней в плоском графе.
3. Приведите простейшие примеры неплоских графов.
Литература:
1. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов
Н/Д: Феникс 2014. – 380с.
2. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 – 495с.
3. Турецкий В.Я.Математика и информатика – 3-е издание, Т 86 испр. и доп. – М: ИНФРА – М,
2000 – 560с.
4. Методическая копилка учителя математики www.metod-kopilka.ru
Практическое занятие № 4
20 графических упражнений для детей, которые действительно поднимают планку
Студенты-математики часто спрашивают: «Но когда я буду использовать это в реальной жизни?» Сбор данных и создание карт имеют множество реальных применений, поэтому дети должны понимать эти навыки. Помогите им освоить гистограммы, линейные графики, точечные диаграммы, круговые диаграммы и многое другое с помощью этих веселых и творческих графических заданий!
1.
 Составьте одну или две опорные диаграммы.
Составьте одну или две опорные диаграммы.Якорные диаграммы могут помочь учащимся математики запомнить части диаграммы и способы использования различных типов для демонстрации данных.
Подробнее: Преподавание на высшем уровне
2. Познакомьтесь с графиками с помощью карманной таблицы.
Карманные карты очень удобны! Используйте их для построения графиков занятий, проводя опросы в классе и добавляя ответы учащихся в каждый столбец или строку.
Узнать больше: Класс Мисс Жирафа
3. Перекусить и поработать с угощениями.
Дайте каждому учащемуся несколько петель Froot и попросите их составить график цветов. Они могут перекусить ими, когда они будут готовы!
Узнайте больше: Планирование игрового времени
4. Используйте игрушки, чтобы сделать пиктограмму.
Совершите набег на ящик с игрушками и используйте игрушечные машинки, поезда и все, что у вас есть под рукой, чтобы создавать простые пиктограммы из реальной жизни. Сортировка по цвету, длине, типу, количеству колес… возможности безграничны.
Сортировка по цвету, длине, типу, количеству колес… возможности безграничны.
Узнайте больше: Мама Жизнь стала проще
5. Нарисуйте график задачи с бутылкой воды.
Если ваши ученики все еще получают удовольствие от попыток решить задачу с бутылкой с водой, превратите это увлечение в урок построения графиков. Веселье + обучение = круто.
Подробнее: Create Dream Explore
6. Измерьте и начертите свои большие пальцы.
Графические задания, подобные этому, объединяют два математических занятия в одном. Дети работают над своими навыками измерения, а затем графически изображают свои результаты.
Подробнее: Эми Лемонс
7. Прогуляйтесь на природе.
Выйдите на улицу и прогуляйтесь, собирая ветки, камни, цветы и листья. Когда вы вернетесь, создайте график для представления ваших находок.
Узнайте больше: Учеба миссис Джей развлекается
8.
 Чаша и график.
Чаша и график.Кто не любит математические занятия, которые поднимают детей со стула и сжигают лишнюю энергию? Им понравится играть в боулинг на уроках — купите недорогой набор для боулинга в долларовом магазине или научитесь делать свои собственные по ссылке.
Подробнее: Пораженный первым
9. Подбросьте монетку.
Подбрасывание монеты — это простой способ получения данных для гистограммы. Единственная проблема может заключаться в том, чтобы заставить детей остановиться!
Подробнее: Класс Мисс Жирафа
10. Постройте всплывающую гистограмму.
Насколько крут этот график? Всплывающая гистограмма выводит данные прямо со страницы. Нажмите на ссылку, чтобы узнать, как это делается.
Подробнее: Комната Рунде
11. Нарисуйте графически количество букв в вашем имени.
Вот умный способ показать гистограммы, которые идут горизонтально, а не вертикально. Найдите это и другие упражнения, которые можно использовать с книгой Хризантема по ссылке.
Найдите это и другие упражнения, которые можно использовать с книгой Хризантема по ссылке.
Дополнительные сведения: One Sharp Bunch
12. Цельтесь в цель.
Зацепите мишень для дротиков на липучке в долларовом магазине или сделайте мишень из бумаги и помпонов. Дети будут в восторге, стремясь к цели, чтобы собрать данные, прежде чем они начертят свои выводы.
Подробнее: Эми Лемонс
13. Читайте книги и составляйте таблицы.
Проведите опрос своего класса, чтобы найти их любимые книги, которые вы прочитали в последнее время. Затем составьте график итоговой диаграммы, чтобы увидеть, какой из них наиболее популярен.
Подробнее: Лягушки, феи и планы уроков
14. Следите за погодой.
Некоторые графические действия позволяют легко увидеть связь в реальном мире, и это одно из них. Студенты отслеживают ежедневные температуры и используют их для построения графиков и прогнозов.
Подробнее: Умный учитель
15. Сыграйте в крестики-нолики.
Создание хороших графиков важно, но не менее важно знать, как их читать и интерпретировать данные. В этой бесплатной печатной форме детям предлагается ответить на вопросы, основываясь на информации, представленной в виде простой гистограммы.
Подробнее: Первый класс a la Carte
16. Сосчитайте кегли, чтобы построить круговую диаграмму.
В этом упражнении так много математических навыков! Дети строят круговую диаграмму, используя конфеты, а затем вычисляют правильные дроби и проценты, представленные данными.
Подробнее: Обучение с видом на горы
17. Составьте круговую диаграмму из цветов глаз.
Цвет глаз — еще один интересный способ построить круговую диаграмму, также называемую круговой диаграммой. Объедините это с уроком анатомии глаза, чтобы получить двойной удар!
Подробнее: Детский сад миссис Ли
18.
 Распечатывайте графики на стикерах.
Распечатывайте графики на стикерах.Знаете ли вы, что можно печатать на стикерах с помощью простого шаблона? Это меняет жизнь! Используйте этот хак, чтобы делать заметки, которые можно использовать для всех видов графических действий. Получите инструкции здесь.
19. Постройте точечный график с помощью M&Ms.
Старшие учащиеся начальной школы начинают изучать диаграммы рассеяния, которые показывают, как фрагменты данных соответствуют друг другу. Познакомьте их с тем, как они работают с M&M’s.
Подробнее: Математика = Любовь
20. Создайте карту города в координатной плоскости.
Координатные плоскости — самая сложная форма графика, но научиться наносить на них точки проще, чем кажется. Нам нравится это невероятно веселое занятие, которое превращает координатную плоскость в карту города… и детям это тоже понравится.
Подробнее: Для такого времени
У нас так много отличных ресурсов для обучения математике K-5! Проверьте их все здесь.
Кроме того, получите более 65 приложений STEAM для детей и подростков.
Занятия по построению графиков и теории вероятностей Практическое развлечение для детей — гордимся тем, что учимся в начальной школе
Обучение с графическими заданиями — одно из самых увлекательных занятий по математике в году. Попробуйте эти идеи для практических занятий в классе!
Графические упражнения и уроки вероятностей
Детям может быть трудно понять, что такое данные и как их организовать. Например, если вы высыпаете пакет кеглей в кучу и спрашиваете его/ее, сколько там красных кеглей, они, вероятно, не смогут этого сделать. Смысл графика в том, чтобы организовать данные понятным образом. Другими словами, организация данных в виде графика помогает детям легко отвечать на вопросы о данных.
Графики также позволяют детям практиковать свои навыки сортировки и наблюдения, когда они распределяют предметы по группам. В классе вы можете сортировать предметы по цвету, размеру, количеству и другим признакам. В результате молодые учащиеся знакомятся с сортировкой информации и ее графическим отображением. Самое главное, они развивают математические навыки, которые они будут использовать на протяжении всей своей жизни!
В классе вы можете сортировать предметы по цвету, размеру, количеству и другим признакам. В результате молодые учащиеся знакомятся с сортировкой информации и ее графическим отображением. Самое главное, они развивают математические навыки, которые они будут использовать на протяжении всей своей жизни!
Дети также могут многое узнать о том, как вероятность проявляется в нашей повседневной жизни. Используя занятия в классе и игры, изучение вероятности становится приятным временем обучения. Понимание приходит легко с идеями, перечисленными здесь!
Типы графиков
Обучайте анализу данных с помощью графических упражнений, и вы просвещаете и поощряете визуальную перспективу чисел. В свою очередь, математика оживает благодаря полезным и применимым в жизни навыкам построения графиков. Будь то раскрашивание гистограммы или создание линейного графика, эти различные графические действия дадут детям инструменты, необходимые им для понимания построения графиков и анализа данных.
- Метки для диаграмм — Использование меток и диаграмм — это простой способ познакомить детей с графиками. Дети считают предметы и подсчитывают их, создавая визуальное представление собранных ими данных.
- Круговые диаграммы/круговые диаграммы — Они позволяют детям легко понять данные. Начните со сравнения двух вещей на круговой диаграмме, используя два разных цвета для отображения информации. По мере того, как они овладевают этим навыком, они могут сравнивать больше предметов.
- Пиктограммы – Картинки стоят тысячи слов. Это, безусловно, относится к пиктограммам. Пиктограммы используют изображения для отображения информации, что делает их отличной отправной точкой для детей.
- Линейные графики – Линейные графики позволяют легко отображать и сравнивать большое количество информации одновременно. Это можно сделать с помощью нескольких линий разных цветов, что упрощает сравнение нескольких результатов.

Практические занятия по построению графиков
Рисование графиков может быть очень увлекательным и обычно является любимым разделом года. Используйте практические методы для графического отображения данных. Эти методы удовлетворяют потребности кинестетических и визуальных учащихся. Кроме того, это просто увлекательный способ обучения для всех детей! Эти графические действия могут быть легко выполнены с помощью нескольких основных материалов.
- Play Connect Four – Помимо того, что это игра, Connect 4 также может использоваться для графического представления информации. Просто пометьте строки и столбцы соответствующим образом, а затем соедините кусочки, чтобы создать гистограмму!
- Sticky Notes — Sticky Notes можно использовать для создания графика на доске. Например, нарисуйте график на доске, а затем попросите детей ответить на вопрос, прикрепив стикер в нужное место.
- Lego – кубиков Lego отлично подходят для построения графиков.
 Дети могут складывать блоки Lego вместе, чтобы создать трехмерную графическую модель.
Дети могут складывать блоки Lego вместе, чтобы создать трехмерную графическую модель. - График человека — Чтобы дети двигались и веселились, создайте график человека! Если вы рисуете цвет рубашек, которые носят дети, попросите детей выстроиться в линию на сетке, приклеенной скотчем к полу. Все дети в белых рубашках выстраиваются в одну колонку, дети в желтых — в следующую и так далее.
- Сортировка с помощью Candy — Еще одна альтернатива раскрашиванию графика на листе бумаги — использование сортируемых элементов в качестве манипуляции. Например, при сортировке M&Ms или Skittles по цветам разместите эти элементы на графике, расположив их стопкой в соответствующем столбце. Сортировка также забавна с сортировкой карточек.
- Fruit Loops — Fruit Loops, наложенные на шпажки, — это удобный способ построить график по цвету. Чтобы создать график, просто воткните деревянные шпажки в коробку, выровняв их равномерно.
 Дайте детям горсть фруктовых петель и наденьте их на шпажки по цвету. Чем больше фруктовых петель на шпажке, тем выше она будет, что дает детям отличное представление о том, что такое график.
Дайте детям горсть фруктовых петель и наденьте их на шпажки по цвету. Чем больше фруктовых петель на шпажке, тем выше она будет, что дает детям отличное представление о том, что такое график. - Coin Flip — Создайте график, подбрасывая монету. При каждом подбрасывании монеты дети могут записывать, выпали ли они орлом или решкой.
- Онлайн-игры – Дети любят играть в онлайн-игры. Удобно, что есть много онлайн-игр для построения графиков, например, Fuzz Bugs на ABCya. Найдите игру, подходящую для возраста и уровня навыков класса, а затем организуйте ее в качестве основного занятия для небольшой группы.
- Дегустация яблок — Это вкусный способ создать гистограмму! Нарежьте красное, желтое и зеленое яблоко и предложите детям попробовать по кусочку каждого цвета. Затем дети могут проголосовать за свой любимый цвет яблока, создав график класса с данными.
- Данные о кубиках — Соберите кубики и пустой график, чтобы сыграть в игру «бросай и рисуй».
 Чтобы играть, дети бросают кости и отмечают на графике выпавшее число. Они продолжают это, получая больше данных для графика с каждым броском.
Чтобы играть, дети бросают кости и отмечают на графике выпавшее число. Они продолжают это, получая больше данных для графика с каждым броском.
Темы для графических занятий
Дети лучше учатся, когда есть личная связь с темой. Другими словами, опрос класса по определенной теме или мнению — это один из способов связать детей с тем, что они изучают. Спросите их, какая у них любимая еда или вид спорта. Выясните, когда у каждого ребенка день рождения или какого цвета рубашка на нем. Используйте эти данные, чтобы создать график вместе, как весь класс. Это поможет представить концепцию таким образом, чтобы они могли понять, а также смоделировать правильный способ сбора информации и отображения ее на графике.
- Дни рождения — Создайте диаграмму класса, которая показывает месяц дня рождения каждого ребенка. Это не только познакомит вас с графикой, но и станет отличным способом запомнить и отпраздновать день рождения каждого ребенка.

- Любимые цвета – Проведите опрос о любимых цветах и нарисуйте информацию всем классом. Альтернативой этому может быть уже перечисление нескольких цветов, и дети должны решить, какой из этих цветов является их любимым.
- Продукты для завтрака — Спросите детей, что они ели на завтрак этим утром, и постройте график с этой информацией. В качестве альтернативы другой график может включать любимые продукты для завтрака.
- Домашние животные – Расспросите класс о домашних животных, которые есть у них дома. Один из способов сделать это — выяснить, сколько у них домашних животных, и представить эту информацию в виде графика. Вы также можете просмотреть типы домашних животных, которые у них есть, например, кошек, собак, рыб и т. д.
- Краска для волос – Попросите детей встать и собраться в небольшие группы в соответствии с цветом волос. Используйте эту информацию для создания графа классов.

- Варианты обеда – Этот опрос можно проводить каждый день. Дети могут перемещать магнит со своим именем на график вариантов обеда. Этот график может включать горячий обед, упакованный ланч, салат-бар или любые другие варианты обеда, доступные в школе.
- Занятия/Спорт — Узнайте, какими видами спорта занимаются дети или чем они занимаются, и создайте график для этого.
Вероятностные игры и занятия
Обучение детей теории вероятности включает в себя предоставление им практического опыта, демонстрирующего вероятность в повседневной жизни. Есть несколько забавных игр и занятий, которые вы можете сделать в классе, чтобы дать своим ученикам. Они дают возможность узнать, что такое вероятность, и как использовать это понимание для принятия решений или прогнозирования результатов. Они смогут ответить на такие вопросы, как «Насколько вероятно, что это произойдет?» и «Какова вероятность того, что это произойдет?»
- Игры в кости – Существует множество способов использовать кости для обучения вероятности.
 Попросите учащихся бросить один кубик и узнать вероятность того, что выпадет определенное число. Или вы можете попросить их бросить два кубика, чтобы предсказать вероятность того, что два числа дадут в сумме шесть. Вы, вероятно, можете придумать больше вероятностных игр с костями, которые просты по своей природе, как в этих двух примерах.
Попросите учащихся бросить один кубик и узнать вероятность того, что выпадет определенное число. Или вы можете попросить их бросить два кубика, чтобы предсказать вероятность того, что два числа дадут в сумме шесть. Вы, вероятно, можете придумать больше вероятностных игр с костями, которые просты по своей природе, как в этих двух примерах.
- Карточные игры – Простые карточные игры могут быть интересным способом поговорить о вероятности. Сыграйте в «Старую деву» и узнайте вероятность получения карты «Старая дева». Сыграйте в игру на совпадение, такую как Speed или Slapjack, и обсудите вероятность выигрышных ходов или получения «дикой» карты и т. д.
- Словарная практика – Расскажите о вероятности того, что события произойдут, и используйте вероятностный словарь. Например, пусть дети нарисуют на своих досках линию, один конец которой будет обозначать «верно», а другой — «невозможно». Затем попросите их отметить свои ответы на такие вопросы, как «Насколько вероятно, что завтра нам подадут пиццу в столовой?» или «Какова вероятность того, что завтра будет облачно?» и т.
 д.
д. - Игры-спиннеры – Используйте круговую диаграмму, разделенную на несколько равных частей и помеченную цветом или номером. Используйте карандаш и скрепку в качестве простого спиннера. Затем попросите учащихся оценить вероятность того, что спиннер приземлится на определенные участки. Попробуйте эти вероятностные игры со спиннерами здесь, чтобы получить больше удовольствия!
- Конфеты — Разноцветные конфеты, такие как M&M’s, Skittles, мармеладки — это вкусный способ попрактиковаться в вероятности. Предложите учащимся угадать вероятность того, что они вытащат один цвет из слепого мешка или коробки, и если они верны, они смогут его съесть!
- Игры на совпадение – Используйте игральные карты или настоящую настольную игру на совпадение, чтобы обсудить вероятность нахождения совпадения.
- Онлайн-игры – Если вы найдете отличную онлайн-игру на вероятность, такую как игра мистера Нуссбаума, это будет плюсом.
 Дети могут играть на ноутбуках или планшетах в классе и видеть вероятность в действии. Он также проверяет их знания и вознаграждает их немедленными результатами и мотивирующей графикой.
Дети могут играть на ноутбуках или планшетах в классе и видеть вероятность в действии. Он также проверяет их знания и вознаграждает их немедленными результатами и мотивирующей графикой.
Детские книги по графикам и вероятностям
Чтение книг может помочь детям научиться рисовать графики и анализировать данные. Например, эти книги по анализу данных помогут детям научиться строить графики, знакомя их с различными видами графиков. От круговых диаграмм до гистограмм дети будут изучать анализ данных, отображая информацию в понятной форме.
- Лимонад на продажу Стюарт Дж. Мерфи – Продажа лимонада включает в себя много информации… вот почему персонажи этой книги решили создать график! Следуйте за персонажами и узнайте больше о графическом отображении информации в увлекательной и увлекательной форме.
- The Great Graph Contest Лорин Лиди – Эта книга знакомит читателей со всеми видами графиков. От гистограмм до диаграмм Венна читатели узнают, как графики могут помочь упорядочить информацию в доступной для понимания форме.

- «Тэлли О’Мэлли» Стюарта Дж. Мерфи — Сколько серых машин или зеленых футболок видят эти персонажи по пути на пляж? Ответ легко найти, поскольку персонажи подсчитывают свои ответы, играя в игру, когда они видят, кто может заметить больше всего.
- Семейное воссоединение Бонни Бадер – Гэри Графф, главный герой этой книги, должен выполнить графическое задание. Он выполняет свое задание на воссоединении семьи, одновременно узнавая много нового о математике и своей семье.
- «Математика тигра: обучение построению графиков у тигренка», Энн Уайтхед Нагда — В этой книге рассказывается о жизни тигренка, который растет в зоопарке. Помимо того, что они больше узнают о тиграх, дети также получат базовые математические навыки построения графиков, включая круговые диаграммы и гистограммы.
- Лучшие каникулы на свете Стюарт Дж. Мерфи — Mathstart издает книги, которые помогают обучать таким понятиям, как вероятность, как в этой книге.
 Используйте его, чтобы помочь учащимся понять концепцию визуального рассказа.
Используйте его, чтобы помочь учащимся понять концепцию визуального рассказа. - Вероятно, Пенни Лорин Лиди . В этой увлекательной книге о девушке по имени Лиза рассматривается понятие вероятности. Лиза пытается выполнить домашнее задание.
- Вероятно, фисташковый, Стюарт Дж. Мерфи – Пополните словарный запас, полезный для понимания вероятностей, с помощью милой истории о персонаже по имени Джек, которому не повезло.
- Это возможность Брюса Голдстоуна – Автор учит детей тому, что возможно или невозможно, на примерах.
- Облачно, возможны фрикадельки Джуди Барретт — Это любимая история о городе, в котором погода была совсем не нормальной. Еда упала с неба! Детям нравится эта история, в которой также есть элементы случайности и вероятности.
Ресурсы для обучения построению графиков и вероятности
Упражнения, показанные в этом посте, доступны в различных ресурсах, которые можно найти на Teachers Pay Teachers. Нажмите на изображения выше, чтобы перейти к устройству, деятельность которого показана на фотографии. Узнайте, почему учителям нравится программа Mindful Math для детского сада, первого и второго классов.
Нажмите на изображения выше, чтобы перейти к устройству, деятельность которого показана на фотографии. Узнайте, почему учителям нравится программа Mindful Math для детского сада, первого и второго классов.
Детский сад Графический и сортировочный отдел
Первый класс Графический и денежный отдел
Второй класс Анализ данных, графики и вероятностный блок
Что учителя говорят о модулях Mindful Math Graphing Units
«Моим ученикам понравились задания, которые проводились с этим модулем». ~ Кимберли К.
«Это невероятный ресурс. Глубоко и очень увлекательно!» ~ Кейтлин Д.
«Горжусь тем, что являюсь математическими единицами Первоначального общества! Такой всесторонний способ преподавания математики — повышение грамотности, обучение в целых и малых группах, самостоятельная практика, игры, занятия в центре, ведение дневника и многое другое. Замечательно построены и легко различимы». ~ Лия Дж.
БЕСПЛАТНАЯ графика
Получите бесплатную копию настольной игры Grocery Graphing Board Game , нажав на изображение ниже и зарегистрировавшись!
Бесплатные коврики для обзора математики
Вы хотите предоставить своим ученикам ценный обзор по математике? Попробуйте тренировочные листы Math Mat!
Получите бесплатный образец, нажав на изображение ниже.
Графики деятельности и вероятностные классные материалы
Имейте под рукой хорошие ресурсы для обучения построению графиков и анализу данных. Самое главное, использование манипуляций при построении графиков поможет сделать обучение более значимым для детей. В дополнение к кубикам и счетным медведям, наличие карманных диаграмм и графических ковриков также поможет детям сортировать данные вместе, когда они графически изображают то, что они изучают. Настройте различные графические занятия для учебных центров, предоставив детям множество различных способов практиковаться в построении графиков. В этих уроках построения графиков и сортировки есть все необходимое для этого.
- Карманная диаграмма с двумя или тремя колонками упрощает создание диаграммы как целого класса. Покажите график в классе, чтобы дети лучше познакомились с концепциями построения графиков.
- Возьмите несколько счетчиков медведей и листы активности медведей, чтобы повеселиться.
 Дети получат массу практических навыков построения графиков, выполняя каждую карточку с заданием.
Дети получат массу практических навыков построения графиков, выполняя каждую карточку с заданием. - График и отображение дней рождения с помощью этой карманной диаграммы. Он включает в себя стираемые ламинированные карточки, поэтому его можно использовать в классе из года в год. Кубики Mathlink
- можно использовать для построения трехмерной гистограммы важной информации. В результате детям будет весело складывать блоки, создавая простой график.
- Готовы заставить детей двигаться и веселиться, пока они учатся? Этот напольный коврик для графики — то, что нужно. Дети будут двигаться, создавая огромный график на полу в классе.
- При сравнении данных карманная диаграмма Венна может помочь организовать информацию в удобном для понимания виде.
- Игральные карты — основной предмет в классе для вероятностных игр. Возьмите этот набор из 8 карточек с простым дизайном и цветами, которые идеально подходят для детей.
- Хотите кубик, который увидит весь класс? Это отличный вариант, который также можно писать и стирать!
- Versatiles идеально подходят для различных уроков в классе, включая вероятность и статистику!
- Используйте эти готовые счетчики вероятностей в своих играх и занятиях — они идеально подходят для различных возможностей обучения.

Поиск правильных графических упражнений является ключом к успеху в обучении анализу данных. Дети учатся этому важному математическому навыку благодаря четкому обучению, практике и повторению. Однако самое главное, чтобы обучение было интересным. Вышеупомянутые действия сделают это для ваших студентов.
Найдите больше математических мероприятий
Образец, которые дети любят
Подсчет книг и видео
Teach Dellow Time Time
. Sense Email Series
Подпишитесь на серию рассылок по строительным номерам, наполненных эффективными стратегиями, обязательными заданиями и БЕСПЛАТНЫМИ ресурсами для создания распорядка в вашем классе. Все, что вам нужно, чтобы помочь детям развить их чувство числа и в то же время весело провести время!
Имя
Личный адрес электронной почты
Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.
Я хочу получить бесплатный курс по электронной почте.
Эта форма собирает информацию, которую я буду использовать для отправки еженедельных электронных писем со стратегиями, рекламными акциями и ресурсами. Отписаться в любое время. Работает на ConvertKit25 Творческие занятия по рисованию, которые понравятся детям
В школах иногда недооценивают важность построения графиков. Начиная с раннего возраста, графика должна быть в верхней части вашего списка. Это способ дать детям другую точку зрения на числа и научить их быстро упорядочивать, сравнивать и обсуждать различные идеи и информацию. К счастью, учителям и родителям доступно множество творческих занятий по рисованию! Мы составили список из 25 различных графических заданий, которые понравятся вашим ученикам!
1. Графическая настольная играНаучите своих малышей, как сделать простую гистограмму, подобную этой, с помощью веселья и красок! Им понравятся разные картинки и, конечно же, тактильное дополнение к броску кубика!
Подробнее: Гордимся тем, что являемся начальным классом
2. Графический рисунок напольного коврика
Графический рисунок напольного коврика Такая интерактивная диаграмма очень важна для формирования детского мышления. Выйдите на улицу и соберите что-нибудь из природы или используйте фигурки, чтобы построить график этих милых людей.
Подробнее: Pre Kinders
3. Графические строительные блокиМилый способ совместить игру с математикой. Учащимся понравится это графическое занятие, основанное на сопоставлении! Это будет очень просто для вас, чтобы объяснить, и для студентов, чтобы понять.
Подробнее: Планирование игрового времени
4. Графика AppleЭтот очаровательный урок по построению графиков поможет учащимся различать цвета и лучше группировать объекты по их цветам.
Узнайте больше: Fun-A-Day
5. График ошибок Это очень милое графическое упражнение с ошибками можно легко превратить в интерактивное занятие с гистограммой. Просто отправьте учащимся шаблон и попросите их заполнить его дома!
Просто отправьте учащимся шаблон и попросите их заполнить его дома!
Узнайте больше: Life Over C’s
6. Графики под водойГрафик, подобный этому пиктограмме под водой, прекрасно сочетается с классной комнатой, оформленной в морской тематике. Нам нравится использовать его в нашем детском саду.
Узнать больше: Scribd
7. Напольный коврик для носковОчень забавная базовая гистограмма, включающая личные вещи учащихся, отлично подходит для дистанционного обучения, домашнего обучения или просто занятий на выходных! Вашим детям понравится подбирать и упорядочивать свои носки.
Подробнее: Days With Grey
8. Цветовая диаграмма кнопокВсплывающая гистограмма идеально подходит для любого класса юных учеников! Просто расскажите о любимом цвете вашего ученика и отметьте его имена. Они будут рады видеть свои имена на дисплее!
Подробнее: Нет времени на карточки
9. График высоты
График высоты Еще одна замечательная гистограмма, которая поможет учащимся ответить без путаницы. Студентам понравится смотреть на свой рост по сравнению с другими в классе.
Узнать больше: Смотри, что я умею! Учебный центр
10. Сколько букв в графикеПопулярных типов ресурсов для подсчета букв в именах ваших учеников очень мало. Почему бы не включить эти уроки непосредственно в ваши уроки математики!
Узнайте больше: Диана Нуньес
11. Графики M&MКто не любит граф с вкусными угощениями? Позвольте учащимся изобразить свои M&M’s на графике перед тем, как съесть их!!
Подробнее: Ducks ‘n a Row
12. Графики динозавров Учащимся начальных классов, изучающим математику, понравится эта захватывающая игра про динозавров. Спиннер действует как простой генератор линейных графиков для учащихся, и им будет очень весело генерировать свои собственные ответы.
Узнайте больше: Обучение на стороне картофеля фри
13. Рыбный графикУченикам младших классов понравится такая форма графика. К этому моменту они должны понять идею гистограммы, но будут рады использовать одну из своих любимых закусок, чтобы сделать ее!
Узнать больше: Instagram
14. Спортивная графикаПо мере того, как мы начинаем осваивать графики, учащиеся захотят отметить что-то более интересное. Ваши детки любят баскетбол? Им обязательно понравится эта спортивная диаграмма.
Узнайте больше: Учитель математики Routty
15. Графики VisualЗнание различий между графиками очень важно для всего вашего графического подразделения. Составление якорной диаграммы, подобной приведенной ниже, вместе с вашими учениками будет постоянно приносить им пользу.
Узнать больше: Stallings in Second
16. График вращения формы
График вращения формы Если у детей появится повод использовать спиннер, это всегда будет увлекательным уроком. Урок, подобный этому, идеально подходит для вводного урока по построению графиков. Возвращаем детей к этой идее.
Узнайте больше: Практическое обучение Life Over C’s
17. Разбивка пиктограммыСтикеры отлично подходят для разбора различных систем. Графика не исключение. Мощная графическая программа, подобная этой, заложит знания вашего ученика на прочной основе.
Подробнее: Математика PISD
18. Баночка с сердечкамиКо дню святого Валентина ученики должны были быть в курсе мастер-гистограмм. Предложите учащимся заполнить забавную банку сердечной деятельности, подобную этой.
Узнать больше: Эми Лемонс
19. График броска кубиков Простое упражнение, которое можно использовать в классе или дома, а также использовать в качестве интерактивной гистограммы. Студенты смогут легко понять и использовать ресурсы из дома для выполнения этого задания.
Студенты смогут легко понять и использовать ресурсы из дома для выполнения этого задания.
Дополнительная информация: Начальная школа Вайракей
20. Забавный рисунок фруктовСупер простой генератор гистограмм для самых маленьких умов. Это простой способ для студентов создавать свои собственные гистограммы. Его можно использовать в группах, на станциях или в качестве занятия в целом.
Узнайте больше: Life Over C’s
21. Наглядные материалы средней школыХороший способ показать учащимся различные наглядные материалы — распечатать графики на плакатах и повесить их в классе. Это поможет учащимся постоянно видеть и помнить о различных типах графиков и диаграмм.
Подробнее: Учителя платят учителям
22. Графики координатных плоскостей Координатные плоскости — очень интересная часть построения графиков. Графики в средней школе приобретают совершенно новый смысл, и что-то увлекательное, например создание этого медведя, — это такой увлекательный способ научить учеников и позволить им попрактиковаться в своих навыках построения графиков.
Узнайте больше: Math Crush
23. График поиска сокровищМоим ученикам ПОНРАВИЛОСЬ это занятие по поиску сокровищ. Это отличный способ стимулировать сотрудничество и участие учащихся. Им также понравятся маленькие картинки, которые заставят почувствовать настоящую охоту за сокровищами.
Узнайте больше: Математические материалы Тейлора Дж.
24. График снежного дняИспользуются ли в вашей школе пакеты для защиты от снега? Я всегда люблю отправлять домой задания по рисованию со студентами в снежные дни или перед ними. Им нравятся эти занятия, и очень легко найти графические занятия на зимнюю тематику, подобные приведенным ниже.
Узнайте больше: Разберитесь в математике
25. Трехмерные гистограммы Держите трехмерные гистограммы в своих инструментах учителя! Веселое и увлекательное занятие, наполненное красками и амбициями, вашим учащимся понравится не только создавать, но и демонстрировать на экране.
Подробнее: Runde’s Room
10 лучших диаграмм управления проектами для планирования проектов
Диаграммы управления проектами очень помогают менеджерам проектов планировать, планировать и отслеживать ход выполнения проектов любого масштаба. Существует много типов диаграмм управления проектами, и по одной для каждого этапа жизненного цикла проекта, например, диаграммы инициации или закрытия проекта.
Существуют также схемы планирования, диаграммы и матрицы для каждой из 10 ключевых областей управления проектом, таких как управление стоимостью, графиком, ресурсами или заинтересованными сторонами.
К счастью для менеджеров проектов, есть много альтернатив, когда дело доходит до выбора диаграммы управления проектом для облегчения усилий по планированию проекта. На самом деле, использование этих диаграмм часто необходимо руководителям проектов. Вам нужно будет использовать диаграмму Ганта или структурную структуру работы, чтобы построить план проекта, который является основой вашего проекта.
Что такое диаграммы управления проектами?
Диаграммы управления проектами — это визуальное представление данных, которые превращают сложные концепции управления проектами в легко усваиваемые активы. Они в основном используются для планирования проектов и имеют множество форм, таких как блок-схемы, сетевые диаграммы или гистограммы. Отличными примерами являются диаграммы Ганта, диаграммы PERT, диаграммы CPM и диаграммы WBS.
Диаграммы управления проектом особенно полезны, когда вы сообщаете сложную информацию о планировании проекта. Они визуализируют данные и превращают сложные концепции, такие как расписание или объем вашего проекта, в удобоваримые данные для команды управления проектом и заинтересованных сторон.
Данные из графиков планирования проекта еще более полезны, когда они связаны с программным обеспечением для управления проектами в реальном времени, таким как ProjectManager. Программное обеспечение может взять статическую диаграмму и превратить ее в динамический инструмент для планирования, выполнения и отчетности. Начните бесплатно работать с ProjectManager уже сегодня.
Начните бесплатно работать с ProjectManager уже сегодня.
Топ-10 таблиц управления проектами
Прежде чем решить, какая диаграмма управления проектами лучше всего подходит для вас, важно сначала решить, какую методологию управления проектами вы будете использовать, поскольку существуют различия между каскадным и гибким планированием проектов. Также важно отметить, что вам понадобятся различные диаграммы управления проектами, поскольку каждая из них служит различным целям планирования проекта, таким как создание графика проекта, распределение ресурсов проекта, планирование работы над проектом и многое другое.
Ниже мы выбрали 10 лучших диаграмм управления проектами для планирования проектов, чтобы вы могли решить, какие из них лучше всего подходят для вашего проекта.
1. Диаграммы Ганта
Опытные менеджеры проектов знакомы с диаграммой Ганта. Это динамическая гистограмма, которая показывает график проекта на временной шкале. Хотя диаграммы Ганта начинались как базовый инструмент, они со временем стали более совершенными и включают в себя заманчивые функции, такие как зависимости задач, которые отмечают, когда одна задача связана с другой.
Хотя диаграммы Ганта начинались как базовый инструмент, они со временем стали более совершенными и включают в себя заманчивые функции, такие как зависимости задач, которые отмечают, когда одна задача связана с другой.
Диаграммы Ганта необходимы для современного планирования и составления графиков проектов, поскольку они позволяют руководителям проектов визуализировать все действия, составляющие проект, на временной шкале. Они также полезны для отслеживания прогресса после начала фазы выполнения.
С появлением новых вычислительных мощностей диаграммы Ганта превратились из простой гистограммы в важный инструмент управления проектами, который позволяет менеджерам проектов определять критический путь, назначать задачи, устанавливать зависимости между задачами, создавать график проекта и многое другое. Вот почему большинство современных программ для планирования проектов теперь включают диаграммы Ганта.
Онлайн-диаграммы Ганта для большей гибкости
Все диаграммы Ганта не равны; в других программах для управления проектами есть диаграммы Ганта, но их функциональность невелика. ProjectManager предлагает функции диаграммы Ганта, которые еще не рассматривались конкурентами.
ProjectManager предлагает функции диаграммы Ганта, которые еще не рассматривались конкурентами.
Для начала ProjectManager может импортировать список задач и расписание из статической электронной таблицы. Если ваш план был разработан в Microsoft Project, но вы хотите перенести этот план в сеть, чтобы поделиться им со своей командой, знайте, что ProjectManager упрощает импорт файлов Microsoft Project.
Когда у вас есть план проекта в ProjectManager, наша онлайн-диаграмма Ганта представляет собой диаграмму управления проектом на стероидах. Вы можете связать зависимости задач, чтобы предотвратить блокировку членов команды. Вы также можете назначать задачи непосредственно из представления Ганта, которое представляет собой интерактивную временную шкалу проекта, которую вы можете настраивать в режиме реального времени. Комментарий на уровне задачи и все обновления состояния мгновенно отражаются на диаграмме Ганта, которая в реальном времени переносится на панель мониторинга с показателями проекта, которые можно фильтровать и делиться ими.
Для получения дополнительной информации о диаграммах Ганта посмотрите короткое видео ниже. В нем описаны все способы, с помощью которых диаграммы Ганта могут помочь вам составить подробный и эффективный план проекта.
2. Диаграмма структуры распределения работ (WBS)
Одним из аспектов планирования проекта является организация проектной деятельности, результатов и сроков. Вот где может пригодиться структура распределения работ (WBS). Это способ взять задачи, которые должна выполнить команда, и разделить их на управляемые разделы.
WBS представляет собой ориентированную на результат иерархическую декомпозицию работы, которую должна выполнить команда проекта. Другими словами, это отличный способ визуализировать задачи, которые необходимо выполнить для завершения проекта. Он действует как представление более высокого уровня, чем диаграмма Ганта, что полезно для сложных проектов. WBS может быть представлен в виде списка, древовидной диаграммы, электронной таблицы или столбца на диаграмме Ганта.
Если у вас есть эта информация, собранная в нашем шаблоне диаграммы WBS, если вам нужен более динамичный инструмент с большим количеством опций, подключите его к программному обеспечению ProjectManager для структурной декомпозиции работ.
При перемещении диаграммы WBS в ProjectManager содержимое отображается в различных представлениях программного обеспечения, включая диаграмму Ганта, список задач и доску канбан, визуальный инструмент рабочего процесса. Онлайн-диаграмма Ганта превращает диаграмму WBS в инструмент для планирования проектов.
3. Блок-схема
Блок-схемы — еще один инструмент, который руководители проектов должны иметь в своем наборе инструментов при планировании проекта. Эти диаграммы помогают визуализировать процессы как способ повышения эффективности проекта. Блок-схема представляет собой графическое отображение цели проекта и помогает создать логический порядок работы, необходимой для достижения этой цели. Планирование проекта — это контроль, и блок-схема дает менеджеру проекта инструмент для осуществления контроля над задачами, ресурсами и временем. Это означает, что все процессы, включая планирование и мониторинг, для повышения эффективности основаны на блок-схеме.
Это означает, что все процессы, включая планирование и мониторинг, для повышения эффективности основаны на блок-схеме.
Процесс планирования начинается с оценки и разработки содержания проекта. Это может привести к индикатору уровня проекта или системе показателей проекта, оба из которых будут включены в план проекта. За планом следуют задачи, ресурсы, бюджеты, графики и т. д., каждая из которых сводится к коммуникациям, управлению рисками, контролю изменений, управлению качеством и т. д.
Наконец, этап утверждения. В случае одобрения план проекта готов. Если нет, блок-схема возвращается к началу, чтобы начать заново.
4. Диаграмма критического пути (CPM)
Еще одним инструментом визуального планирования является диаграмма критического пути (основанная на методе критического пути, или CPM). Он используется для отображения действий, необходимых для завершения проекта. Диаграмма иллюстрирует продолжительность каждого действия и предшествующего действия, как они связаны и отстают (количество времени между двумя действиями).
Диаграмма критического пути помогает руководителям проектов разбить более обширный проект на необходимые действия для успешного выполнения проекта. Эти действия представлены на диаграмме в виде прямоугольников. Между этими действиями или прямоугольниками есть линии, которые представляют поток, чтобы показать, как каждое действие связано и взаимосвязано.
Цель использования диаграммы критического пути — позволить руководителям проектов рассчитать общую продолжительность проекта. Критический путь состоит из критических действий, но также показаны некритические действия. Некритические действия обеспечивают большую гибкость, поскольку они не оказывают существенного влияния на проект.
5. Матрица RACI
RACI — это аббревиатура, означающая «ответственный, подотчетный, консультируемый и информированный». Матрица RACI — это диаграмма, которая помогает распределить обязанности в управлении проектами. Эта таблица помогает руководителям проектов определять заинтересованные стороны в своих проектах и оценивать каждый уровень участия. Это можно сделать, отметив рядом с каждым начальный R, A, C или I, чтобы классифицировать вовлеченность.
Это можно сделать, отметив рядом с каждым начальный R, A, C или I, чтобы классифицировать вовлеченность.
Например, ответственный участник означает, что он несет прямую ответственность за задачу. Ответственный определяет того, кто делегирует и проверяет работу. Консультация означает, что вам нужен вклад и отзывы этого человека о проделанной работе, а информирование — это лица, которым необходимо быть в курсе хода работы.
Это полезно для распределения обязанностей членов команды по проекту. Но его также можно использовать для управления заинтересованными сторонами. Матрица RACI помогает менеджеру проекта выяснить, какие заинтересованные стороны должны знать, что и как часто они должны быть в курсе хода проекта.
6. Диаграмма PERT
Этот визуальный инструмент управления проектами отлично подходит для планирования задач и сроков проекта. PERT — это еще одна аббревиатура, обозначающая метод оценки и анализа проекта (или программы). Он обеспечивает графическое представление задач проекта, расписания и сроков.
Диаграмма PERT не является диаграммой Ганта, хотя и похожа на нее. Диаграммы Ганта — это гистограммы, а PERT — произвольная форма. Диаграммы PERT состоят из узлов, прямоугольников или кругов, которые обозначают вехи. Соединительные стрелки показывают, что должно быть выполнено между узлами, и они представляют продолжительность каждой задачи.
Некоторые диаграммы Ганта не показывают зависимости задач, но все диаграммы PERT показывают. Они используют параллельные стрелки направления, чтобы указать ряд задач, которые должны быть выполнены в определенной последовательности. Расходящиеся стрелки указывают на работу, которую можно выполнять параллельно.
7. Схема рабочего процесса
Диаграммы рабочих процессов наглядно показывают структуру процесса, проекта или задания. Это делается в виде блок-схемы. Диаграммы рабочих процессов обычно используются, чтобы показать полный бизнес-процесс и потоки информации, помочь сотрудникам понять свои роли и обязанности, выявить избыточность и узкие места и избежать рисков.
Эта схема управления проектом может быть создана с помощью программного обеспечения или нарисована вручную. Какой бы путь вы ни выбрали, вы получите значительную ценность от схемы рабочего процесса. Они помогают с операциями и повышают эффективность за счет оптимизации работы. Они также предоставляют документацию по юридическим, нормативным и аудиторским требованиям.
Это отличный инструмент для четкой коммуникации в организации. Визуальные инструменты часто легче усваиваются независимо от того, какой отдел на них смотрит. Диаграмма рабочего процесса также является способом усиления безопасности. Схемы рабочих процессов надежно отслеживают информацию и гарантируют, что ваша организация устранит любые бреши в системе безопасности.
8. Матрица рисков
Риски могут быть хорошими и плохими, и руководители проектов хотят либо воспользоваться этими неожиданными возможностями, либо смягчить влияние проблем на проект. Матрица рисков используется при планировании проекта для выявления и планирования устранения рисков по мере их возникновения в качестве проблем в проекте.
В матрице рисков перечислены риски, которые могут возникнуть на основе опыта и исторических данных. Матрица представляет вероятность появления риска в проекте и влияние, которое он окажет, если он действительно проявится. Риски классифицируются по степени вероятности и серьезности.
Этот инструмент помогает руководителям проектов управлять рисками проекта. Он также сообщает проектной команде и заинтересованным сторонам о рисках, которые могут стать проблемами в проекте. Это позволяет командам быстро выявлять эти проблемы и решать их.
9. Таблица этапов
Диаграмма вех — это наглядная временная шкала, которая помогает руководителям проектов планировать важные события в расписании проекта. Вехи — это важные события в проекте, такие как выполнение плана проекта или завершение одной фазы проекта и начало следующей.
Каждая вертикальная линия диаграммы вех показывает одну веху. Слева от вехи находится описание вехи, а также горизонтальная шкала времени, отображающая весь проект. Диаграмма вех помогает вашей команде, заинтересованным сторонам и клиентам быть в курсе основных событий проекта.
Диаграмма вех помогает вашей команде, заинтересованным сторонам и клиентам быть в курсе основных событий проекта.
Создание вех в вашем расписании и отслеживание их на протяжении всего проекта — это один из способов не сбиться с графика. Совместное использование диаграммы вех сообщает об основных событиях в проекте и гарантирует, что все знают о них. Это похоже на предварительное уведомление о больших сроках, которые должны быть соблюдены.
10. Диаграмма выгорания
В гибком управлении проектами диаграмма выгорания используется для визуального представления того, насколько быстро команда проекта обрабатывает пользовательские истории клиента, и показывает описание функций, над которыми ведется работа. Эти описания даны с точки зрения конечного пользователя. Диаграмма выгорания показывает усилия команды по сравнению с полным спринтом.
Работа, которую еще предстоит выполнить, показана на вертикальной оси. Время, прошедшее с начала проекта, показано по горизонтали. Это представляет как прошлое, так и будущее, чтобы каждый мог видеть, где он находится. Диаграмма выгорания регулярно обновляется, чтобы убедиться, что она точная.
Это представляет как прошлое, так и будущее, чтобы каждый мог видеть, где он находится. Диаграмма выгорания регулярно обновляется, чтобы убедиться, что она точная.
Существует два типа диаграмм выработки: одна используется для спринтов или коротких итераций, когда их agile-команда работает над пользовательскими историями, а другая — диаграмма выработки продукта. Последний показывает работу, которая осталась для всего проекта, в то время как первый — это только то, что осталось сделать.
ProjectManager и диаграммы управления проектами
Диаграммы управления проектом — отличные наглядные пособия и полезные инструменты для настройки процедур вашего проекта, но статические документы могут сделать не так много. Когда вы начнете планировать и выполнять проект, вам понадобится программное обеспечение для управления проектами, чтобы связать команды и упростить работу. ProjectManager — это программное обеспечение для управления проектами, которое автоматически обновляется данными в режиме реального времени, чтобы помочь вам лучше управлять своим проектом.
Отслеживание времени и затрат с помощью информационных панелей в реальном времени
При работе со статическими документами вам необходимо вводить данные и вручную обновлять диаграммы управления проектами, но наше программное обеспечение сделает эту работу за вас. Панели мониторинга в режиме реального времени автоматически собирают оперативные данные из проекта, обрабатывают числа и отображают результаты в диаграммах проекта. Эти шесть показателей проекта включают время, стоимость, рабочую нагрузку и многое другое. Все они обновляются в режиме реального времени, чтобы дать вам обзор вашего проекта в любое время. Там также нет никаких настроек.
Использование канбан-досок для управления задачами
После того, как вы приступите к выполнению проекта, вам понадобится окно в процесс и инструмент, который даст вашей команде возможность самостоятельно управлять своей работой. Наши канбан-доски визуализируют рабочий процесс, позволяя руководителям проектов видеть, где находятся их команды с точки зрения производства, и выявлять любые потенциальные препятствия. Затем они могут перераспределять ресурсы, чтобы команды работали на полную мощность. Между тем, команды могут управлять своим невыполненным заданием и сотрудничать при планировании спринтов.
Затем они могут перераспределять ресурсы, чтобы команды работали на полную мощность. Между тем, команды могут управлять своим невыполненным заданием и сотрудничать при планировании спринтов.
В отличие от диаграмм управления проектами, наше программное обеспечение достаточно гибко, чтобы предоставить вам инструменты, которые вы хотите использовать. Наши многочисленные представления проектов означают, что менеджеры могут планировать на диаграммах Ганта, команды могут использовать представления списков, чтобы отмечать свои задачи, заинтересованные стороны могут просматривать календари, чтобы убедиться, что вехи выполнены, и все представления используют одни и те же данные в реальном времени. Есть один источник правды, благодаря которому всем лучше работать вместе, сотрудничать, обмениваться файлами и комментировать на уровне задач.
Связанный контент
Ознакомьтесь с нашими руководствами, блогами и шаблонами, где вы можете получить подробную информацию о дополнительных схемах и схемах планирования проекта, чтобы вы могли использовать их во всех своих проектах для достижения лучших результатов.
- Как составить матрицу распределения обязанностей
- Как сделать сетевую диаграмму проекта
- Введение в диаграммы приоритета
- Стрелочные диаграммы для проектов
- Ганта, PERT и сетевая диаграмма
Планирование может решить или разрушить проект, поэтому вам нужно иметь в своем распоряжении лучшие инструменты при выполнении процесса. ProjectManager — это онлайн-программное обеспечение для управления проектами, которое помогает планировать, выполнять, отслеживать и составлять отчеты по всем вашим проектам. Он без проблем работает с описанными выше схемами планирования проекта и имеет надежный набор инструментов управления проектами для управления ресурсами, временем и стоимостью. Узнайте, как это может помочь вам спланировать свой проект, воспользовавшись бесплатной 30-дневной пробной версией сегодня.
Все о графе задач Gradle — Том Грегори
Мощной функцией Gradle является возможность устанавливать зависимости между задачами, создавая граф задач или дерево. Это здорово, потому что вам нужно запустить только интересующую вас задачу, а любые другие необходимые задачи запускаются автоматически. В этой статье вы узнаете все о графе задач Gradle, о том, как добавлять в него задачи и как его распечатать.
Это здорово, потому что вам нужно запустить только интересующую вас задачу, а любые другие необходимые задачи запускаются автоматически. В этой статье вы узнаете все о графе задач Gradle, о том, как добавлять в него задачи и как его распечатать.
Задачи и зависимости задач
Задача Gradle — это единица работы, которую необходимо выполнить в вашей сборке. Действительно распространенные примеры в проекте Java включают:
- компиляция кода с помощью задачи
compileJava - создание jar-файла с помощью задачи
jar - создание всего проекта с помощью задачи
buildРабота. Хитрость заключается в том, что те задачи, которые, казалось бы, делают много, напримерbuild, состоят только из зависимостей от других задач.Определение зависимостей задач
В качестве быстрого напоминания, если у нас есть две задачи taskA и taskB , которые печатают свое имя, то мы можем сказать, что taskB зависит от taskA , используя функцию
dependOn.
задача задачаA() { сделатьпоследний { печатать имя } } задача задачаB() { сделатьпоследний { печатать имя } зависит от задачиA }Итак, когда мы запустим
./gradlew taskB, мы получим этот вывод, показывающий, что запускается taskA , за которым следует taskB .> Задача :taskA задача А > Задача: задачаB задачаB ПОСТРОИТЬ УСПЕШНО в 1с
Эта простая концепция, расширенная для включения цепочек многих задач, — это то, как создаются общие задачи, которые мы используем каждый день в Gradle.
Граф задач Gradle
Граф задач — это структура, которая формируется из всех зависимостей между задачами в сборке Gradle.
 Продолжая наш пример задачи
Продолжая наш пример задачи buildв проекте с примененным плагиномjava, его график задачи выглядит следующим образом.Здесь вы видите все различные задачи, составляющие
сборказадача. Пунктирные линии представляют 90 954 зависимых от 90 955 взаимосвязей между задачами. Итак, глядя на верхний раздел,buildзависит отassemble, который зависит отjar, который зависит отклассов, который зависит как отcompileJava, так и отprocessResources.Итак, сборка
На диаграмме видно, что задачи попадают в одну из двух категорий:
- задачи, которые выполняют действие — например, задача
jarимеет связанное с ней действие, которое идет и создает jar файл. Эти типы задач могут зависеть или не зависеть от других задач.
Эти типы задач могут зависеть или не зависеть от других задач. - агрегированные задачи — эти задачи предназначены только для того, чтобы предоставить вам удобный способ выполнить группировку функций. Например, вместо того, чтобы запускать
checkисобирают задачипо отдельности, задачаbuildпросто объединяет их вместе.
Значит, сборка
Печать графа задач
Преимущества понимания структуры графа задач:
- вы можете запускать в нем любую задачу : если вам нужно только создать файл
jar, нет необходимости запускать сборку - это может помочь отладить проблемы, связанные с задачами : если у вас есть сложный граф задач, возможно, с вашими собственными пользовательскими задачами, то понимание графа задач является ключом к решению таких вопросов, как «Почему myAwesomeTask не работает?»
Звучит хорошо, но как нам распечатать график задачи? Что ж, сам Gradle не поддерживает эту функциональность, но, к счастью, есть несколько плагинов, которые ее поддерживают.
 Лучшее, что я нашел, это 9Плагин 0011 gradle-taskinfo .
Лучшее, что я нашел, это 9Плагин 0011 gradle-taskinfo .Давайте применим его к простому проекту Java в нашем build.gradle .
плагины { идентификатор 'java' id 'org.barfuin.gradle.taskinfo' версия '1.0.5' }Он предоставляет новую задачу
tiTree, которую мы запускаем вместе с задачей, дерево задач которой нас интересует../gradlew tiTree build
Что выводит этот вывод
> Задача: tiTree :сборка (org.gradle.api.DefaultTask) +--- :собрать (org.gradle.api.DefaultTask) | `--- :jar (org.gradle.api.tasks.bundling.Jar) | `--- :классы (org.
 gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :check (org.gradle.api.DefaultTask)
`--- :test (org.gradle.api.tasks.testing.Test)
+--- :классы (org.gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :testClasses (org.gradle.api.DefaultTask)
+--- :compileTestJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :классы (org.gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :processTestResources (org.gradle.language.jvm.tasks.ProcessResources)
gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :check (org.gradle.api.DefaultTask)
`--- :test (org.gradle.api.tasks.testing.Test)
+--- :классы (org.gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :testClasses (org.gradle.api.DefaultTask)
+--- :compileTestJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :классы (org.gradle.api.DefaultTask)
| +--- :compileJava (org.gradle.api.tasks.compile.JavaCompile)
| `--- :processResources (org.gradle.language.jvm.tasks.ProcessResources)
`--- :processTestResources (org.gradle.language.jvm.tasks.ProcessResources)
Круто! Вывод показывает ту же структуру, что и диаграмма ранее (забавно, что 😉).
 Плагин также выводит нам тип задачи, например, мы можем видеть, что
Плагин также выводит нам тип задачи, например, мы можем видеть, что compileJava— это задача типаorg.gradle.api.tasks.compile.JavaCompile.Спасибо Barfuin за этот замечательный плагин, о котором вы можете узнать больше на GitLab.
Навигация по графу задач программно
Если вы хотите сами получить доступ к графу задач Gradle во время сборки, к счастью, это довольно просто с 9Интерфейс 0954 org.gradle.api.execution.TaskExecutionGraph . Это в основном позволяет вам:
- получить все задачи в графе
- получить зависимости конкретной задачи
- добавить прослушиватель, который будет выполняться до или после выполнения задач
Давайте попробуем несколько примеров в рамках проекта Gradle, который применяется плагин
java.Получение всех задач в графе задач
При использовании графа задач мы должны определить замыкание, которое будет вызываться, когда граф задач будет готов, иначе мы получим Информация о задании недоступна.
 Ошибка . В этом закрытии мы можем распечатать список всех задач в графе, вызвав
Ошибка . В этом закрытии мы можем распечатать список всех задач в графе, вызвав getAllTasksproject.gradle.taskGraph.whenReady { println project.gradle.taskGraph.getAllTasks() }Когда мы запускаем
./gradlew build, он выводит это.[задача ':compileJava', задача ':processResources', задача ':classes', задача ':jar', задача ':assemble', задача ':compileTestJava', задача ':processTestResources', задача ':test Classes», задача «:test», задача «:check», задача «:build»] ПОСТРОИТЬ УСПЕШНО в 859РС
Содержит все задачи из приведенных выше графических диаграмм задач.

Что такое закрытие? Это способ определения блока кода таким образом, чтобы его можно было передать как переменную и выполнить позже.
Запрос зависимостей задачи
Функция
getDependenciesпринимает задачу в качестве входных данных и возвращает ее прямые зависимости. Давайте изменим замыкание, переданноеwhenReady, на следующее.проект.gradle.taskGraph.whenReady { println project.gradle.taskGraph.getDependencies (сборка как задача) }Выполнение
./gradlew buildтеперь печатает это.[задача ': сборка', задача ': проверка'] BUILD SUCCESSFUL in 893ms
Что показывает, что прямыми зависимостями задачи
buildявляютсяassemble иcheck.
Добавление прослушивателя задач
Наконец, давайте определим закрытие, которое будет выполняться после запуска каждой задачи, используя функцию
afterTask.проект.gradle.taskGraph.whenReady { project.gradle.taskGraph.afterTask {задача -> println "Делаем важные вещи после $task" } }Когда мы запускаем
./gradlew jar, мы получаем этот вывод.> Задача: скомпилировать Java UP-TO-DATE Делаем важные вещи после задачи ':compileJava' > Задача: ProcessResources АКТУАЛЬНО Делать важные вещи после задачи ':processResources' > Задача: классы АКТУАЛЬНЫ Выполнение важных дел после задачи ':classes' > Задача :jar АКТУАЛЬНО Делать важные вещи после задачи ':jar' ПОСТРОИТЬ УСПЕШНО за 798 мс 3 задачи, требующие действия: 3 актуальные
Наше закрытие вызывалось после выполнения каждой задачи.

Для получения полной информации об этих и других функциях ознакомьтесь с документацией для
TaskExecutionGraph.Подведение итогов
Вы только что узнали о задачах и о том, как зависимости между ними формируют граф задач Gradle . График задач можно красиво визуализировать с помощью плагина
taskinfo, который помогает нам понять график задач для конкретной задачи. Для еще большего контроля Gradle предлагает интерфейсTaskExecutionGraph, позволяющий нам подключать пользовательскую логику там, где это необходимо.Хотите узнать больше о Gradle?
Ознакомьтесь с полной подборкой руководств по Gradle.concepts/task-system/task-graph/task-graph · Twister2
Граф задач является предпочтительным выбором для обработки крупномасштабных данных. Это упрощает процесс параллелизма задач и имеет возможность динамически определять зависимость между те задачи. Узлы графа задач состоят из вершин задач и ребер, в которых вершины задач представляют вычислительные единицы приложения, а ребра представляют коммуникационные ребра между этими вычислительными единицами.
 Другими словами, он описывает детали того, как данные
потребляется между этими единицами. Каждый узел графа задач содержит информацию о входных и
его выход. Граф задач преобразуется в граф выполнения, как только происходит фактическое выполнение.
Другими словами, он описывает детали того, как данные
потребляется между этими единицами. Каждый узел графа задач содержит информацию о входных и
его выход. Граф задач преобразуется в граф выполнения, как только происходит фактическое выполнение.График задач в Twister2
Слой задач обеспечивает абстракцию более высокого уровня поверх коммуникационного уровня, чтобы скрыть основные детали выполнения и сообщения от пользователя. Расчеты моделируются как графы задач на слое задач, которые можно создавать статически или динамически. узел в граф задач представляет собой задачу, тогда как ребро представляет собой канал связи между вершинами. Каждый узел в графе задач содержит информацию о входе и выходе. Задача может быть долговременный (потоковый граф) или кратковременный (потоковой граф без циклов) в зависимости от типа применения. Граф задач «TG» обычно состоит из набора вершин задач «TV» и ребер задач (TE), которые математически обозначен как График задач
(TG) -> (TV, TE)
Статические и динамические графы задач
Графы задач могут быть определены двумя способами, а именно статическим и динамическим графом задач.

- Статический граф задач — структура полного графа задач известна во время компиляции.
- Динамический граф задач — структура графа задач неизвестна во время компиляции и программы динамически определять структуру графа задач во время выполнения.
Следующие три важных момента следует учитывать при создании и планировании задачи. экземпляры графа задач.
- Декомпозиция задач — определение независимых задач, которые могут выполняться одновременно
- Группировать задачи — группировать задачи на основе зависимости от других задач.
- Упорядочить задачи — упорядочить задачи, удовлетворяющие ограничениям других задач.
(Ссылка: шаблоны для параллельного программирования, глава 3 (2) и https://patterns.eecs.berkeley.edu/?page_id=609)
Направленный граф задач и неориентированный граф задач
Существует два типа графов задач, а именно направленный граф задач и неориентированный граф задач. В направлении граф задач, ребра в графе задач, которые соединяют вершины задач, имеют направление, как показано на рис.
 1, тогда как в неориентированном графе задач ребра в графе задач, соединяющие задачу
вершины не имеют направления, как показано на рис. 2. Настоящая система задач поддерживает только направленный поток данных.
график задач.
1, тогда как в неориентированном графе задач ребра в графе задач, соединяющие задачу
вершины не имеют направления, как показано на рис. 2. Настоящая система задач поддерживает только направленный поток данных.
график задач.График задач потоковой передачи
Под потоком понимается процесс обработки неограниченной последовательности блоков данных. Потоковое приложение который может непрерывно потреблять единицы входного потока и производить единицы выходного потока. Потоковое граф задач в основном отвечает за создание и выполнение потоковых приложений.
График пакетной задачи
Пакетная обработка относится к процессу обработки ограниченной последовательности единиц данных. Пакетные приложения в основном потребляет ограниченные блоки данных и производит блоки данных. График пакетной задачи в основном отвечает за создание и выполнение пакетных приложений.
График задач в Twister2
Система графов задач в Twister2 в основном предназначена для поддержки графа задач направленного потока данных который состоит из вершин задачи и ребер задачи.

- Вершины задачи представляют исходную и целевую вершины задачи
- Ребро задачи представляет ребра, соединяющие вершины задачи
Граф задач в Twister2
- поддерживает итеративную обработку данных. Например, в алгоритме кластеризации K-средних в конце каждая итерация, точки данных и центроиды сохраняются в наборе данных, который будет использоваться для следующая итерация
- Запрещены циклы, автопетли или циклы
Подробно описывает, как данные потребляются между вершинами задачи.
- Исходная задача — расширяет BaseSource и реализует описанный ниже интерфейс Receptor.
- Compute Task — реализует описанный ниже интерфейс IFunction.
- Sink Task — расширяет BaseSink и реализует интерфейс Collector.
Сведения о реализации
ITaskGraph
Это основной интерфейс, который в первую очередь отвечает за создание вершин и ребер задач.
 между этими вершинами, удаление вершин задач и ребер задач и другие.
между этими вершинами, удаление вершин задач и ребер задач и другие.BaseDataflowTaskGraph
Это базовый класс для графа задач потока данных, который состоит из методов для определения внутреннего и внешние границы задач, а также входящие и исходящие границы задач. Он проверяет вершины задачи и создает ребро направленного потока данных между исходной и целевой вершинами задачи. Он также выполняет проверки, такие как повторяющиеся имена для задачи, повторяющиеся границы между одними и теми же двумя задачами, самозацикливание на графе задач и циклы на графе задач. Некоторые из основных методов, доступных в этот класс
addTaskVertex(TV sourceTaskVertex, TV targetTaskVertex) addTaskEge(TV sourceTaskVertex, TV targetTaskVertex, TE taskEges) removeTaskVertex(TV taskVertex), removeTaskEdge(TE taskEdge) validateTaskVertex (ТВ исходная/целевая вершина) логическое обнаружениеSelfLoop (Set taskVertex) обнаружить цикл (вершина ТВ, установить задачуVertexSet, установить исходную задачу, установить целевую задачу) логическое значение содержитTaskEdge(TE taskEdge)DataflowTaskGraph
Это основной класс, который расширяет BaseDataflowTaskGraph, сначала он проверяет граф задач, а затем сохранить направленные ребра в карту задач, которая состоит из исходной вершины задачи и целевой вершины задачи.

- задачи, которые выполняют действие — например, задача

 ) и повседневной жизни.
) и повседневной жизни.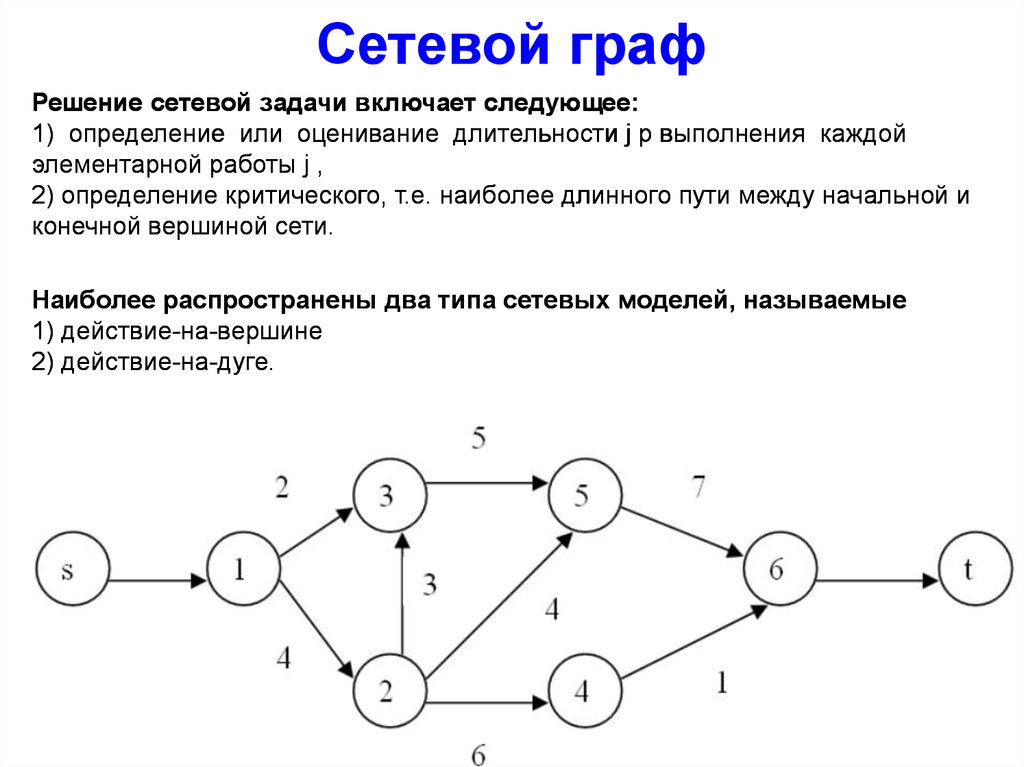 Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.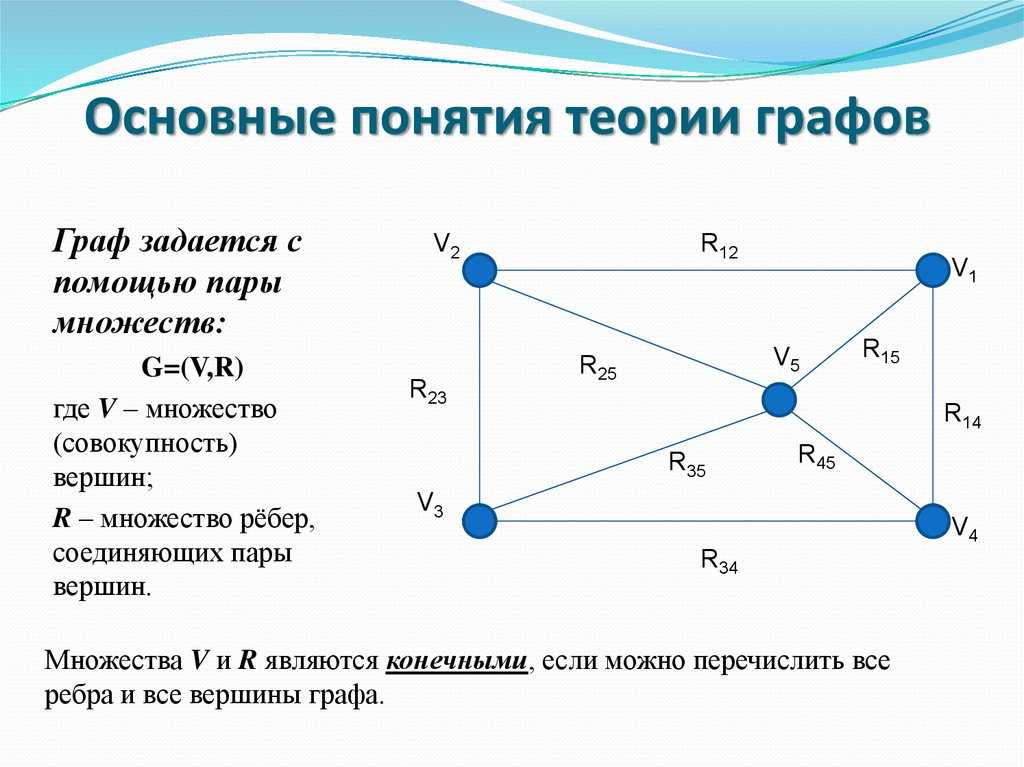 Линия указывает на связь между двумя точками.
Линия указывает на связь между двумя точками.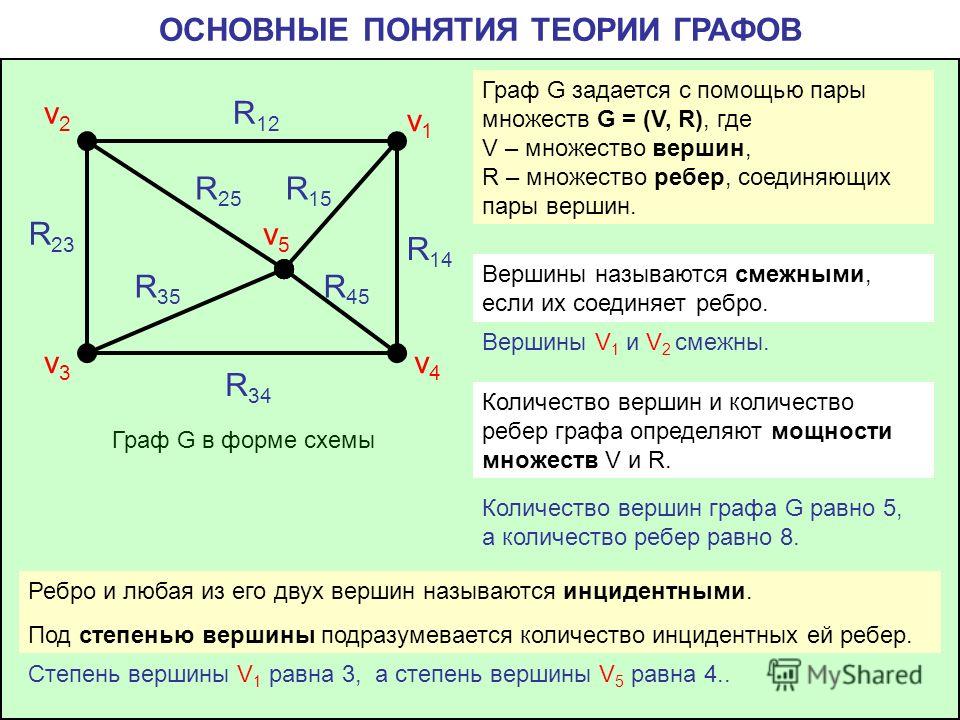
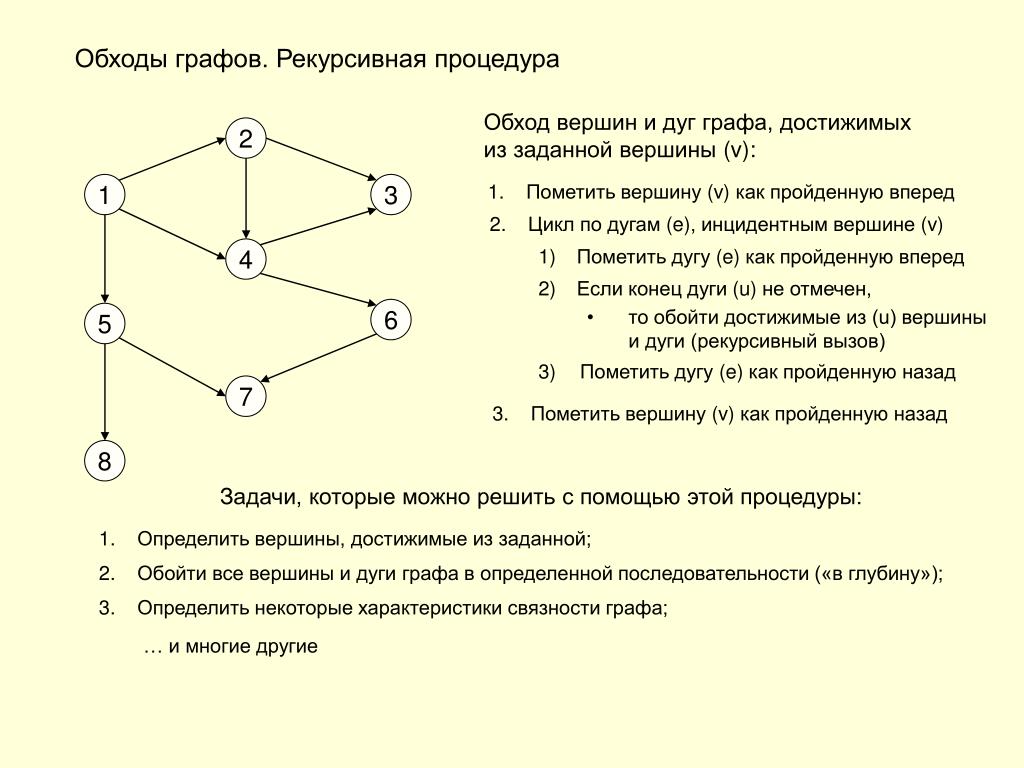 Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева.
Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева. Получается граф (2) дающий решение задачи.
Получается граф (2) дающий решение задачи.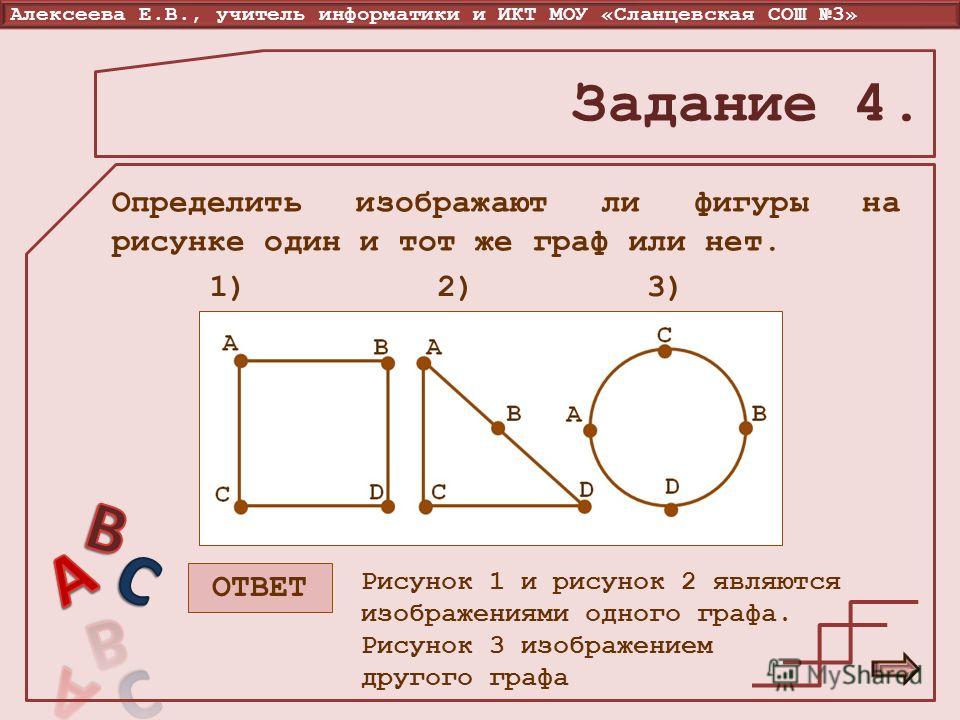
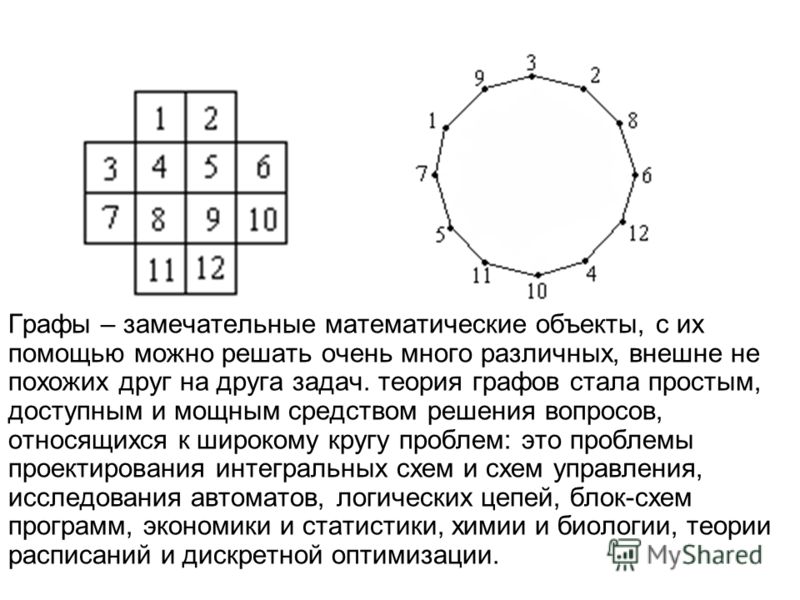 Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?
Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места? Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .
Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .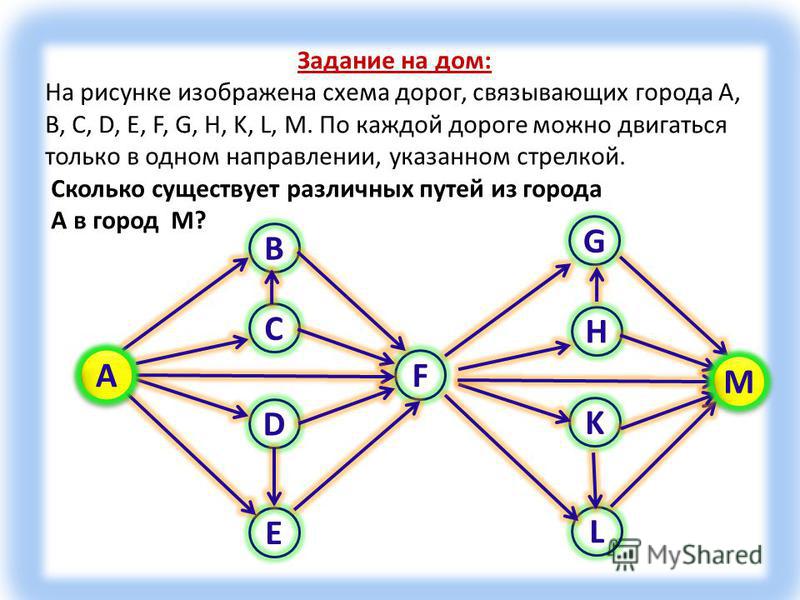 Информатика дает инструмент для познания любой научной дисциплины.
Информатика дает инструмент для познания любой научной дисциплины.