Наименьшее общее кратное / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Наименьшее общее кратное
Задача:
Петя строит железную дорогу из частей, длина которых 4 см, а Сережа, из частей длина которых 6 см. Какую наименьшую протяженность дорожного полотна построят мальчики равной длины?
Решение:
Длина дороги, построенной мальчиками, должна делиться нацело на 4 и 6, так как части, из которых строят дорогу Петя и Сережа равны 4 см и 6 см соответственно, то есть длина построенной железной дороги должна быть кратной и 4, и 6.
Числа кратные 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60…
Числа кратные 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60…
То есть общими кратными чисел 4 и 6 являются числа (выделено синим):
12, 24, 36, 48, 60.
Но наименьшим из них является 12. Это число называется наименьшим общим кратным.
То есть наименьшая протяженность дорожного полотна равной длины у Пети и Сережи 12 см.
| Наименьшее натуральное число, которое делится нацело на каждое из двух данных натуральных чисел, то есть кратно каждому из них, называют наименьшим общим кратным этих чисел. |
Наименьшее общее кратное чисел и обозначают так: НОК(; ), то есть мы можем записать НОК(4; 6) = 12.
Нахождение наименьшего общего кратного:
1 способ:
Найдем НОК(12; 15).
Выбираем наибольшее из двух чисел, в нашем случае это число 15, и записываем числа кратные ему, до тех пор, пока не получим число, которое будет кратно второму числу, в нашем случае числу 12.
Получаем: 15, 30, 45, 60.
Число 60 является наименьшим общим кратным чисел 12 и 15, то есть НОК(12; 15) = 60.
2 способ:
Разложим данные числа на простые множители:
12 = 223 15 = 35.
Далее для выписываем простые множители, которые входят в разложение первого числа, и добавляем множители из разложения второго числа, которых нет в разложении первого, то есть в нашем случае, это множитель 5.
Итак, мы получим 4 множителя 2235, произведение данных множителей равно числу 60, которое является наименьшим общим кратным чисел 12 и 15, то есть мы снова получили НОК(12; 15) = 60.
Таким же образом можно найти НОК трех и более чисел.
Чтобы найти НОК нескольких натуральных чисел, надо:
|
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.
3 способ:
Найдем НОК(2520; 4620). Для это разложим данные числа на простые множители и запишем разложение в виде произведения степеней:
2 520 = 23325171 4 620 = 22315171111.
Далее используем правило:
|
В нашем случае:
- Встречается только в одном разложении: 111.
- Степени с бóльшими показателями: 23, 32, 51, 71.
- Находим произведение данных степеней, то есть искомый наименьшее общее кратное: НОК(2520; 4620) = 2332517111 = 27 720.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 167, Мерзляк, Полонский, Якир, Учебник
Номер 172, Мерзляк, Полонский, Якир, Учебник
Номер 175, Мерзляк, Полонский, Якир, Учебник
Номер 242, Мерзляк, Полонский, Якир, Учебник
Номер 359, Мерзляк, Полонский, Якир, Учебник
Номер 372, Мерзляк, Полонский, Якир, Учебник
Номер 525, Мерзляк, Полонский, Якир, Учебник
Задание 185, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 203, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 45, Мерзляк, Полонский, Якир, Учебник
Номер 46, Мерзляк, Полонский, Якир, Учебник
Номер 47, Мерзляк, Полонский, Якир, Учебник
Номер 48, Мерзляк, Полонский, Якир, Учебник
Номер 349, Мерзляк, Полонский, Якир, Учебник
Номер 529, Мерзляк, Полонский, Якир, Учебник
Номер 562, Мерзляк, Полонский, Якир, Учебник
Номер 670, Мерзляк, Полонский, Якир, Учебник
Номер 692, Мерзляк, Полонский, Якир, Учебник
Номер 693, Мерзляк, Полонский, Якир, Учебник
Как найти общее кратное чисел » задачи
НОД и НОК »
НАЙТИ НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ ЧИСЕЛ 44 И 24.
 ПОДРОБНО.
ПОДРОБНО.
Решение: Число должно делиться без остатка и на 44, и на 24, т. е. оно должно быть кратным и 44 и 24. Выпишем числа, кратные 44. Получим:
88, 150, 132, 176, 220, 264, 308,352,396
Затем выпишем числа, кратные 24. Получим:
48, 72, 96, 120, 144, 168, 192, 216,240, 264, 288,
Общими кратными чисел 44 и 24 будет число 264. Наименьшим из них является 264. Это число называют наименьшим общим кратным чисел 44 и 24.Найти наименьшее общее кратное чисел 12 и 15.
Решение: Что бы найти НОК надо:
1. разложить числа на простые множители
2. Написать разложение одного числа (лучше наибольшее)
3. Дополнить его теми множетялими из разложения другого числа, которых нет в написанном разложении
4. вычислить полученное произведение
Это число и будит НОК данных чисел.
12|2. 15|3
6| 2 5|5
3 | 3. 1|
1 |
НОК (12и15)=3×5×2×2=6012:2=6:2=3:3=1
15:3=5:5=1
общее число на которое делим 3-это и есть наименьшее общее кратноеНайти наименьшее общее кратное чисел: 1) 12 и 15; 2)16 и 32; 3)8 и 15.

Решение: 1) НОК(12;15)=60 2) НОК(16;32)=32 3) НОК(8;15)=1201) разложим числа на простые множители
12=4*3=2*2*3
15=3*5 = 3*5
к большему числу добавим недостающие множители
НОК (12,15)= 15 * 2*2 = 60
2)
16=2*8 = 2*2*2*2
32=4*8= 2*2*2*2*2
НОК (16,32) = 32
3)
8=2*4=2*2*2
15=3*5
НОК = 15*8 = 120Найти наименьшее общее кратное чисел 144и125
Решение: 144 : 2 = 72 125 : 5 = 25
72 : 2 = 36 25 : 5 = 5
36 : 2 = 18 5 : 5 = 1
18 : 2 = 9 125 = 5 * 5 * 5
9 : 3 = 3
3 : 3 = 1
144 = 2 * 2 * 2 * 2 * 3 * 3
НОК (144 и 125) = 144 * 125 = 18 000 — наименьшее общее кратное
Числа 144 и 125 — взаимно простые, так как у них нет общих делителей, кроме единицы.Математика 6 класс найти наименьшее общее кратное чисел 7875 и 4725
Решение: 7875 : 3 = 2625 4725 : 3 = 1575
2625 : 3 = 875 1575 : 3 = 525
875 : 5 = 175 525 : 3 = 175
175 : 5 = 25 175 : 5 = 35
35 : 5 = 7 35 : 5 = 7
7 : 7 = 1 7 : 7 = 1
7875 = 3 * 3 * 5 * 5 * 5 * 7 4725 = 3 * 3 * 3 * 5 * 5 * 7
НОК (7875 и 4725) = 3 * 3 * 3 * 5 * 5 * 5 * 7 = 23 625 — наименьшее общее кратное
23 625 : 7 875 = 3 23 625 : 4 725 = 5найти НОК (Наименьшее Общее Кратное) у чисел 105, 95, 63.
 И нужно не только НОК, но и как его вычислили.
И нужно не только НОК, но и как его вычислили.
Решение: 105 5 95 5 63 3 нок(105,95,63)=1
21 3 19 19 21 3
7 7 1 7 7
1 1105 = 3 · 5 · 7
95 = 5 · 19
63 = 3 · 3 · 7
Наименьшее общее кратное = 3 · 3 · 5 · 7 · 19 = 59851) как начинается ряд чисел кратных числу 5? Какое число стоит в этом ряду на двенадцатом месте? на сотом месте?
2) Назовите несколько общих кратных чисел 5 и 4 расскажите, как можно найти их наименьшее общее кратное.
Решение: 1. Разложить числа на простые множители.2. Выписать простые множители которые входят в состав одного из них.3. Добавить к этим множителям все те, которые есть в разложении остальных, но нет в выбранном.4. Найти произведение всех выписанных сомножителей. Данный способ универсален. С его помощью можно найти наименьшее общее кратное любого количества натуральных чисел.
5
60
500
20, 40.60
а чтоб найти нок надо разложить на простые множители ( там долго объяснять помотри в интернетеНайти наибольший делитель и наименьшее общее кратное чисел 10 и 15, 19 и 57.
Решение: НОК 10 и 15:10 = 5 * 2
15 = 5 * 3
Общее зачеркиваем и пишем один раз и на все остальные умножаем В данный момент это 5. Значит:
5 * 2 * 3 = 30
Выводится что НОК 10 и 15 является 30
НОД 10 и 15:
10 = 5 * 2
15 = 5 * 3
Общее пишем один раз, но на остальные не умножаем. Здесь это 5. Значит НОД чисел 15 и 10 будет 5.
НОК 19 и 57
19 — это простое число
57 = 3 * 19
Здесь:
19 * 3 = 57
Значит НОК для чисел 19 и 57 будет 57
НОД 19 и 57
19 простое число
57 = 3 * 19
А здесь получается просто 19, значит для чисел 19 и 57 НОД это 19
Надо найти общий делитель и наименьшее общее кратное чисел 30 и 45.

Решение: 1. Раскладываем числа на простые множители
30=2*3*5
45=3*3*5
2. Сравниваем множители
3*5 одинаковые, а 2 и 3 отличаются
3. Берём большее число, это 45=3*3*5
4. Смотрим, какого множителя, который есть в 30 не хватает.
Не хватает 2.
5. Умножаем 45 на 2
45*2=90 это и есть наименьшее общее кратное
НОК(30;45)=90
90:30=3
90:45=2
6. Находим НОД, наибольший общий делитель
30=2*3*5
45=3*3*5
Это 3*5=15 это и есть НОД.
НОД(30;45)=15
30:15=2
45:15=3Найти наибольший общий делитель и наименьшее общее кратное чисел 18и36 и зз и44
Решение:
Общий делитель нескольких чисел – это число, которое является делителем для каждого из этих чисел. Например, общими делителями чисел 24, 30 и 18 являются числа 2, 3 и 6.
Наибольший общий делитель (обозначается НОД) – это наибольшее число из общих делителей. Например, НОД (24, 30,18) = 6.
Например, НОД (24, 30,18) = 6.
Общее кратное нескольких чисел – это число, которое является кратным каждому из этих чисел. Например, для чисел 3 и 6 общими кратными являются 12, 24, 36 и т. д.
Наименьшее общее кратное (обозначается НОК) – это наименьшее из общих кратных. Наименьшее общее кратное чисел (НОК) – это такое минимальное число, которое делится без остатка на каждое из этих чисел.
Например, НОК (3,6) = 6, НОК (24,30,18) = 360.
НОД и НОК можно найти, применяя разложение чисел на простые множители.
Например,
24 = 2 · 2 · 2 · 3 = 23 · 3.
30 = 2 · 3 · 5
18 = 2 · 3 · 3 = 2 · 32
В нашем примере множители, которые входят в разложение каждого числа – это 2 и 3. Их минимальная степень – это единица.
Тогда НОД (24,30,18) = 2 · 3 = 6.
Если НОД (a, b) = 1, то числа a и b называют взаимно простыми. Например, числа 15 и 8 являются взаимно простыми, хотя каждое из них – составное.
Для определения НОК нужно выписать все множители, которые встречаются хотя бы в одном из разложений данных чисел. Затем каждый такой множитель следует взять с наибольшим показателем, с которым он входит в одно из чисел, после чего нужно произвести умножение.
Например,
24 = 2 · 2 · 2 · 3 = 23 · 3.
30 = 2 · 3 · 5
18 = 2 · 3 · 3 = 2 · 32
В нашем примере множители, которые входят в разложение каждого числа – это 2, 3 и 5. Их максимальные степени – это соответственно 3,2 и 1.
Тогда НОК (24,30,18) = 23 · 32 · 5 = 360.18 2 36 2 НОД=2*3*3*2*3*3=324
9 3 18 3
3 3 6 3
1 3 3
12 3 > >>
Онлайн урок: Наименьшее общее кратное по предмету Математика 6 класс
Мы узнаем, что такое кратные числа, познакомимся с историей этого понятия и научимся находить одно и то же кратное различных чисел.
Если первое натуральное число делится на второе нацело, то второе называют делителем первого числа.
Пример
1) найти 10 кратных чисел для
2) из них найти общие кратные
3) наименьшее общее кратное чисел 3 и 5
Решение:
1. Кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27,30.
Кратные 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
2. Общие кратные 3 и 5: 15, 30. На самом деле общих кратных будет больше, но в нашем примере было ограничение в 10 кратных чисел.
3. Из 15 и 30 меньшим будет первое. Значит, оно и будет тем, что нам требуется.
Наименьшее натуральное число, кратное каждому из взятых в отдельности, будет наименьшим общим кратным всех взятых чисел вместе.
Наименьшее общее кратное чисел x и y обозначают НОК (x, y)
Как же можно найти этот НОК?
I способ: начинаем перебирать кратные у самого большого из взятых чисел.
- Найдем НОК чисел 12 и 18. Самое большое из них — это число 18
- Посчитаем числа, кратные 18: 18, 36, 54, 72, 90…
- Посчитаем числа, кратные 12: 12, 24, 36, 48, 60, 72, 84…
- Среди них находим наименьшее число, которое делится нацело на оба эти числа, — 36. Значит оно является НОК 12 и 18
НОК (12, 18)=36
II способ: расписываем числа в виде разложения на простые множители.
- Распишем все данные нам числа в виде разложения на простые множители
- Выпишем разложение одного из чисел (лучше сразу взять разложение наибольшего из них)
- Дополним в эту запись множители, которые входят в разложения других чисел, но которых нет в данном
- Перемножим то, что получилось, и запишем результат
Например:
$$\mathbf{20 = 2\cdot2\cdot5}$$
$$\mathbf{15 = 3\cdot5}$$
В этих разложениях встречаются числа 3, 5, 2, 2
Поэтому, \(\mathbf{НОК (20, 15) = 2\cdot2\cdot3\cdot5 = 60}\)
Пример 1
Запишите НОК чисел a и b в виде разложения на множители, если:
А) \(\mathbf{a = 2\cdot2\cdot3\cdot3, b = 2\cdot2\cdot3\cdot7}\)
Б) \(\mathbf{a = 2\cdot2\cdot3, b = 2\cdot37}\)
В) \(\mathbf{a = 2\cdot2\cdot163, b = 2\cdot2\cdot17}\)
Г) \(\mathbf{a = 2\cdot43, b =2\cdot5\cdot5\cdot7}\)
Д) \(\mathbf{a = 2\cdot2\cdot3\cdot3\cdot5\cdot5, b = 2\cdot2\cdot2\cdot5}\)
Е) \(\mathbf{a = 2\cdot2\cdot2\cdot2, b = 2\cdot2\cdot3\cdot5}\)
Решение:
А) \(\mathbf{НОК (2\cdot2\cdot3\cdot3, 2\cdot2\cdot3\cdot7) = 2\cdot2\cdot3\cdot7\cdot3 = 252}\)
Б) \(\mathbf{НОК (2\cdot2\cdot3, 2\cdot37) = 2\cdot37\cdot2\cdot3 = 444}\)
В) \(\mathbf{НОК (2\cdot2\cdot163, 2\cdot2\cdot17) = 2\cdot2\cdot163\cdot17 = 11084}\)
Г) \(\mathbf{НОК (2\cdot43, 2\cdot5\cdot5\cdot7) = 2\cdot5\cdot5\cdot7\cdot43 = 15050}\)
Д) \(\mathbf{НОК (2\cdot2\cdot3\cdot3\cdot5\cdot5, 2\cdot2\cdot2\cdot5) = 2\cdot2\cdot3\cdot3\cdot5\cdot5\cdot2 = 1800}\)
Е) \(\mathbf{НОК (2\cdot2\cdot2\cdot2, 2\cdot2\cdot3\cdot5) = 2\cdot2\cdot3\cdot5\cdot2\cdot2 = 240}\)
Пример 2
Найдите наименьшее общее кратное чисел:
А) 15 и 25
Б) 10 и 6
В) 100 и 84
Г) 36 и 69
Д) 74 и 12
Е) 96 и 50
Решение:
А)
\(\mathbf{15 = 3\cdot5}\)
\(\mathbf{25 = 5\cdot5}\)
\(\mathbf{НОК (15; 25) = 5\cdot5\cdot3 = 75}\)
Б)
\(\mathbf{10 = 2\cdot5}\)
\(\mathbf{6 = 2\cdot3}\)
\(\mathbf{НОК (10; 6) = 2\cdot5\cdot3 = 30}\)
В)
\(\mathbf{100 = 2\cdot2\cdot5\cdot5}\)
\(\mathbf{84 = 2\cdot2\cdot3\cdot7}\)
\(\mathbf{НОК (100; 84) = 2\cdot2\cdot5\cdot5\cdot3\cdot7 = 2100}\)
Г)
\(\mathbf{36 = 2\cdot2\cdot3\cdot3}\)
\(\mathbf{69 = 3\cdot23}\)
\(\mathbf{НОК (36; 69) = 3\cdot23\cdot2\cdot2\cdot3 = 828}\)
Д)
\(\mathbf{74 = 2\cdot37}\)
\(\mathbf{12 = 2\cdot2\cdot3}\)
\(\mathbf{НОК (74; 12) = 2\cdot37\cdot2\cdot3 = 444}\)
Е)
\(\mathbf{96 = 2\cdot2\cdot2\cdot2\cdot2\cdot3}\)
\(\mathbf{50 = 2\cdot5\cdot5}\)
\(\mathbf{НОК (96; 50) = 2\cdot2\cdot2\cdot2\cdot2\cdot3\cdot5\cdot5 = 2400}\)
У меня есть дополнительная информация к этой части урока!
Закрыть
«Крат» в древней Руси XI века значило дословно «раз».
Получается, что «многократно» расшифровывается как «много раз».
Самим понятием кратности часто пользуются в обиходе. Например, бывают разные виды годов, которые получились при использовании нашего математического понятия. На каждые обычные три года из 365 дней приходится один, в котором 366 дней. Это связано с тем, что в таком году в феврале 29 дней, а не 28. Этот год называется високосным.
Если число, обозначающее год, будет кратно 4, то такой год будет високосным, а если не кратно, тогда год обычный. Например, 2018 — год обычный, потому что 2018 не делится без остатка на 4. Следующий за ним 2019 будет тоже обычным. А вот 2020 год будет уже точно високосным.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
- НОК больше либо равен всем данным числам, для которых его ищут
- Если есть пара чисел и одно из них делится на другое, то НОК для них будет наибольшее из этих чисел
Алгоритм нахождения НОК согласно этому свойству:
Проверить, не будет ли самое большое из данных чисел делиться на другие из них.
Если делится, тогда это число будет НОК всех данных чисел.
Если не делится, то проверить, не будет ли делиться на остальные числа удвоенное большее число, утроенное и т.д.
Так проверять до тех пор, пока не найдется самое маленькое число, которое будет делиться на каждое из остальных чисел.
Например, НОК (18, 54) = 54; НОК (27, 81) = 81
- Для взаимно простых чисел НОК можно найти как их произведение.
- НОК(x, x) = x.
- НОК(x, 1) = x.
Пример 1
Выясните, будут ли числа 35 и 88 взаимно простыми?
Найдите НОК чисел 35 и 88. Равно ли оно произведению 35 и 88?
Найдите НОК получившегося произведения.
Решение:
\(\mathbf{35 = 5\cdot7}\)
\(\mathbf{88 = 2\cdot2\cdot2\cdot11}\)
Одинаковых множителей, кроме 1, в разложениях чисел 35 и 88 не нашлось. Можно сделать вывод, что они взаимно простые.
\(\mathbf{НОК (35; 88) = 5\cdot7\cdot2\cdot2\cdot2\cdot11 = (5\cdot7)\cdot(2\cdot2\cdot2\cdot11)= 35\cdot88 =3080}\)
Наименьшее общее кратное чисел 35 и 88 находится как произведение этих чисел.
Пример 2
Найдите наименьшее общее кратное чисел:
а) 45 и 135; б) 34 и 170
Равно ли оно одному из данных чисел?
Решение:
а)
\(\mathbf{45 = 3\cdot3\cdot5}\)
\(\mathbf{135 = 3\cdot3\cdot3\cdot5}\)
\(\mathbf{НОК (45; 135) = 3\cdot3\cdot5\cdot3 = 135}\) и равно одному из чисел — 135;
б)
\(\mathbf{34 = 2\cdot17}\)
\(\mathbf{170 = 2\cdot5\cdot17}\)
\(\mathbf{НОК (34; 170) = 2\cdot5\cdot17=170}\) и равно одному из данных чисел — 170
Пример 3
Вдоль дороги от пункта А поставлены столбы через каждые 75 м. Эти столбы решили заменить другими, поставив их на расстоянии 30 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А.
Эти столбы решили заменить другими, поставив их на расстоянии 30 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А.
Решение:
Надо найти НОК (75; 30).
\(\mathbf{75=3\cdot5\cdot5}\)
\(\mathbf{30=2\cdot3\cdot5}\)
\(\mathbf{НОК (75; 30)= 3\cdot5\cdot5\cdot2 = 150}\)
Ответ: расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, равно 150 м.
У меня есть дополнительная информация к этой части урока!
Закрыть
По разобранным примерам видно, что в НОК не входит наибольший общий делитель чисел.
Получаем такое свойство: произведение любой пары натуральных чисел равно произведению их наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК)
\(\mathbf{A\cdot b = НОД (A; b) \cdot НОК (A; b)}\)
Пример использования формулы:
НОК (143; 91) — ?
\(\mathbf{143\cdot91 = НОД (143; 91) \cdot НОК (143; 91)}\)
Используем алгоритм Евклида:
\(\mathbf{НОД (143; 91) = НОД (52; 91) = НОД (52; 39) = НОД (13; 39) = 13}\)
\(\mathbf{143\cdot91 = 13\cdotНОК (143; 91)}\)
\(\mathbf{НОК (143; 91) = (143\cdot91) : 13 = 1001}\)
\(\mathbf{НОК (143; 91) = 1001}\)
Итак, можно выделить еще один, уже третий по счёту алгоритм вычисления НОК:
его можно применять для пары чисел, для которых уже найден их НОД.
Рациональнее его применять в задачах на нахождение НОД и НОК, так как тогда он даёт выигрыш во времени решения таких задач. Во всех других случаях вы потратите почти в два раз больше времени, если выберете этот алгоритм, а не предыдущие два.
Разберём пример.
Нужно найти НОД и НОК чисел 24 и 12.
Первым шагом вычислим НОД этих чисел:
\(\mathbf{24 = 2\cdot2\cdot2\cdot3}\)
\(\mathbf{12 = 2\cdot2\cdot3}\)
\(\mathbf{НОД (12; 24) = 2\cdot2\cdot3 = 12}\)
Теперь для нахождения НОК чисел 24 и 12, нужно найти их произведение и полученный результат разделить на их НОД, который мы посчитали в первом шаге.
Произведение чисел 24 и 12, равно 288
288 : 12 = 24
В частном получили 24. Значит НОК чисел 24 и 12 равно 24
НОК (12; 24) = 24
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Понятие кратных чисел используется не только при нахождении НОК. {3}}\) грамм.
{3}}\) грамм.
В жизни используются и другие из этих приставок в основном в науке или производстве.
Пройти тест
НОД и НОК
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9.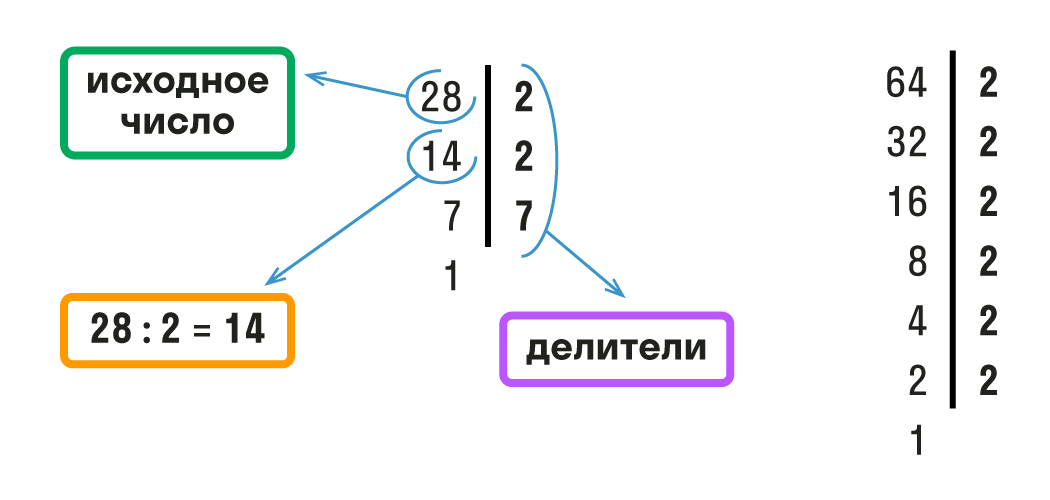 Теперь попробуем прочитать это определение:
Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
Теперь выпишем кратные обоих чисел:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Показать решение
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Показать решение
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Показать решение
Задание 4. Найдите НОК чисел 40 и 32
Найдите НОК чисел 40 и 32
Решение:
Показать решение
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Показать решение
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Показать решение
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Показать решение
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Показать решение
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Показать решение
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Показать решение
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Показать решение
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Показать решение
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
Показать решение
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Показать решение
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Показать решение
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Наименьшее общее кратное (НОК): определение, примеры и свойства
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Определение 1Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
Пример 1Согласно данному выше определению для числа 12 общими кратными числами будут 3 и 2. Также число 12 будет общим кратным для чисел 2, 3 и 4. Числа 12 и -12 являются общими кратными числами для чисел ±1, ±2, ±3, ±4, ±6, ±12.
В то же время общим кратным числом для чисел 2 и 3 будут числа 12, 6, −24, 72, 468, −100 010 004 и целый ряд любых других.
Если мы возьмем числа, которые делятся на первое число из пары и не делятся на второе, то такие числа не будут общими кратными. Так, для чисел 2 и 3 числа 16, −27, 5 009, 27 001 не будут общими кратными.
Так, для чисел 2 и 3 числа 16, −27, 5 009, 27 001 не будут общими кратными.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Если вспомнить свойство делимости относительно противоположных чисел, то получается, что некоторое целое число k будет общим кратным данных чисел точно также, как и число –k. Это значит, что общие делители могут быть как положительными, так и отрицательными.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Пример 2Предположим, что нам даны k целых чисел a1, a2, …, ak. Число, которое мы получим в ходе умножения чисел a1·a2·…·ak согласно свойству делимости будет делиться на каждый из множителей, который входил в изначальное произведение. Это значит, что произведение чисел a1, a2, …, ak является наименьшим общим кратным для этих чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Фактически, их число бесконечно.
Предположим, что у нас есть некоторое число k. Тогда произведение чисел k·z, где z – это целое число, будет являться общим кратным чисел k и z. С учетом того, что количество чисел бесконечно, то и количество общих кратных бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Определение 2Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Наименьшее общее кратное существует для любого количества данных чисел. Наиболее употребимой для обозначения понятия в справочной литературе является аббревиатура НОК. Краткая запись наименьшего общего кратного для чисел a1, a2, …, ak будет иметь вид НОК(a1, a2, …, ak).
Наименьшее общее кратное чисел 6 и 7 – это 42. Т.е. НОК (6,7)=42. Наименьшее общее кратное четырех чисел -2, 12, 15 и 3 будет равно 60. Краткая запись будет иметь вид НОК (-2, 12, 15, 3)=60.
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Теорема 1Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b, деленному на наибольший общий делитель чисел a и b, то есть, НОК(a, b)=a·b:НОД(a, b).
Доказательство 1Предположим, что мы имеем некоторое число M, которое кратно числам a и b. Если число M делится на a, также существует некоторое целое число z, при котором справедливо равенство M=a·k. Согласно определению делимости, если M делится и на b, то тогда a·k делится на b.
Если мы введем новое обозначение для НОД(a, b) как d, то сможем использовать равенства a=a1·d и b=b1·d. При этом оба равенства будут взаимно простыми числами.
При этом оба равенства будут взаимно простыми числами.
Мы уже установили выше, что a·k делится на b. Теперь это условие можно записать следующим образом:
a1·d·k делится на b1·d, что эквивалентно условию a1·k делится на b1 согласно свойствам делимости.
Согласно свойству взаимно простых чисел, если a1 и b1 – взаимно простые числа, a1 не делится на b1 при том, что a1·k делится на b1, то b1 должно делиться k.
В этом случае уместно будет предположить, что существует число t, для которого k=b1·t, а так как b1=b:d, то k=b:d·t.
Теперь вместо k подставим в равенство M=a·k выражение вида b:d·t. Это позволяет нам прийти к равенству M=a·b:d·t. При t=1 мы можем получить наименьшее положительное общее кратное чисел a и b, равное a·b:d, при условии, что числа a и b положительные.
Так мы доказали, что НОК(a, b)=a·b:НОД(a, b).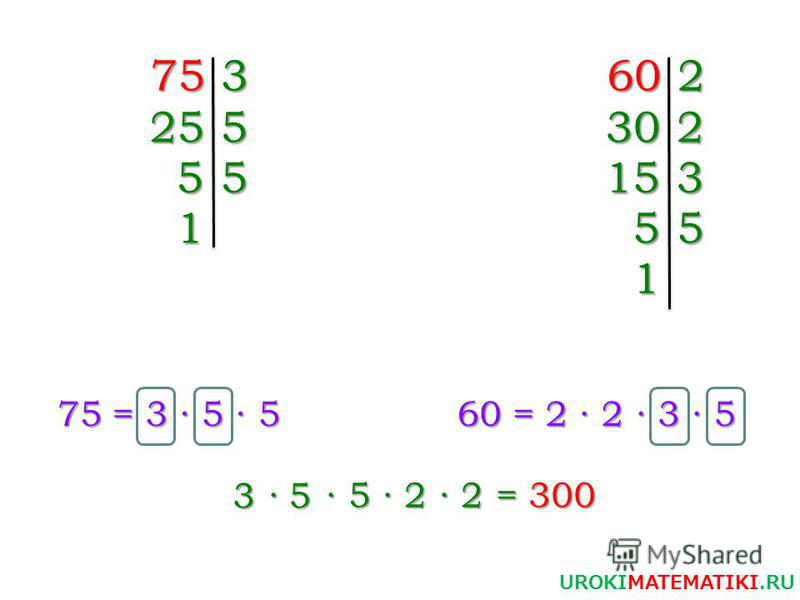
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Определение 3Теорема имеет два важных следствия:
- кратные наименьшего общего кратного двух чисел совпадает с общими кратными этих двух чисел;
- наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.
Обосновать эти два факта не составляет труда. Любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t. Так как a и b взаимно простые, то НОД(a, b)=1, следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b.
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Теорема 2Предположим, что a1, a2, …, ak – это некоторые целые положительные числа. Для того, чтобы вычислить НОК mk этих чисел, нам необходимо последовательно вычислить m2=НОК(a1, a2), m3=НОК(m2, a3), …, mk=НОК(mk-1, ak).
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
- общие кратные чисел a1 и a2 совпадают с кратными их НОК, фактически, они совпадают с кратными числа m2;
- общие кратные чисел a1, a2 и a3 совпадают с общими кратными чисел m2 и a3, следовательно, совпадают с кратными числа m3;
- общие кратные чисел a1, a2, …, ak совпадают с общими кратными чисел mk-1 и ak, следовательно, совпадают с кратными числа mk;
- в связи с тем, что наименьшим положительным кратным числа mk является само число mk, то наименьшим общим кратным чисел a1, a2, …, ak является mk.
Так мы доказали теорему.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
LCM Калькулятор — наименьшее общее кратное
Использование калькулятора
Наименьшее общее кратное ( LCM ) также называется наименьшим общим кратным ( LCM ) и наименьшим общим делителем ( LCD) . Для двух целых чисел a и b, обозначаемых НОК(a,b), НОК является наименьшим положительным целым числом, которое без остатка делится как на a, так и на b. Например, НОК(2,3) = 6 и НОК(6,10) = 30.
Для двух целых чисел a и b, обозначаемых НОК(a,b), НОК является наименьшим положительным целым числом, которое без остатка делится как на a, так и на b. Например, НОК(2,3) = 6 и НОК(6,10) = 30.
НОК двух или более чисел — это наименьшее число, которое делится без остатка на все числа в наборе.
Калькулятор наименьших множителей
Найдите НОК набора чисел с помощью этого калькулятора, который также показывает шаги и способы выполнения работы.
Введите числа, для которых вы хотите найти LCM. Вы можете использовать запятые или пробелы для разделения чисел. Но не используйте запятые в своих числах. Например, введите 2500, 1000 и не 2500, 1000 .
Как найти наименьший общий кратный НОК
Этот калькулятор НОК с пошаговыми инструкциями находит НОК и показывает работу, используя 6 различных методов:
- Список мультипликаторов
- Простая факторизация
- Метод пирога/лестницы
- Метод деления
- Использование наибольшего общего делителя GCF
- Диаграмма Венна
Как найти LCM путем перечисления кратных
- Перечислите кратные каждого числа, пока хотя бы одно из кратных не появится во всех списках
- Найдите наименьшее число из всех списков
- Этот номер LCM
Пример: LCM(6,7,21)
- Кратность 6: 6, 12, 18, 24, 30, 36, 42 , 48, 54, 60
- Кратность 7: 7, 14, 21, 28, 35, 42 , 56, 63
- Кратность 21: 21, 42 , 63
- Найдите наименьшее число из всех списков.
 У нас это выделено жирным шрифтом выше.
У нас это выделено жирным шрифтом выше. - Итак, LCM(6, 7, 21) равно 42
Как найти НОК с помощью простой факторизации
- Найдите все простые множители каждого заданного числа.
- Перечислите все найденные простые числа столько раз, сколько раз они встречаются чаще всего для данного числа.
- Умножьте список простых множителей, чтобы найти LCM.
ЛКМ (a,b) вычисляется путем нахождения простой факторизации как a, так и b. Используйте тот же процесс для LCM из более чем 2 номеров.
Например, для LCM (12,30) мы находим:
- Разложение 12 на простые множители = 2 × 2 × 3
- Разложение числа 30 на простые множители = 2 × 3 × 5
- Используя все простые числа, найденные так часто, как каждое из них встречается чаще всего, мы получаем 2 × 2 × 3 × 5 = 60
- Следовательно, НОК (12,30) = 60.

Например, для LCM (24 300) мы находим:
- Разложение числа 24 на простые множители = 2 × 2 × 2 × 3
- Разложение числа 300 на простые множители = 2 × 2 × 3 × 5 × 5
- Используя все простые числа, найденные так часто, как каждое из них встречается чаще всего, мы получаем 2 × 2 × 2 × 3 × 5 × 5 = 600
- Следовательно, LCM (24 300) = 600.
Как найти НОК с помощью простой факторизации с использованием экспонент
- Найдите все простые множители каждого заданного числа и запишите их в виде экспоненты.
- Перечислите все найденные простые числа, используя наибольший показатель степени, найденный для каждого из них.
- Перемножьте список простых множителей с показателями, чтобы найти LCM.

Пример: НОК(12,18,30)
- Простые множители числа 12 = 2 × 2 × 3 = 2 2 × 3 1
- Простые множители числа 18 = 2 × 3 × 3 = 2 1 × 3 2
- Простые множители 30 = 2 × 3 × 5 = 2 1 × 3 1 × 5 1
- Перечислите все найденные простые числа столько раз, сколько раз они встречаются чаще всего для любого заданного числа, и перемножьте их вместе, чтобы найти НОК.
- 2 × 2 × 3 × 3 × 5 = 180
- Вместо этого, используя показатели степени, перемножьте каждое из простых чисел с наивысшей степенью
- 2 2 × 3 2 × 5 1 = 180
- Итак, НОК(12,18,30) = 180
Пример: LCM(24,300)
- Простые множители числа 24 = 2 × 2 × 2 × 3 = 2 3 × 3 1
- Простые множители 300 = 2 × 2 × 3 × 5 × 5 = 2 2 × 3 1 × 5 2
- Перечислите все найденные простые числа столько раз, сколько раз они встречаются чаще всего для любого заданного числа, и перемножьте их вместе, чтобы найти НОК.

- 2 × 2 × 2 × 3 × 5 × 5 = 600
- Вместо этого, используя показатели степени, перемножьте каждое из простых чисел с наивысшей степенью
- 2 3 × 3 1 × 5 2 = 600
- Итак, НОК(24 300) = 600
Как найти НОК с помощью метода торта (лестничного метода)
Метод торта использует деление для нахождения НОК набора чисел. Люди используют метод пирога или лестницы как самый быстрый и простой способ найти LCM, потому что это простое деление.
Метод торта такой же, как метод лестницы, метод ящика, метод факторного ящика и метод сетки ярлыков для поиска LCM. Блоки и сетки могут выглядеть немного по-разному, но все они используют деление на простые числа для нахождения НОК.
Найдите LCM (10, 12, 15, 75)
- Запишите свои числа в слое торта (ряд)
Торт/Лестница
10
12
15
75
- Разделите номера слоев на простое число, которое делится на два или более числа на уровне следующего слоя, и занесите результат в слой.

Торт/Лестница
2
10
12
15
75
- Если какое-либо число в слое не делится без остатка, просто запишите это число.
ТОК/ЛЕДИ
2
10
12
15
75
5
6
15
75
- Продолжение. Продолжительные разделительные слои торта на первичные номера.
- Когда больше нет простых чисел, которые без остатка делятся на два или более числа, все готово.
Cake / Ladder
2
10
12
15
75
3
5
6
15
75
5
5
2
5
25
- LCM является произведением чисел в форме буквы L, левого столбца и нижнего ряда. 1 игнорируется.
- НОК = 2 × 3 × 5 × 2 × 5
- мкм = 300
- Следовательно, НОК(10, 12, 15, 75) = 300
Как найти LCM методом деления
Найти LCM(10, 18, 25)
- Запишите свои числа в верхней строке таблицы
Таблица делений
10
18
25
- Начиная с наименьших простых чисел, разделите ряд чисел на простое число, которое делится без остатка хотя бы на одно из ваших чисел, и занесите результат в следующая строка таблицы.

Таблица делений
10
18
25
- Если какое-либо число в строке не делится без остатка, просто уменьшите это число.
Таблица делений
10
18
25
- Продолжайте делить строки на простые числа, которые делятся без остатка хотя бы на одно число.
- Когда в последней строке результатов все 1, все готово.
Таблица делений
10
18
25
- НОК представляет собой произведение простых чисел в первом столбце.
- НОК = 2 × 3 × 3 × 5 × 5
- мл = 450
- Следовательно, НОК(10, 18, 25) = 450
Как найти LCM с помощью GCF
Формула для нахождения LCM с использованием наибольшего общего делителя GCF набора чисел:
НОК(a,b) = (a×b)/GCF(a,b)
Пример: найти НОК(6,10)
- Найдите GCF(6,10) = 2
- Используйте формулу LCM по GCF для расчета (6×10)/2 = 60/2 = 30
- Итак, НОК(6,10) = 30
Множитель — это число, которое получается, когда вы можете без остатка разделить одно число на другое. В этом смысле множитель также известен как делитель.
В этом смысле множитель также известен как делитель.
Наибольший общий делитель двух или более чисел — это наибольшее число, разделяемое всеми делителями.
Наибольший общий делитель GCF такой же, как:
- HCF — Наибольший общий делитель
- НОД — Наибольший общий делитель
- HCD — Наибольший общий делитель
- GCM — Наибольшая общая мера
- HCM — Высшая общая мера
Как найти НОК с помощью диаграмм Венна
Диаграммы Венна изображаются в виде перекрывающихся кругов. Они используются для отображения общих элементов или пересечений между двумя или более объектами. При использовании диаграмм Венна для нахождения НОК простые множители каждого числа, которые мы называем группами, распределяются среди перекрывающихся кругов, чтобы показать пересечения групп. После того, как диаграмма Венна будет завершена, вы можете найти LCM, найдя объединение элементов, показанных в группах диаграммы, и перемножив их вместе.
Как найти НОК десятичных чисел
- Найдите число с наибольшим количеством знаков после запятой
- Подсчитайте количество знаков после запятой в этом числе. Назовем этот номер Д. .
- Для каждого из ваших чисел переместите D знаков после запятой вправо. Все числа станут целыми.
- Найти НОК набора целых чисел
- Для вашего LCM переместите десятичные разряды D влево. Это LCM для исходного набора десятичных чисел.
Свойства
НОКНОК ассоциативен:
НОК(a, b) = НОК(b, a)
НОК коммутативен:
НОК(a, b, c) = НОК( НОК(a, b), c) = LCM(a, LCM(b, c))
НОК распределительный:
НОК(da, db, dc) = dLCM(a, b, c)
НОК связан с наибольшим общим делителем (НОК):
НОК(a,b) = a × b/НОК(a,b) и
НОК(a,b) = a × b/НОК(a,b) )
Ссылки
[1] Zwillinger, D. (Ed.). Стандартные математические таблицы и формулы CRC, 31-е издание, Нью-Йорк, штат Нью-Йорк: CRC Press, 2003, с. 101.
(Ed.). Стандартные математические таблицы и формулы CRC, 31-е издание, Нью-Йорк, штат Нью-Йорк: CRC Press, 2003, с. 101.
[2] Вайсштейн, Эрик В. Наименьший общий множитель. Из MathWorld — Веб-ресурс Wolfram.
LCM 12, 15 и 18
Калькуляторы Ресурсы для обучения математике
- Домашняя страница
- Математические функции
- Калькулятор LCM
- lcm of 12, 15 и 18
НОК 12, 15 и 18 равен 180. Комплексная работа дает больше информации о том, как найти МОК чисел 12, 15 и 18, используя простые множители и специальные методы деления, а также пример использования математика и реальные задачи.
что такое lcm 12, 15 и 18?
lcm (12 15 18) = (?)
12 => 2 x 2 x 3
15 => 3 x 5
18 => 2 x 3 x 3
= 2 x 3 x 2 x 5 x 3
= 180
пкм (12, 15 и 18) = 180
180 — это lcm чисел 12, 15 и 18.
, где
12 – целое положительное число,
15 – целое положительное число,
180 – lcm 12, 15 и 18,
{2,
3} в {2 х 2 х 3, 3 х 5, 2 х 3 х 3} являются наиболее повторяющимися факторами 12, 15 и 18,
{2, 5, 3} в {2 х 2 х 3, 3 х 5, 2 x 3 x 3} — другие оставшиеся множители 12, 15 и 18.
Использование в математике: НОК 12, 15 и 18 12, 15 и 18 можно использовать:
- , чтобы найти наименьшее число, которое точно делится на 12, 15 и 18.
- , чтобы найти общие знаменатели для дробей, имеющих 12, 15 и 18 в качестве знаменателей при сложении или вычитании разнородных дробей.
Использование в реальных задачах: 12, 15 и 18 lcm
разное расписание происходит вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуации, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 12 секунд, B звонит через 15 секунд и C многократно звонит через 18 секунд. Ответ заключается в том, что все колокола A, B и C звонят вместе через 180 секунд в первый раз, через 360 секунд во второй раз, через 540 секунд в третий раз и так далее.
Важные примечания: 12, 15 и 18 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 12, 15 и 18:
- Повторяющиеся и неповторяющиеся простые множители 12, 15 и 18 следует умножить, чтобы найти наименьшее общее кратное 12, 15 и 18 при решении lcm методом простых множителей.

- Результаты lcm 12, 15 и 18 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.
Для значений, отличных от 12, 15 и 18, используйте этот инструмент ниже:
В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm числа 12, 15 и 18, используя либо метод простых множителей, либо метод специального деления. .
Пример решения с использованием метода простых множителей:
Что такое НОК 12, 15 и 18?
шаг 1
Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 12
B = 15
C = 18
Что нужно найти:
найдите lcm числа 12, 15 и 18
шаг 2 Найдите простые делители
Простые множители 12 = 2 x 2 x 3
Простые множители 15 = 3 x 5
Простые множители 18 = 2 x 3 x 3
шаг 3 Определите повторяющиеся и неповторяющиеся простые делители чисел 12, 15 и 18 :
{2, 3} — наиболее повторяющиеся множители, а {2, 5, 3} — неповторяющиеся множители 12, 15 и 18.
шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 12, 15 и 18:
= 2 x 3 x 2 x 5 x 3
= 180
lcm(20 и 30) = 180
Следовательно,
lcm 12, 15 и 18 равно 180
Пример решения с использованием специального метода деления:
Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 12, 15 и 18.
шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что нужно найти:
Входные параметры и значения:
Целые числа: 12, 15 и 18
Что нужно найти:
lcm (12, 15, 18) = ?
шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми. Формат:
12, 15 и 18
шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (12, 15 и 18), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами. Перенесите целое число на следующую строку, если какое-либо целое число из 12, 15 и 18 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:
Перенесите целое число на следующую строку, если какое-либо целое число из 12, 15 и 18 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:
| 2 | 12 | 15 | 18 |
| 2 | 6 | 15 | 9 |
| 3 | 3 | 15 | 9 |
| 3 | 1 | 5 | 3 |
| 5 | 1 | 5 | 1 |
| 1 | 1 | 1 |
step 4 Multiply the divisors to find the lcm of 12, 15 и 18:
= 2 x 2 x 3 x 3 x 5
= 180
НОК(12, 15, 18) = 180
Наименьшее общее кратное для трех чисел 12, 15 и 18 равно 180
Что такое наименьшее общее кратное? Определение, примеры, факты
Множитель — это результат произведения одного числа на другое число.
Например, мы можем получить число, кратное 5, путем умножения 5 на числа 1, 2, 3 и так далее.
Кратные 5: 5, 10, 15, 20, 25…
Если число кратно двум или более числам, оно называется общим кратным. Например, 2 х 5 = 10,
Следовательно, 10 кратно как 2, так и 5. Таким образом, 10 называется общим кратным 2 и 5.
Что такое наименьшее общее кратное (НОК)?
LCM — это сокращение от «наименее распространенное кратное». Наименьшее общее кратное определяется как наименьшее кратное, которое объединяет два или более чисел.
Например: Возьмем два целых числа, 2 и 3.
Кратные 2: 2, 4, 6 , 8, 10, 12 , 14, 16, 18 , 20….
Кратность 3: 3, 6 , 9, 12 , 15, 18 , 21, 24, 27, 30 ….
6, 12 и 18 являются кратными 2 и 3. Число 6 является наименьшим. Следовательно, 6 является наименьшим общим кратным 2 и 3.
Итак, что такое НОК в математике? НОК двух чисел — это наименьшее число, которое делится на оба числа.
Одним из основных применений LCM является нахождение наименьшего общего знаменателя (LCD) двух или более дробей. Он играет важную роль в сложении, вычитании и сравнении двух или более дробей.
Как найти наименьшее общее кратное (НОК)?
Различные методы определения НОК набора чисел:
- Список кратных
- Факторизация простых чисел
- Метод деления
Метод списка кратных
числа в таблице, как показано. Наименьшее общее кратное — это первое общее кратное данных чисел.
Для 12 и 16 номер 48 является LCM.
Метод простой факторизации
Метод простой факторизации включает в себя нахождение простых множителей заданных чисел и определение наименьшего общего кратного (НОК). Например, соедините показанные общие кратные, чтобы найти наименьшее общее кратное чисел 12 и 16, используя разложение на простые множители. Перечислите их вместе с остальными кратными.
НОК = 2 × 2 × 2 × 2 × 3 = 48
Метод деления
В этом методе заданные числа делятся на общие делители до тех пор, пока невозможно дальнейшее деление на то же число. Делители и остатки перемножаются, чтобы получить наименьшее общее кратное.
Делители и остатки перемножаются, чтобы получить наименьшее общее кратное.
Например,
LCM = 2 × 2 × 3 × 4 = 48
Связь между LCM и HCF
Наибольший общий делитель двух или более чисел — это HCF данных чисел. Наименьшее число среди всех общих кратных данных чисел является наименьшим общим кратным двух или более чисел. Предполагая, что a и b являются двумя числами, формула для определения отношения между их LCM и HCF:0003
Пример 1: Найдите НОК чисел 18 и 24, используя метод простой факторизации.
Решение :
LCM = 2 × 2 × 2 × 3 × 3 = 72
Пример 2: Найдите наименьшее количество делится на 9 и 15.
Решение :
9 и 15 — НОК 9 и 15.
НОК = 3 × 3 × 5 = 45
Итак, 45 — наименьшее число, которое делится и на 9, и на 15.
Пример 3: Произведение двух чисел равно 180. Если их ДЧП равно 3, какова их НОК?
Решение:
Наибольший общий делитель (ОДП) равен 3, а произведение чисел равно 180.
НОК равно 60.
Практические задачи
12
8
9
11
Правильный ответ: 12
НОК числа и любого его кратного есть само кратное.
9
11
13
19
Правильный ответ: 13
НОК двух простых чисел есть произведение этих чисел. Поскольку 7a = 91, a = 91/7 = 13
A × B
A ÷ B
A + B
A — B
Правильный ответ: A × B
LCM × HCF = произведение чисел
50
30
15
60
Правильный ответ: 60
LCM 20 и 60 = 60
Часто задаваемые вопросы
Как связаны HCF и LCM двух чисел?
Произведение любых двух чисел в LCM и HCF равно произведению этих двух чисел.
В чем разница между LCM и HCF?
НОК (наименьшее общее кратное) двух или более чисел — это наименьшее число среди всех общих кратных предоставленных чисел. Напротив, HCF (самый высокий общий фактор) является самым высоким числом среди всех общих факторов данных чисел.
Напротив, HCF (самый высокий общий фактор) является самым высоким числом среди всех общих факторов данных чисел.
Почему НОК двух взаимно простых чисел всегда является их произведением?
Единственным общим множителем между двумя взаимно простыми числами является 1. Таким образом, HCF двух взаимно простых чисел всегда равен 1. Если a и b — два взаимно простых числа, то по соотношению между LCM и HCF, получаем
НОК (a, b) × HCF (a, b) = a × b
Поскольку a и b — взаимно простые числа, их HCF всегда равен 1. Итак, мы получаем, что НОК a и b всегда является произведением a и b. 93-8
Нахождение наименьшего общего кратного с помощью метода списка
наименьшее общее кратное двух чисел, также известное как НОК, является наименьшим числом, которое делится на два заданных числа. Здесь предполагается, что задействованные числа являются положительными целыми числами или положительными целыми числами
Здесь предполагается, что задействованные числа являются положительными целыми числами или положительными целыми числами
Но сначала мы должны спросить себя. Чему кратно число?
Предположим, у нас есть два целых положительных числа n и m. Число m кратно числу n, если n может разделить m без остатка. Это означает, что при делении m на n в результате получается нулевой остаток.
Например, 20 кратно 10, поскольку 20 разделить на 10 равно 2 и, что более важно, НЕ имеет остатка.
Другой способ взглянуть на это состоит в том, что кратное числу является произведением данного числа на натуральное или счетное число.
Например, число 54 кратно 6, потому что 54 = 6 х 9. Обратите внимание, что число 6 умножается на счетное число, равное 9.
Следующее понятие может показаться банальным, но оно очень важный. Само число кратно самому себе . Очевидно, что 5 кратно 5, потому что 5 разделить на 5 равно 1 и без остатка.
Или 5 кратно самому себе, так как 5 = 5 х 1, где число 5 умножается на счетное число 1.
Теперь пришло время нам научиться составлять список кратных заданному числу. . Имейте в виду, что для любого заданного положительного целого числа оно имеет бесконечное число кратных .
Давайте посмотрим на числа, кратные 7.
Вот в чем фокус! Чтобы найти числа, кратные 7, начните с написания самого числа, затем мы пропустим счет на 7.
Следовательно, числа, кратные 7, равны 7 , 14 , 21 , 28 , 35 , 19 42 , 49 , 56 , …
Символ « … », также известный как эллипс, означает, что последовательность продолжается без конца, но следует определенной схеме.
Другой способ получения кратных чисел — использовать набор натуральных чисел. Помните, что набор натуральных чисел (также известный как набор счетных чисел) содержит элементы 1, 2, 3, 4, 5, 6, 7, 8, 9. , 10, …
, 10, …
Мы также можем выразить счетные числа в виде множества.
Мы будем использовать набор счетных чисел в качестве множителей для заданного числа, чтобы сгенерировать его множители. Поскольку число имеет бесконечное количество кратных, нам нужно будет указать , сколько кратных мы хотим перечислить. Ради этого урока давайте договоримся написать или перечислить первых восьми (8) кратных числа.
Ниже приведен список первых восьми чисел , кратных 6. Обратите внимание, чтобы найти их, мы умножим 6 на первые восемь элементов набора счетных чисел, которые равны 1, 2, 3, 4, 5, 6. , 7 и 8. Произведения становятся первыми восемью кратными 6.
Давайте рассмотрим другие примеры нахождения кратных чисел. Чем больше примеров вы видите, тем удобнее вам становится с этой концепцией.
◉ Первые пять кратных 3 ☞ 3, 6, 9, 12, 15
◉ Первые семь кратных 10 ☞ 10, 20, 30, 40, 60, 70
◉ Первые восемь кратных 9 ☞ 9, 18, 27, 36, 45, 54, 63, 72
◉ Первые десять кратных 13 ☞ 13, 26, 39, 52, 65, 78, 91, 104, 117, 130
1) Найдите наименьшее общее кратное 3 и 7. чтобы найти кратные числа вступит в игру здесь. Единственная разница в том, что мы найдем кратные двух чисел и перечислим их рядом.
чтобы найти кратные числа вступит в игру здесь. Единственная разница в том, что мы найдем кратные двух чисел и перечислим их рядом.
От нас зависит, сколько множителей мы решим написать. Иногда у нас будет необходимость расширить его, потому что мы не можем найти первое общее кратное только что. Первое число, которое появляется в списке и является общим для обоих чисел, становится наименьшим общим кратным или НОК данных двух чисел.
Итак, давайте запишем первые десять чисел, кратных 3 и 7, и посмотрим, сможем ли мы найти первое совпадение. Если мы сделали это правильно, LCM 3 и 7 будет 21 .
Помните, что ключ здесь предназначен для нахождения общего кратного, имеющего наименьшее значение.
Очень возможно иметь более одного общего кратного. Но когда дело доходит до нахождения наименьшего общего кратного, нас определенно интересует нахождение наименьшего общего кратного. Пожалуйста, проверьте схему ниже. Я надеюсь, что это имеет большой смысл!
Пожалуйста, проверьте схему ниже. Я надеюсь, что это имеет большой смысл!
2) Найдите наименьшее общее кратное 8 и 12.
Надеюсь, вы уже освоились. Давайте разберемся с этим шаг за шагом.
- Перечислите первые десять кратных 8 и 12 .
- Определите множители, общие для обоих списков. Как вы можете видеть на рисунке ниже, общие кратные чисел 8 и 12 равны 24, 48 и 72. Просто чтобы уточнить, это общие кратные 8 и 12 для их первых десяти кратных.
- Общее кратное, имеющее наименьшее значение, является наименьшим общим кратным (НОК) данных двух чисел, равных 8 и 12. В этом случае НОК чисел 8 и 12 равно 24.
3) Что такое LCM 14 и 20 ?
Как видите, проблемы с нахождением НОК двух чисел могут усложняться по мере увеличения числа. Поскольку вы уже знаете процедуру, весь процесс должен быть для вас управляемым.
Распространенная ошибка, которую совершают большинство моих студентов, заключается в том, что они небрежно записывают первые несколько чисел, кратных числу. Так что не попадайтесь в ловушку самодовольства. Применяйте то, что вы узнали, и выполняйте это с целью.
Так что не попадайтесь в ловушку самодовольства. Применяйте то, что вы узнали, и выполняйте это с целью.
Я предлагаю вам сначала проработать это на бумаге, прежде чем нажимать кнопку, чтобы показать решение для каждого шага. Удачи!
- Шаг 1: Запишите первые двенадцать множителей 14 и 20 .
- Шаг 2: Отметьте общие кратные чисел 14 и 20 .
- Шаг 3: Определите наименьшее общее кратное (НОК) чисел 14 и 20 .
4) Что такое LCM 11 и 23 ?
Это не вопрос с подвохом. Я бы сказал, что это совершенно справедливый вопрос для теста. Мы, учителя математики, всегда любим задавать такие задачи, связанные с LCM, чтобы проверить, насколько учащиеся понимают тему.
Так что же делать? Как всегда, для каждой математической задачи постарайтесь сделать шаг назад, чтобы посмотреть на проблему в более широкой картине. Только не привыкайте сразу же решать проблему, не имея хорошего плана. Потому что некоторые задачи могут сначала показаться сложными, что может вызвать математическую тревогу, хотя на самом деле это очень просто, если вы знаете, с чем имеете дело.
Только не привыкайте сразу же решать проблему, не имея хорошего плана. Потому что некоторые задачи могут сначала показаться сложными, что может вызвать математическую тревогу, хотя на самом деле это очень просто, если вы знаете, с чем имеете дело.
Во-первых, что вы можете сказать о двух числах 11 и 23? Они какие-то особенные?
Да! Числа 11 и 23 являются простыми числами. Это означает, что 11 делится только на 1 и само на себя. То же самое относится и к 23, что оно делится только на 1 и само на себя.
Правило гласит, что если a и b — два различных простых числа, то их наименьшее общее кратное (НОК) — это их произведение, то есть a х b.
Поскольку мы уже установили, что 11 и 23 являются простыми числами, их НОК является просто их произведением, которое 11 х 23 = 253. Мы также можем записать наш окончательный ответ в виде НОК (11, 23) = 253,9.0011
Предположим, вы не знаете этого правила. У вас нет другого выбора, кроме как перечислить достаточно кратных для каждого числа, чтобы вы нашли первое совпадение. Ваше обычное решение может выглядеть примерно так, как показано ниже. Представьте себе возможность неправильно записать числа, кратные 11 и 23, и, следовательно, не получить правильный НОК. Да, это может быть очень грязно!
Ваше обычное решение может выглядеть примерно так, как показано ниже. Представьте себе возможность неправильно записать числа, кратные 11 и 23, и, следовательно, не получить правильный НОК. Да, это может быть очень грязно!
Вас также могут заинтересовать:
Использование простой факторизации для поиска LCM
Поиск GCF с использованием метода списка
Использование простой факторизации для нахождения GCF
Наименьшие общие знаменатели
Трудно складывать или вычитать дроби, когда знаменатели не совпадают. Итак, используем общий знаменатель. Обычно проще всего использовать наименее общий знаменатель. Наименьший общий знаменатель — это просто наименьший общий множитель ( ЛКМ ) двух знаменателей.
Пример 1:
Найдите общий знаменатель дробей.
1 6 а также 3 8
Нам нужно найти наименьшее общее кратное
6
а также
8
. Один из способов сделать это — перечислить кратные:
Один из способов сделать это — перечислить кратные:
6 , 12 , 18 , 24 _ , 30 , 36 , 42 , 48 , … 8 , 16 , 24 _ , 32 , 40 , 48 , …
Первое число, встречающееся в обоих списках, 24 , так 24 является ЛКМ. Поэтому мы используем это как наш общий знаменатель.
Перечисление кратных нецелесообразно для больших чисел. Другой способ найти НОК двух чисел — разделить их произведение на их наибольший общий делитель ( ЗКФ ).
Пример 2:
Найдите общий знаменатель дробей.
5 12 а также 2 15
Наибольший общий множитель 12 а также 15 является 3 .
Итак, чтобы найти наименьшее общее кратное, нужно разделить произведение на 3 .
12 ⋅ 15 3 знак равно 3 ⋅ 4 ⋅ 15 3 знак равно 60
Если вы можете найти наименьший общий знаменатель, вы можете переписать задачу, используя эквивалентные дроби у которых одинаковые знаменатели, поэтому их легко складывать или вычитать.
Пример 3:
Добавлять.
5 12 + 2 15
В предыдущем примере мы обнаружили, что наименьший общий знаменатель равен
60
.
Запишите каждую дробь в виде эквивалентной дроби со знаменателем 60 . Для этого умножаем и числитель, и знаменатель первой дроби на 5 , а числитель и знаменатель второй дроби на 4 . (Это то же самое, что умножить на 1 знак равно 5 5 знак равно 4 4 , так что это не меняет значение.)
5 12 знак равно 5 12 ⋅ 5 5 знак равно 25 60 2 15 знак равно 2 15 ⋅ 4 4 знак равно 8 60
5 12 + 2 15 знак равно 25 60 + 8 60 знак равно 33 60
Учтите, что этот метод не всегда может давать результат в минимальных условиях. В этом случае приходится упрощать.
В этом случае приходится упрощать.
знак равно 11 30
Та же идея может использоваться, когда в дробях есть переменные, то есть для сложения или вычитания рациональные выражения .
Пример 4:
Вычесть.
1 2 а − 1 3 б
Два выражения 2 а а также 3 б не имеют общих делителей, поэтому их наименьшее общее кратное есть просто их произведение: 2 а ⋅ 3 б знак равно 6 а б .
Перепишите две дроби с 6 а б в знаменателе.
1 2 а ⋅ 3 б 3 б знак равно 3 б 6 а б 1 3 б ⋅ 2 а 2 а знак равно 2 а 6 а б
Вычесть.
1 2 а − 1 3 б знак равно 3 б 6 а б − 2 а 6 а б знак равно 3 б − 2 а 6 а б
Пример 5:
Вычесть.
Икс 16 − 3 8 Икс
16
а также
8
Икс
имеют общий множитель
8
.



 ПОДРОБНО.
ПОДРОБНО.
 И нужно не только НОК, но и как его вычислили.
И нужно не только НОК, но и как его вычислили.
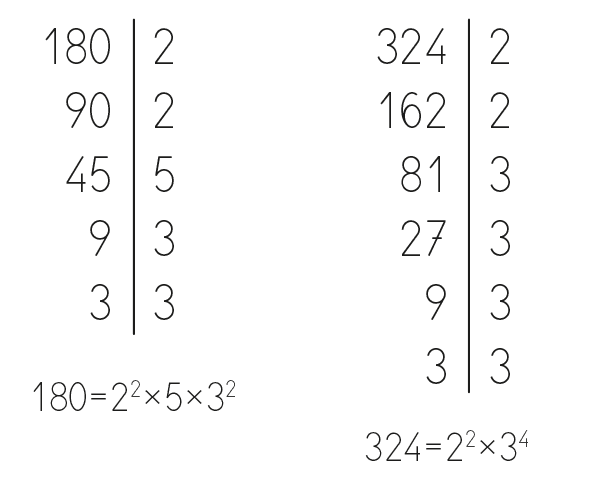
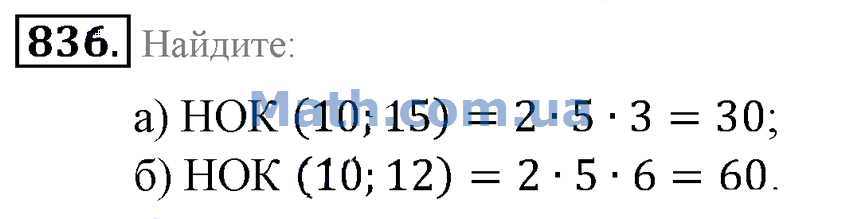 Например, НОД (24, 30,18) = 6.
Например, НОД (24, 30,18) = 6. 
 У нас это выделено жирным шрифтом выше.
У нас это выделено жирным шрифтом выше.



