Как найти тангенс через тангенс — Dudom
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса, тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.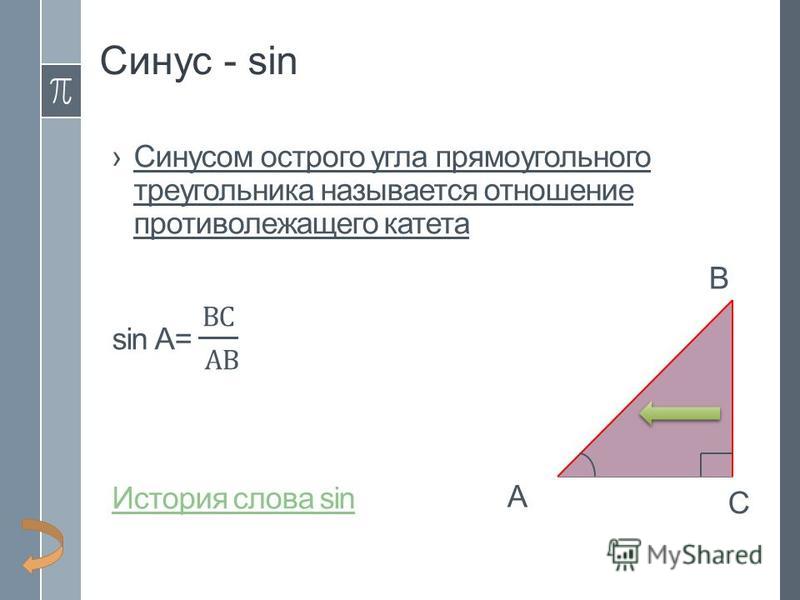
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс – это отношение синуса к косинусу.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.
Значение тангенса показывает не только раскрытие угла α , но и насколько один катет больше другого. При тангенсе угла α , равном 1 , катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.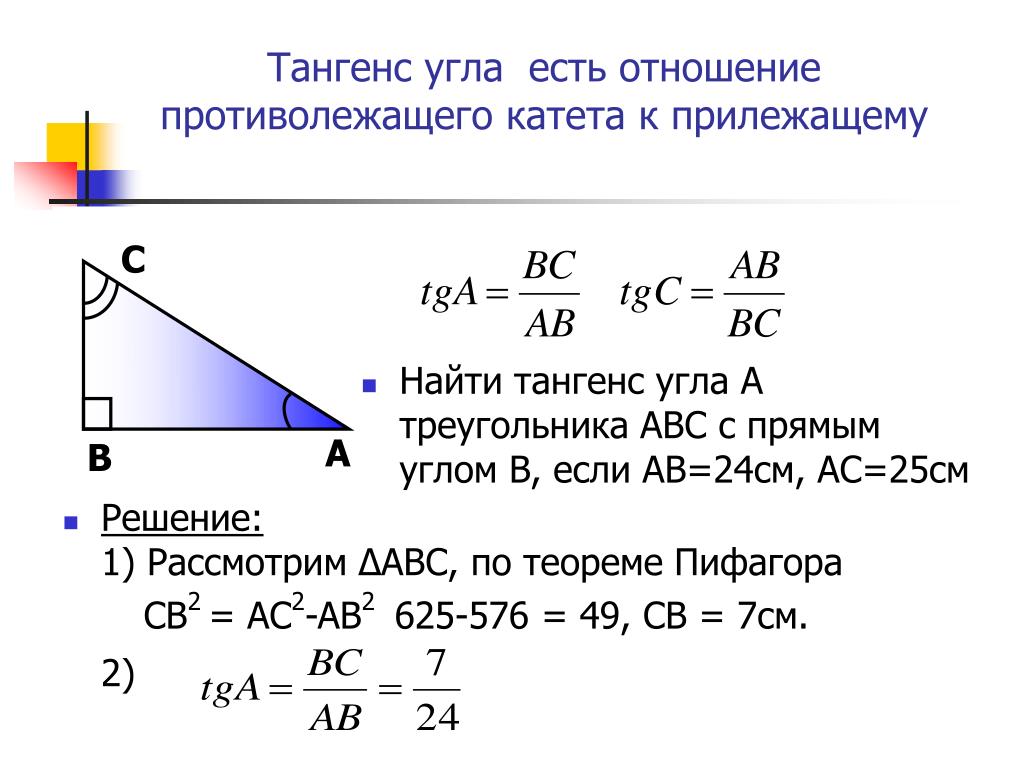
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
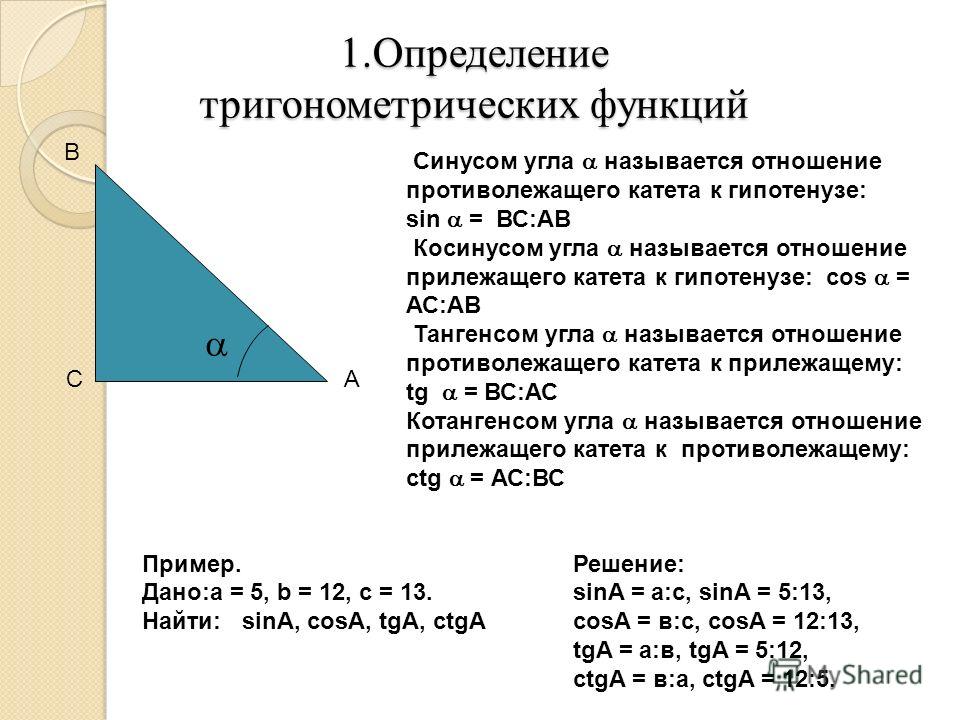
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t.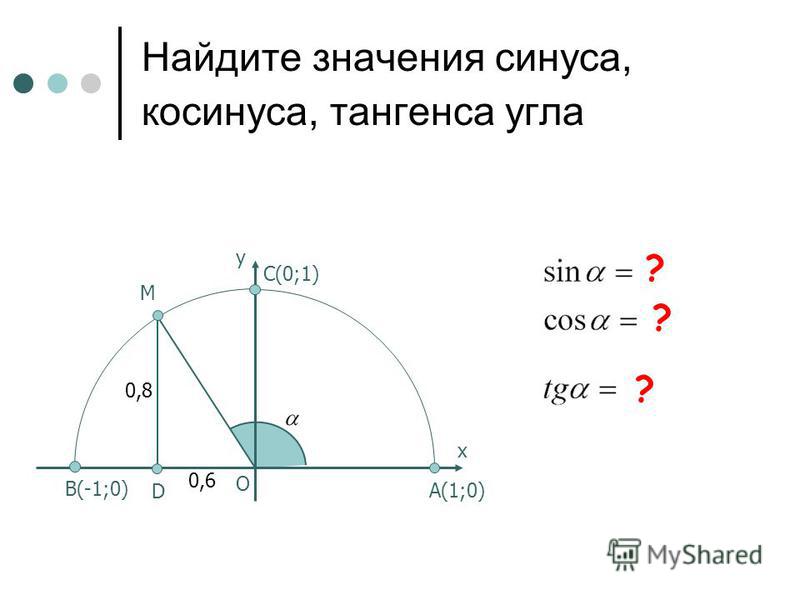 Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс.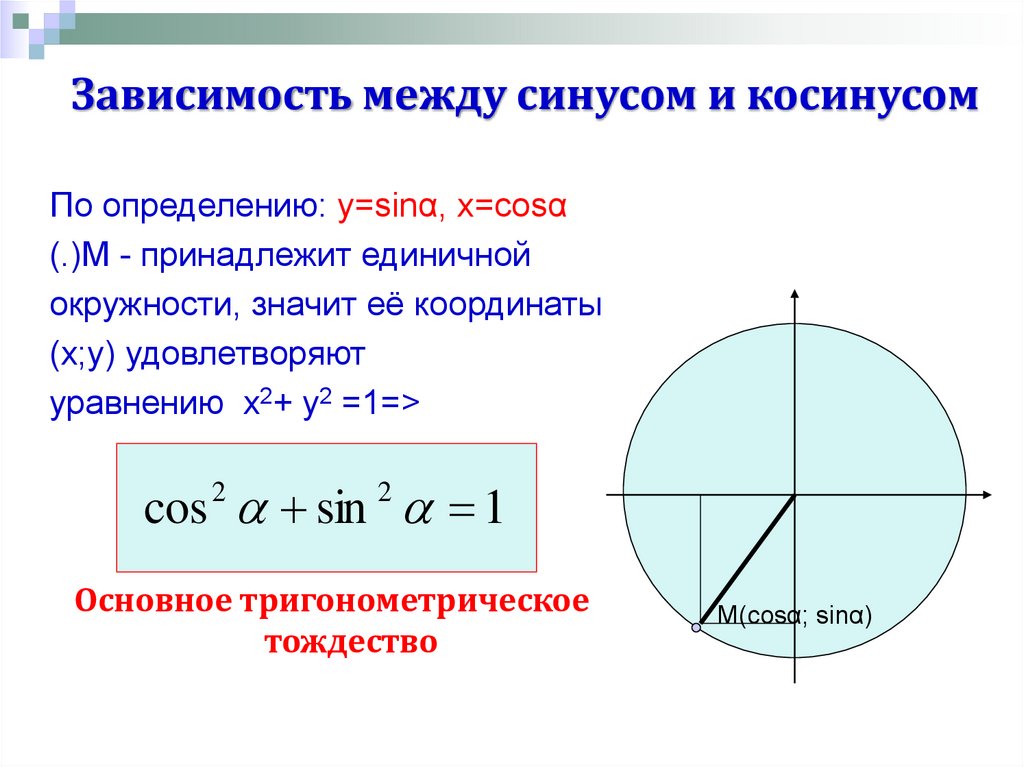 В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Как найти тангенс зная косинус
Содержание
- Линии тригонометрических функций
- Значения основных функций тригонометрии
- Сведение к углу
- Использование формул
- Частные случаи
- Тангенс угла
- Тангенс — это отношение.

- Как найти тангенс угла (формулы)
- Как найти тангенс по клеточкам
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.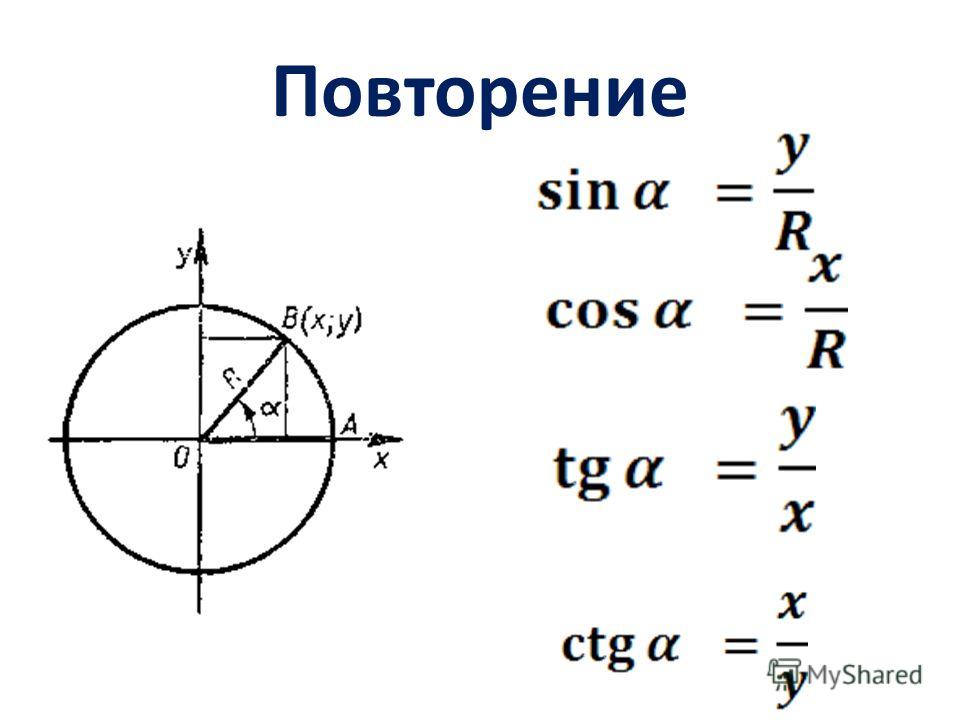
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) .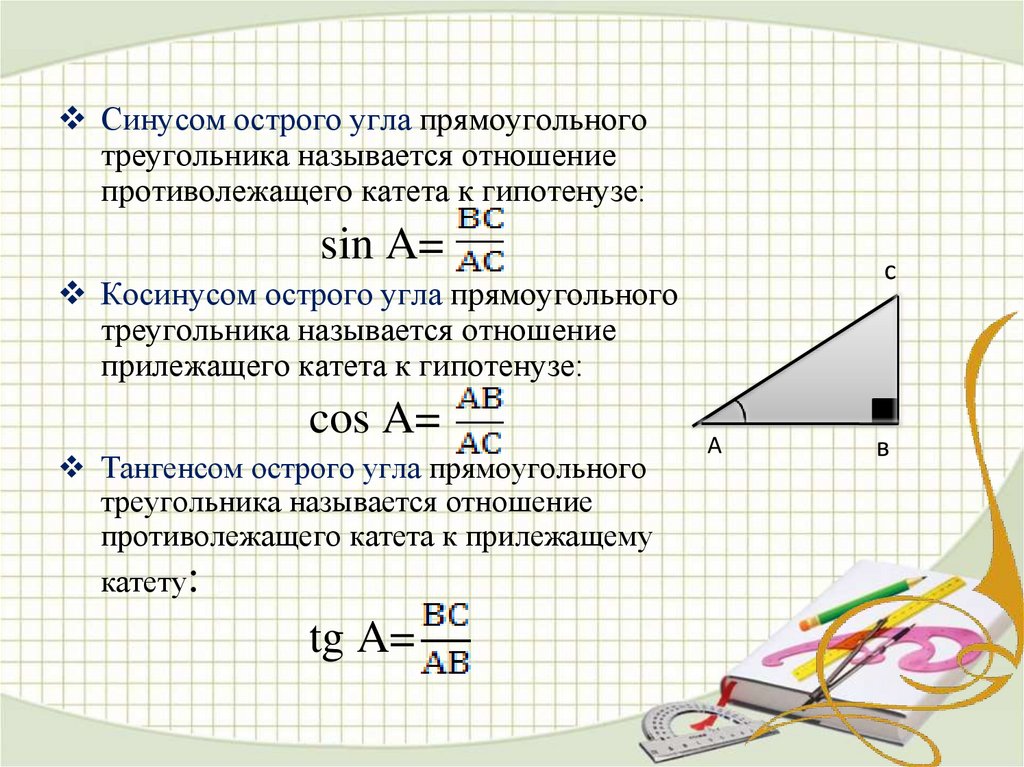 Мы находим значения всех функций кроме тангенса.
Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе.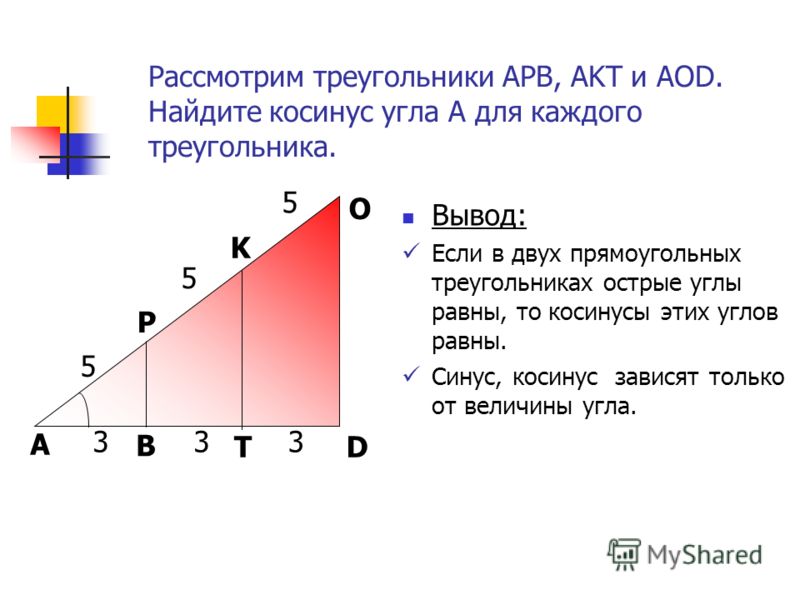 Они используются для наглядного изображения значений.
Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α .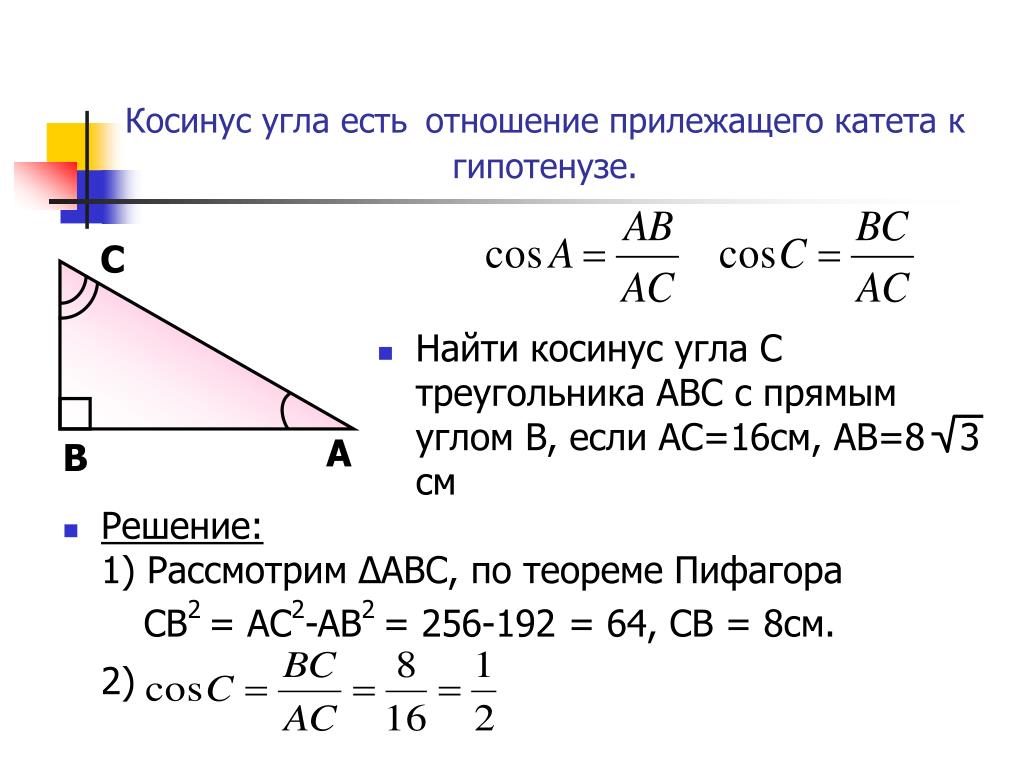 Благодаря этому мы вычисляем значение синуса. Имеем
Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 .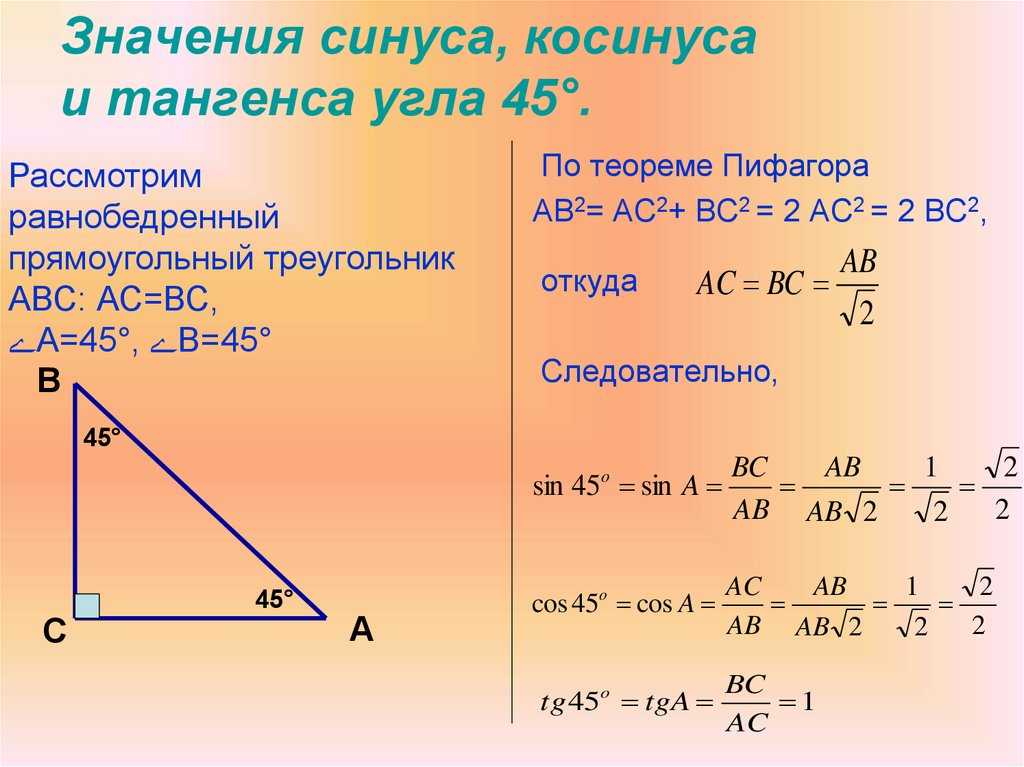 Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
- 10 — 11 классы
- Алгебра
- 5 баллов
ребят, как найти тангенс если известен косинус? и как косинус перевести в синус? напомните. плиз
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса, тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс – это отношение синуса к косинусу.
Вместо «тангенс угла альфа» пишут: tgα.
На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.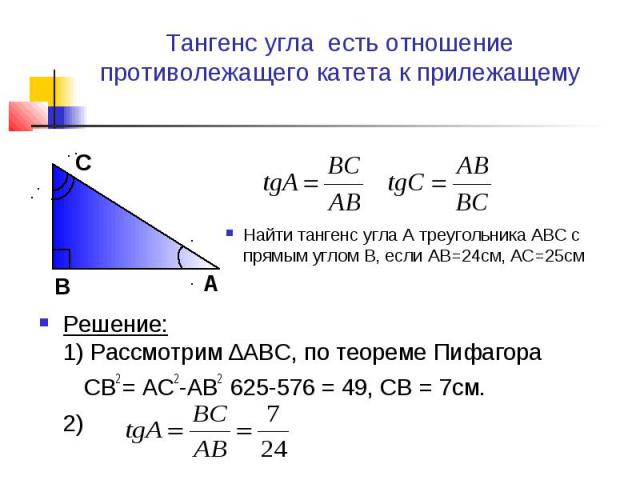 2 = 4 + 16 = 20
2 = 4 + 16 = 20
OB = 2√5
sin AOB = AB / OB = 4 /2√5 = 2 / √5 = 2√5 / 5
cos AOB = AO / OB = 2 / 2√5 = √5 / 5
tg AOB = AB / AO = 4 / 2 = 2
Похожие вопросы
Диагональ куба равна 2 корня из 3 месяца. Найдите площадь его полной поверхности…
Стороны основания прямоугольного параллепипеда равны 2 см и 3 см, а диагональ равная 7 см. Найдите площадь полной поверхности прямоугольного треугольного параллепипеда…
ПОМОГИТЕ, ДАМ 70 БАЛЛОВ
4 задание…
Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π. …
…
С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите косинус угла между прямыми АВ1 и ВС1…
Боковые ребра четырёхугольной пирамиды равны 13 см, а диагональ основания равна 10 корней из 2 см. Найдите высоту пирамиды….
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.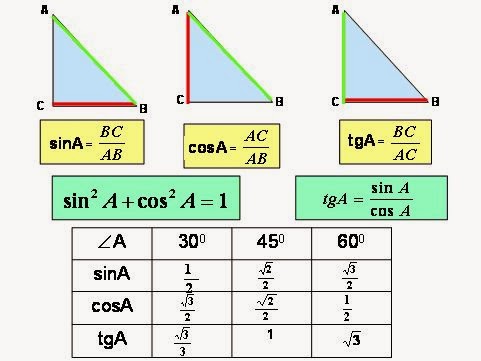 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
SAT Тригонометрия: SOHCATOA и радианы
Тригонометрия и радианы — новые дополнения к разделу SAT Math! Вы любите SOHCATOA и измерения углов ${π}$? Вы ненавидите тригонометрию и радианы и не знаете, что означает SOHCATOA или ${π}/{2}$? Как бы вы ни относились к тригонометрии SAT, не нужно напрягаться. В этом руководстве я расскажу вам все, что вам нужно знать о тригонометрии и радианах для теста SAT по математике, и проведу вас через некоторые практические задачи.
В этом руководстве я расскажу вам все, что вам нужно знать о тригонометрии и радианах для теста SAT по математике, и проведу вас через некоторые практические задачи.
Тригонометрические формулы: синус, косинус, тангенс
Хотя тригонометрия составляет менее 5% всех математических вопросов , вы все равно хотите правильно ответить на эти вопросы, и вы не сможете правильно ответить ни на один вопрос по тригонометрии, не зная следующих формул:
Найти синус угла по мерам сторон треугольника.
$$\sin(x)={\(Мера\:\:\:противоположная\:сторона\:к\:\:угол)}/{\(Мера\:\:\: гипотенуза)}$$
На рисунке выше синус отмеченного угла будет ${a}/{h}$
Найдите косинус угла по сторонам треугольника.
$$\cos(x)={\(Измерение\: из\:\: примыкающее\: сторона\: к\:\: угол)}/{\(Измерение\: из\:\: гипотенуза)}$$
На рисунке выше косинус помеченного угла будет равен ${b}/{h}$.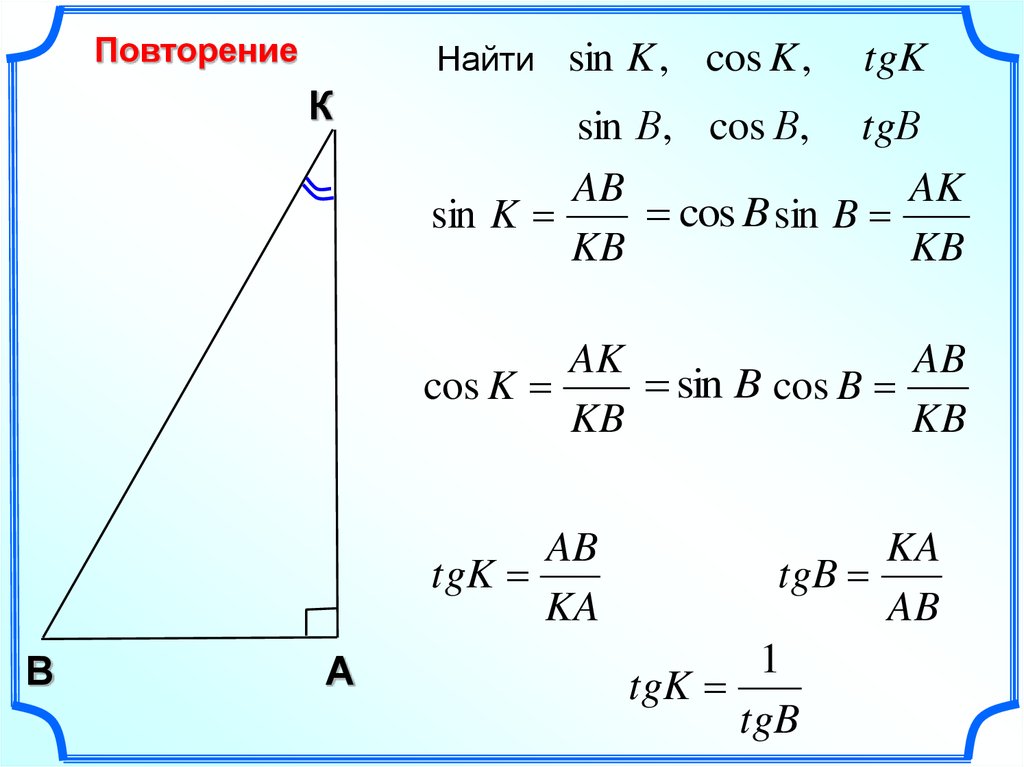
Найдите тангенс угла , зная длины сторон треугольника.
$$\tan(x)={\(Измерение\: от\:\: против\: сторона\: до\:\: угол)}/{\(Измерение\: от\:\: смежные\: сторона\: к\: угол\: угол)}$$
На рисунке выше тангенс помеченного угла равен ${a}/{b}$.
Полезным трюком с памятью является аббревиатура: SOHCAHTOA.
S ine equals O pposite over H ypotenuse
C osine equals A djacent over H ypotenuse
T angent equals O pposite over A djacent
Вы также должны знать соотношение дополнительных углов для синуса и косинуса, то есть $\sin(x°)=\cos(90°−x°)$.
Как применять навыки тригонометрии на SAT Math
Есть два основных типа вопросов по тригонометрии , которые вы увидите в тесте. Я научу вас обращаться к каждому.
Я научу вас обращаться к каждому.
Тип вопроса 1 попросит вас найти синус, косинус или тангенс, используя меры сторон треугольника. Чтобы ответить на эти вопросы, вам нужно будет использовать диаграмму (это означает нарисовать ее, если она вам не дана). Давайте рассмотрим этот пример:
Треугольник ABC — прямоугольный треугольник, угол B которого равен 90°; гипотенуза равна 5, а сторона AB равна 4. Что такое косинус A?
Сначала настройте этот треугольник, используя данную информацию:
Затем укажите необходимую информацию. В этом случае вопрос задан для косинуса А. Мы знаем, исходя из предыдущих формул, что \: угол)}/{\(Мера\: of\: the\: гипотенуза)}$. Определите необходимые части: угол, сторону, прилегающую к углу, и гипотенузу:
У нас есть вся необходимая информация, так что нам просто нужно ввести ее в формулу:
$\cos(A)={\(Мера\: из\:\: примыкающая\: сторона\: к\ : \: угол)}/{\(Мера\:\:\: гипотенуза)}={4}/{5}$.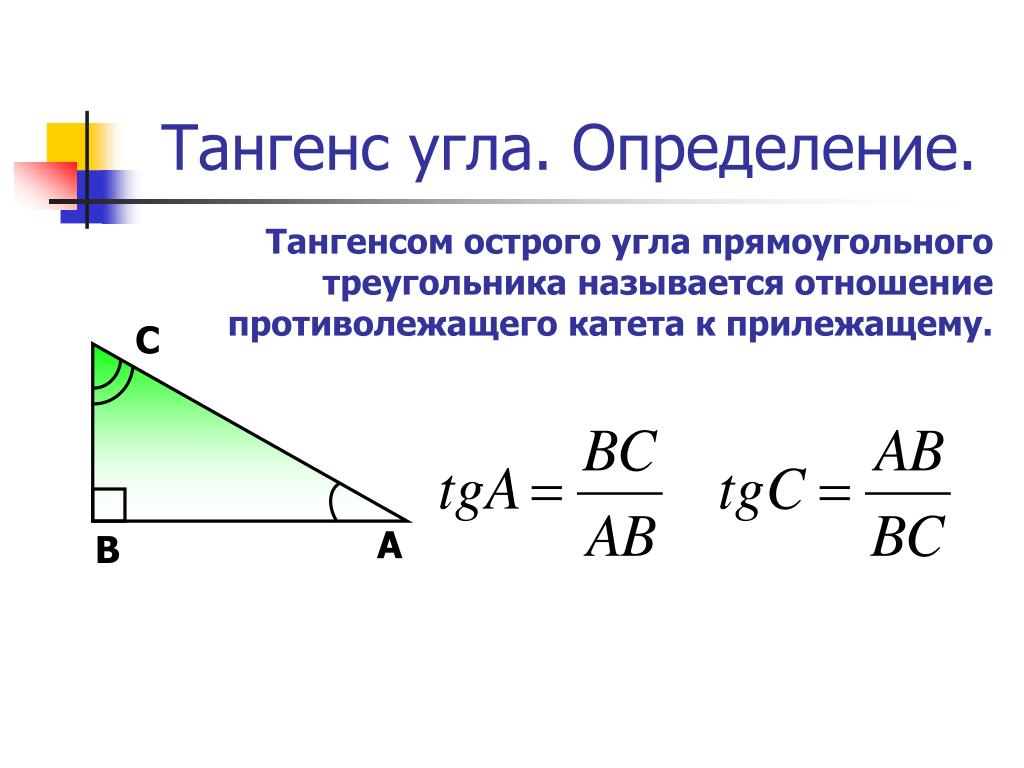
${4}/{5}$ — это ответ.
Немного более сложная версия этого вопроса может попросить вас ввести синус A вместо косинуса A. Если вы посмотрите на диаграмму, вы заметите, что мы не знаем, какова мера стороны, противоположной углу A. (это то, что нам нужно, чтобы найти синус A). 92)}=√{(25)-(16)}=√{9}=3$$
Зная, что мы знаем, что сторона BC равна 3, нам просто нужно подставить это в формулу:
$$\ sin(A)={\(Мера\:\:\:противоположная\:сторона\:к\:\:угол)}/{\(Мера\:\:\:\: гипотенуза)}={ 3}/{5}$$
Тип вопроса 2 попросит вас найти синус, косинус или тангенс угла, используя другой заданный синус, косинус или тангенс угла. Как и в случае с вопросом первого типа, чтобы ответить на эти вопросы, вам нужно будет использовать диаграмму (это означает нарисовать ее, если она вам не дана). Посмотрите этот пример:
В прямоугольном треугольнике ABC, где B — прямой угол, $\cos(A)={4}/{5}$. Что такое грех (С)?
Вы хотите решить эти проблемы, нарисовав диаграмму, но сначала вам нужно выяснить, что и куда должно идти.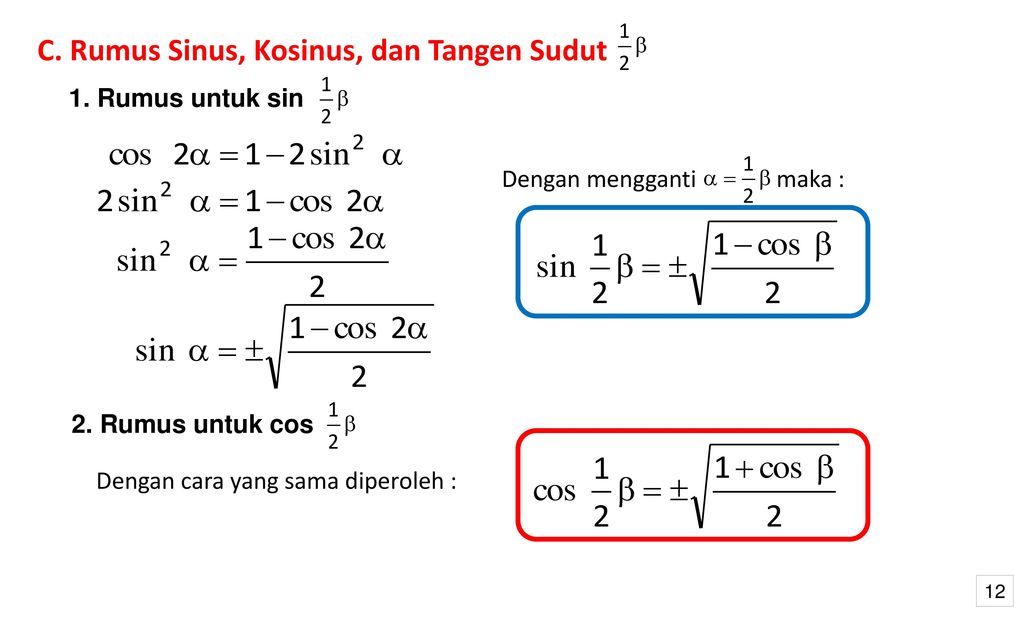 Используйте формулу косинуса, чтобы выяснить, как нарисовать диаграмму.
Используйте формулу косинуса, чтобы выяснить, как нарисовать диаграмму.
$$\cos(A)={\(Измерение\: от\:\:прилегающее\:сторона\:до\:\:угол)}/{\(Измерение\:\:\: гипотенуза)}={4}/{5}$$
Мера прилежащей стороны (AB) = 4
Мера гипотенузы (AC) = 5
Вы можете заметить, что это тот же треугольник из предыдущего примера. В этом случае мы хотим найти косинус C. Мы знаем, основываясь на предыдущих формулах, что }/{Мера\: of\:\: гипотенуза}$. Определите необходимые части: угол, сторону, прилегающую к углу, и гипотенузу.
$$\sin(C)={\(Мера\:\:\:против\:сторона\:к\:\:угол)}/{\(Мера\:\:\: гипотенуза)}={4}/{5}$$
${4}/{5}$ — это ответ.
Немного более сложная версия этого вопроса может попросить вас ввести тангенс C вместо синуса C. Если вы снова посмотрите на диаграмму, вы заметите, что мы не знаем, какова мера стороны, примыкающей к углу C. (это то, что нам нужно, чтобы найти загар A).
В этом случае нам нужно использовать теорему Пифагора (или наши знания о 3-4-5 прямоугольных треугольниках), чтобы найти меру стороны, прилежащей к углу C (BC).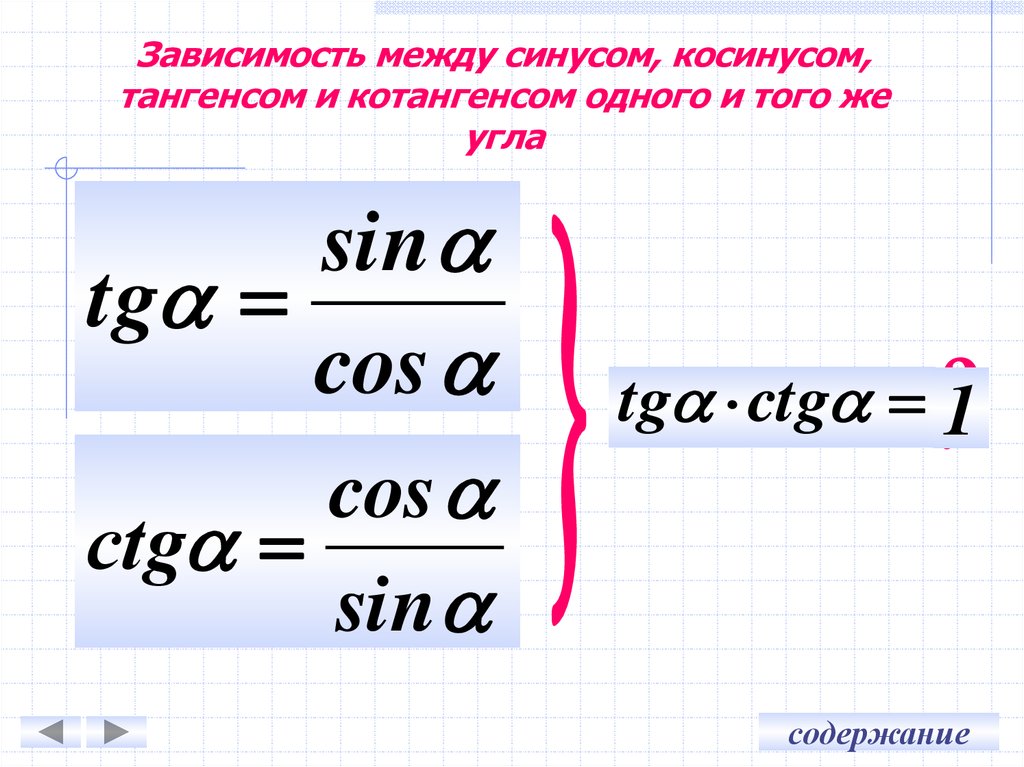 2)}=√{(25)-(16)}=√{9}=3$$
2)}=√{(25)-(16)}=√{9}=3$$
Зная, что мы знаем, что сторона BC равна 3, нам просто нужно подставить ее в формулу:
$$\tan(C)={\(Мера\: of\: the\: напротив \: сторона\: до\:\: угол)}/{\(Измерение\:\:\: смежная\: сторона\: до\:\: угол)}={4}/{3} $$
Теперь, когда мы знаем, как применять необходимые формулы для решения триггерных вопросов, давайте попробуем применить их к некоторым реальным практическим задачам SAT.
Практические задачи по тригонометрии SAT
Пример №1
Объяснение ответа: Треугольник ABC прямоугольный с прямым углом B. Следовательно, AC гипотенуза прямоугольного треугольника ABC, а AB и BC катеты прямоугольного треугольника ABC. По теореме Пифагора
$$AB=√(202)−(162)=√(400)−(256)=√144=12$$
Поскольку треугольник DEF подобен треугольнику ABC с вершиной F соответствующей вершине C, мера угла F равна мере угла C. Следовательно, $\sinF=\sinC$. Из длин сторон треугольника ABC $\sin C={\(Мера\:\:\:против\:сторона\:к\:\:угол)}/{\(Мера\:\: the\: гипотенуза)}={\AB}/{\AC}={12}/{20}={3}/{5}$.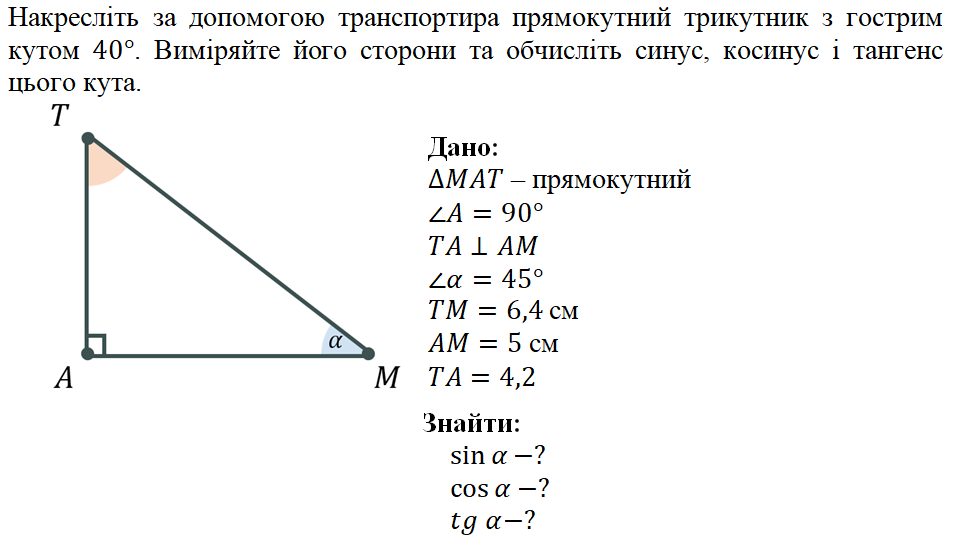 Следовательно, $\sinF={3}/{5}$.
Следовательно, $\sinF={3}/{5}$.
Окончательный ответ: ${3}/{5}$ или 0,6.
Пример #2
Объяснение ответа: Есть два способа решить эту проблему. Более быстрый способ, если вы знаете соотношение дополнительных углов для синуса и косинуса, которое равно $\sin(x°)=\cos(90°−x°)$. Следовательно, $\cos(90°−x°)={4}/{5}$ или 0,8.
Однако вы также можете решить эту проблему, построив диаграмму, используя предоставленную информацию. Это прямоугольный треугольник (каким он должен быть, чтобы использовать синус/косинус), и синус угла x равен ${4}/{5}$, если $\sine={\(противоположная\: сторона)}/{\ гипотенуза}$, то длина противоположной стороны равна 4, а длина гипотенузы 5:
Поскольку два угла треугольника имеют меру x° и 90°, третий угол должен иметь меру $180°−90°−x°=90°−x°$. Из рисунка $\cos(90°−x°)$, равное ${прилегающей\: стороне}/{\: гипотенузе}$, также равно ${4}/{5}$ или 0,8.
Пример №3
Ответ Пояснение: Как и в случае с другой задачей тригонометрии, эту задачу можно решить двумя способами.
Быстрее понять, что x и y являются дополнительными углами (в сумме получается 90°). Затем, используя соотношение дополнительных углов для синуса и косинуса, которое равно $\sin(x°)=\cos(90°−x°)$, вы понимаете, что $\cos(y°)=0,6$.
Однако вы также можете решить эту проблему, построив диаграмму, используя предоставленную информацию. Это прямоугольный треугольник (каким он должен быть, чтобы использовать синус/косинус), а синус угла x равен 0,6. Следовательно, отношение стороны, противоположной углу x°, к гипотенузе равно 0,6.
Сторона, противоположная углу x°, является стороной, примыкающей к углу y°. $\cos(y°)={\(the\: сторона\: примыкающая\: к\:\: y°\: угол)}/{\(the\: гипотенуза)}={6}/{10 }$ равно 0,6.
Ответ: 0,6.
Готовы не просто читать о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Разработанная и написанная экспертами PrepScholar SAT , наша программа SAT адаптируется к вашему уровню навыков по более чем 40 поднавыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.
Нажмите на кнопку ниже, чтобы попробовать!
Радиан
Радиан составляет лишь небольшую часть (около 5%) математических вопросов SAT , но вы все равно хотите правильно ответить на эти вопросы! Радианы — одна из самых сложных концепций. Что нужно знать о радианах?
Определение меры радиана
Обобщенное определение: Радиан является мерой угла (так же, как градус является мерой угла).
Углубленная/концептуальная версия: Радиан — это мера угла, основанная на длине дуги, которую угол пересекает на единичной окружности. Звучит как тарабарщина, я знаю. Позвольте мне сломать его. Единичный круг — это круг радиусом 1 единица. Смотрите картинку:
Gustavb/Wikimedia
Длина окружности (или длина вокруг) этой единичной окружности равна ${2π}$, поскольку ${C=2πr}$ и r=1.
Если бы мера угла равнялась 360°, то мера радиана равнялась бы ${2π}$, поскольку длина дуги, пересекаемой углом 360° на единичной окружности, равнялась бы всей окружности окружности (которую мы уже установлено, что ${2π}$). Вот несколько хороших основных мер радиана, которые следует запомнить:
Вот несколько хороших основных мер радиана, которые следует запомнить:
Градусов | Радиан (точный) |
30° | ${π}/{6}$ |
45° | ${π}/{4}$ |
60° | ${π}/{3}$ |
90° | ${π}/{2}$ |
Как преобразовать угол в градусах в радианы
Чтобы перейти от градусов к радианам, нужно умножить на ${π}$, разделить на 180°. Вот как преобразовать 90° в радианы:
$${90°π}/{180°}$$
$$={π}/{2}$$
Чтобы перейти от радианов к градусам, нужно умножить на 180°, разделить на ${π}$. Вот как преобразовать ${π}/{4}$ в градусы:
$${({π}/{4})(180°)}/{π}$$
$$={({180°π}/{4})/{π}$$
$$=45°$$
Как вычислять тригонометрические функции при эталонных угловых мерах
Эталонные угловые меры (как определены Советом колледжей) равны 0, ${π}/{6}$, ${π}/{4}$, ${π}/{3}$, ${π}/{2}$ радиан, которые равны углам, равным 0°, 30°, 45°, 60° и 90° соответственно.
Вы должны иметь возможность использовать их с тригонометрическими функциями, описанными в предыдущем разделе тригонометрии (синус, косинус и тангенс). Вас не будут спрашивать о значениях тригонометрических функций, требующих калькулятора. 92)}=√{3+1}=√{4}=2$. Таким образом, $\sin(∠AOB)={1}/{2}$.
Следовательно, ∠AOB равен 30°, что равно $30({π}/{180})={π}/{6}$ радиан. Следовательно, значение a равно 6.
Пример #2
Ответ Пояснение: Полный оборот вокруг точки составляет 360° или ${2π}$ радиан. Поскольку центральный угол AOB имеет меру ${5π}/{4}$ радиан, он представляет $/{2π}={5}/{8}$ полного оборота вокруг точки O. Следовательно, сектор, образованный центральным углом AOB имеет площадь, равную ${5}/{8}$ площади всего круга. Ответ: ${5}/{8}$ или в десятичной форме 0,625.
Пример №3
Что из следующего эквивалентно $\cos({3π}/{10})$?
A) $\-cos ({π}/{5})$
B) $\sin ({7π}/{10})$
C) $\-sin ({π}/{5}) $
D) $\sin ({π}/{5})$
Объяснение ответа: Чтобы правильно ответить на этот вопрос, вам нужно понимать как тригонометрию, так и радианы.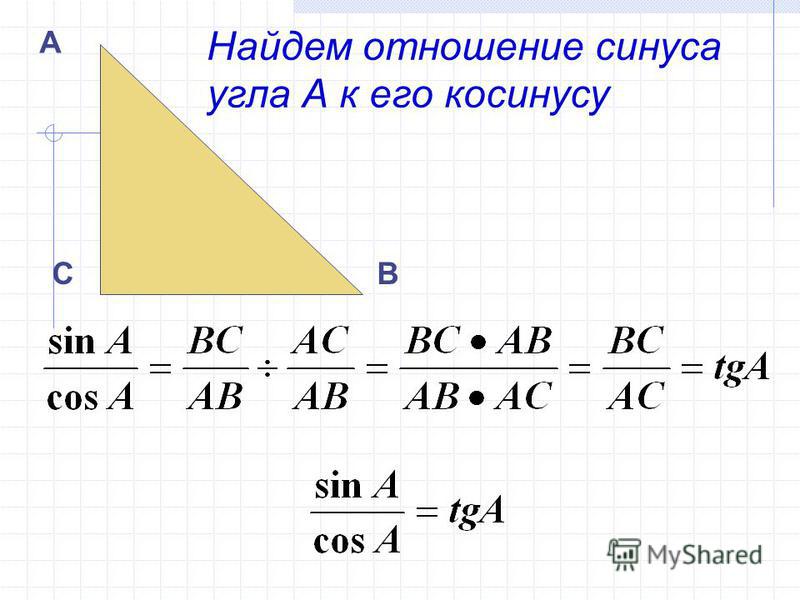 Синус и косинус связаны уравнением $\sin(x)=\cos({π}/{2}-x)$.
Синус и косинус связаны уравнением $\sin(x)=\cos({π}/{2}-x)$.
Чтобы узнать, что эквивалентно $\cos({3π}/{10})$, вам нужно преобразовать ${3π}/{10}$ в форму ${π}/{2} -х$. Для этого нужно составить уравнение:
$${3π}/{10}= {π}/{2}-x$$
Затем найдите x.
$${3π}/{10}-{π}/{2}=-x$$
$${3π}/{10}-{5π}/{10}=-x$$
$$-{2π}/{10}=-x$$
$${2π}/{10}=x$$
$${π}/{5}=x$$
Следовательно, $ \cos({3π}/{10})=\cos({π}/{2}-{π}/{5})=\sin({π}/{5})$. Д — правильный ответ.
Проверьте себя в вопросах тригонометрии SAT!
Практика №1
В треугольнике DCE угол C равен 90°, $\DC=5$ и $\CE=12$. Каково значение $\sin(D)$?
Практическое занятие №2
В прямоугольном треугольнике $\cos({π}/{2}-x)={6}/{8}$. Что такое $\sin(x)$?
Практика №3
В окружности O центральный угол AOB имеет меру ${3π}/{4}$ радиан. Какова часть площади сектора, образованного центральным углом АОВ, от площади круга?
Ответы: #1: ${12}/{13}$, #2: ${6}/{8}$, 3) ${3}/{8}$
Что Следующий?
Теперь, когда вы знаете, как работать с тригонометрией и радианами, убедитесь, что вы готовы ко всем другим математическим темам, которые вы увидите на SAT. Все наши руководства по математике познакомят вас со стратегиями и практическими задачами по всем темам, затронутым в математическом разделе, от целых чисел до отношений, от кругов до многоугольников (и многого другого!).
Все наши руководства по математике познакомят вас со стратегиями и практическими задачами по всем темам, затронутым в математическом разделе, от целых чисел до отношений, от кругов до многоугольников (и многого другого!).
Волнуетесь перед днем экзамена? Убедитесь, что вы точно знаете, что делать и что взять с собой, чтобы успокоиться и успокоить нервы, прежде чем придет время сдавать SAT.
Не хватает времени на математическую секцию SAT? Не ищите ничего, кроме нашего руководства, которое поможет вам побить время и максимизировать свой результат SAT по математике.
Рыбалка, чтобы получить высший балл? Ознакомьтесь с нашим руководством по получению идеальных 800 баллов, написанным отличником.
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег, если вы не улучшите свой результат SAT на 160 или более баллов.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравилось это руководство по математической стратегии, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
Воспользуйтесь нашей 5-дневной бесплатной пробной версией:
У вас есть друзья, которым также нужна помощь в подготовке к экзамену? Поделись этой статьей!
Дора Сейгель
Об авторе
Как репетитор SAT/ACT, Дора помогла многим студентам успешно подготовиться к тестированию. Ей нравится наблюдать за успехами учеников, и она стремится помочь вам добиться этого. Дора получила стипендию на полное обучение в Университете Южной Калифорнии. Она закончила с отличием и набрала 9 баллов.9-й процентиль по ACT. Она также увлечена актерским мастерством, писательством и фотографией.
Дора получила стипендию на полное обучение в Университете Южной Калифорнии. Она закончила с отличием и набрала 9 баллов.9-й процентиль по ACT. Она также увлечена актерским мастерством, писательством и фотографией.
первая в мире тригонометрия обнаружена на древней вавилонской табличке
Древние вавилоняне, жившие около 4000 г. тригонометрию учат в школах.
Наше новое исследование, опубликованное в Historia Mathematica, показывает, что вавилоняне могли построить тригонометрическую таблицу, используя только точные соотношения сторон прямоугольного треугольника. Это совершенно другая форма тригонометрии, не нуждающаяся в привычном современном понятии углов.
В школе нам говорят, что форма прямоугольного треугольника зависит от двух других углов. Угол связан с длиной окружности, которая делится на 360 частей или градусов. Затем этот угол используется для описания отношения сторон прямоугольного треугольника через sin, cos и tan.
Читать далее: Ваш путеводитель по решению следующей вирусной математической онлайн-задачи
Но круги и прямоугольные треугольники сильно отличаются друг от друга, и цена простых значений угла ложится на соотношения, которые очень сложны и должны быть аппроксимированы.
Этот подход восходит к греческому астроному и математику Гиппарху Никейскому (умершему после 127 г. до н. э.). Его называют отцом тригонометрии, потому что он использовал свою таблицу хорд для расчета орбит Луны и Солнца.
Но наше новое исследование показывает, что это был не первый, не единственный и не лучший подход к тригонометрии.
Вавилонская тригонометрия
Вавилоняне открыли свою уникальную форму тригонометрии в древневавилонский период (1900-1600 гг. до н.э.), более чем на 1500 лет раньше, чем греческая форма.
Примечательно, что их тригонометрия не содержит ни одного из признаков нашей современной тригонометрии — она не использует углы и не использует приближение.
У вавилонян было совершенно другое представление о прямоугольном треугольнике.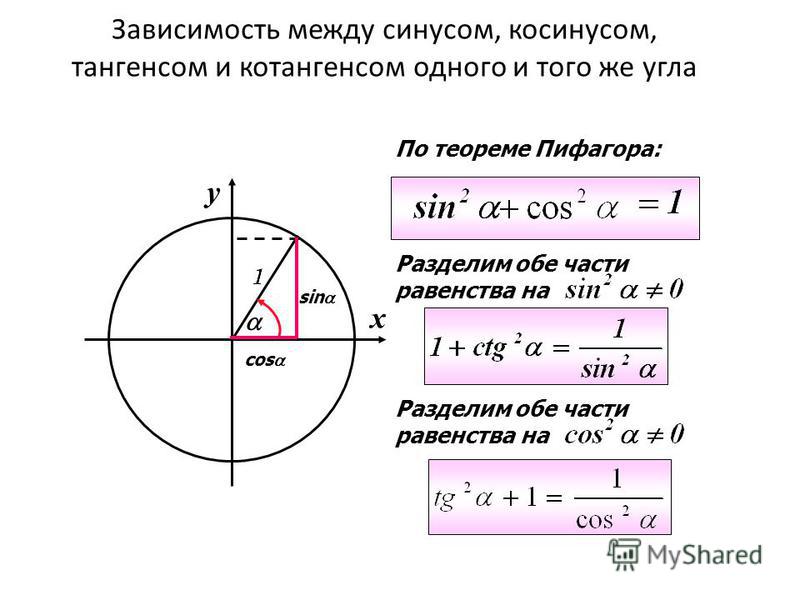 Они видели его как половину прямоугольника, и благодаря своей сложной шестидесятеричной системе счисления (с основанием 60) они смогли построить множество прямоугольных треугольников, используя только точные соотношения.
Они видели его как половину прямоугольника, и благодаря своей сложной шестидесятеричной системе счисления (с основанием 60) они смогли построить множество прямоугольных треугольников, используя только точные соотношения.
Шестидесятеричная система лучше подходит для точного расчета. Например, если вы разделите один час на три, вы получите ровно 20 минут. Но если вы разделите один доллар на три, вы получите 33 цента, а 1 цент останется. Фундаментальное отличие состоит в том, что часы и доллары принято трактовать в разных системах счисления: время — шестидесятеричное, а доллары — десятичные.
Вавилоняне знали, что их шестидесятеричная система счисления допускает более точное деление. Для более сложного примера 1 час, разделенный на 48, равен 1 минуте и 15 секундам.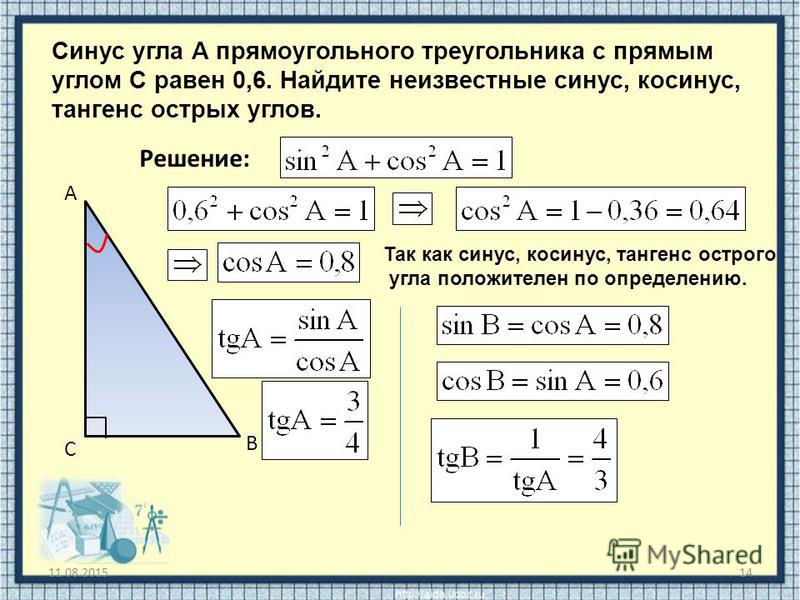
Эта точная арифметика вавилонян также повлияла на их геометрию, которую они предпочитали быть точной. Они смогли создать множество прямоугольных треугольников с точными соотношениями b/l и d/l, где b, l и d — короткая сторона, длинная сторона и диагональ прямоугольника.
Отношение b/l было особенно важно для древних вавилонян и египтян, поскольку они использовали это отношение для измерения крутизны.
Табличка Plimpton 322
Теперь мы знаем, что вавилоняне изучали тригонометрию, потому что у нас есть фрагмент одной из их тригонометрических таблиц.
Плимптон 322 — это разбитая глиняная табличка из древнего города Ларса, расположенного недалеко от Телль-ас-Сенкере в современном Ираке. Табличка была написана между 1822-1762 годами до нашей эры.
В 1920-х годах археолог, академик и искатель приключений Эдгар Дж. Бэнкс продал табличку американскому издателю и филантропу Джорджу Артуру Плимптону.
Плимптон завещал всю свою коллекцию математических артефактов Колумбийскому университету в 1936 году, и сегодня она находится там в Библиотеке редких книг и рукописей. Он доступен в Интернете в рамках Инициативы цифровой библиотеки клинописи.
Он доступен в Интернете в рамках Инициативы цифровой библиотеки клинописи.
В 1945 году выяснилось, что табличка содержит очень сложную последовательность целых чисел, удовлетворяющую уравнению Пифагора a 2 +b 2 =c 2 , известные как пифагорейские тройки.
Это фундаментальное соотношение трех сторон прямоугольного треугольника, и это открытие доказало, что вавилоняне знали это соотношение более чем за 1000 лет до рождения греческого математика Пифагора.
Основное соотношение между длинами сторон прямоугольного треугольника. В наше время это называется теоремой Пифагора, но вавилонянам она была известна более чем за 1000 лет до рождения Пифагора. Plimpton 322 имеет разлинованное место на реверсе, что указывает на то, что предназначались дополнительные ряды. В 1964 году историк науки из Йельского университета Дерек Дж. де Солла Прайс обнаружил закономерность, лежащую в основе сложной последовательности пифагорейских троек, и теперь мы знаем, что изначально она должна была состоять из 38 рядов.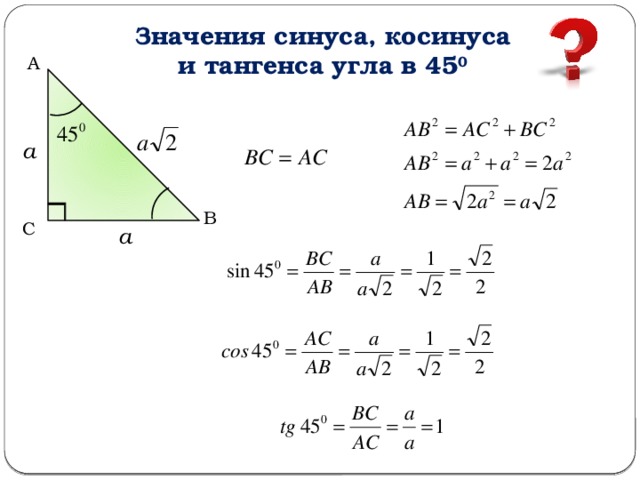
В планшете тоже отсутствуют столбцы, а в 1981 шведский историк математики Йоран Фриберг предположил, что отсутствующие столбцы должны быть отношениями b/l и d/l. Но цель планшета оставалась неясной.
Первые пять строк Plimpton 322 с восстановленными столбцами и десятичными числами.Сохранившийся фрагмент Плимптона 322 начинается с пифагорейской тройки 119, 120, 169. Следующая тройка — это 3367, 3456, 4825. Это имеет смысл, если вы понимаете, что первая тройка представляет собой почти квадрат (который является крайним видом прямоугольника). ), а следующий немного более плоский. На самом деле прямоугольные треугольники медленно, но неуклонно становятся более плоскими на протяжении всей последовательности.
Наблюдайте, как треугольники меняют форму по мере продвижения по списку.
Таким образом, на тригонометрический характер этой таблицы указывают только данные по сохранившемуся фрагменту, но еще более она очевидна из реконструированной таблички.
К этому аргументу следует относиться осторожно, потому что современных понятий, таких как угол, не существовало во время написания Plimpton 322. Как же тогда это может быть тригонометрическая таблица?
По существу тригонометрическая таблица должна описывать три отношения прямоугольного треугольника. Поэтому мы отбрасываем sin и cos и вместо этого начинаем с отношений b/l и d/l. Соотношение, которое заменяет tan, будет тогда b/d или d/b, но ни то, ни другое не может быть точно выражено в шестидесятеричном виде.
Вместо этого информация об этом коэффициенте разбита на три столбца с точными числами. Квадратный индекс и упрощенные значения b и d, чтобы помочь писцу сделать собственное приближение к b/d или d/b.
Без приближения
Самым замечательным аспектом вавилонской тригонометрии является ее точность.

 На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).