8 5 перевести в обыкновенную дробь: Восемь пятых в десятичной дроби

2

Преобразовать в десятичную дробь данное число. Перевод десятичных чисел в обыкновенную дробь

Преобразование обыкновенной дроби в десятичную

Допустим, мы хотим преобразовать обыкновенную дробь 11/4 в десятичную. Проще всего сделать это так:

						2∙2∙5∙5

Это удалось нам потому, что в данном случае разложение знаменателя на простые множители состоит только из двоек. Мы дополнили это разложение еще двумя пятерками, воспользовались тем, что 10 = 2∙5, и получили десятичную дробь. Подобная процедура возможна, очевидно, тогда и только тогда, когда разложение знаменателя на простые множители не содержит ничего, кроме двоек и пятерок.

Если в разложении знаменателя присутствует любое другое простое число, то такую дробь в десятичную преобразовать нельзя. Тем не менее, мы попробуем это сделать, но только другим способом, с которым мы познакомимся на примере всё той же дроби 11/4. Давайте поделим 11 на 4 «уголком»:

В строке ответа мы получили целую часть ( 2 ), и еще у нас есть остаток ( 3 ). Раньше мы деление на этом заканчивали, но теперь мы знаем, что к делимому ( 11 ) можно приписать справа запятую и несколько нулей, что мы теперь мысленно и сделаем. Следом после запятой идет разряд десятых. Ноль, который стоит у делимого в этом разряде, припишем к полученному остатку ( 3 ):

Теперь деление можно продолжать как ни в чем не бывало. Надо только не забыть поставить в строке ответа запятую после целой части:

Теперь приписываем к остатку ( 2 ) ноль, который стоит у делимого в разряде сотых и доводим деление до конца:

В результате получаем, как и раньше,

Попробуем теперь точно таким же способом вычислить, чему равна дробь 27/11:

Мы получили в строке ответа число 2,45, а в строке остатка — число 5 . Но такой остаток нам уже раньше встречался. Поэтому мы уже сразу можем сказать, что, если мы продолжим наше деление «уголком», то следующей цифрой в строке ответа будет 4, затем пойдет цифра 5, потом — снова 4 и снова 5, и так далее, до бесконечности:

27 / 11 = 2,454545454545…

Мы получили так называемую периодическую десятичную дробь с периодом 45. Для таких дробей применяется более компактная запись, в которой период выписывается только один раз, но при этом он заключается в круглые скобки:

2,454545454545… = 2,(45).

Вообще говоря, если делить «уголком» одно натуральное число на другое, записывая ответ в виде десятичной дроби, то возможно только два исхода: (1) либо рано или поздно в строке остатка мы получим ноль, (2) либо там окажется такой остаток, который уже нам раньше встречался (набор возможных остатков ограничен, поскольку все они заведомо меньше делителя). В первом случае результатом деления является конечная десятичная дробь, во втором случае — периодическая.

Преобразование периодической десятичной дроби в обыкновенную

Пусть нам дана положительная периодическая десятичная дробь с нулевой целой частью, например:

a = 0,2(45).

Как преобразовать эту дробь обратно в обыкновенную?

Умножим ее на число 10 k , где k — это число цифр, стоящих между запятой и открывающей круглой скобкой, обозначающей начало периода. В данном случае k = 1 и 10 k = 10:

a ∙ 10 k = 2,(45).

Полученный результат умножим на 10 n , где n — «длина» периода, то есть число цифр, заключенных между круглыми скобками. В данном случае

n = 2 и 10 n = 100:

a ∙ 10 k ∙ 10 n = 245,(45).

Теперь вычислим разность

a ∙ 10 k ∙ 10 n − a ∙ 10 k = 245,(45) − 2,(45).

Поскольку дробные части у уменьшаемого и вычитаемого одинаковы, то у разности дробная часть равна нулю, и мы приходим к простому уравнению относительно a :

a ∙ 10 k ∙ (10 n − 1) = 245 − 2.

Решается это уравнение с помощью следующих преобразований:

a ∙ 10 ∙ (100 − 1) = 245 − 2.

a ∙ 10 ∙ 99 = 245 − 2.

	245 − 2
	10 ∙ 99

Мы специально пока не доводим вычисления до конца, чтобы было наглядно видно, как можно сразу выписать этот результат, опуская промежуточные рассуждения. Уменьшаемое в числителе ( 245 ) — это дробная часть числа

a = 0,2(45)

если в ее записи стереть скобки. Вычитаемое в числителе ( 2 ) — это непериодическая часть числа а , располагающаяся между запятой и открывающей скобкой. Первый сомножитель в знаменателе ( 10 ) — это единица, к которой приписано столько нулей, сколько цифр в непериодической части (k ). Второй сомножитель в знаменателе ( 99 ) — это столько девяток, сколько цифр содержит период (n ).

Теперь наши вычисления можно довести до конца:

Здесь в числителе стоит период, а в знаменателе — столько девяток, сколько цифр в периоде. После сокращения на 9 полученная дробь оказывается равной

Подобным же образом,

Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.

• 
  Обыкновенные дроби

Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.

Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .

• Смешанные дроби

В общем виде смешанная дробь может быть представлена формулой:

Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.

• Десятичные дроби

Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.

Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:

Правила перевода между различными видами дробей

• Перевод смешанной дроби в обыкновенную

Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную.

В общем виде это будет выглядеть следующим образом:
Рассмотрим использование этого правила на конкретных примерах:

• Перевод обыкновенной дроби в смешанную

Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).

Для примера переведем дробь 439/31 в смешанную:
​​

• Перевод обыкновенной дроби

В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.

Например:

В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.

Неправильная дробь — это один из форматов записи обыкновенной дроби.

Как и у любой обыкновенной дроби, у нее есть число над чертой (числитель) и под ней — знаменатель. Если числитель больше знаменателя, это и есть отличительный признак неправильности дроби. В эту форму можно перевести смешанную обыкновенную дробь. Десятичную тоже можно представить в неправильной обыкновенной форме записи, но лишь в том случае, если перед разделительной запятой стоит число, отличное от нуля.

Инструкция

В смешанном формате обыкновенной дроби числитель и знаменатель отделены от целой части пробелом. Чтобы перевести такую запись в , сначала умножьте ее целую часть (число, стоящее перед пробелом) на знаменатель дробной части. Полученное значение прибавьте к числителю. Рассчитанная таким способом величина будет числителем неправильной дроби, а в ее знаменатель поставьте знаменатель смешанной дроби без каких-либо изменений. Например, 5 7/11 в формате обыкновенной неправильной можно записать так: (5*11+7)/11 = 62/11.

Для перевода десятичной дроби в неправильный обыкновенный формат записи определите количество разрядов после запятой, отделяющей целую часть от дробной — оно равно числу цифр справа от этой запятой. Полученное число используйте в качестве показателя степени, в которую вам нужно возвести десятку, чтобы рассчитать знаменатель неправильной дроби. Числитель получается без каких-либо расчетов — просто уберите запятую из десятичной дроби. Например, если исходная десятичная дробь равна 12,585, в числителе соответствующей ей неправильной должно стоять число 10³ = 1000, а в знаменателе — 12585: 12,585 = 12585/1000.

Как и любые обыкновенные дроби, можно и нужно сокращать. Для этого после получения результата описанными в предыдущих двух шагах способами попытайтесь подобрать наибольший общий делитель для числителя и знаменателя. Если это удастся сделать, разделите на найденное по обе стороны дробной черты. Для примера из второго шага таким делителем будет число 5, поэтому неправильную дробь можно сократить: 12,585 = 12585/1000 = 2517/200. А для примера из первого шага общего делителя нет, поэтому сокращать результирующую неправильную дробь не нужно.

Видео по теме

Десятичные дроби более удобны для автоматизированных расчетов, чем натуральные. Любая натуральная дробь может быть переведена в натуральную либо без потери точности, либо с точностью до заданного количества знаков после запятой, в зависимости от соотношения между числителем и знаменателем.

Инструкция

При необходимости округлите результат до требуемого количества знаков после запятой. Правила округления следующие: если в старшем из удаляемых разрядов расположена цифра от 0 до 4, то следующий по старшинству разряд (который не удаляется) не изменяется, а если цифра от 5 до 9 — увеличивается на единицу. В случае если последней из этих операций подвергнут разряд с цифрой 9, осуществляется перенос единицы в другой, еще более старший разряд, как столбиком. Учтите, что , округляя до доступного количества знакомест, осуществляет эту операцию не всегда . Иногда в его памяти имеются скрытые разряды, не выводимые на индикатор. Логарифмическая , обладая малой точностью (до двух знаков после запятой), зачастую при этом справляется с округлением в нужную сторону лучше.

Обнаружив, что после запятой повторяется определенная последовательность цифр, поместите эту последовательность в скобки. О ней говорят, что она находится « », поскольку она повторяется периодически. Например, число 53,7854785478547854… можно записать как 53,(7854).

Правильная дробь, значение которой больше единицы, состоит из двух частей: целой и дробной. Вначале поделите числитель дробной части на ее знаменатель. Затем результат деления сложите с целой частью. После этого при необходимости округлите результат до необходимого количества знаков после запятой либо найдите периодичность и выделите ее скобками.

Десятичные дроби удобны в обращении. Их распознают калькуляторы и многие компьютерные программы. Но порой бывает необходимо, к примеру, составить пропорцию. Для этого придется перевести десятичную дробь в обычную дробь. Это не составит труда, если совершить небольшой экскурс в школьную программу.

Инструкция

Сократите дробную часть получившегося . Для этого числитель и знаменатель дроби нужно разделить на один и тот же делитель. В данном случае это число «5». Итак, «5/10» преобразуется в «1/2».

Подберите число, чтобы результат его умножения на знаменатель был 10. Рассуждения ведите от обратного: можно ли превратить число 4 в 10? Ответ: нет, потому что 10 не делится на 4. Тогда 100? Да, 100 делится на 4 без остатка, в итоге получается 25. Умножьте числитель и знаменатель на 25 и запишите ответ в десятичном виде:
¼ = 25/100 = 0,25.

Не всегда можно воспользоваться методом подбора, существует еще два способа. Принцип их практически один и тот же, различается лишь запись. Один из них – постепенное выделение десятичных знаков. Пример: переведите дробь 1/8.

Очень часто в школьной программе математики дети сталкиваются с проблемой, как перевести обычную дробь в десятичную. Для того чтобы перевести обычную дробь в десятичную, вспомним для начала, что такое обычная дробь и десятичная дробь. Обычная дробь – это дробь вида m/n , где m – числитель, а n – знаменатель. Пример: 8/13; 6/7 и т.д. Дроби делятся на правильные, неправильные и смешанные числа. Правильная дробь – это когда числитель меньше знаменателя: m/n, где m 3. Неправильную дробь всегда можно представить в виде смешанного числа, а именно: 4/3 = 1 и 1/3;

Перевод обычной дроби в десятичную

Теперь рассмотрим, как перевести смешанную дробь в десятичную. Любую обыкновенную дробь, будь она правильной или не правильной, можно перевести в десятичную. Для этого нужно числитель разделить на знаменатель. Пример: простая дробь (правильная) 1/2. Делим числитель 1 на знаменатель 2, получаем 0,5. Возьмем пример 45/12, сразу видно, что это дробь неправильная. Здесь знаменатель меньше числителя. Превращаем неправильную дробь в десятичную: 45: 12 = 3,75.

Перевод смешанных чисел в десятичную дробь

Пример: 25/8. Сначала мы превращаем смешанное число в неправильную дробь: 25/8 = 3х8+1/8 =3 и 1/8; затем делим числитель равный 1 на знаменатель равный 8, столбиком или на калькуляторе и получим десятичную дробь равную 0,125. В статье приведены самые легкие примеры перевода в десятичные дроби. Поняв методику перевода на простых примерах, вы легко сможете решать самые сложные из них.

Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?

Пример первый

У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.

Пример второй

Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.

Пример третий

И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.

Вывод

1. Разбиваем дробь на целую и дробную части.
2. Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.
3. Записываем дробь в обыкновенном виде.
4. Сокращаем числитель и знаменатель дроби.
5. Записываем полученную дробь.
6. Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.

На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.

Представить число в виде десятичной дроби. Перевод обыкновенной дроби в десятичную дробь и обратно, правила, примеры

Десятичной дробью называется дробь, у которой знаменатель представляет собой натуральную степень числа 10. Такой, например, является дробь Эту дробь можно записать в следующей форме: выписать в строку цифры числителя и отделить запятой справа столько из них, сколько нулей содержится в знаменателе, а именно:

В такой записи цифры, стоящие слева от запятой, образуют целую часть, а цифры, стоящие справа от запятой, — дробную часть данной десятичной дроби.

Пусть p/q — какое-либо положительное рациональное число. Из арифметики хорошо известен процесс деления, позволяющий представлять число в виде десятичной дроби. Сущность процесса деления состоит в том, что сначала находят, какое наибольшее целое число раз q содержится в p; если p — кратное q, то на этом процесс деления и заканчивается. В противном случае, появляется остаток. Далее находят, сколько в этом остатке содержится десятых долей q, и на этом шаге процесс может закончиться, либо появится новый остаток. В последнем случае находят, сколько в нем содержится сотых долей q, и т. д.

Если знаменатель q не имеет никаких других простых делителей, кроме 2 или 5, то через конечное число шагов остаток окажется равным нулю, процесс деления закончится и данная обыкновенная дробь обратится в конечную десятичную дробь. В самом деле, в указанном случае всегда можно подобрать такое целое число, что после умножения на него числителя и знаменателя данной дроби получится равная ей дробь, у которой знаменатель будет представлять натуральную степень десяти. Такой, например, является дробь

которую можно представить так:

Однако, не производя этих преобразований, разделив числитель на знаменатель, читатель получит тот же результат:

Если знаменатель несократимой дроби имеет по меньшей мере один простой делитель, отличный от 2 или 5, то процесс деления на q не закончится никогда (никакой из очередных остатков в нуль не обратится).

Выполнив деление, найдем

Для записи результата, получаемого в этом примере, периодически повторяющиеся цифры 0 и 6 заключают в круглые скобки и пишут:

В этом примере и в других подобных случаях действие деления не приводит к окончательному результату в виде десятичной дроби. Можно, обобщая понятие десятичной дроби, все же говорить, что частное 965/132 представлено бесконечной периодической дробью Повторяющиеся цифры 06 называют периодом этой дроби, а их число, равное в нашем примере — длиной периода.

Чтобы уяснить причину явления периодичности дроби, разберем, например, процесс деления на 7. Если деление нацело не выполняется, то появляется остаток, который может иметь только одно из следующих значений: 1, 2, 3, 4, 5, 6. И на каждом из следующих шагов остаток будет иметь снова одно из этих шести значений. Поэтому не позднее чем на седьмом шаге мы неизбежно встретимся с одним из значений остатка, которые раньше уже появлялись, Начиная с этого места, процесс деления приобретет периодический характер. Периодически будут повторяться и значения остатков, и цифры частного. Такое рассуждение применимо и в случае любого другого делителя.

Таким образом, всякая обыкновенная дробь представляется конечной или бесконечной периодической десятичной дробью. Замечательно, что и, обратно, всякая периодическая десятичная дробь представима в виде обыкновенной дроби. Покажем, как выполняется это действие. При этом используется формула суммы бесконечно убывающей геометрической прогрессии (п. 92).

можно понимать так:

здесь члены правой части, начиная со второго, образуют бесконечную геометрическую прогрессию со знаменателем и первым членом

Пользуясь формулой (92. 2):

Ясно, что этот же процесс позволит любую заданную бесконечную периодическую дробь представить в виде обыкновенной дроби (и, как можно показать, именно той, из которой в процессе деления в свою очередь получается данная бесконечная периодическая дробь). Впрочем, здесь имеется одно исключение. Рассмотрим дробь

и применим к ней процесс преобразования в обыкновенную дробь:

Мы пришли к числу 1/2, которое представляется конечной десятичной дробью

Сходный результат получится всякий раз, когда период данной бесконечной дроби имеет вид (9). Поэтому мы отождествляем такие пары чисел, как, например,

Иногда полезно еще допускать записи вида

представляя формально конечные десятичные дроби как бесконечные с периодом (0).

Все сказанное об обращении обыкновенной дроби в десятичную периодическую дробь и обратно относилось к положительным рациональным числам. В случае отрицательного числа можно поступить двояким образом.

1) Взять положительное число, противоположное данному отрицательному, обратить его в десятичную дробь, а затем поставить перед ней знак минус. Например, для — 5/3 получим

2) Данное отрицательное рациональное число представить в виде суммы его целой части (отрицательной) и его дробной части (неотрицательной), а затем обратить в десятичную дробь только эту дробную часть числа. Например:

Для записи чисел, представленных в виде суммы своей отрицательной целой части и конечной или бесконечной десятичной дроби, принято такое обозначение (искусственная форма записи отрицательного числа):

Здесь знак минус ставится не перед всей дробью, а над ее целой частью, чтобы подчеркнуть, что только целая часть отрицательна, а следующая за запятой дробная часть положительна.

Такая запись создает единообразие в записи положительных и отрицательных десятичных дробей и будет использована в будущем в теории десятичных логарифмов (п. 28). Предлагаем читателю для практики проверить переход от одной записи к другой в примерах:

Теперь уже можно сформулировать окончательный вывод: всякое рациональное число может быть представлено бесконечной десятичной периодической дробью, и, обратно, всякая такая дробь задает рациональное число.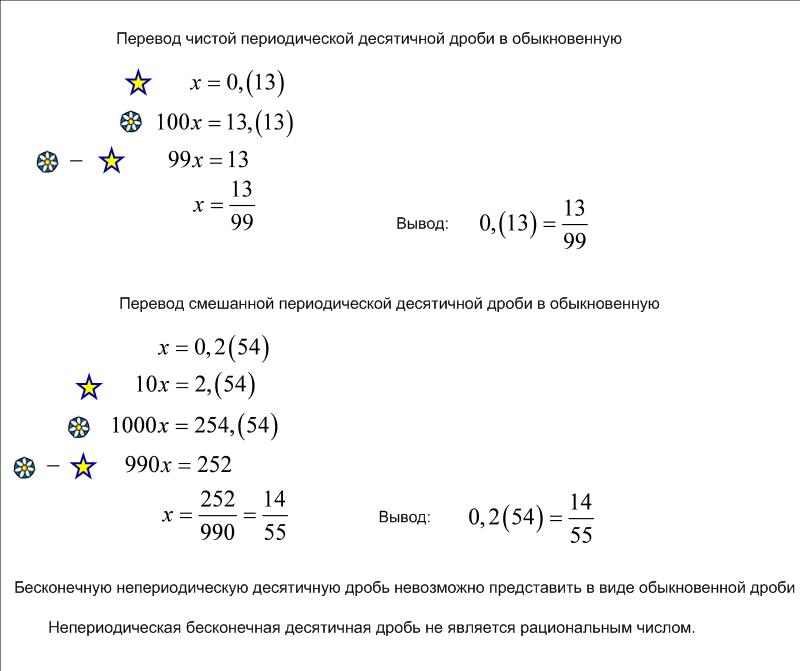 Конечная десятичная дробь допускает акже две формы записи в виде бесконечной десятичной дроби: с периодом (0) и с периодом (9).

Инструкция

Если в виде дроби надо представить целое число , то используйте в качестве знаменателя единицу, а исходное значение ставьте в числитель. Такая форма записи называться неправильной обыкновенной дробью, так как модуль ее числителя больше модуля знаменателя. Например, число 74 можно записать, как 74/1, а число -12 — как -12/1. При необходимости вы можете числитель и знаменатель в одинаковое количество раз — значение дроби в этом случае по-прежнему будет соответствовать исходному числу. Например, 74=74/1=222/3 или -12=-12/1=-84/7.

Если исходное число представлено в формате десятичной дроби , то его целую часть оставьте без изменений, а разделительную запятую замените пробелом. Дробную часть поставьте в числитель, а в качестве знаменателя используйте десятку, возведенную в степень с показателем, равным количеству знаков в дробной исходного числа. Полученную в результате дробную часть можно сократить, разделив числитель и знаменатель на одинаковое число . Например, десятичной дроби 7,625 будет соответствовать обыкновенная дробь 7 625/1000, которая после сокращения примет значение 7 5/8. Такая форма записи обыкновенной дроби смешанной. При необходимости ее можно привести к неправильному обыкновенному виду, умножив целую часть на знаменатель и прибавив результат к числителю: 7,625 = 7 625/1000 = 7 5/8 = 61/8.

Если исходная десятичная дробь является и периодической, то используйте, например, систему уравнений для вычисления ее эквивалента в формате дроби обыкновенной. Скажем, если исходная дробь равна 3,5(3), то можно тождество: 100*x-10*x=100*3,5(3)-10*3,5(3). Из него можно вывести равенство 90*x=318, а , что искомая дробь будет равна 318/90, что после сокращения даст обыкновенную дробь 3 24/45.

Источники:

• Можно Ли Число 450 000 Представить Как Произведение 2 Чисел?

В быту чаще всего встречаются не натуральные числа: 1, 2, 3, 4 и т. д. (5 кг. картофеля), а дробные, нецелые числа (5,4 кг лука). Большинство из них представлены в виде десятичных дробей. Но десятичную дробь представить в виде дроби достаточно просто.

Инструкция

Например, дано число «0,12». Если не эту дробь и представить ее так, как есть, то выглядеть она будет так: 12/100 («двенадцать «). Чтобы избавиться от сотни в , нужно и числитель, и знаменатель поделить на число, которое делит их числа. Это число 4. Тогда, поделив числитель и знаменатель, получается число: 3/25.

Если рассматривать более бытовую , то часто на ценнике у видно, что вес его составляет, к примеру, 0,478 кг или пр. Такое число тоже легко представить в виде дроби :
478/1000 = 239/500. Дробь эта достаточно некрасивая, и если бы была возможность, то эту десятичную дробь можно было бы сокращать и далее. И все тем же методом: подбора числа, которое делит как числитель, так и знаменатель. Это число наибольшим общим множителем. «Наибольшим» множитель потому, что гораздо удобнее и числитель, и знаменатель сразу поделить на 4 (как в первом примере), чем делить дважды на 2.

Видео по теме

Десятичная дробь — разновидность дроби , у которой в знаменателе есть «круглое» число: 10, 100, 1000 и т.д., Например, дробь 5/10 имеет десятичную запись 0,5. Исходя из этого принципа, дробь можно представить в виде десятичной дроби .

Инструкция

Мы живем в цифровом мире. Если раньше главные ценности представляли земля, деньги или средства производства, теперь все решают технологии и информация. Каждый человек, желающий добиться успеха, просто обязан понимать любые числа, в каком бы виде они не были представлены. Кроме обычной десятичной формы записи различают множество других удобных способов представления чисел (в условиях конкретных задач). Рассмотрим наиболее распространенные из них.

Вам понадобится

• Калькулятор

Инструкция

Для представления десятичного числа в виде обыкновенной дроби нужно сначала посмотреть, каким оно является — или вещественным. Целое число не имеет запятой вовсе, или после запятой стоит ноль (или много нулей, что одно и тоже). Если же после запятой есть некоторые числа, то данное число относится к вещественным. Целое число очень легко представить в виде дроби: в числитель идет само число , а в знаменатель — . С десятичной почти так же, только будем умножать обе часть дроби на десять до тех пор, пока не избавимся от запятой в числителе.

В этой статье мы разберем, как осуществляется перевод обыкновенных дробей в десятичные дроби , а также рассмотрим обратный процесс – перевод десятичных дробей в обыкновенные дроби. Здесь мы озвучим правила обращения дробей и приведем подробные решения характерных примеров.

Навигация по странице.

Перевод обыкновенных дробей в десятичные дроби

Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби .

Сначала мы рассмотрим, как обыкновенные дроби со знаменателями 10, 100, 1 000, … представить в виде десятичных дробей . Это объясняется тем, что десятичные дроби по сути являются компактной формой записи обыкновенных дробей со знаменателями 10, 100, … .

После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Теперь обо всем по порядку.

Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби

Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.

«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь после дописывания нулей будет иметь вид .

После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.

Дадим правило перевода правильной обыкновенной дроби со знаменателем 10, или 100, или 1 000, … в десятичную дробь . Оно состоит из трех шагов:

• записываем 0 ;
• после него ставим десятичную запятую;
• записываем число из числителя (вместе с дописанными нулями, если мы их дописывали).

Рассмотрим применение этого правила при решении примеров.

Пример.

Переведите правильную обыкновенную дробь 37/100 в десятичную.

Решение.

В знаменателе находится число 100 , в записи которого два нуля. В числителе находится число 37 , в его записи две цифры, следовательно, эта дробь не нуждается в подготовке к переводу в десятичную дробь.

Теперь записываем 0 , ставим десятичную запятую, и записываем число 37 из числителя, при этом получаем десятичную дробь 0,37 .

Ответ:

0,37 .

Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.

Пример.

Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.

Решение.

Количество цифр в числителе равно 3 , а количество нулей в знаменателе равно 7 , поэтому данная обыкновенная дробь нуждается в подготовке к переводу в десятичную. Нам нужно дописать 7-3=4 нуля слева в числителе, чтобы общее количество цифр там стало равно количеству нулей в знаменателе. Получаем .

Осталось составить нужную десятичную дробь. Для этого, во-первых, записываем 0 , во-вторых, ставим запятую, в-третьих, записываем число из числителя вместе с нулями 0000107 , в итоге имеем десятичную дробь 0,0000107 .

Ответ:

0,0000107 .

Неправильные обыкновенные дроби не нуждаются в подготовке при переводе в десятичные дроби. Следует придерживаться следующего правила перевода неправильных обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби :

• записываем число из числителя;
• отделяем десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.

Разберем применение этого правила при решении примера.

Пример.

Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.

Решение.

Во-первых, записываем число из числителя 56888038009, во-вторых, отделяем десятичной запятой 5 цифр справа, так как в знаменателе исходной дроби 5 нулей. В итоге имеем десятичную дробь 568 880,38009 .

Ответ:

568 880,38009 .

Для обращения в десятичную дробь смешанного числа , знаменателем дробной части которого является число 10 , или 100 , или 1 000, … , можно выполнить перевод смешанного числа в неправильную обыкновенную дробь, после чего полученную дробь обратить в десятичную дробь. Но можно пользоваться и следующим правилом перевода смешанных чисел со знаменателем дробной части 10, или 100, или 1 000, … в десятичные дроби :

• при необходимости выполняем «предварительную подготовку» дробной части исходного смешанного числа, дописав необходимое количество нулей слева в числителе;
• записываем целую часть исходного смешанного числа;
• ставим десятичную запятую;
• записываем число из числителя вместе с дописанными нулями.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.

Пример.

Переведите смешанное число в десятичную дробь.

Решение.

В знаменателе дробной части 4 нуля, в числителе же находится число 17 , состоящее из 2 цифр, поэтому, нам нужно дописать два нуля слева в числителе, чтобы там число знаков стало равно числу нулей в знаменателе. Выполнив это, в числителе окажется 0017 .

Теперь записываем целую часть исходного числа, то есть, число 23 , ставим десятичную запятую, после которой записываем число из числителя вместе с дописанными нулями, то есть, 0017 , при этом получаем искомую десятичную дробь 23,0017 .

Запишем все решение кратко: .

Несомненно, можно было сначала представить смешанное число в виде неправильной дроби, после чего перевести ее в десятичную дробь. При таком подходе решение выглядит так: .

Ответ:

23,0017 .

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями 10, 100, … , но обыкновенные дроби с другими знаменателями. Сейчас мы разберемся, как это делается.

В некоторых случаях исходная обыкновенная дробь легко приводится к одному из знаменателей 10 , или 100 , или 1 000, … (смотрите приведение обыкновенной дроби к новому знаменателю), после чего не составляет труда полученную дробь представить в виде десятичной дроби. Например, очевидно, что дробь 2/5 можно привести к дроби со знаменателем 10 , для этого нужно числитель и знаменатель умножить на 2 , что даст дробь 4/10 , которая по правилам, разобранным в предыдущем пункте, легко переводится в десятичную дробь 0,4 .

В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.

Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел , а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.

Пример.

Переведите обыкновенную дробь 621/4 в десятичную дробь.

Решение.

Число в числителе 621 представим в виде десятичной дроби, добавив десятичную запятую и несколько нулей после нее. Для начала допишем 2 цифры 0 , позже, при необходимости, мы всегда можем добавить еще нулей. Итак, имеем 621,00 .

Теперь выполним деление столбиком числа 621,000 на 4 . Первые три шага ничем не отличаются от деления столбиком натуральных чисел, после них приходим к следующей картине:

Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:

На этом деление закончено, а в результате мы получили десятичную дробь 155,25 , которая соответствует исходной обыкновенной дроби.

Ответ:

155,25 .

Для закрепления материала рассмотрим решение еще одного примера.

Пример.

Переведите обыкновенную дробь 21/800 в десятичную дробь.

Решение.

Для перевода данной обыкновенной дроби в десятичную, выполним деление столбиком десятичной дроби 21,000… на 800 . Нам после первого же шага придется поставить десятичную запятую в частном, после чего продолжить деление:

Наконец-то мы получили остаток 0 , на этом перевод обыкновенной дроби 21/400 в десятичную дробь закончен, и мы пришли к десятичной дроби 0,02625 .

Ответ:

0,02625 .

Может случиться, что при делении числителя на знаменатель обыкновенной дроби мы так и не получим в остатке 0 . В этих случаях деление можно продолжать сколь угодно долго. Однако, начиная с некоторого шага, остатки начитают периодически повторяться, при этом повторяются и цифры в частном. Это означает, что исходная обыкновенная дробь переводится в бесконечную периодическую десятичную дробь . Покажем это на примере.

Пример.

Запишите обыкновенную дробь 19/44 в виде десятичной дроби.

Решение.

Для перевода обыкновенной дроби в десятичную выполним деление столбиком:

Уже сейчас видно, что при делении начали повторяться остатки 8 и 36 , при этом в частном повторяются цифры 1 и 8 . Таким образом, исходная обыкновенная дробь 19/44 переводится в периодическую десятичную дробь 0,43181818…=0,43(18) .

Ответ:

0,43(18) .

В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.

Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.

Понятно, что если обыкновенную дробь можно привести к одному из знаменателей 10, 100, 1 000, … , то полученную дробь легко перевести в конечную десятичную дробь по правилам, разобранным в предыдущем пункте. Но к знаменателям 10, 100, 1 000 и т.д. приводятся далеко не все обыкновенные дроби. К таким знаменателям можно привести лишь дроби, знаменатели которых являются хотя бы одного из чисел 10, 100, … А какие числа могут быть делителями 10, 100, … ? Ответить на этот вопрос нам позволят чисел 10, 100, … , а они таковы: 10=2·5 , 100=2·2·5·5 , 1 000=2·2·2·5·5·5, … . Отсюда следует, что делителями 10, 100, 1 000 и т.д. могут быть лишь числа, разложения которых на простые множители содержат лишь числа 2 и (или) 5 .

Теперь мы можем сделать общий вывод о переводе обыкновенных дробей в десятичные дроби:

• если в разложении знаменателя на простые множители присутствуют лишь числа 2 и (или) 5 , то эту дробь можно перевести в конечную десятичную дробь;
• если кроме двое и пятерок в разложении знаменателя присутствуют другие простые числа, то эта дробь переводится к бесконечную десятичную периодическую дробь.

Пример.

Не выполняя перевод обыкновенных дробей в десятичные, скажите, какие из дробей 47/20 , 7/12 , 21/56 , 31/17 можно перевести в конечную десятичную дробь, а какие — только в периодическую.

Решение.

Разложение на простые множители знаменателя дроби 47/20 имеет вид 20=2·2·5 . В этом разложении присутствуют лишь двойки и пятерки, поэтому эта дробь может быть приведена к одному из знаменателей 10, 100, 1 000, … (в этом примере к знаменателю 100 ), следовательно, может быть переведена в конечную десятичную дробь.

Разложение на простые множители знаменателя дроби 7/12 имеет вид 12=2·2·3 . Так как оно содержит простой множитель 3 , отличный от 2 и 5 , то эта дробь не может быть представлена в виде конечной десятичной дроби, но может быть переведена в периодическую десятичную дробь.

Дробь 21/56 – сократимая, после сокращения она принимает вид 3/8 . Разложение знаменателя на простые множители содержит три множителя, равных 2 , следовательно, обыкновенная дробь 3/8 , а значит и равная ей дробь 21/56 , может быть переведена в конечную десятичную дробь.

Наконец, разложение знаменателя дроби 31/17 представляет собой само 17 , следовательно, эту дробь нельзя обратить в конечную десятичную дробь, но можно обратить в бесконечную периодическую.

Ответ:

47/20 и 21/56 можно перевести в конечную десятичную дробь, а 7/12 и 31/17 — только в периодическую.

Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби

Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?

Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.

Из теоремы о делимости с остатком ясно, что остаток всегда меньше делителя, то есть, если мы выполняем деление некоторого целого числа на целое число q , то остатком может быть лишь одно из чисел 0, 1, 2, …, q−1 . Отсюда следует, что после завершения деления столбиком целой части числителя обыкновенной дроби на знаменатель q , не более чем через q шагов возникнет одна из двух следующих ситуаций:

• либо мы получим остаток 0 , на этом деление закончится, и мы получим конечную десятичную дробь;
• либо мы получим остаток, который уже появлялся ранее, после этого остатки начнут повторяться как в предыдущем примере (так как при делении равных чисел на q получаются равные остатки, что следует из уже упомянутой теоремы о делимости), так будет получена бесконечная периодическая десятичная дробь.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.

Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.

Перевод десятичных дробей в обыкновенные дроби

Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.

Перевод конечных десятичных дробей в обыкновенные дроби

Получить обыкновенную дробь, которая записана в виде конечной десятичной дроби, достаточно просто. Правило перевода конечной десятичной дроби в обыкновенную дробь состоит из трех шагов:

• во-первых, записать данную десятичную дробь в числитель, предварительно отбросив десятичную запятую и все нули слева, если они есть;
• во-вторых, в знаменатель записать единицу и к ней дописать столько нулей, сколько цифр находится после запятой в исходной десятичной дроби;
• в-третьих, при необходимости выполнить сокращение полученной дроби.

Рассмотрим решения примеров.

Пример.

Обратите десятичную дробь 3,025 в обыкновенную дробь.

Решение.

Если в исходной десятичной дроби убрать десятичную запятую, то мы получим число 3 025 . В нем нет нулей слева, которые бы мы отбросили. Итак, в числитель искомой дроби записываем 3 025 .

В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.

Так мы получили обыкновенную дробь 3 025/1 000 . Эту дробь можно сократить на 25 , получаем .

Ответ:

.

Пример.

Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь.

Решение.

Без десятичной запятой исходная десятичная дробь имеет вид 00017 , отбросив нули слева получаем число 17 , которое и является числителем искомой обыкновенной дроби.

В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4 цифры.

В итоге имеем обыкновенную дробь 17/10 000 . Эта дробь несократима, и перевод десятичной дроби в обыкновенную закончен.

Ответ:

.

Когда целая часть исходной конечной десятичной дроби отлична от нуля, то ее можно сразу перевести в смешанное число, минуя обыкновенную дробь. Дадим правило перевода конечной десятичной дроби в смешанное число :

• число до десятичной запятой надо записать как целую часть искомого смешанного числа;
• в числитель дробной части нужно записать число, полученное из дробной части исходной десятичной дроби после отбрасывания в ней всех нулей слева;
• в знаменателе дробной части нужно записать цифру 1 , к которой справа дописать столько нулей, сколько цифр находится в записи исходной десятичной дроби после запятой;
• при необходимости выполнить сокращение дробной части полученного смешанного числа.

Рассмотрим пример перевода десятичной дроби в смешанное число.

Пример.

Представьте десятичную дробь 152,06005 в виде смешанного числа

Чтобы рациональное число m/n записать в виде десятичной дроби, нужно числитель разделить на знаменатель. При этом частное записывается конечной или бесконечной десятичной дробью.

Записать данное число в виде десятичной дроби.

Решение. Разделим в столбик числитель каждой дроби на ее знаменатель: а) делим 6 на 25; б) делим 2 на 3; в) делим 1 на 2, а затем получившуюся дробь припишем к единице — целой части данного смешанного числа.

Несократимые обыкновенные дроби, знаменатели которых не содержат других простых делителей, кроме 2 и 5 , записываются конечной десятичной дробью.

В примере 1 в случае а) знаменатель 25=5·5; в случае в) знаменатель равен 2, поэтому, мы получили конечные десятичные дроби 0,24 и 1,5 . В случае б) знаменатель равен 3, поэтому результат нельзя записать в виде конечной десятичной дроби.

А можно ли без деления в столбик обратить в десятичную дробь такую обыкновенную дробь, знаменатель которой не содержит других делителей, кроме 2 и 5? Разберемся! Какую дробь называют десятичной и записывают без дробной черты? Ответ: дробь со знаменателем 10; 100; 1000 и т. д. А каждое из этих чисел — это произведение равного количества «двоек» и «пятерок». На самом деле: 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 и т.д.

Следовательно, знаменатель несократимой обыкновенной дроби нужно будет представить в виде произведения «двоек» и «пятерок», а затем домножить на 2 и (или) на 5 так, чтобы «двоек» и «пятерок» стало поровну. Тогда знаменатель дроби будет равен 10 или 100 или 1000 и т.д. Чтобы значение дроби не изменилось — числитель дроби умножим на то же число, на которое умножили знаменатель.

Представить в виде десятичной дроби следующие обыкновенные дроби:

Решение. Каждая из данных дробей является несократимой. Разложим знаменатель каждой дроби на простые множители.

20=2·2·5. Вывод: не хватает одной «пятерки».

8=2·2·2. Вывод: не хватает трех «пятерок».

25=5·5. Вывод: не хватает двух «двоек».

Замечание. На практике чаще не используют разложение знаменателя на множители, а просто задаются вопросом: на сколько нужно умножить знаменатель, чтобы в результате получилась единица с нулями (10 или 100 или 1000 и т. д.). А затем на это же число умножают и числитель.

Так, в случае а) (пример 2 ) из числа 20 можно получить 100 умножением на 5, поэтому, на 5 нужно умножить числитель и знаменатель.

В случае б) (пример 2 ) из числа 8 число 100 не получится, но получится число 1000 умножением на 125. На 125 умножается и числитель (3) и знаменатель (8) дроби.

В случае в) (пример 2 ) из 25 получится 100, если умножить на 4. Значит, и числитель 8 нужно умножить на 4.

Бесконечная десятичная дробь, у которой одна или несколько цифр неизменно повторяются в одной и той же последовательности, называется периодической десятичной дробью. Совокупность повторяющихся цифр называется периодом этой дроби. Для краткости период дроби записывают один раз, заключая его в круглые скобки.

В случае б) (пример 1 ) повторяющаяся цифра одна и равна 6. Поэтому, наш результат 0,66… запишется так: 0,(6) . Читают: нуль целых, шесть в периоде.

Если между запятой и первым периодом есть одна или несколько не повторяющихся цифр, то такая периодическая дробь называется смешанной периодической дробью.

Несократимая обыкновенная дробь, знаменатель которой вместе с другими множителями содержит множитель 2 или 5 , обращается в смешанную периодическую дробь.

При слове «дроби» у многих бегут мурашки. Потому что вспоминается школа и задания, которые решались на математике. Это являлось обязанностью, которую необходимо было выполнить. А что если относиться к заданиям, содержащим правильные и неправильные дроби, как к головоломке? Ведь многие взрослые решают цифровые и японские кроссворды. Разобрались в правилах, и все. Так же и здесь. Стоит только вникнуть в теорию — и все встанет на свои места. А примеры превратятся в способ потренировать мозг.

Какие виды дробей существуют?

Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.

В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.

Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.

Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.

Второй вид записи — десятичная дробь. О ней отдельный разговор.

Чем отличаются неправильные дроби от смешанных чисел?

По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.

Все зависит от конкретной ситуации. Иногда в заданиях удобнее использовать неправильную дробь. А порой необходимо перевести ее в смешанное число и тогда пример решится очень легко. Поэтому, что использовать: неправильные дроби, смешанные числа, — зависит от наблюдательности решающего задачу.

Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.

Как представить смешанное число в виде неправильной дроби?

Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.

Для этой цели потребуется выполнить действия по такому алгоритму:

• умножить знаменатель на целую часть;
• прибавить к результату значение числителя;
• записать ответ над чертой;
• знаменатель оставить тем же.

Вот примеры того, как записать неправильные дроби из смешанных чисел:

• 17 ¼ = (17 х 4 + 1) : 4 = 69/4;
• 39 ½ = (39 х 2 + 1) : 2 = 79/2.

Как записать неправильную дробь в виде смешанного числа?

Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:

• разделить числитель на знаменатель до получения остатка;
• записать частное на месте целой части смешанного;
• остаток следует разместить над чертой;
• делитель будет знаменателем.

Примеры такого преобразования:

76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.

108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.

Как целое число превратить в неправильную дробь?

Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:

• умножить целое число на нужный знаменатель;
• записать это значение над чертой;
• разместить под ней знаменатель.

Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.

Пример : 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.

Два подхода к решению заданий с разными числами

В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.

В первом подходе смешанное число будет представлено в виде неправильной дроби.

После выполнения действий, описанных выше, получится такое значение: 13/5.

Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.

При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.

При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.

Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5: 14/11 = 13/5 х 11/14 = 143/70.

Во втором подходе неправильная дробь обращается в смешанное число.

После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.

Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.

При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.

Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.

Чему равно число 8,5 в виде дроби? (Преобразовать 8,5 в дробь)

Хотите преобразовать 8,5 в дробь? Если это так, вы находитесь в правильном месте! В этом пошаговом руководстве мы точно покажем вам, что представляет собой дробная форма числа 8,5, и покажем, как именно его вычислить, чтобы вы могли преобразовать любое десятичное число в дробь. Пойдем!

Хотите быстро узнать или показать учащимся, как преобразовать число 8,5 в дробь? Включи это очень быстрое и веселое видео прямо сейчас!

Существует множество причин, по которым вам может понадобиться преобразовать десятичную дробь в дробь. Самая распространенная причина в том, что ваш учитель сказал вам! Но помимо этого, десятичная форма дроби позволяет очень легко сравнивать две дроби, не задумываясь об этом.

Перед тем, как мы начнем, краткий обзор. Число над дробной чертой является числителем, а число под дробной чертой — знаменателем. Если вы много работали с дробями, вы, вероятно, уже знаете это, но никогда не помешает перепроверить!

Итак, первое, что нужно сделать, это показать вам, что любое число может быть дробью, если вы используете 1 в качестве знаменателя. Взгляните:

8,5 / 1

Что мы действительно хотим сделать, так это полностью избавиться от десятичных знаков, чтобы числитель в нашей дроби был целым числом. Для этого нам нужно посчитать числа после запятой, в данном случае это 5.

Чтобы получить целую дробь, нам нужно умножить и числитель, и знаменатель на 10, если после запятой стоит одно число, на 100, если два числа, на 1000, если три числа, и на 10000, если. .. ну, вы поняли идею!

В нашем случае 5 — это 1 цифра, поэтому нам нужно умножить числитель и знаменатель на 10.

Теперь нам просто нужно выполнить это умножение, чтобы получить целую дробь:

8,5 x 10 / 1 х 10 знак равно 85 / 10

Следующим шагом будет упрощение этой дроби, а для этого нам нужно найти наибольший общий делитель (НОД). Иногда это также называют:

• Наибольший общий делитель (НОД)
• Наивысший общий множитель (HCF)
• Наибольший общий знаменатель (НОД)

GCF может быть немного сложно вычислить вручную, но вы можете использовать наш удобный калькулятор GCF, чтобы вычислить его.

В случае 85 и 10 наибольший общий делитель равен 5. Это означает, что для упрощения дроби мы можем разделить числитель и знаменатель на 5 и мы получим:

85/5 / 10/5 знак равно 17 / 2

Вот и все! Всего за несколько коротких шагов мы выяснили, что такое 8,5 как дробь. Полный ответ для вашего удовольствия ниже:

8 1/2

Примечание: поскольку 85 больше 10, мы еще больше упростили эту дробь до смешанной дроби.

Надеюсь, это руководство помогло вам понять, как преобразовать десятичное число в дробь. Теперь вы можете пойти дальше и конвертировать десятичные дроби в дроби столько, сколько пожелает ваше маленькое сердце!

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Что такое 8,5 как дробь?

• «Что такое 8,5 как дробь?». VisualFractions.com . По состоянию на 5 октября 2022 г. http://visualfractions.com/calculator/decimal-as-fraction/what-is-8-5-as-a-fraction/.

• «Что такое 8,5 как дробь?». VisualFractions.com , http://visualfractions. com/calculator/decimal-as-fraction/what-is-8-5-as-a-fraction/. По состоянию на 5 октября 2022 г.

• Что такое 8,5 как дробь?. VisualFractions.com. Получено с http://visualfractions.com/calculator/decimal-as-fraction/what-is-8-5-as-a-fraction/.

Предустановленный список десятичных дробей

Ниже приведены ссылки на некоторые предустановленные десятичные вычисления, которые обычно ищут:

Что такое 0,25 как дробь?

Что такое 0,50 как дробь?

Что такое 0,75 как дробь?

Что такое 0,100 в виде дроби?

Что такое 0,125 как дробь?

Что такое 0,150 в виде дроби?

Что такое 0,175 в виде дроби?

Что такое 0,200 в виде дроби?

Что такое 0,225 в виде дроби?

Что такое 0,250 как дробь?

Что такое 0,275 в виде дроби?

Что такое 0,300 в виде дроби?

Что такое 0,325 в виде дроби?

Что такое 0,350 как дробь?

Что такое 0,375 как дробь?

Что такое 0,400 в виде дроби?

Что такое 0,425 как дробь?

Что такое 0,450 как дробь?

Что такое 0,475 в виде дроби?

Что такое 0,500 в виде дроби?

Что такое 0,525 как дробь?

Что такое 0,550 как дробь?

Что такое 0,575 в виде дроби?

Что такое 0,600 в виде дроби?

Что такое 0,625 в виде дроби?

Что такое 0,650 в виде дроби?

Что такое 0,675 в виде дроби?

Что такое 0,700 в виде дроби?

Что такое 0,725 как дробь?

Что такое 0,750 как дробь?

Что такое 0,775 в виде дроби?

Что такое 0,800 как дробь?

Что такое 0,825 как дробь?

Что такое 0,850 как дробь?

Что такое 0,875 как дробь?

Что такое 0,900 как дробь?

Что такое 0,925 как дробь?

Что такое 0,950 как дробь?

Что такое 0,975 как дробь?

Что такое 0,1000 в виде дроби?

Чему равно число 1,25 в виде дроби?

Что такое 1,50 как дробь?

Чему равно 1,75 в виде дроби?

Что такое 1,100 как дробь?

Чему равно число 1,125 в виде дроби?

Что такое 1,150 как дробь?

Чему равно 1,175 в виде дроби?

Что такое 1. 200 как дробь?

Что такое 1,225 как дробь?

Что такое 1,250 как дробь?

Что такое 1,275 как дробь?

Что такое 1.300 как дробь?

Чему равно число 1,325 в виде дроби?

Что такое 1,350 как дробь?

Что такое 1,375 как дробь?

Что такое 1.400 как дробь?

Чему равно число 1,425 в виде дроби?

Что такое 1,450 как дробь?

Что такое 1,475 как дробь?

Что такое 1.500 как дробь?

Что такое 1,525 как дробь?

Что такое 1,550 как дробь?

Чему равно число 1,575 в виде дроби?

Что такое 1.600 как дробь?

Чему равно число 1,625 в виде дроби?

Что такое 1,650 как дробь?

Что такое 1,675 как дробь?

Что такое 1.700 как дробь?

Что такое 1,725 ​​как дробь?

Что такое 1,750 как дробь?

Что такое 1,775 как дробь?

Что такое 1.800 как дробь?

Что такое 1,825 как дробь?

Что такое 1,850 как дробь?

Что такое 1,875 как дробь?

Что такое 1. 900 как дробь?

Чему равно число 1,925 в виде дроби?

Что такое 1,950 как дробь?

Что такое 1,975 как дробь?

Что такое 1,1000 как дробь?

Чему равно число 2,25 в виде дроби?

Что такое 2,50 как дробь?

Чему равно число 2,75 в виде дроби?

Что такое 2,100 как дробь?

Чему равно число 2,125 в виде дроби?

Что такое 2,150 как дробь?

Чему равно число 2,175 в виде дроби?

Что такое 2.200 как дробь?

Чему равно число 2,225 в виде дроби?

Что такое 2,250 как дробь?

Чему равно число 2,275 в виде дроби?

Что такое 2.300 как дробь?

Чему равно число 2,325 в виде дроби?

Что такое 2,350 как дробь?

Чему равно число 2,375 в виде дроби?

Что такое 2.400 как дробь?

Чему равно число 2,425 в виде дроби?

Что такое 2,450 как дробь?

Чему равно число 2,475 в виде дроби?

Что такое 2.500 как дробь?

Чему равно число 2,525 в виде дроби?

Что такое 2,550 как дробь?

Чему равно число 2,575 в виде дроби?

Что такое 2. 600 как дробь?

Чему равно число 2,625 в виде дроби?

Что такое 2,650 как дробь?

Чему равно число 2,675 в виде дроби?

Что такое 2.700 как дробь?

Чему равно число 2,725 в виде дроби?

Что такое 2,750 как дробь?

Чему равно число 2,775 в виде дроби?

Что такое 2.800 как дробь?

Чему равно число 2,825 в виде дроби?

Что такое 2,850 как дробь?

Чему равно число 2,875 в виде дроби?

Что такое 2.900 как дробь?

Чему равно число 2,925 в виде дроби?

Что такое 2,950 как дробь?

Чему равно число 2,975 в виде дроби?

Что такое 2,1000 как дробь?

Чему равно число 3,25 в виде дроби?

Что такое 3,50 как дробь?

Чему равно число 3,75 в виде дроби?

Что такое 3,100 как дробь?

Чему равно число 3,125 в виде дроби?

Чему равно число 3,150 в виде дроби?

Чему равно число 3,175 в виде дроби?

Что такое 3.200 как дробь?

Чему равно число 3,225 в виде дроби?

Что такое 3,250 как дробь?

Чему равно число 3,275 в виде дроби?

Что такое 3. 300 как дробь?

Чему равно число 3,325 в виде дроби?

Что такое 3,350 как дробь?

Чему равно число 3,375 в виде дроби?

Что такое 3.400 как дробь?

Чему равно число 3,425 в виде дроби?

Чему равно число 3,450 в виде дроби?

Чему равно число 3,475 в виде дроби?

Что такое 3.500 как дробь?

Чему равно число 3,525 в виде дроби?

Чему равно число 3,550 в виде дроби?

Чему равно число 3,575 в виде дроби?

Что такое 3,600 в виде дроби?

Чему равно число 3,625 в виде дроби?

Чему равно число 3,650 в виде дроби?

Чему равно число 3,675 в виде дроби?

Что такое 3,700 в виде дроби?

Чему равно число 3,725 в виде дроби?

Чему равно 3,750 в виде дроби?

Чему равно число 3,775 в виде дроби?

Что такое 3.800 как дробь?

Чему равно число 3,825 в виде дроби?

Чему равно 3,850 в виде дроби?

Чему равно число 3,875 в виде дроби?

Что такое 3,900 как дробь?

Чему равно число 3,925 в виде дроби?

Что такое 3,950 как дробь?

Чему равно число 3,975 в виде дроби?

Что такое 3,1000 в виде дроби?

Чему равно число 4,25 в виде дроби?

Что такое 4,50 как дробь?

Чему равно число 4,75 в виде дроби?

Что такое 4,100 как дробь?

Чему равно число 4,125 в виде дроби?

Чему равно число 4,150 в виде дроби?

Чему равно число 4,175 в виде дроби?

Что такое 4. 200 как дробь?

Чему равно число 4,225 в виде дроби?

Что такое 4,250 как дробь?

Чему равно число 4,275 в виде дроби?

Что такое 4.300 как дробь?

Чему равно число 4,325 в виде дроби?

Что такое 4,350 как дробь?

Чему равно число 4,375 в виде дроби?

Что такое 4.400 как дробь?

Чему равно число 4,425 в виде дроби?

Что такое 4,450 как дробь?

Чему равно число 4,475 в виде дроби?

Что такое 4.500 как дробь?

Чему равно число 4,525 в виде дроби?

Чему равно число 4,550 в виде дроби?

Чему равно число 4,575 в виде дроби?

Что такое 4.600 как дробь?

Чему равно число 4,625 в виде дроби?

Что такое 4,650 как дробь?

Чему равно число 4,675 в виде дроби?

Что такое 4.700 как дробь?

Чему равно число 4,725 в виде дроби?

Чему равно число 4,750 в виде дроби?

Чему равно число 4,775 в виде дроби?

Что такое 4. 800 как дробь?

Чему равно число 4,825 в виде дроби?

Что такое 4,850 как дробь?

Чему равно число 4,875 в виде дроби?

Что такое 4,900 как дробь?

Чему равно число 4,925 в виде дроби?

Что такое 4,950 как дробь?

Чему равно число 4,975 в виде дроби?

Чему равно 4,1000 в виде дроби?

Что такое 5,25 как дробь?

Что такое 5,50 как дробь?

Что такое 5,75 как дробь?

Что такое 5,100 как дробь?

Что такое 5,125 как дробь?

Что такое 5,150 как дробь?

Чему равно число 5,175 в виде дроби?

Что такое 5.200 как дробь?

Что такое 5,225 как дробь?

Что такое 5,250 как дробь?

Что такое 5,275 как дробь?

Что такое 5.300 как дробь?

Что такое 5,325 как дробь?

Что такое 5,350 как дробь?

Что такое 5,375 как дробь?

Что такое 5.400 как дробь?

Что такое 5,425 как дробь?

Что такое 5,450 как дробь?

Чему равно число 5,475 в виде дроби?

Что такое 5. 500 как дробь?

Чему равно число 5,525 в виде дроби?

Что такое 5,550 как дробь?

Чему равно число 5,575 в виде дроби?

Что такое 5.600 как дробь?

Что такое 5,625 как дробь?

Что такое 5,650 как дробь?

Чему равно число 5,675 в виде дроби?

Что такое 5.700 как дробь?

Что такое 5,725 как дробь?

Что такое 5,750 как дробь?

Что такое 5,775 как дробь?

Что такое 5.800 как дробь?

Что такое 5,825 как дробь?

Что такое 5,850 как дробь?

Чему равно число 5,875 в виде дроби?

Что такое 5.900 как дробь?

Что такое 5,925 как дробь?

Что такое 5,950 как дробь?

Что такое 5,975 как дробь?

Что такое 5,1000 как дробь?

Что такое 6,25 как дробь?

Что такое 6,50 как дробь?

Что такое 6,75 как дробь?

Что такое 6,100 как дробь?

Чему равно число 6,125 в виде дроби?

Что такое 6,150 как дробь?

Чему равно 6,175 в виде дроби?

Что такое 6. 200 как дробь?

Чему равно число 6,225 в виде дроби?

Что такое 6,250 как дробь?

Чему равно 6,275 в виде дроби?

Что такое 6.300 как дробь?

Чему равно 6,325 в виде дроби?

Что такое 6,350 как дробь?

Чему равно 6,375 в виде дроби?

Что такое 6.400 как дробь?

Чему равно 6,425 в виде дроби?

Что такое 6,450 как дробь?

Чему равно число 6,475 в виде дроби?

Что такое 6.500 как дробь?

Чему равно число 6,525 в виде дроби?

Что такое 6,550 как дробь?

Чему равно число 6,575 в виде дроби?

Что такое 6.600 как дробь?

Чему равно 6,625 в виде дроби?

Что такое 6,650 как дробь?

Чему равно число 6,675 в виде дроби?

Что такое 6.700 как дробь?

Чему равно 6,725 в виде дроби?

Что такое 6,750 как дробь?

Чему равно 6,775 в виде дроби?

Что такое 6.800 как дробь?

Чему равно 6,825 в виде дроби?

Что такое 6,850 как дробь?

Чему равно 6,875 в виде дроби?

Что такое 6. 900 как дробь?

Чему равно число 6,925 в виде дроби?

Что такое 6,950 как дробь?

Чему равно 6,975 в виде дроби?

Чему равно 6,1000 в виде дроби?

Чему равно число 7,25 в виде дроби?

Что такое 7,50 как дробь?

Что такое 7,75 как дробь?

Что такое 7,100 как дробь?

Что такое 7,125 как дробь?

Что такое 7,150 как дробь?

Чему равно число 7,175 в виде дроби?

Что такое 7.200 как дробь?

Что такое 7,225 как дробь?

Что такое 7,250 как дробь?

Чему равно 7,275 в виде дроби?

Что такое 7.300 как дробь?

Чему равно число 7,325 в виде дроби?

Что такое 7,350 как дробь?

Что такое 7,375 как дробь?

Что такое 7.400 как дробь?

Что такое 7,425 как дробь?

Что такое 7,450 как дробь?

Чему равно число 7,475 в виде дроби?

Что такое 7.500 как дробь?

Чему равно 7,525 в виде дроби?

Что такое 7,550 как дробь?

Чему равно 7,575 в виде дроби?

Что такое 7. 600 как дробь?

Что такое 7,625 как дробь?

Что такое 7,650 как дробь?

Что такое 7,675 как дробь?

Что такое 7.700 как дробь?

Что такое 7,725 как дробь?

Что такое 7,750 как дробь?

Что такое 7,775 как дробь?

Что такое 7.800 как дробь?

Что такое 7,825 как дробь?

Что такое 7,850 как дробь?

Чему равно 7,875 в виде дроби?

Что такое 7.900 как дробь?

Чему равно число 7,925 в виде дроби?

Что такое 7,950 как дробь?

Чему равно 7,975 в виде дроби?

Что такое 7,1000 как дробь?

Что такое 8,25 как дробь?

Что такое 8,50 как дробь?

Что такое 8,75 как дробь?

Что такое 8,100 как дробь?

Чему равно число 8,125 в виде дроби?

Что такое 8,150 как дробь?

Чему равно число 8,175 в виде дроби?

Что такое 8.200 как дробь?

Чему равно число 8,225 в виде дроби?

Что такое 8,250 как дробь?

Чему равно число 8,275 в виде дроби?

Что такое 8. 300 как дробь?

Что такое 8,325 как дробь?

Что такое 8,350 как дробь?

Чему равно число 8,375 в виде дроби?

Что такое 8.400 как дробь?

Что такое 8,425 как дробь?

Что такое 8,450 как дробь?

Чему равно число 8,475 в виде дроби?

Что такое 8.500 как дробь?

Чему равно число 8,525 в виде дроби?

Что такое 8,550 как дробь?

Чему равно число 8,575 в виде дроби?

Что такое 8.600 как дробь?

Чему равно число 8,625 в виде дроби?

Что такое 8,650 как дробь?

Чему равно число 8,675 в виде дроби?

Что такое 8.700 как дробь?

Чему равно число 8,725 в виде дроби?

Что такое 8,750 как дробь?

Чему равно число 8,775 в виде дроби?

Что такое 8.800 как дробь?

Чему равно число 8,825 в виде дроби?

Что такое 8,850 как дробь?

Чему равно число 8,875 в виде дроби?

Что такое 8.900 как дробь?

Что такое 8,925 как дробь?

Что такое 8,950 как дробь?

Чему равно число 8,975 в виде дроби?

Что такое 8,1000 как дробь?

Что такое 9,25 как дробь?

Что такое 9,50 как дробь?

Что такое 9,75 как дробь?

Что такое 9. 100 как дробь?

Чему равно число 9,125 в виде дроби?

Что такое 9,150 как дробь?

Что такое 9,175 как дробь?

Что такое 9.200 как дробь?

Что такое 9,225 как дробь?

Что такое 9,250 как дробь?

Что такое 9,275 как дробь?

Что такое 9.300 как дробь?

Что такое 9,325 как дробь?

Что такое 9,350 как дробь?

Что такое 9,375 как дробь?

Что такое 9.400 как дробь?

Что такое 9,425 как дробь?

Что такое 9,450 как дробь?

Что такое 9,475 как дробь?

Что такое 9.500 как дробь?

Что такое 9,525 как дробь?

Что такое 9,550 как дробь?

Что такое 9,575 как дробь?

Что такое 9.600 как дробь?

Что такое 9,625 как дробь?

Что такое 9,650 как дробь?

Что такое 9,675 как дробь?

Что такое 9.700 как дробь?

Что такое 9,725 как дробь?

Что такое 9,750 как дробь?

Что такое 9,775 как дробь?

Что такое 9. 800 как дробь?

Что такое 9,825 как дробь?

Что такое 9,850 как дробь?

Что такое 9,875 как дробь?

Что такое 9.900 как дробь?

Что такое 9,925 как дробь?

Что такое 9,950 как дробь?

Что такое 9,975 как дробь?

Что такое 9,1000 как дробь?

Случайные вычисления десятичных дробей

Если вы действительно любите преобразование десятичных дробей в дроби и просто не можете насытиться, вот несколько случайных вычислений для вас:

Что такое 38,995 как дробь?

Чему равно число 44,519 в виде дроби?

Чему равно 68,447 в виде дроби?

Чему равно число 44,123 в виде дроби?

Чему равно 68,518 в виде дроби?

Чему равно 79,392 в виде дроби?

Чему равно 74,835 в виде дроби?

Чему равно 53,87 в виде дроби?

Чему равно 19,694 в виде дроби?

Чему равно 65,371 в виде дроби?

Чему равно число 29,58 в виде дроби?

Чему равно число 38,940 в виде дроби?

Чему равно число 89,12 в виде дроби?

Чему равно 57,501 в виде дроби?

Чему равно число 35,556 в виде дроби?

Чему равно число 20,520 в виде дроби?

Чему равно 55,71 в виде дроби?

Чему равно число 8,913 в виде дроби?

Что такое 99,392 как дробь?

Что такое 11,988 в виде дроби?

Чему равно число 51,114 в виде дроби?

Что такое 10,212 как дробь?

Чему равно 68,164 в виде дроби?

Чему равно число 36,114 в виде дроби?

Чему равно число 8,752 в виде дроби?

Чему равно число 81,275 в виде дроби?

Чему равно 72,832 в виде дроби?

Чему равно число 17,115 в виде дроби?

Что такое 11,327 как дробь?

Сколько будет 34. 800 в виде дроби?

Чему равно число 96,721 в виде дроби?

Что такое 97,259 как дробь?

Что такое 92,211 в виде дроби?

Чему равно число 17,332 в виде дроби?

Чему равно 47,358 в виде дроби?

Чему равно число 29,912 в виде дроби?

Чему равно число 4,607 в виде дроби?

Чему равно 78,358 в виде дроби?

Что такое 86,312 в виде дроби?

Чему равно 74,326 в виде дроби?

Чему равно число 97,973 в виде дроби?

Чему равно число 49,460 в виде дроби?

Чему равно число 56,860 в виде дроби?

Чему равно число 21,873 в виде дроби?

Чему равно 65,49 в виде дроби?

Что такое 9,211 как дробь?

Чему равно число 37,330 в виде дроби?

Чему равно 76,819 в виде дроби?

Чему равно 75,80 в виде дроби?

Чему равно число 41,506 в виде дроби?

Чему равно 51,942 в виде дроби?

Чему равно число 80,684 в виде дроби?

Чему равно 73,222 в виде дроби?

Что такое 5,858 как дробь?

Чему равно число 98,153 в виде дроби?

Чему равно число 28,813 в виде дроби?

Чему равно число 86,935 в виде дроби?

Чему равно число 87,47 в виде дроби?

Чему равно число 38,655 в виде дроби?

Что такое 16,951 как дробь?

Чему равно 61,473 в виде дроби?

Что такое 81,132 в виде дроби?

Чему равно число 3,714 в виде дроби?

Чему равно число 37,170 в виде дроби?

Что такое 18,759 как дробь?

Чему равно число 97,77 в виде дроби?

Чему равно число 98,452 в виде дроби?

Чему равно число 23,981 в виде дроби?

Чему равно число 97,672 в виде дроби?

Чему равно 63,867 в виде дроби?

Что такое 91,109 в виде дроби?

Чему равно 71,267 в виде дроби?

Чему равно 52,519 в виде дроби?

Чему равно число 84,987 в виде дроби?

Чему равно 67,98 в виде дроби?

Чему равно число 96,558 в виде дроби?

Что такое 87,900 в виде дроби?

Чему равно 62,381 в виде дроби?

Чему равно число 49,211 в виде дроби?

Чему равно 50,864 в виде дроби?

Чему равно число 8,619 в виде дроби?

Чему равно 72,993 в виде дроби?

Чему равно число 34,135 в виде дроби?

Чему равно число 44,304 в виде дроби?

Чему равно 25,822 в виде дроби?

Чему равно число 89,218 в виде дроби?

Чему равно 60,133 в виде дроби?

Чему равно число 24,749 в виде дроби?

Что такое 50,314 как дробь?

Чему равно число 17,214 в виде дроби?

Чему равно число 94,748 в виде дроби?

Чему равно число 28,654 в виде дроби?

Чему равно число 74,814 в виде дроби?

Чему равно число 15,797 в виде дроби?

Чему равно число 81,764 в виде дроби?

Чему равно число 41,840 в виде дроби?

Чему равно 76,335 в виде дроби?

Чему равно 61,881 в виде дроби?

Чему равно число 37,705 в виде дроби?

Чему равно 59,674 в виде дроби?

Чему равно число 13,816 в виде дроби?

Мэтуэй | Популярные проблемы

93-8

1	Фактор
9	Оценка	квадратный корень из 12
10	Оценка	квадратный корень из 20
11	Оценка	квадратный корень из 50	94
18	Оценка	квадратный корень из 45
19	Оценка	квадратный корень из 32
20	Оценка	квадратный корень из 18	92

Преобразование процентов, десятичных дробей и дробей

Урок 5: Преобразование процентов, десятичных дробей и дробей

/en/fractions/multipliing-and-dividing-fractions/content/

Преобразование дробей, десятичных дробей и 3 процентов 9002 9005 процентов 9005 Когда мы говорим, мы часто используем разные слова, чтобы выразить одно и то же.

Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький 9.0012 . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .

На этом изображении в каждой мерной чашке одинаковое количество сока. Но мы выразили эту сумму тремя способами: в виде дроби, в процентах и ​​в виде десятичной дроби. Поскольку они выражают одно и то же количество, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.

Иногда полезно преобразовать один вид числа в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные числа и проценты, также поможет вам в изучении более сложной математики.

Дроби и десятичные числа

Каждая дробь может быть записана как десятичная и наоборот. Возможно, вы не будете делать это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.

Преобразование дроби в десятичную

Преобразование дроби в десятичную. Мы будем использовать математический навык, который вы уже изучили: длинное деление. Чтобы освежить в памяти этот навык, вы можете просмотреть наш урок «Длинная дивизия».

Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.

• Давайте посмотрим, как мы можем преобразовать 1/4 в десятичную дробь.

• Чтобы преобразовать дробь в десятичную, мы просто разделим числитель…

• Чтобы преобразовать дробь в десятичную, мы просто разделим числитель… на знаменатель.

• В нашем примере мы разделим 1 на 4.

• 1 разделить на 4 будет 0. 1.

• Мы также добавим десятичную точку после 0 сверху.

• Теперь мы можем разделить 10 на 4.

• 10 разделить на 4 равно 2.

• Теперь умножим 4 на 2.

• 4 умножить на 2 равно 8. Итак, мы вычтем 8 из 10.

s
1000 минус

• Поскольку 2 больше 0, мы еще не закончили деление. Мы добавим еще один 0 после запятой и уменьшим его.

• Теперь 20 поделим на 4.

• 20 разделить на 4 равно 5.

• Теперь умножим. 4 умножить на 5 равно 20.

• Когда мы вычитаем 20 из 20, мы получаем 0. 0 означает, что мы закончили деление.

• 1 разделить на 4 равно 0,25.

• Итак, 1/4 равно 0,25.

Попробуйте!

Преобразуйте каждую из этих дробей в десятичное число .

Преобразование десятичного числа в дробь

Теперь сделаем это в обратном порядке. Преобразуем десятичную дробь в дробь.

Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.

• Мы перепишем 0,85 в виде дроби. Чтобы преобразовать десятичную дробь в дробь, мы будем использовать разрядных значений .

• В десятичных дробях число сразу справа от запятой находится в десятых разрядах.

• Место справа от десятого разряда — это сотый разряд .

• Чтобы преобразовать десятичное число, сначала мы проверим разрядное значение последнего числа справа.

• В 0,85 5 стоит на сотых.

• Это означает, что наша десятичная дробь равна 85 сотым. 85 сотых также можно записать как 85/100.

• Теперь у нас есть дробь. Но всегда полезно сокращать дроби, когда это возможно, — это облегчает их чтение.

• Чтобы уменьшить, нам нужно найти наибольшее число, которое равномерно входит в 85 и 100. дробь на 5,

• Сначала разделим числитель. 85 разделить на 5 равно 17.

• Теперь разделим знаменатель. 100 разделить на 5 равно 20. Это означает, что 85/100 можно уменьшить до 17/20.

• Итак, 0,85 равно 17/20.

Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Если вы добавляете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби так, чтобы у них был общий знаменатель .

Попробуй!

Преобразуйте эти десятичные дроби в дроби. Обязательно уменьшите каждую дробь до простейшей формы!

Проценты и десятичные дроби

Знание того, как преобразовывать проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Проценты в реальной жизни».

Преобразование процентов в десятичные

Преобразование процентов в десятичные числа на удивление просто. Это займет всего несколько простых шагов.

Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в десятичные дроби.

• Мы собираемся преобразовать 17% в десятичную дробь.

• Сначала возьмем знак процента…

• Сначала возьмем знак процента… и превратим его в десятичную точку.

• Далее мы переместим десятичную точку два пробелов до осталось .

• Теперь мы переместим десятичную точку на два пробела до слева .

• Мы преобразовали наши проценты в десятичную дробь. 17% равно 0,17.

• Давайте рассмотрим другой пример. На этот раз мы превратим 78% в десятичную дробь.

• Во-первых, мы заменим знак процента на десятичную точку .

• Затем мы переместим десятичную точку два пробела до слева .

• Затем мы переместим десятичную точку на два пробела до слева .

• 78% равно 0,78.

• Давайте рассмотрим другой пример. На этот раз мы превратим 8% в десятичную.

• Во-первых, мы заменим знак процента на десятичную точку .

• Затем мы переместим десятичную точку на два пробела в осталось .

• Затем мы переместим десятичную точку на два пробела до слева .

• Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Поскольку ноль ничему не равен, мы заменим пробел на ноль .

• Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .

• 8% равно 0,08

Почему это работает?

Преобразование процентов в десятичные дроби настолько просто, что вам может показаться, что вы что-то упустили. Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.

Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты выходят за пределы 100, мы просто помещаем проценты больше 100, например:

78% = 78/100

На втором этапе мы преобразуем 78/100 в десятичное число. Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , вот так:

78 ÷ 100 = 0,78

Так почему же мы не показали эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них. Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.

Попробуй!

Преобразуйте эти проценты в десятичные дроби.

Преобразование десятичной дроби в проценты

Теперь обратим то, что вы только что узнали. Преобразуем десятичную дробь в проценты.

Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.

• Мы собираемся преобразовать 0,45 в проценты.

• Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим десятичную точку на два разряда в 9.0011 справа .

• Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим запятую на два знака справа от .

• Теперь заменим десятичную точку знаком процента.

• Мы закончили преобразование нашей десятичной дроби в проценты. 0,45 равно 45%.

• Давайте попробуем другой пример. На этот раз наша десятичная дробь имеет три числа справа от запятой.

• Но мы все равно переместим десятичную точку на два деления вправо.

• Но мы все равно переместим десятичную точку на два деления вправо.

• У нас еще есть число справа от запятой. Число не равно 0, поэтому мы не можем его отбросить.

• Вместо мы сохраним десятичную точку, а добавим знак процента в конце числа.

• Итак, 0,635 равно 63,5%.

Попробуйте!

Вычислите эти десятичные дроби в процентах.

Проценты и дроби

Умение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни. Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.

Преобразование процентов в дроби

При преобразовании процентов в дроби полезно помнить, что проценты всегда выходят за пределы 100. Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».

Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в дроби.

• Преобразуем 30% в дробь.

• В разделе «Введение в проценты» вы узнали, что все проценты выражаются из 100. На самом деле это то, что означает слово 9.0011 процентов означает.

• Таким образом, любой процент равен самому себе больше 100. В нашем примере 30% равно 30/100.

• Теперь мы преобразовали 30% в дробь, но нам еще нужно ее уменьшить.

• 10 — наибольшее число, которое равномерно делится на 30 и 100. Таким образом, мы можем разделить обе части дроби на 10.

• Сначала мы разделим числитель дроби. 30 разделить на 10 равно 3.

• Теперь разделим знаменатель. 100 разделить на 10 равно 10.

• Итак, 30% равно 3/10.

Попробуйте!

Запишите эти проценты в виде дробей. Убедитесь, что уменьшите каждую дробь до простейшей формы.

Преобразование дроби в проценты

Преобразование дроби использует два навыка, которые вы только что изучили: запись дроби в виде десятичной дроби и запись десятичной дроби в виде процентов . Давайте посмотрим, как мы можем использовать эти навыки для преобразования дроби в проценты.

Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.

• Преобразуем 3/6 в проценты.

• Точно так же, как при преобразовании дроби в десятичную, мы разделим числитель на знаменатель .

  No related posts.