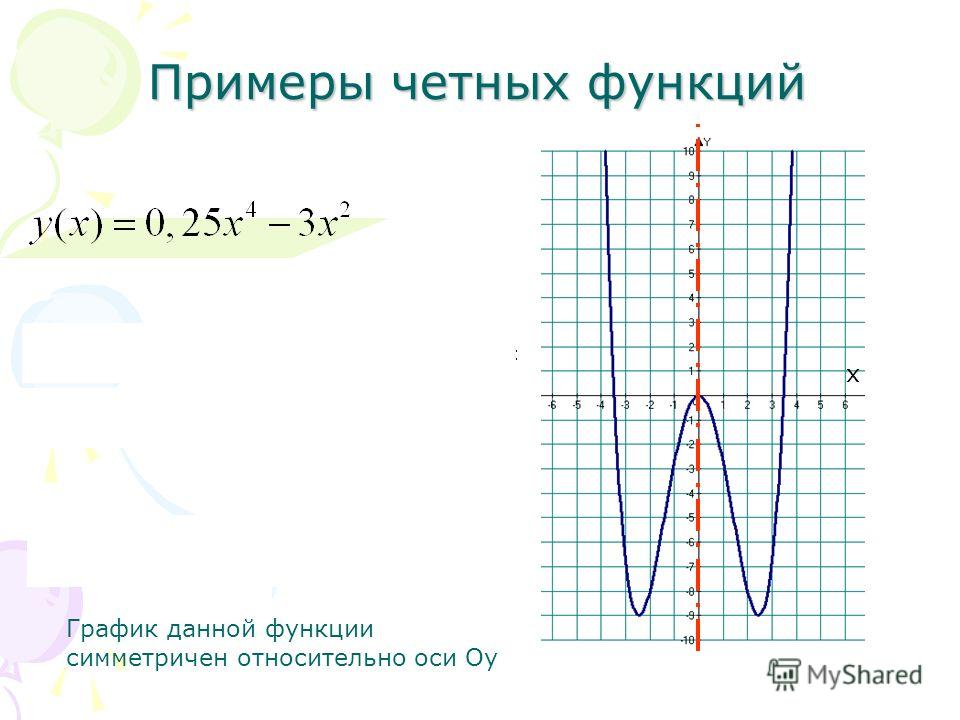
§2. Основные свойства функций. Четность
Функцию , определенную на симметричном относительно нуля множестве Х, называют четной, если для любого верно равенство , и называют нечетной, если для любого верно равенство
Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида, или говорят, что функция свойством четности не обладает.
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
Периодичность
Число называют периодом функции f(x), если для любого выполнены условия и .
Функцию, имеющую период называют периодической.
Если Т – период функции, то для любого число nT также является периодом этой функции.
Если функция имеет
наименьший положительный период, то он
берется в качестве основного.
График периодической функции с периодом Т функции при сдвиге вдоль оси абсцисс на Т переходит в себя.
Тригонометрические функции и — периодические с основным периодом T = , а и — с основным периодом T = .
Пример 1.
Исследовать функции на четность: а); б);
в) при
Решение.
а) Функция определена при , т.е. на множестве, симметричном относительно начала координат и .
Значит, – четная функция.
б) Функция определена при , т.е. на промежутке, симметричном относительно 0;
Значит, — нечетная функция.
в) Хотя формально , но эта функция не обладает свойством четности, т.к. ее область определения несимметрична относительно начала координат.
Пример 2.
Определить, какие из функций являются периодическими, указать их наименьший период: а), б), в) ,
г)
, д) , е).
Решение.
а) периодическая, , т.к. у функции основной период , то , откуда ;
б) периодическая, , т.к. у функции основной период , то , откуда ;
в) непериодическая;
г) периодическая, ;
д) непериодическая;
е) периодическая, .
Самостоятельная работа.
Вариант 1.
1. Исследовать функции на четность: а); б);
в) .
Найти основной период функции: .
Вариант 2.
Исследовать функции на четность: а);
б); в).
Найти основной период функции:
Вариант 3.
Исследовать функции на четность:
а); б); в).
Найти основной период функции: .
Ответы.
Вариант 1: 1а)четная; б)нечетная; в) общего вида; 2) ;
Вариант 2: 1а)нечетная; б) четная; в) общего вида; 2);
Вариант 3: 1а) четная;
б)нечетная; в) общего вида; 2)
.
Дополнительные упражнения.
Найти область определения функции: а);
б); в); г);
д) .
Исследовать функции на четность: а);
б); в) ; г).
Найти основные периоды функций: а); б) ;
в); г).
Ответы.
1.а); б); в);
г); д) .
2.а) четная; б) общего вида; в) четная; г) четная.
3. а) ; б) ; в) ; г) .
§3. Предел функции. Раскрытие простейших неопределенностей.
Пусть функция определена в некоторой окрестности точки .
Число А называется пределом функции при
(в точке ), если для любого , сколь малым бы оно ни было, существует число , зависящее от , такое, что при , удовлетворяющих неравенству , справедливо неравенство .
Если А – предел функции при , то пишут:
или при
.
В самой точке функция может и не существовать, т.е. значение функции может быть не определено.
Аналогично запись означает, что
для любого числа , сколь малым бы оно ни было, существует число , зависящее от , такое, что при всех справедливо неравенство .
Говорят, что предел функции в точке равен бесконечности, и пишут , если
для любого числа , сколь большим бы оно ни было, существует число , зависящее от M, такое, что при всех x, удовлетворяющих неравенству , выполняется неравенство
Справедливы следующие основные теоремы о конечных пределах.
Пусть существуют и , тогда
, где
, если
(Все теоремы верны и при ).
Если некоторый
предел не может быть вычислен ни по
одной из о конечных пределах, ни по
теоремам о бесконечно малых и о бесконечно
больших функциях, то говорят, что этот
предел имеет
неопределенность, и
указывает ее вид.
Основные виды неопределенностей:
,,.
Чтобы вычислить предел, содержащий неопределенность, нужно эту неопределенность раскрыть, то есть преобразовать функцию, стоящую под пределом, так, чтобы неопределенность исчезла.
При вычислении пределов главная задача состоит в том, чтобы научиться раскрывать неопределенности.
Пример 1.
Доказать по определению предела, что .
Решение.
Нам надо доказать, что для любого числа , сколь малым бы оно ни было, существует такое число , что из неравенства следует неравенство .
Зададим и составим неравенство
.
Тогда если взять , то для всех значений , удовлетворяющих условию , будет выполняться неравенство . Следовательно, , что и требовалось доказать.
Пример 2.
Найти
Решение.
Воспользуемся
теоремами о конечных пределах и получим,
что
.
Правило 1
Eсли предел при рациональной дроби имеет неопределенность , то нужно числитель и знаменатель дроби разложить на множители так, чтобы выделить множитель, который стремится к нулю при , и сократить на него.
Пример 3.
Найти .
Решение.
Т.к. пределы числителя и знаменателя равны 0 , применить теорему о пределе частного нельзя, имеем неопределенность вида . Разложим числитель и знаменатель на множители и сократим на общий множитель , который обращает в нуль числитель и знаменатель. Получим
.
Пример 4.
Найти
Решение.
.
Пример 5.
Найти
Решение.
Имеем неопределенность вида . Умножим числитель и знаменатель на выражение, сопряженное числителю , чтобы, получив разность квадратов в числителе и разложив на множители знаменатель, сократить на :
.
Пример 6.
Найти .
Решение.
Имеем неопределенность вида . Умножим числитель и знаменатель на неполный квадрат суммы выражения (), чтобы получить в знаменателе разность кубов. Далее выделим в числителе и знаменателе множитель и сократим на него:
Правило 2
Чтобы раскрыть неопределенность вида , образованную при делением многочленов или иррациональных выражений, нужно вынести за скобки в числителе и знаменателе старшие степени переменной x и сократить дробь под знаком предела.
Пример 7.
Найти .
Решение.
Т.к. числитель и знаменатель дроби неограниченно растут при , то имеем неопределенность .Для ее раскрытия вынесем за скобки в числителе и знаменателе старшую степень переменной и сократим на нее:
.
Здесь учтено, что и при .
Пример 8.
Найти .
Решение.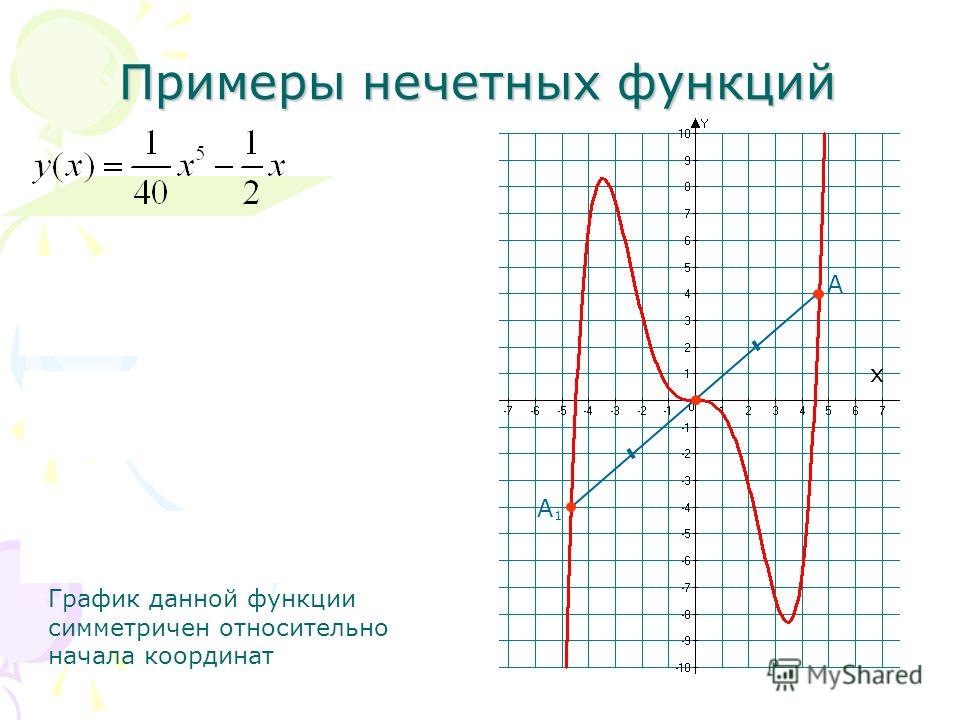
Аналогично рассмотренному в предыдущем примере:
Пример 9.
Найти .
Решение.
Пример 10. Обобщение результатов предыдущих примеров.
Найти , где n и m – натуральные числа, .
Решение.
Имеем неопределенность . Вынесем за скобки в числителе , в знаменателе и получим:
Предел второго множителя равен . Предел первого множителя зависит от соотношения между числами и :
если , то и, следовательно, общий предел бесконечен;
если , то и общий предел ;
если , то и общий предел равен нулю.
Итак, получен результат, которым можно пользоваться для раскрытия неопределенностей , образованных при делением целых многочленов:
.
Например,
так как n = m = 3;
так как n =5, m = 4,
то есть n > m; так как n =5,
m = 6, то есть n < m.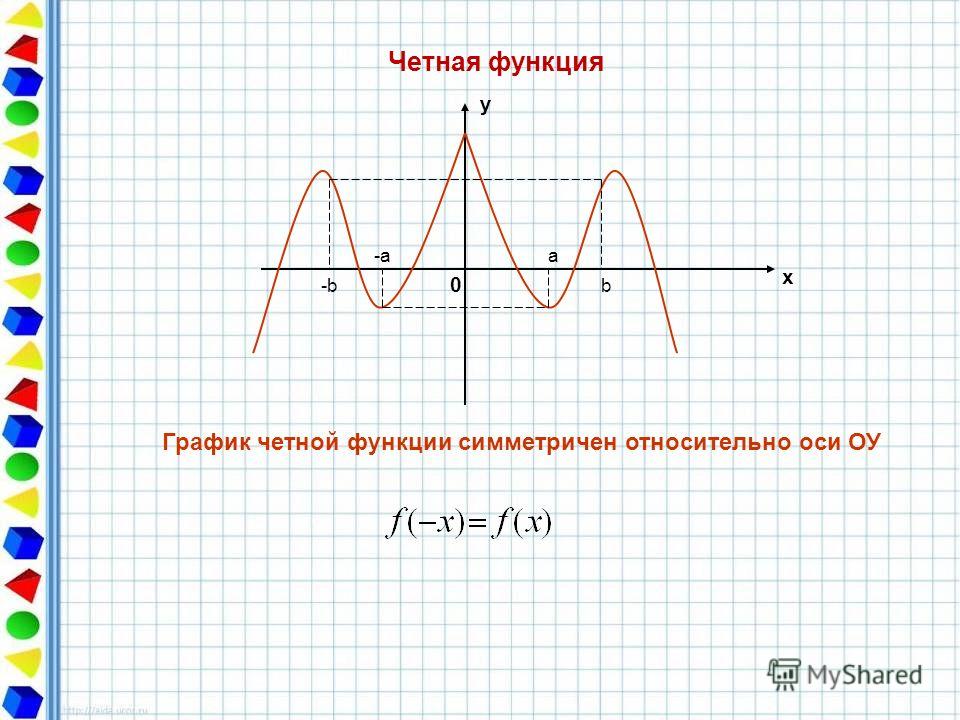
Правило 3.
Случай, когда при или функция представляет разность двух положительных бесконечно больших величин, т.е. неопределенность , можно привести к неопределенности или путем преобразования функции к дроби.
Пример 11.
Найти .
Решение.
Так как знаменатель каждой дроби есть величина бесконечно малая при , а числители есть числа, не равные нулю, то каждая из дробей является бесконечно большой величиной, т.е. имеем неопределенность . Чтобы раскрыть ее, приведем дроби к общему знаменателю:
.
Пример 12.
Найти .
Решение.
Имеем неопределенность . Чтобы раскрыть ее, умножим и разделим выражение на . В результате получим:
.
Т.к. , то дальнейшее решение надо проводить отдельно для и :
Пример 13.
Найти .
Решение.
При
степень
числителя больше степени знаменателя
у обеих дробей /смотри пример 10 / ,значит
имеем неопределенность
. Чтобы раскрыть ее , приведем дроби к
общему знаменателю:
Чтобы раскрыть ее , приведем дроби к
общему знаменателю:
(т.к. степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях).
Самостоятельная работа.
Вариант 1.
Найти: а); б);
в); г).
Вариант 2.
Найти: а); б);
в); г).
Вариант 3.
Найти: а); б);
в); г)
Ответы.
Вариант 1: а); б); в); г) .
Вариант 2: а); б); в); г) .
Вариант 3: а); б); в); г).
Дополнительные упражнения.
а)б)в) 2.а)б)в)
3. 4.
6.
8.
Ответы:
1. а), б) , в);
5.
 ;
;2. а), б) , в) ;
6. ;
3. 7;
7. ;
4.;
8. .
Четность и нечетность функции. (Алгебра 9 класс)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Базовый уровень Сложные задачи
1. Четность и нечетность функции (Алгебра 9 класс)
07.04.20202. Цель урока :
Формирование понятий « четностьнечетность функции»; исследование
функций на четность; определение по
графику четных и нечетных функций;
построение графиков функций, содержащих
модуль, используя при этом свойство
четности и нечетности функций.
3. Понятие симметричности
Если числовое множество Х вместе с каждымсвоим элементом х содержит и противоположный
элемент – х, то Х называют симметричным
множеством
4. Определите симметричное множество или нет:
1.2.
3.
4.
5.
6.
7.
8.
(-6; 6),
[ -7; 7],
[0;+ ∞ ),
(-∞;+∞ ),
(-5; 3),
[-5; 5)
(-∞;-2),(2;+∞ )
(-∞;-8),[8;+∞ )
5. Свойства функций
1) Область определения функций .2) Монотонность функции.
3) Ограниченность функции .
4) Наибольшее и наименьшее значения
функции .
5) Непрерывность .
6) Область значений .
7) Выпуклость
8) Четность, нечетность.
6. Запомнить:
Определение: Функция y(x) называется четной, еслиобласть определения её симметрична относительно
начала координат и выполняется
y(-x) = y(x)
для любого x из области определения этой функции.
График четной функции симметричен относительно оси у.
Определение: Функция y(x) называется нечетной, если
область определения её симметрична относительно
начала координат и выполняется
y(-x) = — y(x)
График нечетной функции симметричен относительно начала
координат.
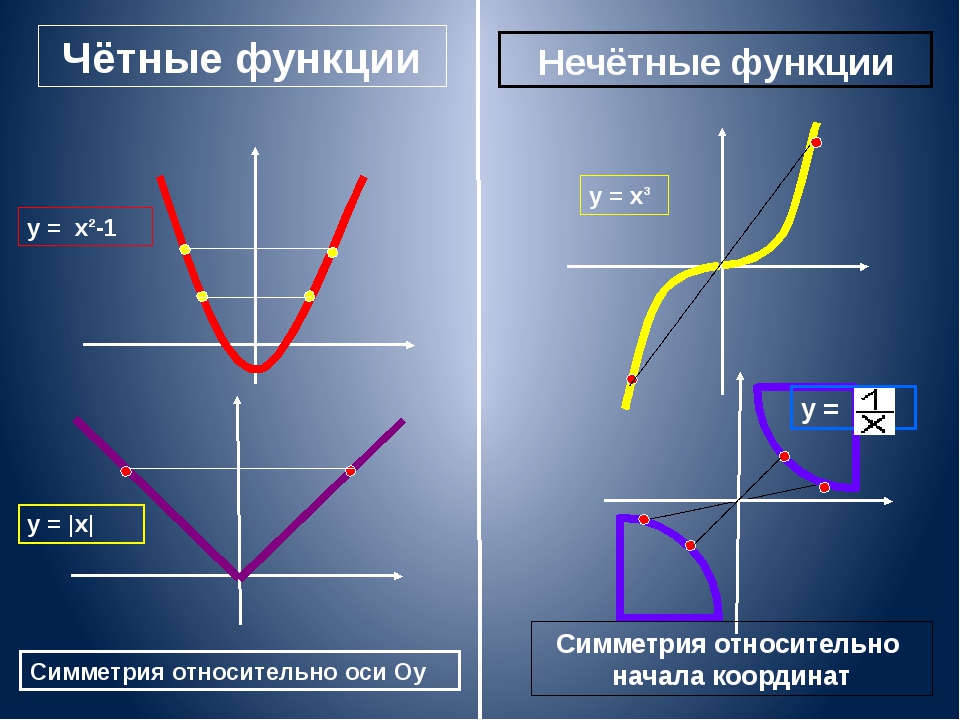
7. Геометрический смысл свойств чётной и нечётной функций.
Чётные функцииy = x²-1
Нечётные функции
y = x³
y =1/х
y = |x|
Симметрия относительно оси Оy
Симметрия относительно
начала координат
9. Алгоритм исследования функции на чётность или нечетность
1)Установить , симметрична ли областьопределения функции
2) Найти f(-x)
3) Сравнить f(-x) и f(x)
Определение
Чётные функции
Нечётные функции
y (- x) = y (x)
y (- x) = — y (x)
Выяснить является ли функция чётной или нечётной.

y = 5 x²- |X|
Решение:
y (- x)=5 •(- x)² — |- x| =
= 5x² — |x|=
= y (x) — четная
y = 7x +x³
Решение:
y (- x)= 7(- x) +(- x)³=
= — 7 x — x³ =- (7x +x³)=
= — y (x)
11. Примеры: Определите, является ли функция четной или нечетной
1. f(x) =3 x2+x42. f(x) = х(5 – x2)
3 . f(x) =4 x6–x2
4.
f(x) = x7+2×3
12. Чётные функции
Функция f(х) называется четной, если область еёопределения симметрична относительно начала координат
и f(-x) = f(x) для любого х из области определения функции.
Графики чётных функций симметричны относительно оси
ординат.
13. График четной функции симметричен относительно оси ординат
График четной функции симметриченотносительно оси ординат
14. График четной функции симметричен относительно оси ординат.
у3
-7
-5
-3
3
5
7
х
15. Укажите график четной функции.
yy
y
1
1
1
0 1
1
x
0 1
x
2
Укажите график четной функции.

0 1
3
x
16. Укажите график четной функции.
yy
y
1
1
0 1
1
1
0 1 x
0 1
2
3
x
Укажите график четной функции.
x
17. Нечётные функции
Функция f(х) называется нечетной, если область еёопределения симметрична относительно начала координат
и f(-x) = -f(x) для любого х из области определения функции.
Графики нечётных функций симметричны относительно
начала координат.
18. График нечетной функции симметричен относительно начала координат
19. График нечетной функции симметричен относительно начала координат.
у4
2
-8
-3
3
-2
-4
8
х
20. Укажите график нечетной функции.
yy
1
0 1
y
1
x
0 1
1
0 1
x
1
3
2
Укажите график нечетной функции.
x
21. Укажите график нечетной функции
yy
y
1
0 1
1
0 1
x
1
0 1
1
x
3
2
Укажите график нечетной функции
x
22.
 Укажите график нечетной функции.y
Укажите график нечетной функции.yy
y
1
0 1
1
x
0 1
1
0 1
x
1
3
2
Укажите график нечетной функции.
x
23. Примеры четных и нечетных функций.
24. Достроить график функции, заданной на рисунке для х < 0 так, чтобы построенная линия была графиком: а) чётной функции; б)
Достроить график функции, заданной на рисункедля х < 0 так, чтобы построенная линия была
графиком:
а) чётной функции;
б) нечётной функции.
Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х
Является ли функция четной, нечетной?
у
3
7
5
3
3
5
7
х
Является ли функция четной, нечетной?
у
4
2
8
3
3
2
4
8
х
Повторение
•Найдите область определения, область значений функций.
•Является ли функция четной или нечетной?
у
4
у
2
1
3
5
х
х
4
4
2
2
4
4
4
—
English Русский Правила
Как определить четность функции по уравнению.
 Как определять четные и нечетные функции. Четная и нечетная функция
Как определять четные и нечетные функции. Четная и нечетная функцияОпределение 1. Функцияназываетсячетной (нечетной ),
если вместе с каждым значением переменной
значение –х также принадлежит
и выполняется равенство
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –х одновременно принадлежат
).
Например, функция
не является четной и нечетной, так как
ее область определения
не симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотя
и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу , так как если
точка
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как если
График нечетной
функции симметричен относительно начала
координат, так как если
принадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f – четная
функция на множествеХ , а функцияg определена на
множестве
,
то функция
–
четная.
д) Если f – нечетная
функция на множествеХ , а функцияg определена на
множестве
и четная (нечетная), то функция
–
четная (нечетная).
Доказательство . Докажем, например, б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функций
и
.
г) Пусть f – четная
функция. Тогда.
Тогда.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию
,
заданную на множествеХ , симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство . Функцию
можно записать в виде
.
Функция
– четная, так как
,
а функция
– нечетная, поскольку.
Таким образом,
,
где
–
четная, а
–
нечетная функции. Теорема доказана.
Определение 2. Функция
называетсяпериодической , если
существует число
,
такое, что при любом
числа
и
также
принадлежат области определения
и выполняются равенства
Такое число T называетсяпериодом функции
.
Из определения 1 следует, что если Т – период функции
,
то и число –Т тоже является
периодом функции
(так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ – основной период функцииf , то остальные периоды кратны ему.
Доказательство . Предположим
противное, то есть что существует периодфункцииf (>0),
не кратныйТ . Тогда, разделивнаТ с остатком, получим
,
где
.
Поэтому
то есть
– период функцииf ,
причем
,
а это противоречит тому, чтоТ –
основной период функцииf .
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
Найдем период функции
. Пусть
Пусть
— период этой функции. Тогда
(так как
.
илиилиили
.
Значение T , определяемое
из первого равенства, не может быть
периодом, так как зависит отх , т.е.
является функцией отх , а не постоянным
числом. Период определяется из второго
равенства:
.
Периодов бесконечно много, при
наименьший
положительный период получается при
:
.
Это – основной период функции
.
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T –
рациональное число, то
и
являются рациональными числами при
рациональномх и иррациональными
при иррациональномх . Поэтому
при любом рациональном числе T .
Следовательно, любое рациональное числоT является периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомn сколь угодно близким к нулю). {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
. Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x}
и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y}
. {2}+1}
. Подставьте в нее следующие значения x {\displaystyle x}
:
{2}+1}
. Подставьте в нее следующие значения x {\displaystyle x}
:
Проверьте, симметричен ли график функции относительно оси Y. Под симметрией подразумевается зеркальное отображение графика относительно оси ординат. Если часть графика справа от оси Y (положительные значения независимой переменной) совпадает с частью графика слева от оси Y (отрицательные значения независимой переменной), график симметричен относительно оси Y. Если функция симметрична относительно оси ординат, такая функция четная.
Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y}
(при положительном значении x {\displaystyle x}
) соответствует отрицательное значение y {\displaystyle y}
(при отрицательном значении x {\displaystyle x}
), и наоборот. Нечетные функции обладают симметрией относительно начала координат. {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Нули функции
Нулём функции называется то значение х , при котором функция обращается в 0, то есть f(x)=0.
Нули – это точки пересечения графика функции с осью Ох.
Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)
Четная функция симметрична относительно оси Оу
Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).
Нечетная функция симметрична относительно начала координат.
Функция которая не является ни чётной,ни нечётной называется функцией общего вида.
Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е. x 2 >x 1 → f(x 2)>f(x 1)
Убывание функции
Функция f(x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. x 2 >x 1 → f(x 2)
Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . Функция f(x) имеет 3 промежутка монотонности:
(-∞ x 1), (x 1 , x 2), (x 3 ; +∞)
Находят промежутки монотонности с помощью сервиса Интервалы возрастания и убывания функции
Локальный максимум
Точка х 0 называется точкой локального максимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0) > f(x)
Локальный минимум
Точка х 0 называется точкой локального минимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0)
Точки локального максимума и точки локального минимума называются точками локального экстремума.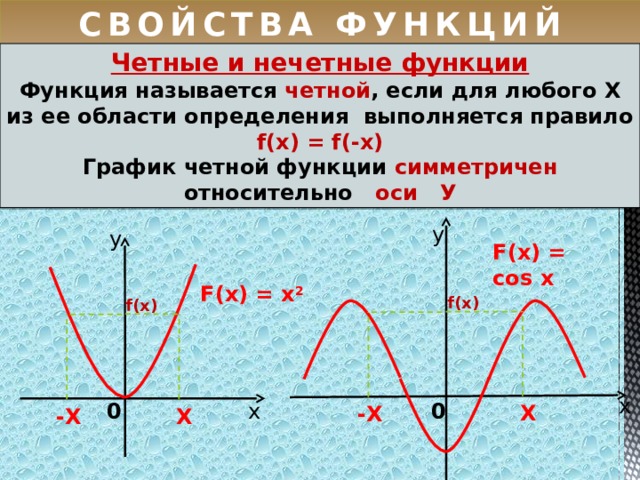
x 1 , x 2 — точки локального экстремума.
Периодичность функции
Функция f(x) называется периодичной, с периодом Т , если для любого х выполняется равенство f(x+T) = f(x) .
Промежутки знакопостоянства
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.
f(x)>0 при x∈(x 1 , x 2)∪(x 2 , +∞), f(x)
Непрерывность функции
Функция f(x) называется непрерывной в точке x 0 , если предел функции при x → x 0 равен значению функции в этой точке, т.е. .
Точки разрыва
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.
x 0 — точка разрыва.
Общая схема для построения графиков функций
1. Найти область определения функции D(y).
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график.
Пример: Исследовать функцию и построить ее график: y = x 3 – 3x
8) По результатам исследования построим график функции:
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x). 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Четные и нечетные функции — Formulasearchengine
From Formulasearchengine
Перейти к навигации Перейти к поиску
Синусоидальная функция и все ее полиномы Тейлора являются нечетными функциями. На этом изображении показан sin(x) и его приближения Тейлора, полиномы степени 1, 3, 5, 7, 9, 11 и 13.
Функция косинуса и все ее полиномы Тейлора являются четными функциями. На этом изображении показан cos(x) и его приближение Тейлора степени 4.
В математике четные функции и нечетные функции являются функциями, которые удовлетворяют определенным соотношениям симметрии относительно аддитивных инверсий. Они важны во многих областях математического анализа, особенно в теории степенных рядов и рядов Фурье. Они названы по четности степеней степенных функций, которые удовлетворяют каждому условию: функция f ( x ) = x n является четной функцией, если n является четным целым числом, и это нечетная функция, если n — нечетное целое число.
Содержание
- 1 Определение и примеры
- 1.1 Четные функции
- 1.2 Дополнительные функции
- 2 Некоторые факты
- 2.1 Непрерывность и дифференцируемость
- 2.2 Алгебраические свойства
- 2.2.1 Свойства уникальности
- 2.2.2 Свойства, включающие сложение и вычитание
- 2.2.3 Свойства, связанные с умножением и делением
- 2.2.4 Свойства, связанные с составом
- 2.2.5 Другие алгебраические свойства
- 2.3 Расчетные свойства
- 2.3.1 Основные свойства исчисления
- 2.3.2 Свойства серии
- 3 гармоники
- 4 См. также
- 5 Примечания
- 6 Каталожные номера
Определение и примеры
Понятие четности или нечетности определено только для функций, область определения и диапазон которых имеют аддитивную обратную. Сюда входят аддитивные группы, все кольца, все поля и все векторные пространства. Так, например, вещественная функция действительной переменной может быть четной или нечетной, как и комплексная функция векторной переменной, и так далее.
Так, например, вещественная функция действительной переменной может быть четной или нечетной, как и комплексная функция векторной переменной, и так далее.
Примеры являются вещественными функциями действительной переменной, чтобы проиллюстрировать симметричность их графиков.
Четные функции
ƒ ( x ) = x 2 является примером четной функции.
Пусть f ( x ) будет вещественной функцией действительной переменной. Тогда f равно даже , если следующее уравнение верно для всех x и -x в области f 9или
- е (х) — е (- х) = 0. {\ displaystyle f (x) -f (-x) = 0. \,}
Геометрически говоря, грань графика четной функции симметрична. относительно оси y , что означает, что его график остается неизменным после отражения относительно оси y .
Примеры четных функций: | х |, х 2 , х 4 , cos( x ) и cosh( x ).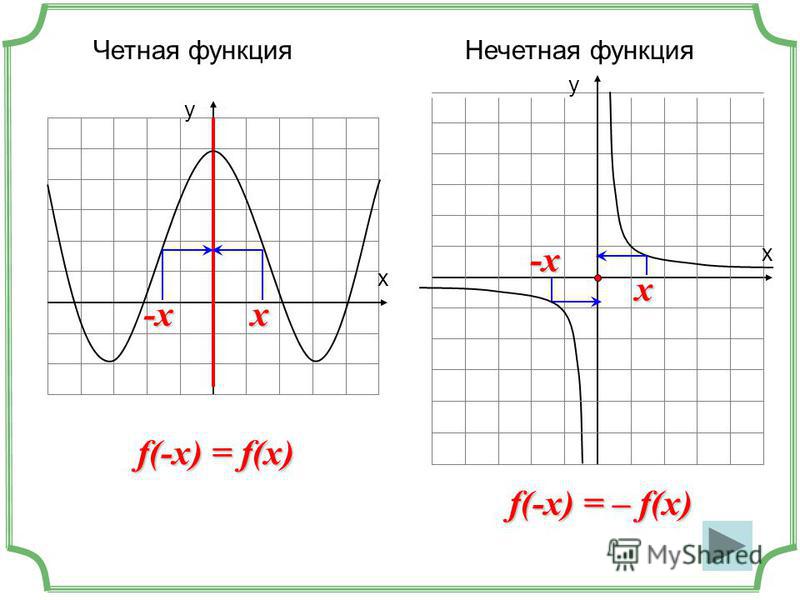
Нечетные функции
ƒ ( x ) = x 3 является примером нечетной функции.
Опять же, пусть f ( x ) будет вещественной функцией действительной переменной. Тогда f равно нечетному , если для всех x и -x в области f : выполняется следующее уравнение , {\ Displaystyle -f (х) = е (- х), \,} или Геометрически график нечетной функции имеет вращательную симметрию с относительно начала координат, что означает, что его график остается неизменным после поворота на 180 градусов вокруг начала координат. Примеры нечетных функций: x , x 3 , sin( x ), sin( x ) и erf( x ). ƒ ( x ) = x 3 + 1 не является ни четным, ни нечетным. Четность или нечетность функции не означает ни дифференцируемость, ни даже непрерывность. Например, функция Дирихле четная, но нигде не непрерывная. Свойства, включающие ряды Фурье, ряды Тейлора, производные и т. д., могут использоваться только тогда, когда можно предположить, что они существуют. При обработке сигналов гармонические искажения возникают, когда синусоидальный сигнал передается через нелинейную систему без памяти, то есть систему, выходной сигнал которой в момент времени t {\ displaystyle t} зависит только от входа в момент времени t { \displaystyle t} и не зависит от ввода в предыдущие моменты времени. Такая система описывается функцией отклика Vout (t) = f (Vin (t)) {\ displaystyle V _ {\ text {out}} (t) = f (V _ {\ text {in}} (t)) }. Тип производимых гармоник зависит от функции отклика f {\ displaystyle f}: [3] Обратите внимание, что это не относится к более сложным сигналам. Например, пилообразная волна содержит как четные, так и нечетные гармоники. После четно-симметричного двухполупериодного выпрямления он становится треугольной волной, которая, кроме смещения постоянного тока, содержит только нечетные гармоники. |CitationClass=citation
}} Зависимость переменной y от переменной x, при которой каждому значению x соответствует единственное значение y, называется функцией. Обозначение y = f (x). Каждая функция обладает рядом основных свойств, таких как монотонность, четность, периодичность и другие. Рассмотрим свойство четности более подробно. Функция y=f(x) вызывается, даже если она удовлетворяет следующим двум условиям: 2. Значение функции в точке x, принадлежащей области видимости функции, должно быть равно значению функция в точке -x. Если построить график четной функции, то он будет симметричен относительно оси Y. 92. На рисунке видно, что график симметричен относительно оси Y. Функция y=f(x) называется нечетной, если она удовлетворяет следующим двум условиям: 1. Область определения данной функции должна быть симметрична относительно точки O. То есть , если некоторая точка а принадлежит области определения функции, то соответствующая точка -а также должна принадлежать области определения данной функции. 2. Для любой точки x, из области определения функции, должно выполняться равенство f(x) = -f(x). 93 симметрична относительно начала координат. Определение 1. Функция вызывается даже ( нечетное ), если вместе с каждым значением переменной Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на вещественной прямой (числа X А — X одновременно принадлежат Функция Функция Функция График четной функции симметричен относительно оси ОУ , так как если точка При доказательстве того, является ли функция четной или нечетной, полезны следующие утверждения. Теорема 1. а) Сумма двух четных (нечетных) функций есть четная (нечетная) функция. б) Произведение двух четных (нечетных) функций есть четная функция. в) Произведение четной и нечетной функции есть нечетная функция. d) Если f четная функция на множестве X , а функция g определяется на множестве e) Если f нечетная функция на множестве X , а функция g определено на множестве Доказательство . Докажем, например, б) и г). б) Пусть г) Пусть f — четная функция. Затем. Аналогично доказываются остальные утверждения теоремы. Теорема доказана. Теорема 2. Любая функция Доказательство . . Функция Определение 2. Функция Такое число T называется период функций Из определения 1 следует, что если T – функция периода Определение 3. Наименьший из положительных периодов функции называется ее основным период. Теорема 3. Если T — основной период функции f , то остальные периоды кратны ему. Доказательство . Предположим противное, т. е. есть функция периода ф (>0), не кратно T . Затем, разделив на Т с остатком, получим т.е. – период функции f , а Хорошо известно, что тригонометрические функции являются периодическими. Основной период (потому что или Значение T , определяемое из первого равенства, не может быть периодом, так как зависит от X , т.е. число. Период определяется из второго равенства: Примером более сложной периодической функции является функция Дирихле Обратите внимание, что если T — рациональное число, то для любого рационального числа T . Следовательно, любое рациональное число T является периодом функции Дирихле. Ясно, что эта функция не имеет главного периода, так как существуют положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное число можно получить, выбрав n произвольно близко к нулю). Теорема 4. Если функция f устанавливается на множество X и имеет период T , а функцию g множество на множестве Доказательство . Таким образом, имеем , т. Например, начиная с , потому что х имеет период Определение 4. Функции, не являющиеся периодическими, называются непериодическими . . Для этого используйте миллиметровую бумагу или графический калькулятор. Выберите любое количество числовых значений для независимой переменной x (\displaystyle x) и подставьте их в функцию для вычисления значений зависимой переменной y (\displaystyle y). Положите найденные координаты точек на координатную плоскость, а затем соедините эти точки, чтобы построить график функции. 9(2)+1). Подставляем в него следующие значения x (\displaystyle x): Проверить, симметричен ли график функции относительно оси Y. Симметрия относится к зеркальному отображению графика относительно оси Y. Если часть графика справа от оси у (положительные значения независимой переменной) совпадает с частью графика слева от оси у (отрицательные значения независимой переменной), то график симметричен относительно оси Y. Проверить, симметричен ли график функции относительно начала координат. Началом является точка с координатами (0,0). Симметрия относительно начала координат означает, что положительное значение y (\displaystyle y)(с положительным значением x (\displaystyle x)) соответствует отрицательному значению y (\displaystyle y)(с отрицательным значением x (\displaystyle x)) , наоборот. Нечетные функции имеют симметрию относительно начала координат. Проверить, имеет ли график функции симметрию. Последний тип функции — это функция, график которой не имеет симметрии, то есть нет зеркального отображения как относительно оси у, так и относительно начала координат. Например, задана функция. Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд. Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage. org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com. Некоторые факты
Непрерывность и дифференцируемость
Алгебраические свойства
Свойства уникальности
Свойства, включающие сложение и вычитание
Свойства, связанные с умножением и делением
Свойства, связанные с композицией
Другие алгебраические свойства
 Точно так же любая линейная комбинация нечетных функций является нечетной, и нечетные функции также образуют векторное пространство над действительными числами. Фактически векторное пространство всех вещественных функций представляет собой прямую сумму подпространств четных и нечетных функций. Другими словами, каждая функция f ( x ) может быть однозначно записана как сумма четной и нечетной функций:
Точно так же любая линейная комбинация нечетных функций является нечетной, и нечетные функции также образуют векторное пространство над действительными числами. Фактически векторное пространство всех вещественных функций представляет собой прямую сумму подпространств четных и нечетных функций. Другими словами, каждая функция f ( x ) может быть однозначно записана как сумма четной и нечетной функций:
Свойства исчисления
Основные свойства исчисления
Свойства ряда
Гармоники
См. также
Примечания
Ссылки
Алгоритм проверки функции на четность. Четность функции. Способы задания функции
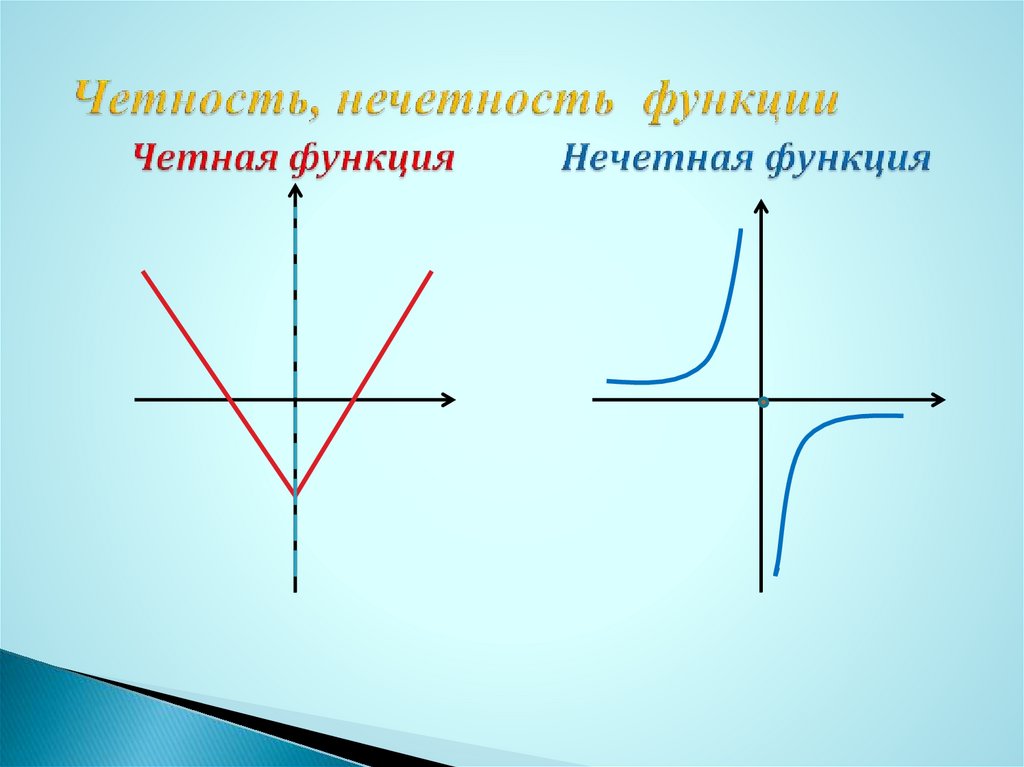 То есть для любой точки x, из области определения функции, должно выполняться равенство f(x) = f(-x).
То есть для любой точки x, из области определения функции, должно выполняться равенство f(x) = f(-x). График четной функции
График нечетной функции
означает — X также принадлежит
и равенство
).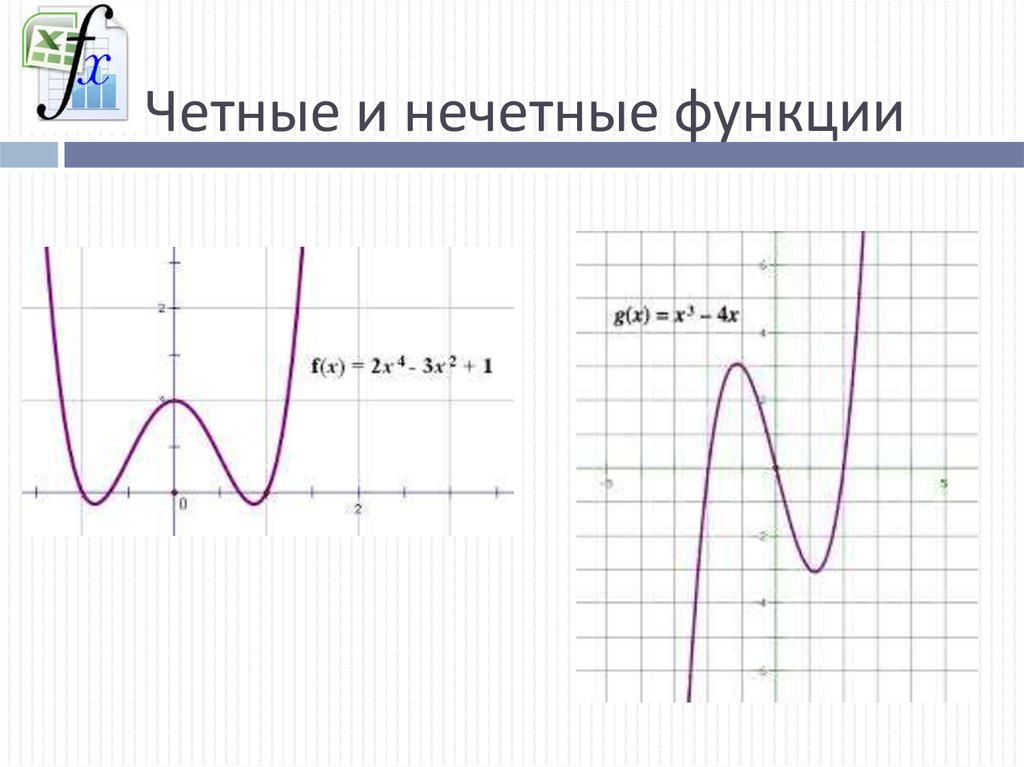 Например, функция
Например, функция
не является четной и нечетной, так как ее область определения
не симметрична относительно начала координат.
четная, т.к.
симметрична относительно начала координат и.
нечетная, потому что
И
.
не является ни четной, ни нечетной, так как, хотя
и симметрична относительно начала координат, равенства (11.1) не выполняются. Например,.
тоже принадлежит графу. График нечетной функции симметричен относительно начала координат, так как если
принадлежит графику, то точка
также принадлежит графику.
, то функция
— четная.
и четное (нечетное), то функция
— четное (нечетное).
И
четные функции. Тогда, следовательно. Случай нечетных функций рассматривается аналогично
и
.
, определенная на множестве X , симметричном относительно начала координат, может быть представлена в виде суммы четной и нечетной функций. Функцию
Функцию
можно записать в виде
четная, так как
, а функция
нечетная, т.к. Таким образом,
, где
— четная, а
— нечетная функция. Теорема доказана.
, вызываемая периодическое издание , если существует число
, такое, что для любых
чисел
И
также принадлежат области определения
и равенства
.
, то число T тоже — период функции
(поскольку при замене Т на — Т равенство сохраняется). Методом математической индукции можно показать, что если T – период функции f , потом и
, тоже точка. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.
, где
. Поэтому
, что противоречит тому, что T является основным периодом функции f . Утверждение теоремы следует из полученного противоречия. Теорема доказана.
и
равно
,
и
. Найдите период функции
. Пусть
— это период этой функции. Тогда
.
.
. Периодов бесконечно много
наименьший положительный период получается при
:
.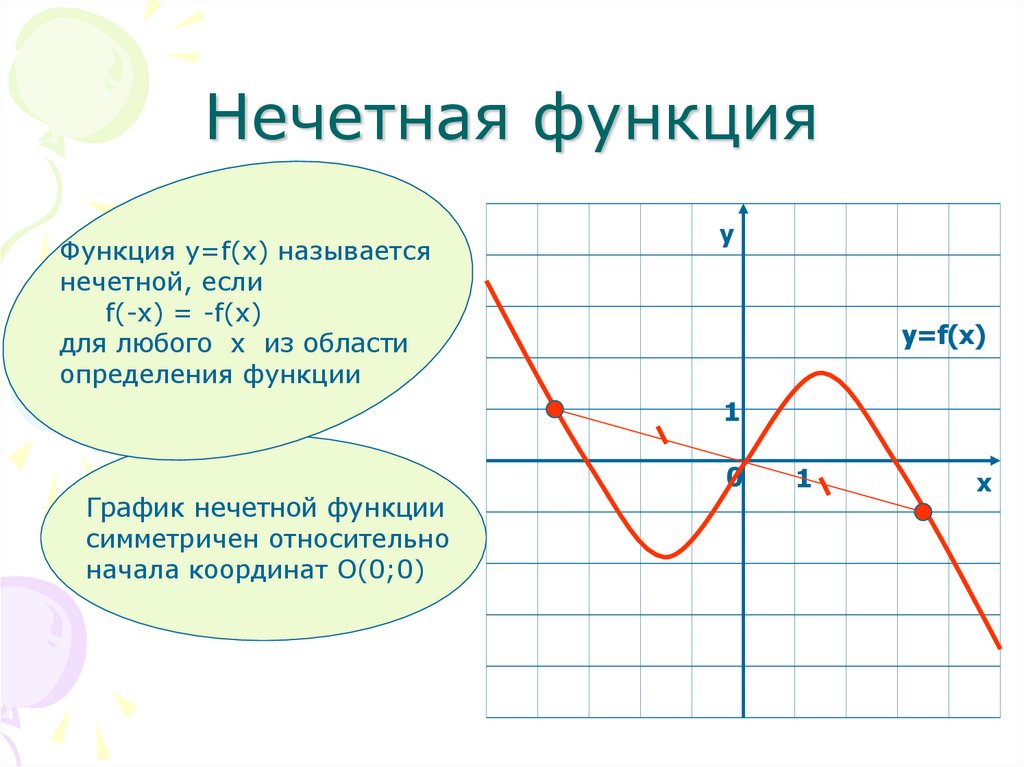 Это основной период функции
Это основной период функции
.
И
— рациональные числа при рациональном X и иррациональные при иррациональном X . Поэтому
, то комплексная функция
тоже имеет период T . е. утверждение теоремы доказано.
е. утверждение теоремы доказано.
, тогда функции
имеют период
.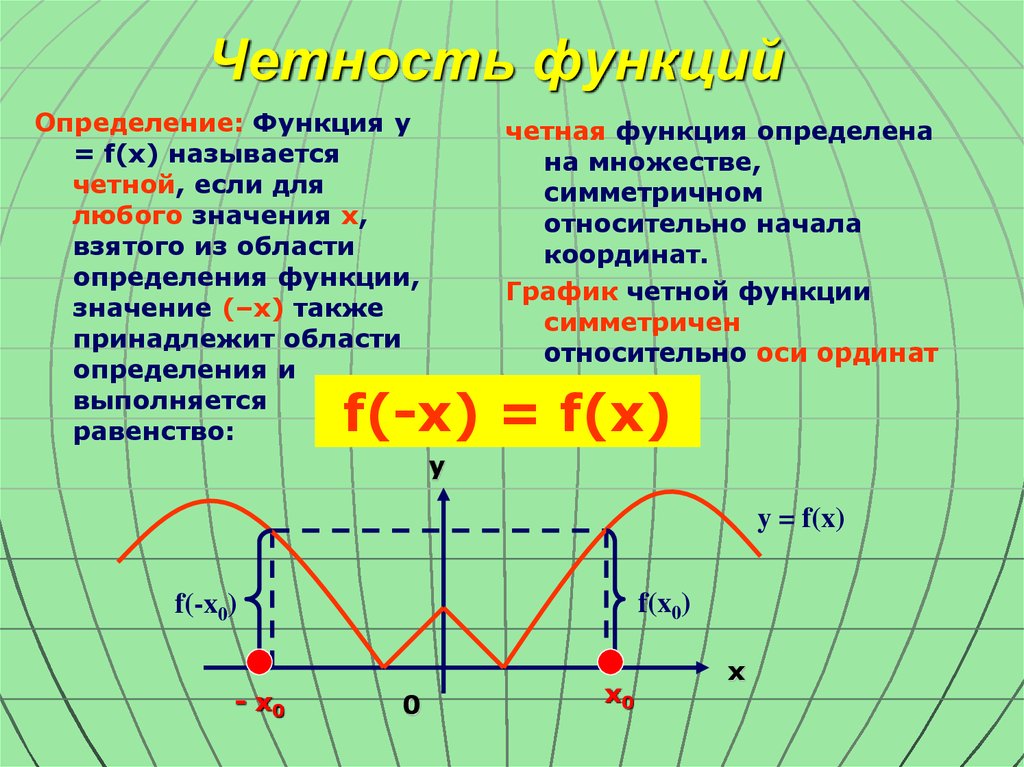 Если функция симметрична относительно оси Y, то она четная.
Если функция симметрична относительно оси Y, то она четная. Таким образом, функция не является ни четной, ни нечетной. 9(2)). Записанная в такой форме функция выглядит четной, потому что имеется четный показатель степени. Но этот пример доказывает, что нельзя быстро определить вид функции, если независимая переменная заключена в круглые скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Таким образом, функция не является ни четной, ни нечетной. 9(2)). Записанная в такой форме функция выглядит четной, потому что имеется четный показатель степени. Но этот пример доказывает, что нельзя быстро определить вид функции, если независимая переменная заключена в круглые скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени. Gale Apps — Технические трудности
 zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.
zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager. java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.
java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer. java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.
java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI. java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.
java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean. invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.
invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps. controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor302.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.
controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor302.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org. springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.
springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org. springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.
springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.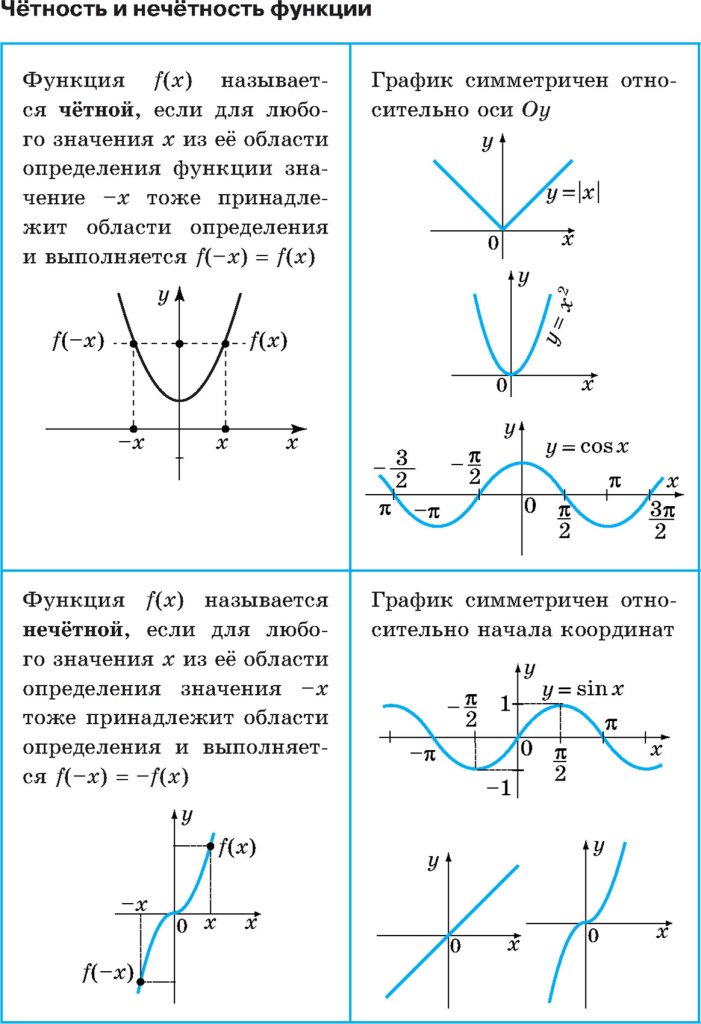 servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.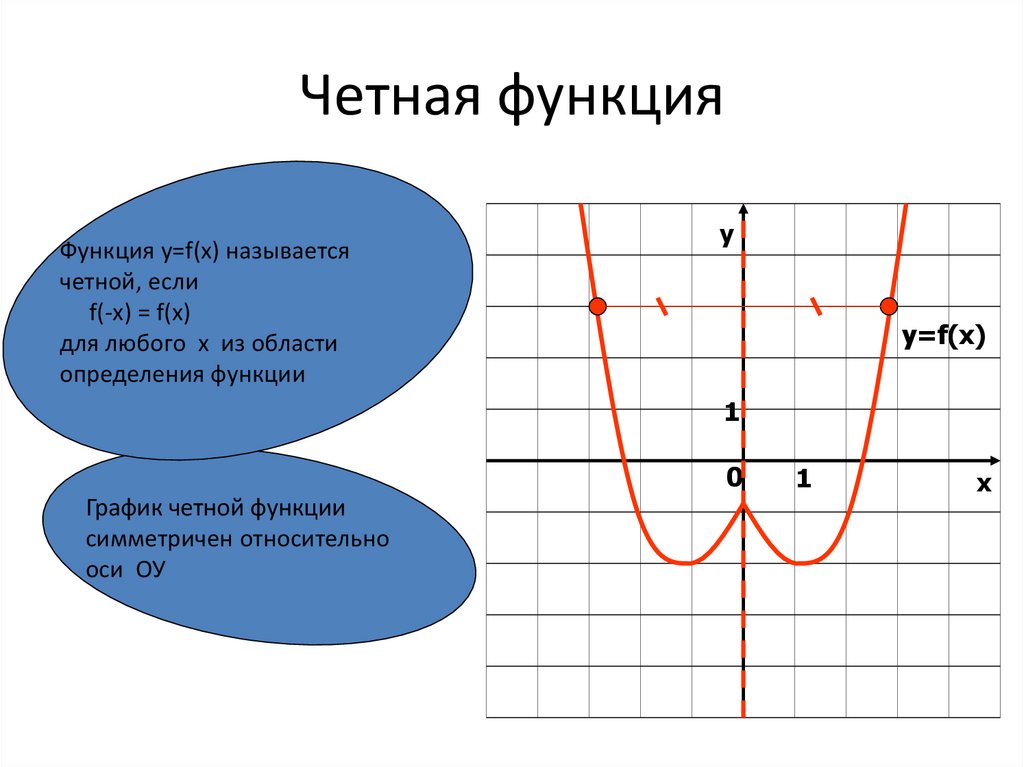 springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.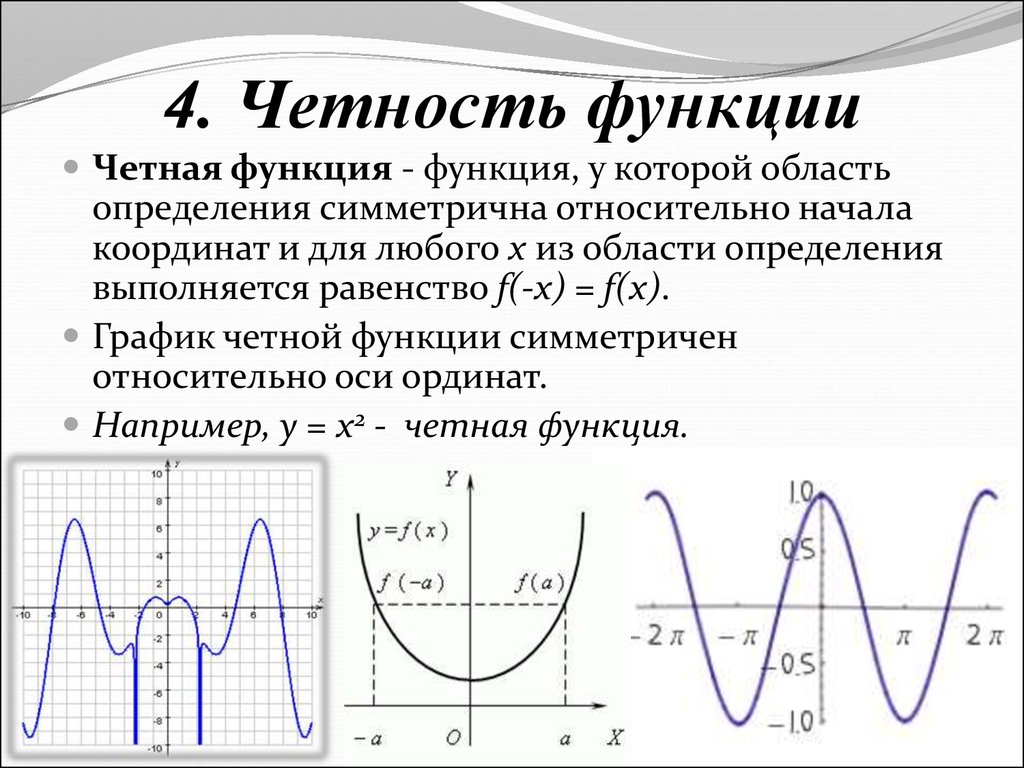 apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.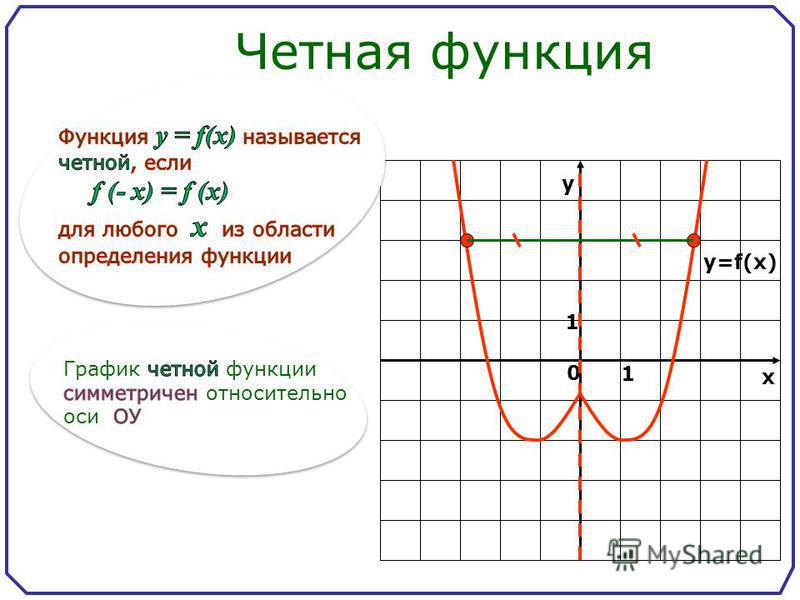 springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org. apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.
apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.

 ;
;