404 Cтраница не найдена
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайта
Найти ближайший филиал Версия для слабовидящих Версия для слабовидящих
КАМЕНСК-УРАЛЬСКИЙ
АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ
Сохраняя традиции, вместе создаем будущее!
Не хватает прав доступа к веб-форме.
Выше сщщбщение успешно отправлено.
-
Сведения об ОО
- Основные сведения
- Структура и органы управления
- Документы
- Образование
- Образовательные стандарты
- Руководство.
 Педагогический состав
Педагогический состав - Педагогический состав
- МТО и оснащенность ОП
- Стипендия и иные виды материальной поддержки
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Противодействие коррупции
- Бесплатная юридическая помощь
- Награды, достижения ОО
- Инновационная деятельность
- Доступная среда
- Международное сотрудничество
-
Летопись техникума
- Страницы летописи
- Руководители
- Нам есть у кого учиться
- Педагоги техникума
- Наша гордость — выпускники
- Достижения
- СМИ о техникуме
- Хранители нашей истории
-
Абитуриентам
- Прием 2022
- Дни открытых дверей
- Специальности/профессии
- Общежитие
- Правила и условия приема
- Документы для поступления
- Подать заявление онлайн
- Студенческая жизнь
- Приемная комиссия
- Мониторинг подачи заявлений и документов
- Зачисление
- Фото-экскурсия
- Инклюзивное образование
- Целевое обучение
-
Студентам
- Расписание
- Заочное отделение
- Документы
- Студенческая жизнь
- Государственная итоговая аттестация
- Центр профориентологии
- Стипендия и иные виды материальной поддержки
- Спорт
- Конференции и олимпиады
- Советы психолога
- Сайты преподавателей
- ЕГЭ для студентов учреждений СПО
- Воспитательная работа
- Целевое обучение
- Выпускникам
-
Сотрудникам
- Документы
- Методическая служба
-
Родителям
- Телефонный справочник
- Информация для Родителей
- Специальности / профессии
- Главная
- ›
- uploads
- ›
- about_the_university
- ›
- 14_sistema-distantsionnogo-obucheniya
- ›
- raspisanie-zanyatiy-na-21-12-27-12
Синус косинус тангенс котангенс числа.
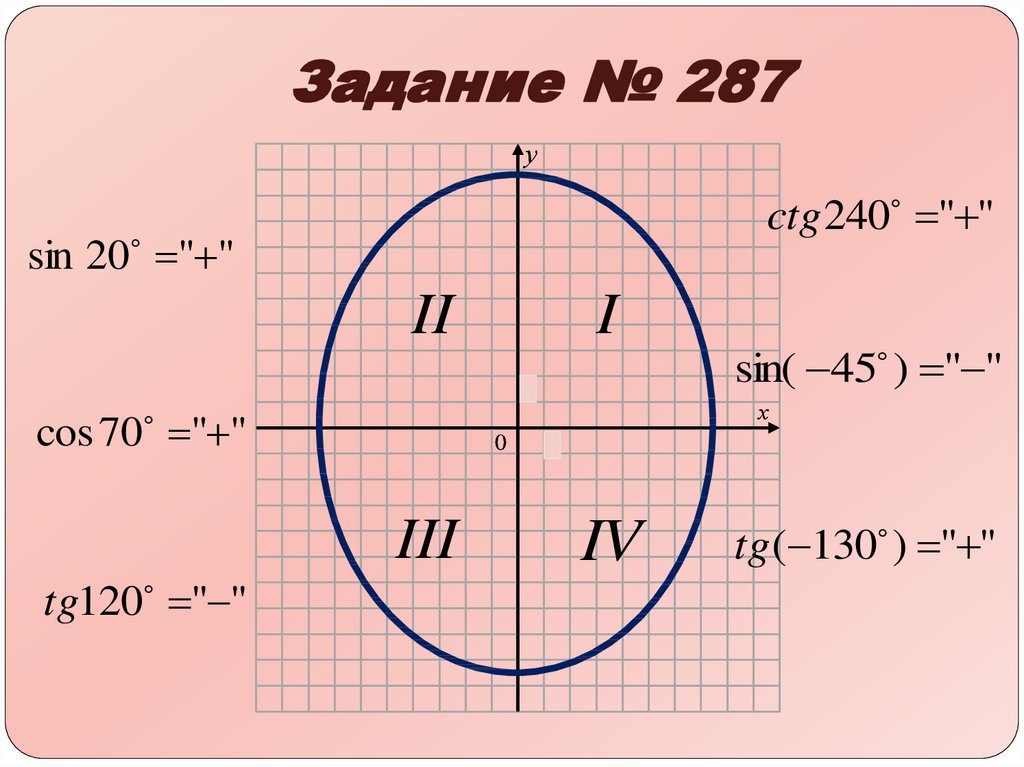 В какой четверти находится угол поворота. Тригонометрия
В какой четверти находится угол поворота. Тригонометрия12+
2 недели назад
Математика от Баканчиковой81 подписчик
Тригонометрия 8-11 класс. Как найти синус, косинус, тангенс или котангенс числа? Сегодня мы ответим на этот вопрос. Если Вы не видели наши предыдущие уроки по теме: «Периодические функции», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Вначале, мы напомним Вам, чему равен период синуса/косинуса, тангенса/котангенса в радианах, и как связаны радианы и градусы. Обратим Ваше внимание на то, что если величина угла тригонометрических функций задана числом – то это угол, заданный в радианах. На примере пяти задач мы покажем Вам, как определять в какой четверти находится угол поворота тригонометрических функций синус, косинус, тангенс и котангенс, если угол задан числом, что позволит Вам легко определять знак функции и находить её значение. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
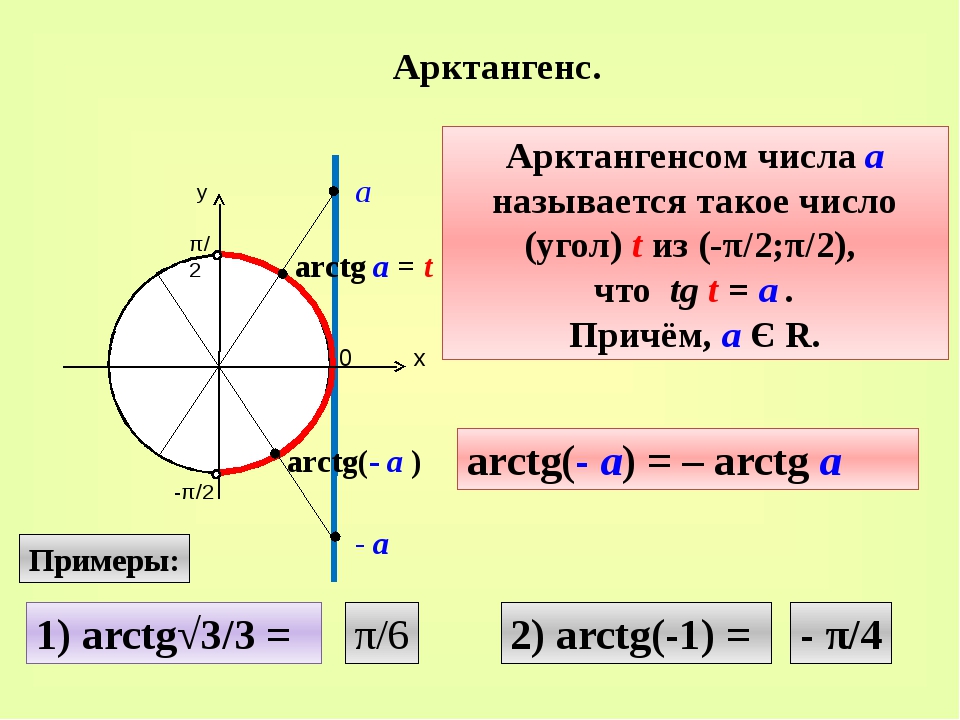 Определение периодической функции. Свойства функции. Алгебра 8-11 класс. https://rutube.ru/video/b25f67fb1e168fdb8b8f5cfddb654749/
Периодические функции в решении задач. Часть 1. Алгебра 8-11 класс. https://rutube.ru/video/e60e96860991be3329b8b4d08571c8c6/
Периодические функции в решении задач. Часть 2. Типовые задания и задачи ЕГЭ. Алгебра 7-11 класс. https://rutube.ru/video/88c985c27ce386702adc84a05b97f9e5/
Как определить знак тригонометрических функций. Часть 3. Тригонометрия 8-11 класс. https://rutube.ru/video/ee737823a02db93694b4ab06a6399847/
Как определить знак выражения с тригонометрическими функциями. Часть 2. Тригонометрия 8-11 класс. . https://rutube.ru/video/48c16739ed1c3f8474a402745d92a879/
Единицы измерения углов. Часть 2. Радиан. https://rutube.ru/video/3a3a7b21273aaaff03296fdc700df9b5/
Знаки тригонометрических функций на единичной окружности. Часть 1. Тригонометрия 8-11 класс. https://rutube.ru/video/46c1d08ad9aa581b687b7f50a9597616/
Определение синуса, косинуса, тангенса и котангенса на единичной окружности.
Определение периодической функции. Свойства функции. Алгебра 8-11 класс. https://rutube.ru/video/b25f67fb1e168fdb8b8f5cfddb654749/
Периодические функции в решении задач. Часть 1. Алгебра 8-11 класс. https://rutube.ru/video/e60e96860991be3329b8b4d08571c8c6/
Периодические функции в решении задач. Часть 2. Типовые задания и задачи ЕГЭ. Алгебра 7-11 класс. https://rutube.ru/video/88c985c27ce386702adc84a05b97f9e5/
Как определить знак тригонометрических функций. Часть 3. Тригонометрия 8-11 класс. https://rutube.ru/video/ee737823a02db93694b4ab06a6399847/
Как определить знак выражения с тригонометрическими функциями. Часть 2. Тригонометрия 8-11 класс. . https://rutube.ru/video/48c16739ed1c3f8474a402745d92a879/
Единицы измерения углов. Часть 2. Радиан. https://rutube.ru/video/3a3a7b21273aaaff03296fdc700df9b5/
Знаки тригонометрических функций на единичной окружности. Часть 1. Тригонометрия 8-11 класс. https://rutube.ru/video/46c1d08ad9aa581b687b7f50a9597616/
Определение синуса, косинуса, тангенса и котангенса на единичной окружности.
Измерение синусоиды
Google Реклама
- • Знать измерения, связанные с синусоидой
- • а.
 Пиковое значение.
Пиковое значение. - • б. Амплитуда.
- • с. Пиковое значение.
- • д. Периодическое время.
- • эл. Средняя стоимость.
- • ф. Среднеквадратичное значение.
Рис. 1.2.1 Характеристики синусоиды
Форма волны представляет собой график, показывающий изменение, как правило, напряжения или тока во времени. Горизонтальная ось показывает течение времени слева направо. Вертикальная ось показывает измеряемую величину (на рис. 1.2.1 это напряжение).
Шесть наиболее важных характеристик синусоиды:
Значение PEAK TO PEAK.
МГНОВЕННОЕ значение.
АМПЛИТУД.
ПИКОВОЕ значение.
ПЕРИОДИЧЕСКОЕ ВРЕМЯ.
СРЕДНЕЕ значение.
Среднеквадратичное значение.
Эти характеристики показаны на рис. 1.2.1.
Значение размаха
Значение размаха до пика представляет собой расстояние по вертикали между вершиной и основанием волны. Он будет измеряться в вольтах на осциллограмме напряжения и может быть обозначен как V PP или V ПК−ПК .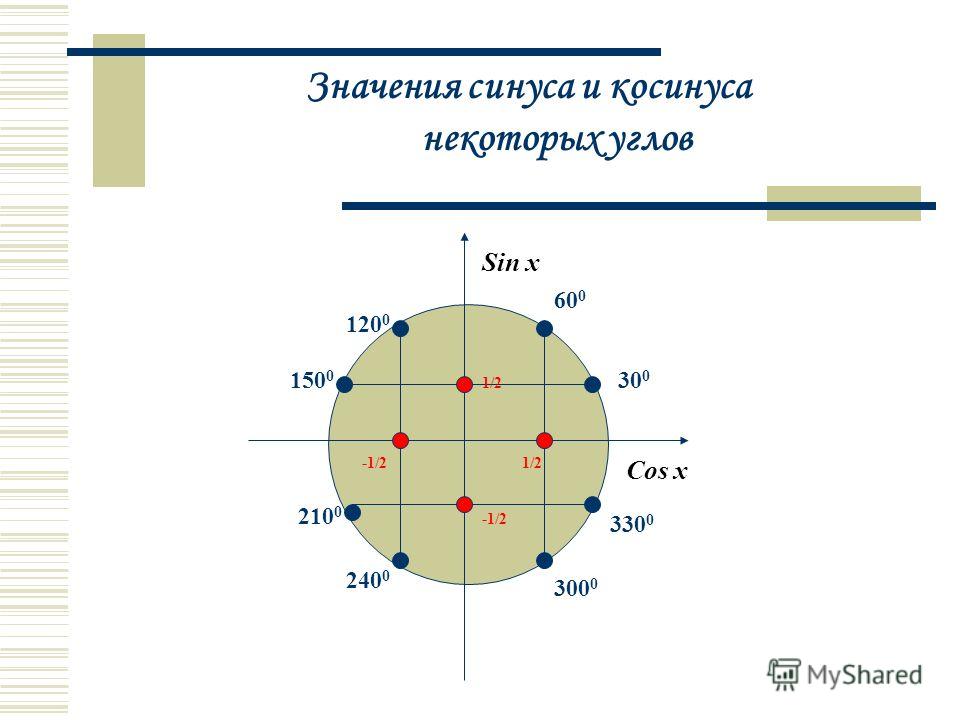 В форме сигнала тока он будет помечен I PP или I PK-PK , поскольку I (не C) используется для представления тока.
В форме сигнала тока он будет помечен I PP или I PK-PK , поскольку I (не C) используется для представления тока.
Мгновенное значение
Это значение (напряжение или ток) волны в любой конкретный момент времени. часто выбирают, чтобы совпасть с каким-то другим событием. Например. Мгновенное значение синусоиды на одной четверти цикла будет равно пиковому значению. См. точку X на рис. 1.2.1.
Амплитуда
АМПЛИТУДА синусоидальной волны – это максимальное расстояние по вертикали в любом направлении от центральной линии волны. Поскольку синусоида симметрична относительно своей центральной линии, амплитуда волны составляет половину от пика до пика, как показано на рис. 1.2.2.
Пиковое значение
ПИКОВОЕ значение волны — это максимальное значение, которого достигает волна выше опорного значения. Обычно используемое эталонное значение равно нулю. В форме сигнала напряжения пиковое значение может быть обозначено как V PK или V MAX (I PK или I MAX в форме тока).
Если измеряемая синусоида симметрична по обе стороны от нуля вольт (или нуля ампер), что означает, что уровень постоянного тока или постоянная составляющая волны составляет ноль вольт, тогда пиковое значение должно быть таким же, как амплитуда, т. е. половина от пикового значения.
Рис. 1.2.2 Определение пикового значения V
PKОднако это не всегда так, если присутствует постоянная составляющая, отличная от нуля вольт, синусоида будет симметрична относительно этого уровня, а не нуля. Нижняя форма волны на рис. 1.2.2 показывает, что пиковое значение теперь может быть даже больше, чем значение размаха (однако амплитуда волны остается неизменной и представляет собой разницу между пиковым значением и «центральной линией»). «формы волны).
Периодическое время и частота
ПЕРИОДИЧЕСКОЕ ВРЕМЯ (обозначается символом T) — это время в секундах, миллисекундах и т. д., необходимое для одного полного цикла волны. Его можно использовать для нахождения ЧАСТОТЫ волны ƒ по формуле T =1/ƒ
Таким образом, если периодическое время волны составляет 20 мс (или 1/50 секунды), то должно быть 50 полных циклов волны. волна за одну секунду. Частота 50 Гц. Обратите внимание, что при использовании этой формулы, если периодическое время указано в секундах, то частота будет в Гц.
волна за одну секунду. Частота 50 Гц. Обратите внимание, что при использовании этой формулы, если периодическое время указано в секундах, то частота будет в Гц.
Рис. 1.2.3 Среднее значение синусоиды
Среднее значение
Среднее значение. Обычно это означает среднее значение только половины цикла волны. Если бы было взято среднее значение полного цикла, оно, конечно, было бы равно нулю, поскольку в синусоидальной волне, симметричной относительно нуля, есть равные отклонения выше и ниже нулевой линии.
Используя только половину цикла, как показано на рис. 1.2.3, среднее значение (напряжение или ток) всегда составляет 0,637 от пикового значения волны.
В AV = В ПК x 0,637
или
I AV = I ПК X 0,637
Однако есть некоторые измерители, которые будут считывать среднеквадратичное значение, они называются «измерителями истинного среднеквадратичного значения».
Среднеквадратичное значение.
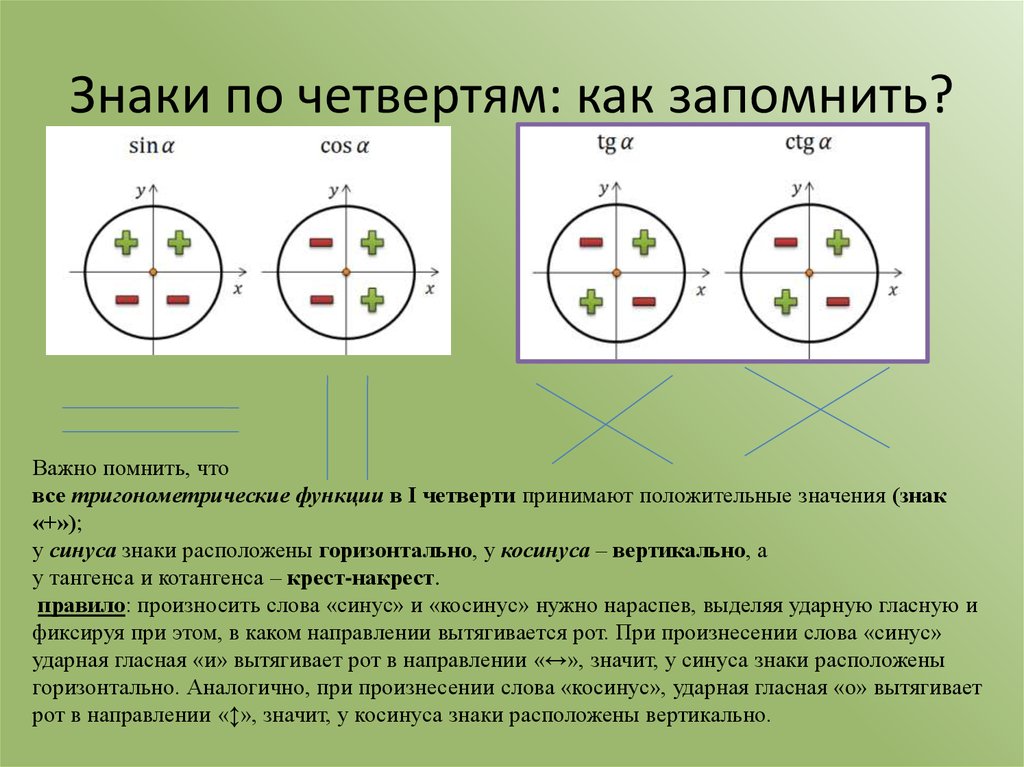
СКЗ или СРЕДНЕКВАДРАТИЧЕСКОЕ значение представляет собой значение эквивалентного постоянного (неизменяющегося) напряжения или тока, которое обеспечивает такую же энергию для цепи, как и измеренная синусоида. То есть, если синусоидальная волна переменного тока имеет среднеквадратичное значение 240 вольт, она будет поставлять в цепь ту же энергию, что и источник постоянного тока 240 вольт.
Можно показать, что среднеквадратичное значение синусоиды составляет 0,707 от пикового значения.
В RMS = V PK x 0,707 и I RMS = I PK x 0,707
Кроме того, пиковое значение синусоиды равно x 1,414 RMS.
Форм-фактор
Если V AV (0,637) умножить на 1,11, получится 0,707, что является среднеквадратичным значением. Эта разница называется форм-фактором волны, и соотношение 1.11 верно только для идеальной синусоиды. Если волна имеет другую форму, изменится либо среднеквадратичное значение, либо среднее значение (или и то, и другое), а также отношение между ними. Это важно при измерении напряжения переменного тока с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение, просто умножая напряжение на 1,11. Поэтому, если измеряемая волна переменного тока не является идеальной синусоидой, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить настоящий измеритель RMS, который фактически вычисляет среднеквадратичное значение несинусоидальных волн.
Это важно при измерении напряжения переменного тока с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение, просто умножая напряжение на 1,11. Поэтому, если измеряемая волна переменного тока не является идеальной синусоидой, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить настоящий измеритель RMS, который фактически вычисляет среднеквадратичное значение несинусоидальных волн.
Сеть (линия) питания
Чтобы продемонстрировать некоторые из этих характеристик при использовании, рассмотрим очень распространенную синусоиду, форму сигнала сети или линии, которая во многих частях мира имеет номинальное напряжение 230 В.
Электрическое оборудование, которое подключается к сети, всегда имеет этикетку с информацией о том, к какому источнику питания может быть подключено это оборудование. Эти метки весьма разнообразны по внешнему виду, но часто имеется изображение синусоиды, показывающее, что переменный ток поставка должна быть использована. Указанное напряжение будет составлять 230 В (или 120 В в США) или диапазон напряжений, включающий эти значения. Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота питания составляет 50 Гц в Европе или 60 Гц в США.
Указанное напряжение будет составлять 230 В (или 120 В в США) или диапазон напряжений, включающий эти значения. Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота питания составляет 50 Гц в Европе или 60 Гц в США.
Из этого небольшого количества информации можно вычислить другие значения:
a. Пиковое напряжение сигнала, как В пик = В RMS x 1,414
b. СРЕДНЕЕ значение сигнала, как V AV = V PK x 0,637
c. Значение PEAK TO PEAK сигнала. Это в два раза больше АМПЛИТУДЫ, которая (поскольку форма сигнала сети симметрична относительно нуля вольт) равна V PK .
Потому что V Кол-во уже известен из а. отсюда следует, что V PP = V PK x 2
d. ПЕРИОДИЧЕСКОЕ ВРЕМЯ, определяемое как T = 1/ƒ
Синусоидальные напряжения — Vpk, Vpk-pk, Vavg, Vrms
Синусоида определяется функцией тригонометрического синуса. При построении графика в виде зависимости напряжения (В) от фазы (θ)
он похож на рисунок справа. Форма волны повторяется каждые 2p
радиан (360°) и симметричен относительно оси напряжения (когда отсутствует смещение постоянного тока). Отображение напряжения и тока
циклическое поведение называется чередующимся; то есть переменный ток (AC). Здесь показан один полный цикл. Основа
уравнение для синусоиды выглядит следующим образом:
При построении графика в виде зависимости напряжения (В) от фазы (θ)
он похож на рисунок справа. Форма волны повторяется каждые 2p
радиан (360°) и симметричен относительно оси напряжения (когда отсутствует смещение постоянного тока). Отображение напряжения и тока
циклическое поведение называется чередующимся; то есть переменный ток (AC). Здесь показан один полный цикл. Основа
уравнение для синусоиды выглядит следующим образом:
Существует несколько способов определения амплитуды синусоидального сигнала, обычно в виде пикового напряжения (V pk или V p ), размах напряжения (V pp или V pp или V pkpk или V pk-pk ),
среднее напряжение (V avg или V avg ) и среднеквадратичное напряжение (V rms ). Пиковое напряжение
и размах напряжения очевидны, если посмотреть на график выше. Среднеквадратичное и среднее напряжение не так
очевидный.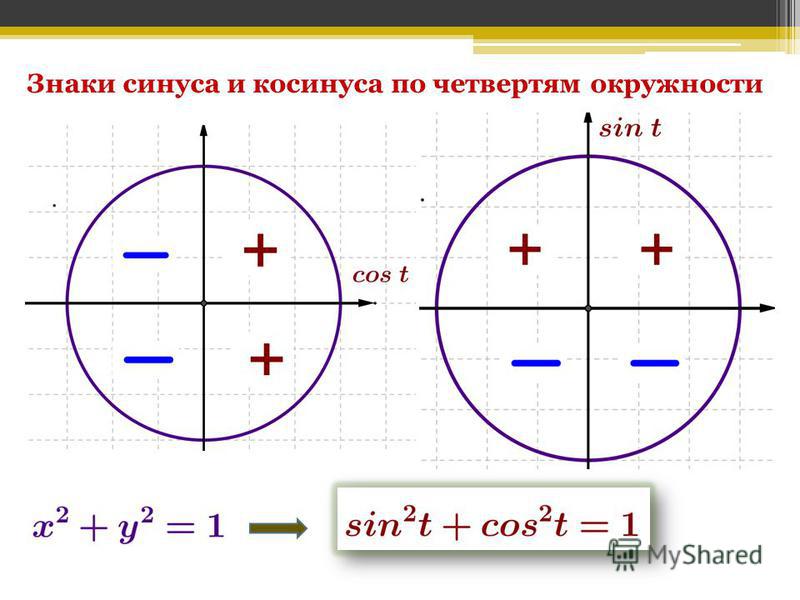
См. также «Напряжения треугольной волны» и Страницы напряжения прямоугольной формы.
Среднеквадратичное напряжение (В
действующее значение )В качестве как следует из названия, V rms вычисляется путем извлечения квадратного корня из среднего значения квадрата напряжения в правильно выбранном интервале. В случае симметричных сигналов, таких как синусоида, четверть периода точно представляет все четыре четверти цикла сигнала. Поэтому допустимо выбирать первую четверть цикл, который проходит от 0 радиан (0°) до p/2 радиан (90°).
В среднеквадратичное значение — значение, которое показывает подавляющее большинство вольтметров переменного тока. Это значение, которое при применении
через сопротивление, производит такое же количество тепла, что и напряжение постоянного тока (DC) той же величины.
производить. Например, 1 В, приложенный к резистору 1 Ом, выделяет 1 Вт тепла. Синусоида 1 В rms через резистор 1 Ом также выделяет 1 Вт тепла.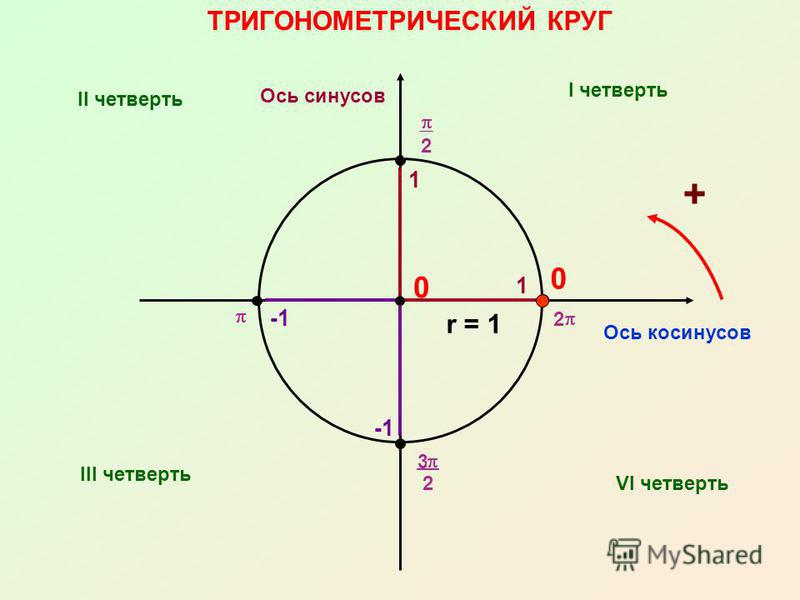

 Педагогический состав
Педагогический состав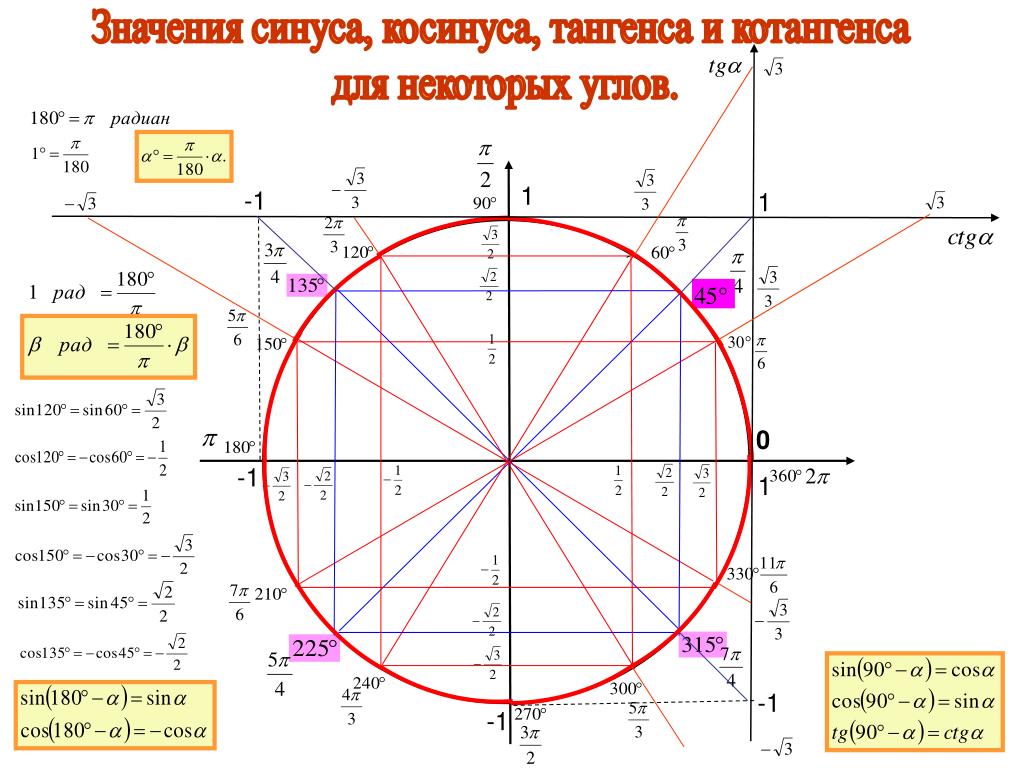 Пиковое значение.
Пиковое значение.