Как доказать что это параллелограмм. Четырехугольник является параллелограммом, если Как доказать что четырехугольник параллелограмм по координатам
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Теорема: Четырехугольник является параллелограммом, если:
- противоположные его углы равны;
- противоположные его стороны попарно равны;
- его диагонали точкой пересечения делятся пополам;
- две его противоположные стороны параллельны и равны.
Доказательство:
A. Пусть в четырехугольнике KLMN углы К и М равны друг другу и равны а, пусть также равны друг другу и равны р углы L и N (рисунок).
B. Пусть в четырехугольнике CDEF стороны CD и FE, а также CF и DE попарно равны (рисунок). Проведем одну из диагоналей четырехугольника, например СЕ. Треугольники CDE и EFC равны по трем сторонам. Поэтому углы DEC и FCE равны. Поскольку эти углы являются внутренними накрест лежащими при прямых DE и CF, пересеченных прямой СЕ, то стороны DE и CF параллельны. Также из равенства углов DCE и FEC получаем, что стороны CD и FE параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник CDEF — параллелограмм.
C. Пусть точка В пересечения диагоналей IL и КМ четырехугольника IKLM делит эти диагонали пополам: IB = BL и KB = ВМ (рисунок). Тогда треугольники KBL и MBI равны по двум сторонам и углу между ними. Это позволяет утверждать, что углы 1MB и LKB равны, а значит, стороны IM и KL параллельны. Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM. Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
Пусть точка В пересечения диагоналей IL и КМ четырехугольника IKLM делит эти диагонали пополам: IB = BL и KB = ВМ (рисунок). Тогда треугольники KBL и MBI равны по двум сторонам и углу между ними. Это позволяет утверждать, что углы 1MB и LKB равны, а значит, стороны IM и KL параллельны. Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM. Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
D. Пусть в четырехугольнике OPQR противоположные стороны ОР и RQ параллельны и равны (рисунок). Проведем диагональ OQ. Полученные углы POQ и RQO равны, так как они являются внутренними накрест лежащими при параллельных прямых ОР и RQ, пересеченных прямой OQ. Поэтому треугольники OPQ и RQO равны по двум сторонам и углу между ними. Значит, их соответствующие углы PQO и ROQ равны.
А поскольку они являются внутренними накрест лежащими углами при прямых PQ и OR, пересеченных прямой OQ, то стороны PQ и OR параллельны. Учитывая параллельность сторон ОР и RQ, по определению параллелограмма утверждаем, что четырехугольник OPQR — параллелограмм.
Учитывая параллельность сторон ОР и RQ, по определению параллелограмма утверждаем, что четырехугольник OPQR — параллелограмм.
Доказательство что ABCD-параллелограмм и получил лучший ответ
Ответ от Николай Цегельник[гуру]
Как доказать, что четырехугольник — параллелограмм
Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
AB ∥ CD, AD ∥ BC.
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
это могут быть пары треугольников
1) ABC и CDA,
2) BCD и DAB,
3) AOD и COB,
4) AOB и COD.
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
4) Четырехугольник — параллелограмм, если у него противоположные стороны попарно равны.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
Николай Цегельник
Мастер
(1657)
Ну правила я написал. Тебе осталось только расписать их под каждый пример. Тут вряд ли кто то будет решать примеры полностью я в том числе. Тем более все 9 примеров. Тут только на 1 пример писанины на пол листа.
Ответ от Александр Ульшин [новичек]
Урок в грузинской школе.
— Гоги, нарисуй на доске равнобэдрэный трэугольник.
— Нарысовал
— А тэпэрь дакажи, што этот трэугольник — равнобэдрэный!
— Мамой клянус!
Ответ от Vercia n [гуру]
1. ВС=АД; ВС||АД > АВСД — параллелограмм
Ответ от 3 ответа [гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Доказательство что ABCD-параллелограмм
Ответ от 3 ответа [гуру]
Признаки параллелограмма.
 Формулировка и доказательства
Формулировка и доказательстваПризнаки параллелограмма. а) Если в выпуклом четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм. б) Если в выпуклом четырёхугольнике противоположные стороны попарно равны, то такой четырёхугольник — параллелограмм. в) Если диагонали выпуклого четырёхугольника, пересекаясь, делятся пополам, то такой четырёхугольник — параллелограмм.
Доказательство первого признака параллелограмма. Если в выпуклом четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник, и известно, что стороны AB и CD равны и параллельны. И надо доказать, что ABCD — параллелограмм. Рассмотрим треугольники ABC и ADC. В них AC — общая сторона, стороны AB и CD равны, и углы BAC и DCA равны как накрест лежащие при ПАРАЛЛЕЛЬНЫХ и СЕКУЩЕЙ. Значит, треугольники равны по первому признаку. Значит, их соответственные углы BCA и DAC равны, а эти углы накрест лежащие при параллельных боковых сторонах и секущей диагонали. То есть боковые стороны тоже параллельны, то есть четырёхугольник — параллелограмм. ЧТД.
То есть боковые стороны тоже параллельны, то есть четырёхугольник — параллелограмм. ЧТД.
Доказательство второго признака параллелограмма. Если в выпуклом четырёхугольнике противоположные стороны попарно равны, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник ABCD. И про него известно, что AB=CD и BC=AD. И надо доказать, что этот четырёхугольник ABCD — параллелограмм.Рассмотрим треугольники ABC и ADC. У них AC — общая сторона, AB=CD и BC=AD значит, треугольники равны по третьему признаку, а значит углы DCA и BAC равны, а они накрест лежащие при верхней и нижней сторонах и секущей диагонали, а значит верхняя и нижняя стороны параллельны. Также углы DAC и BCA равны, а они накрест лежащие при боковых сторонах и секущей диагонали. Значит, и боковые стороны четырёхугольника тоже параллельны, значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказательство третьего признака параллелограмма. Если диагонали выпуклого четырёхугольника точкой своего пересечения делятся пополам, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник ABCD и про него известно, что его диагонали BD и AC точкой своего пересечения E делятся на равные половинки, то есть AE=CE и BE=DE. И надо доказать, что этот четырёхугольник ABCD — параллелограмм. Чтобы доказать, мы рассмотрим треугольники ADE и CBE. В этих треугольниках углы BEC и DEA равны как вертикальные. Стороны BE и DE равны по условию, и стороны AE и CE — тоже равны по условию. Значит, треугольники равны по 1-му признаку. Это значит, что их соответственные углы BCE и DAE равны, а эти углы являются накрест лежащими при двух боковых сторонах и секущей AC, следовательно, боковые стороны четырёхугольника — AD и BC — параллельны. Теперь рассмотрим треугольники EAB и ECD. В этих треугольниках углы BEA и DEC равны, как вертикальные. Стороны BE и DE равны по условию и стороны AE и CE — равны по условию. Следовательно и эти треугольники тоже равны по первому признаку. Это значит, что их соответственные углы BAE и DCE равны, а эти углы являются накрест лежащими при верхней и нижней сторонах AB и CD и секущей диагонали AC.
Доказательство. Вот наш четырёхугольник ABCD и про него известно, что его диагонали BD и AC точкой своего пересечения E делятся на равные половинки, то есть AE=CE и BE=DE. И надо доказать, что этот четырёхугольник ABCD — параллелограмм. Чтобы доказать, мы рассмотрим треугольники ADE и CBE. В этих треугольниках углы BEC и DEA равны как вертикальные. Стороны BE и DE равны по условию, и стороны AE и CE — тоже равны по условию. Значит, треугольники равны по 1-му признаку. Это значит, что их соответственные углы BCE и DAE равны, а эти углы являются накрест лежащими при двух боковых сторонах и секущей AC, следовательно, боковые стороны четырёхугольника — AD и BC — параллельны. Теперь рассмотрим треугольники EAB и ECD. В этих треугольниках углы BEA и DEC равны, как вертикальные. Стороны BE и DE равны по условию и стороны AE и CE — равны по условию. Следовательно и эти треугольники тоже равны по первому признаку. Это значит, что их соответственные углы BAE и DCE равны, а эти углы являются накрест лежащими при верхней и нижней сторонах AB и CD и секущей диагонали AC. Значит, стороны AB и CD тоже параллельны, то есть четырёхугольник ABCD — параллелограмм, ЧТД.
Значит, стороны AB и CD тоже параллельны, то есть четырёхугольник ABCD — параллелограмм, ЧТД.
← Предыдущий урок
Оглавление
Следующий урок →
Когда четырехугольник является параллелограммом?
Я думаю о четырехугольнике, у которого одна пара противоположных сторон параллельна и конгруэнтна. Назовите этот четырехугольник.
Я думаю о четырехугольнике, у которого две пары противоположных сторон равны. Назовите этот четырехугольник.
Я думаю о четырехугольнике, у которого обе пары противоположных углов равны. Назовите этот четырехугольник.
Я думаю о четырехугольнике, диагонали которого пересекаются пополам. Назовите этот четырехугольник.
Если вы ответили «параллелограмм» на все вышеперечисленное, вы правы! Конечно, вы уже знаете, что недостаточно заявить, что я думаю о параллелограмме. В машине есть сомневающиеся, так что придется доказывать.
Противоположные стороны конгруэнтны и параллельны
Ваша первая подсказка «Назови этот четырехугольник» заключалась в том, что одна пара противоположных сторон параллельна и конгруэнтна.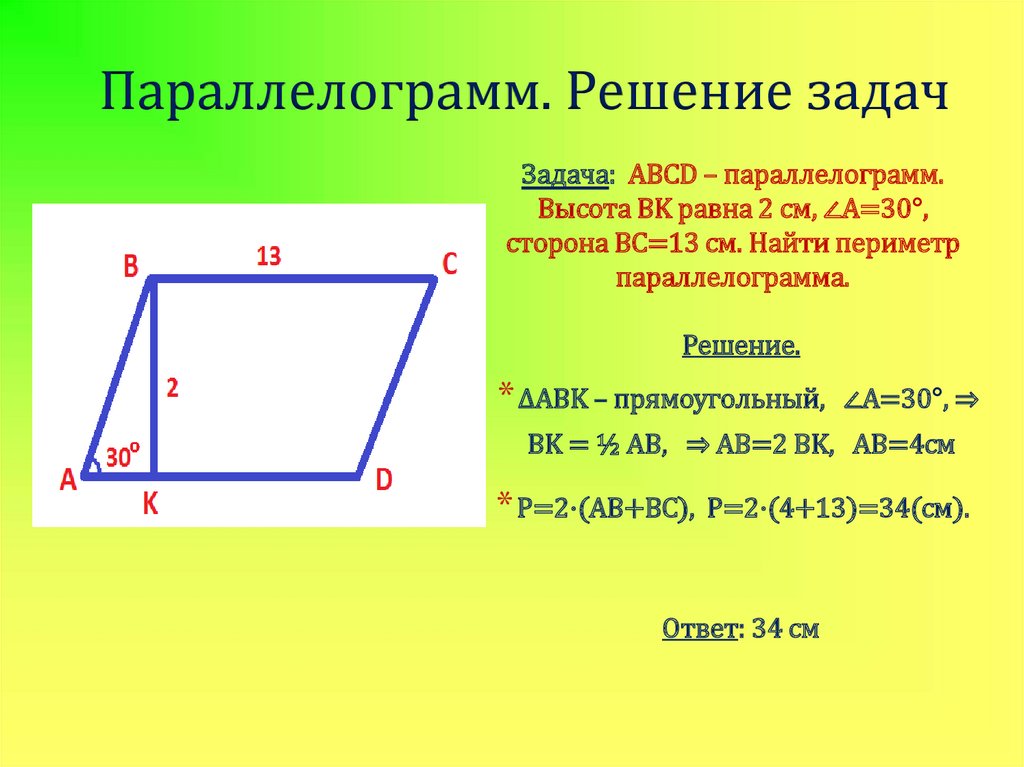 Я назову это теоремой и напишу доказательство в два столбца. Рисунок 16.1 поможет вам визуализировать ситуацию.
Я назову это теоремой и напишу доказательство в два столбца. Рисунок 16.1 поможет вам визуализировать ситуацию.
Рисунок 16.1 Четырехугольник ABCD с ¯BC и ¯BC ~= ¯AD.
- Теорема 16.1 : Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то четырехугольник является параллелограммом.
Вот план игры. Предположим, что ¯BC ¯AD и ¯BC ~= ¯AD. По определению, параллелограмм — это четырехугольник, у которого две пары противоположных сторон параллельны. Вы уже знаете, что одна пара противоположных сторон параллельна. Вам нужно показать, что другая пара противоположных сторон параллельна. Другими словами, нужно показать, что ¯AB ¯CD.
Вы можете посмотреть на этот четырехугольник двумя способами. Первый способ — сосредоточиться на отрезках ¯BC и ¯AD, пересекаемых секущей ¯AC. Тогда BCA и DAC являются альтернативными внутренними углами и равны, так как ¯BC ¯AD. Второй способ — перевернуть его на бок.
| Заявления | Причины | ||||||
|---|---|---|---|---|---|---|---|
| 1. | Четырехугольник ABCD с ¯BC ¯AD и ¯BC ~= ¯AD. | Указано | |||||
| 2. | ¯BC ¯AD CUT с помощью поперечного ¯AC | Определение трансверса | |||||
| 3. | BACD и ACD — ACD | ||||||
| 3. | BACD и ACD — ACD | ||||||
| 3. | ACD ACD — ACD | ||||||
| ACD ACD — ACD | . | ||||||
| 4. | БКА ~= ЦАП | Theorem 10.2 | |||||
| 5. | ¯AC ~= ¯AC | Reflexive property of ~= | |||||
6. | DAC ~= BCA | SAS Postulate | |||||
| 7. | BAC ~ = ACD | CPOCTAC | |||||
| 8. | ¯ab и ¯cd — два сегмента, вырезанные по трансверсуснику ¯ac | .0040 Определение альтернативных внутренних углов | |||||
| 10. | ¯ab ¯cd | Теорема 10.8 | |||||
| 11. | Кваровной ABCD — параллельплама | Кваровдерная ABCD — параллельплама | Кваровдерная ABCD — параллельплама | 040 | . |
Теперь, когда вы правильно назвали этот четырехугольник, вы можете перейти к следующему четырехугольнику.
Две пары конгруэнтных сторон
Во второй игре «Назови этот четырехугольник» у четырехугольника было две пары конгруэнтных сторон. Давайте запишем это как теорему и отложим ее.
- Теорема 16.2 : Если обе пары противоположных сторон четырехугольника конгруэнтны, то этот четырехугольник является параллелограммом.

У нас есть визуал на рис. 16.2. У нас есть параллелограмм ABCD с ¯AB ~= ¯CD и ¯BC ~= ¯AD. План игры состоит в том, чтобы разделить четырехугольник на два треугольника с помощью диагонали ¯AC. Используйте постулат SSS, чтобы показать, что два треугольника конгруэнтны, и используйте CPOCTAC, чтобы сделать вывод, что альтернативные внутренние углы конгруэнтны, а противоположные стороны должны быть параллельны. Если мы покажем это для обеих пар противоположных сторон, то получим параллелограмм по определению. Пришло время написать подробности.
Рисунок 16.2 Четырехугольник ABCD с ¯AB ~= ¯CD и ¯BC ~= ¯AD
| Заявления | Причины | ||
|---|---|---|---|
| 1. | Квадратный ABCD с ¯AB ~ = ¯CD и ¯BC ~ = ¯AD | . | Рефлексивное свойство ~= |
| 3. | ABC ~= CDA | SSS Постулат | |
| 4. | BAC ~= DAC | CPOCTAC | |
5. | ¯BC и ¯AD — два сегмента, вырезанные по трансверляльному ¯AC | Определение Angle Angle | . Углы интерьера|
| 7. | ¯BC ¯AD | Теорема 10,8 | |
| 8. | ¯ab и ¯cd — это два сегмента, вырезанные по трансверсл ¯caC | 000000000000000.0041 | |
| 9. | BAC и ACD — альтернативные внутренние углы | Определение альтернативных внутренних углов | |
| 10. | ¯ab ¯cd | ТООРЕМА 10.8 | Определение параллелограмма |
И снова сладкий вкус победы! Вы правильно назвали этот четырехугольник. Следующий!
Две пары равных углов
Третье описание четырехугольника включало конгруэнтность обеих пар противоположных углов. Я сформулирую теорему и воспользуюсь рис. 16.3, чтобы провести вас через доказательство.
Рисунок 16.3 Четырехугольник ABCD, где A ~= C и B ~= D.
- Теорема 16.3 : Если обе пары противоположных углов четырехугольника равны, то четырехугольник является параллелограммом.
Начать нужно с углов. Поскольку суммы внутренних углов четырехугольника в сумме составляют 360º, можно показать, что mA + mB = 180º, или что A и B являются дополнительными углами. Теперь вы можете посмотреть на этот четырехугольник в следующем свете: ¯BC и ¯AD — два отрезка, пересекаемые секущей ¯AB. Обычно секущей была ¯AC, но на этот раз вы будете использовать ¯AB. Поскольку два ваших угла по одну сторону от трансверсали являются дополнительными, теорема 10.10 говорит вам, что ¯BC ¯AD. Аналогичное рассуждение показывает, что ¯AB ¯CD.
| Заявления | Причины | |
|---|---|---|
| 1. | Квадратный ABCD с ~ = C и B ~ = D | Данный |
| 2. | .мА + мБ + мКл + мД = 360º | Внутренние углы четырехугольника в сумме дают 360º |
3. | мА + мБ + мА + мБ = 360º | Замена (шаги 1 и 2) |
| 4. | мА + мБ = 180º | Алгебра |
| 5. | A и B являются дополнительными углами | Определение дополнительных углов |
| 6. | ¯BC и ¯AD два отрезка, разделенные секущей ¯AB | Определение секущей |
| 7. | ¯ до н.э. ¯ | н.э.Теорема 10.10 |
| 8. | ¯AB и ¯CD — два отрезка, пересекаемые секущей ¯AD | Определение поперечного сечения |
| 9. | мА + мД = 180º | Замена (шаги 1 и 4) |
| 10. | A и D являются дополнительными углами | Определение дополнительных углов |
| 11. | ¯AB ¯CD | Теорема 10.10 |
| 12. | Четырехугольник ABCD является параллелограммом | Определение параллелограмма |
Диагонали, делящиеся пополам
Ах, последняя игра этой серии! Если у вас есть четырехугольник, диагонали которого делят друг друга пополам, то ваш четырехугольник является параллелограммом.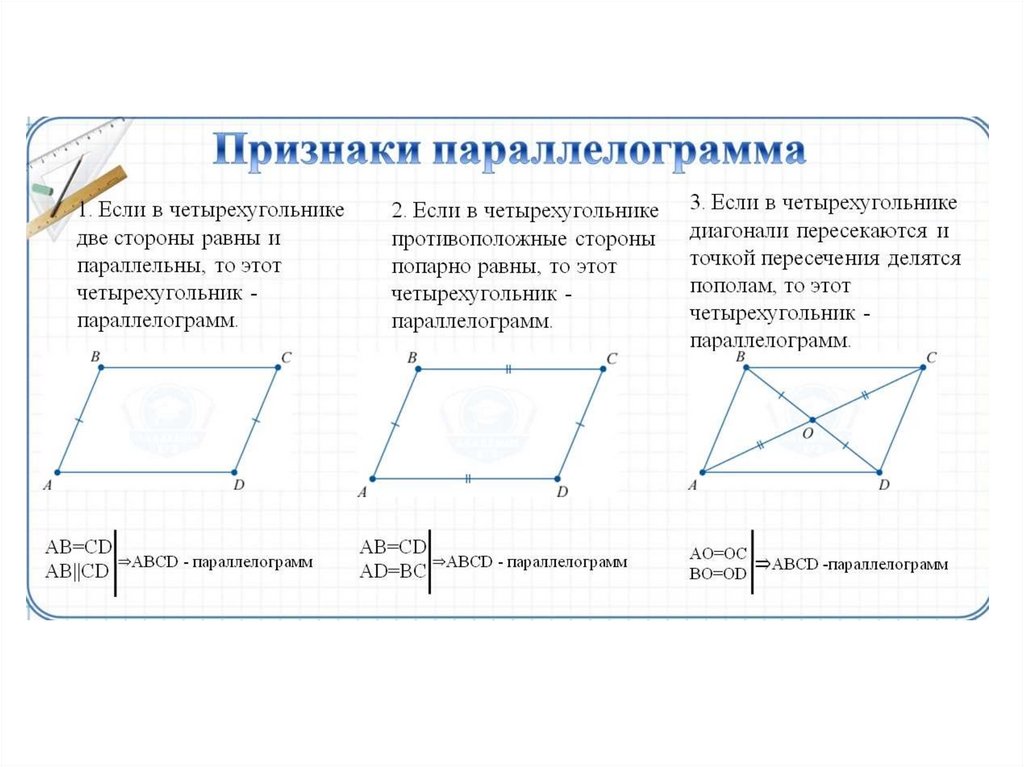 На рис. 16.4 показан параллелограмм ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
На рис. 16.4 показан параллелограмм ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
Рисунок 16.4 Четырехугольник ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
- Теорема 16.4 : Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом.
Если вы посмотрите на рис. 16.4, план игры для доказательства этой теоремы должен прозвучать громко и ясно. Вы воспользуетесь теоремой 16.2: пары противоположных сторон параллелограмма равны. Две диагонали делят параллелограмм на четыре треугольника. Поскольку диагонали делят друг друга пополам, ¯AM ~= ¯MC и ¯BM ~= ¯MD. Поскольку вертикальные углы конгруэнтны, вы можете использовать постулат SAS, чтобы показать, что AMB ~= BMC и AMB ~= DMC. Отсюда нужно применить CPOCTAC, чтобы показать, что обе пары противоположных сторон конгруэнтны.
| Заявления | Причины | |
|---|---|---|
1. | Четырехугольник ABCD с диагоналями ¯AC и ¯BD, которые пересекаются в точке M и делят друг друга пополам | Дано |
| 2. | ¯AM ~= ¯MC и ¯BM ~= ¯MD | Определение деления пополам |
| 3. | AMB ~= CMD и AMD ~= BMC | Теорема 8.1 |
| 4. | драм ~= BMC и AMB ~= DMC | Постулат САС |
| 5. | ¯BC ~= ¯AD и ¯AB ~= ¯CD | КПОКТАК |
| 6. | Четырехугольник ABCD является параллелограммом | .Теорема 16.2 |
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , член Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Раздел 4.2: Доказательство того, что четырехугольник является параллелограммом
Section_4_2Section_4_1По определению параллелограмма, мы знаем, что если обе пары противоположных сторон четырехугольники параллельны, то этот четырехугольник параллелограмм. Есть и другие способы доказать, что четырехугольник является параллелограммом, и здесь мы устанавливаем теоремы, которые помогут нам в этом.
- Теорема 4.5:
Если обе пары противоположных сторон четырехугольника равны, то
четырехугольник является параллелограммом.
Доказательство (схема). Вводя диагональ и доказывая, что два образовавшихся треугольника равны, мы можем получить пары чередующихся внутренние углы равны. Это приводит к противоположным сторонам четырехугольник параллельный, что делает четырехугольник a параллелограмм.
- Теорема 4.
 6:
Если одна пара противоположных сторон четырехугольника равны и
параллельны, то этот четырехугольник является параллелограммом.
6:
Если одна пара противоположных сторон четырехугольника равны и
параллельны, то этот четырехугольник является параллелограммом.
Доказательство (схема): Опять же, введя диагональ и доказав конгруэнтных треугольников, мы можем показать, что обе пары противоположных сторон четырехугольники конгруэнтны; то у нас есть параллелограмм Теорема 4.5.
- Теорема 4.7: Если обе пары противоположных углов четырехугольника равны, то четырехугольник является параллелограммом.
| Дано: $\угол A\конг
\angle C$ и $\angle B\cong \angle D$ Докажите, что $ABCD$ параллелограмм. | |
Доказательство:
Теорема 3.14 мы знаем, что сумма мер углов a
четырехугольник равен 360. Следовательно, $m\угол A+m\угол B+m\угол
C+m\угол D=360$.
Поскольку известно, что обе пары противоположных углов четырехугольника
$ABCD$ конгруэнтны, $m\угол A=m\угол C$ и $m\угол B=m\угол
Д$. Таким образом, $2m\угол A+2m\угол D=360$; затем $m\угол A+m\угол
Д=180$. Таким же образом мы можем показать, что $m\angle C+m\angle
Д=180$. Так как внутренние углы одной стороны являются дополнительными,
$\overline{AB}\parallel\overline{CD}$ и
$\overline{AD}\parallel\overline{BC}$. Это делает $ABCD$
параллелограмм по определению.
Таким образом, $2m\угол A+2m\угол D=360$; затем $m\угол A+m\угол
Д=180$. Таким же образом мы можем показать, что $m\angle C+m\angle
Д=180$. Так как внутренние углы одной стороны являются дополнительными,
$\overline{AB}\parallel\overline{CD}$ и
$\overline{AD}\parallel\overline{BC}$. Это делает $ABCD$
параллелограмм по определению.
- Теорема 4.8:
Если диагонали четырехугольника делят друг друга пополам, то
четырехугольник — параллелограмм.
Доказательство теоремы 4.8 аналогично доказательствам теорем 4.5 и 4.6 и оставим в качестве упражнения.
Часто мы говорим, что параллельные линии есть «везде». равноудаленных». Следующая теорема установит эту идею для нас.
- Теорема 4.9: Если $\ell$ и $m$ — две параллельные прямые и точки $A$ и $B$ лежат на $\ell$, то расстояние от $A$ до прямой $m$ равно расстоянию от $B$ до строки $m$.
| Дано: $\ell\parallel
m$, $\overline{AC}\perp m$ и $\overline{BD}\perp m$ Докажите: $\overline{AC}\cong \overline{BD}$ | |
Доказательство: В главе 3 мы установили, что если две строки
были перпендикулярны одной прямой, то они были параллельны каждой
другое (теорема 3.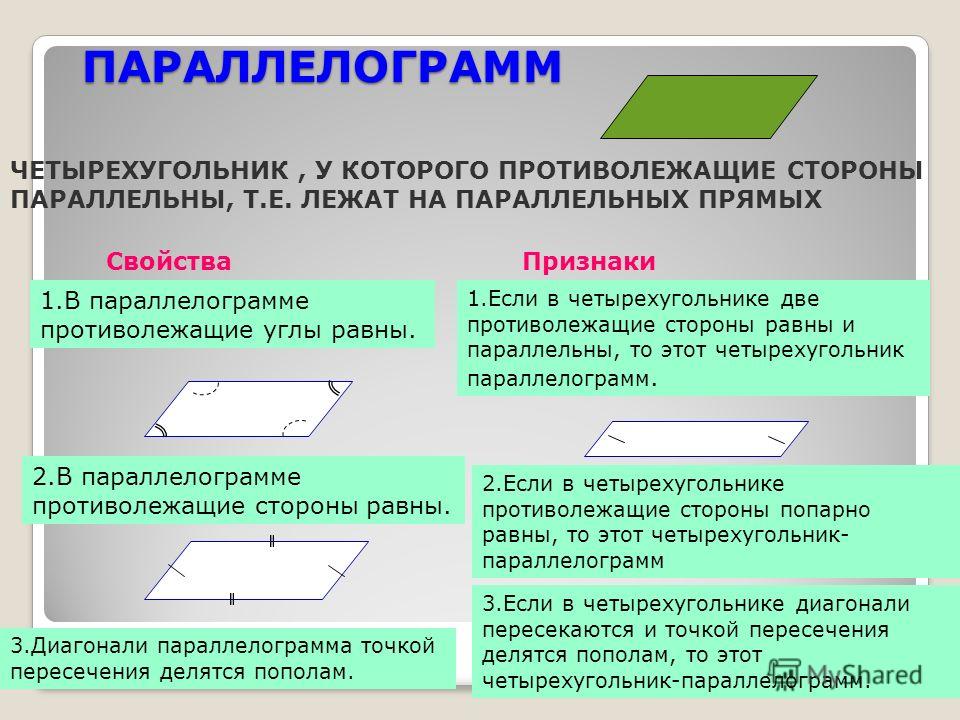 3). Это значит, что
$\overline{AC}\parallel\overline{BD}$. Нам дано, что $\ell
\параллельно м$; поэтому $\overline{AB}\parallel\overline{CD}$.
Так как обе пары противоположных сторон четырехугольника $ABCD$ равны
параллельны, по определению четырехугольник является параллелограммом.
Противоположные стороны параллелограмма равны (теорема 4.1).
Следовательно, $\overline{AC}\cong\overline{BD}$.
3). Это значит, что
$\overline{AC}\parallel\overline{BD}$. Нам дано, что $\ell
\параллельно м$; поэтому $\overline{AB}\parallel\overline{CD}$.
Так как обе пары противоположных сторон четырехугольника $ABCD$ равны
параллельны, по определению четырехугольник является параллелограммом.
Противоположные стороны параллелограмма равны (теорема 4.1).
Следовательно, $\overline{AC}\cong\overline{BD}$.
Пример: Учитывая, что плоскости $m$ и $n$ параллельны и $\overline{AC}\parallel\overline{BD}$, докажите, что $ABDC$ является параллелограмм.
Решение:
Поскольку $\overline{AC}\parallel\overline{BD}$, существует плоскость
содержащие точки $A$, $B$, $C$ и $D$. Этот самолет
пересекает две параллельные плоскости $m$ и $n$. Следовательно
линии пересечения будут параллельны. Следовательно
$\overline{AB}\parallel\overline{CD}$. Поскольку обе пары
противоположные стороны четырехугольника $ABDC$ параллельны, четырехугольник
является параллелограммом.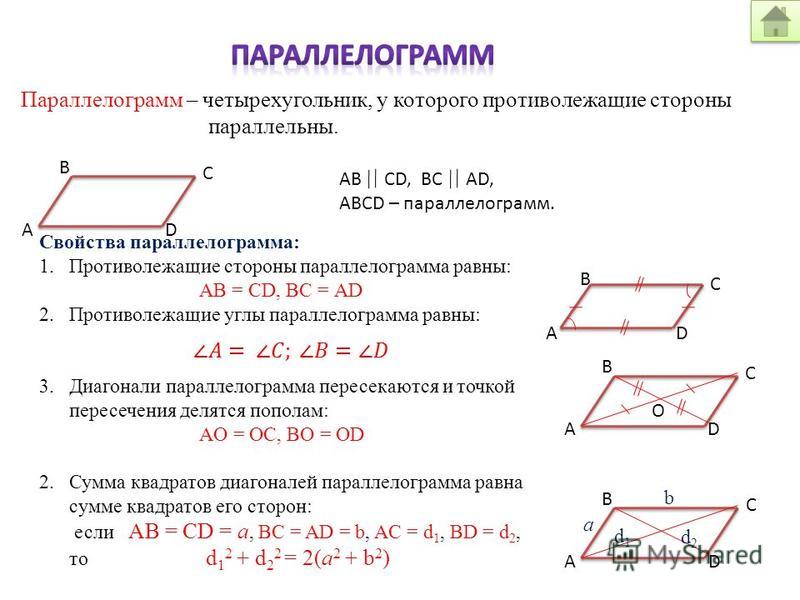 | |
Как и в конце предыдущего раздела, собираем здесь свойства, которыми может обладать четырехугольник, которые позволили бы вам утверждают, что это параллелограмм.
|
|
Что действительно важно, так это то, что вы понимаете разницу между
список выше и список в Разделе 4.1. Они выглядят очень
похожи, но есть большая
разница. Если вы напишете в качестве причины в доказательстве: «Противоположные стороны
параллелограмма конгруэнтны», вы уже должны знать (из
предыдущий шаг), что четырехугольник является параллелограммом.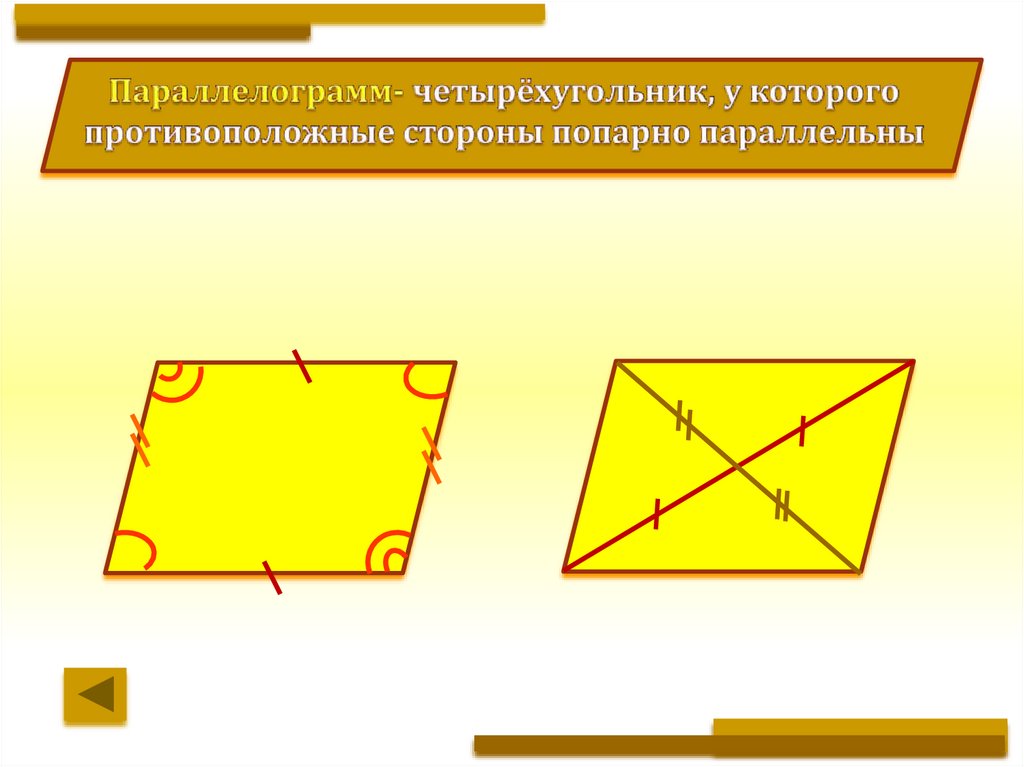


 6:
Если одна пара противоположных сторон четырехугольника равны и
параллельны, то этот четырехугольник является параллелограммом.
6:
Если одна пара противоположных сторон четырехугольника равны и
параллельны, то этот четырехугольник является параллелограммом.