Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Формула радиуса вписанной окружности в треугольник (r):
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности равнобедренный треугольник
1.
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
a — сторона квадрата
Формула радиуса вписанной окружности в квадрат (r):
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
Радиус вписанной окружности в правильный многоугольник
a — сторона многоугольника
N — количество сторон многоугольника
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Формула радиуса вписанной окружности в шестиугольник, (r):
Как найти радиус вписанной в треугольник abc окружности: формула, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Нахождение радиуса вписанной в треугольник окружности
ru Математика Геометрия Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
- Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Примеры задач
Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.
где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:
где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формула радиуса— Что такое формула радиуса? Примеры
Прежде чем мы начнем с формулы радиуса, давайте вспомним, что такое радиус.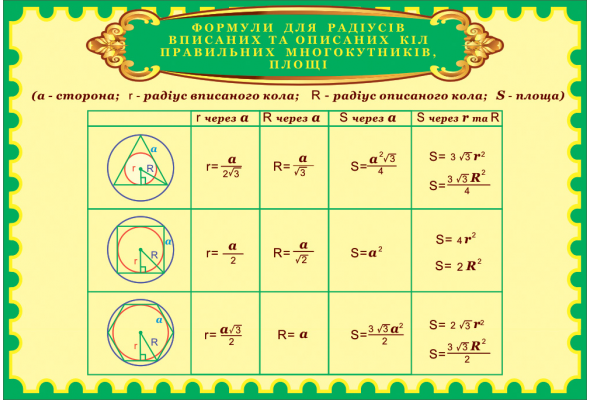 Радиус является одной из важных частей круга. Радиус – это расстояние от центра круга до любой точки на его окружности, что означает прямая линия, соединяющая центр круга с любой точкой на его окружности, называется радиусом. Поскольку на его окружности бесконечное количество точек, это означает, что круг имеет бесконечное число радиусов, и каждый радиус круга равноудален от центра круга.
Радиус является одной из важных частей круга. Радиус – это расстояние от центра круга до любой точки на его окружности, что означает прямая линия, соединяющая центр круга с любой точкой на его окружности, называется радиусом. Поскольку на его окружности бесконечное количество точек, это означает, что круг имеет бесконечное число радиусов, и каждый радиус круга равноудален от центра круга.
Мы можем найти радиус круга, когда известны диаметр, площадь или длина окружности.
Формулы радиуса
Формула радиуса 1: Радиус равен половине длины диаметра. Если диаметр круга известен, то формула радиуса выражается следующим образом:
Формула радиуса = Диаметр/2 или D/2 единиц
Формула радиуса 2: Радиус – это отношение длины окружности к 2π. Если длина окружности известна, то формула радиуса выражается так:
Формула радиуса = длина окружности/2π или единиц C/2π
Формула радиуса 3: Мы можем вывести формулу радиуса, используя формулу площади круга, которая представляет собой Площадь = π(Радиус) 2 . Если известна площадь круга, то формула радиуса выражается так:
Если известна площадь круга, то формула радиуса выражается так:
Формула радиуса = √(Площадь/π) единиц
Давайте изучим формулу радиуса на нескольких примерах решения.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры формулы радиуса
Пример 1: Найдите радиус круга, диаметр которого составляет 24 дюйма. (Подсказка: используйте формулу радиуса, когда известен диаметр)
Решение: Мы будем использовать формулу радиуса, когда известен диаметр окружности. Что выражается как.
Радиус = Диаметр/2
Г = 24 дюйма
R = 24/2 = 12 дюймов
Ответ: Радиус данной окружности равен 12 дюймам.
Пример 2: Найдите радиус круга, длина окружности которого составляет 4π единиц. (Подсказка: используйте формулу радиуса, если длина окружности известна)
(Подсказка: используйте формулу радиуса, если длина окружности известна)
Решение:
Мы будем использовать следующую формулу радиуса, чтобы найти радиус окружности.
Радиус = Окружность/2π
C = 4πединиц
Радиус = 4π/2π = 2 единицы
Ответ: Радиус данной окружности равен 2 единицам.
Пример 3: Найдите радиус круга, площадь которого 4π единиц 2 . (Подсказка: используйте формулу радиуса, когда известна площадь круга)
Решение:
Мы будем использовать следующую формулу радиуса, чтобы найти радиус круга.
Формула радиуса = √(Площадь/π)
Площадь = 4π единиц 2
R = √(4π/π)
Радиус = 2 единицы
Ответ: Радиус данной окружности равен 2 единицам.
Часто задаваемые вопросы о формуле радиуса
Что такое формула радиуса, когда известна площадь круга?
Если площадь круга указана в квадратных единицах, то легко вывести формулу радиуса, как показано ниже:
Площадь = π(радиус) 2
Формула для радиуса = √(площадь/π) единиц
Какая формула радиуса, если известен диаметр круга?
Если диаметр окружности дан в единицах «x», то легко вывести формулу радиуса, как указано ниже:
Диаметр = 2р.
Формула радиуса = диаметр/2 единицы
Что такое формула радиуса, когда известна длина окружности?
Если длина окружности дана в единицах x, то легко вывести формулу радиуса, как указано ниже:
Окружность = 2πr.
Формула для радиуса = длина окружности/2π единиц
Как найти длину окружности с помощью формулы радиуса?
Если задан радиус круга, то путем подстановки данных значений в следующую формулу радиуса мы можем легко найти длину окружности.
Формула для радиуса = длина окружности/2π.
C = 2πr единиц.
Радиус круга — определение, формула, примеры решений и часто задаваемые вопросы
Формула радиуса равна половине диаметра круга. Расстояние между центром и окружностью круга называется радиусом круга. Диаметр окружности — это наибольшая хорда любой окружности, проходящая через ее центр, она всегда вдвое больше радиуса.
Что такое радиус?
Радиус — это отрезок, соединяющий центр круга или сферы с его периферией или границами.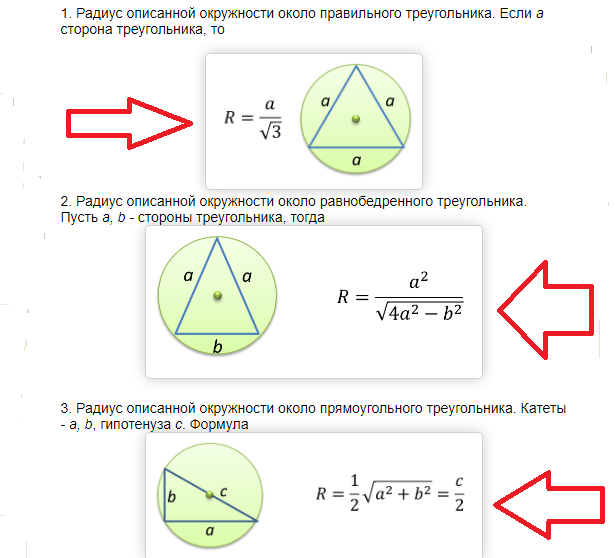 Это компонент кругов и сфер, который обычно обозначается аббревиатурой «r». Множественное число слова «радиус» — «радиусы», которое используется при одновременном обсуждении более чем одного радиуса. Диаметр круга или сферы — это самый длинный отрезок, соединяющий все точки, находящиеся на противоположной стороне от центра, при этом радиус равен половине длины диаметра.
Это компонент кругов и сфер, который обычно обозначается аббревиатурой «r». Множественное число слова «радиус» — «радиусы», которое используется при одновременном обсуждении более чем одного радиуса. Диаметр круга или сферы — это самый длинный отрезок, соединяющий все точки, находящиеся на противоположной стороне от центра, при этом радиус равен половине длины диаметра.
Radius Formula
Radius of a circle is calculated with some specific formulas which are given below in the table
Формула радиуса из диаметра
Radius in Terms of Diameter d ⁄ 2 Радиус с точки зрения окружности C ⁄ 2π Радиус в терминах области √ (a π) √ (a π) √ (a π π) √ (a π) √ (A0149 где
d — диаметр,
C — длина окружности,
A — площадь.
Радиус равен половине диаметра. то есть Диаметр = 2 × радиус . Диаметр — это наибольшая хорда любого круга.
Формула радиуса из длины окружностиРадиус = диаметр / 2
Длина окружности – это измерение периметра окружности, ее формула представлена как
C = 2πr
, где,
C — окружность
R — это Radius
π — это постоянное со значением 3,14
отношение длины окружности к 2π. Формула радиуса с использованием длины окружности:
Формула радиуса из площадиРадиус = длина окружности / 2π
Пространство, занимаемое кругом, называется его площадью. Формула для Площадь круга = πr 2 квадратных единиц определяет отношение радиуса любого круга к его площади. Здесь r представляет радиус, а константа π равна 3,14159. Формула радиуса с использованием длины окружности выглядит следующим образом:
Здесь r представляет радиус, а константа π равна 3,14159. Формула радиуса с использованием длины окружности выглядит следующим образом:
Как рассчитать радиус окружности?Радиус = √(Площадь / π) единиц
Радиус окружности можно найти с помощью трех основных формул радиуса в зависимости от различных условий, когда дан диаметр, когда дана площадь, и когда известна длина окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.
- Если Диаметр известен. Радиус = диаметр / 2
- Если длина окружности известна. Радиус = Окружность / 2π
- Если площадь известна. Радиус = √(Площадь круга/π)
Например,
- Если диаметр равен 28 см, то радиус R = 28/2 = 14 см
- Когда длина окружности круг равен 66 см, тогда радиус R = 66/2π = 10,5 см
- Когда площадь круга равна 154 см 2 , тогда радиус равен R = √(154/π) = 7 см
Радиус сферы
Сфера представляет собой твердую трехмерную форму. Радиус сферы — это расстояние между ее центром и любой точкой на ее поверхности. Радиус сферы легко вычислить, если задан объем сферы или площадь поверхности сферы.
Радиус сферы — это расстояние между ее центром и любой точкой на ее поверхности. Радиус сферы легко вычислить, если задан объем сферы или площадь поверхности сферы.
Радиус сферы (когда задан объем) R = 3 √{(3V) / 4π} единиц
где
V представляет объем
π является константой со значением приблизительно 3,14
Радиус сферы (если задана площадь поверхности) R = √(A / 4π) единиц
где
A 490920 представляет площадь поверхности 0 π константа со значением приблизительно 3,14
Уравнение радиуса окружности
Уравнение окружности на декартовой плоскости с центром (h, k) задается как (x − h) 2 + ( у — к) 2 = г 2 . Где (x, y) — геометрическое место любой точки на окружности круга, а «r» — радиус круга. Если начало координат (0,0) становится центром окружности, то ее уравнение задается как x 2 + y 2 = r 2 .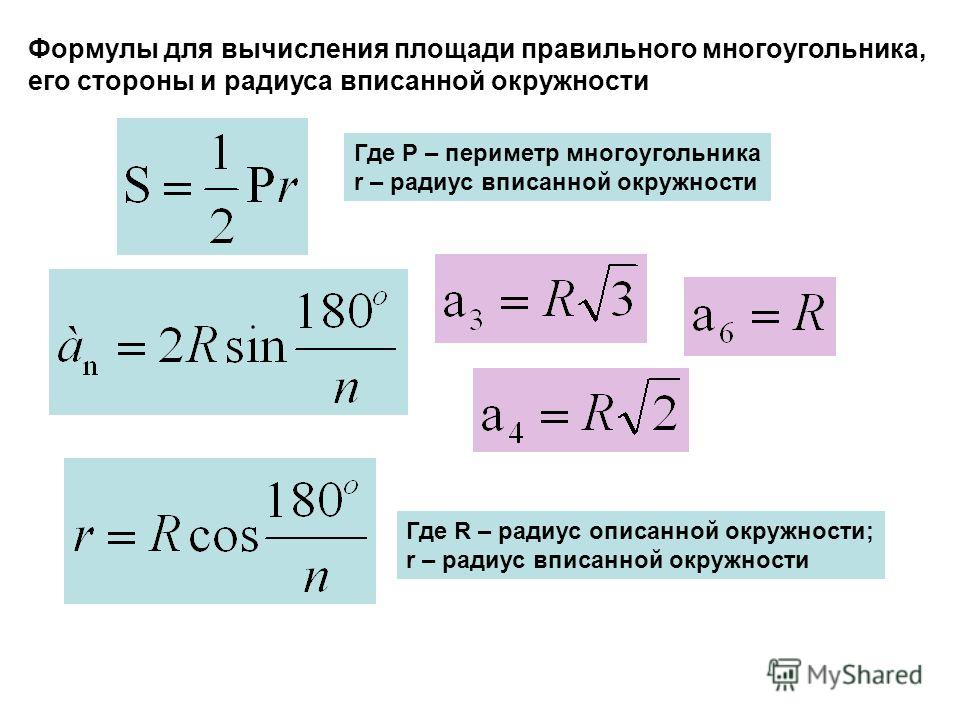 Для нахождения радиуса окружности используется следующая формула:
Для нахождения радиуса окружности используется следующая формула:
(Радиус) r = √( x 2 + y 2 )
Решенный пример по формулам радиуса
радиус окружности, диаметр которой равен 18 см.
Решение:
Дано, диаметр круга = D = 18 см
Радиус круга с помощью диаметра,
радиус = (диаметр ⁄ 2)
= 18 ~ 2 см
= 9 см.Следовательно, радиус окружности равен 9 см.
Пример 2: Найдите радиус круга с длиной окружности 14 см.
Решение:
Радиус круга с длиной окружности 14 см можно рассчитать по формуле
Радиус = Окружность / 2π
r = C / 2π
r = 14 / 2π {значение π = 22/7}
r = (14 × 7) / (2 × 22)
r = 98 / 44
r = 2,22 см
Следовательно, радиус данной окружности равен 2,22 см
Пример 3: Найдите площадь и длину окружности, радиус которой равен 12 см. (Возьмем значение π = 3,14)
(Возьмем значение π = 3,14)
Решение:
Дано: Радиус = 12 см.
Площадь круга = π r 2
= 3,14 × (12) 2a = 452,6 см 2
Сейчас округа круга,
C = 2πr
C = 2 × 3,14 × 12C = 2πr
C = 2 × 3,14 × 12.
Следовательно, площадь круга равна 452,6 см 2 , а длина окружности равна 75,36 см
Пример 4. Чему равен радиус круга, если площадь равна 42 м 2 ?
Решение:
Дано: Площадь круга, A = 42 м 2 .
Радиус круга с использованием площади можно рассчитать по формуле: радиус = √(A/π). Так, радиус длина окружности 13,36 м
Пример 5. Найдите диаметр окружности, зная, что площадь окружности численно равна удвоенной длине ее окружности.
Дано,
Площадь круга = 2 × окружность
, мы знаем,
Площадь круга = π r 2
Окружность = 2πrСледовательно,
=> π r 2 = 2.
× 2 × π × r
=> r = 4
Следовательно,
диаметр = 2 × радиус
=> Диаметр = 2 × 4
= 8 единиц
FAQS на радиусе
Вопрос 10177 FAQ : Каков радиус единичного круга?
Ответ:
Единичная окружность – это окружность с радиусом в 1 единицу
Вопрос 2: Каково соотношение между радиусом и диаметром окружности?
Ответ:
Диаметр круга в два раза больше радиуса круга.
Диаметр = 2 × радиус
Вопрос 3: Найдите радиус окружности, зная площадь.
Ответ:
Когда площадь круга дана, формула для радиуса – это радиус,
R = √(A/π) единиц
где
A – площадь круга.
Связанные ресурсы
- Квадрат
- Треугольник
- Трапеция
Диаметр круга в два раза больше радиуса, или радиус равен половине диаметра.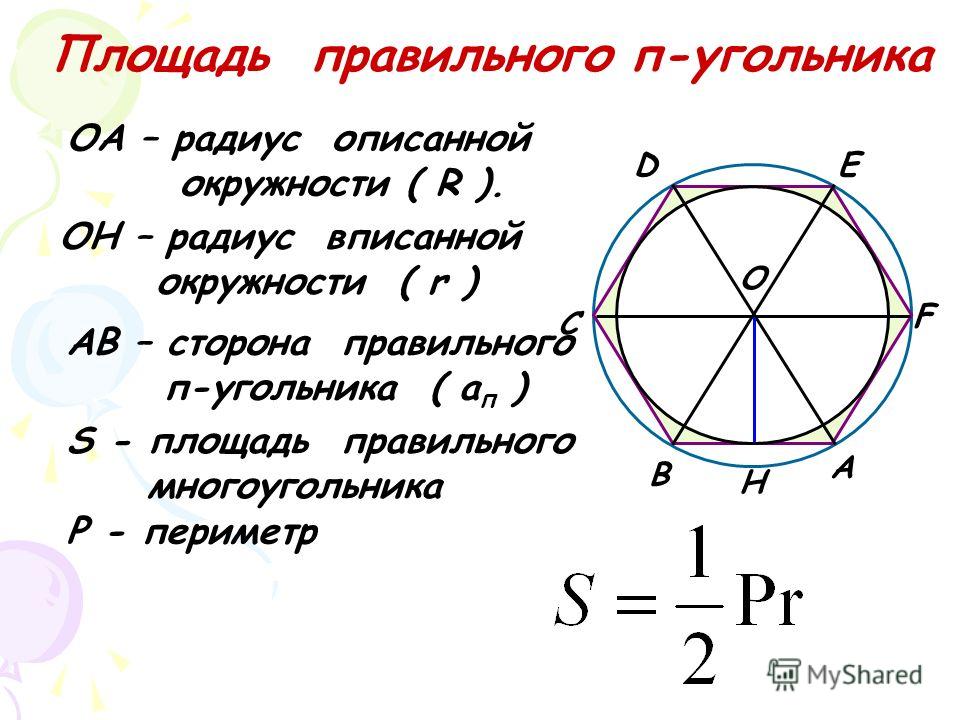

 × 2 × π × r
× 2 × π × r