Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Серединный перпендикуляр к отрезку |
| Окружность описанная около треугольника |
| Свойства описанной около треугольника окружности. Теорема синусов |
| Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию.
Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2.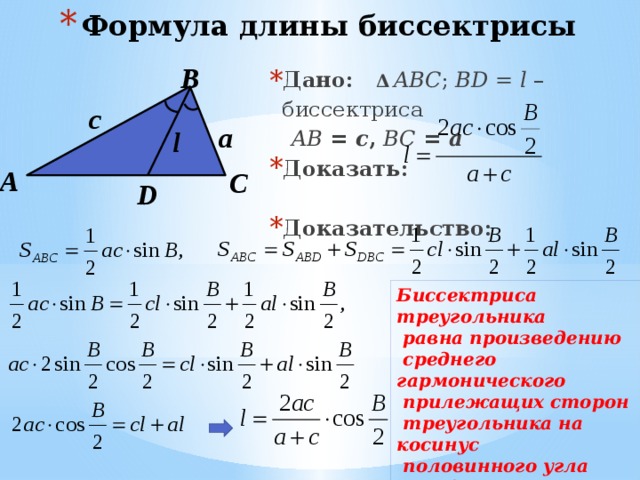
Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.
Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | |
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов | Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Площадь треугольника | Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Радиус описанной окружности | Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Серединные перпендикуляры к сторонам треугольника |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |
Около любого треугольника можно описать окружность. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |
Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.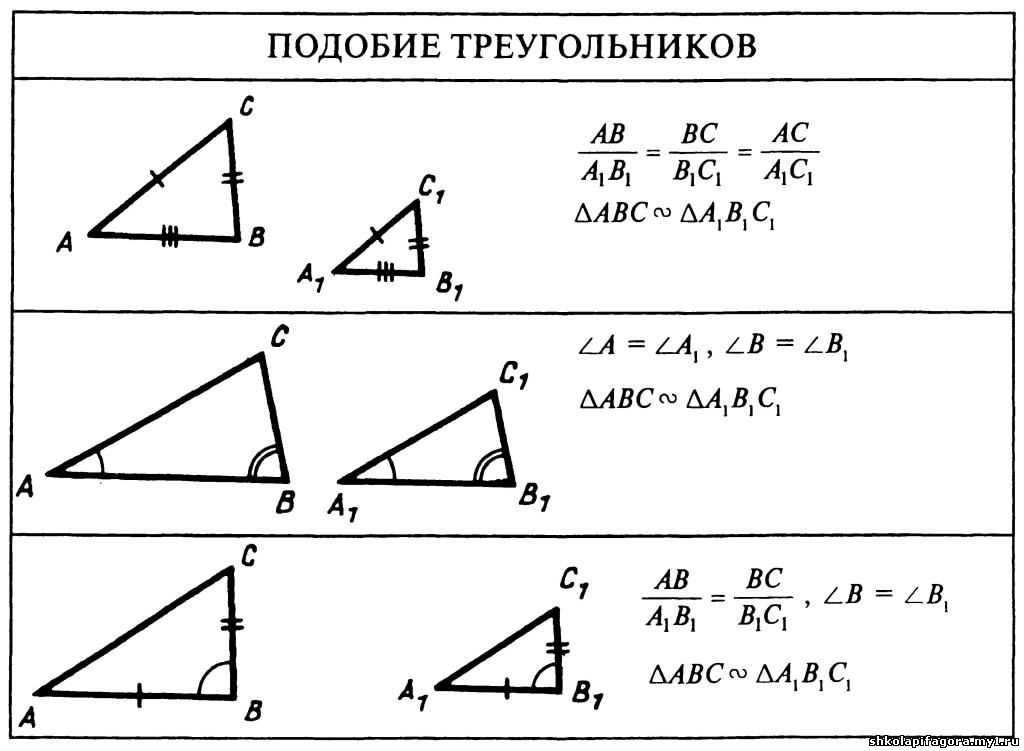
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).
Рис.6
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)
Рис.7
справедливы равенства:
.
Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
l = 2Rsin φ . | (1) |
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Рис.8
Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Теорема синусов доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Прямоугольный треугольник формулы — Математическая шкатулка
mathembox 14 комментариев
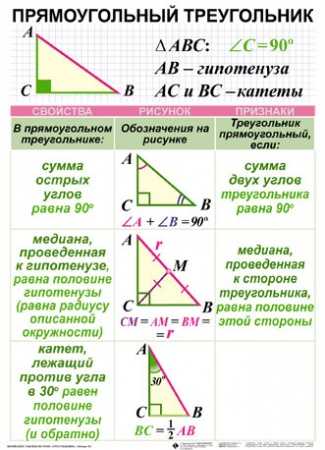
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.
Прямоугольный треугольник: основные формулы
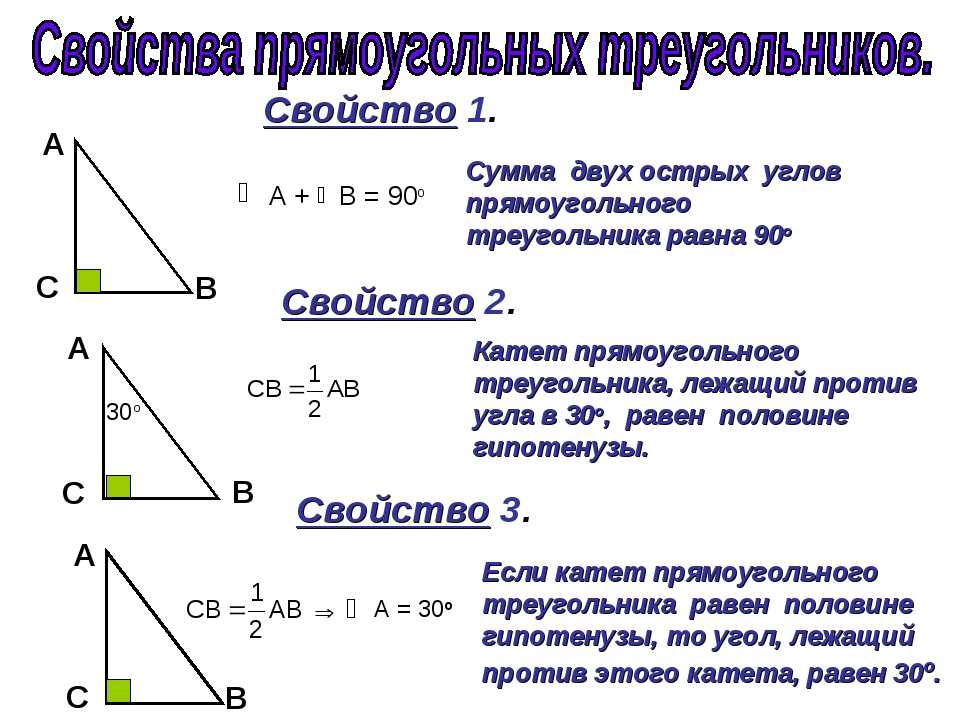
- Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
- Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. AB2 = AC2 + CB2
Прямоугольный треугольник: формулы площади и проекции
- Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
- Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH2 = AH·BH.
- Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA2 = AB·AH; CB2 = AB·BH.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
- Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
- Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.
Прямоугольный треугольник: формулы тригонометрия
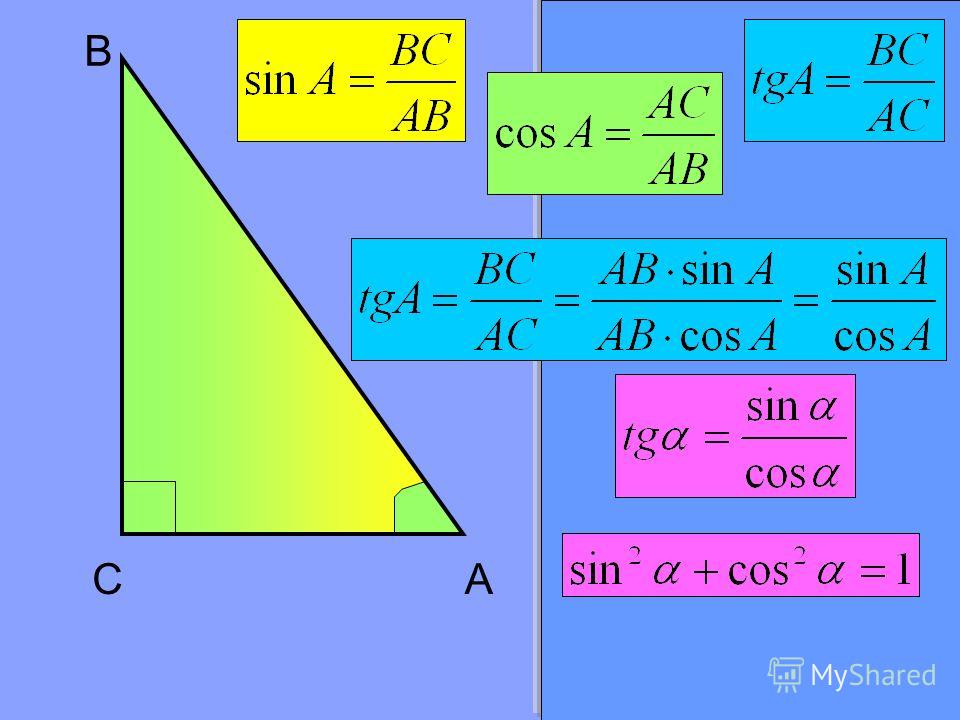
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
- Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
- Основное тригонометрическое тождество: cos2α + sin2α = 1.
- Теорема косинусов: b2 = a2 + c2 – 2ac·cosα.
- Теорема синусов: CB :sinA = AC : sinB = AB.
ctgα = AC:BC.Прямоугольный треугольник: формулы для описанной окружности
- Радиус описанной окружности равен половине гипотенузы : R=AB:2.
- Центр описанной окружности лежит на середине гипотенузы.
Прямоугольный треугольник: формулы для вписанной окружности
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.
Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.
В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.
Решение:
- Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
- По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.
Ответ: AB = 28.
ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)
Формулы, Формулы по геометрии прямоугольный треугольник, формулыКак найти недостающий угол треугольника (видео и примеры)
, написанный
Малкольм МакКинси
, проверенные на фактах
Пол Маццола
Англы в Triangle
A треугольник – простейший из возможных многоугольников. Это двумерная (плоская) форма с тремя прямыми сторонами, образующими внутреннее замкнутое пространство. У него три внутренних угла . Одна из самых первых концепций, которую следует изучать в геометрии, заключается в том, что сумма внутренних углов треугольников равна 9.0017 180° . Но откуда ты знаешь? Как вы можете доказать, что это правда? Давай выясним!
Как найти угол треугольника
У вас может быть треугольник, в котором отмечены и измерены только два угла.
Теперь, когда вы уверены, что внутренние углы всех треугольников в сумме составляют 180° , вы можете быстро вычислить недостающее измерение. Вы можете сделать это одним из двух способов:
Вычесть два известных угла из 180° .
Подставьте два угла в формулу и используйте алгебру: a+b+c=180°
Как найти недостающий угол треугольника
Два известных угла треугольника: 37° и 24° . Каков недостающий угол?
Мы можем использовать два разных метода, чтобы найти наш недостающий угол:
Как найти угол треугольникаВычесть два известных угла из 180° :
Подставить два угла в формулу и использовать алгебру: a + b + c = 180°
Формула угла треугольника
Нарисуем треугольник и обозначим его внутренние углы тремя буквами: a , b и c . Наш образец будет иметь сторону ac по горизонтали внизу и ∠b наверху.
Теперь, когда мы обозначили наши углы, у нас есть формула, на которую мы можем ссылаться для углов. Это a + b + c = 180° , что говорит нам о том, что если мы сложим все наши углы, они всегда будут равны 9.0017 180 .
Теперь давайте проведем линию, параллельную стороне ac , которая проходит через точку b (где вы также найдете ∠b ).
Теорема о чередующихся внутренних углах Чтобы найти недостающий угол в треугольникеЭта новая параллельная прямая создала два новых угла по обе стороны от ∠b . Мы обозначим эти два угла ∠z и ∠w слева направо. Сторону ab нашего треугольника теперь можно рассматривать как поперечную, линию, пересекающую две параллельные линии.
Альтернативные внутренние углы Теорема
КАБОР Альтернативные углы внутренних углов , мы знаем, что ♂ — конгресс (равна) с ♂ , а ♂ — это конгресс с тром .
Мы тебя потеряли? Не отчаивайся! Теорема о чередующихся внутренних углах говорит нам, что поперечное сечение двух параллельных прямых создает конгруэнтные альтернативные внутренние углы.
Чередующиеся внутренние углы лежат между параллельными прямыми по разные стороны от секущей. В нашем примере ∠a и ∠z являются альтернативными внутренними углами, а также ∠c и ∠w .
Теперь у нас есть три угла нашего треугольника, тщательно перерисованные и имеющие общую точку Point b . У нас есть ∠z в качестве замены для ∠a , затем ∠b и, наконец, ∠w в качестве замены для ∠c . И посмотрите, они образуют прямую линию!
Прямая измеряет 180° . Это тот же тип доказательства, что и доказательство параллельных прямых. Три угла любого треугольника всегда дают в сумме 180° или прямая линия. Теорема суммы углов треугольника
Сумма углов треугольника равна 180° доказательство
Для выполнения этого удивительного математического трюка вам понадобятся четыре вещи. Вам понадобится линейка, ножницы, бумага и карандаш. На листе бумаги нарисуйте аккуратный большой треугольник.
Любой треугольник — разносторонний, равнобедренный, равносторонний, остроугольный, тупоугольный — какой угодно.
Пометьте внутренние углы (вершины, образующие внутренние углы) тремя буквами, например R-A-T . Вырежьте треугольник, оставив небольшую рамку вокруг него, чтобы вы могли видеть все три края.
Теперь оторвите три угла вашего треугольника. Не используйте ножницы, потому что вам нужны зубчатые края, которые помогут вам не перепутать их с прямыми сторонами, которые вы нарисовали. У вас будет три меньших треугольных бита, каждый с внутренним углом, обозначенным R , A или T . Каждый маленький кусочек имеет две аккуратные стороны и шероховатый край.
У вас также будет грубый шестиугольник, который является оставшейся частью исходного большого треугольника.
Возьмите три маленьких отмеченных уголка и сложите их вместе так, чтобы необработанные края были далеко от вас. Единственный способ сделать это — заставить их выстроиться в прямую линию.
Три внутренних угла RAT в сумме образуют прямой угол, также называемый прямой линией.
Есть; ты сделал это!
Резюме урока
Если вы внимательно изучили этот урок, то теперь вы можете определить и обозначить три внутренних угла любого треугольника, и вы можете вспомнить, что сумма внутренних углов всех треугольников составляет
Что вы узнали:
С помощью этого видео и урока вы научились:
Определять и обозначать три внутренних угла любого треугольника
Вспомнить, что сумма внутренних углов всех треугольников составляет 180°
Продемонстрировать доказательство суммы внутренних углов треугольников
Применить формулу суммы внутренних углов любого треугольника
Вычислить недостающее измерение любого внутреннего угла любого треугольника
Репетиторы 90180° . Вы также можете продемонстрировать доказательство суммы внутренних углов треугольников и применить формулу a + b + c = 180° , где a , b и c – внутренние углы треугольника.
Кроме того, вы можете вычислить недостающее измерение любого внутреннего угла любого треугольника, используя два разных метода.Формулы геометрии Треугольники | Свойства, определение и примеры
ВведениеВ реальном мире мы часто сталкиваемся с треугольниками, которые представляют собой двумерные (2D) формы с тремя сторонами и тремя углами.
Треугольник — это трехсторонний многоугольник в геометрии, который имеет три ребра и три вершины. Одной из наиболее значимых характеристик треугольников является то, что сумма их внутренних углов равна 180 градусам.
В этой статье вы узнаете больше о треугольниках, их свойствах и различных формулах для нахождения конкретных измерений.
Что такое треугольники?Определение
Треугольники — это многоугольники с тремя (3) сторонами и (3) внутренними углами. Обозначается символом △.
Части треугольника
Треугольник имеет три (3) вершины, три (3) стороны и три (3) угла.
В приведенном ниже треугольнике у нас есть следующее:Три вершины — это L, M и N.
Три стороны: сторона LM, сторона MN и сторона NL.
Три угла: ∠LMN, ∠MLN и ∠NLM.
Классификация треугольников
Треугольники классифицируются по сторонам и углам. Треугольники можно разделить на разносторонние, равнобедренные или равносторонние в зависимости от длины их сторон. Треугольники могут быть острыми, тупоугольными или прямыми, в зависимости от их углов.
В таблице ниже показано, как треугольники классифицируются на основе их сторон и углов.
Сумма углов треугольникаClassification of Triangles by their Sides Classification of Triangles by their Angles
Equilateral Triangle
An equilateral triangle has three equal-length sides.
Остроугольный треугольник
Все углы остроугольного треугольника меньше 90 градусов.
Равнобедренный треугольник
Две стороны равнобедренного треугольника имеют одинаковую длину.
Прямоугольный треугольник
Одна сторона прямоугольного треугольника составляет угол 90 градусов.
Разносторонний треугольник
Разносторонний треугольник не имеет равных сторон.
Тупоугольный треугольник
Тупоугольный треугольник имеет угол больше 90 градусов.Сумма внутренних углов треугольника всегда равна 180 градусам.
Сумма ∠s треугольника = ∠1 + ∠2 + ∠3 = 180°
Пример
Найдите величину недостающего угла x ниже.
Решение
Поскольку сумма углов треугольника равна 180 градусам, получаем
x + 120° + 46° = 180°
x + 166° = 180°0272 x = 14°Следовательно, недостающий угол x равен 14°.
Периметр треугольникаПериметр треугольника равен сумме его сторон. Скажем, например, на иллюстрации ниже; периметр можно рассчитать по формуле
Периметр = x + y + z
Пример
Найдите периметр треугольника, показанного ниже.
Решение
Так как периметр △ является суммой всех трех сторон, мы имеем,
Периметр = 3 см + 6 см + 7 см
Периметр = 16 смСледовательно, периметр треугольника равен 16 см.
Площадь треугольникаОбласть, ограниченная периметром треугольника или его тремя сторонами, называется площадью треугольника.
Основание и высота известны
Определяется путем деления произведения основания и высоты треугольника на два. Она всегда измеряется в квадратных единицах.
Площадь треугольника = ½ × основание × высота
Допустим, на рисунке внизу основание NM, а высота LO. Таким образом, площадь треугольника определяется как
Площадь ∆LMN = ½ × NM × LO
Например, мы хотим найти площадь треугольника ниже,
Чтобы вычислить площадь ∆QRS, мы
Площадь ∆QRS = ½ × 14 м × 5 м
Площадь ∆QRS = ½ × 70 м 2
Площадь ∆QRS = 35 м 2
Отсюда площадь ∆QRS равна 35 м 2 .Формула Герона
Дана формула Герона для вычисления площади разностороннего треугольника.
Площадь=$\sqrt{S (S – a)(S – b)(S – c)}$
, где переменная S – полупериметр, а стороны – a, b и c.
Формула S=$\frac{a+b+c}{2}$ дает полупериметр S.
Например, мы хотим найти площадь разностороннего треугольника со сторонами 81, 93, и длиной 121 см.
Решение:
Найдем полупериметр разностороннего треугольника по формуле S=$\frac{a+b+c}{2}$. Следовательно, имеем
S=$\frac{81+93+121}{2}$
S=$\frac{295}{2}$
S=147,50 см.
Поскольку мы уже знаем, что полупериметр данного разностороннего треугольника равен 147,50 см, воспользуемся теперь формулой Герона, чтобы найти его площадь.
Площадь=$\sqrt{S (S-a)(S-b)(S-c)}$
Площадь=$\sqrt{147,50 (147,50-81)(147,50-93)(147,50-121)}$
Площадь= $\sqrt{147,50 ( 66,50)(54,50)(26,50)}$
Площадь=$\sqrt{14166287,19}$
Площадь≈3763,81 см2
Следовательно, площадь данного масштабного треугольника равна 3763,81 квадратного сантиметра.
Теорема ПифагораТеорема Пифагора, также известная как теорема Пифагора, утверждает, что при прямом угле квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух меньших стороны. Следовательно, мы используем формулу
a 2 + b 2 = c 2
, где сторона c — длина гипотенузы, а a и b — две другие стороны.
Чтобы лучше понять это, давайте посмотрим на изображение ниже,
Мы видим, что у нас есть три квадрата со сторонами a, b и c. Обратите внимание, что у нас есть прямоугольный треугольник, сформированный из этих длин. Допустим, на стороне а 3 единицы, а на стороне b 4 единицы. По теореме Пифагора мы можем вычислить сторону с.
C 2 = A 2 + B 2
C 2 = 3 2 + 4 2
C 2 = 2
C 2 = 2
C 2 = 2
C 2 907 = 2
C 2 = 2
C 2 . $\sqrt{25}$
c = 5Следовательно, гипотенуза или самая длинная сторона прямоугольного треугольника равна 5 единицам длины. 92}$
Примеры
Пример 1
Если две другие стороны прямоугольного треугольника равны 8 см и 15 см, определите длину гипотенузы.
Решение
Предположим, что сторона a = 8 часов, а сторона b = 15. Следовательно, для вычисления длины гипотенузы воспользуемся формулой Пифагора c 2 = a 2 + b 2 .
в 2 = а 2 + б 2
Таким образом, длина гипотенузы равна 17 .
в 2 = 8 2 + 15 2
c 2 = 64 + 225
c 2 = 289
c = 289
c = 17Пример 2
Найдите длину основания прямоугольного треугольника.
Решение
В прямоугольном треугольнике мы знаем, что длина гипотенузы (сторона, противоположная прямому углу) равна 10 см, а высота 8 см.
Допустим, что а = 8 см и с = 10 см.Следовательно, по теореме Пифагора для вычисления основания прямоугольного треугольника имеем
b 2 = c 2 – a 2
b 2 = 10 6 7 – 2 2 2 2 2
b 2 = 100 – 64
b 2 = 36
b = 36
b = 6В результате длина основания прямоугольного треугольника составляет 6 см.
Основные тригонометрические функцииТремя основными тригонометрическими функциями прямоугольных треугольников являются синус, косинус и тангенс.
Воспользуемся иллюстрацией ниже, чтобы ознакомиться с частями и основными тригонометрическими функциями синуса, косинуса и тангенса.
∟ используется для обозначения прямого угла треугольника
θ (тета) используется для обозначения одного из углов прямоугольного треугольника, но не прямого угла
o используется для обозначения противоположной стороны угла θ
a используется для обозначения прилежащей стороны угла θ
h используется для обозначения гипотенузы прямоугольного треугольника
Для трех основных тригонометрических функций мы используем мнемонический прием: SOH CAH TOA, где S — синус, C — косинус, а T — тангенс.
Приведены формулы для трех основных тригонометрических функций:
θ=$\frac{opposite}{гипотенуза}$ sin =$\frac{o}{h}$ косинус θ =$\frac{adjacent}{гипотенуза}$ cos θ=$\frac{a}{h}$ тангенс θ=$\frac{противоположный}{adjacent}$ tan θ=$\frac{o}{a}$ Примеры
Пример 1
Найдите длину противоположной стороны угла θ.
Решение
Из приведенных данных мы знаем, что θ=45° и длина прилегающей стороны 10 см. Поскольку вовлеченными частями являются угол , противоположная сторона и смежная сторона, мы будем использовать формулу tan θ=$\frac{o}{a}$. Следовательно, мы имеем
tan θ=$\frac{opposite}{adjacent}$
tan 45°=$\frac{напротив} {10 см}$
( 45° ) 10 см =напротив
( 1 )( 10 см )=напротив
10 см=напротив
Пример 26
Найдите длину гипотенузы.
Решение
Мы знаем, что угол = 60°, а противолежащая сторона имеет длину 12 см. Так как мы должны найти длину гипотенузы, мы будем использовать формулу sin θ=$\frac{opposite}{hypotenuse}$.
Отсюда имеем
sin θ=$\frac{opposite}{гипотенуза}$ 90}$
гипотенуза=$\frac{12 см}{\frac{\sqrt{3}}{2}}$
гипотенуза=8$\sqrt{3}$ см
Следовательно, длина гипотенуза равна 8$\sqrt{3}$ см.
Правила синусов и косинусовДля решения необходимо найти длины сторон треугольника и всех его углов. Правила синусов и косинусов можно использовать при решении любых треугольников. Правило синусов используется, когда известны сторона и противолежащий ей угол. Мы применяем правило косинуса, когда у нас есть либо две стороны и угол между ними, либо три стороны треугольника.
Сторона A — противоположность ♂
Сторона B — противоположность ♂
Сторона C является противоположностью ЧК SO DAIN433333331
The SO
. используется при решении любого треугольника, а не только прямоугольного треугольника. Правило синусов используется, когда известны сторона и противолежащий ей угол.
$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$
$\frac{sinsin A}{a}$ =$\frac{sinsin B}{b}$ = $\frac{sinsin C}{c}$
Обратите внимание, что мы будем использовать только две части формулы, а не три.
Вычисление сторон
При вычислении длины стороны следует использовать правило синусов, где длины сторон являются числителями.
$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$
Пример
Найдите длину a в рисунок ниже.
Решение
На данном рисунке нам известны два угла А и В и сторона а. Будем использовать формулу 90}$ x sin 85°
a≈8,79
Вычисление углов
При вычислении угловых мер треугольника следует использовать правило синусов, где угловые меры являются числителями.
$\frac{A}{sinsin a}$ =$\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$
Пример
Найдите недостающий угол в рисунок ниже.
Решение
Поскольку мы знаем, что ∠C = 70°, c = 11 и b = 9, мы будем использовать правило синусов,
$\frac{B}{sinsin b}$ =$\frac {C}{sinsin c}$ 90}{11}$ x 9
sin B=0,769 ( 3 десятичных знака)
Используйте обратную функцию ( sin -1 ), чтобы найти угол B.
∠B=0,769
∠B≈50,26° ( 2 десятичных знака мест )
Следовательно, ∠B имеет длину 50,26°.Правило косинуса
Правило косинуса можно использовать в треугольниках, где вы пытаетесь связать все три стороны с углом. Ниже приведены следующие формулы: 2bc} $
где сторона a — недостающий угол
стороны b и c — известные углы
∠A — угол напротив стороны a стороны необходимы для вычисления длины недостающей стороны треугольника. В этом сценарии мы будем использовать формулуa 2 =b 2 +c 2 – 2bc coscos A
Помните, что a – это недостающая сторона, b и c – длины двух других сторон.
сторон, а ∠A — угол, противоположный стороне a.Пример
Вычислить длину недостающей стороны.
Решение
На данном рисунке есть информация: ∠A=95°, b=20, c=29. Теперь подставим известные значения в формулу, чтобы найти недостающую сторону а.
A 2 = B 2 +C 2 — 2BC COSCOS A
A 2 = 20 2 +29 2 — 2 (20) (29) (Cost Coscos 2 — 2 (20) (Cospos 9) (Costs 9) (Coscos
.a 2 = 1342,100662
a = $\sqrt{1342,100662}$ 92}{2bc}$Помните, что ∠A — недостающий угол, b и c — длины двух других сторон, а a — сторона, противоположная ∠A.
Пример
Вычислите величину ∠A на рисунке ниже.
Решение
На данном рисунке нас просят найти меру ∠A по трем сторонам треугольника с размерами 6, 9 и 13 единиц. Сторона, противоположная ∠A, равна 9 единицам, поэтому мы должны использовать ее как сторону a.
92}{2x6x13}$cos A=$\frac{124}{156}$
cos A≈0,795 (3 знака после запятой)
Используйте обратную функцию (cos -1 ), чтобы найти угол A.
∠A=0,795
∠A≈37,34° ( 2 знака после запятой )Следовательно, недостающий угол A равен 37,34° по правилу косинусов.
Список формул геометрии ТреугольникиНазвание Определение 5 9 Формула 6 Периметр треугольника Периметр треугольника равен сумме его сторон. Периметр = x + y + z Площадь треугольника Область, ограниченная периметром треугольника или его тремя сторонами, называется площадью треугольника. Площадь треугольника = ½ × основание × высота
Формула Герона
Площадь = $\sqrt{S (S-a)(S-b)(S-c)}$
Формула S = $\frac{a+b +c}{2}$ дает полупериметр S. Теорема Пифагора Теорема Пифагора, также известная как теорема Пифагора, утверждает, что при прямом угле квадрат на гипотенузе (сторона напротив прямого угла) равен сумме квадратов с двух меньших сторон. a 2 +b 2 =c 2 Основные тригонометрические функции касательная. Мнемоническое устройство: SOH CAH TOA
sinsin θ=$\frac{opposite}{hypotenuse}$
coscos θ=$\frac{adjacent}{гипотенуза}$
tantan θ=$\frac{opposite}{adjacent }$Правило синусов Правило синусов можно использовать при решении любого треугольника, а не только прямоугольного. Правило синусов используется, когда известны сторона и противолежащий ей угол. $\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$ $\frac{A}{sinsin a}$ = $\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$ 92}{2bc}$
, где сторона a — недостающий угол, стороны b и c — известные углы∠A — угол, противоположный стороне a (3) внутренние углы. Обозначается символом △.Список основных формул для работы с треугольниками приведен в таблице ниже.
Геометрические формулы Треугольники
Периметр треугольника
Периметр треугольника равен сумме его сторон.
Периметр = x + y + z
Площадь треугольника
Область, ограниченная периметром треугольника или его тремя сторонами, называется площадью треугольника.
Основание и высота известны
Определяется путем деления произведения основания и высоты треугольника на два. Она всегда измеряется в квадратных единицах.
Площадь треугольника = ½ × основание × высота
Формула Герона
Дана формула Герона для вычисления площади разностороннего треугольника.
Площадь=$\sqrt{S (S-a)(S-b)(S-c)}$
, где переменная S — полупериметр.
Формула S = $\frac{a+b+c}{2}$ дает полупериметр S.Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, утверждает, что при прямом угле квадрат гипотенузы (сторона напротив прямого угла) равен сумме квадратов двух меньших сторон.
a 2 +b 2 =c 2
где сторона c — гипотенуза, а два других катета прямоугольного треугольника — a и b.
Основные тригонометрические функции
∟ используется для обозначения прямого угла треугольника
θ (тета) используется для обозначения одного из углов прямоугольного треугольника, но не прямого угла
o используется для представления противоположной стороны угол θ
a используется для обозначения прилежащей стороны угла θ
h используется для обозначения гипотенузы прямоугольного треугольника
Мнемонический прием для трех основных тригонометрических функций — SOH CAH TOA.sinsin θ=$\frac{opposite}{гипотенуза}$
coscos θ=$\frac{adjacent}{гипотенуза}$
tantan θ=$\frac{opposite}{adjacent}$
Правила синуса и косинуса
сторона a противоположна ∠A
сторона b противоположна ∠B
сторона c противоположна ∠C
Часто задаваемые вопросы по формулам геометрии ТреугольникиПравило синусов
$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$ \frac{c}{sinsin C}$
$\frac{sinsin A}{a}$=$\frac{sinsin B}{b}$=$\frac{sinsin C}{c}$Косинус Правило
а 2 92}{2bc}$Какие существуют типы треугольников?
Треугольники классифицируются по сторонам и углам.
Треугольники можно разделить на разносторонние, равнобедренные или равносторонние в зависимости от длины их сторон. Треугольники могут быть острыми, тупоугольными или прямыми, в зависимости от их углов.Типы треугольников по их сторонам
Равносторонний треугольник
У равностороннего треугольника три стороны одинаковой длины.Равнобедренный треугольник
Две стороны равнобедренного треугольника имеют одинаковую длину.Разносторонний треугольник
Разносторонний треугольник не имеет равных сторон.Типы треугольников по их углам
Остроугольный треугольник
Все углы остроугольного треугольника меньше 90 градусов.Прямоугольный треугольник
Одна сторона прямоугольного треугольника составляет угол 90 градусов.Тупоугольный треугольник
Тупоугольный треугольник имеет угол больше 90 градусов.Как вычислить площадь треугольника?
Для вычисления площади треугольника используется следующая формула:
Площадь треугольника=1/2×основание×высота
По какой формуле определяется недостающая сторона прямоугольного треугольника?
Теорема Пифагора, также известная как теорема Пифагора, утверждает, что при прямом угле квадрат гипотенузы (сторона, расположенная напротив прямого угла) равен сумме квадратов двух меньших сторон. Следовательно, мы используем формулу 92}$
c=$\sqrt{36+64}$
c=$\sqrt{100}$
c=10
Какие пифагорейские тройки?
Пифагоровы тройки, представленные в виде ( a, b, c ), представляют собой набор из трех положительных целых чисел, которые могут быть сторонами прямоугольного треугольника. A Pythagorean triple satisfies the Pythagorean theorem equation a 2 + b 2 = c 2 ,
Examples of Pythagorean Triples are as follows:
( 3, 4, 5 ) (6, 8, 10) (9, 12, 15) (12, 16, 20) (15, 20, 25) (5, 12, 13) ( 10, 24, 26) (15, 36, 39) (20, 48, 52) (25, 60, 65) (10 7, 8, 9 25) , 50) (21, 72, 75) (28, 96, 100) (35, 120, 125) (8, 15, 17) (16, 225, 289) ( 24 , 45 , 51 ) (32, 60, 68) (40, 75, 85) (9, 40, 41) (18, 80, 82) (27, 120, 123) ( (27, 120, 123) ( (27, 120, 123) 36, 160, 164 ) (45, 200, 205 ) Треугольники (тема моды) Рабочие листы
Площадь треугольников (тема мороженого) Рабочие листы
Пространственные навыки: ThemedW Solstices Worksheets (Треугольники и четырехугольники)Мы тратим много времени на изучение и сбор информации на этом сайте.
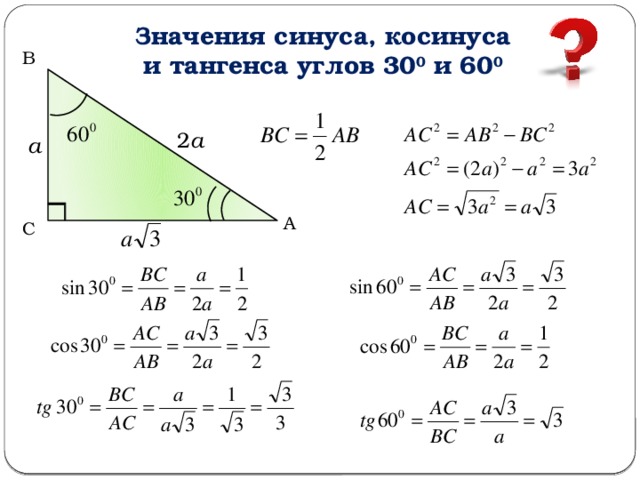
Кроме того, вы можете вычислить недостающее измерение любого внутреннего угла любого треугольника, используя два разных метода.
В приведенном ниже треугольнике у нас есть следующее:
$\sqrt{25}$ 
Допустим, что а = 8 см и с = 10 см.
SO DAIN
сторон, а ∠A — угол, противоположный стороне a.
92}{2x6x13}$
Обозначается символом △.
Треугольники можно разделить на разносторонние, равнобедренные или равносторонние в зависимости от длины их сторон. Треугольники могут быть острыми, тупоугольными или прямыми, в зависимости от их углов.
