Рациональные числа, зачем нужны рациональные числа, в чем их особенность
Рациональным числом называют число, которое можно записать в виде отношения mn, где m — целое число, a n — натуральное число. Чтобы понимать значение рационального числа, необходимо знать, что такое натуральные числа, целые числа, дроби (правильные \(\frac{2}{3}\), неправильные \(\frac{3}{2}\), бесконечные периодические 0,(4) и смешанные \(4 \frac{2}{3}\),). Натуральные числа представляют собой числа, которые мы используем при счете (1, 2, 3…). В свою очередь целые числа – это натуральные числа, а также противоположные им и ноль (1, 2, 0, -1, -2…). Дробью называется число, записанное в виде отношения mn (\(\frac{2}{3}\)), где m – целое, а n – натуральное число. Понятие дроби берет свое начало еще с древних времен, когда людям в торговых делах и бытовых нуждах требовалось определить часть какого-либо целого.
История рациональных чисел началась с возникновением финансово-кредитных отношений между людьми.
Чтобы в численном виде представить задолженность человека, нужно было записывать числа, противоположные натуральным. Так появились отрицательные числа (-3, -167). А для того, чтобы записывать часть целого (например, возвращение долга частями), стали использовать дроби. Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).
Для усвоения материала приведем пример задания на определение рациональных чисел из ряда чисел.
Задача. Даны числа: -34, 480, 0,11, \(\frac{1}{2}\), 8. Какие из них рациональные?
Решение.
Рассмотрим отдельно каждое из заданных чисел:
- Число -34 – целое число;
- Число 480 – натуральное число;
- Число 0,11 = \(\frac{11}{100} \) – десятичная дробь;
- Число \(\frac{1}{2}\) — правильная дробь;
- Число 8 – натуральное число.
Каждое из заданных чисел можно представить в виде дроби с целым и натуральным знаменателем.
Значит, все 5 чисел являются рациональными числами.
Ответ: все числа являются рациональными.
Чтобы хорошо понимать специфику рациональных чисел, нужно усвоить два правила:
- Сумма рациональных чисел является рациональным числом.
- Произведение рациональных чисел является рациональным числом.
Теория в математике очень важна. Умение отличать натуральные числа от целых, рациональные от иррациональных поможет Вам не запутаться и не ошибиться в практике. Удачи!
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Рациональные числа 8 класс онлайн-подготовка на Ростелеком Лицей
115. Рациональные числа
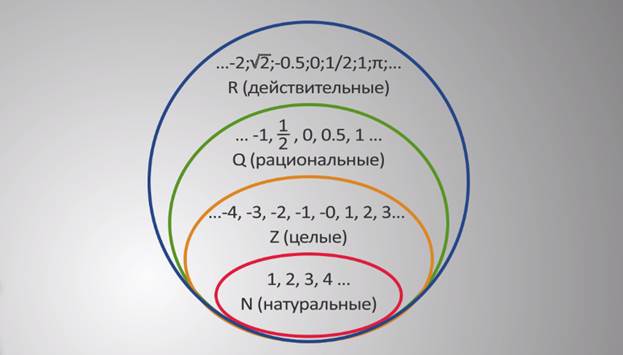
Мы уже знаем, что числа, которые употребляются при счете предметов, называются натуральными.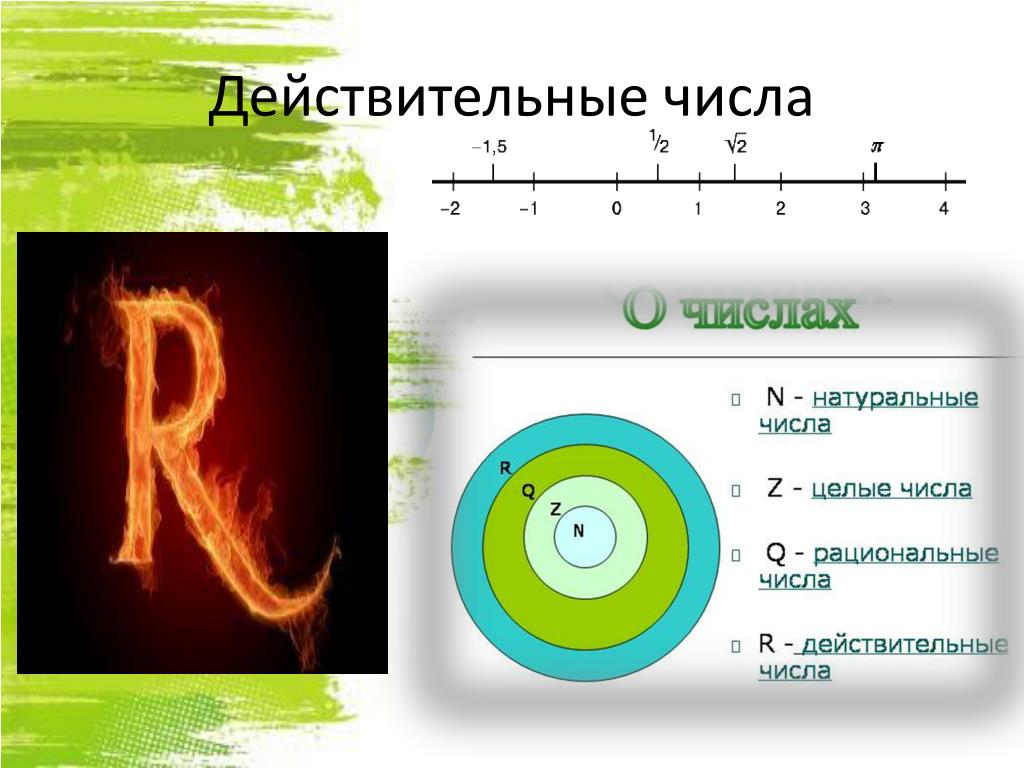
Натуральные числа, противоположные им и ноль называются целыми. Но кроме целых чисел есть дробные. Целые и дробные числа вместе составляют рациональные числа.
Отрицательные числа были введены в использование позднее, чем дроби. Долгое время эти числа считали «несуществующими» или «ложными». Положительные и отрицательные числа служат для описания изменений величин. Если величина растёт, то говорят, что её изменение положительно, а если она убывает, то изменение называют отрицательным.
Множество натуральных чисел обозначается буквой N (от латинского naturalis – естественный, природный).
Множество целых чисел обозначается Z (от немецкого Zahl – число).
Множество рациональных чисел обозначается буквой Q (от французского quotient – отношение).
Если мы хотим написать, что некое число принадлежит множеству натуральных, целых или рациональных чисел, то используем значок принадлежности.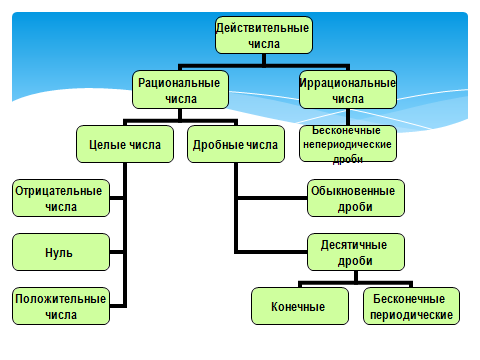
Например, 2∈N или 0∈Z. Если мы хотим написать, что некое число не принадлежит некоему множеству, то пишем так: -2∉N.
Множества можно изображать на рисунках с помощью кругов. Такой способ изображения множеств придумал математик Леонард Эйлер. Поэтому изображения множеств получили название круги Эйлера.
Если мы хотим обозначить, что некое множество целиком входит в другое (то есть является его подмножеством), то используем знак принадлежности без средней перегородки – ⊂.
N⊂Z⊂Q (множество натуральных чисел является подмножеством множества целых чисел, а множество целых чисел является подмножеством множества рациональных чисел).
Введем понятие разности множеств. Разностью множеств А и В является такое множество, элементы которого принадлежат А, но не принадлежат В. Например, разностью множеств целых и натуральных чисел будет множество, состоящее из целых отрицательных чисел и нуля.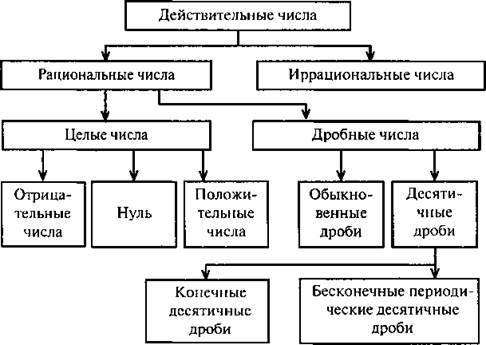
Всякое рациональное число можно представить в виде дроби mn, где m – целое число, а n – натуральное. Одно и то же рациональное число можно представить в таком виде разными способами. Например, 23=46=1015 или 5=51=153.
Среди дробей, с помощью которых записывается данное рациональное число, всегда можно указать дробь с наименьшим знаменателем, которая является несократимой. Для целых чисел такая дробь имеет знаменатель 1.
Рассмотрим вопрос о представлении рациональных чисел в виде десятичных дробей.
Представим дробь 14 в виде десятичной дроби. Для этого разделим ее числитель на знаменатель. Получим 0,25.
Попробуем представить в виде десятичной дроби дробь 837. Получим 0,216216216…
Сколько бы мы не продолжали деление, мы не получим в остатке ноль. В частном же будет повторяющаяся последовательность чисел после запятой. Такая дробь называется бесконечной десятичной периодической дробью.
Повторяющаяся последовательность записывается в скобках: 0,(216) и читается это так: «нуль целых, двести шестнадцать в периоде».
357,025555… = 357,02(5)
триста пятьдесят семь целых, 2 сотых и 5 в периоде.
Любое рациональное число можно представить в виде конечной десятичной дроби либо в виде бесконечной десятичной периодической дроби.
Если знаменатель дроби можно разложить на множители, которые представляют собой степени чисел 2 или 5, то такую обыкновенную дробь можно представить в виде конечной десятичной дроби.
1.1 Что такое числа? Рациональные числа
У нас есть много видов чисел, но все они начинаются с натуральных чисел , которые \(1, 2, 3\) и так далее.
Если вы посчитаете свои цифры и пальцы ног, вы придете к \(20\) (большинство из вас), и это натуральное число. Мы
можем в нашем воображении считать, что эти натуральные числа продолжаются вечно, после миллиона, миллиарда,
триллион и так далее.
В начальной школе вы изучали не только эти числа, но и то, как над ними можно производить действия.
Какие операции?
Есть сложения, вычитания, умножения и деления .
Вы можете сложить два натуральных числа вместе, и вы всегда получите еще одно натуральное число, как в известный факт, что один и один два.
С вычитанием дело обстоит сложнее. Если вычесть число, например число \(5\), из
само по себе, вы получаете что-то новое, что-то, что вовсе не является натуральным числом. Мы называем это числом \(0\) или ноль . И если вы вычтете число, снова скажем \(5\), из меньшего числа, скажем \(3\), тогда
вы получаете нечто новое, а именно отрицательное целое число, которое в данном случае равно \(-2\), называемое 
Вы можете использовать числа, чтобы подсчитать количество копеек, которые у вас есть в кармане. Таким образом, у вас может быть пять пенни в твой карман. Ноль — это количество пенни, которое у вас было бы, если бы в вашем кармане была дырка, а все те, что вы положили в сразу выпал снова.
Теперь предположим, что вы идете в магазин, и владелец магазина достаточно глуп, чтобы отдать вам должное. Предположим далее, что у вас было пять копеек, и вы купили какую-то дорогую вещь стоимостью 11 копеек. Тогда отрицательное целое, \(-6\), представляет собой тот факт, что у вас не только нет пенни, но если бы вы получили еще шесть, вы были бы обязаны сдайте их, чтобы заплатить за этот предмет. Шесть – это количество пенни, которое вы должны были бы своему кредитору, если бы заплатить ему ваши \(5\) пенни, и он отдал вам предмет, а остальные деньги одолжил вам.
Таким образом, чтобы приспособиться к вычитанию и иметь возможность представлять «сумму долга» числами, мы расширяем естественный
числа, включающие числа \(0\) и отрицательные значения натуральных чисел.
Весь этот набор цифр,
положительные натуральные числа, их отрицательные значения и 0 называется набором из целых чисел и обозначается
буквой \(Z\).
Мы можем взять любые два члена \(Z\) и добавить их или вычесть их и в любом случае получить еще один член \(З\).
Я все это знаю, но я очень заржавел в реальных сложениях и вычитаниях. Я ошибаюсь в большинстве время я пытаюсь сделать их.
Большинство людей делают ошибку примерно один раз из десяти сложений или вычитаний однозначных цифр, которые они совершают. выполнять. Это означает, что если они добавляют или вычитают многозначные числа, например \(1234123\) и \(5432121\), у них есть отличный шанс получить неправильный ответ.
К счастью, сегодня это не имеет значения. Вы можете легко проверить сложения и вычитания на калькуляторе или
в электронной таблице и посмотрите, получите ли вы один и тот же ответ несколько раз.
К сожалению, я обычно делаю
ошибка при вводе чисел для сложения или вычитания, или сложения вместо вычитания, или выполнения чего-либо еще в равной степени
абсурд. Все, что это означает сегодня, это то, что я должен сделать каждый расчет по крайней мере три раза, чтобы иметь разумное
шанс на правильность. Правда, количество моих усилий в три раза больше, чем могло бы быть, но в три раза очень мало
усилия по-прежнему очень мало усилий.
Если у вас есть эта проблема, вам лучше всего добавлять или вычитать в электронной таблице. Тогда вы можете посмотреть на свой вычисления и использовать свое суждение относительно того, имеет ли это смысл. Вот несколько правил проверки на смысл.
Когда вы добавляете положительные числа, результат должен быть больше, чем оба из двух «сумм» , которые
вы добавили. Если одно из чисел положительное, а другое отрицательное, величина (значение, если вы игнорируете любое
знак минус) суммы должен быть меньше, чем величина большего из двух, а знак должен быть
то из слагаемого с большей величиной.
Кроме того, младшие значащие цифры ваших чисел должны правильно складываться или вычитаться, если вы игнорируете остальные. За например, если вы вычтете \(431\) из \(512\), то последняя цифра ответа должна быть \(1\), что равно \(2\) минус \(1\).
Если ваша проверка выдает что-то подозрительное, попробуйте еще раз вычислить, будучи более осторожным, особенно с входными данными.
Операция вычитания 5 из другого числа, отменяет операцию добавления \(5\) к другой номер. Таким образом, если вы выполняете обе операции, прибавляете пять, а затем вычитаете пять или наоборот, вы снова откуда вы начали: \(3 + 5 — 5 = 3\).
Сложение \(5\) и вычитание \(5\) считаются обратными операциями друг к другу из-за this property: Выполнение их одно за другим равносильно бездействию.
Кстати, почему \(0\) не является натуральным числом?
Я понятия не имею.
Так люди определяли натуральные числа давным-давно, и никто особо не заботился об их изменении.
это определение.
Еще в начальной школе вы также столкнулись с понятием умножения на . Это что-то вы можете сделать с двумя целыми числами, которые дадут третье, называемое их произведением . Ты был (я надеюсь) вынужден выучить таблицу умножения, которая дает произведение каждой пары однозначных чисел и затем научился использовать эту таблицу для умножения чисел с большим количеством цифр.
Я никогда не был хорош в этом .
В старину нужно было уметь делать эти вещи, сложения и умножения, хотя бы для того, чтобы уметь обращаться с деньги и совершать обычные покупки, не подвергаясь мошенничеству.
Теперь вы можете использовать калькулятор или компьютерную электронную таблицу, чтобы сделать эти вещи, если вы знаете, как вводить целые числа и
, чтобы нажать кнопки \(+\) или \(-\) или \(*\) и = соответственно.
( К сожалению, этот факт заставил педагогов поверить, что им не нужно заставлять учеников проходить нудное изучение таблицы умножения.
Это наносит большой вред тем, кто этого не делает, из-за того, как работает наш мозг. оказывается что чем больше времени мы тратим на любую деятельность в детстве и даже во взрослом возрасте, тем больше площадь мозга получает то, что посвящено этой деятельности, и чем больше она становится, тем лучше мы справимся с этой деятельностью.
Таким образом, вы тратите меньше времени на изучение таблицы умножения, что приводит к уменьшению площади вашего мозг посвящен вычислениям, что препятствует вашему дальнейшему математическому развитию.
Ваши математические способности будут прямо пропорциональны количеству времени, которое вы посвящаете математике.
думаю об этом.
И это зависит от вас. )
Как только мы познакомимся с умножением, возникает естественный вопрос: как мы можем отменить умножение? Что это обратная операция, скажем, к умножению на \(5\), так что умножение, а затем выполнение этого равносильно выполнению ничего такого? Эта операция называется деление. Итак, вы научились делить целые числа. операция, обратная умножению на \(x\) — это деление на \(x\) , (если только \(x\) не равно \(0\)).
Теперь возникает проблема: если мы попытаемся разделить \(5\) на \(3\), мы не получим целое число. Итак, как мы и должны были
расширить натуральные числа до целых, чтобы приспособить операцию вычитания, мы должны расширить
наши числа из целых чисел включают также соотношения целых чисел , например \(\frac{5}{3}\), если мы хотим сделать
деление определено для каждой пары ненулевых целых чисел.
И мы хотим иметь возможность определять разделение, где бы мы ни находились.
Можно.
Отношения целых чисел называются рациональными числами, и вы получаете единицу для любой пары целых чисел, если второе целое число, называемое знаменателем, не равно нулю. Соотношения типа \(\frac{5}{3}\), которые сами по себе не являются целыми числами, называется дроби.
После того, как мы ввели дроби, мы хотим предоставить правила их сложения и вычитания, а также правила умножения. и разделив их. Это начинает усложняться, но, к счастью для нас, у нас есть калькуляторы и электронные таблицы. которые могут делать все это без каких-либо жалоб, если у нас хватит ума ввести то, что мы хотим сделать.
Есть одна вещь, которую мы не можем делать с нашими рациональными числами, — делить на \(0\). Дивизия, в конце концов,
является действием отмены умножения.
Но умножение любого числа на 0 дает результат \(0\). Нет способа
верни из этого произведения \(0\) то, на что ты умножил \(0\), чтобы получить его.
Конечно, складывать и умножать (а также вычитать и делить) дроби сложнее, чем делать это для целые числа. Чтобы умножить, скажем, \(\frac{a}{b}\) на \(\frac{c}{d}\), новый числитель является произведением старого единицы (а именно \(ac\)) и новый знаменатель является произведением старых (\(bd\)), поэтому произведение равно \(\frac{ac}{bd}\): \(\frac{a}{b}*\frac{c}{d} = \frac{ac}{bd}\).
Обратная операция умножения на \(\frac{c}{d}\) — это умножение на \(\frac{d}{c}\), и эта обратная операция по определению операция деления на \(\frac{c}{d}\). Произведение любого числа на обратное всегда равно \(1\). Это означает, что \(\frac{d}{d}\) всегда \(1\) для любого \(d\), отличного от \(0\).
Таким образом, \(\frac{a}{b}\), деленное на \(\frac{c}{d}\), равно \(\frac{a}{b}\), умноженному на величину, обратную \(\frac{ CD}\)
что равно \(\frac{a}{b}\), умноженному на \(\frac{d}{c}\).
Ответ: \(\frac{ad}{bc}\).
Добавление немного сложнее. Понятие сложения можно применять как к объектам, так и к числам в следующий смысл. Мы знаем, например, что \(3+5\) равно \(8\). Значит, если у нас есть 3 редиски и выкопаем \(5\) больше, у нас будет \(8\) редиски (при условии, что никто не ел первую \(3\)). И то же самое верно для любые другие предметы вместо редиски. Это говорит нам, как складывать дроби с одинаковыми знаменателями. Таким образом \(\frac{3}{a} + \frac{5}{a}\) — это \(\frac{8}{a}\), в котором \(\frac{1}{a}\) заменено редька. Мы применяем общее правило добавления подобных вещей к объекту \(\frac{1}{a}\).
Чтобы сложить дроби с разными знаменателями, нужно сначала изменить их так, чтобы знаменатели были одинаковыми,
затем добавьте числители, как вы добавляли числа. Самый простой способ сделать это — сделать новый знаменатель
продукт старых. Таким образом, чтобы найти \(\frac{a}{b} + \frac{c}{d}\), вы сначала умножаете первый член на
\(\frac{d}{d}\), а второй на \(\frac{b}{b}\), получив \(\frac{ad}{bd} + \frac{cb}{bd} \) и ответ
\(\frac{ad+cb}{bd}\).
Вы можете сделать то же самое для вычитания.
Вас, вероятно, заставляли выносить за скобки общие члены в числителе и знаменателе в этом ответе в школе, но вам не нужно делать это при вводе ответа в электронную таблицу, что значительно усложняет сложение дробей легче, когда вы используете электронные таблицы.
В чем разница между целыми, целыми и натуральными числами?
Система счисления, любой из различных наборов символов и, следовательно, правила их использования для обозначения чисел, которые обычно указывают, какое процентное соотношение объектов присутствует в данном наборе, или, другими словами, система счисления представляет собой математическое представление чисел данный набор. Давайте посмотрим на различные типы чисел в десятичной системе счисления,
Типы чисел
В системе счисления есть разные виды чисел, к комплексным числам относятся все виды чисел, как действительные, так и мнимые, в действительных числах есть рациональные и иррациональные числа.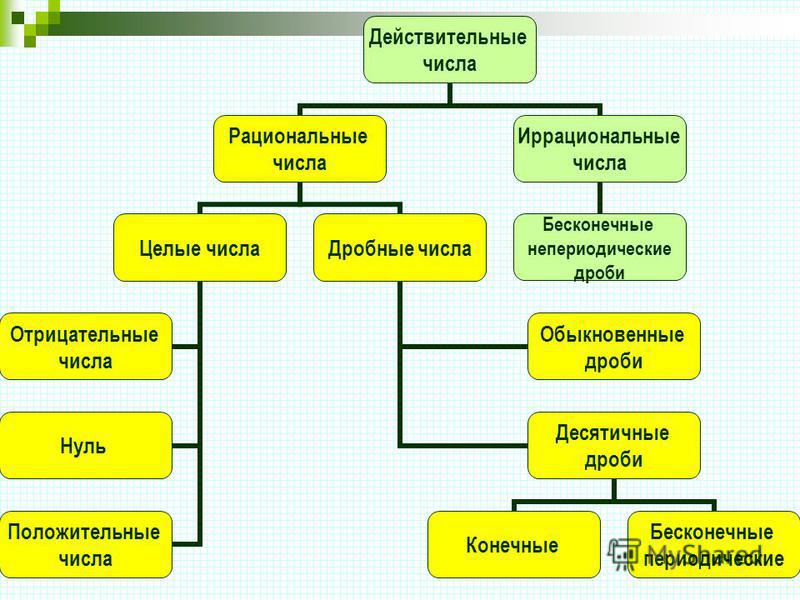
Существуют целые числа, идущие от отрицательной бесконечности к положительной бесконечности, целые числа, идущие от 0 до положительной бесконечности, являются целыми числами, а целые числа, которые генерируются от 1 до бесконечности, являются натуральными числами.
Целые числа
Если построен набор полностью натуральных чисел, целых чисел и отрицательных чисел, то такой набор называется набором целых чисел. Он может быть положительным, отрицательным или нулевым. Например: 2, 5, -9, -17 , 112 и т. д.
Рациональные числа
Рациональное число может быть определено как любое число, которое может быть представлено в виде p/q, где q больше 0. Например, 2/5, 22 /7, 4/3 и т. д.
Целые числа
Целые числа — это часть системы счисления, в которую входят все положительные целые числа от 0 до бесконечности. Эти числа существуют в числовой строке. Следовательно, все они действительные числа. Полный набор натуральных чисел рядом с «0» называется целыми числами.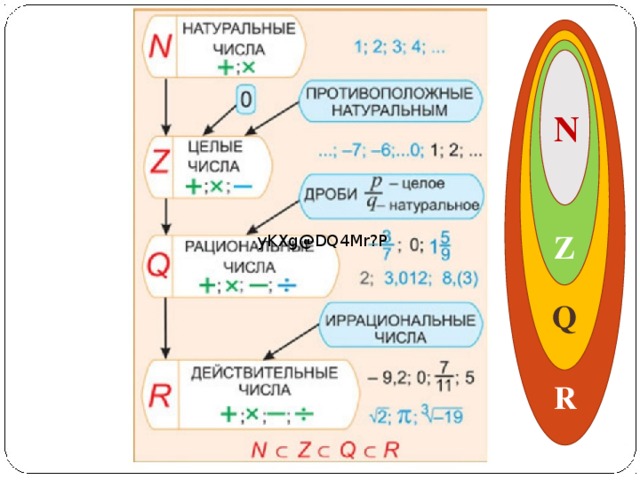
Целые числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , …
Натуральные числа
Натуральные числа — это часть системы счисления, в которую входят все положительные целые числа от 1 до бесконечности. Натуральные числа — это 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , …
Разница между целыми числами, целыми числами и натуральными числами
Основное различие между целыми числами и натуральными числами заключается в том, что целые числа включают 0 а натуральные числа генерируются из 1 и, следовательно, не содержат 0. Однако целые числа включают числа от отрицательной бесконечности до положительной бесконечности. Ниже приведена точка, показывающая основную разницу между целыми числами, целыми числами и натуральными числами,
- Для целых чисел счет начинается с отрицательной бесконечности, в натуральных числах счет начинается с 1, а в целых числах счет начинается с 0.
- Можно сказать, что каждое натуральное число является целым числом, но все целые числа не являются натуральными числами.
. Однако все натуральные и целые числа являются целыми числами, а не наоборот. - Например: {-∞,…-1, 0, 1, 2,….+∞} — набор целых чисел, {0, 1, 2, 3, 4,…} — набор целых чисел, а {1, 2, 3, 4,…} — набор натуральных чисел.
- Целые числа представлены как I , натуральные числа представлены как N , целые числа представлены как W .
. Однако все натуральные и целые числа являются целыми числами, а не наоборот.W = {I} – {-∞, ….-1}
N = {W} – {0}
Примеры задач
Вопрос 1. Можем ли мы сказать, что 7 равно обоим целое число и натуральное число?
Ответ:
Да , 7 — это и целое, и натуральное число.
Вопрос 2: Укажите, верно или нет данное утверждение: «все натуральные числа являются целыми числами»?
Ответ:
Верно, что все натуральные числа являются целыми числами, но не наоборот.
Вопрос 3. Является ли 5 целым и натуральным числом?
Ответ:
Да, 5 — это и натуральное, и целое число.
Вопрос 4: Является ли 0,7 целым числом?
Ответ:
Нет , это десятичное число.
Вопрос 5: «-17» — это целое или натуральное число?
Ответ:
Нет , -17 не является ни натуральным, ни целым числом.
Вопрос 6: Распределите данные числа по категориям: Целые, целые и натуральные числа,
-3, 77, 34,99, 1, 100
Ответ:
Numbers Integers Whole numbers Natural numbers -3 yes no no 77 yes yes yes 34.
