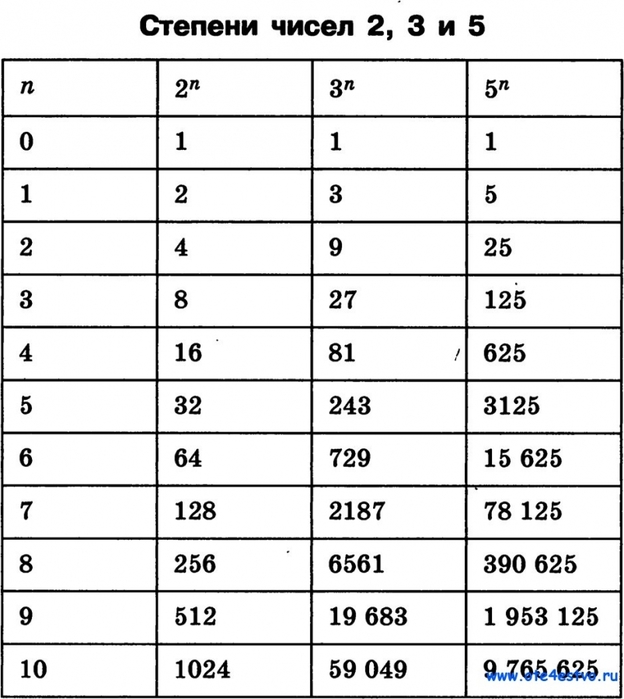
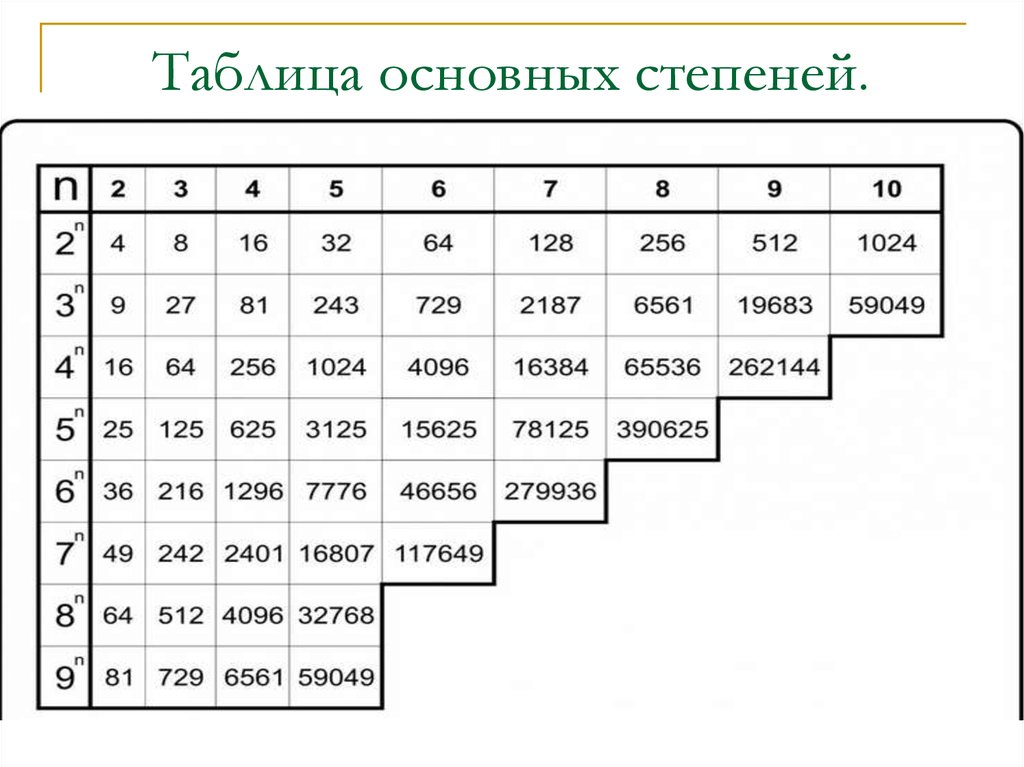
- экспоненциальная форма
- выражение, записанное с показателем степени, где нижняя часть является основанием, а надстрочная часть является экспонента или индекс
Упражнение 3.1. Запись многократного умножения в экспоненциальной форме
Используйте свой калькулятор, чтобы проверить эти ответы.
- \[2 \раз 2 \раз 2 =\]
- \[2 \times 2 \times 2 \times 2 \times 2 \times 2 =\]
- \[3 \раз 3 \раз 3 =\]
- \[3 \раз 3 \раз 3 \раз 3 \раз 3 \раз 3 =\]
Запишите каждое из этих произведений в экспоненциальной форме.
Сравнение показателей степени с помощью неравенств
Когда нам нужно сравнить два числа, записанные в экспоненциальной форме, иногда проще сначала вычислить ответ для каждого.
Рабочий пример 3.1: Сравнение показателей степени
Сравните следующее. Используйте знак \(<\), \(>\) или \(=\) между двумя числами.
9{6} \конец{выравнивание*}\] временный текстЦелые числа в экспоненциальной форме
При умножении положительного (или отрицательного) целого числа на отрицательное (или положительное) целое число необходимо соблюдать осторожность.
посмотрите, когда знак изменится с \(-\) на \(+\) или с \(+\) на \(-\).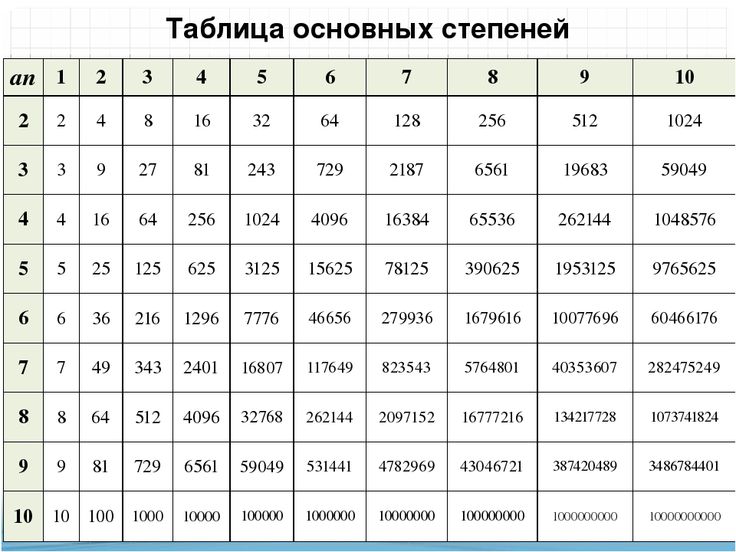
Помните, что при умножении или делении двух отрицательных целых чисел получается положительное число. Если знаки двух целых чисел различны, то результат умножения или деления будет отрицательным число.
Упражнение 3.3. Запишите многократное умножение целых чисел в экспоненциальная форма
\[- 2 \раз (- 2) \раз (- 2) =\]
\[- 2 \раз (- 2) \раз (- 2) = ( — 2 \раз — 2) \раз ( — 2) = 4 \раз ( — 2) = — 8\]
\[- 2 \раз (- 2) \раз (- 2) \раз (- 2) =\]
\[- 2 \раз (- 2) \раз (- 2) \раз (- 2) = ( — 2 \раз (- 2)) \раз ( — 2 \раз (- 2)) = 4 \раз 4 = 16\]
\[- 5 \раз (- 5) =\]
\[- 5 \раз (- 5) = 25\]
\[- 5 \раз (- 5) \раз (- 5) =\]
\[- 5\ \раз (- 5) \раз (- 5) = ( — 5\ \раз (- 5) )) \times ( — 5) = 25 \times ( — 5) = — 125\]
\[- 1 \times (- 1) \times (- 1) =\]
\[- 1\ \ раз \ (- 1)\ \раз \ (- 1)\ = \ ( — 1\ \раз \ (- 1))\ \раз \ ( — 1)\ = \ 1\ \раз \ ( — 1)\ «=» \ — 1\]
\(- 1 \раз (- 1) \раз (- 1) \раз (- 1) =\)
\[- 1\ \раз \ (- 1)\ \раз \ (- 1)\ \раз \ (- 1)\ = \ ( — 1\ \раз \ (- 1))\ \раз \ ( — 1\ \раз \ (-
1))\ = \ 1\ \раз \ 1\ = \ 1\] 9{6} &&\text{Истина.
}
\конец{выравнивание*}\]
\[\начать{выравнивать*}
&&\text{Показатель степени — четное число, поэтому ответ будет положительным с обеих сторон.}
\конец{выравнивание*}\]
Рациональные числа в экспоненциальной форме
Обыкновенные дроби и десятичные дроби являются примерами рациональных чисел .
- рациональное число
- число, которое можно записать как отношение двух целых чисел
Десятичные дроби должны иметь ограниченное количество знаков после запятой или повторяться. образец после запятой – считать рациональным числом.
Давайте посмотрим на дроби и десятичные числа в экспоненциальной форме. Возведение в квадрат или куб дроби или десятичной дроби дробь ничем не отличается от возведения в квадрат или куба целого числа.
Упражнение 3.
5. Нахождение квадратов дробей и десятичных знаков
Найдите значение квадрата следующих дробей.
- \[\фракция{1}{2}\]
- \[\фракция{1}{4}\]
- \[\фракция{4}{7}\]
Чтобы найти значение квадрата дроби, мы начинаем с умножения данной дроби на сам.
- \[\frac{1}{2} \times \frac{1}{2} = \frac{1 \times 1}{2 \times 2} = \frac{1}{4}\]
- \[\ \frac{1}{4} \times \frac{1}{4} = \frac{1 \times 1}{4 \times 4} = \frac{1}{16}\]
- \[\frac{2}{3} \times \frac{2}{3} = \frac{2 \times 2}{3 \times 3} = \frac{4}{9}\]
- \[\frac{4}{7} \times \frac{4}{7} = \frac{4 \times 4}{7 \times 7} = \frac{16}{49{2}} = \фракция{9}{121}\]
Выполните эти расчеты.
В научной записи число выражается двумя частями: число от \(1\) до \(10\), умноженное на степень \(10\). Показатель степени всегда должен быть целым числом.
Упражнение 3.7. Запись больших чисел научными обозначение
Запишите следующие числа в экспоненциальном представлении.
- \[367\ 000\ 000\] 9{3} = \text{2,05} \times 1\000 = 2\050\]
Как вводить экспоненты в Google Docs
Вам нужно записать одно число как степень другого в документе Google? Узнайте, как вводить показатели в Google Docs, здесь.
Photo Credit — iStockPhoto
Google Docs — отличное приложение для набора обычного письменного текста. Иногда, однако, вам может понадобиться добавить немного математики.
Не всегда сразу понятно, как вводить даже самые простые показатели степени, например 3 9.0553 2 . Однако, как только вы узнаете, как это сделать, добавление показателей в ваши Документы Google станет легкой задачей.
Существует несколько различных способов ввода показателей в Google Docs, в зависимости от того, какими они будут. Если вы хотите узнать, как вводить показатели степени в Документах Google, выполните следующие действия.
Как вводить показатели в Google Docs с надстрочным индексом
Способ написания показателя степени заключается в том, что он имеет меньший размер шрифта, чем остальная часть текста, и приподнят, так что верхняя часть текста выше, чем остальная часть текста. Вы можете добиться этого эффекта, используя форматирование верхнего индекса в Документах Google.
Для ввода показателей степени в Документах Google с использованием надстрочного индекса:
- Откройте документ Документов Google.
- Введите букву или число в качестве основания степени.
- Откройте меню Формат .
- Наведите указатель мыши на Текст и выберите Верхний индекс .
- Введите показатель степени.
- Еще раз нажмите меню Формат .
- Выбрать Очистить форматирование .
- Теперь вы можете продолжать печатать как обычно.
- Повторяйте описанные выше шаги каждый раз, когда вы хотите добавить в текст новый показатель степени.
Как использовать верхний индекс с сочетанием клавиш в Документах Google
Существует сочетание клавиш для включения форматирования верхнего индекса в Документах Google. Это сочетание клавиш может сэкономить много времени, если вам нужно добавить к тексту несколько показателей степени.
Чтобы использовать верхний индекс в Документах Google с помощью сочетания клавиш:
- Откройте документ Google.
- Введите символ, который вы хотите использовать в качестве основания вашего показателя степени.
- Нажмите сочетание клавиш Ctrl+. или Cmd+. на Mac, чтобы включить форматирование верхнего индекса.
- Введите показатель степени.
- Нажмите Ctrl+. или Cmd+. еще раз, чтобы отключить форматирование верхнего индекса.
- Продолжайте печатать как обычно.
Как вводить экспоненты в Документах Google с помощью специальных символов
Если вы используете однозначное число, вы также можете вставить его, используя специальный символ. Этот метод не будет работать, если ваш показатель не является одним из ограниченного числа показателей, доступных в Документах Google.
Чтобы ввести показатель степени в Документах Google с помощью специальных символов:
- Откройте документ.
- Введите символ, который вы хотите использовать в качестве основания вашего показателя степени.
- Откройте меню Вставить .
- Выберите Специальные символы .
- В раскрывающихся списках выберите Символ и Верхний индекс .
- Выберите один из символов надстрочного индекса и нажмите на него.
- Специальный символ будет вставлен в ваш текст. Внешний вид специального символа немного отличается от надстрочного текста — показатель степени не выходит за пределы высоты основного символа.
- Закройте окно Специальные символы и продолжайте вводить как обычно.
Как вводить показатели степени в Документах Google с помощью инструмента формул
Вы также можете вводить показатели степени в Документах Google с помощью инструмента формул. Этот метод особенно полезен, если ваш показатель степени представляет собой алгебраический термин, а не просто число.
Для ввода показателей степени в Документах Google с помощью инструмента Equation:
- Откройте документ и поместите курсор туда, где вы хотите, чтобы базовое число появилось, но пока не вводите базовое число.
