Как вместо галочки поставить степенной регистр?
- python
2
Вот так, но универсального решения нет, это для конкретно степени 2 символ UTF-8:
a = 4
print('a = 2\u00B2')
Вывод:
a = 2²
Ссылка на таблицы кодов для степеней
Ссылка на таблицы кодов для остальных математических символов
3
Есть таблица символов юникода, оттуда можно брать.
Можно скопировать отсюда: https://unicode-table.com/ru/sets/superscript-and-subscript-numbers/
1
Немного дополню ответ Danis’a, правда только для целочисленных значений и немного уродски выглядит в консоли )))
indexes = {"0": "\u2070",
"1": "\u00B9",
"2": "\u00B2",
"3": "\u00B3",
"4": "\u2074",
"5": "\u2075",
"6": "\u2076",
"7": "\u2077",
"8": "\u2078",
"9": "\u2079",
"-": "\u207B"
}
def degree(a: int):
degrees = ""
temp = str(a)
for char in temp:
degrees += indexes[char] or ""
return "a = " + temp + degrees
if __name__ == "__main__":
print(degree(1024))
print(degree(-1024))
print(degree(int(input("Введите число: "))))
Вывод:
a = 1024¹⁰²⁴ a = -1024⁻¹⁰²⁴ Введите число: -659897 a = -659897⁻⁶⁵⁹⁸⁹⁷
UPDATE
Ну и немного подправил, чтобы юзабельно было (может кому и пригодится):
def degree(digit: int, deg: int):
degrees = ""
temp = str(deg)
for char in temp:
degrees += indexes[char] or ""
return "a = " + str(digit) + degrees
if __name__ == "__main__":
print(degree(1024, 56))
a, b = map(int, input("Введите число и степень: "). split())
print(degree(a, b))
split())
print(degree(a, b))
Вывод:
a = 1024⁵⁶ Введите число и степень: 23 5698 a = 23⁵⁶⁹⁸
dict_ = {
0: "\u2070",
1: "\u00B9",
2: "\u00B2",
3: "\u00B3",
4: "\u2074",
5: "\u2075",
6: "\u2076",
7: "\u2077",
8: "\u2078",
9: "\u2079"
}
a = 4
print("a = ", str(a) + dict_[2])
1
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Как поставить степень числа на компьютере и телефоне
Давайте разберёмся, как набрать число в квадрате, кубе или напечатать показатель степени больше трёх. А ещё, как поставить степень на смартфоне с Android и отобразить степени в виде верхнего индекса в html-коде.
А ещё, как поставить степень на смартфоне с Android и отобразить степени в виде верхнего индекса в html-коде.
Знака степени на клавиатуре нет, поэтому будем использовать несколько вариантов. Они зависят от вашего устройства, операционной системы и текстового редактора, в котором вы работаете.
Варианты набора степени числа:
- Скопировать знак и вставить в нужное место.
- Использовать комбинации клавиш Alt + Num (степень ¹²³).
- Применить инструменты Word или Google Документы.
- Воспользоваться таблицей символов Windows.
- Открыть дополнительные символы на смартфоне.
- Обернуть нужную степень тегом <sup> в коде веб-страницы.
Скопировать знак степени от 0 до 9
Выделите требуемую вам степень, скопируйте и вставьте в нужное место.
Как поставить степень¹²³ на клавиатуре сочетанием клавиш Alt + Num
Сочетания цифр и клавиши Alt работают в Ворде и любом текстовом редакторе для Windows.
Переключаем клавиатуру на En.
Для написания символа первой степени¹ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 0 1 8 5. Отпустите Alt — получится ¹.
Для написания второй степени (квадрата)² следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 0 1 7 8. Отпустите Alt — получится ².
Для написания третьей степени (куба)³ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 0 1 7 9. Отпустите Alt — получится ³.
Набрать степень более трёх ⁴⁵⁶⁷⁸⁹, сочетанием клавиш увы, не получится.
Для ноутбуков, у которых на клавиатуре нет цифрового блока, нужно дополнительно нажать клавишу Fn и использовать функциональные клавиши с цифрами.
Как поставить степень в Word
Первый способ
Напишите число, где последняя цифра (или цифры) — это требуемая степень. Выделите последний знак и нажмите кнопку надстрочного знака x² на панели инструментов.
Этот метод можно использовать как для написания цифр, так и для написания букв или знаков.
Если по каким-то причинам кнопка надстрочного знака x² не работает, используйте комбинацию клавиш Ctrl, ⇑Shift и ⩲.
Второй способ
При работе в ворде устанавливаем курсор в нужное место → вкладка Вставка → Символ → Другие символы… → Набор: надстрочные и подстрочные. Выделяем нужный знак → Вставить.
Программа запомнит ваш выбор. В следующий раз достаточно будет открыть набор ранее использованных символов.
Как поставить степень в Google Документы
Напишите число, где последняя цифра (или цифры) — это требуемая степень. Выделите последний знак → Формат → Текст → X² Надстрочный.
Как поставить степень в таблице символов Windows
Коллекция символов есть не только в ворде. В Windows существует своя таблица с символами — программа charmap.exe. Для её вызова нажимаем Пуск → Выполнить → charmap.exe → ОК.
В окне таблицы найдите знак нужной степени. Выделите его, нажмите кнопку Выбрать и Копировать.
Выделите его, нажмите кнопку Выбрать и Копировать.
Остаётся лишь вставить символ в нужное место сочетанием клавиш Ctrl и V.
Как поставить степень на телефоне Android
Зажмите нужную клавишу с цифрой (от 0 до 9) и тапните по надстрочному показателю степени.
HTML
Тег <sup> отображает текст в виде верхнего индекса.
645<sup>5</sup> = 6455
Главная | Powerball
Победители джекпота
Матч 5 +
Power Play
Победители на 2 миллиона долларов
Матч 5
$1 миллион победителей
Следующий розыгрыш
Приблизительный джекпот
Денежная сумма:
Цифры
- Выигрышные номера
- Прошлые чертежи
Поиск прошлых чертежей
Дата начала
Дата окончания
Сила 9
9 способов победить!
Есть 9 способов выиграть приз в Powerball®.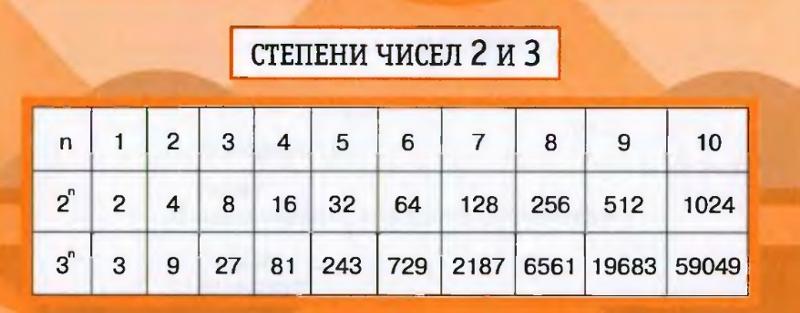
Все призы устанавливаются в денежной форме, за исключением Главного приза.
В Калифорнии суммы призовых выплат являются одинаковыми и определяются продажами и количеством победителей.
- Главный приз
- 1 миллион долларов
- 50 000 долларов
- 100 долларов
- 100 долларов
- $7
- $7
- 4 доллара
- 4 доллара
- Главный приз
- 2 миллиона долларов
- 100 000 долларов
- 200 долларов
- 200 долларов
- 14 долларов
- 14 долларов
- $8
- $8
- Главный приз
- 2 миллиона долларов
- 150 000 долларов
- 300 долларов
- 300 долларов
- 21 доллар
- 21 доллар
- 12 долларов
- 12 долларов
- Главный приз
- 2 миллиона долларов
- 200 000 долларов
- 400 долларов
- 400 долларов
- 28 долларов
- 28 долларов
- 16 долларов
- 16 долларов
- Главный приз
- 2 миллиона долларов
- 250 000 долларов
- 500 долларов
- 500 долларов
- 35 долларов США
- 35 долларов США
- 20 долларов
- 20 долларов
- Главный приз
- 2 миллиона долларов
- 500 000 долларов
- 1000 долларов
- 1000 долларов
- 70 долларов
- 70 долларов
- 40 долларов
- 40 долларов
Посмотреть таблицу призов и шансов
Призы Powerball
- Главный приз
- 1 миллион долларов
- 50 000 долларов
- 100 долларов
- 100 долларов
- $7
- $7
- 4 доллара
- 4 доллара
- Главный приз
- 2 миллиона долларов
- 100 000 долларов
- 200 долларов
- 200 долларов
- 14 долларов
- 14 долларов
- $8
- $8
- Главный приз
- 2 миллиона долларов
- 150 000 долларов
- 300 долларов
- 300 долларов
- 21 доллар
- 21 доллар
- 12 долларов
- 12 долларов
- Главный приз
- 2 миллиона долларов
- 200 000 долларов
- 400 долларов
- 400 долларов
- 28 долларов
- 28 долларов
- 16 долларов
- 16 долларов
- Главный приз
- 2 миллиона долларов
- 250 000 долларов
- 500 долларов
- 500 долларов
- 35 долларов США
- 35 долларов США
- 20 долларов
- 20 долларов
- Главный приз
- 2 миллиона долларов
- 500 000 долларов
- 1000 долларов
- 1000 долларов
- 70 долларов
- 70 долларов
- 40 долларов
- 40 долларов
Коэффициенты Powerball
- Главный приз
- 1 миллион долларов
- 50 000 долларов
- 100 долларов
- 100 долларов
- $7
- $7
- 4 доллара
- 4 доллара
- 1 из 292 201 338,00
- 1 из 11 688 053,52
- 1 из 913 129,18
- 1 из 36 525,17
- 1 из 14 494,11
- 1 из 579,76
- 1 из 701,33
- 1 из 91,98
- 1 из 38,32
Коэффициенты при наличии множителя 10X
- 10x
- 5x
- 4x
- 3x
- 2x
- Приз выиграл раз 10
- Приз выиграл раз 5
- Приз выиграл раз 4
- Приз выиграл раз 3
- Выиграно раз 2
- 1 из 43
- 1 из 21,5
- 1 в 14,33
- 1 из 3,31
- 1 из 1,79
Коэффициенты, когда 10-кратный множитель недоступен
- 5x
- 4x
- 3x
- 2x
- Приз выиграл раз 5
- Приз выиграл раз 4
- Приз выиграл раз 3
- Выиграно раз 2
- 1 из 21
- 1 из 14
- 1 из 3,23
- 1 из 1,75
Играй как профессионал
x
Как
Powerball® стоит 2 доллара за игру. В Айдахо и Монтане Powerball поставляется в комплекте с Power Play по минимальной цене покупки 3 доллара за игру.
В Айдахо и Монтане Powerball поставляется в комплекте с Power Play по минимальной цене покупки 3 доллара за игру.
Выберите пять цифр от 1 до 69для белых шаров; затем выберите одно число от 1 до 26 для красного Powerball.
Выберите свои номера на игровом листе или позвольте лотерейному терминалу выбрать ваши номера случайным образом.
Джекпот Powerball растет до тех пор, пока он не будет выигран.
Игроки получают приз, угадав один из 9 способов выиграть.
x
Где
В Powerball играют в 45 штатах, Вашингтоне, Пуэрто-Рико и на Виргинских островах США!
Розыгрыши Powerball проводятся каждый понедельник, среду и субботу в 10:59.вечера. ЕТ.
Время закрытия продаж варьируется за один-два часа до розыгрыша, в зависимости от юрисдикции продажи.
Чтобы узнать, где посмотреть рисунки, нажмите здесь.
x
Power Play
Попросите Power Play® при покупке Powerball!
За дополнительный 1 доллар за игру функция Power Play может умножить призы, не связанные с джекпотом, в 2, 3, 4, 5 или 10 раз!
Номер множителя выбирается случайным образом перед каждым розыгрышем.
Множитель 10X используется только в том случае, если объявленный аннуитет джекпота составляет 150 миллионов долларов или меньше.
Приз за 5 совпадений с Power Play всегда составляет 2 миллиона долларов.
x
Multi-Draw
Играйте одним и тем же набором чисел в нескольких розыгрышах!
Выберите количество последовательных розыгрышей, которые вы хотите разыграть, в разделе «Несколько розыгрышей» или «Предварительная игра» вашего игрового билета или сообщите продавцу, сколько розыгрышей вы хотите сыграть.
Количество мульти-розыгрышей или предварительных розыгрышей, доступных для покупки, зависит от юрисдикции продажи.
bg_image
https://s3.amazonaws.com/cdn.powerball.com/drupal/files/2017-12/how-tall-desktop_0.jpg
Как TALL
стоит 40 миллионов долларов?
Джекпот Powerball в размере 40 миллионов долларов может показаться не таким уж большим, но спросите себя: действительно ли 40 миллионов долларов — это небольшая сумма? Является ли Смитсоновский институт в Вашингтоне небольшим зданием?
Если бы вам нужно было сложить 100-долларовые купюры, взгляните на высоту, которую могут достичь деньги при каждой предполагаемой сумме джекпота.
145 ft
Smithsonian Institution
Washington, DC
305 ft
Statue of Liberty
New York City
455 ft
Great Pyramid
Egypt
805 ft
Bloomberg Tower
New York Город
1063 фута
Эйфелева башня
Париж
1776 футов
Всемирный торговый центр One
Нью-Йорк
2717 футов
Бур-Халифадж0015Дубай
3458 футов
Уиллис Тауэр X2
Чикаго
40 миллионов долларов 85 миллионов долларов 125 миллионов долларов 225 миллионов долларов 300 миллионов долларов 500 миллионов долларов 750 миллионов долларов 1 миллиард долларов
Используйте ползунок, чтобы увидеть размер джекпота своей мечты.
Результат поиска
Следите за выигрышными номерами в Powerball!
Подпишитесь на бесплатную рассылку по электронной почте и следите за тем, куда направляется джекпот Powerball.
Спасибо, что подписались на нашу рассылку новостей!
Видео-урок: Степени и показатели для рациональных чисел
Стенограмма видео
В этом видео мы научимся определять основание и показатель степени в формулах степени, записывать их в показательных и расширенные формы и оценивают простые степени.
Начнем с того, что вспомним, что можем
представить многократное умножение как степень. Например, два в пятой степени
определяется как произведение пяти двоек, как показано. Мы называем два основанием, а пять — основанием.
экспонента. Мы можем распространить это определение на
общие рациональные основания. В этом случае, если 𝑛 является положительным
целое число, а 𝑎 над 𝑏 — рациональное число, то 𝑎 над 𝑏 в 𝑛-й степени будет
быть продуктом 𝑛 множества 𝑎 над 𝑏. Например, мы можем оценить
половина в третьей степени, или половина в кубе, путем умножения половины на половину
и еще раз половина. Вспоминая наши правила умножения
дроби, мы просто умножаем числители и знаменатели отдельно. Это дает нам один больше восьми, или
одна восьмая.
Вспоминая наши правила умножения
дроби, мы просто умножаем числители и знаменатели отдельно. Это дает нам один больше восьми, или
одна восьмая.
Мы также можем следовать тому же процессу в обратном порядке. Представим, что мы хотим написать дробь 27 на восемь в экспоненциальной форме. Начнем с факторизации числителя и знаменатель на простые числа следующим образом. 27 равно трем, умноженным на три умножить на три, а восемь равно двум умножить на два умножить на два. Затем мы можем разделить умножение, что дает нам три на два, умноженное на три, на два, умноженное на три больше двух. Таким образом, 27 больше восьми произведение трех лотов из трех на два и, следовательно, может быть записано как три на два. два в кубе.
Теперь рассмотрим несколько примеров
с участием степеней рациональных чисел.
Какую терминологию мы используем для опишите половину в выражении половина в пятой степени и пять в выражение половина в пятой степени?
Начнем с того, что вспомним, что выражение вида 𝑎 в 𝑛-й степени называется экспоненциальным выражением или 𝑛-я степень 𝑎. Мы называем 𝑎 основанием выражение и 𝑛 показатель степени или степени. В этом вопросе имеем выражение половина в пятой степени. Половина — это число, которое берется в силу, а пятерка есть сама сила. Таким образом, мы можем сделать вывод, что в выражение половина в пятой степени, половина называется основанием выражение, а пять называется показателем степени выражения.
В нашем следующем примере мы упростить выражение, переписав его в экспоненциальной форме.
Сколько будет четыре больше 11, умноженное на
четыре больше 11 умножить на четыре больше 11 умножить на четыре больше 11 умножить на
четыре больше 11 умножить на четыре больше 11 умножить на четыре больше 11? Это вариант (А) четыре одиннадцатых до
сила отрицательной семерки? (B) Четыре одиннадцатых в степени
Семь. (C) Четыре одиннадцатых в степени
девять. (D) Семь одиннадцатых в степени
четыре. Или (E) двадцать восемь одиннадцатых до
сила семи.
(C) Четыре одиннадцатых в степени
девять. (D) Семь одиннадцатых в степени
четыре. Или (E) двадцать восемь одиннадцатых до
сила семи.
Мы могли бы вычислить это выражение
путем умножения всех числителей и всех знаменателей. Это даст нам следующее
выражение, которое мы могли бы вычислить с калькулятором или без него. Тем не менее, пять вариантов в этом
вопрос дается как полномочия. Это означает, что вместо
оценивая выражение, мы можем упростить, вспомнив, что многократное умножение
можно записать в экспоненциальной форме. В частности, в этом вопросе мы
умножают семь партий из четырех одиннадцатых. Мы знаем, что произведение семи
много из четырех одиннадцатых можно записать, возведя четыре одиннадцатых в степень
Семь. И, таким образом, мы можем сделать вывод, что
правильный ответ — вариант (Б). Выражение в вопросе
эквивалентно четырем одиннадцатым в степени семь.
Выражение в вопросе
эквивалентно четырем одиннадцатым в степени семь.
Теперь мы будем использовать информацию, которую мы до сих пор видели, чтобы определить ключевое свойство степеней рациональных чисел. Так как положительная целая степень a рациональная база определяется повторным умножением, мы можем показать, что если 𝑛 является натуральное число и 𝑎 над 𝑏 — рациональное число, то 𝑎 над 𝑏 до 𝑛-й мощность равна 𝑎 в 𝑛-й степени, деленной на 𝑏 в 𝑛-й степени. Другими словами, мы можем повысить числитель и знаменатель степени отдельно.
Теперь рассмотрим пример, где мы можем применить это.
Найти отрицательное значение шесть пятых в кубе, давая ответ в простейшей форме.
Мы можем оценить выражение в
этот вопрос двумя способами. Во-первых, напомним, что отрицательный
шесть на пять в кубе можно записать как многократное умножение.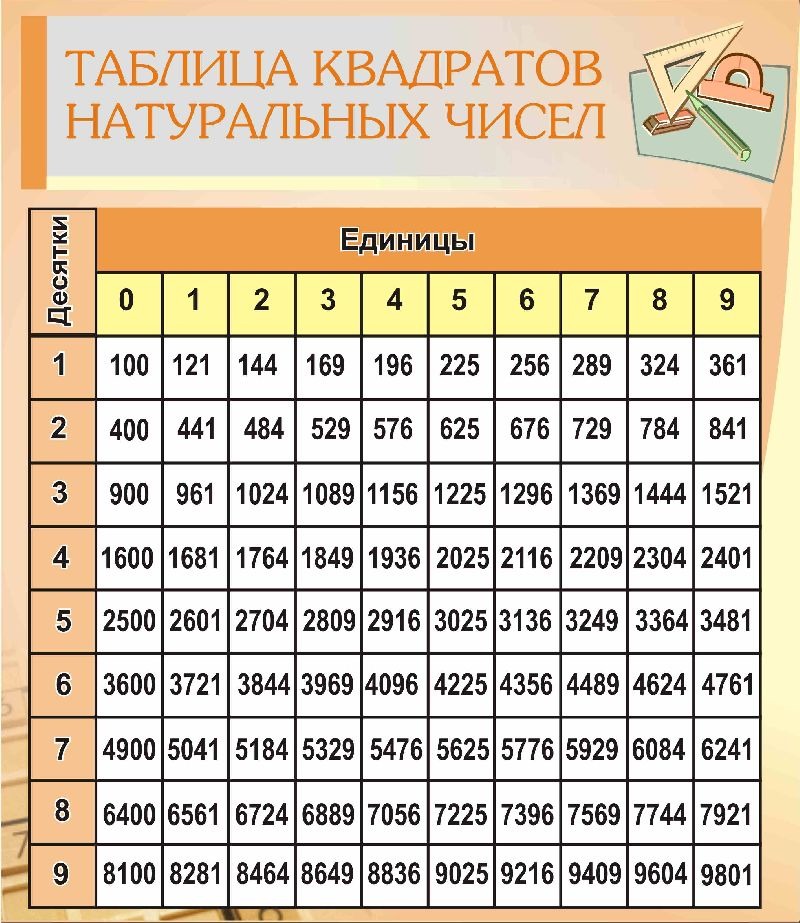 Это продукт трех партий
минус шесть на пять, как показано. Тогда мы можем умножить числители
и знаменатели отдельно, что дает нам отрицательные шесть, умноженные на отрицательные шесть
умножить на минус шесть на пять умножить на пять умножить на пять. Умножение трех отрицательных чисел
дает отрицательный ответ, поэтому числитель отрицательный 216. Знаменатель упрощается до
125. Значение минус шесть больше пяти
в кубе отрицательно 216 больше 125.
Это продукт трех партий
минус шесть на пять, как показано. Тогда мы можем умножить числители
и знаменатели отдельно, что дает нам отрицательные шесть, умноженные на отрицательные шесть
умножить на минус шесть на пять умножить на пять умножить на пять. Умножение трех отрицательных чисел
дает отрицательный ответ, поэтому числитель отрицательный 216. Знаменатель упрощается до
125. Значение минус шесть больше пяти
в кубе отрицательно 216 больше 125.
Мы также можем вычислить выражение
напоминая общий результат для степеней рациональных чисел. Если 𝑛 — натуральное число и 𝑎
над 𝑏 — рациональное число, то 𝑎 над 𝑏 в 𝑛-й степени равно 𝑎
𝑛-я степень, деленная на 𝑏 в 𝑛-й степени. Это означает, что мы можем переписать
минус шесть на пять в кубе как минус шесть в кубе на пять в кубе, что еще раз
упрощается до отрицательного 216 вместо 125.
В нашем следующем примере мы рассмотреть проблему в контексте.
Найдите выражение для объема данного куба, длина стороны которого два 𝑥 больше пяти.
Начнем с того, что вспомним, что объем куба определяется кубом длины его стороны. Это означает, что если куб имеет сторону длина 𝑙, то его объем 𝑙 умножается на 𝑙 умножается на 𝑙, что равно 𝑙 в кубе. В этом вопросе нам говорят, что длина стороны на два 𝑥 больше пяти. Это означает, что его объем задан выражением два 𝑥 на пять в кубе. Вспоминая, что для любого рационального число 𝑎 над 𝑏 и любое целое число 𝑛 𝑎 над 𝑏 в 𝑛-й степени равно 𝑎 𝑛-я степень делится на 𝑏 в 𝑛-й степени, наше выражение упрощается до двух 𝑥 в кубе над пятью в кубе.
Далее вспоминаем, что для умножения
одночлены, умножаем коэффициенты и складываем степени разделяемых
переменные. Это означает, что два 𝑥 умножаются
на два 𝑥 умножить на два 𝑥 равно восьми 𝑥 в кубе. А так как пять в кубе это 125, то наш
выражение упрощается до восьми 𝑥 в кубе на 125. Это выражение для
объем куба, длина стороны которого два 𝑥 больше пяти.
Это означает, что два 𝑥 умножаются
на два 𝑥 умножить на два 𝑥 равно восьми 𝑥 в кубе. А так как пять в кубе это 125, то наш
выражение упрощается до восьми 𝑥 в кубе на 125. Это выражение для
объем куба, длина стороны которого два 𝑥 больше пяти.
Теперь мы рассмотрим один последний пример, где нам нужно оценить алгебраическое выражение, используя результаты для степени рациональных чисел.
Если 𝑥 равно трем больше двух и 𝑦 равно отрицательному четырем на пять, найдите значение 𝑥 в квадрате 𝑦 минус 𝑥𝑦 в кубе, давая ответ в виде дроби в простейшей форме.
Мы начнем этот вопрос с
подставляя значения 𝑥 и 𝑦 в наше выражение. 𝑥 в квадрате 𝑦 минус 𝑥𝑦 в кубе
поэтому равно трем на два в квадрате, умноженному на минус четыре на пять
минус три на два умножить на минус четыре на пять в кубе. Следующим нашим шагом будет оценка
степени, напомнив, что если 𝑛 — натуральное число, а 𝑎 над 𝑏 — рациональное
число, то 𝑎 над 𝑏 в 𝑛-й степени равно 𝑎 в 𝑛-й степени над 𝑏
в 𝑛й степени. Это означает, что три больше двух
квадрат равен трем в квадрате на два в квадрате, что равно девяти на два в квадрате.
четыре. Точно так же отрицательная четверка
пять в кубе равно отрицательным четырем в кубе на пять в кубе. А это равно минус 64
более 125. Таким образом, наше выражение упрощает
до девяти на четыре умножить на минус четыре на пять минус три на два
умножить на минус 64 больше 125.
Это означает, что три больше двух
квадрат равен трем в квадрате на два в квадрате, что равно девяти на два в квадрате.
четыре. Точно так же отрицательная четверка
пять в кубе равно отрицательным четырем в кубе на пять в кубе. А это равно минус 64
более 125. Таким образом, наше выражение упрощает
до девяти на четыре умножить на минус четыре на пять минус три на два
умножить на минус 64 больше 125.
Мы можем упростить первую часть
наше выражение путем деления числителя и знаменателя на четыре. Точно так же мы можем разделить
числитель и знаменатель второй части нашего выражения на два. И наше выражение упрощается до
отрицательные девять пятых минус отрицательные 96 на 125. Это, в свою очередь, упрощается до отрицательных
девять на пять плюс 96 на 125. Наконец, чтобы сложить дроби,
у нас должны быть одинаковые знаменатели, поэтому мы умножаем числитель и знаменатель
нашу первую дробь на 25. Выражение становится отрицательным 225
более 125 плюс 96 на 125. Наконец, мы добавляем числители,
что дает нам отрицательное значение 129 на 125. Поскольку нет общих множителей
кроме единицы, это значение 𝑥 в квадрате 𝑦 минус 𝑥𝑦 в кубе как дробь в
его простейшая форма.
Выражение становится отрицательным 225
более 125 плюс 96 на 125. Наконец, мы добавляем числители,
что дает нам отрицательное значение 129 на 125. Поскольку нет общих множителей
кроме единицы, это значение 𝑥 в квадрате 𝑦 минус 𝑥𝑦 в кубе как дробь в
его простейшая форма.
Сейчас мы закончим это видео,
повторение ключевых моментов. Мы видели, что в выражении
преобразуем 𝑏 в 𝑛-ю степень, мы называем 𝑏 основанием, а 𝑛 степенью или показателем степени. Определим положительные целые степени
повторным умножением, известным как расширенная форма. В общем, если 𝑎 над 𝑏 является
рациональное число и 𝑛 — натуральное число, то 𝑎 над 𝑏 в 𝑛-й степени есть
произведение 𝑛 множества 𝑎 больше 𝑏, как показано на рисунке. Наконец мы увидели, что можем
оценить мощность рационального числа, оценив мощность числителя и
знаменатель отдельно.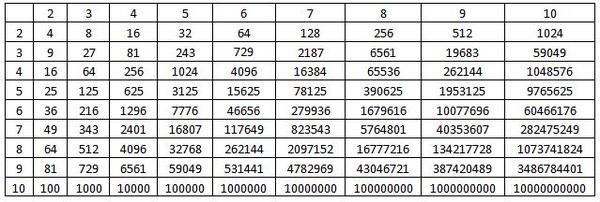

 split())
print(degree(a, b))
split())
print(degree(a, b))