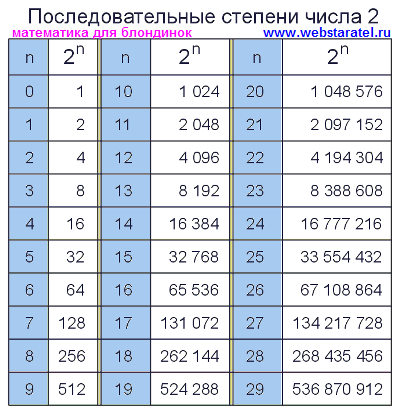
Степени двойки от 0 до 16
Используя наш сайт, вы подтверждаете, что прочитали и поняли политику о куки , политику конфиденциальности и пользовательское соглашение. Stack Overflow на русском — это сайт вопросов и ответов для программистов. Регистрация займёт не больше минуты. Подскажите, пжл, алгоритм.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Список степеней двойки
- Задачи / Является ли число степенью двойки
- Возведение в степень
- A1 Ответы и решения
- Системы счисления и их применение
1024 (число) - Таблица степеней
- Способы перевода чисел из одной системы счисления в другую
- Научный форум dxdy
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: PCM декодирование простыми словами об импульсно кодовой модуляции — ИКМ.
Список степеней двойки
Преподаватели Анкеты лучших репетиторов. Найти репетитора Заполните форму запроса, и вам подберут подходящего репетитора. Библиотека Методические статьи, пособия, задачники. Вузы Ведущие российские вузы и их преподаватели.
Репетиторам Регистрация в базе данных преподавателей. Форум Задайте вопрос крупнейшему сообществу репетиторов. Книга отзывов Отзывы учеников о работе репетиторов. Ломоносова, факультет вычислительной Баумана, приборостроительный Ломоносова, факультет В 2-х частях. Бененсон , А. Могилев, Н. Пак, Е. Поиск по базе преподавателей :. Часы работы: с до Учебники по информатике. Темы: авторские статьи , информатика. Автор: Бабичев Сергей Анатольевич.
Сдающим ЕГЭ и не только… Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую.
Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке. Например, нужно перевести число 10 в двоичную систему: Результат записываем в обратном порядке снизу вверх. И как тут собрать все единички с нулями и ни одной не пропустить? В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и ричными системами и двоичной.
Это разделы А1, В Но есть и задачи с другими системами счисления, как например, в разделе B7. Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией. Таблица степеней числа 2: 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 2 4 8 16 32 64 Она легко получается умножением предыдущего числа на 2.
Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните. Таблица двоичных чисел от 0 до 15 c ричным представлением: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Перевод целых чисел Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число Нам нужно разложить это число на слагаемые, равные степеням двойки.
Ищем ближайшую к степень двойки, не превосходящую его. Вычитаем из , получаем Повторим шаги 1 и 2, пока не останется 1 или 0.
Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда Квадрат основания всегда будет , куб Способ 1 : Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2 : Распишем слагаемые как степени двойки друг под другом, начиная с большего. Вот и всё. Ответ — столько, сколько слагаемых степеней двойки в таком его представлении. У их 5. Теперь пример попроще. Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 квадрат 5.
Тогда подберем коэффициент для 5 2. Это 2. Ну и, наконец, совсем лёгкие переводы между 8- и ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для ричной четырьмя.
При этом все ведущие нули обязательны, кроме самого старшего разряда. Переведем в двоичную систему число 8. Переведем в 8-ричную систему число C25 Теперь рассмотрим перевод обратно в десятичную.
Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
Перевод отрицательных чисел Здесь нужно учесть, что число будет представлено в дополнительном коде. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1. Итак, переведем число в двоичную систему. Число займёт у нас один байт. Дополним слева нулями до размера байта, 8 разрядов, получаем Получаем К результату прибавляем 1, получаем ответ В дополнительном коде они будут записаны одинаково Перевод дробных чисел Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале.
То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.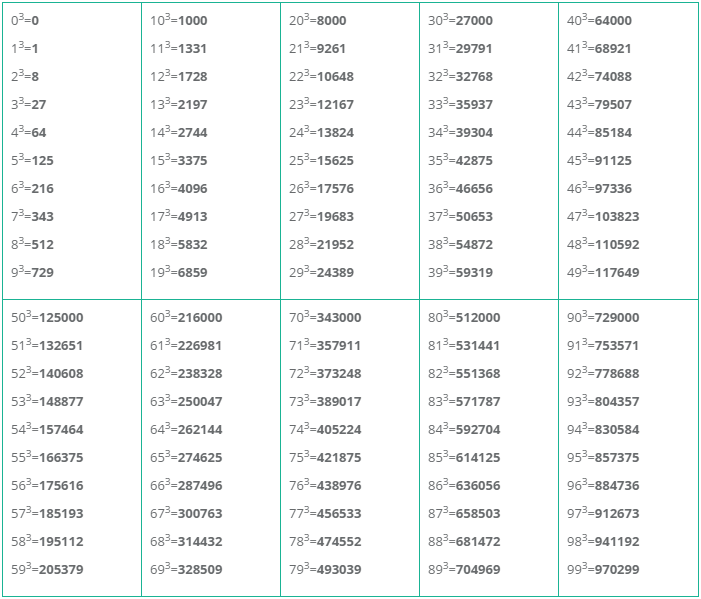
Переведем число 0, в двоичную систему. Остановимся пока на 6-м знаке. Если число было 5,, то в двоичном виде оно будет , Условия использования.
Мобильная версия.
Задачи / Является ли число степенью двойки
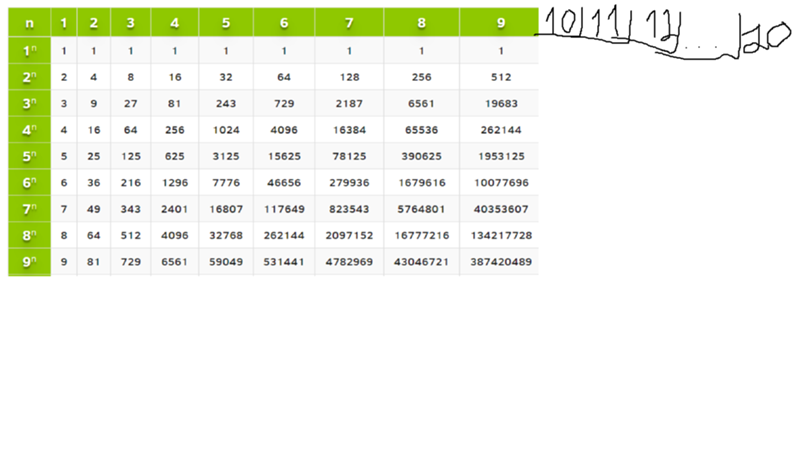
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности , геометрии и математике! Также на сайте работает форум , на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
всего две цифры, начертание которых заимствовано из десятичной системы и выглядит, как 0 и 1. Степени двойки в десятичном виде 21 22 23 системах, часто внизу пишут основание системы: степеней двойки до 16 ( табл.
Возведение в степень
Таблица степеней числа 2 два последовательно представляет число 2 два в степени от 0 нуля до 29 двадцати девяти. Все результаты сведены в таблицу, которую можно скачать бесплатно. Число 2 в нулевой степени. Начинается таблица с нулевой степени числа два. Как известно, любое число в нулевой степени равняется единице. Поэтому два в нулевой степени равняется единице. Число 2 в первой степени. Если любое число возвести в первую степень, это число останется неизменным.
A1 Ответы и решения
Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Мегапосты: Криминальный квест HR-истории Путешествия гика. Войти Регистрация. Как найти показатель степени двойки за O 1 с помощью последовательности де Брёйна Алгоритмы Из песочницы Аперитив Всем, наверное, известно, как посчитать количество бит в числе.
Хочу представить вам самый простой способ перевода чисел из двоичной системы счисления в десятиричную и обратно. Стандартные решения предполагают математические вычисления, я же предложу простую схему даже для гуманитарного мозга.
Системы счисления и их применение
Бит это двоичное число, которое, как правило принимает либо 0 либо 1. Если говорить о конечном проявлении в физической форме в компьютере, то как правило это состояния «свободно», «занято» или «нет сигнала» и «есть сигнал». Вот именно от сюда проявляется важность двойки и ее степенней. Так как бит это очень уж маленькая единица измерения даже для переменных, не говоря уже о подсчете информации на энергонезависимых источниках памяти жесткие диски, флешки. В современных компьютерных системах 1 байт равен 8 битам.
1024 (число)
Пусть нам надо перевести число 10 в двоичную систему. Воспользуемся методом деления на новое основание 2 :. Попробуем совершить обратное действие:. Получается, что самая старшая цифра 1 умножается на 2 6 , следующая — на 2 5 , дальше — на 2 4 и т. Получаем такую сумму:. Если выполнить каждое умножение, то получится такая сумма:. Если всё это сложить, то получится число
Тогда, например, в 5-м конверте будет 16 у.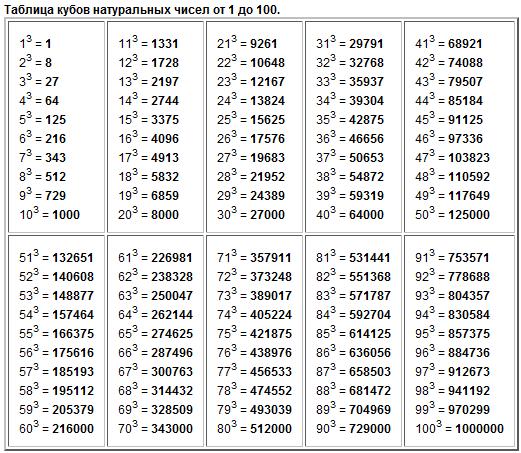
е., в м — у.е., в м N0. Пусть 2n — максимальная степень двойки, не превосходящая N, то есть 2n не класть, то можно получить таким образом любое число от 0 до – 1.
Таблица степеней
Одномерный массив степени двойки Здравствуйте! Помогите, пожалуйста! Среди заданной последовательности целых чисел найти степени двойки Среди заданной последовательности целых чисел найти степени двойки.
Способы перевода чисел из одной системы счисления в другую
Называется она вполне ожидаемо: последовательность степеней двойки. Тем не менее, она обладает весьма примечательными свойствами. Понятно, что суммарное их количество равно. Кто похитрей, могут углядеть в этой последовательности геометрическую прогрессию.
Компьютеры работают с числами. Причём в подавляющем большинстве случаев число разрядов в этих числах ограничено [2].
Научный форум dxdy
Среди степеней двойки вновь и вновь встречаются числа, начинающиеся с единицы. Как часто они встречаются? Иными словами, какова вероятность того, что произвольно взятая степень двойки начинается цифрой 1? Уточним постановку задачи.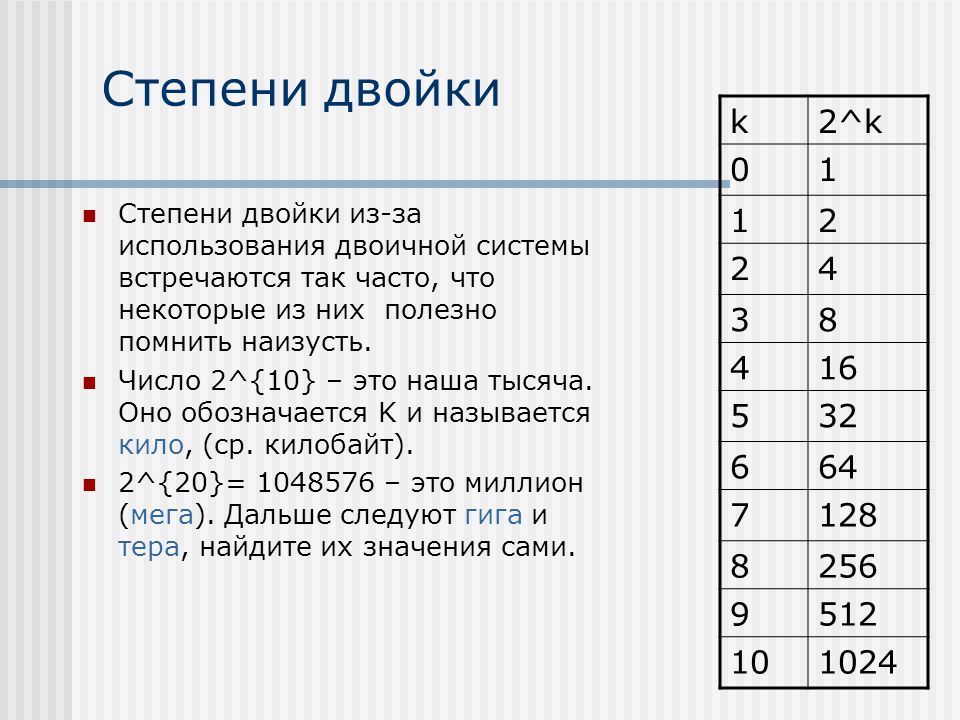
Поэтому двоичная запись числа 10 содержит 10 разрядов. Эти разряды будем нумеровать справа налево, начиная с 0. Самый правый разряд последний, если считать слева — нулевой, второй справа предпоследний — первый, …, самый левый восьмой справа — седьмой справа.
Число 2 | Математика, которая мне нравится
Пишите об интересных свойствах числа
. Картинки приветствуются!
Для начала выкладываю свойства, которые прислал Лейб Александрович Штейнгарц.
1. В Ветхом Завете рассказывается о Всемирном потопе, в котором спасся только праведник Ной и его семья, так как Всевышний оповестил его о предстоящем бедствии и подал мысль построить ковчег (корабль). И Бог также дал Ною наказ: для сохранения жизни на земле взять на борт ковчега всех животных по ПАРАМ.
2. Из Библии:
“И создал Бог два светила великие: светило большее, для управления днем, и светило меньшее, для управления ночью”.
3. У человека имеется:
две руки,
две ноги,
два уха,
два глаза.
4. Если конечное множество состоит из n элементов, то количество всех его подмножеств можно вычислить по такой формуле:
Например, пусть множество состоит из трех элементов:
. Тогда у него имеется
подмножеств
.
5. Число 2 — основание простейшей двоичной системы счисления, широко используемой в вычислительной технике.
6. Два – наименьшее простое число.
При этом оно – единственное чётное простое число.
7. 1. Одна из главных аксиом в геометрии формулируется так: “Через любые ДВЕ точки можно провести одну и только одну прямую”.
8. Люди и многие животные делятся на ДВЕ категории по половому признаку.
9. В декартовой системе координат на плоскости каждая точка однозначно определяется ДВУМЯ своими координатами.
10. Единственный из показателей корня, который не пишется – это корень ВТОРОЙ степени, то есть квадратный корень.
11. ДВА – это наименьшее возможное количество диагоналей в многоугольнике.
12. При помощи всего лишь ДВУХ спичек можно составить много символов, которые используются в математике. Например:
Плюс.
Знак умножения.
Так на калькуляторах и в языках программирования обозначается операция “возведения в степень”.
Обозначение угла.
Слово “перпендикулярно”.
Слово “параллельно”.
Буквой
обычно обозначают переменную в уравнениях, а также ее используют в качестве аргумента функции.
Символ “меньше“.
Символ “больше“.
Символ модуля (абсолютной величины).
Так обозначают единицу измерения веса “тонна”, а иногда кратко обозначают слово “теорема”.
Так обозначают единицу измерения веса “грамм”, а также кратко обозначают слово “год”.
Так в логике обозначают символ “конъюнкция” (слово “и”).
Так в логике обозначают символ “дизъюнкции” (слово “или”).
Так в логике обозначают символ “отрицания” (слово “не”).
Римская цифра 2.
Римская цифра 5.
Римская цифра 10.
Римская цифра 50.
Как проверить, является ли число степенью двойки
Как узнать, является ли число степенью двойки?
Это легко сделать, если оно представлено в виде 2 n , где n — целое число. Например, 2 12 , 2 0 и 2 -37 являются степенью двойки. Это по определению. Но как насчет произвольных положительных чисел, таких как 16 392, 524 288 или 0,00390625? Являются ли они степенью двойки? Вот как сказать — если их можно упростить до вида 2 n , они есть; если не могут, то нет.
Мы рассмотрим это в два этапа. Во-первых, мы увидим, как преобразовать известные степени двойки, используя простую арифметику, в форму 2 n . Затем мы увидим, как проверить, является ли произвольное число степенью двойки.
(Если вы ищете информацию о том, как определить, является ли число в компьютере степенью двойки, см. мои статьи «Как выглядят степени двойки внутри компьютера» и «Десять способов проверить, является ли Целое число — это степень двойки в С».)
Преобразование степени двойки в форму 2
nНекоторые числа вы сразу узнаете как степени двойки, несмотря на то, что они не представлены в форме 2 n . Например: 2, 4, 8, 16, 1/2, 1/4, 1/8, 0,5 и 0,25. Если вы разбираетесь в компьютерах, вы распознаете и другие степени двойки, такие как 256, 1024, 4096 и даже 65 536. Но как насчет степеней двойки, которые вы не запомнили?
В общем, чтобы показать, что число является степенью двойки, вам понадобится процедура, то есть алгоритм, чтобы представить его в виде 2 п .
Используемый алгоритм зависит от того, работаете ли вы с положительной или отрицательной степенью двойки (вам не нужен алгоритм, чтобы сказать вам, что 1, то есть 2 0 , является степенью двойки).
Преобразование положительных степеней двойки
Самый простой способ преобразовать положительную степень двойки в форму 2 n — это подсчитать число n из делений на 2, которое требуется, чтобы получить частное 1. Для например, для числа 524 288 требуется 19делений до 1, что дает 2 19 :
- 524 288/2 = 262 144
- 262 144/2 = 131 072
- 131 072/2 = 65 536
- 65 536/2 = 32 768
- 32 768/2 = 16 384
- 16 384/2 = 8 192
- 8 192/2 = 4 096
- 4096/2 = 2048
- 2048/2 = 1024
- 1024/2 = 512
- 512/2 = 256
- 256/2 = 128
- 128/2 = 64
- 64/2 = 32
- 32/2 = 16
- 16/2 = 8
- 8/2 = 4
- 4/2 = 2
- 2/2 = 1
Этот пример раскрывает свойство, общее для всех положительных степеней двойки: все промежуточные частные также являются степенями двойки.
На самом деле частные образуют нисходящую последовательность последовательных неотрицательных степеней двойки. Для числа 524 288 последовательность частных такова: 2 18 , 2 17 , 2 16 , …, 2 1 , 2 0 .
Преобразование отрицательных сил двух
Чтобы преобразовать отрицательную степень двойки в форму 2 n , подсчитайте число n из умножений на 2, которое требуется для получения произведения 1, затем инвертируйте n. Например, число 0,00390625 требует 8 умножений, чтобы получить 1, что дает 2 -8 :
- 0,00390625*2 = 0,0078125
- 0,0078125*2 = 0,015625
- 0,015625*2 = 0,03125
- 0,03125*2 = 0,0625
- 0,0625*2 = 0,125
- 0,125*2 = 0,25
- 0,25*2 = 0,5
- 0,5*2 = 1,0
Этот пример раскрывает несколько свойств, общих для всех отрицательных степеней двойки. Во-первых, обратите внимание, что все промежуточные продукты являются степенями двойки.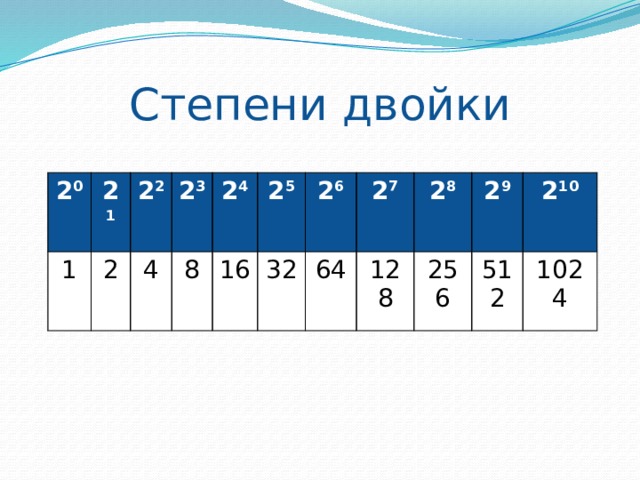
На самом деле произведения образуют восходящую последовательность последовательных неположительных степеней двойки. Для числа 0,00390625 последовательность продуктов 2 -7 , 2 -6 , 2 -5 , … , 2 -1 , 2 0 . Также все продукты, кроме последнего, заканчиваются на цифру 5; все отрицательные степени двойки в десятичной форме заканчиваются на 5!
Этот алгоритм работает так же хорошо для отрицательных степеней двойки, выраженных в виде дробей. Например, 1/128 равно 2 -7 :
- 1/128*2 = 1/64 .
- 1/64*2 = 1/32
- 1/32*2 = 1/16
- 1/16*2 = 1/8
- 1/8*2 = 1/4
- 1/4*2 = 1/2
- 1/2*2 = 1
С дробями работать не нужно; вместо этого вы можете выполнить одно из следующих действий:
- Обработать знаменатель как положительную степень двойки, преобразовать его с помощью алгоритма деления, а затем инвертировать показатель степени 9.
0050 - Преобразование дроби в десятичную и преобразование с помощью алгоритма умножения
0050Проверка того, является ли произвольное число степенью двойки
К этому моменту мы продемонстрировали наши алгоритмы на числах, которые, как известно, являются степенями двойки. Но что, если вы не знаете, что число — это степень двойки? Вам подскажут те же алгоритмы.
Проверка положительных целых чисел
Для целого числа больше 1, которое делает его кандидатом на положительную степень двойки, используйте алгоритм «повторного деления на 2».
Число, которое равно , а не степени двойки, будет иметь частные — на самом деле все они — которые не являются степенями двойки. Итак, если вы признаете, что частное не является степенью двойки, вы можете остановиться; исходное число не является степенью двойки. Конечно, это помогает только в том случае, если вы можете распознать степень двойки, чего вы не можете, потому что используете этот алгоритм!
Надежный способ прекратить проверку — найти частное, не считая 1, которое является нечетным.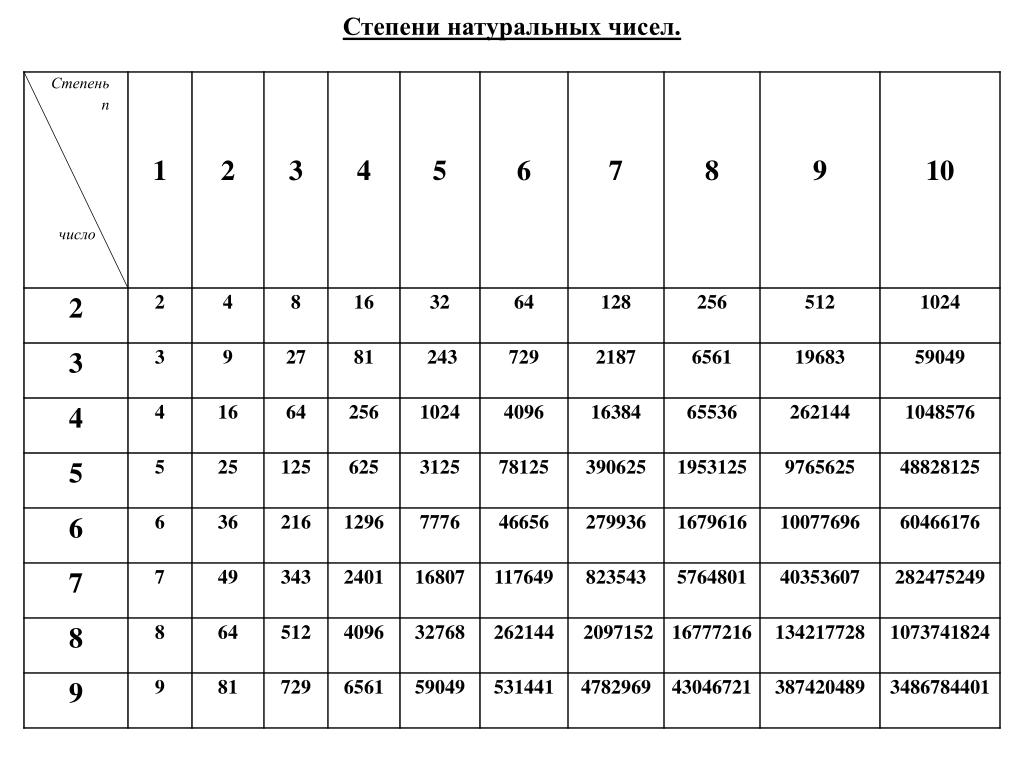
Это означает, что частное и, следовательно, само число не может быть степенью двойки. Например, 16,39Число 2 не является степенью двойки, поскольку после трех делений оно возвращает нечетное частное:
- 16 392/2 = 8 196
- 8 196/2 = 4 098
- 4098/2 = 2049
Другой пример — число 524 289, которое изначально нечетное, поэтому оно не является степенью двойки.
Проверка положительных десятичных знаков
Для десятичного значения от 0 до 1, которое делает его кандидатом на отрицательную степень двойки, используйте алгоритм «повторного умножения на 2».
Число, равное , а не степень двойки будет иметь продукты — на самом деле, все они — которые не являются степенями двойки. Как это вам поможет? Отрицательная степень двойки оканчивается на «5», поэтому число, которое не может быть степенью двойки (это не означает, что число, оканчивающееся на 5 , должно быть степенью двойки). Если вы заметили продукт с последней цифрой, отличной от 5, исходное число не является степенью двойки.
Если вам не нравится этот ярлык, просто выполните алгоритм до конца. Это означает вычисление произведений до тех пор, пока последнее произведение не станет равным или превысит 1. Если число не является отрицательной степенью двойки, последнее произведение никогда не будет точно равно 1.
Вот несколько примеров:
Является ли 0,0390625 степенью двойки?
Нет, потому что это дает произведение больше 1:
- 0,0390625*2 = 0,078125
- 0,078125*2 = 0,15625
- 0,15625*2 = 0,3125
- 0,3125*2 = 0,625
- 0,625*2 = 1,25
Я тщательно выбрал этот пример. Все произведения не только оканчиваются на 5, но и выглядят как степени двойки (они были бы степенями двойки, если бы их сдвинули на одну позицию вправо). Если бы вы не были обмануты этим по пути, вы могли бы перестать размножаться.
Является ли 0,0178125 степенью двойки?
Нет, так как произведение (пятое) не оканчивается на 5:
- 0,0178125*2 = 0,035625
- 0,035625*2= 0,07125
- 0,07125*2 = 0,1425
- 0,1425*2 = 0,285
- 0,285*2 = 0,57
Опять же, если вы заметили продукт, который не был степенью двойки до этого момента, вы могли бы остановиться.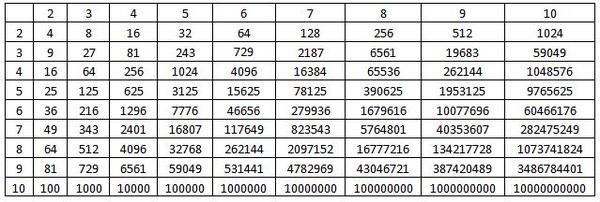
Является ли 0,00390626 степенью двойки?
Нет. Оно не заканчивается на 5, точка.
Проверка положительных дробей
Для дроби в наименьшем выражении и в форме 1/d, что делает ее кандидатом на отрицательную степень двойки, у вас есть несколько вариантов:
- Считайте знаменатель целым положительным числом и проверьте это с использованием алгоритма деления
- Преобразуйте дробь в десятичную и проверьте ее с помощью алгоритма умножения
- Проверьте дробь напрямую, используя алгоритм умножения
Чтобы использовать вариант 3, умножьте числитель на 2 и уменьшайте дробь на каждом шаге, чтобы получить произведение. Вы можете перестать проверять любое из этих условий, что означает, что исходное число не является степенью двойки:
- Продукт не является дробной частью
- Произведение представляет собой дробную единицу, но его знаменатель нечетный
- Произведение представляет собой дробную единицу, но вы понимаете, что его знаменатель не является степенью двойки
Если вы дойдете до 1, поздравляю — число равно степени двойки.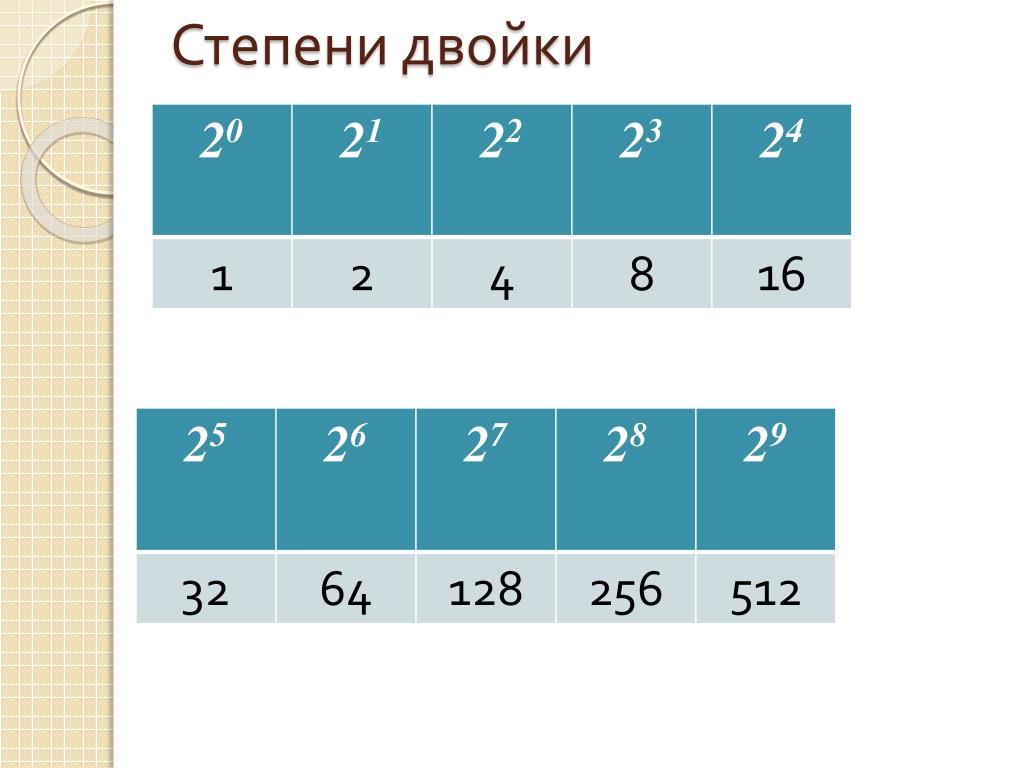
Вот пример:
- 1/48*2 = 1/24
- 1/24*2 = 1/12
- 1/12*2 = 1/6
- 1/6*2 = 1/3
1/48 не является степенью двойки, потому что знаменатель четвертого произведения равен 3, а это нечетно. В любом случае, вы, вероятно, знали с самого начала, что 48 — это не степень двойки.
Упражнения
Определите, какие из следующих являются степенями двойки, и задайте их форму как 2 n :
- 4 294 967 296
- 3 145 728
- 0,0009765625
- 0,046875
- 131 072
- 1/294,912
Ответы
- 2 32
- Не степень двойки (частное становится нечетным только после 20-го деления, так что вам может потребоваться некоторое время, чтобы определить это)
- 2 -10
- Не степень двойки (произведение не становится 1; после 4 умножений оно равно 0,75, а после 5 умножений равно 1,5)
- 2 17
- Не степень двойки (после 15 умножений на дробь знаменатель произведения нечетный)
Изучение сил числа 2 – Кубок Чар
Требуется двое
При любом интересе к компьютерам и вычислениям невозможно избежать сил числа 2.
x (2 моркови x) или 2 с надстрочным индексом x). Я решил писать свои показатели более словесно, чтобы избежать общих странностей с Unicode. Оставив это в стороне, давайте вместе взглянем на некоторые шаблоны и свойства, связанные со степенями числа 2.
В пересчете на два
Существует реальная вероятность того, что кто-то спросит вас, каково точное значение степени двойки во время технического собеседования. По своему опыту я сталкивался с вопросами о двойках в степенях 7, 8, 10, 16, 20, 30, 32 и 40. Прежде чем мы перейдем к самому интересному, давайте рассмотрим некоторые практические применения степеней числа 2. 2 в вычислительной технике.
2 в степени от 0 до 8 важно знать, и их не должно быть слишком сложно запомнить, поскольку все, что они требуют, — это некоторые вычисления в уме. Начните с 2 в степени 0, что равно 1. Удвойте его — вы получите 2, что равно 2 в степени 1. Удвойте еще раз, и вы получите 4, что является значением 2 в степени 2. Этот шаблон удвоение предыдущего значения не меняется.
Этот метод должен привести вас как минимум к 2 в степени 8. Запоминание этих значений станет более естественным по мере вашего продвижения в ваших приключениях в области компьютерных наук.
Побитно
Что такого особенного в первых 8 степенях числа 2? Обратите внимание, что мы начинаем счет с нуля, то есть с 2 в степени 0 и вплоть до 2 в степени 7. Эти числа составляют первый байт в адресной организации компьютера. Если вы слышали или знаете, что байт состоит из 8 бит, вы, возможно, уже догадались, в каком направлении мы движемся со значением подсчета первых 8 степеней двойки. Давайте проверим, каково двоичное представление этих первых восьми выглядеть так:
| Power of 2 | Decimal Value | Binary Representation |
| 0 | 1 | 0000 0001 |
| 1 | 2 | 0000 0011 |
| 2 | 4 | 0000 0111 |
| 3 | 8 | 0000 1111 |
| 4 | 16 | 0001 1111 |
| 5 | 32 | 0011 1111 |
| 6 | 64 | .
Начиная с 2 в степени 0, мы получаем 0000 0001. Затем мы заменяем ноль с самой правой стороны на 1 для каждой итерации по показателю степени 2. В конце концов мы получаем все восемь двоичных цифр 1111. 1111, что равно 2 в степени 7. Что действительно круто в том, что степени 2 идут дальше 7 в качестве показателя степени, так это то, что вы можете добавить еще 2 в степени 0 (0001) слева и повторять шаблон вечно. То же, что и на графике выше, но красивее!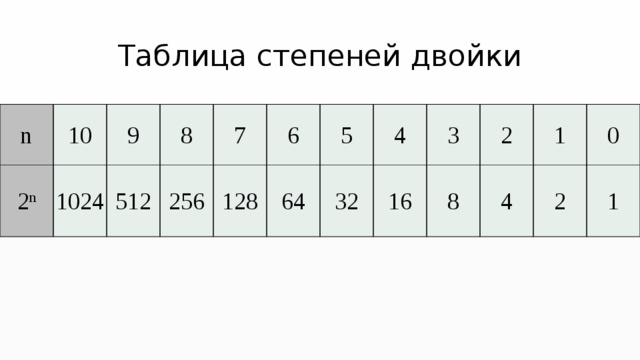
Это повлияет на встроенные системы и структуры данных с временным представлением.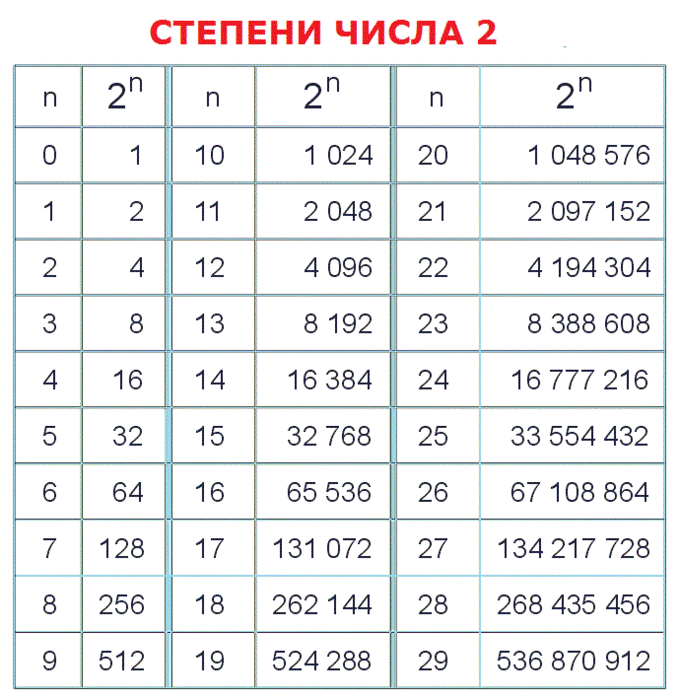
2 в степени 86 — это наибольшая степень двойки, которая не содержит нуля — насколько мы подсчитали. Это число равно 77 371 252 455 336 267 181 195 264. Если мы пройдем еще немного дальше 2 в степени 168, мы найдем наибольшую степень 2 (пока что), которая не содержит все десять цифр. При ошеломляющих 374 144 419156 711 147 060 143 317 175 368 453 031 918 731 001 856, по иронии судьбы оно не содержит числа 2.
Попробуйте ввести 2 в степени 1023 в свой калькулятор или калькулятор Google. Вроде нормально, да? Теперь попробуйте 2 в степени 1024. Мы достигли предела, потому что это максимальное число, которое может поместиться в число двойной точности с плавающей запятой. Вы обнаружите, что многие программы не могут представить это число, например, калькуляторы и даже Microsoft Office. Число 1024 вам знакомо? Если вы помните, 2 в степени 10 равно 1024.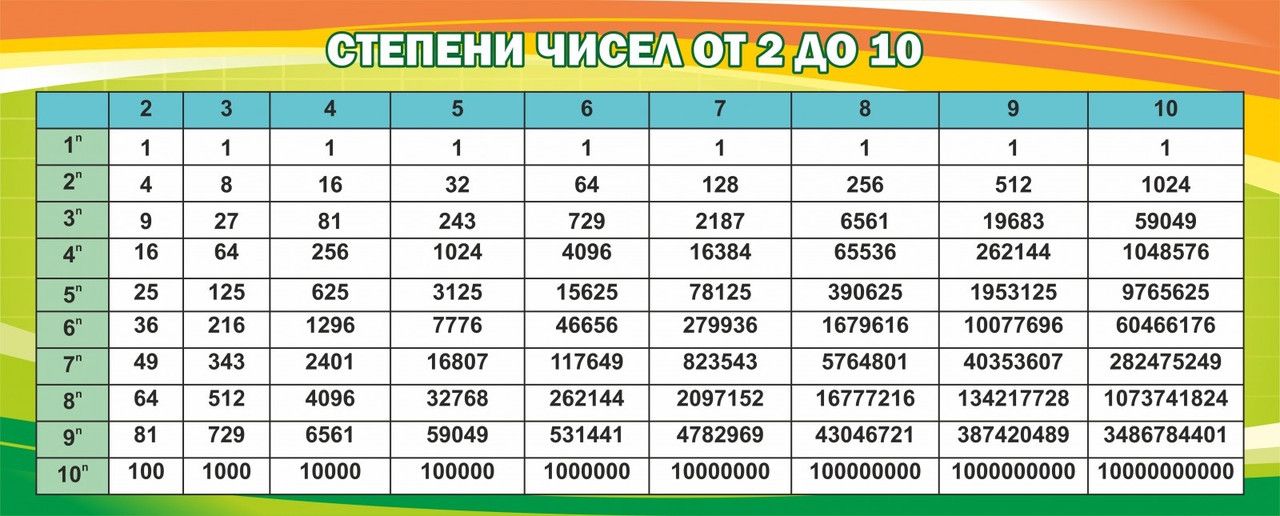
Двоично-рациональные дроби — это дроби со степенью двойки в знаменателе. «Вежливое число» — это число, которое может быть представлено в виде суммы последовательных положительных целых чисел, что означает, что это в точности те числа, которые равны 9.0207, а не в степени 2.
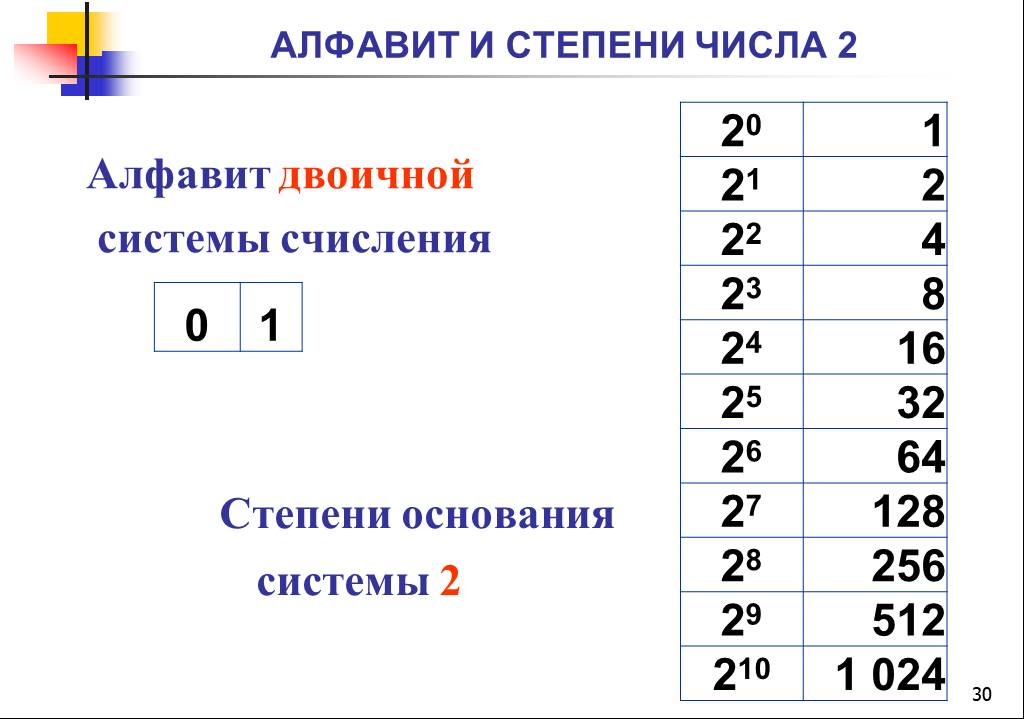Это равно 1,09.9 511 627 776, что примерно равно одному триллиону. Если бы вы собирались сделать вывод, что я собирался сказать вам, что это количество байтов в терабайте, вы были бы правы.