Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три».
Если в матрице один столбец
или одна строка
,
то такие матрицы также называют векторами.
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице
.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
Действие второе. Умножение матрицы на число.
Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
Сначала рассмотрим то, чего делать НЕ НАДО:
Вносить дробь в матрицу НЕ НУЖНО- это только затрудняет дальнейшие действия с матрицей.
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать. Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В этом случае можно и НУЖНО умножить все элементы матрицы на 1/2, так как все числа матрицы делятся на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
Действие пятое. Умножение матриц.
Как умножить матрицы ?
Пример:
Умножить матрицы
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
Пример сложнее:
Умножить матрицы
Формула:
В результате получена так называемая нулевая матрица.
Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицуы
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицы
Ответ.
Как проверить решение? Необходимо выполнить матричное умножение либо
Проверка:
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Пример:
Найти обратную матрицу для матрицы
Обратную матрицу найдем по формуле:
,
где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Как вычислить определитель?
Определитель можно вычислить только для квадратной матрицы.
Обозначения: Если дана матрица
,
то ее определитель обозначают |A|. Также очень часто определитель обозначают латинской буквой D или греческой Δ.
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО.
2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»:
Сразу рассмотрим пример:
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Пример:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс». Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Правило Крамера.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три».
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если D=0, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет/
Если D≠0, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
И, наконец, ответ рассчитывается по формулам:
Пример
Решить систему по формулам Крамера.
Решение:
Решим систему по формулам Крамера.
значит, система имеет единственное решение.
Ответ: ..
Собственно, здесь опять комментировать особо нечего. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения.
Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Пример
Решить систему матричным методом
Решение:
Запишем систему в матричной форме: AX=b, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице A нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице A нужно было бы поставить нули.
.
Согласно формуле нам нужно найти обратную матрицу и выполнить матричное умножение . Алгоритм нахождения обратной матрицы подробно разобран в разделе «Как найти обратную матрицу?»
Обратную матрицу найдем по формуле:
,
где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
Сначала разбираемся с определителем:
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце.
В ходе решения расчет миноров лучше расписать подробно.
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).
Таким образом:
– матрица миноров соответствующих элементов матрицы A.
– матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Теперь записываем обратную матрицу:
Ни в коем случае не вносим в матрицу, это серьезно затруднит дальнейшие вычисления.Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Ответ: .
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три».
Если в матрице один столбец
или одна строка
,
то такие матрицы также называют векторами.
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице
.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 6 из 65Следующая ⇒ Вернемся к нашей матрице
.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит. Проведем «тождественное преобразование» матрицы, которое её не изменит. Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль. Обратный пример: .
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось.
2) Умножение матрицы на число. Пример: Преобразовать:
Как видим, чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Пример: Преобразовать: применив умножение матрицы на дробь.
Сначала рассмотрим то, чего делать НЕ НАДО (это правильно, но усложняет вид):
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если – окончательный ответ задания). И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример: В этом случае можно и НУЖНО умножить все элементы матрицы на (1/2), так как все числа матрицы делятся на 2 без остатка.
Примечание: В теории высшей математики школьным понятием «деление» обычно не пользуются. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». Любое деление – это частный случай умножения.
Транспонирование матрицы Определение: Чтобы транспонировать матрицу, нужно строки исходной матрицы записать в столбцы транспонированной матрицы. Следствие: Если исходная матрица Amn – порядка (размером) «m на n», то матрица, транспонированная к исходной матрице, будет размером «n на m» и иметь вид ATn∙т. Следствие: При операции транспонирования элементы на главной диагонали матрицы (от верхнего левого до нижнего правого) остаются неизменными.
Пример: Транспонировать матрицу . Внимание: не «транспортировать», не «трансвестировать», а «транспонировать»! Строка здесь всего одна и, согласно правилу, её нужно записать в столбец: . Таким образом, DT – это матрица, транспонированная к исходной матрице D. Подчеркнём, что исходная матрица A и транспонированная матрица AT — это две различные, в общем случае, матрицы. A = AT только в особых случаях: если A – симметричная матрица, когда элементы, симметричные относительно главной диагонали исходной матрицы, равны.
Пример пошаговый: Транспонировать матрицу Примечание: В матрице B на главной диагонали расположены элементы: {-1; 4; -6}.
Заполняем места элементов транспонированной матрицы Сначала переписываем первую строку B — в первый столбец BT.: Потом переписываем вторую строку во второй столбец: И, наконец, переписываем третью строку в третий столбец:
Примечание: Транспонировать – это значит прибить матрицу в левом верхнем элементе и повернуть её (исходную матрицу) вокруг главной диагонали на 180°.
Сумма (разность) матриц. Сумма матриц — действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ. Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой. — Такое действие не определено для этих матриц!
Определение: Для того чтобы получить матрицу, равную сумме (разности) двух исходных матриц, необходимо сложить (вычесть) их соответствующие элементы: Пример: Сложить матрицы и В соответствии с определением, запишем: . Для разности матриц, аналогично, находим разность соответствующих элементов: Пример: Найти разность матриц и . А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу H: Примечание: В теории высшей математики школьного понятия «вычитание» нет.
Умножение матриц. Скажем сразу, правило умножения матриц (есть в любом учебнике по алгебре) выглядит очень странно для неподготовленного слушателя, но мы объясним это на конкретных примерах. Прежде всего: «Какие матрицы можно умножать?» Следствие (из строгого определения): Для умножения матрицы K на матрицу L слева необходимо, чтобы число столбцов матрицыKравнялось числу строк матрицыL.
Пример: Можно ли умножить матрицу на матрицу ? , значит, умножать данные матрицы можно. А вот если, в данном случае, матрицы переставить местами, то умножение уже невозможно! , значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла: Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно. Следует отметить, что в ряде случаев можно умножать матрицы и так, и так, но с разным результатом, т. к. в общем случае KL ¹ LK. Например, для матриц и существует как произведение , так и .
Как умножать матрицы? Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей. Начнем с самого простого: Пример: Умножить матрицу на матрицу – попытайтесь сразу уловить закономерность. Поэтому:
Пример сложнее: Умножить матрицу на матрицу Формула: . В таком случае произведение: . В результате мы получили так называемую нулевую матрицу. Попробуйте самостоятельно выполнить умножение . Правильный ответ — . Обратите внимание, что! Это почти всегда так!
Таким образом, переставлять матрицы в произведении нельзя!Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке.
Примеры с матрицами третьего порядка: Умножить матрицу на матрицу . Формула умножения очень похожа на предыдущие формулы: . А теперь попробуйте самостоятельно разобраться в умножении следующих матриц: Умножьте матрицу на матрицу . Вот готовое решение, но постарайтесь сначала в него не заглядывать! .
Нахождение обратной матрицы Смотри, после вычисления определителей, раздел 2.3.
Вычисление определителей
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Мы не будем давать строгое математическое определение определителя, и, вообще, будем стараться минимизировать математическую терминологию, так как большинству читателей легче от этого не станет. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители. Определение:Определитель, или детерминант матрицы, – это единственное для данной матрицы число, оно определяется всеми элементами матрицы и характеризует всю матрицу. Определитель можно вычислить только для квадратной матрицы. Для вектора таким характерным числом является модуль вектора. Для действительного числа произвольного знака таким характерным числом является абсолютное значение, или модуль числа. Но, в отличие от модуля ненулевого вектора или числа, определитель матрицы может иметь любой знак и быть равным нулю, в том числе для ненулевой исходной матрицы. Обозначение: Определитель матрицы обозначается символом данной матрицы в прямых (одинарных, или двойных) скобках, как у модуля вектора, или D, или Δ, или det(A). На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: . Определитель четвертого порядка встречается значительно реже, но о нем тоже поговорим. Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании в строке или столбце D речи не идет. Менять местами числа нельзя! Но если очень хочется, то можно… (На самом деле, есть десяток теорем о детерминантах, об условиях, при которых можно переставлять строки и столбцы, но не отдельные элементы, определителя со сменой (или без смены) знака определителя). Таким образом, если дан определитель, то ничего внутри него не трогаем!
1) Что значит вычислить (найти, раскрыть, решить) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. 2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы.
Определитель матрицы «два на два», его формула: . ЭТО НУЖНО ЗАПОМНИТЬ, по крайней мере, на время изучения высшей математики в ВУЗе. Сразу рассмотрим пример: Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три», его формула: Пример:
Приведенная формула определителя «три на три» длинная и допустить ошибку по невнимательности проще простого. Как избежать промахов? Определитель «три на три»можно раскрыть 10 способами (10-ю способами получить приведённую формулу). Четыре из них – «простые», и шесть – «нормальные».
Начнем с четырёх простых способов «параллельных полосок» Саррюса: 1) два способа дополнительных столбцов; 2) два способа дополнительных строк. Первый способ дополнительных столбцов состоит в том, что справа от определителя приписывают первый и второй столбцы и аккуратно карандашом проводят линии: . Заметим, что элементы на «красных» диагоналях входят в формулу со знаком «плюс», а элементы на «синих» диагоналях входят в формулу со знаком минус.
Пример:
Второй способ дополнительных столбцов состоит в том, что слева, перед определителем приписывают второй и третий (ближе к определителю) столбцы и проводят линии, начиная с главной диагонали.
Первый способ дополнительных строк состоит в том, что снизу от определителя приписывают первую (ближе к определителю) и вторую строки и проводят линии, начиная с главной диагонали.
Второй способ дополнительных строк состоит в том, что сверху от определителя приписывают вторую и третью (ближе к определителю) строки и проводят линии, начиная с главной диагонали.
Во всех четырёх простых способах элементы матрицы, находящиеся на «красных» диагоналях, параллельных главной диагонали, входят в формулу со знаком «плюс». Элементы матрицы, находящиеся на «синих» диагоналях, входят в формулу со знаком минус. Вычисления по остальным простым способам проведите самостоятельно.
Сравните решение «по формуле» и «простые решения». Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим 6 «нормальных» способов для вычисления определителя. Почему «нормальных» Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так. Как Вы заметили, у определителя «три на три» три столбца и три строки. Вычислить определитель можно, разложив его по любой строке или по любому столбцу. Таким образом, получается 6 способов, при этом во всех случаях используется алгоритм одного и того же типа (смотрите в книгах по высшей алгебре теорему Лапласа о разложении определителя матрицы по любой строке или столбцу, но мы обещали нашим студентам «не докучать моралью строгой»). Теорема Лапласа: Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики. В следующем примере будем раскрывать определитель по первой строке. Для этого нам понадобится «матрица знаков»: . Легко заметить, что знаки расположены в шахматном порядке. Примечание: Внимание! «Матрица знаков» – это изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает вам понять алгоритм вычисления определителя. Сначала приведём полное решение. Снова берем наш подопытный определитель и проводим вычисления по теореме Лапласа, разложив его по первой строке:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или, как их еще называют, МИНОРОВ.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё. Запишем рядом исходную матрицу и «матрицу знаков», одинаковую для любой матрицы «три на три»:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец). Сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: Оставшиеся четыре числа записываем в маленький определитель.
Переходим к третьему элементу первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент: Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым. В этом и состоит ценность теоремы Лапласа!
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм. При этом матрица знаков у нас увеличится: В следующем примере раскроем определитель по четвертому столбцу:
Пример: А как это получилось, попробуйте разобраться самостоятельно.
Вычисление обратной матрицы
Что такое обратная матрица? Прежде определим единичную матрицу.
Определение: Единичной матрицей n-го порядка называется такая матрица En, что для любой квадратной матрицы n-го порядка An выполняется соотношение . Можно показать, что у единичной матрицы на главной диагонали расположены единицы, а все остальные элементы равны нулю.
Определение: Обратной матрицей для матрицы An с неравным нулю определителем (|An|¹0) называется такая матрица An-1, для которой выполняется соотношение .
Что необходимо знать и уметь для успешного изучения данного материала? Ответ. Обратную матрицу A-1можно найти по следующей формуле:
где |A| – определитель матрицы A, Ã – матрица алгебраических дополнений исходной матрицы, а ÃT – присоединённая матрица, или транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
(Обозначение Ã читаем «A с тильдой»)
Понятие обратной матрицы, как и понятие определителя, существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения:Как Вы уже, наверное, заметили, обратная матрица обозначается добавлением надстрочного индекса (-1) к символу исходной матрицы. Начнем с простейшего случая – матрицы «два на два». Пример: Найти обратную матрицу для матрицы . Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы. . Важно! У матрицы, определитель которой равен НУЛЮ, обратной матрицы НЕ СУЩЕСТВУЕТ (Это следствие из основной теоремы об обратной матрице). В рассматриваемом примере, как выяснилось, |A| = -2 ¹ 0, а значит, всё в порядке.
2) Находим матрицу миноров элементов. Матрица миноров элементов имеет такие же размеры, как и матрица A, то есть, в данном случае, . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек. Возвращаемся к нашей матрице . . Как найти минор этого элемента матрицы? А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: Оставшееся число в данном случае и является минором данного элемента, которое записываем в нашу матрицу миноров:
Рассматриваем следующий элемент матрицы : Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:
Аналогично рассматриваем элементы второй строки и находим их миноры: Готово. – это и есть матрица миноровсоответствующих элементов матрицы A. 3) Находим матрицу алгебраических дополнений соответствующих элементов. Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: .
— это матрица Ã алгебраических дополнений соответствующих элементов матрицы A.
4) Находим транспонированную матрицу алгебраических дополнений.
— это транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
Ответ. Вспоминаем нашу формулу Всё найдено! Таким образом, искомая обратная матрица:
Ответ лучше оставить в таком виде. НЕ НУЖНОделить каждый элемент матрицы на 2, так как получатся дробные числа.
Как проверить решение? По определению обратной матрицы, необходимо выполнить матричное умножение либо .
6) Проверка:
Получена так называемая единичная матрица(с единицами по главной диагонали и нулями в остальных местах). Таким образом, обратная матрица найдена правильно.
Перейдём к более распространенному на практике случаю – матрице «три на три».
Пример: Найти обратную матрицу для матрицы . Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы B.
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Что такое матрица — Журнал «Код»
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Эксперимент: что нейронка думает о жизни, Вселенной и всём прочем
- Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
- У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
- Векторы можно складывать, вычитать, умножать.
 Это чуть сложнее, чем с обычными числами.
Это чуть сложнее, чем с обычными числами. - У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.
Общая схема матрицыПример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число триПростые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыреПеред матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычисленийУмножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.
Пример умножения матрицы на числоТранспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матрицУмножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
- У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C.
- Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂.
- У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂.
- У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂.
- Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁).

- Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂).
- Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁).
- Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂).

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
Формула умножения матрицПример умножения квадратных матриц размерностью 2×2Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Вынесение минуса из матрицы (внесение минуса в матрицу). — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Вернемся к нашей матрице . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: . Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому-что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
Действие второе. Умножение матрицы на число.
Пример 1
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
В данном случае – на тройку.
Действие третье. Сумма (разность) матриц.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Пример 2
Сложить матрицы и
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример 3
Найти разность матриц ,
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
То есть, вычитание – это частный случай сложения.
УМНОЖЕНИЕ МАТРИЦ
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу можно было умножить на матрицу необходимо, чтобы число столбцов матрицы равнялось числу строк матрицы .
Пример 4
Можно ли умножить матрицу на матрицу ?
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример 5
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
Пример 6
Умножить матрицу на матрицу
Формула:
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение (правильный ответ ).
Обратите внимание, что ! Это почти всегда так!
Таким образом, переставлять матрицы в произведении нельзя!
ПРАКТИКУМ 1
ЗАДАНИЕ N 1
Тема: Действия над матрицами
Даны матрицы
и
Вычислить
Решение:
Для нахождения матрицы необходимо каждый элемент матрицы B умножить на 2. Получим
Каждый элемент разности матриц и равен разности соответствующих элементов матриц.
Значит,
ЗАДАНИЕ N 2
Тема: Действия над матрицами
Даны матрицы и тогда …
Решение:
Напоминаем, что для нахождения матрицы необходимо каждый элемент матрицы A умножить на 3. Получим
Каждый элемент разности матриц и равен разности соответствующих
элементов этих матриц. Значит,
ЗАДАНИЕ N 3
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
Решение:
Напоминаем, что если то элемент матрицы равен сумме произведений элементов i−ой строки матрицы A и соответствующих элементов j−го столбца матрицы В.
Тогда
ЗАДАНИЕ N 4
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
Решение:
Напоминаем, что если , то элемент матрицы равен сумме произведений элементов i-ой строки матрицы A и соответствующих элементов j-го столбца матрицы В.
Тогда
ЗАДАНИЕ N 5
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
Решение:
Напоминаем, что если , то элемент матрицы равен сумме произведений элементов i-ой строки матрицы A и соответствующих элементов j-го столбца матрицы В.
Тогда
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
ЗАДАНИЕ N 1
Тема: Действия над матрицами
Даны матрицы и тогда …
ЗАДАНИЕ N 2
Тема: Действия над матрицами
Даны матрицы и тогда …
ЗАДАНИЕ N 3
Тема: Действия над матрицами
Даны матрицы и тогда …
ЗАДАНИЕ N 4
Тема: Действия над матрицами
Даны матрицы и тогда …
Варианты ответов:
1. 2. 3. 4.
3. 4.
ЗАДАНИЕ N 5
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
ЗАДАНИЕ N 6
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
ЗАДАНИЕ N 7
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
ЗАДАНИЕ N 8
Тема: Умножение матриц
Даны матрицы и . Тогда матрица равна …
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности. Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 3 Матрица – математический объект вида таблицы, имеющий mстрок и nстолбцов. Элементами матрицы могут быть как числа, так и функции. Матрица может быть квадратной. В таком случае m=n. В матрице есть главная диагональ – слева направо и, аналогично, побочная. Матрица может быть треугольной – все элементы ниже\выше главной диагонали равны нули. Матрица может быть диагональной – только элементы главной диагонали не равны нулю. Матрица может быть единичной – все элементы главной диагонали диагональной матрицы равны единице. Матрица может быть нулевой. Матрицы можно: · Сравнивать Матрицы равны, если равны их размерности и содержимое. · Складывать (сумма) Складывать можно только матрицы одной размерности, в таком случае складываются элементы одного индекса. Свойства суммы: § A+B=B+A § (A+B)+C=A+(B+C) § Для матрицы A(m,n) существует такая матрица 0(m,n), что A+0=A · Умножать на число В данном случае каждое из чисел матрицы умножается на число. Свойства: § bcA=b(cA) § b(A+C)=bA+bC § A(b+c)=Ab+Ac · Умножать на матрицу (рассматривается в следующем пункте).
Умножение матриц При умножении матрицы Aна матрицу Bнеобходимо, чтобы число столбцов матрицы Aсовпадало с числом строк матрицы B. Только тогда можно умножать. В таком случае результирующая матрица Cбудет иметь количество строк Aи столбцов B, а её числа будут результатом всех возможных перемножений строк Aна B. Свойства: § Бывают исключения, называемые коммутирующими матрицами. § § § § § Det(A*B)=DetA*DetB Обратная матрица Матрица называется обратной к матрице A, если Где AdT– алгебраическое дополнение, транспонированное. Примечание: алгебраическим дополнением для какого-либо элемента матрицы является определитель исходной матрицы свычеркнутыми строкой и столбцом исходной матрицы, в которых стоял данный элемент. Теорема: для того, чтобы для матрицы существовала обратная, необходимо и достаточно, чтобы матрица имела определитель не равный нулю. Док-во необходимости: Док-во достаточности(док-во неверно!): Пускай, B – алгебраическое дополнение матрицы A. ДомножимB на определитель A в минус первой степени. Докажем, что . В таком случае, если вынести у B за скобку определитель в минус первой степени, то при произведении матриц мы получим на главной диагонали определители, а на всех остальных местах нули. Доможив на определитель, получим единичную матрицу. Свойства обратной матрицы: · · · Ранг матрицы Наибольший порядок не равного нулю минора матрицы Aназывается рангом матрицы A. Ранг не может превышать наименьшее из числа строк\столбцов матрицы. СЛАУ, методы решения. Система Линейных Алгебраических Уравнений (СЛАУ) может быть: · Однородной (все свободные члены равны нулю) и Неоднородной. · Совместной (система имеет одно или более решений) и Несовместной. · Определённой (одно решение) и Неопределённой. · Если решения двух систем одинаковы, то они называются Эквивалентными.
Матричный метод В матричном методе любое СЛАУ представляется, как матричное уравнение , где A–матрица коэффициентов, X–искомая матрица неизвестных и B–матрица свободных коэффициентов. Таким образом, . Метод Крамера Метод (или же правило) Крамера – следствие из матричного метода. Здесь каждый из неизвестных аргументов представляется собой как определитель аргумента поделённый на определитель матрицы СЛАУ, где определитель аргумента – определитель матрицы СЛАУ, в который столбец, принадлежащий искомому аргументу, был заменён на столбец свободных коэффициентов. Метод Гаусса Метод Гаусса использует элементарные преобразования строк для получения из расширенной матрицы СЛАУ треугольной или диагональной расширенной матрицы СЛАУ, которая при домножении на матрицу неизвестных аргументов даёт решение. ⇐ Предыдущая123 Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами » Kupuk.net
В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
- a — действительная часть числа;
- b — мнимая часть;
- i — мнимая единица (квадратный корень из -1).

На приведенном примере показаны варианты.
Простейшие действия с матрицами могут быть разными. К их числу относятся:
- умножение;
- вычитание;
- умножение на число;
- перемножение между собой;
- транспортирование матриц.
Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.
Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.
Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:
Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:
Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.
2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.
3 этап: в итоге получаем:
Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:
Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:
Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:
На рисунке представлен метод решения:
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:
Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.
В рассматриваемом случае он равен -2, поэтому всё в порядке.
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:
3 этап: находят алгебраические дополнения.
4 этап: определяют транспонированную матрицу.
Итогом будет:
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.
В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю.
Это говорит о том, что решение было найдено правильно.
Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:
Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:
Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.
Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
- действия, когда в системе переставляются местами два уравнения;
- произведение одного из уравнений в системе на действительное ненулевое число;
- сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.

Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.
Следует переписать эту систему в матричный вид:
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:
Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:
Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:
На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:
Обращают внимание на последние строки.
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Её необходимо заменить равноценным матричным уравнением.
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:
В итоге получают выражения:
Из представленных уравнений выделяют формулы Крамера:
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.
Вычитание матриц — Свойства
Вычитание матриц относится к вычитанию соответствующих элементов двух или более матриц. Матрица — это математический формат для упорядочивания данных в виде строк и столбцов. Вычитание матриц может быть выполнено посредством поэлементного вычитания матриц. К матрицам можно применять различные операции, такие как сложение, вычитание и умножение. В этой статье мы сосредоточимся в основном на операции вычитания матриц. Вычитание матриц — это процесс вычитания соответствующих элементов матриц.
Вычитание матриц выполняется так же, как сложение матриц. Ограничения сложения матриц применимы и к вычитанию матриц. Вычитание матриц определено только для матриц одинакового размера. Давайте рассмотрим концепцию подробно на примерах.
| 1. | Что такое вычитание матриц? |
| 2. | Вычитание матриц порядка 2 × 2 |
| 3. | Вычитание матриц порядка 3 × 3 |
| 4. | Свойства матричного вычитания |
| 5. | Часто задаваемые вопросы о вычитании матриц |
Что такое вычитание матриц?
Вычитание матриц — операция поэлементного вычитания матриц одного порядка, то есть матриц, имеющих одинаковое количество строк и столбцов. Если количество горизонтальных строк в матрице равно «m», а количество вертикальных столбцов равно «n», то говорят, что матрица имеет размерность «m × n». Для вычитания матриц необходимо, чтобы вычитаемые матрицы были такой же размерности, как мы вычитаем соответствующие элементы матриц.
Для вычитания матриц необходимо, чтобы вычитаемые матрицы были такой же размерности, как мы вычитаем соответствующие элементы матриц.
Вычитание матриц Значение
Вычитание матриц или вычитание матриц возможно только в том случае, если количество строк и столбцов обеих матриц одинаково. При вычитании двух матриц мы вычитаем элементы в каждой строке и столбце из соответствующих элементов в строке и столбце другой матрицы. Рассмотрим две матрицы A и B одного и того же порядка m × n, где m — количество строк, а n — количество столбцов двух матриц, обозначаемых как A = [a ij ] и B = [b ij ]. Теперь разность двух матриц A и B определяется как: A — B = [a ij ] — [b ij ] = [a ij — b ij ], где ij обозначает положение каждого элемента в i -й -й строке и j -м -м столбце. Размер разностной матрицы, то есть A — B, также равен m × n.
Вычитание матриц порядка 2 × 2
Поскольку мы знаем, что вычитание матриц возможно только в том случае, если матрицы имеют равное количество строк и столбцов, следовательно, для вычитания матриц порядка 2 × 2 матрицы должны иметь 2 строки и 2 столбца. Теперь рассмотрим две матрицы A и B размерности 2 × 2. Чтобы вычесть B из A, мы вычтем элементы B из соответствующих элементов A. Общая форма вычитания B из A (порядок 2 × 2) такова :
Теперь рассмотрим две матрицы A и B размерности 2 × 2. Чтобы вычесть B из A, мы вычтем элементы B из соответствующих элементов A. Общая форма вычитания B из A (порядок 2 × 2) такова :
Чтобы лучше понять концепцию вычитания матриц размера 2 × 2, рассмотрим пример двух матриц A и B и вычтем B из A.
Вычитание матриц порядка 3 × 3
Матричное вычитание матриц 3 × 3 подразумевает, что матрицы, которые нужно вычесть друг из друга, имеют 3 строки и 3 столбца. При вычитании матриц мы вычитаем элементы одной матрицы из соответствующих элементов другой матрицы. Общая форма вычитания матриц A и B порядка 3 × 3:
Обратите внимание, что для вычитания матриц матрицы не обязательно должны быть квадратными матрицами. Матричное вычитание прямоугольных матриц также определяется, если порядок матриц одинаков.
Свойства матричного вычитания
Все ограничения на сложение матриц применяются и к вычитанию матриц. Но есть определенные законы, которым матричное вычитание не следует так же, как вычитание чисел. Наиболее важная необходимость для вычитания матриц для сохранения всех этих свойств заключается в том, что вычитание матриц определяется только в том случае, если порядок матриц одинаков.
Но есть определенные законы, которым матричное вычитание не следует так же, как вычитание чисел. Наиболее важная необходимость для вычитания матриц для сохранения всех этих свойств заключается в том, что вычитание матриц определяется только в том случае, если порядок матриц одинаков.
- Количество строк и столбцов должно быть одинаковым для матричного вычитания.
- Вычитание матриц не является коммутативным, то есть A — B ≠ B — A
- Вычитание матриц не является ассоциативным, то есть (А — В) — С ≠ А — (В — С)
- Вычитание матрицы из самой себя приводит к нулевой матрице, то есть A — A = O.
- Вычитание матриц — это прибавление отрицательного значения одной матрицы к другой матрице, то есть A — B = A + (-B).
Важные замечания по вычитанию матриц
- Вычитание матриц возможно, только если матрицы имеют одинаковую размерность.
- Вычитание матриц не является коммутативным и ассоциативным.

- Вычитаем соответствующие элементы матриц для вычитания матриц.
Темы, связанные с вычитанием матриц
- Типы матриц
- Умножение матриц
- Калькулятор сложения матриц
Часто задаваемые вопросы о вычитании матриц
Что такое вычитание матриц?
Вычитание матриц — операция поэлементного вычитания матриц одного порядка, то есть матриц, имеющих одинаковое количество строк и столбцов. При вычитании двух матриц мы вычитаем элементы в каждой строке и столбце из соответствующих элементов в строке и столбце другой матрицы.
Как выполнять вычитание матриц?
Рассмотрим две матрицы A и B одного порядка m × n, где m — количество строк, а n — количество столбцов двух матриц, обозначенных как A = [a ij ] и B = [b ij ]. Теперь разность двух матриц A и B определяется как: A — B = [a ij ] — [b ij ] = [a ij — b ij ], где ij обозначает положение каждого элемента в i -й -й строке и j -й 9-й строкестолбец 0064. Размер разностной матрицы, то есть A — B, также равен m × n.
Размер разностной матрицы, то есть A — B, также равен m × n.
Является ли
Вычитание матриц Коммутативным?Вычитание матриц не является коммутативным, то есть A — B ≠ B — A. Как и вычитание чисел, вычитание матриц также имеет определенные ограничения.
Что является необходимым условием для вычитания матриц?
Для вычитания матриц необходимо условие, чтобы они имели одинаковое количество строк и столбцов. Вычитаемые матрицы должны иметь одинаковую размерность.
Можно ли вычесть две матрицы разного порядка?
Матрицы разных порядков нельзя вычитать, так как при вычитании любых двух матриц мы вычитаем элементы одной матрицы из соответствующих элементов другой матрицы. Если порядки разные, то в одной из матриц отсутствуют соответствующие элементы.
Является ли вычитание матриц ассоциативным?
Вычитание матриц не является ассоциативным, то есть (A — B) — C ≠ A — (B — C). Как и вычитание чисел, вычитание матриц также имеет определенные ограничения.
Сложение и вычитание матриц — ChiliMath
В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.
Если вы знаете, как складывать и вычитать действительные числа, эта тема не вызовет затруднений. Единственное, что требуется для того, чтобы «легально» выполнять операции сложения или вычитания в «мире» матриц, — это убедиться, что заданные матрицы должны иметь одинаковый размер или размерность.
Что означает, что данная матрица имеет одинаковый размер или измерение?
Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размерность, потому что в них одинаковое количество строк и столбцов.
Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:
количество строк x количество столбцов
Позвольте мне показать вам несколько примеров…
Последняя матрица размерностью 5 x 5 также считается «квадратной матрицей», поскольку количество строк и количество столбцов равны. Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что у всех квадратных матриц есть обратные, но первое требование, чтобы матрица имела обратную, состоит в том, что она должна быть сначала квадратной матрицей.
Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что у всех квадратных матриц есть обратные, но первое требование, чтобы матрица имела обратную, состоит в том, что она должна быть сначала квадратной матрицей.
Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.
Я должен подчеркнуть, что для сложения или вычитания двух заданных матриц они должны иметь одинаковый размер или размерность. В противном случае делаем вывод, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разный размер или размерность, не определена!
Теперь давайте рассмотрим общее правило сложения и вычитания матриц с одинаковыми размерами или измерениями.
Предположим, что матрицы A и B состоят из двух строк и двух столбцов (2×2) с некоторыми произвольными элементами или элементами.
«Формулы» для сложения и вычитания матриц показаны ниже.
- Сложите матрицы , добавив соответствующие записи
- Вычтите матрицы , вычтя соответствующие записи
Давайте поработаем над некоторыми проблемами.
Примеры сложения и вычитания матриц
Пример 1 : Выполните указанную операцию для A+C.
Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «измерение», поскольку количество строк и столбцов в них одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне, что можно найти их сумму.
Добавлю соответствующие записи и упрощу.
Вот как это просто!
Пример 2 : Выполните указанную операцию для B+F.
Обратите внимание, что матрица B имеет размерность 2×3, а матрица F имеет размерность 2×2.
Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена. Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.
Пример 3 : Выполните указанную операцию для E-B.
В последних двух примерах показано, как добавлять матрицы. На этот раз мы поговорим о вычитании матриц. Помните, что процессы, связанные как со сложением, так и с вычитанием матриц, очень похожи. Просмотрите «формулу» выше, если вы забыли.
Помните, что процессы, связанные как со сложением, так и с вычитанием матриц, очень похожи. Просмотрите «формулу» выше, если вы забыли.
В этом примере нам нужно найти разницу между матрицей E и матрицей B.
Однако оказывается, что это невозможно, так как они имеют разные размеры или размеры. Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.
Так как я не могу вычитать по элементам из-за того, что элементы двух матриц не имеют прямого соответствия, я должен утверждать, что найти их разницу НЕВОЗМОЖНО. Поэтому наш ответ не определен.
Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или измерениями. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы это знаете, вы будете осторожны в следующий раз, когда столкнетесь с подобной проблемой.
Пример 4 : Выполните указанную операцию для F-D.
При беглом просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов. Большой!
Для начала я вычту соответствующие записи F и D. Единственное предупреждение: будьте очень осторожны при вычитании действительных чисел. Обычно именно здесь возникают распространенные ошибки. Помните, что два соседних отрицательных знака оказываются положительными.
Неплохо, правда?
Пример 5 : Выполните указанную операцию для C-A.
Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3×3). Это позволяет нам выполнять операцию вычитания.
Вычитая по записи, я получил…
Пример 6 : Выполните указанную операцию для (A+C)+(C-A).
Это отличный пример «многоэтапной» задачи, включающей сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой скобкой, а затем добавить их вместе.
Чтобы пропустить некоторые шаги, посмотрите, как мы находили (A+C) в примере 1 и C-A в примере 5.
Пока у нас есть эти частичные ответы… получить требуемый ответ.
Как видите, складывать и вычитать матрицы очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как решить эту проблему.
Пример 7 : Выполните указанную операцию для (A+C)+(C-A).
Это та же проблема, что и в примере 6. Но я хочу решить ее немного по-другому, чтобы продемонстрировать, что есть и другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.
Вот так.
Если рассматривать выражение (A+C)+(C-A) как объединение одинаковых или похожих терминов типа задачи, то имеет смысл, что мы можем быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.
Обратите внимание, что я могу комбинировать C-термины как 2C.
Теперь А-члены должны сокращаться, потому что они имеют противоположные знаки.
Наша исходная задача сводится к 2C, что в два раза больше матрицы C.
Это означает, что я собираюсь умножить каждую запись матрицы C на 2. На самом деле это тема моего другого учебника по алгебре «Скалярное умножение матрицы».
Поскольку
, то 2C решается с помощью…
Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?
Вас также может заинтересовать:
Скалярное умножение
Умножение матриц
Объяснение урока: Сложение и вычитание матриц
В этом объяснении мы узнаем, как складывать и вычитать матрицы, используя свойства их сложения и вычитания.
Если 𝐴
является матрицей 𝑛×𝑚,
он состоит из 𝑛 строк и 𝑚
колонны,
⋮⋮⋱⋮𝑎𝑎⋯𝑎⎞⎟⎟⎠,
а квадратная матрица — это 𝑛×𝑛
матрица, содержащая одинаковое количество строк и столбцов
(𝑚=𝑛),
𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ 𝑎𝑎𝑎 ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠.
Для этого объяснения мы будем только смотреть на матрицы вверх до матриц 3×3 включительно (𝑛,𝑚≤3), но применяются те же правила для большего количества строк и столбцов. Чтобы добавить или вычесть матрицы, вы должны добавить или вычесть их соответствующие элементы.
Мы можем складывать или вычитать матрицы только одного порядка (т. е. обе матрицы имеют одинаковое количество строк и одинаковое количество столбцов друг с другом). Это имеет смысл, потому что вы не можете выполнять эти операции с соответствующие элементы, если обе матрицы не имеют одинаковое количество строк и столбцов.
Добавление и вычитание 𝑛 × 𝑚 𝑚 матрицы:
⎛⎜⎜⎝𝑎𝑎 𝑎𝑎𝑎 ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠+⎛⎜⎜⎜⎝𝑏𝑏 𝑏𝑏𝑏 ⋯ ⋮⋮ ⋱ ⋮ 𝑏𝑏 ⋯ 𝑏 𝑏 𝑏 𝑏 ⎞⎟⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑎+𝑏𝑎+𝑏 ⋯ 𝑎+𝑏𝑎+𝑏𝑎+𝑏 ⋯ 𝑎+𝑏 ⋮⋮ ⋮ 𝑎 𝑎+𝑏𝑎+𝑏 ⋯ 𝑎+𝑏⎞⎟⎟⎟⎠⎛⎜⎜⎝ 𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠ — ⋯ 𝑏𝑏𝑏 𝑏 ⋮⋮ ⋱ ⋮ 𝑏𝑏 ⋯ 𝑏⎞⎟⎟⎟⎠ = ⎛⎜⎜⎜⎝𝑎 — 𝑏𝑎-𝑏 ⋯ 𝑎 — 𝑏𝑎 — 𝑏𝑎 ⋯ 𝑎 — ⋮⋮ ⋮⋮ ⋱ ⋮ 𝑎 — 𝑏𝑎 ⋯ 𝑎 — 𝑏⎞⎟⎟⎟⎠ 100005
Чтобы увидеть это в действии, рассмотрим матрицы 2×2
𝐴=8207,𝐵=−559−8.
Чтобы сложить эти матрицы, мы добавляем соответствующие элементы: 𝐴+𝐵=8207+−559−8=8+(−5)2+50+97+(−8)=379−1.
Чтобы вычесть матрицу 𝐵 из матрицы 𝐴, мы вычитаем каждый элемент в матрице 𝐵 из соответствующего элемента в матрица 𝐴: 𝐴−𝐵=8207−−559−8=8−(−5)2−50−97−(−8)=13−3−915.
Теперь рассмотрим матрицы 3×2 𝐴=673−25−1,𝐵=2380−49.
Опять же, давайте сложим и вычтем эти матрицы, выполнив каждую операцию над соответствующими элементами: 𝐴+𝐵=673−25−1+2380−49=6+27+33+8−2+05+(−4)−1+9=81011−218,𝐴−𝐵 =673−25−1−2380−49=6−27−33−8−2−05−(−4)−1−9=44−5−29−10.
Наконец, рассмотрим матрицы 3×3 𝐴=5622−334−1−5,𝐵=1207−19−58−1.
Повторим те же операции над этими матрицами по
завершая каждую операцию над соответствующими элементами, как и раньше:
𝐴+𝐵=5622−334−1−5+1207−19−58−1=5+16+22+02+7−3+(−1)3+94+(−5)−1+8−5+(−1)=6829−412−17 −6,𝐴−𝐵=5622−334−1−5−1207−19−58−1=5−16−22−02−7−3−(−1)3−94−( −5)−1−8−5−(−1)=442−5−2−69−9−4.
Существуют также свойства сложения матриц, о которых нам следует знать:
- Сложение матриц коммутативно, это означает, что если 𝐴 и 𝐵 две матрицы одного порядка такие, что 𝐴+𝐵 определено, то 𝐴+𝐵=𝐵+𝐴, это означает, что порядок, в котором вы выполняете добавление, не имеет значения. Это происходит из-за коммутативного закона сложения чисел, так как мы выполняем сложение на соответствующих элементах каждой матрицы.
- Сложение матриц является ассоциативным, что означает, что если 𝐴, 𝐵 и 𝐶 три матрицы одного порядка такие, что 𝐵+𝐶, 𝐴+(𝐵+𝐶) и 𝐴+𝐵, (𝐴+𝐵)+𝐶 определены, то 𝐴+(𝐵+𝐶)=(𝐴+𝐵)+𝐶, означает, что сумма трех матриц остается неизменной независимо от того, как они сгруппированы. Ты может сначала найти 𝐴+𝐵, а затем добавить результат в 𝐶 или добавить 𝐴 к 𝐵+𝐶 и получить тот же результат.
- Сложение матриц удовлетворяет аддитивному тождеству, что означает, что если 𝐴
является матрицей, то 𝐴+𝑂=𝑂+𝐴=𝐴,
где 𝑂 — нулевая (или нулевая) матрица того же порядка, что и 𝐴
состоящая из нулей в каждом элементе.
 Нулевая матрица
𝑂 называется аддитивным тождеством для матриц.
Нулевая матрица
𝑂 называется аддитивным тождеством для матриц. - Сложение матриц удовлетворяет аддитивной обратной матрице, что означает, что если 𝐴 является матрицей, то 𝐴+(−𝐴)=(−𝐴)+𝐴=𝑂, где 𝑂 — аддитивная идентичность, а −𝐴 называется аддитивным обратным к 𝐴.
Теперь давайте рассмотрим несколько примеров, чтобы попрактиковаться и углубить наше понимание, начиная с добавления две матрицы 1×3.
Пример 1. Сложение матриц один на три
Найти (12−1)+(282).
Ответ
В этом примере мы должны выполнить сложение двух матриц 1×3.
Чтобы сложить эти матрицы, мы добавляем соответствующие элементы каждой матрицы: (12−1)+(282)=(1+22+8−1+2)=(3101).
Один и тот же метод выполнения операций над всеми соответствующими элементами двух матриц одного порядка применяется к добавлению больших матриц, как мы можем видеть в нашем следующем примере.
Пример 2.
 Сложение матриц «два на два»
Сложение матриц «два на два»Оценить 811−37+10−131.
Ответ
В этом примере мы должны выполнить сложение двух матриц 2×2.
Для того, чтобы сложить эти матрицы, мы добавляем соответствующие элементы каждой матрицы: 811−37+10−131=8+1011+(−1)−3+37+1=181008.
В следующем примере мы вычтем одну матрицу из другой.
Пример 3. Нахождение разницы между двумя заданными матрицами
Найти 79−50−8−520.
Ответ
В этом примере мы должны найти разницу между матрицами 2×2.
Чтобы вычесть эти матрицы, мы вычитаем соответствующие элементы каждой матрицы: 79−50−8−520=7−89−(−5)−5−20−0=−114−70.
Далее давайте рассмотрим пример, который требует от нас перестановки и решения матричного уравнения, используя наши знания свойств матричного сложения и вычитания.
Пример 4. Сложение и вычитание матриц
Рассмотрим матрицу
𝐴=−1−1513−10.
Предположим, что сумма матриц 𝐴 и 𝐵 это 𝐴+𝐵=10−1012.
Найдите матрицу 𝐵.
Ответ
В этом примере нам нужно найти неизвестную матрицу 𝐵 применяя операции над матрицами 2×3. Так как мы можем только добавлять или вычитать матрицы того же порядка, как мы применяем операции на соответствующих элементах и и данная матрица, и 𝐴 являются матрицами 2 × 3, 𝐵 также должна быть матрицей 2×3.
Чтобы найти 𝐵, переформулируем уравнение сделать 𝐵 предметом и вычесть соответствующие элементы из каждая матрица:𝐴+𝐵=10−1012.
Поскольку сложение матриц коммутативно, мы знаем, что 𝐴+𝐵=𝐵+𝐴. Затем мы можем вычесть матрицу 𝐴 из каждого часть нашего уравнения, оставив 𝐵=10−1012−𝐴.
Следовательно, после замены 𝐴 имеем 𝐵=10−1012−−1−1513−10=1−(−1)0−(−1)−1−50−131−(−1)2−0=21−6 −1322.
Теперь давайте применим наши знания о сложении и вычитании матриц в
пример, который требует от нас выполнения
обратная операция, чтобы найти ответ.
Пример 5. Поиск неизвестной матрицы путем применения операций над матрицами, включающими Нулевая матрица
Учитывая, что 𝑋+−6−865=𝑂, где 𝑂 это 2×2 нулевая матрица, найдите значение 𝑋.
Ответ
В этом примере мы должны найти неизвестную матрицу 𝑋 по применение операций над матрицами 2×2. С тех пор, как мы могут складывать или вычитать матрицы только того порядка, в котором мы применяем операции над соответствующими элементами и данная матрица, и нулевая матрица равны матрицы 2 × 2, 𝑋 также должна быть матрицей 2 × 2.
Чтобы найти неизвестную матрицу 𝑋, мы изменим уравнение, чтобы сделать 𝑋 предметом, а затем мы вычесть соответствующие элементы данной матрицы из нулевая матрица: 𝑋+−6−865=𝑂.
Поскольку сложение матриц коммутативно, мы можем вычесть заданную матрицу из каждой части нашего уравнения. Как
первая матрица является нулевой матрицей, это имеет эффект переключения
знаки на каждом элементе второй матрицы:
𝑋=𝑂−−6−865=0000−−6−865=0−(−6)0−(−8)0−60−5=68−6−5.
В нашем последнем примере мы будем использовать наши знания о коммутативности сложения матриц, чтобы помочь нам выполнить вычисление, включающее сложение и вычитание трех матриц.
Пример 6. Коммутативные и ассоциативные свойства операций над матрицами
Учитывая, что 𝐴=43−13,𝐵=−1023,𝐶=−5107, найти 𝐴+𝐵−𝐶.
Ответ
В этом примере мы должны выполнить операции сложения и вычитания над тремя матрицами 2×2.
Для этого мы выполняем каждую операцию над соответствующим элементы каждой матрицы: 𝐴+𝐵−𝐶=43−13+−1023−−5107=4+(−1)−(−5)3+0−1−1+2−03+3−7 =821−1.
Сложение матриц коммутативно, поэтому, если мы рассматриваем вычитание матрицы как эквивалентное сложению отрицательных матрицы, мы можем видеть, что мы могли бы выполнить вычисление несколькими различными способами и все равно получить то же самое ответ:
Сложение матриц также ассоциативно, поэтому мы можем сгруппировать элементы разными способами и все равно получаю один и тот же ответ:
Ключевые точки
- Чтобы добавить две матрицы, нам нужно добавить каждый соответствующий элемент.

- Чтобы вычесть одну матрицу из другой, нам нужно вычесть соответствующие элементы.
- Для выполнения этих операций порядок каждой матрицы должен быть одинаковым.
- Сложение матриц коммутативно и ассоциативно.
- Сложение матриц удовлетворяет аддитивному тождеству и аддитивным обратным свойствам.
: Сложение и вычитание матриц
Стенограмма видео
В этом видео мы собираемся научиться складывать и вычитать матрицы, используя свойства их сложения и вычитание.
Напомним, что матрица – это массив
чисел. Они располагаются рядами и
столбцы, и каждое число затем упоминается как элемент. Размеры матрицы дают
количество строк и столбцов, поэтому эта матрица на экране состоит из двух строк и трех столбцов.
и поэтому является матрицей два на три. Учитывая все это, матрица
сложение, да и вычитание, довольно просты. Чтобы добавить или вычесть пару
матрицы, мы просто добавляем или вычитаем их соответствующие элементы. При этом, однако, мы должны наложить
ограничение. Возьмите эту пару два на два
матрицы. Мы видим, что первый элемент
в сумме этих матриц есть 𝑎 плюс 𝑒. Второй элемент в первой строке
это 𝑏 плюс 𝑓 и так далее.
Чтобы добавить или вычесть пару
матрицы, мы просто добавляем или вычитаем их соответствующие элементы. При этом, однако, мы должны наложить
ограничение. Возьмите эту пару два на два
матрицы. Мы видим, что первый элемент
в сумме этих матриц есть 𝑎 плюс 𝑒. Второй элемент в первой строке
это 𝑏 плюс 𝑓 и так далее.
Отсюда следует, что если мы добавим
элементы в матрицах, нам нужно убедиться, что каждый элемент в нашем первом
матрице есть что добавить во вторую и наоборот. Поэтому мы можем только добавить или
вычитание матриц одинакового порядка. У них обязательно должны быть одинаковые
количество строк и столбцов, чтобы мы могли выполнять сложение матриц или
вычитание. Матрицы также обладают многими
свойства сложения и вычитания, свойственные действительным числам. В частности, сложение матриц
коммутативный; то есть это можно делать в любом порядке. Он также удовлетворяет добавке
свойство идентичности. И это если мы добавим ноль
матрица, матрица, все элементы которой равны нулю, мы получаем оригинал
матрица. Итак, давайте посмотрим на действительно
просто пример.
Он также удовлетворяет добавке
свойство идентичности. И это если мы добавим ноль
матрица, матрица, все элементы которой равны нулю, мы получаем оригинал
матрица. Итак, давайте посмотрим на действительно
просто пример.
Вычислить матрицу, элементы которой восемь, 11, минус три, семь плюс матрица, элементы которой равны 10, минус один, три, один.
Мы знаем, что для сложения матриц мы
просто добавьте соответствующие им элементы. И, конечно, это работает только в том случае, если
порядок каждой матрицы одинаков, другими словами, если каждая матрица имеет одинаковую
количество строк и столбцов. Теперь обе наши матрицы имеют два
строки и два столбца. Их порядок два на два. Теперь порядок тот же, поэтому мы
знаем, что мы можем продолжить и добавить матрицы. Это условность, конечно,
начните с элемента в первой строке и первом столбце. Итак, мы собираемся начать с восьми
в нашей первой матрице и 10 во второй. И так элемент в первой строке
и первый столбец суммы этих матриц будет равен восьми плюс 10, т.е.
курс 18. Теперь мы переходим к элементу в
первую строку, но второй столбец. Итак, это 11 в нашей первой матрице.
и отрицательный в нашем втором. Их сумма равна 11 плюс минус
один. Это то же самое, что 11 минус один,
что просто 10.
Итак, мы собираемся начать с восьми
в нашей первой матрице и 10 во второй. И так элемент в первой строке
и первый столбец суммы этих матриц будет равен восьми плюс 10, т.е.
курс 18. Теперь мы переходим к элементу в
первую строку, но второй столбец. Итак, это 11 в нашей первой матрице.
и отрицательный в нашем втором. Их сумма равна 11 плюс минус
один. Это то же самое, что 11 минус один,
что просто 10.
Теперь перейдем к элементам
во втором ряду. Мы начнем с отрицательной тройки в
наша первая матрица и три в нашей второй. На этот раз их сумма отрицательна
три плюс три, что равно нулю. И так первый элемент в нашем
вторая строка суммы этих матриц равна нулю. Осталась одна пара элементов
разобраться, а это семь в первой матрице и один во второй. И, конечно, их сумма семь
плюс один, что равно восьми. Тогда сумма наших двух матриц равна
матрица, элементами которой являются 18, 10, ноль и восемь.
Тогда сумма наших двух матриц равна
матрица, элементами которой являются 18, 10, ноль и восемь.
Теперь, когда мы рассмотрели, как добавить пара матриц, давайте посмотрим, как мы вычитаем пару.
Найдите матрицу семь, девять, минус пять, ноль минус матрица восемь, минус пять, два, ноль.
Теперь мы знаем, что можем добавить или
вычитание матриц, если их порядок одинаков. У нас есть пара два на два
матрицы здесь, так что мы можем перейти к следующему шагу. Чтобы вычесть пару матриц, мы
просто вычтите соответствующие элементы. Традиционно начнем с
первый элемент первой строки. Итак, в нашей первой матрице это
семь, а в нашей второй матрице восемь. Соответствующий элемент в
результат разности этих двух матриц будет семь минус восемь, что равно
отрицательный. Теперь, конечно, вычитание матриц,
точно так же, как вычитание с действительными числами, не является коммутативным. Мы не можем изменить порядок, поэтому мы
абсолютно необходимо сделать семь минус восемь, а не наоборот.
Мы не можем изменить порядок, поэтому мы
абсолютно необходимо сделать семь минус восемь, а не наоборот.
Элемент в первой строке и Второй столбец получается путем вычисления девяти минус минус пять. Теперь, конечно, когда мы вычитаем отрицательный, это то же самое, что добавить положительный. Так что мы собираемся работать девять плюс пять, что равно 14. Далее мы будем иметь дело с первый элемент во второй строке. Итак, в нашей первой матрице это минус пять, а в нашем втором — два. Так что у нас будет минус пять минус два, что минус семь. Наш самый последний элемент в разница между нашими двумя матрицами равна нулю минус ноль, что, конечно, нуль. И так результат вычитания наши две матрицы представляют собой матрицу два на два, элементы которой равны единице, 14, минус семь, ноль.
Сейчас мы рассмотрим, как
найти неизвестную матрицу, применяя операции с нулевой матрицей.
Учитывая, что 𝑋 плюс матрица, элементы — отрицательные шесть, отрицательные восемь, шесть, пять равны нулю, где ноль — это нулевая матрица два на два, найдите значение 𝑋.
Начнем, конечно, с того, что вспомним
что мы имеем в виду, когда говорим, что матрица является нулевой матрицей. Это квадратная матрица, в других
слова, матрица с равным количеством строк и столбцов, элементы или элементы которой
все равны нулю. И в этом случае два на два
нулевая матрица — показанная матрица. Поэтому мы можем переписать нашу матрицу
уравнение как 𝑋 плюс минус шесть, минус восемь, шесть, пять равно нулю, нулю, нулю,
нуль. Теперь пытаемся найти значение
из 𝑋. Итак, учитывая уравнение, которое мы имеем сейчас
написано, что мы можем сделать вывод о 𝑋? Ну, одно мы знаем
что если мы добавим пару матриц, мы просто добавим элементы. И мы можем сделать это только в том случае, если
матрицы одного порядка. Мы не могли добавить, например,
матрицу два на два к матрице два на три, и мы не можем добавить матрицу два на два к
просто число с одним значением.
И мы можем сделать это только в том случае, если
матрицы одного порядка. Мы не могли добавить, например,
матрицу два на два к матрице два на три, и мы не можем добавить матрицу два на два к
просто число с одним значением.
Таким образом, для этого матричного уравнения
имеет смысл, 𝑋 также должна быть матрицей два на два. Теперь, чтобы решить это матричное уравнение,
мы на самом деле собираемся выполнить аналогичный набор шагов для решения обычного
уравнение. Мы собираемся вычесть эту матрицу
минус шесть, минус восемь, шесть, пять с обеих сторон уравнения. Когда мы вычтем его из
в левой части, конечно, мы просто получим матрицу 𝑋. Итак, 𝑋 это ноль, ноль, ноль, ноль
минус матрица, элементами которой являются отрицательные шесть, отрицательные восемь, шесть, пять. Теперь, как когда мы добавляем пару
матриц, и мы добавляем их элементы, чтобы вычесть пару матриц, мы вычитаем
отдельные их элементы.
Элемент в первой строке и первый столбец будет равен нулю минус минус шесть. Теперь, конечно, вычитая отрицательное то же самое, что добавить положительное. Так что это то же самое, что делать ноль плюс шесть, что шесть. Затем мы делаем ноль минус минус восемь. И еще раз, это то же самое, что и делать ноль плюс восемь, что равно восьми. Теперь перейдем к элементам второй ряд, поэтому получаем ноль минус шесть. И, конечно же, просто минус шесть. И, наконец, мы собираемся работать ноль минус пять, и это минус пять. Итак, матрица два на два 𝑋 равна шесть, восемь, минус шесть, минус пять.
Этот пример иллюстрирует
что-то действительно важное. Мы видим, что сложение матрицы
удовлетворяет аддитивному обратному свойству. Теперь аддитивная обратная величина
число — это то, что вы добавляете к числу, чтобы получить ноль, и обычно это просто находит
изменение знака исходного числа. Если мы посмотрим на наш пример здесь, мы
можно увидеть, что мы изменили знак отдельных элементов. И так матрицы шесть, восемь,
отрицательные шесть, отрицательные пять — это аддитивная обратная матрица отрицательных шести,
минус восемь, шесть, пять.
Если мы посмотрим на наш пример здесь, мы
можно увидеть, что мы изменили знак отдельных элементов. И так матрицы шесть, восемь,
отрицательные шесть, отрицательные пять — это аддитивная обратная матрица отрицательных шести,
минус восемь, шесть, пять.
Сейчас мы рассмотрим другой пример, который включает в себя решение матричного уравнения.
Рассмотрим матрицу 𝐴, которая имеет элементы отрицательный один, отрицательный один, пять, 13, отрицательный один, ноль. Предположим, что сумма матриц 𝐴 а 𝐵 равно 𝐴 плюс 𝐵 равно единице, нулю, отрицательной единице, нулю, единице, двум. Найдите матрицу 𝐵.
Нам дано, что сумма
матрицы 𝐴 и 𝐵 представляют собой матрицу размера два на три. Имеет два ряда и три
столбцы. Мы также знаем, что можем добавить
матрицы, просто добавляя их отдельные элементы. Но это означает, что матрицы
которые мы добавляем, должны быть того же порядка. И так, чтобы можно было сложить матрицу 𝐴
и 𝐵, где 𝐴 также является матрицей два на три, а результатом является матрица два на три.
матрица, сама 𝐵 должна быть матрицей два на три. Теперь мы можем решить эту матрицу
уравнение, как и любое другое нормальное уравнение. Мы собираемся вычесть 𝐴 из
обе стороны. Но, конечно, 𝐴 — это матрица, поэтому мы
можно записать это как 𝐵 равно единице, нулю, отрицательной единице, нулю, единице, двум минус матрица
элементами которого являются отрицательная единица, отрицательная единица, пять, 13, отрицательная единица и ноль.
И так, чтобы можно было сложить матрицу 𝐴
и 𝐵, где 𝐴 также является матрицей два на три, а результатом является матрица два на три.
матрица, сама 𝐵 должна быть матрицей два на три. Теперь мы можем решить эту матрицу
уравнение, как и любое другое нормальное уравнение. Мы собираемся вычесть 𝐴 из
обе стороны. Но, конечно, 𝐴 — это матрица, поэтому мы
можно записать это как 𝐵 равно единице, нулю, отрицательной единице, нулю, единице, двум минус матрица
элементами которого являются отрицательная единица, отрицательная единица, пять, 13, отрицательная единица и ноль.
Теперь, как и при добавлении
матрицы, мы можем вычитать матрицы, вычитая их отдельные элементы. И так начнем с первого
элемент в нашей первой матрице и первый в нашей второй. Это один минус минус один. Но, конечно, когда мы вычитаем
отрицательный, это то же самое, что добавить положительный. Так что это похоже на разработку одного
плюс один, что равно двум. Повторяем этот процесс с
второй элемент каждой матрицы. Теперь мы работаем ноль минус
отрицательная единица, что равно нулю плюс единица, что равно единице. Переходим к третьему
элемент. Это отрицательный в первом
матрица и пять во второй. Итак, мы делаем минус один минус пять,
что минус шесть.
Так что это похоже на разработку одного
плюс один, что равно двум. Повторяем этот процесс с
второй элемент каждой матрицы. Теперь мы работаем ноль минус
отрицательная единица, что равно нулю плюс единица, что равно единице. Переходим к третьему
элемент. Это отрицательный в первом
матрица и пять во второй. Итак, мы делаем минус один минус пять,
что минус шесть.
Теперь повторим это с элементы второй строки. У нас есть ноль минус 13, то есть минус 13. Далее вычисляем один минус отрицательный. И, конечно же, это то же самое, что и один плюс один, то есть два. И тогда наш окончательный расчет два минус ноль, что, конечно, просто два. Итак, мы нашли матрицу 𝐵. Это матрица два на три с элементы два, один, минус шесть, минус 13, два, два.
В нашем последнем примере мы
подумайте, как мы можем распространить это на работу с более чем двумя матрицами.
Учитывая, что 𝐴 равно матрица четыре, три, минус один, три; 𝐵 минус один, ноль, два, три; 𝐶 это минус пять, один, ноль, семь, найти 𝐴 плюс 𝐵 минус 𝐶.
Перепишем это выражение, используя
заданные матрицы. Это четыре, три, минус один,
три плюс минус один, ноль, два, три минус минус пять, один, ноль, семь. Теперь мы знаем, как складывать и вычитать
матрицы. Пока матрицы имеют
том же порядке, другими словами, они имеют одинаковое количество строк и одинаковое количество
столбцы, мы добавляем или вычитаем их соответствующие элементы. Но так же, как работать с реальным
чисел, сложение коммутативно. Другими словами, это можно сделать в
любой порядок, но не вычитание. Мы также знаем, что когда мы рассматриваем
порядок действий, если у нас есть сложение и вычитание в одном и том же
расчет, мы просто двигаемся слева направо. И так начнем с принятия
первый элемент в первой строке каждой матрицы. Это четыре, минус один и
минус пять.
И так начнем с принятия
первый элемент в первой строке каждой матрицы. Это четыре, минус один и
минус пять.
Мы используем индекс для определения
первый элемент в первой строке как 𝑎 под единицей. И так мы получаем четыре плюс минус
один минус минус пять. Четыре плюс минус один равно трем,
а затем мы собираемся вычесть минус пять. Так что это то же самое, что добавить
пять. Таким образом, мы получаем три плюс пять, что равно
равно восьми. Итак, это первый элемент в
Первый ряд. Тогда 𝑎 sub one two — это элемент
в первой строке и втором столбце. Итак, три плюс ноль минус
один. Три плюс ноль будет три, и тогда
мы делаем три минус один, что равно двум. Теперь мы переходим к рассмотрению
элемент во второй строке и первом столбце. Это минус один плюс два минус
нуль. А так как минус один плюс два
единица, мы получаем единицу минус ноль, что равно единице.
Наш последний элемент определяется 𝑎 саб два два. Это элемент во втором строку и второй столбец. Это три плюс три минус Семь. Три плюс три равно шесть, поэтому мы получаем шесть минус семь как отрицательную единицу. А так осталось поставить это обратно в свою матричную форму. 𝐴 плюс 𝐵 минус 𝐶 это матрица два на два, элементами которой являются восемь, два, один, отрицательная единица.
Теперь мы собираемся повторить ключ
баллы из этого урока. В этом видео мы узнали, что мы
может добавлять или вычитать матрицы, добавляя или вычитая их соответствующие
элементы. Мы также видели, однако, что это только
работает, если порядок каждой матрицы одинаков, другими словами, если они имеют одинаковые
количество строк и такое же количество столбцов. Мы видели, что сложение матриц
коммутативный; это можно делать в любом порядке, в отличие от матричного вычитания. И так же, как работать с реальным
чисел, сложение матриц также удовлетворяет свойству аддитивной идентичности и
аддитивное обратное свойство.
И так же, как работать с реальным
чисел, сложение матриц также удовлетворяет свойству аддитивной идентичности и
аддитивное обратное свойство.
Добавление и матрицы вычитания Добавление матрицы справедливо простой, и делается мудрый вход.
Мне нужно добавить пары записей, а затем упростите для окончательного ответа: Итак, ответ: До сих пор вы были
можно добавить любые две вещи, которые вы хотели: числа, переменные, уравнения,
и так далее.
С добавлением матриц по записи, я должен добавить 1 и 4, 2 и 5, 0 и 7, и 3 и 8. Но что мне добавить к 6 а на 9? В первой матрице нет соответствующих элементов, которые можно добавить к этим элементам во второй матрице. Итак, ответ: Я не могу добавить это матрицы, потому что они не одного размера . Всегда так: Чтобы можно было сложить две матрицы, они должны быть одного размера. Если они не одного размера (если они не имеют одинаковых «размеров»), то сложение «не определено» (не делает математических смысл). Работы по вычитанию проходные, слишком. Авторские права Элизабет Стапель 2003-2011 Все права защищены
А и В имеют одинаковый размер, каждый из которых равен 2 3 матрицы, так что я могу вычитать, работает на входе: Однако А и С не одного размера, так как A это 2 3 и С это 2 2. Таким образом, это вычитание не определено. А С не определено, потому что А и С не одного размера. Сложение и вычитание матриц, где определено (то есть, где матрицы имеют одинаковый размер, поэтому сложение и вычитание имеют смысл), можно превратить в домашние задания.
Во-первых, я упрощу левую часть немного, добавив по записи: Поскольку равенство матриц работает по входу,
Я могу сравнить записи, чтобы создать простые уравнения, которые я могу решить. Верх | Вернуться к индексу
|
|
|
Вычитание матриц – объяснение и примеры
Есть $ 4 $ основных операций, которые мы можем выполнять с матрицами. Это сложение, вычитание, скалярное умножение и матричное умножение. Матричное вычитание — одна из них, и мы рассмотрим ее в этой статье.
Это сложение, вычитание, скалярное умножение и матричное умножение. Матричное вычитание — одна из них, и мы рассмотрим ее в этой статье.
Примечание. Деление матрицы не является определенной операцией. Мы можем разделить матрицу только на скалярное число. Чтобы узнать больше о матричном делении, нажмите здесь.
Определим вычитание матриц:
Вычитание матриц — это операция вычитания двух матриц одного размера путем вычитания соответствующих элементов.
Эта статья покажет, при каких условиях возможно вычитание матриц, вычитание матриц и несколько примеров, показывающих этот процесс.
Когда можно вычитать матрицы?
Можем ли мы вычесть любые матрицы?
Нет!
Мы можем вычитать $2$ матрицы, только если они имеют одинаковую размерность. То есть, если матрицы $2$ имеют одинаковое количество строк и столбцов, то и только тогда мы можем вычитать матрицы $2$ вместе.
Напомним, что измерение матрицы — это количество строк и количество столбцов. Если в матрице есть $a$ строк и $b$ столбцов, мы можем сказать, что матрица имеет размеры $a\times b$ (произносится как $a$-by-$b$). Чтобы узнать больше о размерах матрицы, ознакомьтесь с этой статьей!
Помните, матрица, полученная в результате операции вычитания матриц, будет той же размерности, что и матрицы, из которых она получена.
Как вычитать матрицы?
После того, как мы пришли к выводу, что матрицы имеют одинаковые размеры, мы вычитаем $ 2 $ матрицы, вычитая соответствующие элементы друг друга . Рассмотрим Matrix $ A $ и Matrix $ B $, показанные ниже:
$ A = \begin{bmatrix} { 0 } & { 4 } \\ { – 3} & { – 3 } \end {bmatrix} $
$ B = \begin{bmatrix} { – 9 } & 0 \\ 2 & { – 2 } \end {bmatrix} $
Обе матрицы $ A $ и $ B $ имеют $ 2 $ строк и $ 2 $ столбцы. Следовательно, размерность матриц $ 2 \times 2 $, что делает их равными. Это означает, что мы можем вычесть матрицы $2$, вычитая каждую соответствующую запись друг из друга. Процесс показан ниже:
Это означает, что мы можем вычесть матрицы $2$, вычитая каждую соответствующую запись друг из друга. Процесс показан ниже:
$ A – B = \begin{bmatrix} { 0 – – 9 } & { 4 – 0 } \\ { – 3 – 2 } & { – 3 – – 2 } \ end {bmatrix } $
$ A – B = \begin{bmatrix} { 0 + 9} & { 4 – 0 } \\ { – 3 – 2 } & { – 3 + 2 } \end {bmatrix} $
$ A – B = \begin{bmatrix} { 9 } & { 4 } \\ { – 5 } & { – 1 } \end {bmatrix} $
Теперь рассмотрим две матрицы, показанные ниже:
$ A = \begin{bmatrix} { 0 } & { – 1 } \\ 10 & 2 \ end {bmatrix} $
$ B = \begin{bmatrix} { – 5 } & 0 \\ 6 & 0 \\ 3 & 7 \\ 4 & { – 7 } \end {bmatrix} $
Is $ А – В$ определены?
№
Матрица $A$ имеет размерность $2\times 2$. Матрица $B$ имеет размерность $4\times 2$. Поскольку размеры обеих матриц не равны, вычитание матрицы не определено! Мы не можем вычесть Матрицы $A$ и $B$, потому что не будет соответствующей записи для каждого элемента Матрицы $A$ и Матрицы $B$.
Правила вычитания матриц
Мы можем написать $ 4 $ правила для вычитания матриц. Показано ниже:
- Вычитать можно только матрицы одинаковой размерности (т.е. количество строк первой матрицы должно быть равно количеству строк второй матрицы. Также количество столбцов первой матрицы должно быть равно количеству столбцов вторая матрица.)
- Матрица, полученная в результате вычитания матриц, будет иметь ту же размерность, что и исходные матрицы, из которых она получена.
- Вычитание матриц НЕ коммутативно (т. е. $ A – B \neq B – A $). Когда вы меняете порядок матриц и вычитаете, он дает другой ответ (точно так же, как действительные числа).
- Вычитание матриц является НЕ ассоциативным (т. е. $ (A – B) – C \neq A – (B – C) $).
Давайте рассмотрим несколько примеров Вычитания матриц .
Пример 1 Проверить, определено ли матричное вычитание между матрицей $A$ и матрицей $B$. Если да, вычтите их.
Если да, вычтите их.
$ A = \begin{bmatrix} { 0 } & { – 5 } \\ { – 5 } & { 0 } \end {bmatrix} $
$ B = \begin{bmatrix} { 3 } & { – 4 } \\ { 0 } & { – 5 } \end {bmatrix} $
Решение
Для определения вычитания матриц размерность каждой матрицы должна быть одинаковой.
Матрица $A$ является матрицей размера $2\times 2$. Матрица $B$ также является матрицей $2\times 2$. Таким образом, матричное вычитание между Matrix $A$ и $B$ определено.
Теперь давайте вычтем вместе матрицы $2$, вычитая каждый соответствующий элемент матрицы $B$ из каждого соответствующего элемента матрицы $A$. Показано ниже:
$ A – B = \begin{bmatrix} { 0 – 3 } & { – 5 – – 4 } \\ { – 5 – 0 } & { 0 – – 5 } \end {bmatrix} $
$ A – B = \begin{bmatrix} { – 3 } & { – 5 + 4 } \\ { – 5 } & {0 + 5 } \end{bmatrix} $
$ A – B = \begin {bmatrix} { – 3 } & { – 1 } \\ { – 5 } & { 5 } \end{bmatrix} $
Пример 2
Для матриц $ 2 $, показанных ниже, найдите $С-Д$.
$ C = \begin{bmatrix} { 1 } & { – 1 } \\ 1 & { – 1 } \\ 7 & { – 7 } \end {bmatrix} $
$ D = \begin{bmatrix} { 1 } & { – 2 } & { – 1 } \\ { – 1 } & 0 & { – 1 } \end {bmatrix} $
Решение
Размер матрицы $C$ равен $3\times 2$. Размерность матрицы $D$ равна $2\times 3$. Несмотря на то, что размеры эквивалентны, мы не можем вычесть матрицу $D$ из матрицы $C$. Порядок размеров также важен. Матрица $3\times 2$ не равна матрице $2\times 3$. Таким образом, мы не можем вычесть матрицу $D$ из матрицы $C$.
Мы также можем решать основные алгебраические уравнения с вычитанием матриц. Рассмотрим пример, показанный ниже.
Пример 3Найдите значения $ a $ и $ b $ по следующему уравнению:
$ \begin{pmatrix} { 1 } & { 2 } \\ b & { – 6 } \ end {pmatrix} – \begin{pmatrix} { a } & { – 1 } \\ 0 & { – 3 } \ end {pmatrix} = \begin{pmatrix} { 7 } & { 3 } \\ { – 2 } & { – 3 } \end {pmatrix} $
Решение
Мы можем вычесть соответствующие записи, чтобы найти $ a $ и $ b $. Сначала вычтем соответствующие элементы для $a$ и найдем переменную:
Сначала вычтем соответствующие элементы для $a$ и найдем переменную:
$ 1 – a = 7 $
$ a = 1 – 7 $
$ a = – 6 $
Теперь найдем значение $ b $, вычитая соответствующие записи для $ b $:
$ b – 0 = – 2 $
$ b = – 2 $
Теперь вы можете попробовать несколько практических вопросов и посмотреть, правильно ли вы ответили на них или нет. Ответы ниже.
Практические вопросы- Рассмотрим следующие матрицы $ 3 $:
$ P = \begin{pmatrix} { – 2 } & { – 2 } \\ 1 & { 1 } \end {pmatrix} $
$ Q = \begin{pmatrix} { – 3 } & { – 3 } \\ { – 3 } & { – 3 } \end {pmatrix} $
$ R = \begin{pmatrix} 1 & 1 \\ 7 & { – 2 } \\ 3 & { – 7 } \end {pmatrix} $
Найти:- $ P – Q $
- $ Q – R $
- $ Q – P $
- Найти значения $ a $, $ b $ и $ c $, заданные следующим уравнением:
$ \begin{pmatrix} { 3 } & { 2 } & 0 \\ b & { – 2 } & 3 \\ 11 & a & -2 \end {pmatrix} – \begin{pmatrix} { 3 } & { 2 } & c \\ 5 & { – 5 } & 3 \\ { – 4 } & { 6 } & 10 \end {pmatrix} = \begin{pmatrix} { 0 } & { 0 } & -9\\ 12 & { 3 } & 0 \\ 15 & -3 & { – 12 } \end {pmatrix} $
Обратите внимание, что, поскольку матричное вычитание не является коммутативным , ответ на часть $ A $ и часть $ C $ будет другим. Ответы показаны ниже.
Ответы показаны ниже.
- Обе матрицы $P$ и $Q$ являются матрицами размера $2\times 2$. Таким образом, мы вычитаем матрицы $2$, вычитая соответствующие элементы. Показано ниже:
$ P – Q = \begin{pmatrix} { – 2 – – 3 } & { – 2 – – 3 } \\ { 1 – – 3 } & {1 – – 3 } \end {pmatrix} $
$ P – Q = \begin{pmatrix} { – 2 + 3 } & { – 2 + 3 } \\ {1 + 3 } & {1 + 3 } \end {pmatrix} $
$ P – Q = \begin{pmatrix } { 1 } & { 1 } \\ { 4 } & { 4 } \end {pmatrix} $ - Мы не можем вычесть матрицу $R$ из матрицы $Q$, потому что их размеры не совпадают. Матрица $Q$ является матрицей размера $ 2 \times 2$, а матрица $R$ является матрицей размера $3 x 2$.
- Ответ на эту часть вопроса будет отличаться от ответа на часть $ A $, поскольку вычитание матриц не является коммутативным. Вычтем Матрицу $P$ из Матрицы $Q$.
$ Q – P = \begin{pmatrix} { – 3 – – 2 } & { – 3 – – 2 } \\ { – 3 – 1 } & { – 3 – 1 } \end {pmatrix} $
$ Q – P = \begin{pmatrix} { – 3 + 2 } & { – 3 + 2 } \\ { – 4 } & { – 4 } \end {pmatrix} $
$ Q – P = \begin{pmatrix} { – 1 } & { – 1 } \\ { – 4 } & { – 4 } \end {pmatrix} $


 Все правила по сольфеджио
Все правила по сольфеджио


 А именно: строку номер «m» исходной матрицы в столбец номер «m» транспонированной матрицы. После транспонирования новой матрице выдают особый знак: к символу исходной матрицы справа сверху добавляют большую букву T, или штрих.
А именно: строку номер «m» исходной матрицы в столбец номер «m» транспонированной матрицы. После транспонирования новой матрице выдают особый знак: к символу исходной матрицы справа сверху добавляют большую букву T, или штрих.

 Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения. Т. е., как |A|, или ||A||, или латинской буквой D, или греческой буквой Δ, или det(A) для матрицы A. При этом вместо A в новые скобки может быть вписана вся таблица.
Т. е., как |A|, или ||A||, или латинской буквой D, или греческой буквой Δ, или det(A) для матрицы A. При этом вместо A в новые скобки может быть вписана вся таблица. Знаки вопроса (?) в вышерассмотренных примерах – это совершенно обыкновенные числа.
Знаки вопроса (?) в вышерассмотренных примерах – это совершенно обыкновенные числа.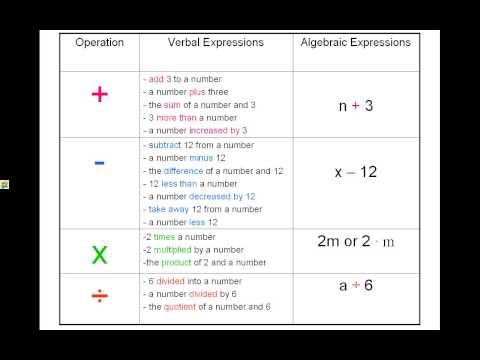


 Термин надо запомнить. Минор – маленький, точнее, по смыслу в данном случае, — определитель уменьшенной матрицы.
Термин надо запомнить. Минор – маленький, точнее, по смыслу в данном случае, — определитель уменьшенной матрицы.
 Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше будет также раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше будет также раскрыть определитель по какому-нибудь другому столбцу или другой строке. Вы должны уметь вычислять определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые операции с матрицами.
Вы должны уметь вычислять определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые операции с матрицами. Чаще, конечно, требуется найти обратную матрицу для матрицы «три на три», но мы настоятельно рекомендуем изучить более простое задание, чтобы усвоить общий принцип решения.
Чаще, конечно, требуется найти обратную матрицу для матрицы «три на три», но мы настоятельно рекомендуем изучить более простое задание, чтобы усвоить общий принцип решения. Сначала рассмотрим левый верхний элемент
Сначала рассмотрим левый верхний элемент Именно у тех чисел, которые обведены в кружок! Получим:
Именно у тех чисел, которые обведены в кружок! Получим:
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.082 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.082 с.) Это чуть сложнее, чем с обычными числами.
Это чуть сложнее, чем с обычными числами. 

 ..
..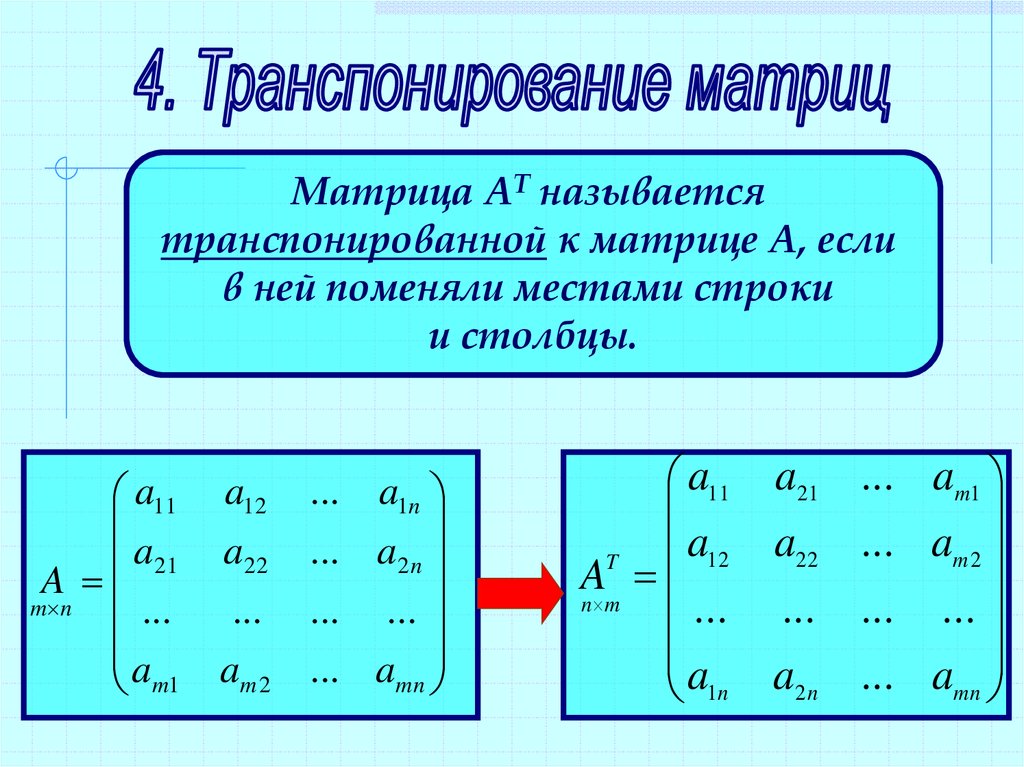





 Это говорит о том, что решение было найдено правильно.
Это говорит о том, что решение было найдено правильно.
