Расчет сложной электрической цепи постоянного тока: Методы расчета сложных электрических цепей постоянного тока — Начало. Основы. — Справочник

Содержание

Задание №1 — Расчет сложной электрической цепи постоянного тока

Оглавление

Задание №1 — Расчет сложной электрической цепи постоянного тока 3

1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа. 4

1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов 8

Задание № 2 — Расчет электрической цепи переменного синусоидального тока 17

Активная мощность. Единица измерения — ватт (W, Вт). 26

Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар) 26

Указания к выбору варианта задания

Электрические схемы, предлагаемые для расчета, пронумерованы. Соответствие варианта и расчетной схемы обозначено в таблице №1 и одинаково для обеих групп. Значения сопротивлений резисторов для студентов групп, номера которых заканчиваются цифрой 1 и 2 приведены в таблицах №3 и №4 соответственно. Значения ЭДС, действующих в ветвях, приведены в таблице №2 (первая строка для всех студентов группы, номер которой заканчивается цифрой 1, вторая строка – для группы, номер которой заканчивается цифрой 2).

Внутренними сопротивлениями источников ЭДС следует пренебречь.

Содержание работы

1. Рассчитать токи во всех ветвях электрической цепи

а) методом непосредственного применения правил Кирхгофа;

б) методом контурных токов;

в) методом узловых потенциалов.

Результаты расчетов свести в таблицу.

2. Составить и решить уравнение баланса мощностей.

Рисунок 1.1

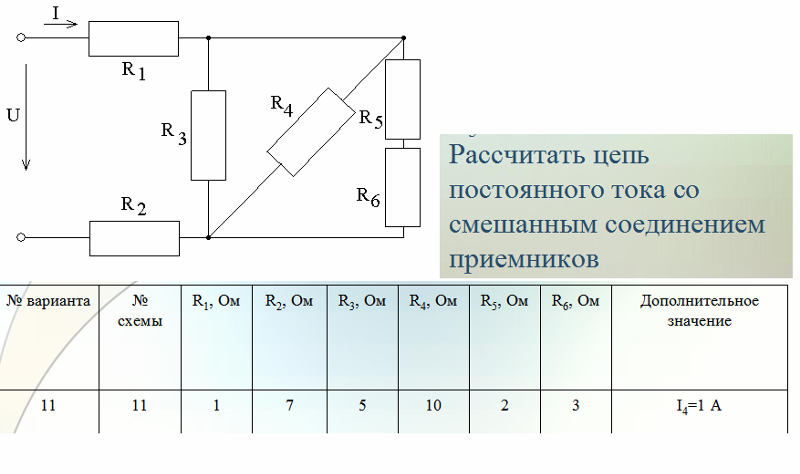
Таблица 1.1 – Значения параметров, вариант 10

R1, Ом

R2, Ом

R3, Ом

R4, Ом

R5, Ом

R6, Ом

R7, Ом

R8, Ом

Е1,

Е3,

Е5,

Е8,

1.

1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа.

Рисунок 1.2 – Исследуемая схема цепи

Составим систему уравнений, согласно законам Кирхгофа для цепи (рисунок 1.2):

(1)

Решим систему матричным методом:

Находим токи в ветвях:

₍₂₎

i₁ = -0,257(A), i₃ = 0,599(A), i₄ = -0,342(A), i₅ = 0,854(A), i₆ = -0,144(A), i₈ = 0,656(A),

1.2 Расчёт токов в ветвях методом контурных токов.

Для схемы (1.2 обход по часовой стрелке) составим систему уравнений:

(3)

Решая систему, получаем:

Находим токи в контурах:

₍₄₎

Рассчитаем токи в ветвях:

₍₅₎

₍₆₎

₍₇₎

₍₈₎

₍₉₎

₍₁₀₎

i₁ = -0,257(A), i₃ = 0,599(A), i₄ = -0,342(A), i₅ = 0,854(A), i₆ = -0,144(A), i₈ = 0,656(A),

1.

3 Расчёт токов во всех ветвях схемы методом узловых потенциалов

Найдём проводимости ветвей схемы.

g₁ = 0,067(См), g₂₃ = 0,027 (См), g₄ = 0,045 (См),

g₅ = 0,026(См), g₆₇= 0,023 (См), g₈ = 0,033 (См).

Рисунок 1.3

Запишем уравнения в матричной форме (φа=0):

₍₁₁₎

Решая систему, получаем:

Находим токи в контурах:

₍₁₂₎

Рассчитаем токи в ветвях:

₍₁₃₎

₍₁₄₎

₍₁₅₎

₍₁₆₎

₍₁₇₎

₍₁₈₎

i₁ = -0,257(A), i₃ = 0,599(A), i₄ = -0,342(A), i₅ = 0,854(A), i₆ = -0,144(A),

i₈ = 0,656(A),

Таблица 1. 2 – Результаты расчётов

	i₁	i₃	i₄	i₅	i₆	i₈
Законы Кирхгофа	-0,257	0,599	-0,342	0,854	-0,144	0,656
Метод контурных токов	-0,257	0,599	-0,342	0,854	-0,144	0,656
Метод двух узлов	-0,257	0,599	-0,342	0,854	-0,144	0,656

1. 4 Баланс мощностей.

Уравнение баланса мощностей:

(19)

Суммарная мощность источников:

(20)

Суммарная мощность приёмников:

(21)

Контрольные вопросы по теме

«Расчет электрических цепей постоянного тока»

Дайте определение электрической цепи и ее схемы замещения.

Электрическая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитных процессов, в которых могут быть описаны с помощью понятий сила тока и напряжение.

Схема замещения — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.

Какими моделями пользуются при описании свойств идеальных и реальных источников электродвижущей силы (Э. Д.С.)?

Источник напряжения — идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от протекающего через него тока.

Какими моделями пользуются при описании свойств идеальных и реальных источников тока?

Источник тока – это идеализированный элемент ЭЦ, ток которого не зависит от напряжения на его зажимах.

Чем отличаются линейные и нелинейные элементы электрических цепей?

Элементы, ВАХ которых являются прямыми линиями, называются линейными. Электрические цепи, имеющие только линейные элементы, называются линейными электрическими цепями.

Элементы, ВАХ которых не являются прямыми линиями, называются нелинейными. Электрические цепи, имеющие хотя бы один нелинейный элемент, называются нелинейными.

Какие электрические цепи называются линейными электрическими цепями постоянного тока?

Элементы электрической цепи, ВАХ которых представляют собой прямые линии, называются линейными элементами, а цепи, состоящие из таких элементов, работающие от источника постоянного тока – линейными электрическими цепями постоянного тока.

Дайте определения ветви, узла и контура электрической цепи.

Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.

Узел цепи в электронике — точка, в которой соединяются три (или более) проводника электрической цепи. Узел (наряду с контуром) является базовым понятием, необходимым при анализе электрических цепей.

Контур — это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи, и есть замкнутый контур.

Сформулируйте первое правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается в первом правиле Кирхгофа?

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю.

При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным.

Сформулируйте второе правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается во втором правиле Кирхгофа?

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю.

Докажите, что при последовательном соединении элементов в электрической цепи эквивалентное сопротивление равно сумме их сопротивлений.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: .

Так как ток в цепи один:

Докажите, что при параллельном соединении элементов в электрической цепи эквивалентная проводимость равна сумме их проводимостей.

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора).

Для двух параллельно соединённых резисторов их общее сопротивление равно: .

Если , то общее сопротивление равно:, то естьэквивалентная проводимость равна сумме проводимостей.

Приведите пример расчета электрической цепи методом непосредственного применения правил Кирхгофа.

Пример приведён в работе.

Приведите пример расчета электрической цепи методом контурных токов.

Пример приведён в работе.

Приведите пример расчета электрической цепи методом узловых потенциалов.

Пример приведён в работе.

Приведите пример расчета электрической цепи методом эквивалентного генератора.

Метод эквивалентного генератора используется при расчёте сложных схем, в которых одна ветвь выделяется в качестве сопротивления нагрузки, и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки. В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви, содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.

ЭДС эквивалентного генератора определяется по формуле:

где: —проводимость участка цепи, равная

Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а также, в случае более сложных схем, применяют преобразование треугольник-звезда.

После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:

Параметры иможно так же определить по исходной схеме из опытовхолостого хода икороткого замыкания .

По опыту холостого хода Для определенияв исходной схеме убирают сопротивление нагрузки и полученную схему рассчитываютметодом узловых потенциалов. Через полученные значения потенциалов определяют

Значение обычно определяется из опыта короткого замыкания, для этого в исходной схеме сопротивление нагрузки заменяют проводом и пометоду контурных токов определяют ток в проводе. После этого эквивалентное сопротивление генератора определяется по формуле:

Приведите пример расчета электрической цепи методом эквивалентных преобразований.

Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, каким они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.

Одним из наиболее часто встречающихся случаев смешанного соединения сопротивлений.

Исходная схема содержит параллельное соединение ветвей, содержащих и, т.е.. И этот участок с параллельным соединением включен последовательно с.

Поэтапным преобразованием эта цепь сводится к эквивалентному сопротивлению

Как и для чего составляется уравнение баланса мощностей при расчете электрической цепи? Приведите пример его составления.

Для проверки правильности расчёта электрической цепи. Пример приведён в работе.

Методы расчета сложных электрических цепей

Оглавление:

Сложной электрической цепью называют разветвленную цепь с несколькими источниками электрической энергии.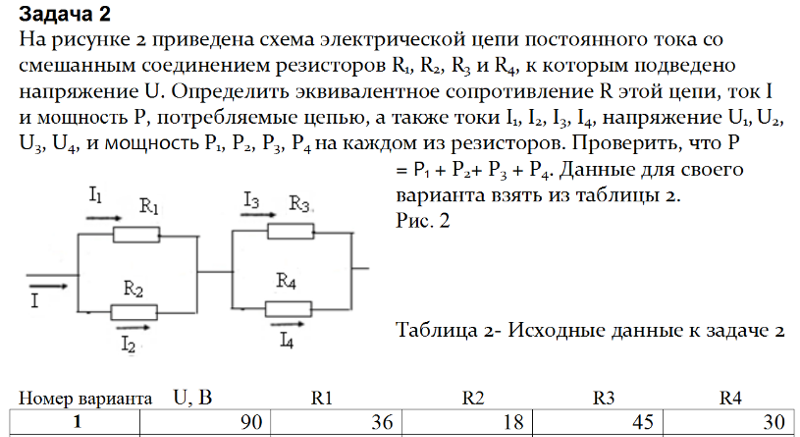 Применение методов эквивалентных преобразований в таких цепях, как правило, не эффективно, так как не позволяют упростить ее до одноконтурной цепи или цепи с двумя узлами. Для расчета таких цепей используют более общие методы.

Метод непосредственного применения законов Кирхгофа

Метод заключается в составлении системы уравнений с применением первого и второго законов Кирхгофа для заданной электрической цени, решение которой позволяет определить токи всех ветвей цепию.

Реализация этою метода, как и любого другого метода расчета сложной электрической цени, начинается с предварительного анализа ее схемы с целью определения числа узлов , числа ветвей , числа независимых контуров , числа ветвей с источниками токов, выяснения возможности упрощения схемы.

Прежде всего определяют число неизвестных токов, которое равно — . Для каждой ветви задают положительное направление тока.

Далее по первому закону Кирхгофа составляют — 1 независимых уравнений.

Затем по второму закону составляют уравнений. При этом выбирают независимые контуры, не содержащие источников тока.

Общее число составленных по первому и второму законам Кирхгофа должно быть равно числу неизвестных токов.

Рассмотрим применение законов Кирхгофа для определения токов в ветвях цепи, схема которой приведена на рис. 1.25. Пусть ЭДС идеальных источников напряжения , сопротивления . Требуется определить все токи схемы с помощью метода непосредственного применения законов Кирхгофа.

Схема содержит 6 ветвей с неизвестными токами и четыре узла. Па схеме узлы обозначены арабскими цифрами, показаны принятые направления токов и направления обхода контуров А, Б и В.

Составим систему из 6 уравнений. Уравнения по первому закону Кирхгофа запишем для узлов 1, 2, 3, уравнения по второму закону Кирхгофа запишем для контуров А, Б, В:

Решив эту систему уравнений, получим . Отрицательное значение тока , указывает на то, что выбранное при составлении уравнений направление этого тока не соответствует действительности. Правильное направление — от узла 3 к узлу 4.

Для проверки вычислений с помощью программы схемотехнического моделирования Micro Сар выполнен анализ по постоянному току схемы, изображенной на рис. 1.25. Изображенные на рис. 1.26,а значения токов ветвей (в мА) подтверждают правильность выполненных расчетов. Изображенные на рис. 1.26,б узловые потенциалы схемы (в В) позволяют определить направление токов ветвей.

Метод контурных токов

Метод контурных токов наиболее часто применяется на практике для расчета сложных цепей, так как он позволяет находить все неизвестные величины при числе уравнений, меньшем числа неизвестных величин.

По этому методу в каждом независимом контуре схемы вместо действительных токов в ветвях вводят условный контурный ток. Действительный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току. Действительный ток в любой ветви, принадлежащей нескольким контурам равен алгебраической сумме контурных токов, проходящих через эту ветвь.

Уравнения для расчета контурных токов составляются по второму закону Кирхгофа. При этом учитываются напряжения на всех пассивных элементах контура от собственного контурного тока и в смежных элементах -от контурных токов соседних контуров. Направление контурного тока в независимом контуре выбирают произвольно. Направление обхода контура обычно выбирают совпадающим с направлением собственного контурного тока.

Падение напряжения при прохождении тока смежного контура в элементе принимают положительным, если направление тока в смежном контуре совпадает с направлением обхода, Если направление тока смежного контура не совпадает с направлением обхода, падение напряжения считают отрицательным. Значение ЭДС берется со знаком плюс, если направление обхода контура совпадает с положительным направлением ЭДС, и со знаком минус — если не совпадает.

Метод контурных токов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.27. Схема имеет три независимых контура: А, Б, В. Через сопротивления каждого контура проходит свой контурный ток . Направления обхода каждого контура совпадает с направлением контурного тока этого контура. ЭДС идеальных источников напряжения , сопротивления и .

Уравнения, составленные по второму закону Кирхгофа, для контуров А, Б и В:

Подставив в эту систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим

Действительные токи ветвей схемы:

Полученные значения полностью совпадают с результатами ранее проделанного расчета этой же цени по методу непосредственного применения Законов Кирхгофа.

Метод узловых потенциалов

Потенциал любой точки электрической цепи определяется напряжением между данной точкой и точкой цепи с потенциалом равным нулю.

Метод узловых потенциалов заключается в том, что вначале полагают равным нулю потенциал некоторого базисного узла и для оставшихся ( -1) узлов составляют уравнения по первому закону Кирхгофа: алгебраическая сумма токов всех ветвей, подключенных к рассматриваемому узлу равна нулю. , полученными при выполнении с помощью программы Micro-Сар анализа по постоянному току схемы, изображенной на рис. 1.28,а.

Применив обобщенный закон Ома для каждой ветви схемы, получим искомые токи:

Полученные значения токов совпадают с результатами расчета этой цепи методом непосредственного применения законов Кирхофа и методом контурных токов.

Направления найденных токов указаны на графе цепи на рис. 1.28,6. Графом цепи называют такое изображение схемы электрической цепи, в котором все ветви заменены линиями, источники напряжения закорочены, а источники тока разомкнуты. Все ветви и все узлы сохраняются.

Метод узловых потенциалов имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа.

Метод двух узлов является частным вариантом метод узловых потенциалов. Он применяется в тех случаях, когда анализируемая схема содержит только два узла (для определенности узлы и ) и большое число параллельных ветвей, содержащих и не содержащих источники ЭДС. Согласно методу двух узлов межузловое напряжение

где — алгебраическая сумма произведений ЭДС ветвей (ЭДС считаются положительными, если они направлены к узлу , и отрицательными, если от узла к узлу ) на проводимости этих ветвей; — сумма проводимости всех ветвей, соединяющих узлы и .

Эта теория взята со страницы помощи с заданиями по электротехнике:

Помощь по электротехнике

Возможно эти страницы вам будут полезны:

ДЗ — Расчёт сложной цепи постоянного тока

Выполнение домашнего задания № 1 (первая часть)

Тема «Расчёт сложной цепи постоянного тока »

Методические указания

Цель работы: освоение методов анализа линейных электрических цепей постоянного тока.

Задание:

1) Начертить схему согласно варианту.

2) Определить количество ветвей, узлов и контуров.

3) Составить уравнения по первому и второму законам Кирхгофа.

4) Определить токи всех ветвей методом узловых потенциалов и методом контурных токов.

5) Составить и рассчитать баланс мощностей.

6) Определить ток в ветви (номер ветви в таблице соответствует номеру резистора в схеме) методом эквивалентного генератора.

7) Определить показания приборов.

8) Построить потенциальную диаграмму.

9) Сделать выводы.

2. Указания по оформлению расчетно-графической работы

1) Начертить схему в соответствии с номером варианта (схема Приложение 1, таблица Приложение 2). Номер варианта соответствует номеру в учебном журнале.

2) Домашнее задание выполняется на листах формата А4 с одной стороны листа, желательно использовать компьютерные программы.

3) Выполнить чертеж схемы и её элементов в соответствии с ГОСТом.

4) Образец оформления титульного листа представлен в Приложении 3.

5) Каждый пункт задания должен иметь заголовок. Формулы, расчёты, диаграммы должны сопровождаться необходимыми пояснениями и выводами. Полученные значения сопротивлений, токов, напряжений и мощностей должны заканчиваться единицами измерения в соответствии с системой СИ.

6) Графики (диаграммы) должны выполняться на мм бумаге с обязательной градуировкой по осям и указанием масштабов по току и напряжению.

7) Если студент сделал ошибки при выполнении домашнего задания, то исправление проводится на отдельных листах с заголовком «Работа над ошибками » .

8) Срок выполнения домашнего задания 5 неделя семестра.

3. Теоретическое введение

3.1 Топологические компоненты электрических схем

Количество ветвей — р

б) узел – q место соединения трех и более ветвей, узлы бывают потенциальные или геометрические рис. 1

Рис. 1

Четыре узла геометрических (abcd) и три потенциальных (abc) так как потенциалы узлов с и d равны: φс = φd

в) Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвленной электрической цепи – abcd , рис. 1. Независимый контур имеющий хотя бы одну новую ветвь.

3.2. Баланс мощностей

Составляем уравнения для определения мощности приемника:

ΣР_пр = Σ I²·R

Составляем уравнения для определения мощности источника:

ΣP_ист =Σ E·I

Баланс сходится при условии равенства уравнений мощностей источника и приемника, т.е.: ΣР_пр = ΣP_ист

Баланс считается сошедшимся, если погрешность не сходимости составляет не более 2%.

3.3. Эквивалентные преобразования пассивных участков электрической цепи

Соединения бывают: последовательное, параллельное и смешанное, звезда, треугольник, мостовое.

1. Последовательное соединение, когда ток в каждом элементе один и тот же.

Свойства последовательного соединения:

а) Ток цепи и напряжения зависит от сопротивления любого из элементов;

б) Напряжение на каждом из последовательно соединенных элементов меньше входного;

U_i< U

в) Последовательное соединение является делителем напряжения.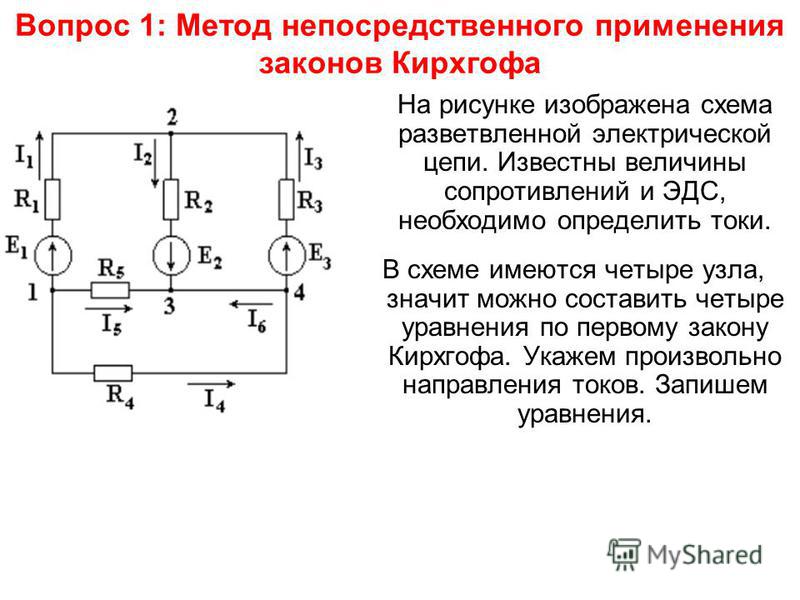

2. Параллельное соединение

Соединение, при котором все участки цепи присоединяются к одной паре узлов, находящихся под воздействием одного и того же напряжения.

Свойства параллельного соединения:

1) Эквивалентное сопротивление всегда меньше наименьшего из сопротивлений ветвей;

2) Ток в каждой ветви всегда меньше тока источника. Параллельная цепь является делителем тока;

3) Каждая ветвь находится под одним и тем же напряжением источника.

3. Смешанное соединение

Это сочетание последовательных и параллельных соединений.

Метод эквивалентных преобразований

Решение любой задачи с одним источником питания с помощью законов Ома, Кирхгофа и умением сворачивания схемы.

3.4 Методы расчета электрических цепей с несколькими источниками питания

3.4.1 Метод с помощью законов Кирхгофа.

Самый точный метод, но с его помощью можно определять параметры схемы с небольшим количеством контуров (1-3).

Алгоритм:

1. Определить количество узлов q, ветвей p и независимых контуров;

2. Задаться направлениями токов и обходов контуров произвольно;

3. Установить число независимых уравнений по 1-ому закону Кирхгофа (q — 1) и составить их, где q-количество узлов;

4. Определить число уравнений по 2-ому закону Кирхгофа (p – q + 1) и составить их;

5. Решая совместно уравнения, определяем недостающие параметры цепи;

6. По полученным данным производится проверка расчетов, подставляя значения в уравнения по 1-ому и 2-ому законам Кирхгофа или составив и рассчитав баланс мощностей.

Пример:

Запишем эти уравнения согласно правилам:

для узла «а » I₁ — I₂ — I₄ = 0

для узла «b » I₄ — I₅ — I₃ = 0

для контура 1 R₁·I₁+R₂·I₂ = E₁ — E₂

для контура 2 R₄·I₄+R₅·I₅ — R₂·I₂ = E₂

для контура 3 R₃·I₃ — R₅·I₅ =E₃

Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+ » , если нет, то с «- » .

Составим уравнения баланса мощностей:

P_пр= R₁·I₁² + R₂·I₂² + R₃·I₃² + R₄·I₄² + R₅·I₅²

P_ист= E₁·I₁ + E₃·I₃ — E₂·I₂

3.4.2 Метод контурных токов

Используя этот метод, сокращается число уравнений, а именно исключаются уравнения по 1-ому закону Кирхгофа. Вводится понятие контурный ток (таких токов в природе не бывает – это виртуальное понятие), составляются уравнения по второму закону Кирхгофа.

Рассмотрим наш пример рис. 2

Рис.2

Контурные токи обозначены I_м, I_н, I_л, заданы их направления, как показано на рис.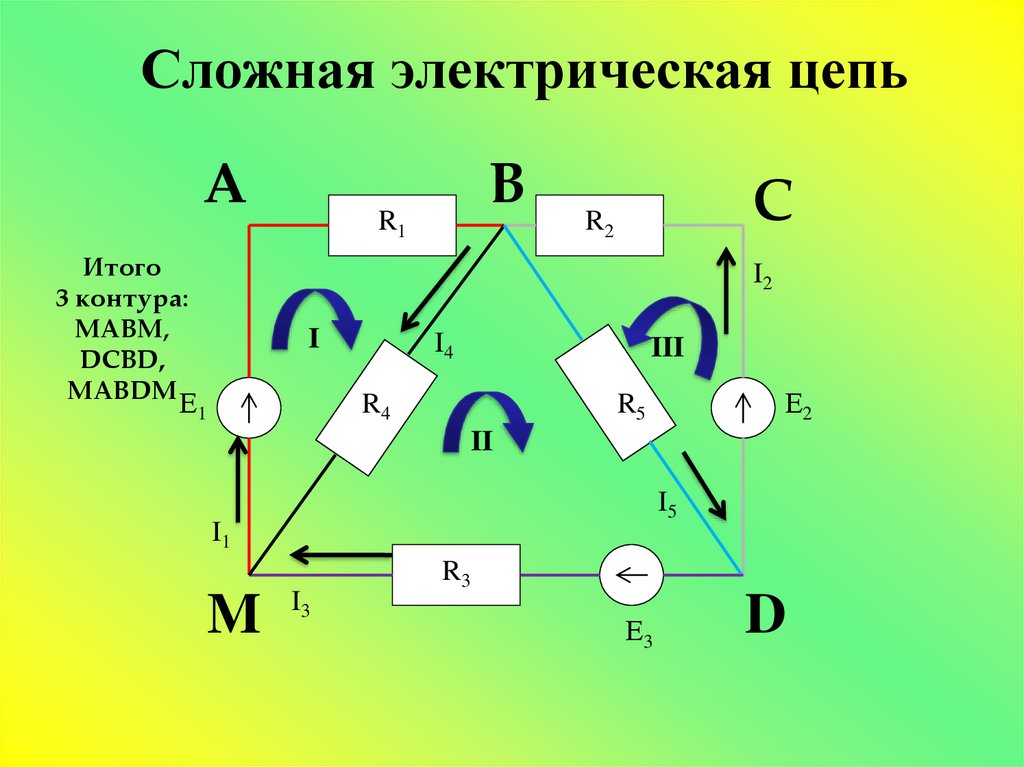 2

Алгоритм решения:

1. Запишем действительные токи через контурные: по внешним ветвям I₁= I_м,

I₃= I_л, I₄= I_н и по смежным ветвям I₂= I_м — I_н, I₅= I_н — I_л

2. Составим уравнения по второму закону Кирхгофа, так, как контура три, следовательно будет и три уравнения:

для первого контура I_м·(R₁ + R₂) — I_н·R₂ = E₁ — E₂, знак «– » перед I_н ставится потому, что этот ток направлен против I_м

для второго контура — I_м·R₂ + (R₂ + R₄+ R₅) ·I_н — I_л·R₅ = E₂

для третьего контура — I_н·R₅ + (R₃ + R₅) ·I_л = E₃

3. Решая полученную систему уравнений, находим контурные токи

4. Зная контурные токи, определяем действительные токи схемы (см. пункт 1.)

3.4.3 Метод узловых потенциалов

Предлагаемый метод самый эффективный из предложенных методов.

Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы.

Если схема содержит n-узлов, то уравнений будет (n-1):

Заземлим любой узел схемы φ = 0;
Необходимо определить (n-1) потенциалов;
Составляются уравнения согласно первому закону Кирхгофа по типу:

φ₁·G₁₁ + φ₂·G₁₂ +…+ φ_(n-1)·G_1,(n-1) = I₁₁

φ₁·G₂₁+ φ₂·G₂₂ +…+ φ_(n-1₎·G_2,(n-1) = I₂₂

…………………………………………………

φ₁·G_(n-1),1 + φ₂·G_(n-1),2 +…+ φ_(n-1₎·G_(n-1),(n-1) = I _{(n-1), (n-1)}

где I₁₁… I ₍_n_{-1), (}_n_-1) узловые токи в ветвях с ЭДС подключенных к данному узлу, G_kk_{– собственная проводимость (сумма проводимостей ветвей в узле k), G_km_{– взаимная проводимость (сумма проводимостей ветвей соединяющие узлы k и m), взятая со знаком «– » .}}

Токи в схеме определяются по обобщенному закону Ома.

Пример:

φ_а( + + ) — φ_b = E₁ + E₂

φ_b(++) — φ_a = — E₃

определив потенциалы φа и φb, найдем токи схемы. Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см. лекция 1).

Правильность расчета токов проверяется с помощью законов Кирхгофа и баланса мощностей.

3.4.4 Метод двух узлов

Метод двух узлов это частный случай метода узловых потенциалов. Применяется в случае, когда схема содержит только два узла (параллельное соединение).

Алгоритм:

Задаются положительные направления токов и напряжение между двумя узлами произвольно;
Уравнение для определения межузлового напряжения

где G – проводимость ветви, J – источники тока;

Правило: G·E и J берутся со знаком «+ » , если Е и J направлены к узлу с большим потенциалом;
Токи схемы определяются по обобщенному закону Ома

Пример:

Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см.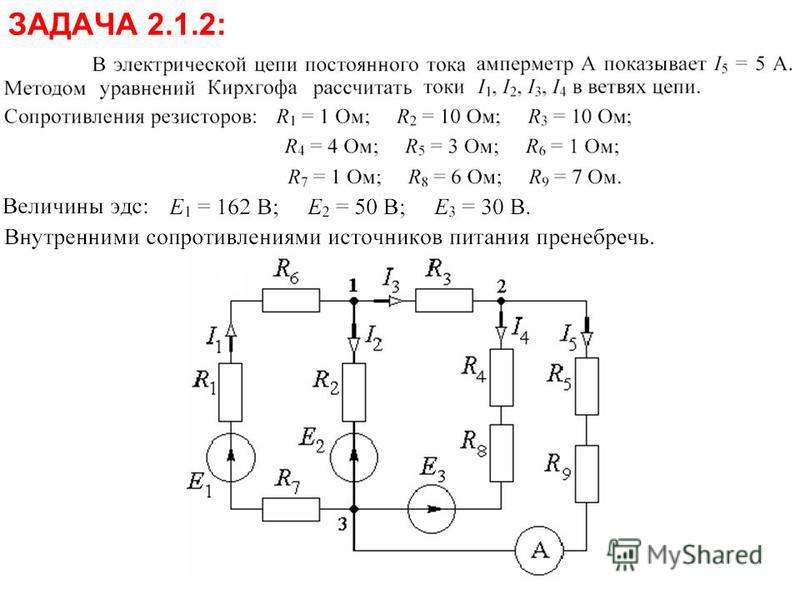 лекция 1).

3.4.5 Метод активного двухполюсника

Данный метод применяется, когда необходимо рассчитать параметры одной ветви в сложной схеме. Метод основан на теореме об активном двухполюснике: «Любой активный двухполюсник может быть заменен эквивалентным двухполюсником с параметрами Е_экв и R_экв или J_экв и G_экв, режим работы схемы при этом не изменится » .

Алгоритм:

1. Разомкнуть ветвь, в которой необходимо определить параметры.

2. Определить напряжение на разомкнутых зажимах ветви, т.е. при режиме холостого хода Е_экв = U_хх любимым методом.

3. Заменить активный двухполюсник, т.е. схему без исследуемой ветви, пассивным (исключить все источники питания, оставив их внутренние сопротивления, не забывая, что у идеальной ЭДС R_вн = 0, а у идеального источника тока R_вн = ∞). Определить эквивалентное сопротивление полученной схемы R_экв.

4. Найти ток в ветви по формуле I = E_экв/(R+R_экв) для пассивной ветви и

I = E ± E_экв/(R+R_экв) для активной ветви.

3.5 Построение потенциальной диаграммы

Распределение потенциалов в электрической цепи можно представить с помощью потенциальной диаграммы.

Потенциальная диаграмма представляет собой зависимость φ(R) в виде графика, на котором по вертикальной оси отложены значения потенциалов последовательного ряда точек выбранного контура, а по горизонтальной – сумма значений сопротивлений последовательно проходимых участков цепи этого контура. Построение потенциальной диаграммы начинается из произвольно выбранной точки контура, потенциал которой принят за нулевой φ₁ = 0. Последовательно обходим выбранный контур. Если построение диаграммы начали в точке 1, то и закончиться она должна в этой же точке 1. Скачки потенциала на графике соответствуют включенным в цепь источникам напряжения.

1.1. Определение показаний приборов

Вольтметр измеряет напряжение (разность потенциалов) между двумя точками в электрической цепи. Для определения показания вольтметра необходимо составить уравнение по второму закону Кирхгофа по контуру, в который входит измеряемое напряжение.

Ваттметр показывает мощность участка электрической цепи, которая определяется по закону Джоуля – Ленца.

4. Пример:

Дано: R₁ = R₅ =10 Ом, R₄ = R₆= 5 Ом, R₃ = 25 Ом, R₂ = 20 Ом, Е₁ =100 В, Е₂ =80 В, Е₃ =50 В

Определить токи в ветвях разными методами, составить и рассчитать баланс мощностей.

Решение:

1) Метод контурных токов

Так как три контура, то будет три контурных тока I₁₁, I₂₂, I₃₃. Направления этих токов выбираем по часовой стрелке рис 3. Запишем настоящие токи через контурные:

I₁= I₁₁ — I₃₃, I₂= — I₂₂, I₃= — I₃₃, I₄= I₁₁, I₅= I₁₁— I₂₂

Запишем уравнения по второму закону Кирхгофа для контурных уравнений в соответствии с правилами.

Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+ » , если нет, то с «– » .

Решим систему уравнений математическим методом Гаусса или Крамера.

Решив систему, получаем значения контурных токов:

I₁₁= 2,48 А, I₂₂ = — 1,84 А, I₃₃ = — 0,72 А

Определим настоящие токи: I₁= 3,2 А, I₂= 1,84 А, I₃= 0,72 А, I₄= 2,48 А, I₅= 4,32 А

Проверим правильность расчёта токов, подставив их в уравнения по законам Кирхгофа.

Составим уравнения для расчёта баланса мощностей:

Из расчёта видно, что баланс мощностей сошёлся. Погрешность меньше 1%.

2) Метод узловых потенциалов

Решаем туже задачу методом узловых потенциалов

Составим уравнения:

Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы. Заземлим любой узел схемы φ_с= 0.

Решая систему уравнений, определяем потенциалы узлов φ_a_{и_{φ_b}}

φ_a= 68 B φ_b_{= 43,2 B}

По обобщенному закону Ома определяем токи в ветвях. Правило: ЭДС и напряжение берутся со знаком «+ » , если их направления совпадают с направлением тока, и со знаком «– » , если нет.

3)Построение потенциальной диаграммы внешнего контура

Определим значение потенциалов узлов и точек схемы.

Правило: обходим контур против часовой стрелки, если ЭДС совпадает с обходом тока, то ЭДС бреется с «+ » (φ_е).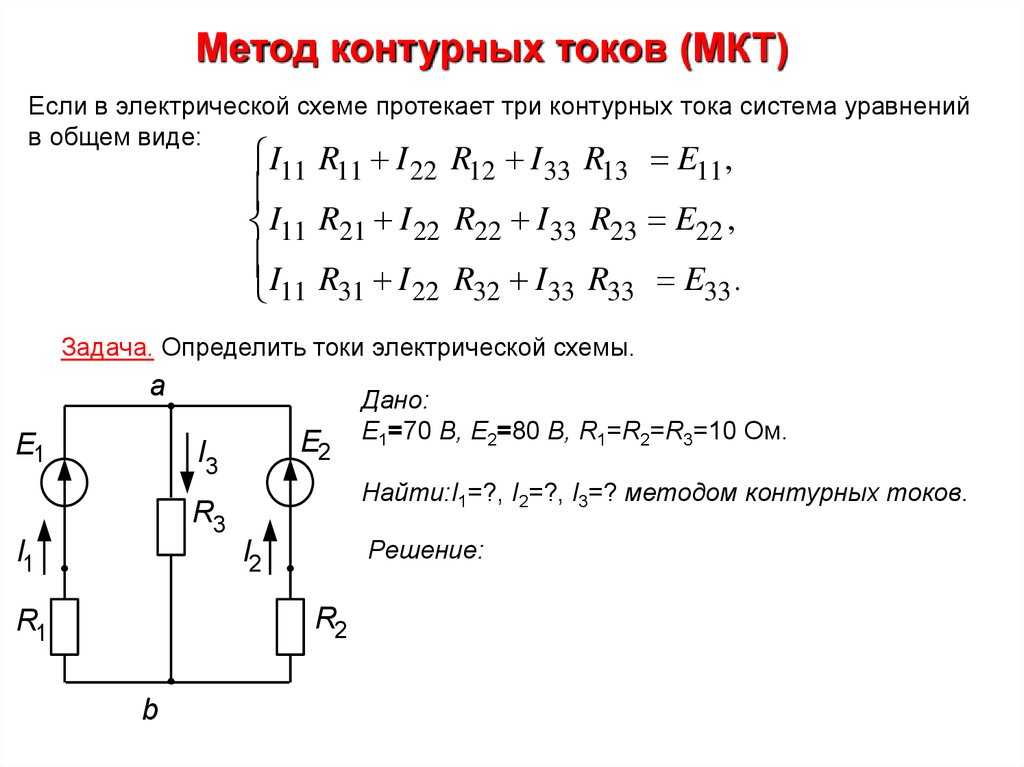 Если ток по обходу, то падение напряжения на резисторе, т.е «- » (φ_b).

Потенциальная диаграмма:

Список рекомендуемой литературы

Бессонов Л.А. Теоретические основы электротехники. В 2-х томах. М.: Высшая школа, 1978.
Электротехника и электроника. Учебник для вузов. / Под редакцией В.Г.Герасимова. — М.: Энергоатомиздат, 1997.
Сборник задач по электротехнике и основам электроники. / Под редакцией В.Г. Герасимова. Учебное пособие для вузов.- М.: Высшая школа, 1987.
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. Учебник для вузов – М.: Энергоатомиздат, 1985.
Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. Учебное пособие для студентов вузов. – М.: Энергоатомиздат, 1984.
Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника, -М.: Энергоатомиздат, 1987.

Контрольные вопросы

Свойства последовательной цепи
Свойства параллельной цепи
Правила составления баланса мощностей
Правила составления уравнений по первому закону Кирхгофа
Как определяется мощность источника питания?
Независимый контур. Напишите уравнение по 2-ому закону Кирхгофа любого контура Вашей схемы.
Правила составления уравнений по 2-ому закону Кирхгофа
Как определяется мощность приемника?
Как определить количество уравнений по 1-ому закону Кирхгофа?
Алгоритм метода эквивалентного генератора
Как включается вольтметр в цепь?
Как включается амперметр в цепь?
Как определить количество уравнений по 2-ому закону Кирхгофа?
С помощью какого закона определяем ток в ветви, в методе эквивалентного генератора?
В чём смысл метода эквивалентных преобразований?

Приложение 1

Схема 1 и данные для группы СМ3 – 41

Схема 1 и данные для группы СМ3 – 42

Приложение 2.

Для группы СМ3 – 41

Для группы СМ3 – 42

Выполнение домашнего задания № 1 вторая часть

по курсу «Электротехника и электроника »

тема «Расчёт линейных цепей синусоидального тока »

Методические указания

Цель работы: освоение анализа электрических цепей однофазного синусоидального тока с использованием символического метода.

Задание

1) Изучить теоретическое введение и методические указания по выполнению домашнего задания.

2) Начертить схему с элементами согласно варианту.

3) Определить количество узлов, ветвей и независимых контуров.

4) Определить количество уравнений по первому и второму законов Кирхгофа.

5) Составить уравнения по первому и второму законов Кирхгофа.

6) Рассчитать эквивалентное сопротивление схемы и определить характер цепи.

7) Определить токи в ветвях методом эквивалентных преобразований.

Записать токи в алгебраической, показательной и во временной форме.

8) Составить и рассчитать баланс мощностей. Определить коэффициент мощности цепи.

9) Рассчитать напряжения на элементах и построить векторную диаграмму токов и напряжений всей цепи.

10) Определить показания приборов.

11) Начертить схему замещения исходя из характера цепи. Ввести в схему замещения дополнительный элемент, обеспечивающий в цепи резонанс напряжений. Рассчитать напряжения и ток, построить векторную диаграмму.

12) Ввести в схему замещения дополнительный элемент, обеспечивающий в цепи резонанс токов. Рассчитать напряжение и токи, построить векторную диаграмму.

13) Собрать исходную схему в среде MULTISIM. Поставить приборы и измерить токи, напряжение и мощность.

Указания по оформлению расчетно-графической работы

9) Выписать параметры сопротивлений ветвей схемы в соответствии с номером варианта (таблица приложение1). Номер варианта соответствует номеру в учебном журнале.

10) Домашнее задание выполняется на листах формата А4 с одной стороны листа, желательно использовать компьютерные программы.

11) Выполнить чертеж схемы и её элементов в соответствии с ГОСТом. Схема представлена в приложении 2.

12) Образец оформления титульного листа представлен в приложении 2.

13) Каждый пункт задания должен иметь заголовок. Формулы, расчёты, диаграммы должны сопровождаться необходимыми пояснениями и выводами. Полученные значения сопротивлений, токов, напряжений и мощностей должны заканчиваться единицами измерения в соответствии с системой СИ.

14) Графики (векторные диаграммы) должны выполняться на миллиметровой бумаге с обязательной градуировкой по осям и указанием масштабов по току и напряжению.

15) При работе с программой MULTISIM необходимо в рабочем поле собрать схему, подключить в ветви амперметры. Перевести картинку с результатами в Word. Амперметры убрать из ветвей. Подключить вольтметр и ваттметр и измерить напряжение и мощность. Перевести картинку с результатами в Word. Результаты включить в отчет.

16) Если студент сделал ошибки при выполнении домашнего задания, то исправление проводится на отдельных листах с заголовком «Работа над ошибками » .

17) Срок выполнения домашнего задания 10 неделя семестра.

Теоретическое введение

3.1 Временная форма представления электрических величин, при синусоидальных воздействиях

Аналитическое выражение мгновенных значений тока, ЭДС и напряжения определяется тригонометрической функцией:

i(t) = I_msin(ωt + ψ_i)

u(t) = U_m sin(ωt + ψ_u)

e(t) = E_m sin(ωt + ψ_e),

где I_m, U_m, E_m— амплитудные значения тока, напряжения и ЭДС.

(ωt + ψ) — аргумент синуса, который определяют фазовый угол синусоидальной функции в данный момент времени t.

ψ — начальная фаза синусоиды, при t = 0.

i(t), u(t) временные формы тока и напряжения.

По ГОСТу ƒ = 50 Гц, следовательно, ω = 2πƒ = 314 рад/сек.

Временную функцию можно представить в виде временной диаграммы, которая полностью описывает гармоническую функцию, т.е. дает представление о начальной фазе, амплитуде и периоде (частоте).

3.2 Основные параметры электрических величин

При рассмотрении нескольких функций электрических величин одной частоты интересуются фазовыми соотношениями, называемой углом сдвига фаз.

Угол сдвига фаз φ двух функций определяют как разность их начальных фаз. Если начальные фазы одинаковые, то φ = 0 , тогда функции совпадают по фазе, если φ = ± π, то функции противоположны по фазе.

Особый интерес представляет угол сдвига фаз между напряжением и током: φ = ψ_u — ψ_i

На практике используют не мгновенные значения электрических величин, а действующие значения. Действующим значением называют среднеквадратичное значение переменной электрической величины за период.

Для синусоидальных величин действующие значения меньше амплитудных в √2 раз, т.е.

Электроизмерительные приборы градуируются в действующих значениях.

3.3 Применение комплексных чисел

Расчет электрических цепей с использованием тригонометрических функций весьма сложен и громоздок, поэтому при расчете электрических цепей синусоидального тока используют математический аппарат комплексных чисел. Комплексные действующие значения записываются в виде:

Синусоидальные электрические величины, представленные в комплексной форме, можно изображать графически. На комплексной плоскости в системе координат с осями +1 и +j, которыми обозначены положительные действительная и мнимая полуоси, строятся комплексные векторы. Длина каждого вектора пропорциональна модулю действующих значений. Угловое положение вектора определяется аргументом комплексного числа. При этом отсчет положительного угла ведется против часовой стрелки от положительной действительной полуоси.

Пример: построение вектора напряжения на комплексной плоскости рисунок 1.

Напряжение в алгебраической форме записывается:

Длина вектора напряжения:

Комплексное сопротивление выражается через комплексные действующие значения напряжения и тока в соответствии с законом Ома:

3.4 Законы Ома и Кирхгофа в комплексной форме

Закон Ома в комплексной форме:

• Анализ цепей синусоидального тока происходит при условии, что все элементы цепи R, L, C идеальны (таблица 1).

• Электрическое состояние цепей синусоидального тока описывается теми же законами и рассчитываются теми же методами, что и в цепях постоянного тока.

Первый закон Кирхгофа в комплексном виде:

Второй закон Кирхгофа в комплексном виде:

Сводная таблица идеальных элементов и их свойств.

Таблица 1

3.5 Баланс мощностей в цепях синусоидального тока

Для приемников вычисляем раздельно активную мощность

и реактивную мощность

При выполнении реальных расчетов мощности источников и приемников могут несколько отличаться. Эти погрешности обусловлены погрешностями метода, округления результатов расчётов.

Точность выполненного расчета схемы оценивают с помощью относительной погрешности при вычислении баланса активных мощностей

δ_Р% =

и реактивных мощностей

δ_Q% =

При выполнении расчетов погрешности не должны превышать 2%.

3.6 Определение коэффициента мощности

Электрооборудование энергетически выгодно эксплуатировать, если он совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.

Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование.

λ = P/S = cosφ ≤ 1

Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.

3.7 Резонансы в цепях синусоидального тока

3.7.1 Резонанс напряжений

Режим работы RLC цепи рисунок 2 или LC—цепи, при условии равенства реактивных сопротивлений X_C= X_L, когда общее напряжение цепи совпадает по фазе с её током , называется резонансом напряжения.

X_C= X_L – условие резонанса

Признаки резонанса напряжения:

1. Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1

2. Ток в цепи будет наибольшим и как следствие P_max= I²_maxR мощность тоже максимальна, а реактивная мощность равна нулю.

3. Резонансная частота

Резонанс можно достигнуть, изменяя L, C или ω.

Векторные диаграммы при резонансе напряжений

LC цепь RLC цепь

3.7.2. Резонанс токов

Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.

Условие резонанса токов: разность реактивных проводимостей параллельных ветвей равна 0

В₁ – реактивная проводимость первой ветви,
В₂– реактивная проводимость второй ветви
Признаки резонанса токов:
Реактивные составляющие токов ветвей равны I_PC= I_PL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
и совпадают по фазе
RLC – цепь                                                                                      Векторная диаграмма
LC – цепь                                                                             Векторная диаграмма

Методические указания
4. 1 Начертить схему с элементами согласно варианту.
Схема рисунок 1 преобразуем согласно варианту ( Z₁ – RC, Z₂ – R, Z₃ – RL).
Рисунок 1 Исходная схема
4.2 Рассмотрим схему рисунок 2, и запишем уравнения по законам Кирхгофа.
Схема содержит два узла, два независимых контура и три ветви.
            Рисунок 2 Схема с элементами
Запишем первый закон Кирхгофа для узла а:
Запишем второй закон Кирхгофа для первого контура:
Запишем второй закон Кирхгофа для второго контура:
4.3 Определим эквивалентное сопротивление цепи.
Свернём схему рис 2.

По эквивалентному сопротивлению определяется характер цепи и чертится схема замещения.
Рисунок 3 свернутая схема
4.4 Определяем токи в ветвях схемы рисунок 2, методом эквивалентных преобразований: зная эквивалентное сопротивление, определяем ток первой ветви .
Рассчитываем ток в комплексной форме по закону Ома в соответствии со схемой рисунок 3:
Чтобы определить токи в остальных ветвях, нужно найти напряжение между узлами «ab » рисунок 2:
Определяем токи:
4.5 Запишем уравнения баланса мощностей:
где I₁, I₂, I₃– действующие значения токов.
Определение коэффициента мощности
Расчёт коэффициента мощности проводят, определив активную и полную мощности:    P/S = cosφ . Используем рассчитанные мощности, которые найдены при расчёте баланса.
модуль полной мощности .
4.6 Рассчитаем напряжения на элементах, используя схему рисунок 2:

4.7 Построение векторной диаграммы
Построение векторной диаграммы ведется после полного расчета всей цепи, определения всех токов и напряжений. Построение начинаем с задания осей комплексной плоскости [+1; +j]. Выбираются удобные для построения масштабы для токов и напряжений. Сначала строим на комплексной плоскости вектора токов (рисунок 4), в соответствии с первым законом Кирхгофа для схемы 2. Сложения векторов осуществляется по правилу параллелограмма.
Рисунок 4 векторная диаграмма токов
Затем строим на комплексной плоскости вектора рассчитанных напряжений проверка по таблице 1 рисунок 5.
Рисунок 5 Векторная диаграмма напряжений и токов
4.8 Определение показаний приборов
Амперметр измеряет ток, проходящий через его обмотку. Он показывает действующее значение тока в ветви, в которую он включен. В схеме (рис.1) амперметр показывает действующее значение (модуль) тока . Вольтметр показывает действующее значение напряжения между двумя точками электрической цепи, к которым он подключен. В рассматриваемом примере (рис.1) вольтметр подключен к точкам а и b.
Вычисляем напряжение   в комплексной форме:
Ваттметр измеряет активную мощность, которая расходуется на участке цепи, заключенном между точками, к которым подключена обмотка напряжения ваттметра, в нашем примере (рис. 1) между точками   а и b.
Активную мощность, измеряемую ваттметром, можно вычислить по формуле
                   ,
где — угол между векторами   и .
В этом выражении   действующее значение напряжения, на которое подключена обмотка напряжения ваттметра, и   действующее значение тока, проходящего через токовую обмотку ваттметра.
Или рассчитываем полную комплексную мощность
ваттметр покажет активную мощность Р.
4.9 Расчёт резонансных цепей
4.9.1 Добавить в схему замещения элемент для получения резонанса напряжений. Например, схема замещения представляет RL цепь. Тогда необходимо добавить последовательно включённый конденсатор С – элемент. Получается последовательная RLC цепь.
Рассчитать ток и все напряжения цепи в комплексной форме, при выполнении условия резонанса, построить векторную диаграмму, см.теоретическое введение пункт 3.7.1
4.9.2 Добавить в схему замещения элемент для получения резонанса токов. Например, схема замещения представляет RL цепь. Тогда необходимо добавить параллельно включённый конденсатор С – элемент.

Рассчитать проводимости ветвей, токи и напряжения, при выполнении условия резонанса. Построить векторную диаграмму, см.теоретическое введение пункт 3.7.2
5. Собрать схему в среде MULTISIM. Поставить приборы и измерить токи, напряжение и мощность.
Сборка схемы в среде Multisim 10.1. На рисунке 6 рабочее окно в среде Multisim. Панель приборов располагается справа.
Рисунок 6 рабочее окно в среде Multisim
Разместить на рабочем поле необходимые для схемы элементы. Для этого на верхней панели инструментов слева нажмём кнопку «Place Basic » (см. Рисунок 7 ). Выбор резистор: появится окно «Select a Component » , где из списка «Family » выбрать «Resistor » . Под строкой «Component » появятся номинальные значения сопротивлений, выбираем нужное нажатием левой кнопки мыши или же непосредственным введением в графу «Component » необходимого значения. В Multisim используются стандартные приставки системы СИ (см. Таблицу 1)
Таблица 1
Рисунок 7
В поле «Symbol » выбираем элемент. После выбора, нажимаем кнопку «OK » и размещаем элемент на поле схемы нажатием левой кнопки мыши. Далее можно продолжать размещение необходимых элементов или нажать кнопку «Close » , чтобы закрыть окно «Select a Component » . Все элементы можно поворачивать для более удобного и наглядного расположения на рабочем поле. Для этого необходимо навести курсор на элемент и нажать левую кнопку мыши. Появится меню, в котором надо выбрать опцию «90 Clockwise » для поворота на 90° по часовой стрелке или «90 CounterCW » для поворота на 90° против часовой стрелки. Размещённые на поле элементы необходимо соединить проводами. Для этого наводим курсор на клемму одного из элементов, нажимаем левую кнопку мыши. Появляется провод, обозначенный пунктиром, подводим его к клемме второго элемента и снова нажимаем левую кнопку мыши. Проводу так же можно придавать промежуточные изгибы, обозначая их кликом мыши (см. Рисунок 8). Схему необходимо заземлить.
Подключаем к цепи приборы. Для того, чтобы подсоединить вольтметр, на панели инструментов выбираем «Place Indicator » , в списке Family » открывшегося окна выбираем тип элемента «Voltmetr_V » , приборы перевести в режим измерения переменного тока (АС).
Измерение токов
Соединив все размещённые элементы, получаем разработанную схему рисунок .
На панели инструментов выбираем «Place Source » . В списке «Family » открывшегося окна выбираем тип элемента «Power Souces » , в списке «Component » — элемент «DGND » .
Измерение напряжения
Измерение мощности
6. Контрольные вопросы
1. Сформулируйте законы Кирхгофа и объясните правила составления системы уравнений по законам Кирхгофа.
2. Метод эквивалентных преобразований. Объясните последовательность расчета.
3. Уравнение баланса мощностей для цепи синусоидального тока. Объясните правила составления уравнения баланса мощностей.
4. Объясните порядок расчета и построения векторной диаграммы для Вашей схемы.
5. Резонанс напряжений: определение, условие, признаки, векторная диаграмма.
6. Резонанс токов: определение, условие, признаки, векторная диаграмма.
7. Объясните, как рассчитать показания приборов (амперметра, вольтметра, ваттметра).
8. Сформулируйте понятия мгновенного, амплитудного, среднего и действующего значений синусоидального тока.
9. Напишите выражение для мгновенного значения тока в цепи, состоящей из соединенных последовательно элементов R и L, если к зажимам цепи приложено напряжение   .
10. От каких величин зависит значение угла сдвига фаз между напряжением и током на входе цепи с последовательным соединением R , L , C ?
11. Как определить по экспериментальным данным при последовательном соединении сопротивлений R , X_L и X_C_{значения величин   Z , R , X , Z_К , R_К , L , X_C , C ,cosφ , cosφ_К?}
12. В последовательной RLC цепи установлен режим резонанса напряжений. Сохранится ли резонанс, если:
а) параллельно конденсатору подключить активное сопротивление;
б) параллельно катушке индуктивности подключить активное сопротивление;
в) последовательно включить активное сопротивление?
13. Как должен изменяться ток I в неразветвленной части цепи при параллельном соединении потребителя и батареи конденсаторов в случае увеличения емкости от С = 0 до С = ∞ , если потребитель представляет собой:
а) активную,
б) емкостную,
в) активно-индуктивную,
г) активно-емкостную нагрузку?
6. Литература
1. Бессонов Л.А. Теоретические основы электротехники- М.: Высшая школа, 2012г.
2. Беневоленский С.Б., Марченко А.Л. Основы электротехники. Учебник для ВУЗов – М.,Физматлит, 2007г.
3. Касаткин А.С., Немцов М.В. Электротехника. Учебник для вузов- М.: В. ш, 2000г.
4. Электротехника и электроника. Учебник для вузов, книга 1. / Под редакцией
В.Г.Герасимова. — М.: Энергоатомиздат, 1996г.
4. Волынский Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника, -М.:
      Энергоатомиздат, 1987г.
Приложение 1
Схема группа 1
Схема группа 2
Приложение 2
Расчет сложных электрических цепей постоянного тока
Похожие презентации:
Электрическая цепь постоянного тока
Электрические цепи постоянного тока
Анализ сложной линейной электрической цепи постоянного тока
Анализ сложной линейной электрической цепи постоянного тока
Электрические цепи постоянного тока
Анализ сложной линейной электрической цепи постоянного тока
Цепи постоянного тока
Электротехника и электроника. Электрические цепи постоянного тока. (Лекция 1)
Электрические цепи постоянного тока
Расчет цепи постоянного тока
Тема:
«Расчет сложных
электрических цепей
постоянного тока»
Тема: «Сложные электрические цепи
постоянного тока»
План урока:
1. Строение сложной электрической цепи.
2. Законы Кирхгофа, область их применения.
3. Алгоритм расчета сложной электрической
цепи постоянного тока.
Из каких элементов состоит простейшая
электрическая цепь постоянного тока?
5. Густав Роберт Кирхгоф /1824г.-1887г./ Немецкий физик, внес огромный вклад в развитие математической физики и электричества.
По каким признакам
классифицируются электрические
цепи?
• По виду тока цепи подразделяются на
цепи постоянного и переменного тока.
• По характеру параметров элементов
цепи разделяются на линейные и
нелинейные.
•По наличию или отсутствию в цепи
источника электрической энергии цепи
делятся на активные (А) и пассивные (П).
•По степени сложности – цепи бывают
простые (неразветвлённые) и сложные
(разветвлённые).
11. Электрическая цепь
R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
I3
Е3
12. Зададим направление токов во всех ветвях цепи
В
А
С
R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
M
I3
Е3
D
13. Сложная электрическая цепь
А
В
R1
Итого
m=5 ветвей,
из них 3ветвей
активные
С
R2
I2
I4
Е1
R4
Е2
R5
Итого
n=3 узловых точек
I5
I1
M
R3
I3
Е3
D
15. Дайте формулировку I закону Кирхгофа
Алгебраическая сумма токов в узле
электрической цепи равна нулю.
n
I
i 1
i
0
При этом направленный к узлу ток принято считать
положительным, а направленный от узла — отрицательным.
Количество уравнений по первому закону
Кирхгофа определяется по формуле (n-1)
Количество уравнений по первому
закону Кирхгофа (n-1) =3-1=2
Для узла M: I3+I4-I1=0
Для узла B: I1+I2-I4-I5=0
17.
Вывод:1.Рассматривая строение сложной
электрической цепи:
а) задали произвольно направление
токов во всех ветвях цепи и их
обозначили;
б) определили общее количество ветвей;
в) определили количество ветвей с
источниками тока;
г) определили количество узлов.
19. Сложная электрическая цепь
А
Итого
3 контура:
MABM,
DCBD,
MABDM
В
R1
С
R2
I2
I
Е1
I4
III
R4
Е2
R5
II
I5
I1
M
I3
R3
Е3
D
20. II закон Кирхгофа
В замкнутом контуре электрической цепи
алгебраическая сумма ЭДС равна
алгебраической сумме падения
напряжения .
n
n
U E
i 1
i
i 1
i
Количество уравнений по второму закону Кирхгофа
определяется по формуле
m-(n-1)
21. Сложная электрическая цепь
В R
А
С
R
1
2
I2
Итого:
составляем 3
контурных Е
1
уравнения
I4
I
R4
III
II
I5
I1
M
Е2
R5
I3
R3
Е3
D
При составлении уравнений ЭДС и токи, совпадающие с
выбранным направлением обхода контура будем брать со
знаком (+), а несовпадающие – со знаком (–).
Количество уравнений по второму
закону Кирхгофа определяется по
формуле m-(n-1) =5-(3-1)=3
Для I контура: E1= I1R1+I4R4
Для II контура: E2+Е1=I2R2+I5R5+I1R1
Для III контура: E3= I3R3- I4R4+ I5R5
Вывод:
1.Рассмотрели строение сложной цепи постоянного тока.
а) Обозначили номера токов, выбрав их направления
произвольно.
б) Определили общее количество ветвей.
в) Определили количество ветвей с источниками тока.
г) Определили количество узлов и обозначили их
произвольно.
2. Определили количество уравнений по первому закону
Кирхгофа (n-1)= 3-1=2.
3. Составили уравнения по первому закону для любых узлов.
4. Определили количество уравнений по второму закону
Кирхгофа m-(n-1)=5-(3-1)=3.
5. Выбрали контуры и направления их обхода.
6. Составили уравнения по второму закону для выбранных
контуров.
24. Алгоритм расчета:
1.Рассмотрение строения сложной цепи постоянного тока:
а) обозначение номера токов, выбрав их направления
произвольно;
б) определение общего количества ветвей;
в) определение количества ветвей с источниками тока;
г) определение количества узлов и произвольное их
обозначение.
2. Определение количества уравнений по первому закону
Кирхгофа (n-1)= 3-1=2.
3. Составление уравнения по первому закону для любых узлов.
4. Определили количество уравнений по второму закону Кирхгофа
m-(n-1)=5-(3-1)=3.
5. Выбор контуры и направления их обхода.
6. Составление уравнения по второму закону для выбранных
контуров.
7. Объединение уравнение в систему и их решение.
English Русский Правила
Алгоритм расчета сложной электрической цепи постоянного тока.

Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

КАТЕГОРИИ:
Археология
Биология
Генетика
География
Информатика
История
Логика
Маркетинг
Математика
Менеджмент
Механика
Педагогика
Религия
Социология
Технологии
Физика
Философия
Финансы
Химия
Экология

ТОП 10 на сайте
Приготовление дезинфицирующих растворов различной концентрации
Техника нижней прямой подачи мяча.
Франко-прусская война (причины и последствия)
Организация работы процедурного кабинета
Смысловое и механическое запоминание, их место и роль в усвоении знаний
Коммуникативные барьеры и пути их преодоления
Обработка изделий медицинского назначения многократного применения
Образцы текста публицистического стиля
Четыре типа изменения баланса
Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации
Практические работы по географии для 6 класса
Организация работы процедурного кабинета
Изменения в неживой природе осенью
Уборка процедурного кабинета
Сольфеджио. Все правила по сольфеджио
Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 5 из 18Следующая ⇒
Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системылинейных уравнений c lнеизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)
Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.
Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:
1. Выбирают положительные направления токов в ветвях электрической цепи.
2. Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.

3. Выбирают (l—k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.
4. Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.
5. Решают систему из (l—m) линейных уравнений любым удобным способом.
Более наглядно методика составления системы уравнений для данного способа расчета сложных электрических цепей показана на рисунке ниже.

На рисунке изображена схема сложной электрической цепи, содержащей 4 узла и 6 ветвей (k=4, l=6). Для расчета цепи необходимо составить систему из 6 линейных уравнений. Предварительно выберем направления токов в каждой из ветвей. По первому закону Кирхгофа (формула 1.20) составляем 3 уравнения (k-1=4-1=3), например для узлов A, B и C. Вместо любого из этих узлов для составления уравнения можно взять узел D, на результат расчетов это не повлияет. Оставшиеся 3 уравнения (l—k+1-m=6-4+1-0=3) придется составлять по второму закону Кирхгофа.
Для этого выбираем 3 независимых контура электрической цепи и для каждого из них выберем направление обхода. Составляем для каждого выбранного контура уравнение по второму закону Кирхгофа (формула 1.21). Получаем систему из 6 линейных уравнений с 6 неизвестными, которую и решаем любым удобным способом.
Магнитное поле. Сила Лоренца.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющая электромагнитного поля^[2].
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментамиэлектронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).
Кроме этого, оно возникает в результате изменения во времени электрического поля.
Основной силовой характеристикой магнитного поля является вектор магнитной индукции (вектор индукции магнитного поля)^[3]^[4]. С математической точки зрения —векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
F = IBΔl sin α
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
I = q n υ S.
Выражение для силы Ампера можно записать в виде:
F = q n S Δl υB sin α.
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна
F_Л = q υ B sin α.
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или поправилу буравчика. Взаимное расположение векторов , и для положительно заряженной частицы показано на рис. 1.18.1.
Рисунок 1.18.1. Взаимное расположение векторов , и Модуль силы Лоренца численно равен площади параллелограмма, построенного на векторах и помноженной на заряд q
Сила Лоренца направлена перпендикулярно векторам и
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, ²⁰Ne и ²²Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источникаS, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся вскрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условииE = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q₁ = q₂) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10^–4.
Рисунок 1.18.4. Селектор скоростей и масс-спектрометр
Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ_┴ вектора а шаг спирали p – от модуля продольной составляющей υ_|| (рис. 1.18.5).
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 10⁶ K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемыерадиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.

⇐ Предыдущая12345678910Следующая ⇒

Читайте также:

Техника прыжка в длину с разбега
Организация работы процедурного кабинета
Области применения синхронных машин
Оптимизация по Винеру и Калману

Последнее изменение этой страницы: 2016-04-20; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы!

infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176. 9.44.166 (0.012 с.)

Сложные электрические цепи постоянного тока

Стр 1 из 2Следующая ⇒
В сложной электрической цепи постоянного тока (Таблица 2)
определить токи на всех участках цепи. Задачу решить двумя любыми методами
Таблица 2
Вариант № Данные для расчётов Схема электрической цепи
Е₁=136В; Е₂=80В; R₁ = 194 Ом; R₂ =76 Ом; R₃ = 240 Ом; R₄ =120 Ом. _. r₁= 6 Ом; r₂= 4 Ом. Рис.12
Е₁=150В; Е₂=170В; R₁ = 29,5Ом;R₂ =24 Ом; R₃ = 40 Ом; r₁= 0,5 Ом; r₂= 1 Ом. Рис.13
Е₁=68В; Е₂=40В; R₁ = 97Ом;R₂ =38Ом; R₃ = 120 Ом; R₄=60Ом; r₁= 3 Ом; r₂= 2 Ом. Рис.14
Е₁=45В; Е₂=60В; R₁ = 2 Ом;R₂ =14.5 Ом; R₃ = 15 Ом; R₄ =5 Ом 5 r₁= 0,5 Ом; r₂= 0,5Ом. Рис.15
Е₁=30В; Е₂=40В; R₁ =10Ом;R₂ =2 Ом; R₃ = 3Ом; R₄ = R₅=12Ом; r₁= 2Ом; r₂= 1Ом. Рис.16
Вариант № Данные для расчётов Схема электрической цепи
Е₁=90В; Е₂=120В; R₁ = 4Ом;R₂ =29 Ом; R₃ = 30 Ом; R₄ =10Ом; r₁= 1Ом; r₂= 1Ом. Рис.17
Е₁=120В; Е₂=144В; R₁ = 3,6Ом;R₂ =6,4 Ом; R₃ = 6 Ом; R₄ =4 Ом r₁= 0,4 Ом; r₂= 1,6 Ом. Рис.18
Е₁=160В; Е₂=200В; R₁ = 9Ом;R₂ =19 Ом; R₃ = 25 Ом; R₄ =100Ом; r₁= 1Ом;r₂= 1 Ом. Рис.19
Е₁=60В; Е₂=72В; R₁ = 1,8Ом;R₂ =3,2 Ом; R₃ = 3 Ом; R₄ =2Ом; r₁= 0,2Ом; r₂= 0,8 Ом. Рис.20
Е₁=80В; Е₂=100В; R₁ = 9Ом;R₂ =19 Ом; R₃ = 25 Ом; R₄ =100Ом; r₁= 1Ом; r₂= 1 Ом. Рис. 21

Решение задачи 2 требует знаний методов расчёта сложной электрической цепи и ее участков, законов Кирхгофа, методики определения эквивалентного сопротивления цепи. Перед решением задачи изучите методики расчётов сложных электрических цепей постоянного тока и рассмотрите соответствующие им типовые примеры.
Методические указания к решению задачи 2:
2.1. Метод наложения токов
Метод наложения является одним из методов расчета сложных цепей с несколькими источниками.

Сущность расчета цепей методом наложения сводится к следующему:
1. В каждой ветви рассматриваемой цепи направление тока выбирается произвольно.
2. Количество расчетных схем цепи равно количеству источников в исходной схеме.
3. В каждой расчетной схеме действует только один источник, а остальные источники заменяются их внутренним сопротивлением.
4. В каждой расчетной схеме методом свертывания определяют частичные токи в каждой ветви. Частичным называется условный ток, протекающий в ветви под действием только одного источника. Направление частичных токов в ветвях вполне определенно и зависит от полярности источника.
5. Искомые токи каждой ветви рассматриваемой схемы определяются как алгебраическая сумма частичных токов для этой ветви. При этом частичный ток, совпадающий по направлению с искомым, считается положительным, а несовпадающий — отрицательным. Если алгебраическая сумма имеет положительный знак, то направление искомого тока в ветви совпадает с произвольно выбранным, если отрицательный, то направление тока противоположно выбранному.
Пример 2.1. Метод наложения токов
Определить токи во всех ветвях цепи, схема которой приведена на рисунке 22, если задано Е₁ = 40 В; Е₂ = 30 В; R₀₁ = R₀₂ = 0,4 Ом; R₁ = 30 Ом; R₂=R₃ = 10 Ом; R₄=R₅ = 3,6 Ом.
Рисунок 22 Рисунок 23
Рисунок 24
Устанавливается, что количество ветвей и соответственно различных токов в цепи (рисунок 22) равно пяти, и произвольно выбирается направление этих токов.

Количество расчетных схем две, так как в цепи два источника.
Вычисляются частичные токи, созданные в ветвях первым источником (I’) Для этого изображается та же цепь, только вместо Е₂ — его внутреннее сопротивление (R₀₂). Направление частичных токов в ветвях указаны в схеме (рисунок 23).
Вычисление этих токов производится методом свертывания

Тогда первые частичные токи в цепи (рисунок 23), имеют следующие значения:

Вычисляются частичные токи, созданные вторым источником (I’’). Для этого изображается исходная цепь, заменив в ней первый источник (Е₁) его внутренним сопротивлением (R₀₁). Направления этих частичных токов в ветвях указаны на схеме (рисунок 24).
Вычислим эти токи, пользуясь методом свертывания.

.

Вторые частичные токи в цепи (рисунок 24) имеют следующие значения:

Следовательно, искомые токи в рассматриваемой цепи (рисунок 22) определяются алгебраической суммой частичных токов (см. рисунок 22, 23 и 24) и имеют следующие значения:
Ток I_АБ имеет знак «-», следовательно, его направление противоположно произвольно выбранному, т. е. I_АБ направлен из точки А в точку Б.

2.2. Метод узлового напряжения

Расчет сложных разветвленных электрических цепей с несколькими источниками можно осуществить методом узлового напряжения, если в этой цепи имеются только два узла. Напряжение между этими узлами и называется узловым. U_АБ — узловое напряжение схемы (рисунок 25).
Величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:

,

Для определения знаков алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т. е. от одного узла к другому (рисунок 25). Тогда ЭДС источника, работающего в режиме генератора, берут со знаком «+», а источника, работающего в режиме потребителя, — со знаком «-».

Рисунок 25

Для цепи, изображенной на рисунке 25, узловое напряжение определяется выражением:

,

Где – проводимость первой ветви; — проводимость второй ветви; – проводимость третей ветви.

Узловое напряжение (U_АБ) может получиться как положительным так и отрицательным. Определив узловое напряжение (U_АБ), можно вычислить токи в каждой ветви.

Узловое напряжение для первой ветви:

,

Так как источник E₁ работает в режиме генератора. Откуда

,

Для второй ветви, источник которой E₂ работает в режим потребителя:

,

Откуда

,

Для третьей ветви , так как условно выбранное направление тока I₃ указывает, что точки Б ( ) больше, чем потенциал точки А ( ). Тогда:

,

Знак «-» в вычисленном значении тока указывает, что условно выбранное направление тока данной ветви противоположно выбранному.

Пример 2.2. Метод узлового напряжения

Рисунок 26

В ветвях схемы (рисунок 26) требуется определить токи, если R₁ = 1,7 Ом; R₀₁ = 0,3 Ом; R₂ = 0,9 Ом; R₀₂ = 0,1 Ом; R₃=4 Ом; E₁ = 35 В; E₂ = 70 В.

Определяем узловое напряжение U_АБ

Где ; ; ;

тогда

Определяем токи в ветвях:

Как видно, направление токов I₁ и I₃ противоположно выбранному. Следовательно, источник Е₁ работает в режиме потребителя.

2.3. Метод узловых и контурных уравнений

Законы Кирхгофа лежат в основе расчета сложных электрических цепей методом узловых и контурных уравнений.

Составление системы уравнений по законам Кирхгофа (методом узловых и контурных уравнений) осуществляется в следующем порядке:

1. Число уравнений равно числу токов в цепи (число токов равно числу ветвей в рассчитываемой цепи). Направление токов в ветвях выбирается произвольно.

2. По первому закону Кирхгофа составляется (n-1) уравнений, где n- число узловых точек в схеме.

3. Остальные уравнения составляются по второму закону Кирхгофа.

В результате решения системы уравнений определяем искомые величины для сложной электрической цепи (например, все токи при заданных значениях ЭДС источников Е и сопротивлений резисторов R). Если в результате расчета какие-либо токи получаются отрицательными, это указывает на то, что их направление противоположно выбранному.

Пример 2.3. Метод узловых и контурных уравнений

Рисунок 27

Составить необходимое и достаточное количество уравнений по законам Кирхгофа для определения всех токов в цепи (рисунок 27) методом узловых и контурных уравнений.

Решение. В рассматриваемой сложной цепи имеется 5 ветвей, а следовательно, и 5 различных токов, поэтому для расчета необходимо составить 5 уравнений, причем два уравнения по первому закону Кирхгофа (в цепи n=3 узловых точки А, Б и В) и три уравнения — по второму закону Кирхгофа (контур обходим по часовой стрелке и внутренним сопротивлением источников пренебрегаем, т. е. R₀=0). Составляем уравнения:

1) (для точки А)

2) (для точки Б)

3) (для контура А, а, Б)

4) (для контура А, Б, б, В)

5) (для контура А, В, в)

Обходим контуры по часовой стрелке.

2.4. Метод контурных токов

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления. Так для схемы (рисунок 28) необходимо составить и рассчитать систему, составленную из 7-ми уравнений (по законам Кирхгофа).

Рисунок 28

Ту же задачу можно рассчитать, составив и решив только 4 уравнения по 2-му закону Кирхгофа, если воспользоваться методом контурных токов.

Для этой цели в схеме выделим т независимых контура, в каждом из которых произвольно направим контурный ток (I_I, I_II, I_III, I_IV). Контурный ток — это расчетная величина, измерить которую невозможно. Как видно, отдельные ветви схемы входят в два смежных контура. Тогда действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров:

Для определения контурных токов составляем т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства) и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).

Таким образом, для схемы (рисунка 28) составляем 4 уравнения. Со знаком плюс записываются ЭДС и падения напряжения (по разные стороны знака равенства), действующие в направлении контурного тока, со знаком минус, направленные против контурного тока

Определив контурные токи, рассчитав систему уравнений, вычисляем действительные токи в рассматриваемой цепи.

Пример 2.4. Метод контурных токов

Рисунок 29

Определить токи на всех участках сложной цепи (рисунок 29), если Е₁= 130 В; Е₂=40 В; Е₃=100 В; R₁ = 1 Ом; R₂ = 4,5 Ом; R₃==2 Ом; R₄=4 Ом; R₅ = 10 Ом; R₆ = 5 Ом; R₀₂=0,5 0м» R₀₁ = R₀₃ = О Ом.

Решение. Составляем три уравнения по второму закону Кирхгофа для определения контурных токов I_I, I_II ,I_III (направление контурных токов вsбрано произвольно)

Подставляем числовые значения данных величин:

Из уравнения 2 определяем ток I_I:

Подставляем его значение в уравнение 1:

Подставляем ток I_I в уравнение 3:

Из уравнения 3 вычтем уравнение 1:

Из уравнения 3 определим контурный ток I_III:

Тогда (из уравнения 2) получим:

Найдём реальные токи в заданной цепи:

Проверим правильность решения для 1го контура:

Решение правильное.

Вопросы к контрольной работе №1.

Вариант 1

1. Статические характеристики ЭТМ: пределы прочности при растяжении, сжатии и изгибе. Стандартные образцы, устройства и способы испытаний.

2. Определения, классификация и назначение методов и средств измерений.

Вариант 2

1. Электропроводность, факторы, влияющие на проводимость Удельное сопротивление. Единицы измерения. Температурный коэффициент удельного сопротивления и его физический смысл. Диэлектрическая проницаемость (ε). Тангенс угла диэлектрических потерь (tg δ).

2. Погрешности. Классификация погрешностей; причины их возникновения, способы обнаружения и пути устранения.

Вариант 3

1. Металлы и сплавы, применение в припоях. Маркировка припоев. Условия и факторы, влияющие на выбор марки припоя.

2. Устройство, типовые детали и узлы показывающих электроизмерительных приборов.

Вариант 4

1. Электрическая прочность диэлектриков. Способы и устройства для испытаний на электрическую прочность.

2. Принцип действия, устройство и область применения измерительных механизмов и приборов магнитоэлектрической, системы.

Вариант 5

1. Тепловые характеристики ЭТМ: температура плавления, вспышки и размягчение материалов, теплостойкость, морозостойкость, стойкость к термоударам, температурные коэффициенты.

2. Принцип действия, устройство и область применения измерительных механизмов и приборов электромагнитной, системы.

Вариант 6

1. Физико-химические характеристики: кислотное число, вязкость, влагостойкость, химическая стойкость, тропикостойкость, радиационная стойкость материалов.

2. Принципы действия, устройство, схемы включения и область применения измерительных механизмов и приборов электродинамической систем.

Вариант 7

1. Проводниковая медь. Получение меди. Физические, механические и электрические свойства меди. Мягкая медь. Твёрдая медь. Марки меди по ГОСТу. Применение меди.

2. Принципы действия, устройство, схемы включения и область применения измерительных механизмов и приборов ферродинамической системы.

Вариант 8

1. Определение контакта. Неподвижные, разрывные и скользящие контакты, их устройство. Требования, предъявляемые к контактным материалам.

2. Принципы действия, устройство, схемы включения и область применения измерительных механизмов и приборов индукционной системы.

Вариант 9

1. Сплавы высокого сопротивления: манганин, константан, нихром, фехраль. Их свойства, марки по ГОСТу и применение.

2. Магнитоэлектрические измерительные механизмы с преобразователями: термоэлектрические приборы, выпрямительные приборы, вибрационные и логометрические.

Вариант 10

1. Тугоплавкие материалы вольфрам и молибден, их свойства и применение.

2. Динамические характеристики ЭТМ: вибропрочность и ударная вязкость. Стандартные образцы, устройства и способы испытаний.

КОНТРОЛЬНАЯ РАБОТА №2

Задача 1.

12Следующая ⇒
Читайте также:

Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
Вернемся к основам. Ниже приведены простые формулы для расчета электроэнергии для однофазной цепи переменного тока, трехфазной цепи переменного тока и цепи постоянного тока. Вы можете легко найти электрическую мощность в ваттах, используя следующие формулы электрической мощности в электрических цепях .
Содержание
Основная формула электрической мощности в цепях переменного и постоянного тока
Формулы мощности в цепях постоянного тока
P = V x I
P = I ² x R
Р = В ² / Р
Формулы мощности в однофазных цепях переменного тока
P = V x I x Cos Ф
P = I ² x R x Cos Ф
P = В ² / R (Cos Ф)
Формулы мощности в трехфазных цепях переменного тока
P = √3 x V _L x I _L x Cos Ф
P = 3 x V _Ph x I _Ph x Cos Ф
P = 3 x I ² x R x Cos Ф
P = 3 (V ²/R) x Cos Ф
Где:
P = мощность в ваттах
В = напряжение в вольтах
I = ток в амперах
R = сопротивление в омах (Ом)
Cos Ф = Коэффициент мощности
Формулы мощности переменного тока в сложных цепях:
Комплексная мощность и полная мощность:
Когда в цепи есть катушка индуктивности или конденсатор, мощность становится комплексной мощностью «S» , что означает, что она состоит из двух частей, т. и мнимая часть. Величина Комплексной мощности называется Полная мощность |S|.

Где
P — реальная мощность
Q — реактивная мощность
Активная или активная мощность и реактивная мощность:
Действительная часть представляет собой комплексную мощность «S», известную как активную или действительную мощность «P» , а мнимую часть известную как реактивную мощность «Q».
S = P + jQ
P = V I cosθ
Q = V I sinθ
Где
θ — фазовый угол между напряжением и током.
Коэффициент мощности:
Коэффициент мощности «PF» — это отношение активной мощности «P» к полной мощности «|S|» . Математически коэффициент мощности представляет собой косинус угла θ между реальной мощностью и кажущейся мощностью.

Где
|S| = √ (стр. ² +Q ²)
Другие формулы, используемые для коэффициента мощности:
Cosθ = R/Z
Где:
Cosθ = коэффициент мощности
2
R = Сопротивление
Z = импеданс (сопротивление в цепях переменного тока, т.е. X _L , X _C и R , известные как Индуктивное реактивное сопротивление , Емкостное реактивное сопротивление и Сопротивление соответственно).
Cosθ = кВт/кВА
Где
Cosθ = коэффициент мощности
кВт = реальная мощность в ваттах
кВА = полная мощность в вольт-амперах или ваттах
Дополнительные формулы, используемые для коэффициента мощности.
Cosθ = P / V I
Cosθ = кВт/кВА
Cosθ = Истинная мощность/Полная мощность
Активная мощность однофазного и трехфазного тока
Где
В _{среднеквадратичное значение} & I _{среднеквадратичное значение} – среднеквадратичное значение напряжения и тока соответственно.
В _L-N и I _L-N — это фазное напряжение и ток соответственно.
В _L-L и I _L-L — линейное напряжение и ток соответственно.
Cosθ – коэффициент мощности PF.
Реактивная мощность однофазного и трехфазного тока:
Где
θ = фазовый угол, т.е. разность фаз между напряжением и током.
В следующей таблице показаны различные формулы электрической мощности в цепях переменного и постоянного тока.
Количество DC Переменный ток (1 фаза) Переменный ток (3 фазы)
Мощность
(Ш)
Р = В х I
P = I ² х R
Р = В ² / Р
P = V x I x Cos Ф
P = I ² x R x Cos Ф
P = В ² / R (Cos Ф)
P = √3 x V _L x I _L x Cos Ф
P = 3 x V _Ph x I _Ph x Cos Ф
P = 3 x I ² x R x Cos Ф
P = 3 (V ² / R) x Cos Ф
Связанные формулы и уравнения Посты:
Основные формулы и уравнения электротехники
Основные формулы электрических величин
Формулы и уравнения в области электротехники и электроники
Показать полную статью
Связанные статьи
Кнопка «Вернуться к началу»
Учебник по физике: комбинированные цепи
Ранее в уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательных соединений или посредством параллельных соединений. Когда все устройства в цепи соединены последовательным соединением, тогда цепь называется последовательной цепью. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательных и параллельных соединений в цепи; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательных, так и параллельных соединений в одной и той же цепи. В этом случае лампочки А и В соединены параллельным соединением, а лампочки С и D — последовательно. это пример комбинированная схема .
При анализе комбинированных цепей крайне важно хорошо понимать концепции, относящиеся как к последовательным, так и к параллельным цепям. Поскольку в комбинированных схемах используются оба типа соединений, понятия, связанные с обоими типами цепей, применимы к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии
Ток одинаков во всех резисторах; этот ток равен току в батарее.
Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи.
Общее сопротивление набора резисторов равно сумме значений отдельных сопротивлений,
Р _до = Р ₁ + Р ₂ + Р ₃ + … Параллельные цепи
Падение напряжения одинаково на каждой параллельной ветви.
Сумма токов в каждой отдельной ветви равна току вне ветвей.
Эквивалентное или общее сопротивление набора резисторов определяется уравнением 1/R _экв. = 1/R ₁ + 1/р ₂ + 1/р ₃ . ..
Каждое из приведенных выше понятий имеет математическое выражение. Сочетание математических выражений вышеприведенных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной цепи.
Анализ комбинированных цепей
Основная стратегия анализа комбинированных цепей включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной цепи в последовательную. После преобразования в последовательную цепь анализ можно проводить обычным образом. Ранее в Уроке 4 метод определения эквивалентного сопротивления параллельных ветвей равен, тогда общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
This method is consistent with the formula

1 / R _eq = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ + . ..
где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, то необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе урока 4.
Применяя понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную цепь можно преобразовать в последовательную цепь. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения полного сопротивления цепи. Рассмотрим следующие диаграммы ниже. На схеме А представлена комбинированная схема с резисторами R ₂ и R ₃, размещенными в параллельных ветвях. Два резистора по 4 Ом, соединенные параллельно, эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы соединены последовательно, можно использовать формулу для полного сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления равна
R _tot = R ₁ + R ₂ + R ₃ + …
Таким образом, на диаграмме B полное сопротивление цепи равно 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже двумя примерами.
Пример 1:
Первый пример — самый простой случай — параллельно расположенные резисторы имеют одинаковое сопротивление. Целью анализа является определение тока на входе и падения напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательных резистора на 8 Ом эквивалентны одному резистору на 4 Ом. Таким образом, два ветвящихся резистора (R ₂ и R ₃) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор на 4 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление равно
Ом.0394 R _to = R ₁ + 4 Ом + R ₄ = 5 Ом + 4 Ом + 6 Ом
R _to = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
I _tot = ΔV _tot / R _tot = (60 В) / (15 Ом)
я _до = 4 ампера
Расчет тока 4 А представляет собой ток в месте расположения батареи. Но резисторы R ₁ и R ₄ включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
I _tot = I ₁ = I ₄ = 4 А
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я ₂ + I ₃ должен равняться 4 Ампер. Существует бесконечное число возможных значений I ₂ и I ₃, которые удовлетворяют этому уравнению. Поскольку значения сопротивлений равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 Ампер.
I ₂ = I ₃ = 2 А
Теперь, когда ток в каждом отдельном резисторе известен, уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждый резистор. Эти расчеты показаны ниже.
ΔV ₁ = I ₁ • R ₁ = (4 А) • (5 Ом)
ΔV ₁ = 20 В
ΔV ₂ = I ₂ • R ₂ = (2 А) • (8 Ом)
ΔV ₂ = 16 В
ΔV ₃ = I ₃ • R ₃ = (2 А) • (8 Ом)
ΔV ₃ = 16 В
ΔV ₄ = I ₄ • R ₄ = (4 А) • (6 Ом)
ΔV ₄ = 24 В

Теперь анализ завершен, и результаты представлены на диаграмме ниже.

Пример 2:
Второй пример представляет собой более сложный случай — параллельно расположенные резисторы имеют разное значение сопротивления. Цель анализа та же — определить ток на входе и падение напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить по обычной формуле для эквивалентного сопротивления параллельных ветвей: 2 + 1/R ₃ …
1 / R _eq = 1 / (4 Ом) + 1 / (12 Ом)
1 / R _экв. = 0,333 Ом ^-1
R _экв. = 1 / (0,333 Ом ^-1 )
R _экв. = 3,00 Ом
На основании этого расчета можно сказать, что два ответвленных резистора (R ₂ и R ₃ ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор на 3 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление равно
R _to = R ₁ + 3 Ом + R ₄ = 5 Ом + 3 Ом + 8 Ом
Ч _до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
I _to = ΔV _to / R _to = (24 В) / (16 Ом)
I _to = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Но резисторы R ₁ и R ₄ включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
I _tot = I ₁ = I ₄ = 1,5 А
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я ₂ + I ₃ должен равняться 1,5 Ампер. Существует бесконечное множество значений I ₂ и I ₃, которые удовлетворяют этому уравнению. В предыдущем примере два резистора, включенных параллельно, имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями. В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Определение величины тока потребует использования уравнения закона Ома. Но чтобы его использовать, нужно сначала знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от направления в более простом случае, показанном в предыдущем примере.
Для определения падения напряжения на параллельных ветвях сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R ₁ и R ₄ ). Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV ₁ = I ₁ • R ₁ = (1,5 А) • (5 Ом)
ΔV ₁ = 7,5 В
ΔВ ₄ = I ₄ • R ₄ = (1,5 А) • (8 Ом)
ΔV ₄ = 12 В
Эта схема питается от источника 24 В. Таким образом, кумулятивное падение напряжения заряда, пересекающего петлю цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R ₁ и R ₄). Падение напряжения на ветвях должно составлять 4,5 вольта, чтобы компенсировать разницу между 24 вольтами и 19 вольтами.Падение 0,5 В на R ₁ и R ₄ . Таким образом,
ΔV ₂ = V ₃ = 4,5 В
Зная падение напряжения на параллельно соединенных резисторах (R ₁ и R ₄ ), можно использовать уравнение (Ом) ΔV = I • R) для определения тока в двух ветвях.

I ₂ = ΔV ₂ / R ₂ = (4,5 В) / (4 Ом)
I ₂ = 1,125 А 906:00
I ₃ = ΔV ₃ / R ₃ = (4,5 В) / (12 Ом)
I ₃ = 0,375 А
Теперь анализ завершен, и результаты представлены на диаграмме ниже.

Разработка стратегии
Два приведенных выше примера иллюстрируют эффективную концептуальную стратегию анализа комбинационных цепей. Подход требовал твердого понимания последовательностей и параллельных концепций, обсуждавшихся ранее. Такие анализы часто проводятся для решения физической задачи для заданного неизвестного. В таких ситуациях неизвестность обычно варьируется от проблемы к проблеме. В одной задаче номиналы резисторов могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче можно указать ток в батарее и несколько номиналов резисторов, а неизвестная величина станет сопротивлением одного из резисторов. Различные проблемные ситуации, очевидно, потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум вышеприведенным примерам проблем.
Начинающему ученику предлагаются следующие рекомендации по решению задач комбинированной схемы:
Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте схематические символы, подобные показанным в примере выше.
Приступая к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записывая известные значения и приравнивая их к символу, такому как I _tot , I ₁ , R ₃ , ΔV ₂ и т. д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
Знать и использовать соответствующие формулы эквивалентного сопротивления последовательно и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
Превратите комбинированную цепь в строго последовательную, заменив (мысленно) параллельную часть одним резистором, сопротивление которого равно эквивалентному сопротивлению параллельной части.
Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будут определены с помощью этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при расчете I ₂ важно подставить в уравнение значения ΔV ₂ и R ₂.
Для дальнейшей практики анализа комбинированных цепей рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.

Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).

Посетите: DC Circuit Builder

Проверьте свое понимание
1. Комбинированная схема показана на схеме справа. Используя схему, ответьте на следующие вопросы.
а. Ток в точке А равен _____ (больше, равно, меньше) току в точке В.
b. Ток в точке B равен _____ (больше, равно, меньше) току в точке E.
с. Ток в точке G равен _____ (больше, равно, меньше) току в точке F.
d. Ток в точке E равен _____ (больше, равно, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равно, меньше) току в точке F.
f. Ток в точке А равен _____ (больше, равно, меньше) току в точке L.
g. Ток в точке H равен _____ (больше, равно, меньше) тока в точке I.

2. Рассмотрим комбинированную цепь на схеме справа. Используя схему, ответьте на следующие вопросы. (Считать, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
b. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
с. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
d. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A равна _____ (больше, равно, меньше) разности электрических потенциалов (падению напряжения) между точками B и K.

3. Используйте понятие эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.

4. Проанализируйте следующую цепь и определите значения полного сопротивления, полного тока, а также падения тока и напряжения на каждом отдельном резисторе.

5. По схеме вопроса №4 определите …
а. … номинальная мощность резистора 4.
б. … скорость, с которой энергия потребляется резистором 3.

Последовательная цепь постоянного тока — инженерное мышление
Изучите основные принципы последовательной цепи постоянного тока, от напряжения, тока, сопротивления и потребляемой мощности до использования мультиметра. В конце вам также предстоит решить задачу с ответами.
Прокрутите вниз, чтобы посмотреть обучающее видео на YouTube.
Помните, что электричество опасно и может привести к летальному исходу, вы должны иметь квалификацию и компетентность для выполнения любых электромонтажных работ.
Что такое последовательная цепь постоянного тока?
Когда мы соединяем компоненты в электрическую цепь, мы можем соединять их либо последовательно, либо параллельно, или мы можем комбинировать их для создания последовательно-параллельной цепи. В этой статье подробно описывается тип серии, который является самым основным, мы рассмотрим другие типы в других статьях, которые вы можете прочитать ЗДЕСЬ .
Если мы поместим два компонента в линию, конец к концу или с каким-либо проводом между ними, то они будут соединены последовательно. У электронов есть только один путь, по которому они могут пройти, поэтому все они будут проходить через каждый из компонентов.

через GIPHY
Просто отметим, что в этих анимациях мы используем поток электронов от отрицательного к положительному. Возможно, вы привыкли видеть обычный ток, который меняется от положительного к отрицательному. Электронный поток — это то, что происходит на самом деле, первоначальная теория была традиционной, но ее все еще учат, потому что ее легко понять. Просто знайте о двух и о том, какой из них мы используем.
Сопротивление в последовательных цепях
Каждый компонент будет иметь определенное сопротивление, сопротивление противодействует приложенному напряжению. Мы измеряем сопротивление в единицах Ом с символом Ом Ω.
В последовательных цепях; мы находим полное сопротивление цепи, просто складывая все сопротивления вместе. Мы маркируем каждый резистор заглавной буквой R и нумеруем их R1, R2, R3 и т. д.
Общее сопротивление отображается с заглавной буквы R и нижним индексом T, который представляет общее сопротивление или общее сопротивление.
Рассчитать общее сопротивление последовательной цепи очень просто, мы просто складываем значение сопротивления каждого резистора.
Допустим, у нас есть цепь с одним резистором, это наш R1, и он имеет значение 10 Ом. Каково наше общее сопротивление? Ну это просто, полное сопротивление 10 Ом.
Если затем добавить в цепь второй резистор R2 с сопротивлением 5 Ом, общее сопротивление составит 15 Ом, 10 Ом + 5 Ом.
Если мы добавим еще один резистор на 5 Ом, то общее сопротивление составит 20 Ом.
На самом деле провода тоже будут добавлять некоторое сопротивление, но оно очень мало, вам, возможно, придется учитывать это в зависимости от того, насколько точным должен быть ваш проект.
Ток в серии
Ток — это поток электронов. Это как вода, которая течет по трубе. Чем больше ток, тем больше электронов течет. Мы измеряем ток в амперах, но инженеры склонны сокращать их до ампер. Обозначается заглавной буквой А.
Мы подробно рассмотрели ток в нашей предыдущей статье, посмотрите ЗДЕСЬ .
Мы измеряем ток, помещая амперметр в цепь, через которую проходят электроны. Это похоже на счетчик воды в том смысле, что через него должна пройти вода, чтобы мы могли ее измерить. Мы можем подключить мультиметр к цепи, чтобы также измерить ток.
Мультиметр должен быть подключен к цепи для снятия показаний, через него будет протекать ток. Измеритель добавит некоторое сопротивление в цепь, но это настолько мало, что мы обычно можем его игнорировать.
Если у вас еще нет мультиметра, мы настоятельно рекомендуем вам его приобрести, он необходим для устранения неполадок и улучшения вашего понимания. Купить их можно по ссылке ниже.
Мы можем рассчитать общий ток цепи, разделив напряжение на сопротивление.
Если мы подключим резистор 10 Ом к батарее 9 В, 9 В ÷ 10 Ом даст нам 0,9 А.
Если мы добавим в цепь еще один резистор на 5 Ом, это даст нам сопротивление 15 Ом, поэтому 9 В ÷ 15 Ом = 0,6 А.
Затем, если мы добавим еще один резистор на 5 Ом, это даст нам сопротивление 20 Ом, поэтому
9 В ÷ 20 Ом = 0,45 А.
Мы видим, что по мере того, как мы увеличиваем сопротивление цепи, ток уменьшается, поэтому проходит меньше электронов, а это означает, что мы можем выполнять меньше работы. Мы можем визуализировать это, соединив светодиод с резистором в цепи. Чем выше сопротивление; тем тусклее будет светодиод.
Мы также можем использовать резисторы для защиты компонентов в цепи. Если мы используем резистор 100 Ом с сопротивлением 9V, ток будет около 0,09 А или 90 мА, и это приведет к перегоранию светодиода. Если мы используем резистор 450 Ом; ток будет около 0,02 А или 20 мА, поэтому светодиод должен быть в порядке. Если мы используем резистор 900 Ом, ток будет 0,01 А или 10 мА, а светодиод будет очень тусклым.
В последовательной цепи; ток одинаков во всей цепи. Это важно помнить. Как подробно описано ниже; если мы поместим счетчик в любое место, мы получим одно и то же показание. Это потому, что электроны могут течь только по одному пути, и все они движутся вместе в одном и том же направлении, поэтому
ток должен быть одинаковым. Неважно, где мы измеряем или где размещаем резистор, даже если мы поменяем порядок резисторов, ток будет одинаковым в любом месте последовательной цепи.
Последовательное напряжение
Помните, что напряжение — это сила, выталкивающая электроны, это как давление в трубе. Чем выше давление; чем больше воды может протекать, тем выше напряжение; тем больше электронов может течь. Мы можем видеть, что, изменяя напряжение на лампе, как показано ниже, яркость лампы увеличивается по мере увеличения напряжения.
Если мы поместим в цепь батарею на 9 В, мы подадим на цепь напряжение 9 В. Мы можем увеличить это, соединив батареи последовательно.
Итак, если мы поместим две батареи 9 в цепь последовательно, мы получим 18 В, три батареи 9 В дадут нам 27 В.
Возьмем 9-вольтовую батарею и добавим в цепь резистор R1 сопротивлением 10 Ом. Если мы используем мультиметр для измерения резистора, мы получим показание напряжения 9 В. Если мы добавим еще один резистор 10 Ом, мы получим показание 9 В на двух резисторах, но мы получим показание 4,5 В, если мы будем измерять на любом из резисторов по отдельности. Таким образом, резисторы делят напряжение.
Если мы заменим резистор R2 резистором 5 Ом, общее напряжение снова будет 9 В, и это то, что мы увидим, если измерим два резистора. Но если мы измерим на резисторе 10 Ом, мы увидим напряжение 6 В, а если мы измерим на резисторе 5 Ом, мы увидим 3 В.
Если мы добавим в цепь еще один резистор R3 с сопротивлением 5 Ом, мы снова получим общее падение напряжения на 3 резисторах 9 В. На резисторе R1 10 Ом читаем 4,5 В, на резисторе R2 5 Ом читаем 2,25 В, а на последнем резисторе R3 5 Ом снова 2,25 В.
Мы можем объединить эти показания, чтобы найти напряжение на разных участках цепи. Например, если мы измеряем от батареи и через R1, мы видим 4,5 В. Если мы измерим от батареи между R1 и R2, мы получим 6,75 В, потому что 4,5 В + 2,25 В.
Таким образом, в отличие от тока, где он одинаков во всей цепи, напряжение будет разным во всей последовательной цепи.

через GIPHY
Это показывает нам, что напряжение уменьшается с каждым резистором, поэтому резистор создает падение напряжения. Это цель резистора, чтобы уменьшить напряжение или давление. Происходит то, что резистор создает более трудный путь для прохождения электронов, и по мере прохождения они будут сталкиваться с другими электронами. Это столкновение преобразует энергию в тепло. Столько же
электронов будут входить и выходить из резистора, у них просто будет меньше энергии или давления, поэтому произойдет падение напряжения.
Расчет падения напряжения
Мы можем рассчитать падение напряжения на каждом резисторе отдельно, умножив общий ток в цепи на сопротивление компонента. Помните, что в последовательных цепях ток везде одинаков. Общее падение напряжения будет суммой всех отдельных падений напряжения вместе взятых.
Первая схема, там был резистор 10 Ом сам по себе. В цепи был ток 0,9Таким образом, 0,9 А х 10 Ом = 9 В. Таким образом, падение напряжения на резисторе равно 9 В, как и на источнике напряжения.
Во второй цепи резисторы 10 Ом и 5 Ом вместе, и ток в этой цепи равен 0,6 А, поэтому падение напряжения на первом резисторе составляет 0,6 А x 10 Ом = 6 В, на втором резисторе 5 Ом, а ток было то же самое, поэтому 0,6 А x 5 Ом = 3 В. Общее падение напряжения составляет 6В + 3В = 9В.
Третья цепь имеет резисторы на 10 Ом и два резистора на 5 Ом, ток в цепи равен 0,45 А, поэтому R1 равен 0,45 А x 10 Ом = 4,5 В, R2 и R3 будут равны 0,45 А x 5 Ом = 2,25 В.
Таким образом, общее падение напряжения составляет 9 В (4,5 В + 2,25 В + 2,25 В).
Потребляемая мощность
Как измерить энергопотребление схемы? Мы можем использовать следующие уравнения:
Либо
Мощность (Вт) = Напряжение ² / Сопротивление
Или
Мощность (Вт) = Напряжение x Ток.
Вам может быть интересно, как резистор может потреблять энергию? Поскольку резистор создает падение напряжения, электроны теряют часть энергии. Куда уходит эта энергия? Электрическая энергия преобразуется в тепло, которое, глядя на некоторые резисторы под тепловизионной камерой, можно увидеть выделяющееся тепло.
Таким образом, потребляемая мощность фактически представляет собой тепло, отводимое от схемы.
В этой цепи сопротивление составляет 10 Ом, батарея обеспечивает 9 В, ток составляет 0,9 А, а схема потребляет 8,1 Вт. Как мы это вычисляем? Используя метод 1, 9 В в квадрате или 9, умноженное на 9, составляет 81, ÷ на 10 Ом составляет 8,1 Вт. В качестве альтернативы 9 В x 0,9 А = 8,1 Вт
В следующей цепи с резистором 10 Ом и резистором 5 Ом общее сопротивление было 15 Ом, а ток 0,6 А, поэтому
9 В в квадрате равно 81, деленное на 15 Ом, составляет 5,4 Вт
или 9 В x 0,6 А = 5,4 Вт.
В цепи с резисторами 10 Ом и двумя резисторами 5 Ом общее сопротивление цепи составило 20 Ом, а ток 0,45 А, поэтому
9 В в квадрате равно 81, деленное на 20 Ом, равно 4,05 Вт
или 9 В x 0,45 А = 4,05 Вт
Проблема: светодиод подключен к батарее 9 В, и ток в цепи должен быть ограничен максимальным значением 0,02 А или 20 мА, иначе светодиод перегорит. Если мы подключимся к этим резисторам, какой будет примерный ток в цепи и не сгорит ли светодиод?
Ответ: Сначала нам нужно рассчитать общее сопротивление цепи. Мы делаем это, складывая все номиналы резисторов.
100+15+30+310+5 = сопротивление 460 Ом
Теперь рассчитаем ток, разделив напряжение цепи на сопротивление.
9 В ÷ 460 Ом = 0,0195 А
Это меньше нашего максимума 0,02 А, так что все должно быть в порядке.

Что такое цепь постоянного тока
Цепь постоянного тока или цепь постоянного тока — это цепь, имеющая одно направление напряжения и тока. Чтобы быть более конкретным, эта цепь имеет только одно направление или однонаправленный поток электрического заряда. Одним из простейших примеров постоянного напряжения является батарея.
Если DC — это сокращение от «Постоянный ток», то AC — это сокращение от «Переменный ток». Идея «прямого» или «переменного» — это «направление» их потока зарядов.
Основы теории постоянного тока
Если кто-то попросит вас дать определение цепи постоянного тока, можете ли вы дать свое лучшее и самое простое объяснение? Из некоторой литературы, книг или журналов они могут дать вам наиболее полное объяснение. Но нам почему-то достаточно узнать о них самое простое определение и сразу перейти к анализу схемы.
Как следует из названия, Direct Current означает, что он использует только одно направление. Здесь мы знаем еще одно важное слово, и это «полярность». Полярность указывает «направление» точно так же, как нам нужно знать перед анализом электрической цепи.
Цепь постоянного тока — это цепь, имеющая только одну полярность, одно направление напряжения или тока. Эта схема имеет постоянное значение, нулевую частоту или медленно почти не меняющееся среднее значение напряжения или тока.
Другое объяснение:
Источник постоянного напряжения всегда имеет постоянное напряжение.
Через источник постоянного тока всегда проходит постоянный ток.
В заключение, цепь постоянного тока – это цепь, в которой напряжение и ток в каждой части цепи имеют постоянное значение.
Возможно, вас смущает мысль, что аббревиатура постоянного тока — постоянный ток. Вот почему DC также относится к « постоянной полярности ». Цепь постоянного тока может иметь переменное напряжение, но она не будет пересекать отрицательную полярность или наоборот, как показано на графике напряжения выпрямителя ниже.
Выше приведен общий график цепи постоянного тока, где он никогда не пересекает другую полярность.
Что такое цепь постоянного тока
Цепь постоянного тока представляет собой электрическую цепь, состоящую только из
источников постоянного напряжения и/или тока,
резистивных нагрузок (резисторов).
Эта цепь не зависит от времени. Если цепи не нужны какие-либо прошлые значения ее напряжения и тока, мы можем предположить, что цепь является цепью постоянного тока.
Ему не нужно его прошлое значение, поэтому он не использует никаких сложных вычислений, состоящих из изменяющегося во времени, переходного периода или чего-то подобного.
Нам нужно только проанализировать его расчет в стационарном режиме, конечно, с решением для постоянного тока.
Имейте в виду, что не каждую электрическую цепь можно решить с помощью решения постоянного тока. Приготовьтесь использовать другое решение, если в схеме есть индуктивная (индуктор) и емкостная (конденсатор) нагрузки.
Кроме того, безопасно называть цепь цепью постоянного тока, если она питается от источников постоянного тока (батареи или источника постоянного тока).
Применение цепи постоянного тока
Постоянный ток обычно используется в приложениях сверхнизкого и низкого напряжения, особенно для аккумуляторов и солнечных элементов. Большинству наших электронных устройств также требуется постоянное напряжение и источник питания постоянного тока.
Имейте в виду, что когда мы используем электрические устройства постоянного тока, мы должны обращать внимание на полярность, иначе вы ее нарушите. Даже если ваши устройства имеют элемент диодного моста, все же разумно подключить правильную полярность.
Существует также много применений постоянного напряжения в автомобильной промышленности.
Возьмем, к примеру, разрабатываемые электромобили, они используют батареи, что означает постоянное напряжение. В дизельных двигателях тяжелых транспортных средств, грузовиков, сельскохозяйственной техники и т. д. также используются системы постоянного напряжения.
Источники питания постоянного тока также используются в телекоммуникационных технологиях.
Этот источник питания будет поддерживать линии связи для абонентов, если во время работы возникнут перебои. Преобразователь постоянного тока также популярен в качестве источника питания для устройств связи.
Для повышения эффективности передачи энергии высокого напряжения используется электричество постоянного тока. Это связано с тем, что при передаче на большие расстояния потери от высокого напряжения постоянного тока (HVDC) ниже и дешевле.
Простая электрическая цепь постоянного тока
Электрическая цепь постоянного тока, в которой электрический заряд течет от более высокого потенциала к более низкому. Вот почему символ источника постоянного напряжения или батареи имеет обозначение высокого и низкого потенциала.
Символ выше обозначает общий источник постоянного напряжения, где:
Более высокий потенциал представлен положительным символом
Более низкий потенциал представлен отрицательным символом
Символом выше является батарея, где:
Более длинная линия с положительным символом представляет более высокий потенциал.
Более короткая линия представляет более низкий потенциал.
Двигаясь дальше, давайте перейдем к приведенной ниже простой электрической схеме постоянного тока. Мы будем использовать фонарик, чтобы сделать простую электрическую схему постоянного тока.
Из диаграммы выше мы можем заключить, что нашими частями простой электрической цепи постоянного тока на этот раз являются:
Батарея,
Выключатель и
Лампочка.
Следующим нашим вопросом будет «как загорится лампочка в простой цепи постоянного тока». Это очень просто, потому что если у него нет выключателя, лампочка всегда будет гореть, пока батарея не высохнет.
Эта простая схема лампочки может показать нам, как ведет себя цепь постоянного тока, когда к цепи приложен постоянный ток или постоянное напряжение.
Есть два условия:
Когда выключатель замкнут, ток течет к лампочке и включает ее.
Когда выключатель разомкнут, ток не течет к лампочке и выключает ее.
Конечно, только эту схему можно улучшить для повышения безопасности, потому что мы подключаем батарею к лампочке только с помощью проводника. Имейте в виду, что каждое электрическое устройство, элементы и компоненты имеют пороговые значения как для напряжения, так и для тока.
Перегрузка по току в цепи приведет к перегоранию лампочки, и вам нужно купить другую.
Вспоминая, как мы изучаем закон Ома, мы можем применить его здесь.
Использование

Мы можем уменьшить ток, увеличив сопротивление или уменьшив напряжение.
Вы можете забыть о снижении напряжения, потому что мы используем аккумулятор с фиксированным значением напряжения. Затем мы можем только добавить резистор, чтобы уменьшить или ограничить ток, протекающий через лампочку.
Вот как сделать собственную простую цепь постоянного тока.
Пример анализа цепи постоянного тока
Что такое цепь постоянного тока и в каком направлении она течет?
Дочитав до этого места, вы должны были ответить себе на этот вопрос. Просто понаблюдайте за цепью постоянного тока в течение секунды, и вы узнаете направление тока. Наш следующий фокус:
Сколько тока течет в этом направлении?
Чтобы ответить на этот вопрос, мы будем использовать последовательную цепь постоянного тока, как показано ниже:
Протекание тока цепи постоянного тока обозначается буквой I вместе с направлением стрелки. Напряжение в цепи постоянного тока представлено V.
Мы можем предположить, что V — это батарея, тогда R1 и R2 могут быть любыми резистивными нагрузками, такими как лампочки.
Поскольку существует только один путь тока, ток будет одинаковым во всех точках цепи. Или мы можем записать это в математическом выражении:

Напряжение в цепи постоянного тока представляет собой сумму падений напряжения на элементах цепи. В этом случае напряжение источника V равно сумме падений напряжения на резисторах R1 и R2.
Следовательно, мы можем преобразовать его в математическое уравнение:

Получив эти два уравнения, мы можем свободно использовать закон Ома, чтобы найти нужную переменную.
Используя закон Ома:

Таким образом,

Мы ограничимся последовательной цепью постоянного тока и не будем продолжать параллельную цепь постоянного тока.
Теория и законы цепи постоянного тока
Чтобы полностью понять электрическую цепь, обязательно прочитайте:
Электрическое напряжение,
Электрический ток и
Электроэнергия.
Не забудьте выучить:
Элементы электрической цепи,
Узлы, ответвления и петли,
Последовательный резистор и
Параллельный резистор.
При работе с простой цепью постоянного тока мы всегда можем использовать:
Закон Ома
Закон Кирхгофа
Кроме того, когда цепь становится все более сложной и сложной, вы начнете изучать и использовать методы анализа ниже:
Анализ узлов,
Анализ суперузлов,
Анализ сетки,
Анализ суперсети и
Преобразование звезды-дельты.
Иногда описанные выше методы анализа усложняют задачу многочисленными уравнениями, поэтому мы будем использовать приведенную ниже теорему анализа:
Суперпозиция,
Преобразование источника,
Теорема Тевенина,
Теорема Нортона о максимальной мощности и
передача.
Часто задаваемые вопросы
Что такое цепь постоянного тока?
Цепь постоянного тока — это цепь, которая имеет только одну полярность, одно направление напряжения или тока. Эта схема имеет постоянное значение, нулевую частоту или медленно почти не меняющееся среднее значение напряжения или тока.
Что является примером цепи постоянного тока?
Самый простой пример цепи постоянного тока — это фонарик, в котором мы подключаем только батарею, переключатель и лампочку или светодиод.
В какой стране используется постоянный ток?
Мы можем сказать, что каждая страна использует постоянный ток, если они все еще используют постоянное напряжение. Конечно, большинство электронных устройств, которые мы используем, также работают от электричества постоянного тока.
Анализ схемы для читфекта Dummies
BY: John Santiago и
Обновленный: 01-26-2022
Из книги: Анализ схемы для Dummies
Анализ схемы Dummies
. Купить на Амазоне
При анализе цепей вам необходимо знать некоторые основные законы, электрические величины, взаимосвязи и теоремы.
Закон Ома является ключевым уравнением устройства, которое связывает ток, напряжение и сопротивление. Используя законы Кирхгофа, вы можете упростить сеть резисторов, используя один эквивалентный резистор. Вы также можете выполнить такой же расчет, чтобы получить эквивалентную емкость и индуктивность для сети конденсаторов или катушек индуктивности.
Для более сложных схем могут пригодиться методы анализа узловых напряжений и тока сетки. А если вы хотите попробовать разные нагрузки для конкретной схемы источника, вы можете использовать эквивалент Тевенина или Нортона.
Три основных закона для работы со схемами
На самом базовом уровне анализ схем включает расчет тока и напряжения для конкретного устройства. Вот тут-то и появляются уравнения устройства и соединения. Уравнения устройства описывают взаимосвязь между напряжением и током для конкретного устройства.
Одним из наиболее важных уравнений устройства является закон Ома, который связывает ток (I) и напряжение (В) с использованием сопротивления (R) , , где R IS A Constant: V = IR или 4 I = V/R или 4 I = V/R или 4 I = V/R или 44.
Вам необходимо знать два уравнения связи: закон Кирхгофа для тока (KCL) и закон Кирхгофа для напряжения (KVL):
Электрические величины и единицы измерения
Определенные электрические величины, отношения и электрические единицы необходимо знать при анализе и характеристике поведения схемы. Следующая таблица поможет вам сохранить эту информацию в чистоте.
Эквивалентное сопротивление, емкость и индуктивность
При анализе цепей можно упростить сети, состоящие только из резисторов, конденсаторов или катушек индуктивности, заменив их одним эквивалентным устройством. Следующие уравнения показывают эквивалентные последовательные и параллельные соединения для комбинаций только резистора, только конденсатора и только катушки индуктивности.
Методы анализа сложных цепей
При работе со сложными цепями, такими как схемы с большим количеством петель и узлов, можно использовать несколько приемов, чтобы упростить анализ. Следующие методы анализа цепей пригодятся, когда вы хотите найти напряжение или ток для определенного устройства. Они также полезны, когда у вас есть много устройств, подключенных параллельно или последовательно, устройства, образующие петли, или несколько устройств, подключенных к определенному узлу.
Анализ напряжения узла: Узлы — это определенные точки в цепи. Когда к определенной точке подключено много устройств, вы можете сделать этот узел опорным узлом и думать о нем как о имеющем напряжение 0 В. Затем вы используете его в качестве опорной точки для измерения напряжения для определенного узла.
С помощью анализа узловых напряжений вы находите неизвестные узловые напряжения в цепи с помощью токового закона Кирхгофа. После нахождения узловых напряжений вы используете ток-напряжение ( i-v ) взаимосвязи, такие как закон Ома, для определения токов устройств и использование узловых напряжений для определения напряжений устройств.
Текущий анализ сетки: Сетка представляет собой петлю без устройств, заключенных в петлю, где границы сетки — это те устройства, которые образуют петлю. Анализ токов сетки позволяет находить неизвестные токи сетки в цепи с помощью закона напряжения Кирхгофа (KVL). Уравнения сетки представляют собой уравнения КВЛ с неизвестными токами сетки в качестве переменных. После нахождения токов сетки вы используете i – v отношения для определения напряжения устройства.
Суперпозиция: Для линейных цепей с независимыми источниками вы можете использовать суперпозицию, чтобы найти выходное напряжение и ток для конкретного устройства. Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника.
Эквиваленты Thévenin/Norton: Анализ цепи может стать утомительным, если вы пробуете разные нагрузки с одной и той же цепью источника. Чтобы избавить себя от работы, замените схему источника эквивалентами Тевенина и Нортона. Теорема Тевенина говорит, что вы можете заменить линейную сеть источников и резисторов между двумя терминалами одним независимым источником напряжения (V _T ) последовательно с одним резистором (R _T ) , and Norton’s theorem says you can replace the linear network of sources and resistors with one independent current source (I _N ) in parallel с одним резистором (R _N ) — см. следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткого замыкания), если они имеют одинаковые отношения напряжения и тока на клеммах.
Finding the Thévenin or Norton equivalent requires calculating the following variables: V _T = V _OC , I _N = I _SC , и R _T = R _N = 4 V 49445 = 4. V 4944444444.1444 /I _SC (где T означает Thévenin, OC означает нагрузку холостого хода, N означает нагрузку Norton, а 5 означает нагрузку короткого замыкания). Если вы хотите проанализировать различные нагрузки, подключенные последовательно к цепи источника, полезен эквивалент Тевенина; когда нагрузки подключены параллельно цепи источника, лучшим выбором будет аналог Norton. Два эквивалента связаны друг с другом преобразованием источника.
Об этой статье
Эта статья взята из книги:
Анализ схем для чайников,
Об авторе книги:
Джон М. Сантьяго-младший, доктор наук, служил в ВВС США (USAF). ) в течение 26 лет. В течение этого времени он занимал различные руководящие должности в области управления техническими программами, разработки приобретений и поддержки исследований в области эксплуатации. Находясь в Европе, он руководил более чем 40 международными научными и инженерными конференциями/семинарами.
Эту статью можно найти в категории:
Схема ,
Закон Кирхгофа для сложных цепей | ОРЕЛ
Закон Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша цепь более сложная? Вы можете проектировать электронику, которая имеет как параллельное, так и последовательное сопротивление, и закон Ома начинает нарушаться. Или что, если у вас нет источника постоянного тока? В этих ситуациях, когда вы не можете использовать только V = IR, пришло время встать на плечи Ома и использовать закон Кирхгофа. Здесь мы рассмотрим, что такое закон Кирхгофа о цепях и как его использовать для анализа напряжения и тока в сложных электрических цепях.
Что такое закон Кирхгофа?
Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться исключительно на закон Ома для определения напряжения или тока. Здесь пригодится закон Кирхгофа о цепях, который позволяет рассчитать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Есть два варианта закона Кирхгофа, в том числе:
Закон тока Кирхгофа: Для анализа полного тока сложной цепи
Закон Кирхгофа о напряжении : для анализа полного напряжения сложной цепи
Если объединить эти два закона, получится Закон Кирхгофа о цепях
Как и любой другой научный или математический закон, названный в честь его создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом. Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент в периодической таблице имеет свою уникальную длину волны. Открытие этой закономерности позволило дуэту открыть два новых элемента, цезий и рубидий.
Густав Кирхгоф (слева) и Роберт Бунзен (справа)
Позже Кирхгоф применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил много темных линий в солнечном спектре длин волн. Это было вызвано тем, что солнечный газ поглощал световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.
Чуть ближе к дому в мире электроники Кирхгоф объявил свой свод законов для анализа тока и напряжения для электрических цепей в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа основана на фундаменте, изложенном в законе Ома, и помогла проложить путь для анализа сложных цепей, на который мы полагаемся сегодня.
Первый закон – Текущий закон Кирхгофа
Закон тока Кирхгофа гласит, что количество тока, входящего в узел, равно количеству тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выйти. Вы можете определить узел, в котором два или более пути соединены через общую точку. На схеме это будет точка соединения, соединяющая два пересекающихся сетевых соединения.
Взгляните на изображение ниже, чтобы наглядно понять этот Закон. Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону токов Кирхгофа отношение между этими токами, входящими в узел и выходящими из узла, можно представить как I 1 + I 2 = I 3 + I 4 + I 9,1489
Закон тока Кирхгофа, ток на входе должен быть равен току на выходе. (Источник изображения)
Когда вы сбалансируете это уравнение как алгебраическое выражение, вы сделаете вывод, что ток, входящий в узел и выходящий из него, всегда будет равен 0, или 3 + -I 4 + -I 5 ) = 0 Все должно уравновеситься, и Кирхгоф назвал этот принцип Сохранение заряда .
Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже у нас есть схема с четырьмя узлами: A, C, E и F. Ток сначала течет от источника напряжения и разделяется в узле A, который затем течет через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы течь через резисторы R3, R4 и R5 , где он встречается с узлом E и узлом F.
(Источник изображения)
Чтобы подтвердить закон тока Кирхгофа в этой цепи, нам нужно предпринять следующие шаги:
Расчет полного тока цепи
Рассчитать ток, протекающий через каждый узел
Сравните входной и выходной токи в определенных узлах, чтобы подтвердить закон Кирхгофа о токе.
1. Расчет общего тока
Здесь мы используем закон Ома, чтобы получить общий ток нашей цепи с I = V/R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, соединенных параллельно, которое составляет:
Начиная с узла AC, мы получаем следующее сопротивление для параллельных резисторов R1 и R2:
И переходя к Node CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:
Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы затем можем подставить в закон Ома I = V/R , чтобы получить полный ток в нашей цепи:
2. Расчет узловых токов
Теперь, когда мы знаем, что из нашей цепи вытекает 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся законом Ома в виде I = V/R , чтобы получить ток для каждой ветви узла.
Во-первых, нам нужны напряжения для узловых ветвей AC и CF:
Затем мы можем рассчитать ток для каждой ветки узла:
3. Подтвердить действующий закон Кирхгофа
После расчета тока для каждой ветви узла у нас теперь есть две различные точки отсчета, которые мы можем использовать для сравнения наших входных и выходных токов. Это позволит нам проанализировать нашу схему и подтвердить закон тока Кирхгофа следующим образом:
Второй закон – закон напряжения Кирхгофа
Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром общее напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что падение напряжения происходит всякий раз, когда ток протекает через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Законом сохранения энергии . Опять же, то, что входит, должно выйти.
Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение будет встречаться с пассивной составляющей, что вызовет отчетливое падение напряжения.
Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:
Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает. В приведенном ниже примере у нас есть две известные переменные: общее напряжение и падение напряжения на резисторе R1.
(Источник изображения)
Что нам нужно вычислить, так это падение напряжения на R2, и мы можем использовать закон Кирхгофа о напряжении, чтобы вычислить это со следующим соотношением:
Поскольку общее падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления отсутствующей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:
Давайте посмотрим на другой пример. В схеме ниже у нас есть три резистора, соединенных последовательно с 12-вольтовой батареей.
Чтобы подтвердить закон Кирхгофа о напряжении в этой схеме, нам нужно предпринять следующие шаги:
Расчет полного сопротивления цепи
Рассчитать полный ток цепи
Рассчитать ток через каждый резистор
Рассчитайте падение напряжения на каждом резисторе
Сравните источник напряжения с полным падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении
1. Рассчитать общее сопротивление
Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:
2.
Рассчитать общий ток
Теперь, когда мы знаем наше общее сопротивление, мы можем снова использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V/R, , что выглядит так:
3. Рассчитайте ток через каждый резистор
Поскольку все наши резисторы соединены последовательно, через них будет протекать одинаковая величина тока, которую можно выразить следующим образом:
4. Рассчитайте падение напряжения на каждом резисторе
Наш окончательный расчет снова будет использовать закон Ома, чтобы дать нам общее падение напряжения для каждого резистора в виде В = IR , что выглядит следующим образом:
5. Проверка закона Кирхгофа о напряжении
Теперь у нас есть все необходимые данные, включая общее напряжение нашей схемы, а также каждое падение напряжения на каждом из наших резисторов. Собрав все это вместе, мы можем легко подтвердить закон Кирхгофа о напряжении с помощью этого соотношения:
Это также может быть выражено как:
Как видите, общее напряжение равно общему падению напряжения в нашей схеме. То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
Процесс использования закона Кирхгофа о цепях
Теперь, когда вы понимаете, как работает закон Кирхгофа о цепях, у вас есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих законов в дикой природе рассмотрите следующий пошаговый процесс:
Во-первых, начните с маркировки всех известных напряжений и сопротивлений в вашей цепи.
Затем назовите каждую ветвь вашей цепи текущей меткой, например I1, I2, I3 и т. д. Ветвь — это один или группа компонентов, соединенных между двумя узлами.
Затем найдите закон тока Кирхгофа для каждого узла в вашей цепи.
Затем найдите закон Кирхгофа для напряжения для каждого из независимых контуров вашей цепи.
После того, как вы вычислили законы тока и напряжения Кирхгофа, вы можете использовать ваши уравнения, чтобы найти недостающие токи. Готовы попробовать сами? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон Кирхгофа для тока и закон напряжения с небольшой помощью Ома!
Пишите свои ответы в комментариях ниже!
Стоя на плечах Ома
Имея в руках закон Кирхгофа о цепях, у вас теперь есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.
No related posts.

Задание №1 — Расчет сложной электрической цепи постоянного тока

1.

1.

Методы расчета сложных электрических цепей

Метод контурных токов

ДЗ — Расчёт сложной цепи постоянного тока

Расчет сложных электрических цепей постоянного тока

5. Густав Роберт Кирхгоф /1824г.-1887г./ Немецкий физик, внес огромный вклад в развитие математической физики и электричества.

11. Электрическая цепь

12. Зададим направление токов во всех ветвях цепи

13. Сложная электрическая цепь

15. Дайте формулировку I закону Кирхгофа

17.

19. Сложная электрическая цепь

20. II закон Кирхгофа

21. Сложная электрическая цепь

24. Алгоритм расчета:

Алгоритм расчета сложной электрической цепи постоянного тока.

Сложные электрические цепи постоянного тока

Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока

Основная формула электрической мощности в цепях переменного и постоянного тока

Связанные статьи

Учебник по физике: комбинированные цепи

Последовательная цепь постоянного тока — инженерное мышление

Что такое последовательная цепь постоянного тока?

Сопротивление в последовательных цепях

Ток в серии

Последовательное напряжение

Расчет падения напряжения

Потребляемая мощность

Что такое цепь постоянного тока

Часто задаваемые вопросы

Что такое цепь постоянного тока?

Что является примером цепи постоянного тока?

В какой стране используется постоянный ток?

Анализ схемы для читфекта Dummies

Анализ схемы Dummies

Три основных закона для работы со схемами

Электрические величины и единицы измерения

Эквивалентное сопротивление, емкость и индуктивность

Методы анализа сложных цепей

Об этой статье

Эта статья взята из книги:

Об авторе книги:

Эту статью можно найти в категории:

Закон Кирхгофа для сложных цепей | ОРЕЛ

Что такое закон Кирхгофа?

Первый закон – Текущий закон Кирхгофа

1. Расчет общего тока

2. Расчет узловых токов

3. Подтвердить действующий закон Кирхгофа

Второй закон – закон напряжения Кирхгофа

1. Рассчитать общее сопротивление

2.

3. Рассчитайте ток через каждый резистор

4. Рассчитайте падение напряжения на каждом резисторе

5. Проверка закона Кирхгофа о напряжении

Процесс использования закона Кирхгофа о цепях

Стоя на плечах Ома

Добавить комментарий Отменить ответ