Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | |||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. Поделиться:
| ||||||||||||
| |||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||
/ / Перестановки и разбиения. Число перестановок, число сочетаний, число комбинаций. Число различимых разбиений. Число различных последовательностей из N объектов.
..+Nr объектов, содержащих N1 неразличимых объектов типа 2, и Nr неразличимых объектов типа r, или
Определение комбинаторики, этапы развития, основные модели
Из истории комбинаторики
Комбинаторика занимается различным видом соединений, которые могут быть образованы из конечного многообразия элементов. В Индии были известны несколько элементов комбинаторики еще во II в. до н.э. Индийцы могли вычислить числа, которых теперь называют «сочетания».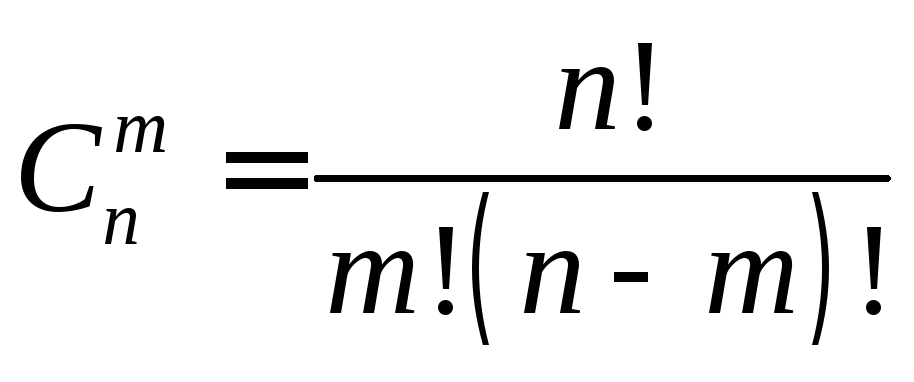
Производился подсчет возможных комбинаций ударных длинных и неударных коротких слогов в поэзии из множества n.
Как научная дисциплина, комбинаторика сформировалась в XVII веке. В книге «Теория и практика арифметики» 1656 года французского автора А. Таке посвящена сочетаниям и перестановке отдельная глава.
Б. Паскаль в «Трактате по арифметическому треугольнику» и «Трактате по числовым порядкам» 1665 года изложил учение о биномиальной динамике. П.Ферма знал о связи математического квадрата и фигурного числа с теорией соединения. После публикации Лейбницем в 1665 году работы «Рассуждение о комбинаторном искусстве», в которой было представлено научное объяснение теории комбинации и перестановки, впервые и появилось определение комбинаторики. Изучать размещения первым стал Я.
Определение комбинаторики
Определение 1Комбинаторика (комбинаторная математика) является разделом математики, который относится к методам подсчета количества предметов определенного происхождения.
В смысле задачи, как правило, понятно, что есть только конечное количество объектов, которые интересуют нас, и все дело в поиске этого числа. Рассмотренные объекты обычно представляют собой определенные комбинации других предметов числа, буквы и так далее. Отсюда и следует определение – комбинаторика.
Для более широкого понимания комбинаторная теория является теорией конечных множественностей; здесь мы рассмотрим лишь задачи расчета, поэтому такого расширенного толкования нам не понадобится. Из сказанного понятно, что в комбинаторике речь идет только о натуральных числах. Может казаться, что поэтому она более «элементарна», чем другие математические разделы, оперирующие богатыми числовыми материалами – отрицательными числами, дробями, иррациональными, комплексными.
Но такая дискуссия была бы поспешной. Практика свидетельствует о том, что многим, кто впервые встречается с комбинаторикой, сложно привыкнуть к комбинаторному рассуждению, более близкому к программированию, чем, к примеру, к математике.
Лучшим способом освоения комбинаторики является решение задач. Начинать, естественно, надо с простых. Именно про простые, типовые и одновременно важнейшие задачи и будет речь ниже. Интересно, что комбинаторика необходима и многим другим разделам математики.
Комбинаторная математика является разделом математики, в котором изучается задача выбора элементов и их расположения по заданным правилам. В теории вероятности используются формулы и методы комбинации для расчета вероятности происходящих событий, а также для получения закона распределения вероятных величин. Это позволяет исследовать закономерности массовых случаев, что очень важно для того, чтобы правильно понимать статистические закономерности, проявляющиеся в технике и природе.
Основное правило комбинаторики
Пусть нужно несколько раз выбирать.
Есть варианты для первого выбора, — для второго, — для третьего и так далее. Если выбор производится каждый раз без ограничений, общее количество возможностей в каждой последовательности выбора равно общему числу возможностей в каждой последовательности выбора:
Теперь поговорим об основных стандартных методах вычисления, используемых в решении комбинационных задач. Рассуждения будут приводиться на следующем примере: Пусть в урне m имеются различные шары с номерами от 1 до m. Из нее извлекают n шаров, при несоблюдении каких-либо условий при извлечении. Каждая модель вычисляет количество возможных результатов.
Число размещений с возвращением
Извлекаются шары наудачу один за другим, а каждый извлеченный шар возвращается обратно в урну, прежде чем извлекается следующий шар. При этом записываются номера шариков в порядке появления. Поэтому мы имеем в виду упорядоченные наборы где каждая может иметь любые значения от 1 до m. Основной принцип сразу дает ответ на полный список исходов.
Число размещений без возвращения
Шары поочередно извлекаются, но в этой модели они возвращаются не обратно в воронку. Мы снова работаем с наборами упорядоченных но с ограничением того, что все различны в них. Конечно же, должно выполняться условие .
Замечание 1Главное правило не применимо напрямую.
Однако, учитывая, что количество шариков в урне на каждом этапе становится меньше на один, мы можем записать их:
Эта модель имеет важную частную особенность – модель перестановки.
Перестановка из различных шаров
Разберемся с моделью при . Тогда все шары извлекаются один за другим без возврата. Результат выбора состоит из набора шаров из m, которые расставлены в некоторой последовательности. Полное число возможностей сопоставимо с количеством всех расположений элементов во множестве
.
Такое число называют факториалом от m и обозначают его:
Сочетание (или неупорядоченный выбор)
Модель заключается в том, что не фиксируется порядок номеров вытягивающихся шаров.
По сравнению с моделями размещения, наборы, отличающиеся лишь порядком движения элементов, рассматриваются как одинаковые.
Число комбинаций без возврата
Шары, которые достали, не возвращаются в урну. Также не фиксируется порядок номеров в процессе извлечения. Иными словами, вы можете представить, что все n шары вынимают сразу один за одним. Таким образом, мы делаем выбор произвольного подмножества n из подмножества m. Из предыдущего рассуждения видно, что упрощенная выборка размеров n создает неупорядоченных, каждая из которых однозначно может быть восстановлена.
Из обсуждений модели известно о том, что число последовательных наборов размером n равно . Обозначим как x исходное число подмножества размера n. Рассуждения, изложенные выше, свидетельствуют о том, что:
Из этого следует, что ответ:
Если умножить числитель и знаменатель на , получим:
Это выражение называется биномиальным коэффициентом, который является важной частью теории вероятности.
Таким образом, тождество верно:
Перестановка из
m шаров, неразличимых внутри группДопустим, у нас есть шары цвета , шары цвета , шары цвета . Цвета разные, шаров одного цвета нет. Конечно, . Сколько различных перестановок в таком случае? Используйте рассуждения для всех первоначальных перестановок без различия шаров одного цвета в соответствии с основным правилом.
Тогда существует новых способов размещения с учетом нумерации.
Рассуждения, которые были проведены для модели, свидетельствуют о том, что число неумеренных перестановок является частным:
Число называется мультиномиальным (или полиномиальным) коэффициентов. Когда , коэффициент становится биномиальным.
Число сочетаний с возвращением
Из урны взяты друг за другом n шары, каждый из вынутых шаров возвращается обратно, прежде чем будет получен следующий шар. При этом может быть, что все вынутые шары регистрируются в неупорядоченном наборе группы, то есть без внимания к порядку их возникновения.
Человеку нередко приходится заниматься задачами, где необходимо подсчитать количество всевозможных способов размещения каких-либо предметов или количество всевозможных способов совершения какого-либо действия. Разные способы или варианты выбора, которые человеку нужно выбирать, составляются в самых разнообразных комбинациях. И целый раздел математики, называемый комбинаторной, занимается поиском ответа на вопрос, сколько комбинаций в этом или ином случае.
Комбинаторика имеет огромное значение в различных областях науки. С комбинаторными величинами приходится иметь дело представителям многих специальностей: ученому – химику, биологу, конструктору, диспетчеру и т.п. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы). В каждой из этих игр приходится рассматривать различные сочетания фигур, и выигрывает тот, кто их лучше изучает, знает выигрышные комбинации и умеет избегать проигрышных. Усиление интереса к комбинаторике в последнее время обуславливается бурным развитием кибернетики.
Использование комбинаторных элементов в различных областях жизнедеятельности показало, что комбинаторные элементы, в том числе сочетания, используются для решения различных ситуаций жизни. Доказана практическая важность комбинаторных элементов в математике. Подтверждена гипотеза о том, что комбинаторная математика является разделом математики, который находится на магистральном этапе развития наук и имеет широкий круг практических направлений.
комбинаторика — Формула для расчета количества возможных позиций для $x$ чисел
спросил
Изменено 4 года, 8 месяцев назад
Просмотрено 1к раз
$\begingroup$
Какую формулу использовать для расчета количества возможных позиций для $x$ чисел?
Допустим, у меня есть $3$ человек в гонке.
Каковы все возможные комбинации порядка, в котором они могут закончить? Предположим, что связи невозможны. Я слышал, что использую факториал, но прошло некоторое время с тех пор, как я использовал факториалы. Так хочу проверить.
- комбинаторика
- факториал
$\endgroup$
1
$\begingroup$
Легко перечислить на троих. Назовем людей $x_1,x_2,x_3$. Возможные порядки показаны ниже.
- $x_1,x_2,x_3$
- $x_1,x_3,x_2$
- $x_2,x_1,x_3$
- $x_2,x_3,x_1$
- $x_3,x_1,x_2$
- $x_3,x_2,x_1$
В общем, в гонке $n$ людей обозначим людей как $x_1,x_2,\ldots,x_n$. Первую позицию может занять любой из $n$ индивидуумов. Следовательно, есть $n$ вариантов для первого места. Теперь, учитывая, что первую позицию занимает $1$ индивидуум, для каждого из $n$ вариантов первой позиции вторая позиция может быть занята любым из оставшихся $n-1$ индивидуумов.
{th}$ позицию может занять любая из оставшихся $n-k+1$ особей. Следовательно, общее количество упорядочений равно $$n \times (n-1) \times \cdots \times (n-k+1) \times \cdots 2 \times 1$$, что равно $n! $.
В вашем случае $n=3$ дает нам $3! = 6$, что соответствует нашему перечислению.
$\endgroup$
1
$\begingroup$
Предположим, в гонке участвует 1 человек. Возможна только одна комбинация.
Второй гонщик (№2) участвует в гонке. Этот человек может быть размещен в 2 местах (перед 1 или позади 1) Теперь есть 2 возможных комбинации 12 21
в гонке участвует 3-й участник. Гонщики 1 и 2 на своих местах, у номер 3 есть 3 возможных места для размещения (спереди, между 1 и 2 или сзади. Поскольку есть 2 возможных положения для 1 и 2, есть 3 * 2 возможных комбинации для 3 гонщиков
12 становится 312, 132 или 123
21 становится 321, 231 или 213
входит 4-й гонщик, есть 4 места, в которые может поместиться этот новый гонщик Всего будет 4*6 возможных комбинаций
n гонщиков n! возможные позиции
$\endgroup$
$\begingroup$
Количество возможностей того, что (1) закончится первым: два, так как мы имеем (1)-(2)-(3) и (1)-(3)-(2).
Немного подумав, мы убедимся, что для любого из трех участников (1), (2), (3) одинаково финишировать на первом месте. Таким образом, всего имеется $\,3!=6\,$ возможностей.
Используя этот ход мыслей и некоторую индукцию, вы можете доказать аналогичный результат для $n\,$ участников: у них есть $\,n!\,$ различных способов закончить гонку.
$\endgroup$
$\begingroup$
Достойные ответы. Однако без дубликатов решение можно объяснить проще.
Поскольку ничьи не участвуют (дубликаты), каждая позиция может иметь на единицу меньше, чем у следующего лучшего финишера, и, таким образом, мы получаем:
3 * 2 * 1 = 6
Если бы в гонке участвовало 5 человек, решение было бы 5 * 4 * 3
$\endgroup$
комбинаторика — Количество комбинаций цифр и букв пароля с учетом ограничений
Задавать вопрос
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 217 раз
$\begingroup$
Пароль состоит из цифр 1-9 и заглавных букв A,B,C,D,E,F,G,H.
Сколько паролей можно составить из четырех цифр и трех букв, если
(а) разрешено повторение?
(b) повторение запрещено?
(c) никакие две цифры не могут стоять рядом друг с другом, и повторение не допускается? 98\mathrm P_6 = 336$, количество комбинаций чисел $=9\times 8\times7\times 6 = 3024$, всего комбинаций = $35\times 336\times 3024 = 35562240$
Мои подходы на запчасти ( а) и б) правильно? Я не уверен, как подойти к части (c) — любые предложения будут очень признательны.
- комбинаторика
$\endgroup$
$\begingroup$
Да, ваш подход правильный. Для c) обратите внимание, что единственный способ иметь четыре цифры без двух соседних, это если пароль выглядит как #@#@#@#, где # представляет цифру, а @ букву.
Если бы у вас было три цифры, было бы больше возможностей. Количество допустимых аранжировок 3#s и 4@s такое же, как количество аранжировок 3#s и 2@s без ограничений.
Чтобы перейти от короткой последовательности, такой как ##@#@, к соответствующей длинной последовательности, добавьте @ между первым и вторым # и еще один между вторым и третьим, чтобы получить #@#@@#@. (Это гарантирует, что в длинной последовательности не может быть двух смежных символов #.)
Всего $\binom 52$ коротких последовательностей, поэтому существует такое же количество допустимых длинных последовательностей. Делая этот трюк, если у вас есть $\ell$ букв и $d$ цифр в длинной последовательности, вы получите $\ell-d+1$ букв и $d$ цифр в короткой последовательности, поэтому количество шаблонов всегда равно $ \binom{\ell+1}d$. (Если $\ell+1 [править] На самом деле тот же результат можно получить и проще — между буквами стоят пробелы $\ell+1$ (включая пробел в начале и пробел в конце), и нужно выбрать $d $ разные пробелы для ввода цифр. $\endgroup$ 4 $\begingroup$ Если разрешено повторение первых цифр в $7 \выберите 4$ способами, то просто поставьте буквы на оставшиеся места.