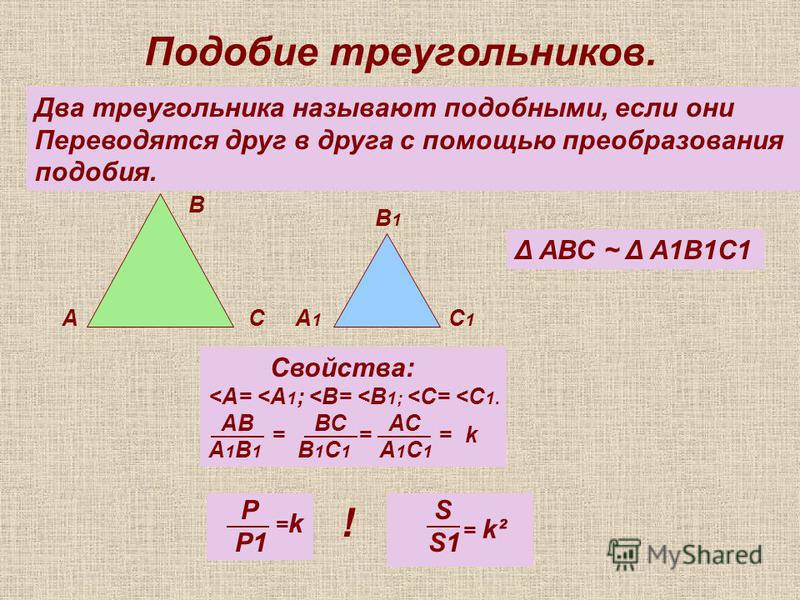
Что дает подобие треугольников: Подобные треугольники — урок. Геометрия, 8 класс.

Содержание

Использование цифрового образовательного комплекса «1С:Школа. Геометрия, 8 кл.» на уроках математики.

Иванова Аниса Габдулхаковна, учитель математики МБОУ СОШ с УИОП №52 города Кирова

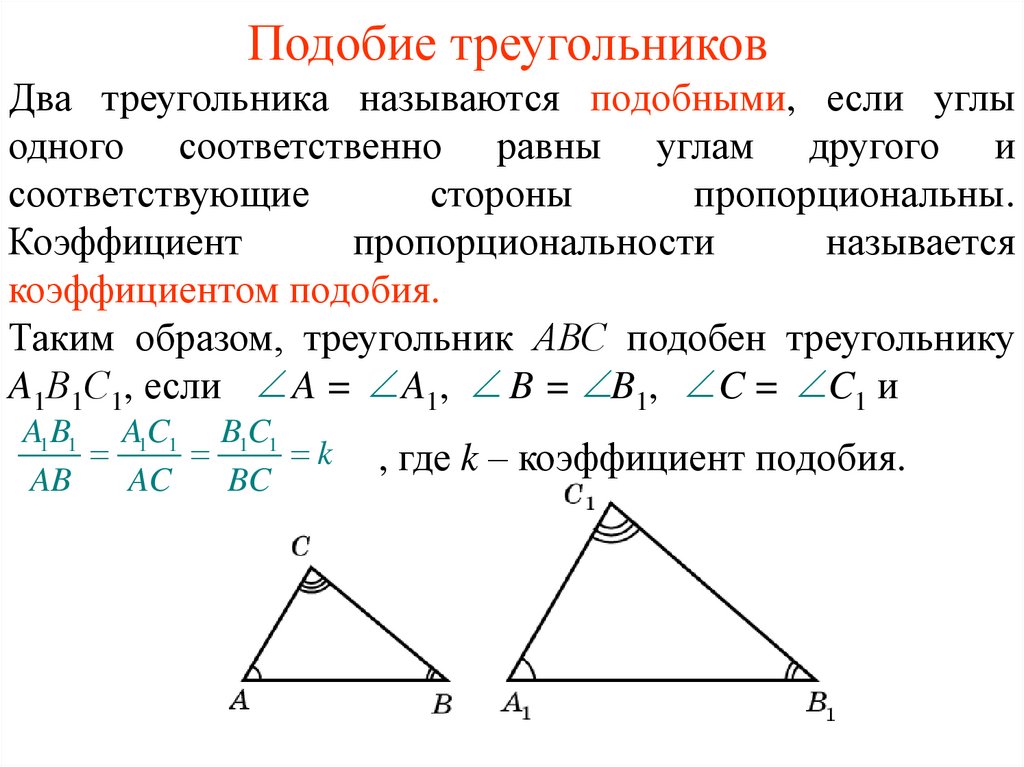
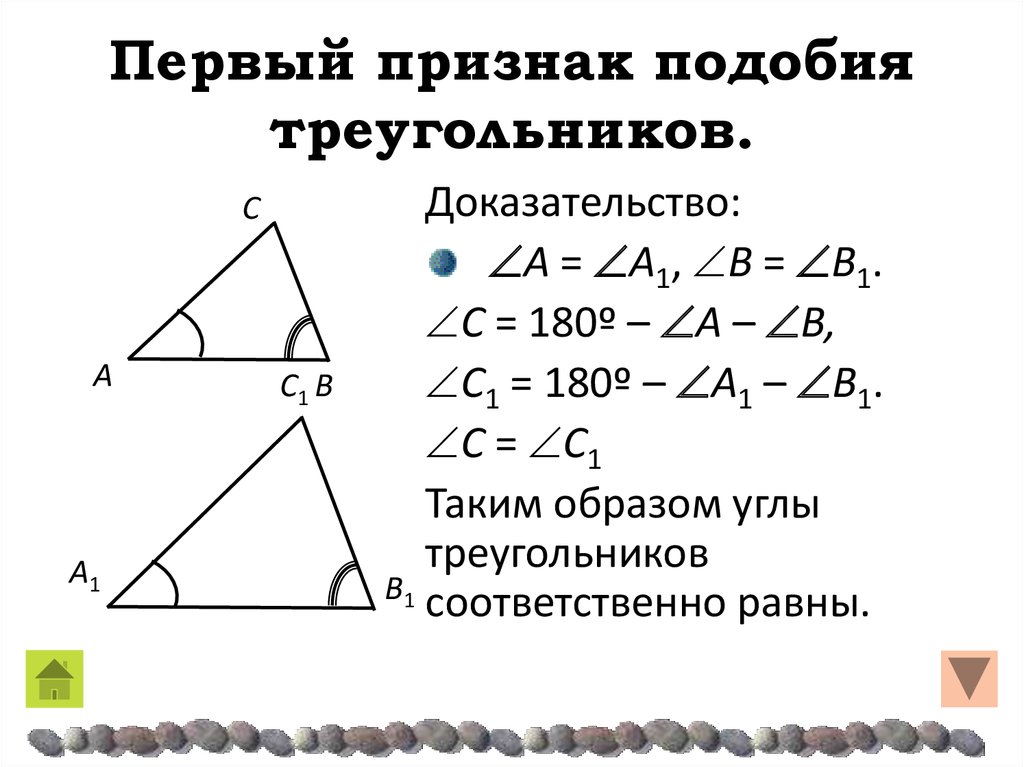
Применение электронных ресурсов по математике серии «1С:Школа» позволяет ученикам успешнее осваивать достаточно сложный учебный материал. На уроках геометрии, используя готовые чертежи со слайдов, доказывать теоремы, решать задачи с проверкой ответов.

Цифровые общеобразовательные ресурсы повышают эффективность учебного процесса, позволяют творчески проводить уроки.

Диск «Геометрия,8 класс-1С: Образование», соответствует УМК Л.С Атанасяна, Б.Ф Бутузова С.Б Кадомцева и др. Также может применяться и с другими УМК.

Мною разработан урок геометрии в 8 классе по теме «Первый признак подобия треугольников». Электронный образовательный ресурс («1С:Школа. Геометрия, 8 кл.»/ГлаваVII. «Подобные треугольники»/Теория/Анимированная презентация) применяется на двух этапах урока :

Усвоение новых знаний и способов действия.
Первичная проверка понимания.

Для объяснения нового учебного материала использую режим постепенного ввода информации, тем самым я акцентирую внимание учащихся на конкретном этапе доказательства теоремы. Такая работа даёт возможность учителю делать дополнительные комментарии, а учащимся корректировать сказанное, лучше концентрироваться на изучаемом вопросе. Слайд используется как опорный конспект при фронтальной работе.

При закреплении изученного материала и первичной проверки понимания, использую ресурс: «1С:Школа. Геометрия, 8 класс» /Глава VII «Подобные треугольники» /Признаки подобия треугольников/ Упражнения. Решаем задачу из учебника № 550. Очень удобно нажатием кнопки «Подтвердить ответ» проверить результат решения.

Благодаря применению цифровых ресурсов, учащиеся на уроках стали более активны. Повышается уровень восприятия информации и качество знаний.

Технологическая карта урока математики по теме: «Первый признак подобия треугольников».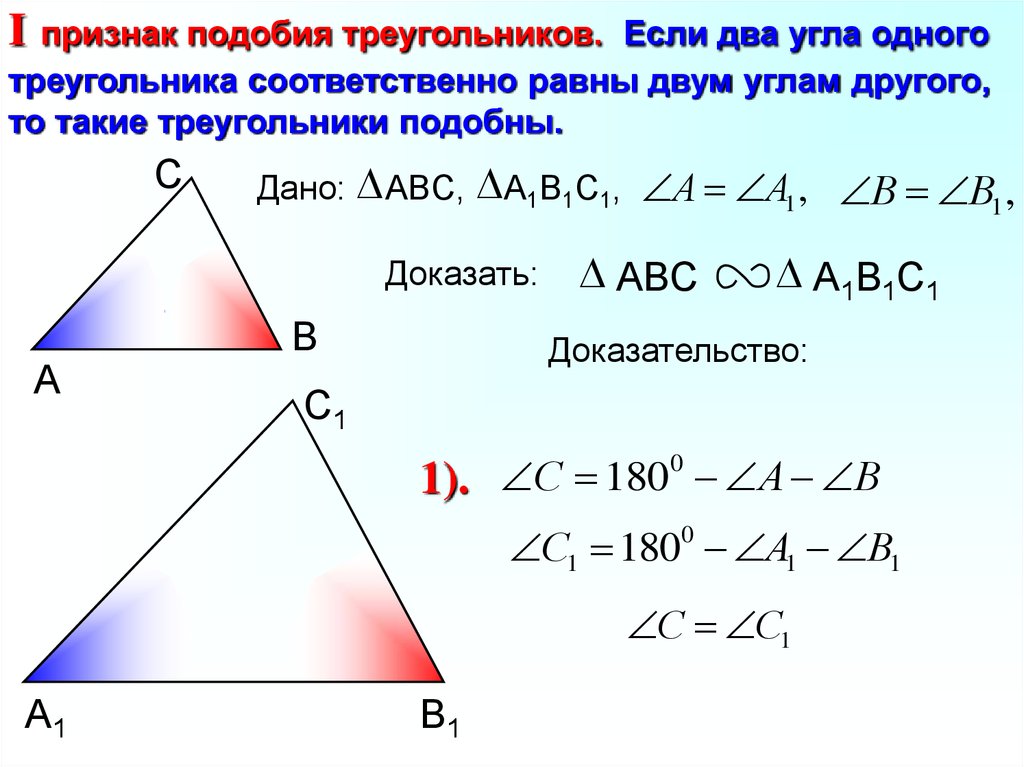

Класс 8

Урок №3 в теме «Подобные треугольники».

Автор УМК Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 7-9 классы: учебник для общеобразовательных учреждений. М.: Просвещение, 2010.

Тип урока: изучения и первичного закрепления нового материала.

Оборудования и средства обучения:

ЦОР: «1С:Школа. Геометрия, 8 кл.», компьютер, медиапроектор, доска, мел, учебник «Геометрия 7-9 классы», чертежные инструменты.

Цели:

образовательная

дать понятия первого признака подобия треугольников,
формировать умение пользоваться этим признаком при
решении задач, способствовать усвоению первого
признака подобия треугольников.

развивающая

создать условия для формирования навыков применения
полученных знаний при решении задач,
создать условия для формирования логического, абстрактного, системного мышления,
способствовать формированию интеллектуальных умений,
развитию математической речи и познавательного интереса.

воспитательная: воспитать интерес к предмету, культуру поведения, волевые качества.

Этапы	Деятельность учителя	Деятельность учеников
Организация начала занятия.	Учитель проверяет готовность рабочего места учащихся, настраивает ребят на урок, создает ситуацию успеха.	Готовят рабочее место, слушают учителя
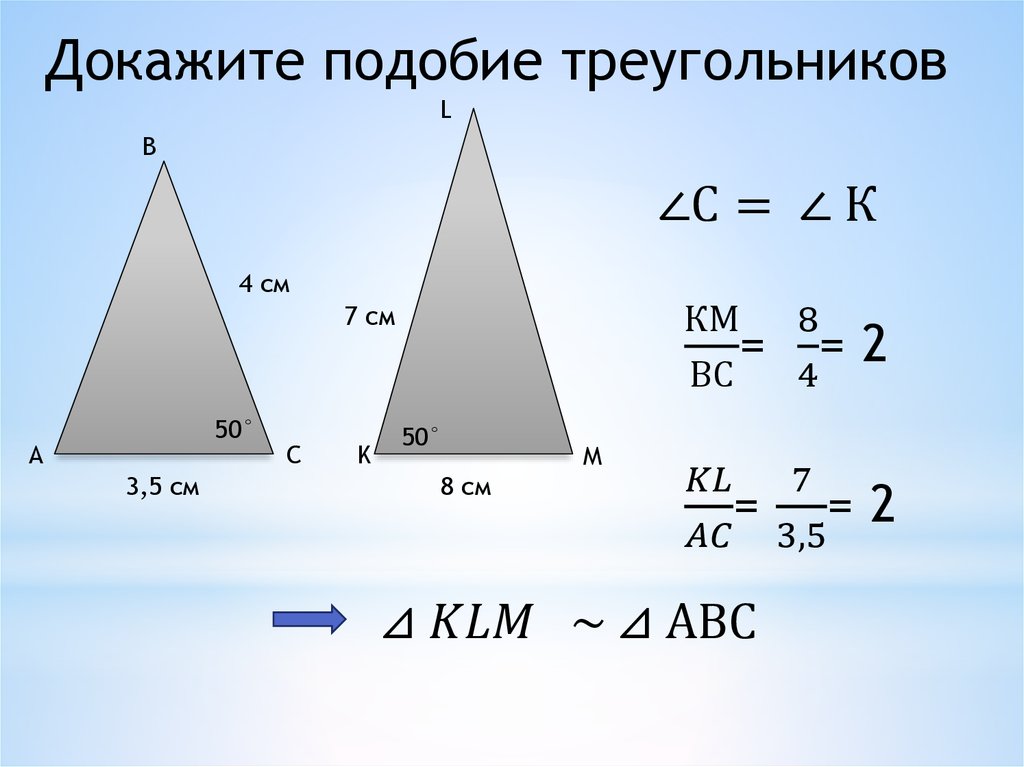
Подготовка к основному этапу занятия.	Учитель задает вопросы по чертежам, построенным на доске. •По рис 1 назовите стороны, между которыми заключен угол A;угол A1? • Что вы можете сказать об углах A и A1 -? • Что вы можете сказать об отношении площадей этих треугольников? •Сформулируйте теорему, запишите её для данного условия. •Что вы можете сказать об углах B и B1 на рисунке 2? •Докажите это. • Как называют равные углы в треугольниках? • Как называют стороны находящиеся напротив равных углов? •Будут ли отрезки AB и A1B1; ACи A1C1 пропорциональными? • Докажите. • Чем является число 2? • Используя данные на чертеже, что можно сказать о треугольниках ABC и A1B1C1-? • Итак, мы доказали подобие треугольников с помощью определения, как вы заметили, доказывали долго, но вы знаете, что в геометрии существуют другие утверждения, которые позволяют это сделать быстро, облегчить работу. •Кто-нибудь догадался о чём идет речь?	отвечают на вопросы AB, AC и A1B1, A1C1 ∠A = ∠A1 один из учеников пишет на доске один ученик, проговаривая, пишет на доске: ∠A=∠A1 (по условию) ∠С=∠С1 (по условию) отсюда следует ∠B=180-(∠A+∠C) ∠B=∠B1 ∠B1=180- (∠A1+∠C1) соответственными сходственными да: 1 ученик пишет на доске = 2 = 2 коэффициентом пропорциональности отвечают: ∆ABC подобен ∆A1B1C1 по определению подобных треугольников т. к. ∠A=∠A1 ∠B=∠B1 ∠C=∠C1 == размышляют, отвечают: о признаках подобия треугольников
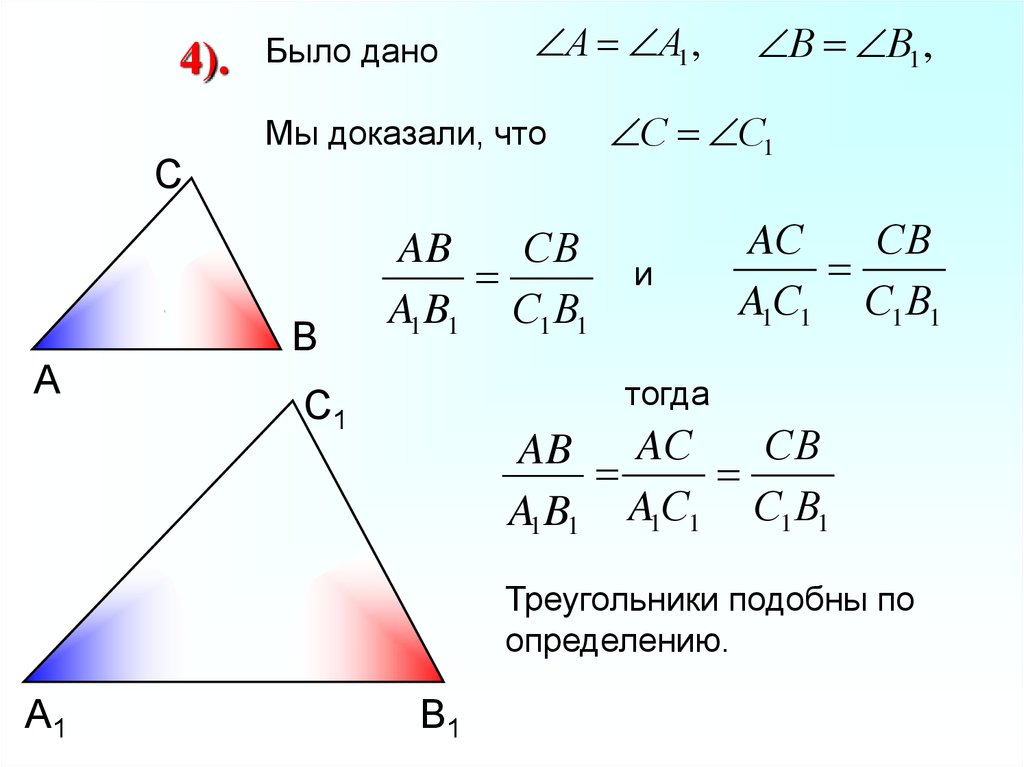
Усвоение новых знаний и способов действий.	Да, речь идет о признаках подобия треугольников, и сегодня мы будем рассматривать один из них. Поэтому тема нашего урока так и называется «Первый признак подобия треугольников». •Учитель открывает по данной теме *слайд* и просит учеников: Прочитайте теорему, выражающую I признак подобия треугольников. •Из данной формулировки надо выбрать, показать по готовому чертежу и записать условие в тетрадь. • Учитель показывает на *слайде* условие из теоремы для коррекции сказанного учениками. • На сегодняшний день доказывать подобие треугольников можем только по определению, а значит, надо будет доказать 2 условия. • Какое первое? • Попробуйте устно доказать первое условие. • Учитель показывает на *слайде* проверку. • Какое второе условие надо доказать? • Что будем использовать для доказательства пропорциональности сходственных сторон? • Попробуем продолжить доказательство. • Учитель показывает на *слайде* проверку сказанному. • Какой можно сделать вывод? • Какой окончательный вывод? Учитель выводит на *слайд* полное доказательство.	записывают в конспект тему урока читают, записывают формулировку в конспект готовые на *слайде* треугольники перечерчивают в тетрадь, проговаривают условие озвучивают и записывают условие в тетрадь отвечают: доказать равенство соответственных углов доказывают, опираясь на устную работу корректируют сказанное и записывают в конспект доказать, что стороны одного треугольника пропорциональны сторонам другого отвечают: использовать утверждение об отношении площадей размышляют, доказывают, используя устную работу вначале урока, проводят аналогию, записывают на доске записывают доказательство в конспект отвечают: сходственные стороны пропорциональны отвечают: данные треугольники подобны по определению подобия треугольников
Первичная проверка понимания Подведение итогов занятия.	• Итак, мы доказали первый признак подобия треугольников, а где он нам может пригодиться? №550 (в учебнике рисунок сверху) •Учитель открывает *слайд* с чертежом. • Нажатием мышки выводит правильный ответ. №550 (в учебнике рисунок снизу) • Учитель открывает *слайд* с чертежом. • Показывает правильный ответ. • Дает анализ и оценку успешности достижения цели и намечает перспективу следующей работы: • Ребята, а по рис 5 сможете доказать подобие треугольников? Сформулируйте теорему ещё раз. •А по рис 6, я вам точно говорю, что треугольники подобны, как вы думаете почему? • Да, здесь будет применяться второй признак подобия треугольников, а ещё есть третий и на следующих уроках мы будем доказывать их.	отвечают: при решении задач комментируя, решают в тетрадях для практики. Проверяют свой ответ с тем, который появился на слайде, убеждаются в правильности или наоборот, найдя ошибку,исправляют её выполняют самостоятельно проверяют ответ получают информацию да, эти треугольники подобны по первому признаку подобия треугольников отвечают: наверное, есть другие признаки подобия треугольников
Информация о домашнем задании, инструктаж по его выполнению.	П. 59 № 554, 555. • Ребята, д/з на следующем уроке проверим с помощью компьютера (на диске есть *слайды* с решением этих заданий). • Учитель проверяет записи в дневниках.	записывают д/з в дневник, внимательно слушают учителя

Подобие треугольников | Методическая разработка по математике (7, 8 класс):

Этапы урока

Деятельность учителя

Методы, технологии, средства обучения

Деятельность учащихся

УУД, которые развиваются на данном этапе урока

Самоопределение к деятельности

Приветствует учащихся, создаёт эмоциональный настрой на урок:

— Выдающийся французский философ, учёный Блез Паскаль утверждал: “Величие человека в его способности мыслить”

— Сегодня мы с вами имеем возможность почувствовать себя великими людьми, открывая знания для себя.

Словесные, ИКТ (показ портрета учёного).

Приветствуют учителя, слушают учителя.

Коммуникативные – умение слушать.

Актуализация опорных знаний, устная работа

Проверяет готовность обучающихся к уроку посредством тренажёров. Каждый год в образовательной среде, как правило, посвящается определённой теме. А вот какая, вы узнаете, когда найдёте значения выражений и поставите в соответствие определённую букву. (Тренажер № 1)

Слово «экология» появилось в нашем языке сравнительно недавно, в XX столетии. В переводе с греческого оно означает учение о сохранении дома, Родины, а в более широком смысле —всей нашей планеты. Что же такое экология сегодня? Экология сегодня – это не только наука, это мировоззрение, отношение к себе, это и политика, и экономика, и культура.

Практические, тренажёры для вычислений.

Выполняют упражнения на тренажёрах для развития вычислительных навыков. В оценочных листах рисуют – солнышко улыбается, если всё хорошо сделал, солнышко хмурится, если сделано плохо (по мнению ребёнка).

Познавательные — контроль и оценка

процесса и результатов деятельности.

Формулирование учебной проблемы

Учитель задаёт вопрос:

-Люди уже давно связывали математические знания с природой.

Предлагаю вам решить древнеегипетскую задачу: У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики эти числа? Сколько мер ячменя уничтожат мыши?

Метод постановки учебной проблемы, диалога, фронтальная работа.

Видят выражения:

Исследуем условие задачи. Назовите: (в ходе обсуждения на доске появляется запись)

Количество кошек

7*7=49

Количество мышей

7*7*7=343

Количество колосьев

7*7*7*7=2401

Количество мер зерна

7*7*7*7*7=16807

Познавательные — самостоятельное выделение и формулирование познавательной учебной цели.

Коммуникативные — инициативное сотрудничество в процессе диалога.

Побуждение к осознанию:

Ученые математики всегда стремились выполнить работу быстрее, используя более удобные формы записи.

– Много разных мнений.

(Осознание противоречия.)

Побуждение к проблеме:

– Так чего мы еще не знаем, какой возникает вопрос

Проблема: Нельзя ли проще записать полученные произведения?

– Какие же действия можно выполнять со степенями?

— Можно, но как?

Открытие нового знания

Тему нашего урока вам поможет сформулировать загадка.
Загадка.

Первый слог возьми из слова «степь»,

Что всегда прекрасною бывает.

Слог второй мы сможем лицезреть,

Если кто в лесу деревья валит. (СТЕ — ПЕНЬ)

Запись

2+2+2+2+2+2=6*2, а как можно записать 2*2*2=.

7*7*7*7*7=75 читается так «7 в степени 5» или «7 в пятой степени».

Число 7 называют основанием степени, 5- показателем степени.

Предлагаю вам сформулировать определение степени с натуральным показателем

Организует самостоятельную работу по изучению нового материала в два тапа:

1 этап: класс делится на 5 групп, каждая из которых работает по учебнику, изучая одно из свойств степени с натуральным показателем.

Технология сотрудничества, работа в малых группах, работа с учебником.

Самостоятельно формулируют тему урока.

Читают текст, обсуждают приведённые в учебнике примеры решения задач, составляют свои по данному свойству, осуществляют взаимопроверку, изученного материала. Каждый ученик заполняет свой оценочный лист.

Познавательные — поиск и выделение необходимой информации, интерпретация её в знаковые системы.

Коммуникативные — инициативное сотрудничество в поиске и сборе информации, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами.

2 этап: работа в динамических парах (парах сменного состава) под девизом “Один ум хорошо, а два лучше!”

Парная работа, технология сотрудничества.

“Слабые” дети получают учебные карточки, сильные работают с заданиями из учебника

№376 (а,в,д,ж,и) № 377 (а, в, д, ж)

Один ученик слушает, другой объясняет.

2. Затем меняются ролями.

3. Потом каждый берет тетрадь своего соседа и проверяет.

5. Результаты выставляются в индивидуальную карточку достижений.

6. Затем каждый партнёр пары создаёт новую пару, в которой вся работа повторяется.

По окончанию работы в каждой паре дети заполняют свой оценочный лист.

Коммуникативные -владение монологической и диалогической формами речи, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

Предметные- выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; рефлексия способов и условий действий.

Первичное закрепление

Проводит интерактивный тест, который проверяется с использование сигнальных карточек.

Проведём анализ полученных результатов.
Какой знак имеет результат возведения положительного числа в натуральную степень?

Какой знак имеет значение степени отрицательного числа с чётным показателем?

С нечётным показателем?

Какое число получается при возведении в степень нуля?

Информационно-коммуникативные технологии, индивидуальная работа.

Выполняют задания устно и демонстрируют своё согласие или несогласие с отвечающим одноклассником с помощью сигнальной карточки.

— Знак «+»

— Знак «-»

— Единица

Предметные — контроль и оценка процесса и результатов деятельности;

Регулятивные — осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание уровня усвоения.

Фронтальная работа.

Фронтальная работа с классом.

Решите задачу экологического содержания.

Древесные отходы, накапливаясь в одном месте без принудительного уплотнения, образует насыпь (кучу) и занимают объем больший, чем они занимали в цельной древесине до обработки последней, а вес единицы объема такой насыпи уменьшается за счет разрыхления. Определите массу 1м3 сосновых щепок, если масса 1см3 равна 0,76 г.

Что нужно знать, чтобы ответить на вопрос задачи?
Как перевести 1м3 в см3?
Ребята, как вы думаете, какое применение можно найти древесным отходам.
Часто на уроках физики, химии и астрономии вы будете сталкиваться с большими числами и степенью числа 10. Думаю, что вам будет интересна следующая информация.

Личностно-ориентированная технология, индивидуальная работа.

Обучающийся на доске записывает решение задачи:

1)1м3=1м*1м*1м=100см*100см*100см=1000 000см3= 106 см3.

1)0,76*106г = 760 000г=760 кг.

Ответ: 760 кг.

— Ответы детей

Сообщение учащегося.

Название больших чисел
Миллиард или биллион – 1000 000 000 = 109
Триллион -1000 000 000 000 = 1012
Квадриллион -1000 000 000 000 000 = 1015
Квинтиллион – 1000 000 000 000 000 000= 1018
Секстиллион -1000 000 000 000 000 000 000= 1021
Септиллион – 1000 000 000 000 000 000 000 000 =1024
Названия степени числа 10:
Дека – 10 (дк) ,Гекто – 102(г) ,Кило — 103(к) ,Мега – 106(М),Гига – 109 (Г),Тера – 1012(Т) .

Предметные — контроль и оценка процесса и результатов учебной деятельности;

Самостоятельная работа

Существует и обратная операция- представление числа в виде степени. Например, 25 = 52, 144 = 122. Для квадратов натуральных чисел от 10 до 99 есть таблица на форзаце учебника. (Рассказ учителя о том, как пользоваться таблицей). Предлагаю вам выполнить самостоятельную работу -математический диктант, записать в виде квадрата числа, которые встретятся в тексте. Итак, экология: факты и цифры.

36 млн. тонн вредных веществ выбрасывается за год автомобильным транспортом.
В США автомобиль есть у каждого второго жителя, а в Африке на 100 человек приходится 9 автомобилей, в России – 81 (число нельзя представить в виде квадрата).
Ежегодно автомобиль в среднем расходует около 4356 кг кислорода и загрязняет воздух, выбрасывая 3249 кг углекислого газа.
225 тыс. человек ежегодно умирает в Европе от заболеваний, связанных с выхлопными газами.
Из 250 000 видов растений Земли десятая часть находится на грани исчезновения.
Растения Земли ежегодно очищают атмосферу, образуя около 400 млрд. т кислорода, обеспечивая всему живому возможность дышать.
В мире ежегодно добывается 1600 млн. м3 древесины
Подсчитано, что для нормальной жизни в промышленном городе на каждого жителя необходимо иметь 25 квадратных метров зеленых насаждений
На 4 года меньше живет средний житель мегаполиса по сравнению с теми, кто живет в сельской местности.
Жизненная ёмкость лёгких пловца 4900 см2.

Сопоставить пример с ответом.

Индивидуальная

Самопроверка, результаты говорят ученики и проверяю тетрадь соседа.

Предметные — контроль и оценка процесса и результатов деятельности;

Рефлексия деятельности, итог урока.

Что нового для себя вы открыли на сегодняшнем уроке?
Во начале урока мы поставили проблему, какую?
Отвечают: «Нельзя ли проще записать полученные произведения?»

Д/З: стр. 90, № 380, № 378.

Коммуникативные — умение структурировать знания; умение осознанно и произвольно строить речевое высказывание в устной форме.

Аналогичные треугольники — Как доказать, определение и теоремы (Видео)

Написано

Малкольм МакКинси

11 января 2023

. Через

Paul Mazzola

Аналогичные Triandgles (определение & теоремы)

Сходство в математике не означает то же самое, что и сходство в повседневной жизни. Подобные треугольники — это треугольники с одинаковой формой, но разными размерами сторон.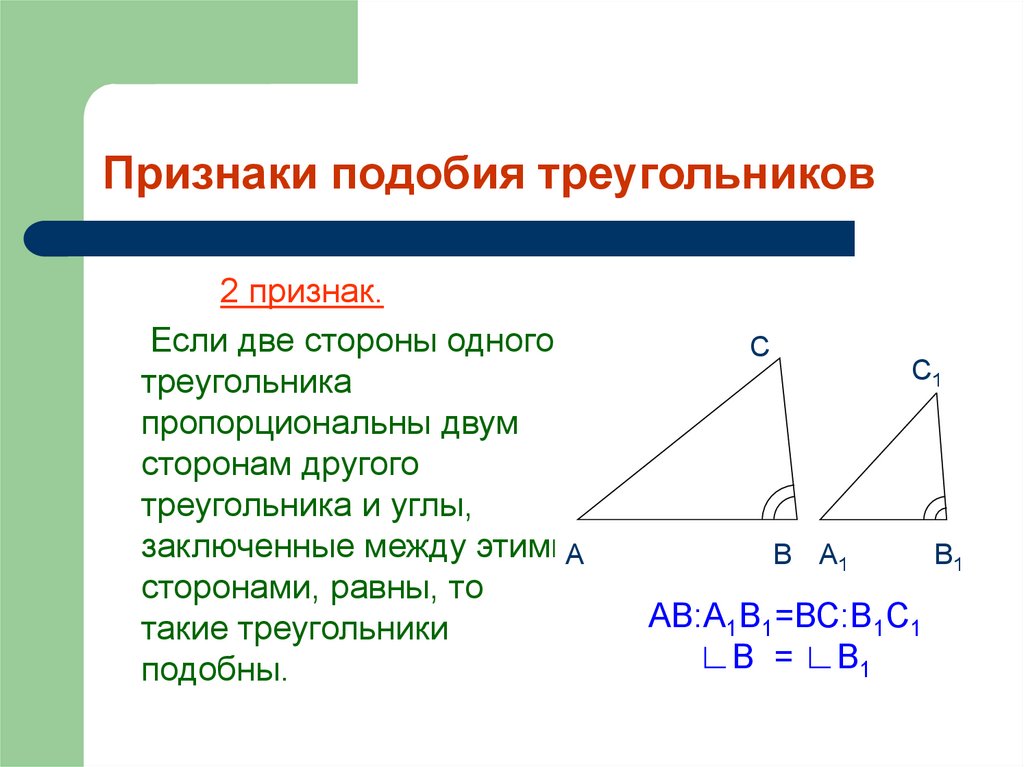

Определение подобных треугольников

Мятное мороженое с шоколадной крошкой и мороженое с шоколадной крошкой похожи, но не одно и то же. Это повседневное использование слова «подобный», но не так, как мы используем его в математике.

В геометрии две фигуры похожи если они имеют одинаковую форму, но разные размеры. У вас может быть квадрат со сторонами 21 см и квадрат со сторонами 14 см ; они были бы похожи. Равносторонний треугольник со сторонами 21 см и квадрат со сторонами 14 см не будут похожи, потому что они разной формы.

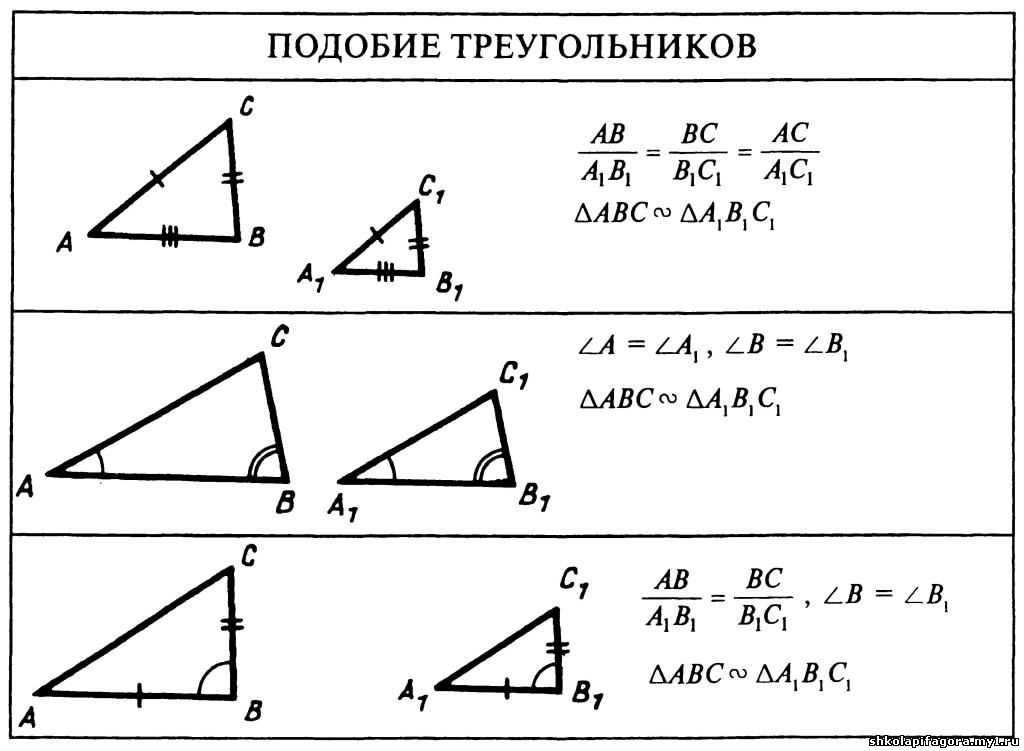
Подобные треугольники легко определить, поскольку к треугольникам можно применить три теоремы. Эти три теоремы, известные как Угол-Угол (AA) , Сторона-Угол-Сторона (SAS) и Сторона-Сторона-Сторона (SSS) , являются надежными методами определения сходства в треугольниках.

Угол-угол (AA)
Сторона-угол-бок (SAS)
Сторона-сторона-сторона (SSS)

Соответствующие углы

В геометрии соответствие означает, что конкретная часть одного многоугольника точно относится к аналогично расположенной части другого. Даже если два треугольника ориентированы по-разному, если вы можете повернуть их, чтобы сориентировать одинаково, и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.

Три теоремы подобия треугольников зависят от соответствующих частей. Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом другого треугольника.

Подобные треугольники Соответствующие углы

Пропорция

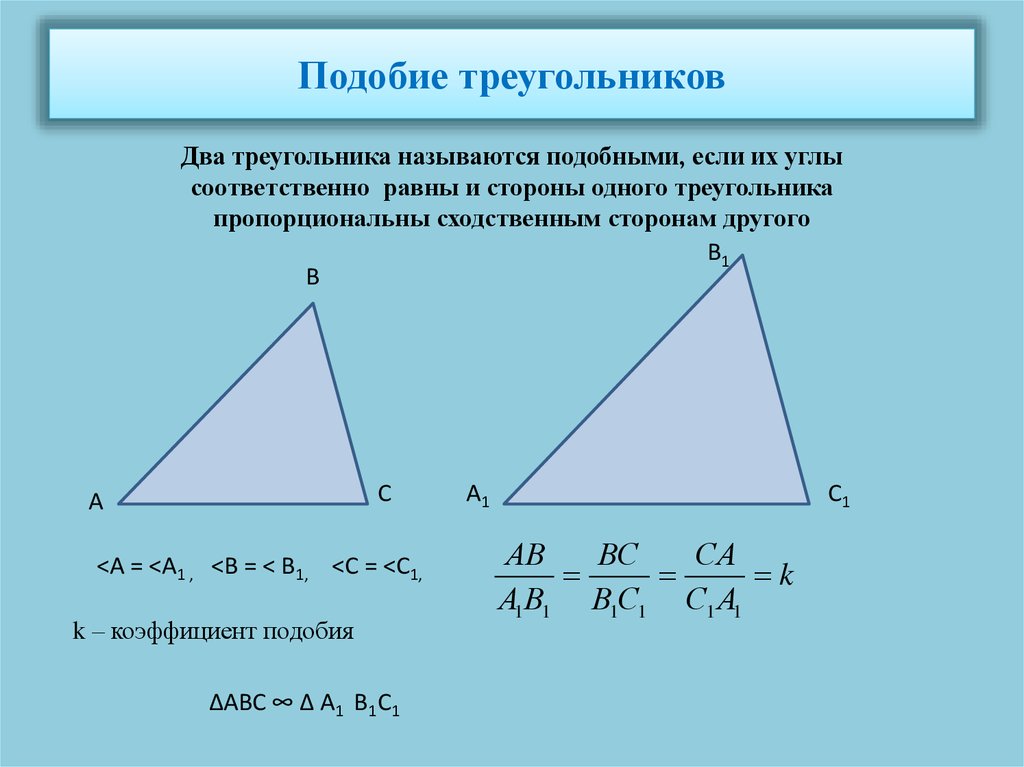
Подобие связано с пропорцией. Треугольники легко оценить по пропорциональным изменениям, которые делают их похожими. Их сравнительные стороны пропорциональны друг другу; их соответствующие углы равны.

Вы можете установить соотношения для сравнения длин сторон двух треугольников. Если отношения конгруэнтны, соответствующие стороны подобны друг другу.

Угол в комплекте

включенный угол относится к углу между двумя парами соответствующих сторон. Вы не можете сравнить две стороны двух треугольников, а затем перепрыгнуть на угол, который не находится между этими двумя сторонами.

Доказательство подобия треугольников

Вот два конгруэнтных треугольника. Чтобы облегчить вам жизнь, мы сделали их равносторонними треугольниками.

Доказательство похожих треугольников

△FOX сравнивается с △HEN . Обратите внимание, что ∠O на △FOX соответствует ∠E на △HEN . Оба ♂ и ♂ — , включены углы между сторонами FO и OX на △ Fox и стороны HE и EN на △ Hen .

Сторона FO соответствует стороне HE ; сторона OX равна стороне EN , а ∠O и ∠E являются вложенными конгруэнтными углами.

Два равносторонних треугольника одинаковы, за исключением букв. Они одного размера, поэтому их 9.0023 одинаковые треугольники . Если бы они оба были равносторонними треугольниками, но сторона EN была вдвое длиннее стороны HE , то они были бы подобными треугольниками .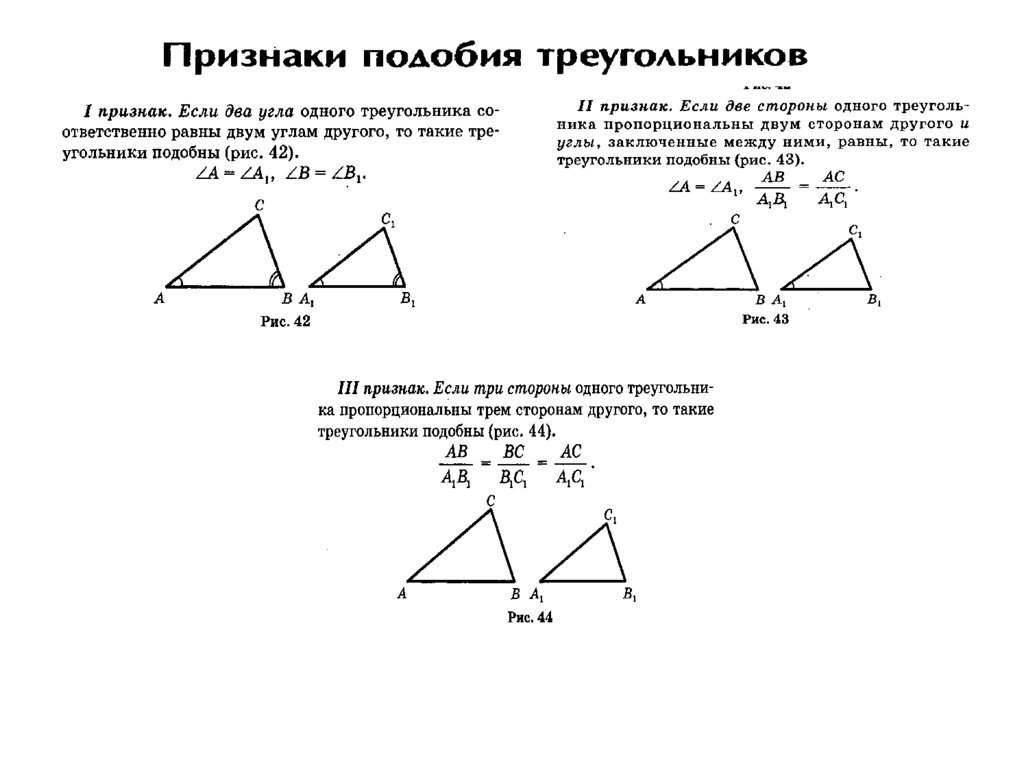

Теоремы подобия треугольников

Теорема об угле-угле (AA)

Угол-угол (AA) говорит, что два треугольника подобны, если они имеют две пары соответствующих углов, которые конгруэнтны. Два треугольника могут быть на 90 099 больше, чем на 90 100, чем похожи; они могут быть идентичными. Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.

Пробуем угол-угол

Вот два разносторонних треугольника △JAM и △OUT . Мы уже отметили два внутренних угла каждого треугольника с помощью геометрического обозначения конгруэнтности: маленьких косых черт.

Одинарная косая черта для внутреннего ∠A и такая же одиночная косая черта для внутреннего ∠U означают, что они совпадают. Обратите внимание, что ∠M соответствует ∠T , потому что у каждого из них есть две косые черты.

Поскольку ∠A сравнимо с ∠U , а ∠M сравнимо с ∠T , теперь у нас есть две пары конгруэнтных углов, поэтому треугольники

4 подобны теореме 900 AA.

Подобие треугольника. Теорема AA (угол-угол)

Хитрости мастерства

Следите за хитростями из учебников, онлайн-задач и учителей математики. Иногда треугольники не ориентированы одинаково, когда вы смотрите на них. Возможно, вам придется повернуть один треугольник, чтобы увидеть, сможете ли вы найти две пары соответствующих углов.

Еще одна задача: на одном треугольнике измерены и определены два угла, а на другом измерены и определены два разных угла.

Поскольку каждый треугольник имеет только три внутренних угла, каждый из идентифицированных углов должен быть конгруэнтным. Вычитая измеренные, идентифицированные углы каждого треугольника из 180°, вы можете узнать меру недостающего угла. Затем вы можете сравнить любые два соответствующих угла на конгруэнтность.

Теорема сторона-угол-сторона (SAS)

Вторая теорема требует точного порядка: сторона, затем прилежащий угол, затем следующая сторона. Теорема Сторона-Угол-Сторона (SAS) утверждает, что если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, а их соответствующие углы равны, то два треугольника подобны.

Пробуем сторона-угол-сторона

Вот два треугольника, расположенных рядом и ориентированных одинаково. △RAP и △EMO идентифицированы стороны размером 37 дюймов на △RAP и 111 дюймов на △EMO , а также стороны 17 на △RAP △2 9002 9002 .3 . Обратите внимание, что угол между идентифицированными и измеренными сторонами в обоих треугольниках одинаков: 47° .

Подобие треугольника — теорема SAS (сторона, угол, сторона)
Является ли отношение 37111\frac{37}{111}11137 таким же, как отношение 1751\frac{17}{51}5117? Да; два соотношения пропорциональны, поскольку каждое из них упрощается до 13\frac{1}{3}31. При одинаковом углу между ними эти два треугольника подобны.
Теорема Side-Side-Side (SSS)
Последняя теорема Side-Side-Side, или SSS . Эта теорема утверждает, что если два треугольника имеют пропорциональные стороны, то они подобны. Это может показаться большим скачком, который игнорирует их углы, но подумайте об этом: единственный способ построить треугольник со сторонами, пропорциональными сторонам другого треугольника, — это скопировать углы.
Пробуем бок-бок-бок
Вот два треугольника: △FLO и △HIT . Обратите внимание, что мы не определили внутренние углы. Стороны △FLO измерить 15 , 20 и 25 см в длину. Стороны △HIT имеют длину 30 , 40 и 50 см .
Сходство треугольников — Теорема SSS (Side Side Side)
Вам необходимо установить отношения соответствующих сторон и оценить их:
Все они представляют собой одно и то же отношение, если упростить. Все они 12\frac{1}{2}21. Таким образом, даже не зная внутренних углов, мы знаем, что эти два треугольника подобны, потому что их стороны пропорциональны друг другу.
Итоги урока
Теперь, когда вы изучили этот урок, вы можете определять и идентифицировать подобные фигуры, а также можете описать требования, чтобы треугольники были подобными (у них должны быть либо две конгруэнтные пары соответствующих углов, либо два пропорциональных соответствующих угла). стороны с включенным соответствующим углом конгруэнтны или все соответствующие стороны пропорциональны).
Вы также можете применить три теоремы подобия треугольников, известные как угол-угол (AA), сторона-угол-сторона (SAS) или сторона-сторона-сторона (SSS), чтобы определить, подобны ли два треугольника.
Как вычислять подобные треугольники в геометрии

Ключевые термины
O Трансформация
O Перевод
O отражение
O Линия отражения
O Вращение
O Центр вращения
DATATIO условие сторона-бок (пропорциональность)
o сторона-угол-бок (пропорциональность) условие
Цели
o Понять, как можно использовать преобразования как метод понимания конгруэнтности и подобия
o Доказать, что два треугольника подобны, используя соответствующие критерии

Другой взгляд на конгруэнтность и подобие
Давайте рассмотрим задачу доказательства того, что два треугольника подобны. Напомним, что конгруэнтность означает, что меры всех трех сторон и всех трех углов одинаковы для двух треугольников. Для подобия достаточно, чтобы углы были равны. Еще один способ взглянуть на конгруэнтность и подобие — с помощью геометрических преобразований . Трансформация, с точки зрения непрофессионала, — это просто движение или изменение фигуры. Четыре основных преобразования — это переводы, отражения, повороты и расширения. Перевод — это просто перемещение всей фигуры на некоторое расстояние, при котором форма и ориентация фигуры остаются неизменными. Перевод показан ниже.
Другим преобразованием является отражение , которое производит зеркальное отражение фигуры. Линия отражения должен быть выбран в качестве «зеркала» для создания отраженной фигуры. Отражение показано ниже.
Вращение , как следует из названия, просто включает «вращение» фигуры вокруг некоторой точки (этот центр вращения может быть либо внутри, либо снаружи фигуры). Ниже показаны два поворота: крайний левый пример имеет центр вращения внутри фигуры, а крайний правый пример имеет центр вращения вне фигуры.
Наконец, расширение — это просто расширение или уменьшение фигуры таким образом, что новая фигура пропорциональна во всех своих размерах.
Если две фигуры конгруэнтны, то одна фигура может быть наложена на другую посредством некоторой комбинации перемещений, отражений и поворотов. Рассмотрим два равных треугольника ниже.
Хотите узнать больше? Пройдите онлайн-курс по геометрии.
Если мы повернем треугольник справа на четверть оборота (против часовой стрелки), а затем отразим его, то в результате получится треугольник, полностью соответствующий треугольнику слева.
Эти математические манипуляции являются более строгим способом сказать, что если мы вырезаем из листа бумаги два треугольника абсолютно одинаковой формы, то эти треугольники останутся одинаковыми независимо от того, как мы поворачиваем, переворачиваем или перемещаем эти кусочки. бумага!
Если два треугольника (или другие фигуры) можно наложить с помощью некоторой серии преобразований, включающей растяжение, то треугольники подобны. Рассмотрим два подобных треугольника, показанных ниже.
Расширяя и перемещая меньший треугольник, мы можем создать идеальное перекрытие большего треугольника. Поскольку расширение необходимо, эти треугольники подобны, но не конгруэнтны.
Практическая задача: Определите ряд преобразований, которые показывают, что треугольники ниже равны.
Решение: Чтобы продемонстрировать, что два приведенных выше треугольника конгруэнтны, нам нужно выполнить ряд преобразований (перемещений, поворотов или отражений), чтобы один треугольник полностью перекрыл другой. Выполним наши преобразования над правым треугольником. При осмотре видим, что треугольник нужно повернуть (на 180°), а затем перевести влево.
Опять же, поскольку треугольники перекрываются, они конгруэнтны (мы также знаем, что треугольники конгруэнтны из данной диаграммы по условию SAS).
Практическая задача : Покажите с помощью ряда преобразований, что приведенные ниже треугольники подобны.
Решение: Если мы сможем найти серию геометрических преобразований (перемещений, вращений, отражений или расширений), которые позволяют нам заставить треугольник справа накладываться на треугольник слева, тогда треугольники подобны. По условию сторона-угол-сторона (пропорциональность) мы уже можем видеть, что треугольники подобны. Чтобы сделать их конгруэнтными, давайте сначала расширим треугольник справа (то есть мы увеличим его в три раза по сравнению с текущим размером).
Затем мы переместим треугольник влево, чтобы показать идеальное перекрытие, тем самым демонстрируя, что треугольники подобны.
Доказательство подобия
Как и в случае конгруэнтности, мы можем указать несколько условий для доказательства подобия треугольников, которые не требуют от нас доказательства конгруэнтности всех трех углов. Опять же, условие подобия состоит в том, что внутренние углы одного треугольника равны углам другого треугольника.
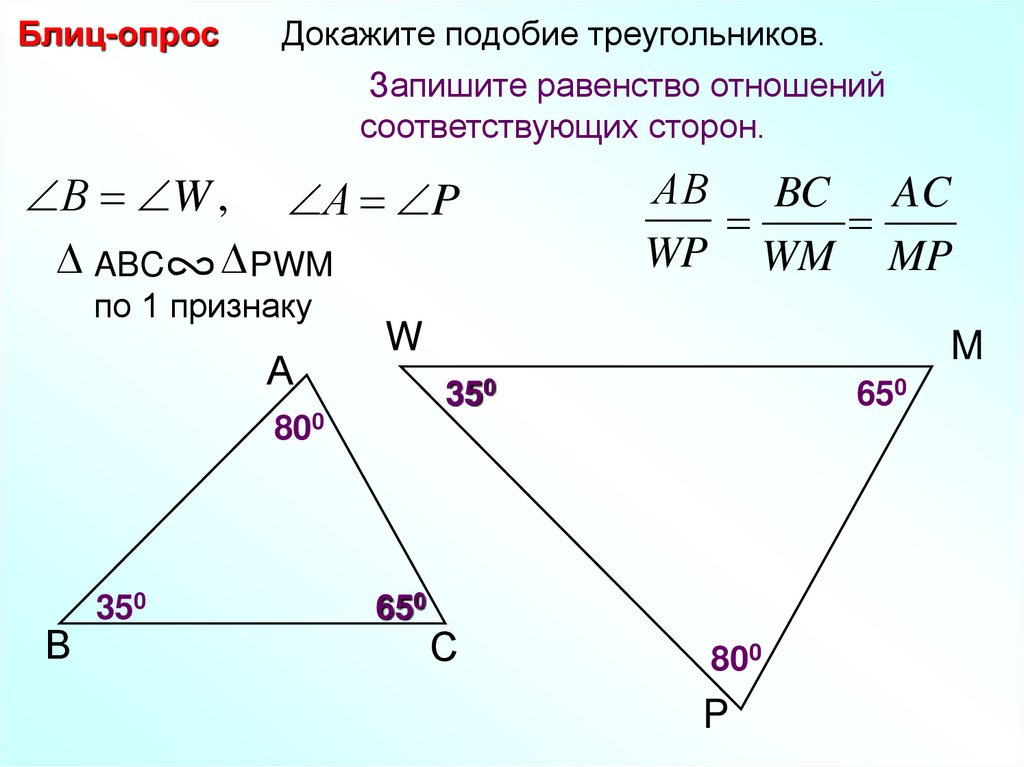
Первое условие, которое мы можем использовать для доказательства подобия, это условие угла-угла . Напомним, что сумма всех углов треугольника всегда равна 180°; таким образом, если два треугольника имеют два конгруэнтных угла, они также должны иметь конгруэнтный третий угол, как показано ниже.
Остальные критерии доказывают сходство через пропорциональность. Одним из этих критериев является условие сторона-сторона-сторона (пропорциональность) , которое просто утверждает, что если все соответствующие стороны двух треугольников пропорциональны (то есть они имеют одну и ту же константу пропорциональности), то они являются подобными треугольниками. . Рассмотрим, например, два треугольника ниже.
Поскольку длина каждой стороны самого правого треугольника составляет половину длины соответствующей стороны крайнего левого треугольника, эти два треугольника подобны. Таким образом, мы также можем заключить, что соответствующие углы двух треугольников равны.
Последний критерий сходства, который мы обсудим, это условие сторона-угол-сторона (пропорциональность) . В этом случае два треугольника подобны, если две соответствующие стороны пропорциональны и углы между ними равны. Рассмотрим два треугольника ниже.
Эти два треугольника подобны, потому что соответствующие помеченные стороны пропорциональны (длина сторон самого правого треугольника в 5/3 раза больше длины сторон самого левого треугольника), а соответствующие углы между ними равны. Таким образом, используя любой из вышеперечисленных критериев, мы можем доказать, что два треугольника равны.
Практическая задача: Докажите, что треугольники ABD и BCD подобны.
Решение : Докажем, что треугольники подобны, используя формат доказательства в два столбца. Обратите внимание, что треугольники имеют равные углы и . Мы также можем разделить треугольники для ясности.
1. Дано
2. , 8 = 2 ∙ 4
3. Даны, 4 = 2 ∙ 2
4. Стоки BC и BD и отчеты 2 и 3
стороны BD и AB пропорциональны
5. Треугольники ABD и BCD Сторона-угол-сторона (соразмерность) условие
подобны
Таким образом, мы показали, что два треугольника подобны.
Практическая задача : Докажите, что любые два равносторонних треугольника подобны.
Решение : Из нашего изучения треугольников мы знаем, что равносторонний треугольник содержит три конгруэнтных угла; таким образом, мера каждого угла в равностороннем треугольнике равна 60°. В результате по условию угол-угол все равносторонние треугольники должны быть подобны друг другу.
Практическая задача : Два равнобедренных треугольника имеют внутренний угол 100°. Докажите, что эти треугольники подобны.
Решение : Начнем с рисования схемы (необязательно в масштабе).
No related posts.