Симплекс метод c: Симплекс-метод. Реализация — Программирование на C, C# и Java

14. В чем особенности симплекс метода?

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.

15. Условие допустимости симплекс-метода.

Два правила выбора вводимых и исключающих переменных в симплекс-методе называются условием оптимальности и условием допустимости.

Условие оптимальности. Выбор переменной, вводимой в список базисных – просматривается последняя строка симплекс-таблицы, среди элементов этой строки выбирается максимальный по абсолютной величине отрицательный элемент. Столбец, в котором стоит этот элемент называется разрешающим.

Условие допустимости. Находят отношения элементов столбца свободных членов к элементам разрешающего столбца. При делении на отрицательный элемент и 0 результат полагают равным +oo. Среди полученных отношений выбирают минимальное. Строка, соответствующая минимальному отношению называется разрешающей. Пусть это будет строка q. Базисная переменная xq соответствующая этой строке выводится из списка базисных.

16. Может ли в ограничениях присутствовать неравенства при решении задачи симплекс методом?

Нет, так как симплекс-метод работает только с задачей в каноническом виде, где в ограничениях могут быть только равенства.

17. Могут ли, при решении задачи симплекс методом, присутствовать отрицательные переменные?

Да, могут.

18. Частные случаи использования симплекс-метода.

Следующие особые случаи, встречающиеся при использовании симплекс-метода:

1) вырожденность

Если на следующей итерации одна из базисных переменных равна нулю, то новое решение называют вырожденным. Наличие вырожденного решения не свидетельствует о какой-либо «опасности» для исследователя и вызывает лишь некоторое неудобство в теоретическом отношении. С практической точки зрения специфика ситуации целиком объясняется наличием в модели, по крайней мере, одного избыточного ограничения.

2) альтернативные оптимальные решения;

3) неограниченные решения;

Когда график целевой функции параллелен одной из прямой ограничений.

Тогда задача имеет бесконечное количество решений.

Или когда пространство решений по крайней мере в одном направлении не ограничено.

4) отсутствие допустимых решений.

19. Двойственная задача линейного программирования.

Любой задаче линейного программирования, называемой исходной или прямой, можно поставить в соответствие другую задачу, которая называется двойственной или сопряженной. Обе эти задачи образуют пару двойственных задач. Каждая из задач является двойственной к другой задаче рассматриваемой пары.

В теории двойственности используются четыре пары двойственных задач:

20. Соотношения между решениями исходной и двойственной задач.

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой, не решая ее, или установив его отсутствие.

Теорема (первая теорема двойственности). Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение; причем значения целевых функций задач на своих оптимальных решениях совпадают.

Если одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.

Теорема (вторая теорема двойственности). Для оптимальных планов прямой и двойственной задачи в каждой паре двойственных условий только одно условие может быть неактивным (нежестким, свободным).

Вторая теорема двойственности иначе называется принципом дополняющей нежесткости. Для ее формулировки нам потребуется ввести классификацию ограничений.

Если взять конкретный план задачи линейного программирования и подставить его в некоторое ограничение, имеющее вид нестрогого неравенства, то оно будет выполняться либо как равенство, либо как строгое неравенство. В случае равенства ограничение для этого плана будет активным (в другой терминологии жестким, связанным), а при неравенстве неактивным (нежестким, свободным)

Симплекс-метод c искусственным базисом — Студопедия

Поделись  

Шаг4.

Шаг3.

Шаг2.

Шаг1.

Симплекс-метод для решения задач линейного программирования

Графический метод решения задач линейного программирования прост и нагляден. Однако, практическое его применение ограничивается задачами, в которых всего две переменных величины. Если условие задачи линейного программирования непротиворечиво, то область её допустимых решений образует выпуклый многогранник в n-мерном пространстве. При этом оптимальное решение, если оно существует, обязательно достигается, в некоторой вершине многогранника (возможно и более чем в одной).

Таким образом, чтобы найти решение задачи линейного программирования достаточно перебрать лишь вершины многогранника области допустимых решений и определить точку (вершину), соответствующую оптимальному решению. Однако, в сложных задачах число вершин может оказаться очень большим, поэтому перебор всех вершин будет затруднен.

Симплекс-метод позволяет осуществить упорядоченный перебор вершин многогранника.

Симплекс-метод позволяет решать задачу линейного программирования, если она задача в виде основной задачи линейного программирования. Если же ограничения имеют вид неравенств, то необходимо от неравенств перейти к равенствам путем введения дополнительных неотрицательных переменных.

Пусть n-количество основных переменных, m- количество дополнительных переменных, тогда N=n+m – число переменных преобразованной системы ограничения.

Затем все переменные задачи должны быть разделены на

базисные , число которых равно m (количество уравнений системы) и свободные ,число которых равно k. Причем, базисные переменные и целевая функция должны быть выражены через свободные. При этом не следует смешивать свободные переменные с основными, а базисные с дополнительными.

Разделение переменных задачи линейного программирования, то есть отыскание первого базисного решения (первого базиса) , довольно сложная задача. Наиболее просто такое разделение переменных на базисные и свободные можно произвести в случае, когда K=N-m=n.

Допустим, что решение задачи линейного программирования существует, причем, оптимальное значение целевой функции конечно.

Рассмотрим алгебру симплекс-метода:

Выбрать «m» переменных, задающих первоначальное допустимое решение системы уравнений (базисное решение). Свободные переменные приравнять к 0. Найти значение базисных переменных.

Проверить, нельзя ли за счет одной из свободных переменных улучшить значение целевой функции, придавая этой переменной отличные от нуля положительные значения. Если это возможно, перейти к шагу 3, в противном случае вычисления прекратить.

Найти предельное значение переменной, за счет которой можно улучшить значение целевой функции. Улучшение значения этой переменной допустимо до тех пор, пока одна из «m» базисных переменных не обратится в 0. Эту переменную исключают из целевой функции и базисного решения, и вводят ту переменную, за счет которой результат может быть улучшен

Разрешить систему «m» — уравнений относительно новых базисных переменных. Исключить эти переменные из целевой функции и вернутся к шагу 2.

Исследование опорного плана на оптимальность, а также весь вычислительный процесс в симплекс –методе целесообразно вести в таблице.

В качестве исходного опорного плана задачи принимаем x₁=0,x₂=0, … , x_k=0, x_k+1=b₁, x_k+2=b₂, … , x_k+m=b_m

Рассмотрим заполнение симплекс таблицы:

В столбце «Базис» записываются переменные, входящие в базис, т.е. базисные переменные.

В столбце «С» записываются коэффициенты при неизвестных целевой функции, являющихся базисными переменными.

В столбце «План» записывают положительные компоненты исходного опорного плана.

В самой верхней строке таблицы записаны коэффициенты целевой функции.

Первые «m» строк таблицы определяются исходными данными задачи: это коэффициенты при переменных в уравнениях-ограничениях.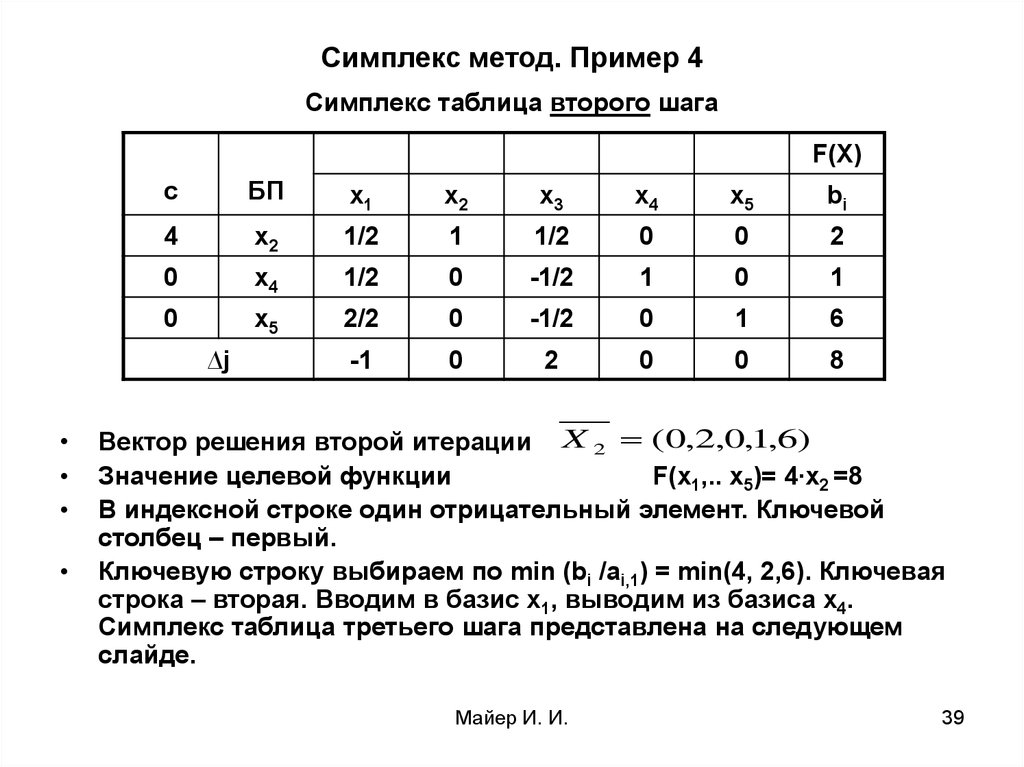

Показатели «m+1» вычисляются .В столбце «План» записывают значение целевой функции при данном опорном плане, а в столбцах «X

j»- значения Δj=Zj-Cj

(j=1,k)

После заполнения таблицы, исходный опорный план проверяется на оптимальность. Для этого просматривают элементы (m+1)-ой строки таблицы. В результате может быть иметь место один из 3-х случаев:

1. Δj≥0 (j=1,k) — в этом случае опорный план является оптимальным

2. Δj<0 – для некоторых j, но все коэффициенты a_ij в столбце Δj≤0. Это означает, что целевая функция не ограничена сверху на множестве планов.

3. Δj<0 – для некоторых индексов j и для каждого такого j , по крайней мере, одно из чисел a_ij >0 . Это означает , что можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится .

Переход от одного опорного плана к другому осуществляется исключением из исходного базиса одной переменной и введением в него новой.

В качестве переменной, вводимой в базис, выбирают ту, которой в строке «m+1» соответствует наибольшее по модулю отрицательное число (например, a_ij ).

Для определения переменной, подлежащей исключению из базиса , находят

min всех a_ij >0 (j=1,m)

Пусть этот min достигается в R-той строке, тогда из базиса будет исключена переменная x_k+r и введена на ее место переменная x_j.

Число a_rj называют направляющим (разрешающим) элементом, а соответствующие ему строка и столбец – направляющими.

Затем находится новый опорный план, т.е. заполняется новый раздел симплекс-таблицы.

Прежде всего заполняется строка вводимой переменной x_j.

Новые элементы этой строки определяются путем деления элементов r-той строки исходного опорного плана на направляющий элемент

В столбце «С» r-той строки нового опорного плана проставляется коэффициент целевой функции, соответствующий новой вводимой переменной.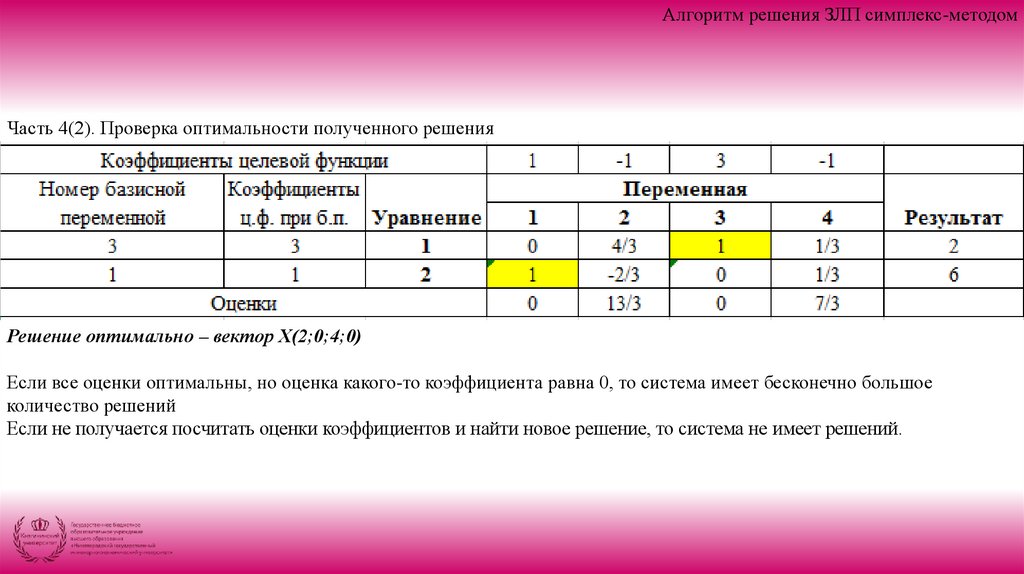

Пересчитаем столбец «план». r-ая строка уже заполнена, в столбце «план»

там стоит число b_r/a_rj.

Пересчет остальных элементов данного столбца ведут по правилу треугольника (правилу 3-х чисел)

Для этого находят три числа:

1. Число, стоящее в предыдущем разделе симплекс-таблицы на месте искомого элемента нового раздела таблицы.

2. Число, стоящее в предыдущем разделе симплекс-таблицы на пересечении строки, в которой находится искомый элемент новой симплекс- таблицы, и столбца, соответствующего переменной, вводимой в базис.

3. Число, стоящее в новом разделе симплекс -таблицы на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимой в базис переменной (выделенной строки)

Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс- таблице, а третье – числу, находящемуся в новой симплекс – таблице.

Для определения искомого элемента новой симплекс – таблицы из первого числа вычитают произведение второго и третьего.

После заполнения столбца «План» пересчитывают матрицу коэффициентов, используя рассмотренное выше правило треугольника. Переменным , входящим в базис, всегда соответствуют в матрице коэффициентов единичные векторы — столбцы. Определяют элементы «m+1» строки нового опорного плана ().

Если все элементы Δ ́j =Z ́j – Cj ≥ 0, то новый опорный план является оптимальным.

Если же среди указанных чисел имеются отрицательные, то используя описанную выше последовательность действий, находят новый опорный план.

Процесс продолжают о тех пор , пока либо не получат оптимальный план задачи , либо не установят ее неразрешимость.

Итак, нахождение оптимального плана симплекс-метода включает следующие этапы :

1. Находят опорный план.

2. Составляют симплекс-таблицу.

3. Выясняют, имеется ли хотя бы одно отрицательное число Δ j. Если нет, то найденный план оптимален, если есть, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.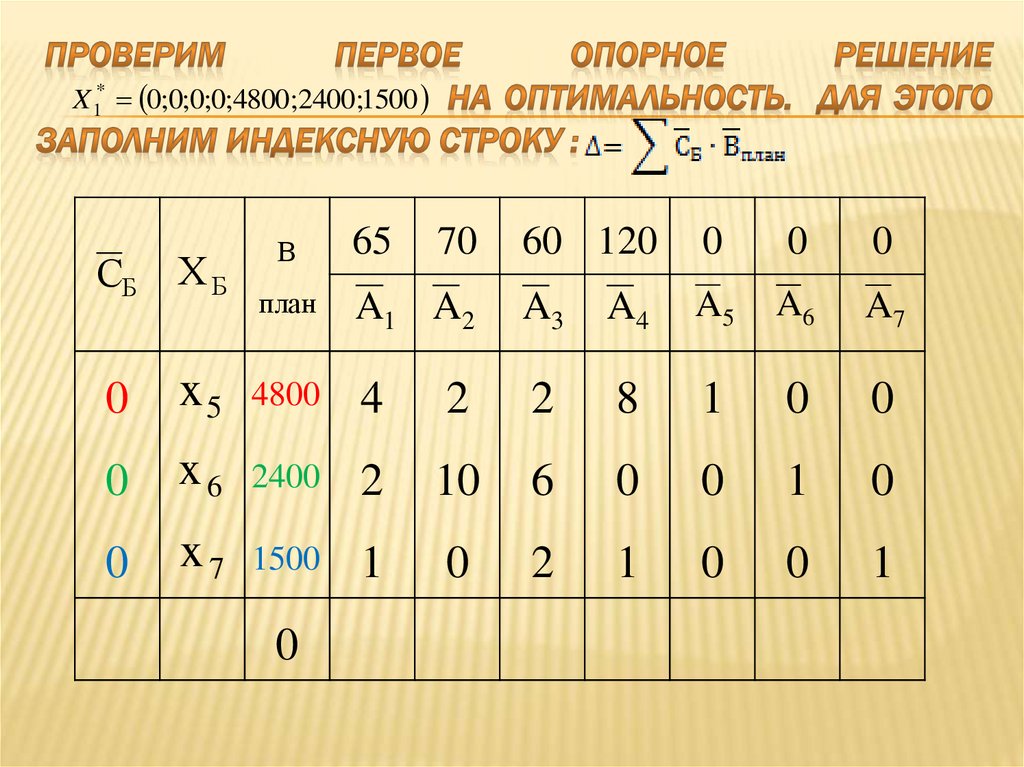

4. Находят направляющую строку и столбец.

Направляющий столбец определяется наибольшим по модулю отрицательным числом Δ j, а направляющая строка – минимальным из отношений столбца «план» и положительных элементов направляющего столбца.

5. Определяют положительные элементы нового опорного плана.

6. Проверяют найденный план на оптимальность. Если план не оптимальный , то возвращаются к пункту 4, а если план оптимален или установлена неразрешимость, то процесс решение задачи закончен.

Пример №1.

Найти решение задачи линейного программирования

Z = x₁ + 3x₂ →max при ограничениях:

x_j ≥0 (j=1,5)

Рассматриваемый алгоритм симплекс- таблицы требует, чтобы задача была приведена к виду ОЗЛП: ограничения заданы в виде системы уравнений, а целевая функция стремилась к максимуму.

Составим симплекс-таблицу:

В первый раздел симплекс-таблицы записываем матрицу коэффициентов системы ограничений.

Выбираем базисные переменные, ими будут те переменные, вектора которых в совокупности образуют единичную матрицу. У нас это х₃, х₄, х₅.

Заполняем вторую и третью колонку симплекс-таблицы.

В колонку «план» записываем столбец свободных членов.

Заполняем индексную (4) строку , и по ней ведем анализ.

В этой строке есть отрицательные элементы, а в соответствующих им столбцам есть положительные элементы. Следовательно ,план можно улучшить.

Выбираем max по модулю отрицательный элемент, ему соответствует переменная х₂, ее будем вводить в базис.

Определим выводимую переменную.

Находим min:

=4 соответствует х₄

х₃ х₄ х₅

Значит выводим из базиса х₄

Разрешающий элемент а₂₂=6

Переходим к заполнению второго раздела симплекс-таблицы

Первой заполняется вторая строка (выделенная строка) . ее элементы находятся путем деления элементов разрешающей строки первого раздела на разрешающий элемент.

Пересчет всех остальных элементов этого раздела ведем по правилу трех чисел.

Вновь анализируем индексную строку и видим, что план можно улучшить.

Вводимой переменной будет х₁ , а выводимой будет х₃ .

Заполнение элементов третьего раздела ведем аналогично.

В индексной строке третьего разделяя все Δj≥0, следовательно, процесс вычисления закончен, найдено оптимальное решение задачи:

Z^* = 15 X^* = (6;3;0;0;21)

Симплекс-таблица позволяет контролировать процесс вычислений, начиная со второго раздела.

Элементы всех строк этого раздела пересчитываются по правилу трех чисел (кроме выделенной строки), а для контроля элементы индексной строки находят так же, как и в первом разделе. Если значения совпали, то ошибок нет.

Пример 2.

Найти решение задачи линейного программирования

Z = 2x₁ − 6x₂ +5х₅→max при ограничениях:

x_j ≥0 (j=1,6)

I-ая итерация.

Вводим х₅, т.к max |-a_ij|=|-5|

Выводим х₄, т.к min

II-ая итерация

Анализ четвертой строки показывает, что задача оптимального решения не имеет. Целевая функция не ограничена сверху, т.к в индексной строке есть отрицательный элемент, а в соответствующем ему столбце нет положительных.

Для построения исходного опорного плана при решении задачи симплекс-методом необходимо, чтобы матрица коэффициентов при переменных, имеющая «m» строк и «n» столбцов (m<n), содержала в себе единичную матрицу порядка «m». Такая матрица получалась после введения дополнительных переменных в исходные ограничения вида «≤». Однако, если исходные ограничения задаются сразу уравнениями, то нет никакой гарантии, что матрица коэффициентов содержит единичную матрицу порядка «m». То же относится и к системе неравенств вида « ≥».

Дополнительные переменные входят в такую систему с коэффициентами «-1». В этих случаях для решения задачи применяется симплекс-метод с искусственным базисом.

В левую часть уравнений вводятся неотрицательные искусственные переменные ω₁, ω₂, …, ω_m , коэффициенты при которых образуют единичную матрицу. Эти же переменные с большими по абсолютной величине отрицательными коэффициентами (-M) включаются в целевую функцию.

В результате расширенная задача принимает вид:

При условиях:

,

Искусственные переменные необходимы для построения исходного плана задачи. В процессе решения они должны выводиться из базиса, т.к. в окончательном плане задачи должны соблюдаться исходные уравнения, а это возможно когда ω_i=0.

Решение задачи линейного программирования методом искусственного базиса включает следующие этапы.

1. Составляют расширенную задачу.

2. Находят опорный план расширенной задачи.

3. С помощью обычных вычислений симплекс-методом исключают искусственные переменные из базиса. Анализ ведут по «m+2» строке. В результате находят опорный план исходной задачи, либо устанавливают ее неразрешимость.

4. Используя найденный опорный план исходной задачи симплекс-методом находят оптимальный план (анализ ведут по «m+1» строке) или устанавливают неразрешимость задачи.

Возможны случаи , когда при оптимизации опорного плана расширенной задачи в «m+2» строке еще остается отрицательное число, но в соответствующем ему столбце нет положительных коэффициентов, следовательно, в базисе остаются несколько искусственных переменных и они не могут быть выведены. Это означает, что исходная задача не имеет искомого решения. Полученный план не удовлетворяет всем поставленным условиям, и окончательный базис будет содержать искусственную переменную.

Пример:

Найти оптимальное решение задачи

F=-2x₁+3x₂−6x₃−x₄→min

при ограничениях

Приведем задачу к виду основной задачи линейного программирования, учитывая, что целевая функция должна стремиться к max

:

F=-2x₁+3x₂−6x₃−x₄→max

Среди векторов, составленных из коэффициентов при неизвестных, только два единичных (х₄ и х₅), поэтому в левую часть третьего уравнения добавим искусственную переменную ω и составим расширенную задачу:

F=-2x₁+3x₂−6x₃−x₄−М ω →max

Теперь задача содержит необходимое количество единичных векторов, образующих базис. Составим симплекс –таблицу

1-ая итерация

План можно улучшить . Анализ ведем по второй индексной строке . Вводимой переменной будет х₃ ,а выводимой ω т.к.

Примечание.

Искусственную переменную всегда стараются вывести первой. Как только ω выведена из базиса , на последующих итерациях столбец ω не заполняется и индексная строка будет одна .



Симплексный метод для LP — библиотека ALGLIB, C++ и C#

Руководство пользователя ALGLIB — Линейное программирование — Симплексный метод

Симплекс-метод — один из двух наиболее часто используемых алгоритмов линейного программирования. (другой популярный подход — метод внутренних точек, который также включен в ALGLIB). ALGLIB реализует так называемый пересмотренный метод двойного симплекса с несколькими существенными улучшениями производительности и стабильности, которые обсуждаются в разделах ниже.

В этой статье представлен общий обзор реализации симплекс-метода в ALGLIB. В нем обсуждаются такие вопросы, как сильные и слабые стороны алгоритма, его стабильность и производительность. API линейного программирования ALGLIB описан в этой отдельной статье.

Содержимое

1 Пересмотренный метод Dual Simplex
Алгоритм
Улучшения
Сравнение с методом внутренней точки
2 Аспекты производительности
C ++ против C#
SIMD и Parallelism
3 Работа с Simplex Solver
4 Раздел

Симплексный метод — это метод активного множества. Каждый шаг симплекс-метода деактивирует одно ограничение коробки и выбирает другое для активации (общие линейные ограничения всегда выполняются). Обычно для метода активного набора O(N+M) шагов требуется для N -мерной задачи с M общими линейными ограничениями.

Симплекс-метод останавливается, когда решатель находит пробную точку (уникально определяемую активным набором), которая достижима в прямом/двойственном порядке. Здесь первичная выполнимость означает, что пробная точка не нарушает ограничений, а двойная осуществимость означает, что нет направлений спуска, «выходящих» из пробной точки. Точка, которая является одновременно прямой и двойственно допустимой, является решением задачи линейного программирования потому что он и локально оптимален, и не нарушает ограничений.

Метод первичного симплекса начинается с пробной точки, которая является первично выполнимой, и повторяется до двойной выполнимости. Двойной симплекс-метод начинается с пробной точки, которая является двойной допустимой, и повторяется до первичной выполнимости. ALGLIB реализует трехфазный двойной симплекс-метод с дополнительным возмущением, нарушающим вырождение:

• Фаза 1 находит начальную двойную допустимую точку путем минимизации суммы двойных недопустимостей возмущенной задачи линейного программирования.
• Фаза 2 начинается с двойной допустимой точки и повторяется до тех пор, пока не будет найдена точка, которая одновременно является и первичной, и двойной допустимой.
• Фаза 3 удаляет возмущение, нарушающее вырождение, из вектора стоимости и выполняет несколько итераций метода простого симплекса для восстановления двойной осуществимости

Наша реализация симплекс-метода имеет следующие улучшения по сравнению с «учебной» версией:

• Обновления Forrest-Tomlin для более быстрого рефакторинга LU
• Тест связанного коэффициента переключения (также известный как длинный двойной шаг) для более длинных шагов.
• Двойное ценообразование с наибольшей крутизной для лучшего выбора остаточной переменной
• Сдвиг (динамические возмущения применяются к вектору стоимости) для лучшей стабильности

Метод внутренних точек, еще один решатель, реализованный в ALGLIB, решает задачу линейного программирования, применяя итерацию Ньютона к линейной целевой функции с дополнительными логарифмическими барьерными членами. Метод внутренних точек в некотором смысле двойственен симплексному методу:

• Симплексный метод имеет очень низкую стоимость итерации, но для сходимости требуется около O(N+M) итераций. В отличие от этого, метод внутренней точки сходится за 10-30 итераций, но стоимость итерации намного выше.
• Симплекс-метод возвращает решения, которые «прилипают к границам», т. Е. Он предпочитает точки, расположенные точно на границе допустимого множества. Метод внутренних точек, как и другие барьерные методы, возвращает точки, приближающиеся к границам изнутри допустимой области. В результате иногда симплекс-метод и метод внутренней точки возвращают несколько разные решения (которые по-прежнему имеют одинаковое значение целевой функции).
• Наконец, метод внутренней точки довольно легко ускорить: общая структура алгоритма очень проста, и большая часть времени уходит на разреженную факторизацию Холецкого/LDLT. В отличие от этого, симплекс-метод представляет собой очень сложный алгоритм с шаблонами доступа к данным, которые трудно оптимизировать.

В этом разделе мы рассмотрим различные факторы, влияющие на эффективность симплекс-метода.

Время выполнения симплекс-метода зависит от того, работаете ли вы с собственным ALGLIB (доступно на C++, C#, Python и других языках). или его полностью управляемая версия (доступна на C#, VB.NET и IronPython). Платформа .NET значительно улучшилась за последние несколько лет. но код C/C++ с интенсивными математическими вычислениями по-прежнему примерно в 2 раза быстрее, чем эквивалентный полностью управляемый код C#. Эта разница в основном объясняется тем, что управляемый код должен проверять каждое обращение к массиву на предмет нарушения границ массива.

В результате предпочтительнее работать с собственным вычислительным ядром. Если вы используете ALGLIB для C++, вы уже на стороне победителя. Пользователи C# могут счесть полезным использовать оболочку C# вокруг собственного ядра (доступно в коммерческой версии). С другой стороны, полностью управляемая версия по-прежнему хорошо оптимизирована — мы пытались добиться наилучшего результата, возможного при условии полного управления.

Известно, что симплексный метод трудно распараллелить и/или ускорить с помощью SIMD. Алгоритм по своей сути является последовательным, со многими недорогими взаимозависимыми шагами и нерегулярными шаблонами доступа к памяти. Таким образом, реализация симплексного метода в ALGLIB не поддерживает SIMD/SMP.

Функциональность линейного программирования предоставляется подпакетом minlp. Класс minlpstate предоставляет общий интерфейс для всех решателей (симплексный метод и метод внутренней точки), поддерживаемых ALGLIB.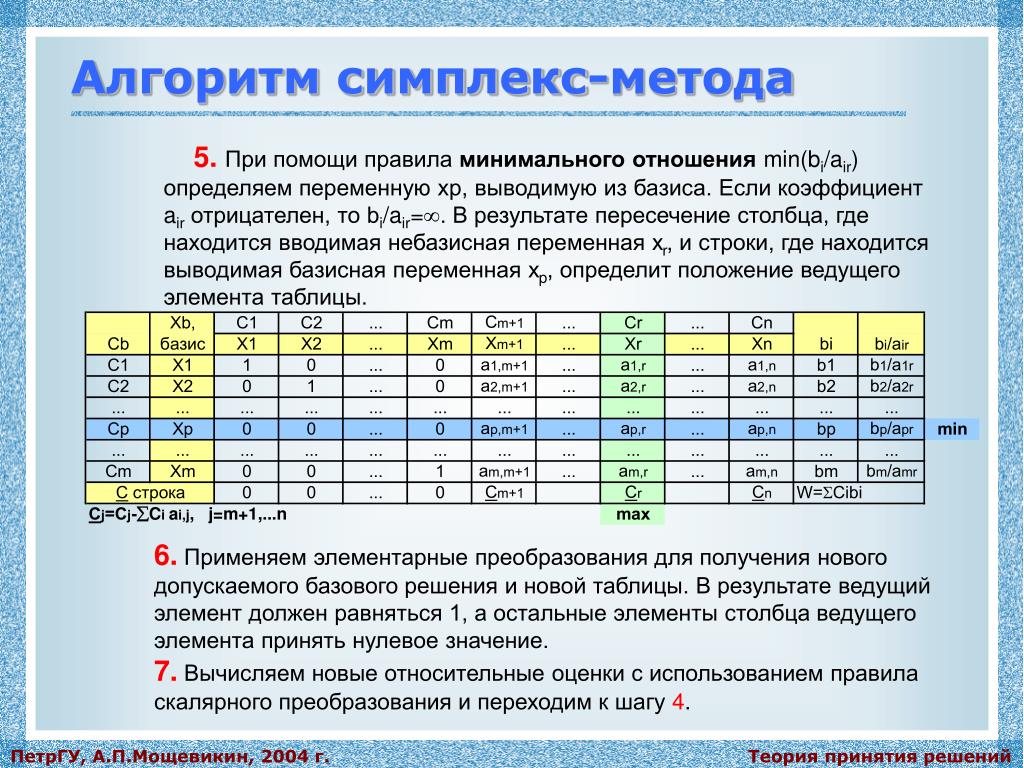 Этот интерфейс описан в этой отдельной статье, в которой объясняется, как задавать и решать задачи линейного программирования с помощью ALGLIB.

Эта статья лицензирована только для личного использования.

Симплексный метод: простой способ. Примерный подход к пониманию… | Виджаясри Айер

Примерный подход к пониманию симплексного метода оптимизации

Симплексный метод, изобретенный Данцигом в 1946 году, до сих пор остается одним из самых элегантных методов решения задач линейного программирования (ЛП). LP занимается поиском оптимального решения линейной функции с учетом некоторых линейных ограничений. Он используется в реальных задачах оптимизации в нескольких областях. Сегодня давайте попробуем понять работу этого алгоритма простым и кратким образом, используя пример, который поможет нам в этом.

Метод

1. Настройка/преобразование LP в стандартную форму максимизации.
2. Настроить начальную симплексную таблицу
3. Определить опорную точку
4. Найти оптимальную таблицу методом Гаусса-Жордана
5. Проверить оптимальность таблицы
6. Найти оптимальное решение

Шаг 1: Преобразовать LP в стандартную форму максимизации

пример:

Задача максимизации

(Примечание: В случае задачи минимизации ее можно преобразовать в задачу двойной максимизации, умножив на -1. )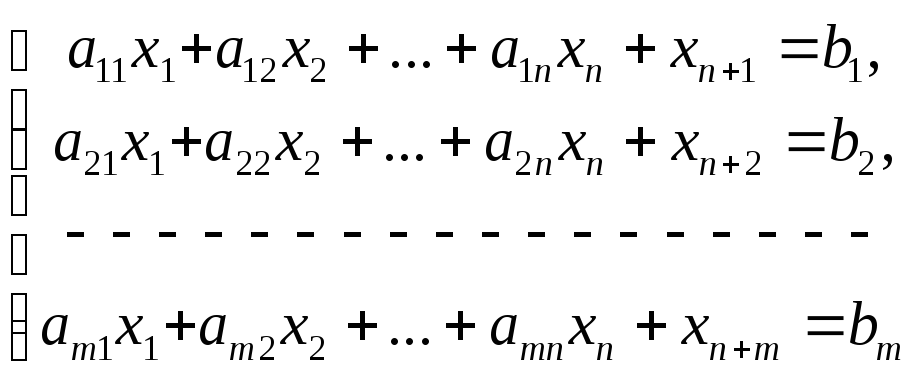

В стандартной форме LP все ограничения являются уравнениями и все переменные неотрицательны . Можно выполнить следующие шаги преобразования, чтобы преобразовать все неравенства в ограничения равенства .

1. Если ограничение имеет тип (x + y ≤ c), используйте резервную переменную «s» (где «s» неотрицательно), так что x+y+s = c.

2. Если ограничение относится к типу (x + y ≥ c), используйте дополнительную переменную «s» (где «s» неотрицательно), так что х+у-с = с .

Используя этот метод преобразования на нашем примере, мы получаем следующую систему уравнений:

Система уравнений в стандартной форме полученный. Это выглядит примерно так:

Таблица 1.1

Шаг 4. Определение опорной точки

В симплексной таблице опорная точка определяется с использованием следующих двух условий

1. Сводная колонка выбирается путем определения самой отрицательной записи в нижней строке таблицы.
2. Сводная строка определяется путем деления констант (столбец C в таблице) на коэффициенты сводной колонки. Строка, содержащая наименьшее частное, будет основной строкой.

(Подробное объяснение этого метода можно найти здесь.)

В нашем примере столбец «y» является сводным столбцом, поскольку он содержит -40, а сводная строка — R3 (строка 3), поскольку 12/ 2 =6 — наименьший коэффициент в сводном столбце. Следовательно, наш опорный элемент равен 2,9.0003 Таблица 1.2

Шаг 3. Определите оптимальные значения, выполнив операции поворота с использованием метода исключения Гаусса-Жордана

После того, как мы определили элемент поворота, мы выполним метод исключения Гаусса (выполним преобразования строк на R1, R2, R3, R4 ). Мы преобразуем опорный элемент в 1 , а все остальные элементы в опорном столбце — в 0. . В этом случае мы будем использовать следующие преобразования строк, чтобы получить результат

9. 0033

R3->R3/2

R1->R1- R3

R2->R2- R3

R4->R4+40R3

Шаги, есть два термина, с которыми вам нужно ознакомиться.

Базовая переменная : Обычно говорят, что сводной столбец представляет базовую переменную. Хотя, если говорить проще, базовой переменной является любая переменная в таблице, которая имеет только один ненулевой элемент, т.е. представляет собой единичную матрицу. В таблице 1.3 y, s1, s2 и P являются основными переменными. Для математического определения, пожалуйста, проверьте здесь.

Небазовая переменная : Небазовая переменная, с другой стороны, не представляет единичную матрицу и имеет более одного ненулевого элемента. В таблице 1.3 s3 и x являются неосновными переменными.

Когда нам нужно определить основное допустимое решение, мы установим все неосновные переменные в 0, что даст нам максимальные значения основных переменных. Установив s3, x = 0, получим y = 6, s1 = 4, s2 = 1, P = 240.

Теперь по симплекс-методу, если в самой нижней строке (т.е. R4) нет отрицательного коэффициента мы можем остановиться здесь. Если нет, то мы повторяем шаги 3 и 4 , пока не удалим все отрицательные члены в нижней строке и не найдем оптимальное решение. В нашей таблице у нас есть -10 в R4, поэтому нам нужно выполнить еще одну итерацию шагов 3 и 4.

Итерация 2

Используя процедуру шага 3, мы идентифицируем нашу новую точку опоры как 1/2 в R2, а столбец «х».

Tableau 1.4

Мы будем использовать следующие преобразования строк, чтобы сделать все записи 0 в сводной таблице 1 в столбце «x».

• R2->2R2
• R1->R1–3/2R2
• R3->R3–1/2R2
• R4 ->R4+10R2

Таблица 1.5

Присвоив неосновным переменным значение 0, мы получаем x =2, y=5 , s1=1 и P = 260. Следовательно, наши оптимальные значения для x и y равны 2,5. Для тех, кто заинтересован в решении таких задач с использованием графического подхода, пожалуйста, обратитесь сюда.