Процентное отклонение с отрицательным числом: формула Excel
Обычная формула для вычисления процентного отклонения прекрасно работает до той поры пока не приходиться работать с отрицательными числами. Проверьте стоит нам изменить значение в процентном отношении на отрицательное число в результате мы получаем ОШИБКУ! То есть формула процентного отклонения с отрицательным числом в числителе: =-10/20-1 или так: =(20—10)/10 в любом случаи формулой будет возвращено ошибочное значение -300%. Возникает вопрос откуда появилось минус триста процентов? Для ответа на этот вопрос и как делать правильно покажем на конкретном примере ниже.
Вычисление процентного отклонения для отрицательных чисел
Почти каждый инвестиционный проект пока еще не вышел на точку окупаемости в первый год приносит больше расходов чем доходов. Для этого при составлении бизнес-плана был заложен в бюджет объем просадки инвестиционного портфеля в пределах -10000$. Допустим объектом для инвестирования были криптовалюты биткоин и за первый очень успешный год доходность инвестиционного портфеля взлетела до +12000$.
Вычисление процентного отклонения отношения между запланированной просадкой инвестиций и фактическим доходом по старой формуле: -10000/12000-1 дает -220%!
Почему же мы получили аж -220% отклонения? Ведь известно то, что доход не только перекрыл расходы и преодолел точку окупаемости, но и принес чистую прибыль в размере аж 12000$! Что ж, проблема возникает в том, что если значение отношения является отрицательным, то математическое вычисление возвращает обратный результат. В математике минус на минус всегда дает плюс, поэтому в нашей формуле нарушаются вычислительные операции. Часто такие ошибки допускаются при работе в Excel с бюджетами где запланированные расходы выражаются в отрицательных числах.
Для решения данной задачи следует использовать функцию =ABS(), которая преобразовывает отрицательное число в положительное. То есть, функция сама найдет модуль числа (его абсолютную величину). На рисунке показано как ведет себя модифицированная формула для вычисления процентного отклонения с отрицательными числами при любых условиях.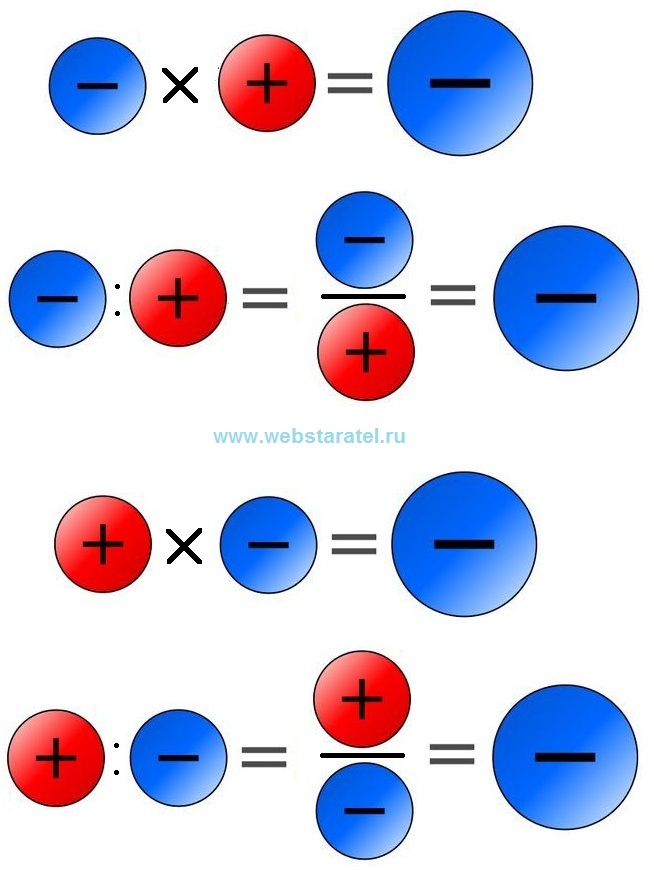
Как видите, чтобы вычисление процентного отклонения в Excel возвращало правильный результат при любых положительных или отрицательных числах в числителе и знаменателе следует использовать такую формулу:
На картинке видно, что доходности инвестиционного портфеля необходимо было преодолеть путь длинною в 220% (22000$), чтобы пройти от -10000$ до +12000$.
Из этого следует что доходность инвестиционного портфеля составила 120% годовых, потому как: (22000-10000)/10000=120%. А если мы при такой доходности инвестируем 10000$, то через год не только вернем вложенные средства, а еще и заработаем 12000$.
Интересный факт! На сегодняшний день среднестатистический показатель рискованных инвестиций составляет всего 70% годовых.
Эти формулы можно смело применять как при отрицательных, так и при положительных значениях. Процентное отклонение возвращается безошибочным в результате вычисления формулой с функцией ABS.
Описание примера работы функции ABS
Функция ABS возвращает абсолютное значение величины для любого числа.
Если мы ведем в ячейке A1 формулу с функцией ABS в аргументах, которой будет указано отрицательное или положительное число, то в результате функция возвращает всегда только положительное число ABS(-100) = 100. Поэтому функция ABS, использованная в выше описанном примере, позволяет преобразовать отрицательнее число в положительное перед математическим вычислением для нахождения процентного отклонения (в данном случаи с отрицательным бюджетом -10 000$).
Читайте также: процентное распределение в Excel.
В результате формула возвращает безошибочное истинное значение, которое теперь можно использовать в дальнейший расчетах и анализах данных.
Отрицательные числа – примеры, правила знаков
4
Средняя оценка: 4
Всего получено оценок: 284.
4
Средняя оценка: 4
Всего получено оценок: 284.
Отрицательные числа тяжело воспринимаются учениками 6 класса математики, поскольку долгое время их учат том, что все результаты вычислений, которые меньше нуля неверны.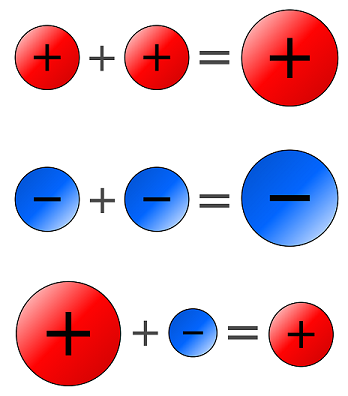
Отрицательные числа
Отрицательным числом называется любое число меньше нуля. Чтобы обозначить, что число меньше нуля, перед ним ставится знак минус.
Среди отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Практически все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Так же важно помнить, что число 0 не относится ни к положительным, ни к отрицательным числам.
Числовая прямая
Числовая прямая это прямая, которая имеет обозначение 0 и единичных отрезков. На числовой прямой все отрицательные числа лежат левее нуля.
Числовую прямую очень удобно использовать для сравнения отрицательных чисел. Чем ближе отрицательное число на числовой прямой к нулю, тем большим значением оно является.
Правило знаков
Умножение и деление отрицательных чисел происходит согласно правилу знаков:
- При умножении или делении отрицательного числа на отрицательное, в результате получится положительное число.
- При умножении или делении положительного числа на отрицательное в результате получится отрицательное число.
- При умножении или делении отрицательного числа на положительное, получится отрицательное число.
Сложение отрицательных чисел
При сложении отрицательных чисел действует все то же правило знаков, только в несколько ином виде. Общая формулировка правила знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». Тогда если к одному отрицательному числу прибавить другое, то получится:
-а+(-в)=-а-в – то есть из отрицательного числа вычитается положительное.
-а-(-в)=-а+в – к отрицательному числу в итоге прибавляется положительное.
Что мы узнали?
Мы поговорили об отрицательных числах. Рассказали, как удобнее сравнивать отрицательные целые числа, а также как правильно подобные числа перемножать между собой, делить, складывать и вычитать.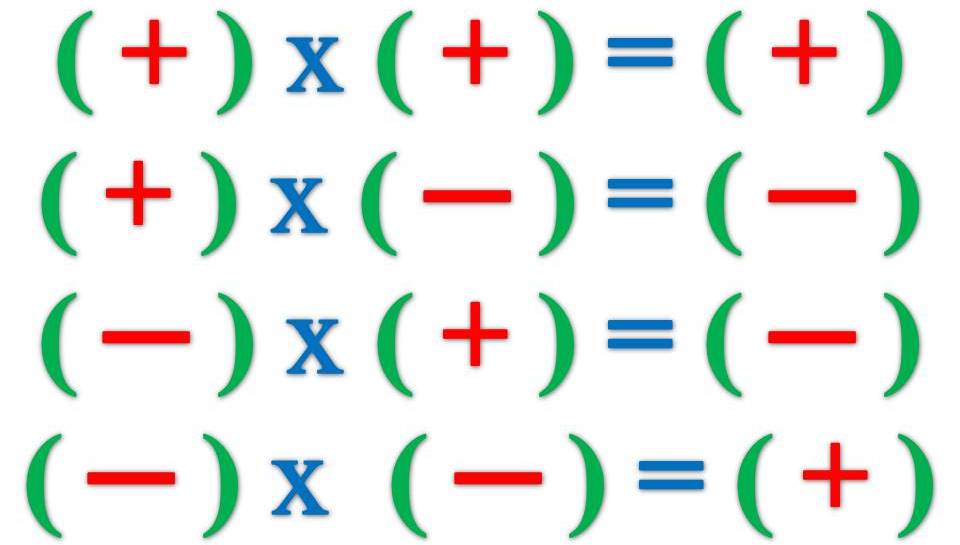
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ярослав Перфильев
5/5
Георгий Григорьев
4/5
Sveta Sveta
4/5
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 284.
А какая ваша оценка?
Я запутался в сложении, вычитании, умножении и делении отрицательных чисел.
Некоторым людям поначалу может быть трудно понять, что делать с отрицательными числами, потому что это требует уровня абстрактного мышления, который не так необходим при работе с положительными числами. Базовые уроки математики часто связаны с физическими, реальными ситуациями, чтобы вы могли лучше визуализировать происходящее. Вас могут спросить: «Если у Джордана 9 кошек, а у Аарона 12 кошек, сколько у них всего кошек?» в качестве иллюстрации сложения или «Если вы хотите дать равное количество шариков каждому из 8 человек, и у вас есть 24 шарика, сколько шариков получит каждый человек?» чтобы проиллюстрировать разделение.
Отрицательные числа нельзя так просто проиллюстрировать реальными примерами. Например, вы можете представить, что у Джордана нет кошек, но что значит для Джордана наличие -4 кошек? Как у него может быть меньше нуля кошек?
Очевидно, что не может. Отрицательные числа требуют от вас абстрактного мышления. Использование числовой линии может помочь вам легче визуализировать математику, но со временем, по мере развития ваших способностей к математическому мышлению, ваша способность понимать абстрактные отрицательные числа улучшится, и вы больше не будете думать об отрицательных числах.
Но до тех пор было бы неплохо просто запомнить несколько правил об отрицательных числах и о том, как их использовать.
Умножение и деление отрицательных чисел
Умножение и деление — две стороны одной медали, и когда дело доходит до отрицательных чисел, они оба подчиняются одним и тем же правилам, которые можно проиллюстрировать простой таблицей:
Второе число положительное (+) | Второе число отрицательное (–) | |
| Первое число положительное (+) | Положительный ответ (+) | Ответ отрицательный (–) |
Первое число отрицательное (–) | Ответ отрицательный (–) | Положительный ответ (+) |
Иными словами, если оба числа имеют одинаковый знак, ответ положительный; если числа имеют разные знаки, ответ отрицательный.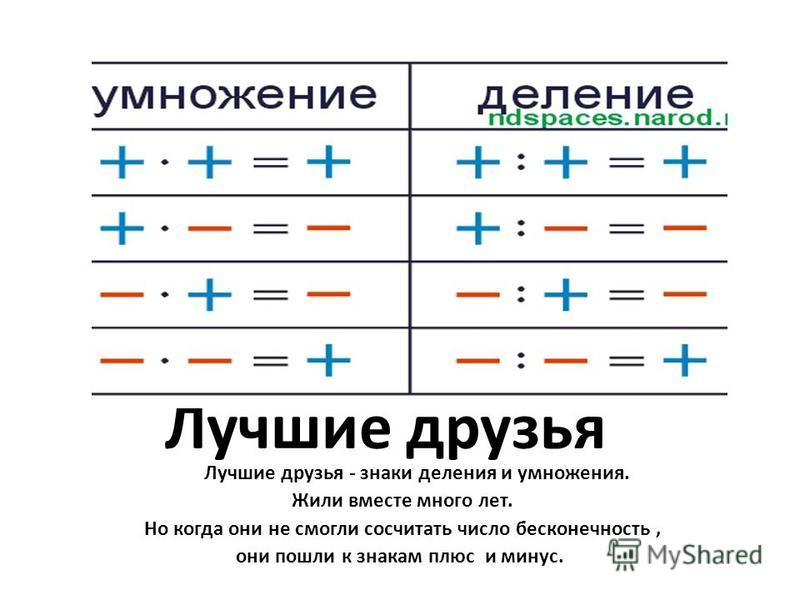
Сложение и вычитание с отрицательными числами
Во-первых, поймите, что сложение и вычитание — это, с одной точки зрения, одно и то же. Вычитание числа — это то же самое, что добавление отрицательного значения этого числа. Например, 4 – 12 равно 4 + –12 (что, поскольку порядок членов не имеет значения при сложении, равно –12 + 4). Имея это в виду, вот правила сложения с отрицательными и положительными числами:
- Если оба числа положительные, то и ответ положительный.
- Если оба числа отрицательные, то и ответ отрицательный.
- Если числа имеют разные знаки, ответ принимает знак большего числа.
- Вычитание отрицательного числа равносильно добавлению его положительного числа. Например, 5 – –4 равно 5 + 4.
Деление отрицательных чисел. Математика 6-го класса
Освойте 7 столпов школьной успеваемости
Улучшите свои оценки и снизьте стресс
Common Core Standard 9 0088 6.
NS.C.5
Математика 6 класса
Как умножать положительные и отрицательные целые числа
Применение одних и тех же правил к отрицательным и десятичным числам.
+/ -= -, -/ -+, -/+ = —
15/ -. 5 = -30
-540/1.2 = -450
-540/1.2 Вот ссылка на полезное видео о том, как делить с десятичной дробью.
Разделение на десятичные десятки
Предальгебра/выражения, уравнения
.
Геометрия/Фигуры
Геометрия/SAT
Геометрия/Плоскость
Привычки к обучению
Геометрия/Основы
Подпись Transcripting Numbering0036
Сегодня мы пройдемся по разделу.
Вот наши примеры. Двадцать разделить на минус два, что минус десять. Отрицательные двенадцать, деленные на отрицательные три, дают положительные четыре. Третий — минус восемнадцать, деленный на плюс девять — минус два. Теперь давайте пройдемся по правилам деления чисел со знаком. Правила аналогичны правилам сложения и вычитания. Если у вас есть отрицание, разделенное на отрицательное, эти два являются парами, поэтому у нас есть положительный результат, поэтому отрицательные значения всегда идут парами. Отрицательное разделить на положительное, у отрицательного нет пары, поэтому ответ отрицательный. Положительное разделить на отрицательное. Опять же, у отрицательного числа нет пары, поэтому ответ отрицательный. Наконец, положительное, деленное на положительное, является положительным. Итак, давайте вернемся и посмотрим на наши первоначальные проблемы в замедленном темпе. Итак, первая проблема — это положительное, деленное на отрицательное. У нас есть только один отрицательный и у него нет партнера, поэтому ответ отрицательный.
На втором у нас есть отрицательные двенадцать, и эта дробь — еще один способ сказать, что деление е делится на отрицательные три. Эти два отрицания являются партнерами и образуют пару, поэтому мой ответ положительный. Третий — минус восемнадцать, деленный на положительную девятку, поскольку у нас есть только один минус, ответ должен быть отрицательным, восемнадцать разделить на девять — два. Итак, наши ответы.
Примеры задач на деление отрицательных чисел
Помните, что «подобные знаки дают положительное число» в отличие от знаков дают отрицательное число»
Деление отрицательного на отрицательное
Деление положительного на отрицательное
Рассмотрим правила деления положительных и отрицательных целых чисел.0036
- При делении двух чисел с одинаковым знаком произведение положительное.
- При делении двух чисел с разными знаками произведение отрицательное.
или…. помните, что….
Подобные знаки дают положительное число, а противоположные знаки — отрицательное число.
или…..
Помните, что минусы должны идти парами.
-4/2 = -2
-15/-5 = 3 Уведомление о применении «Негативы приходят в паре».
Вам также может понравиться ……….
Сложение отрицательных чисел
Умножение положительных и отрицательных чисел
Деление положительных и отрицательных целых чисел
15/-5= -3
В математике числа могут быть как больше нуля, так и меньше нуля. Мы различаем эти числа, называя их либо положительным числом, либо отрицательным числом. Мы используем символ — для обозначения отрицательного числа. На числовой прямой положительное число будет справа от нуля, а отрицательное число будет слева от нуля.
Когда вы делите отрицательные числа, может быть немного сложно определить, будет ли ответ положительным или отрицательным.