Доказательство второго признака равенства треугольников: Второй признак равенства треугольников

Задачи на признаки равенства треугольников: угол-сторона-угол и сторона-сторона-сторона

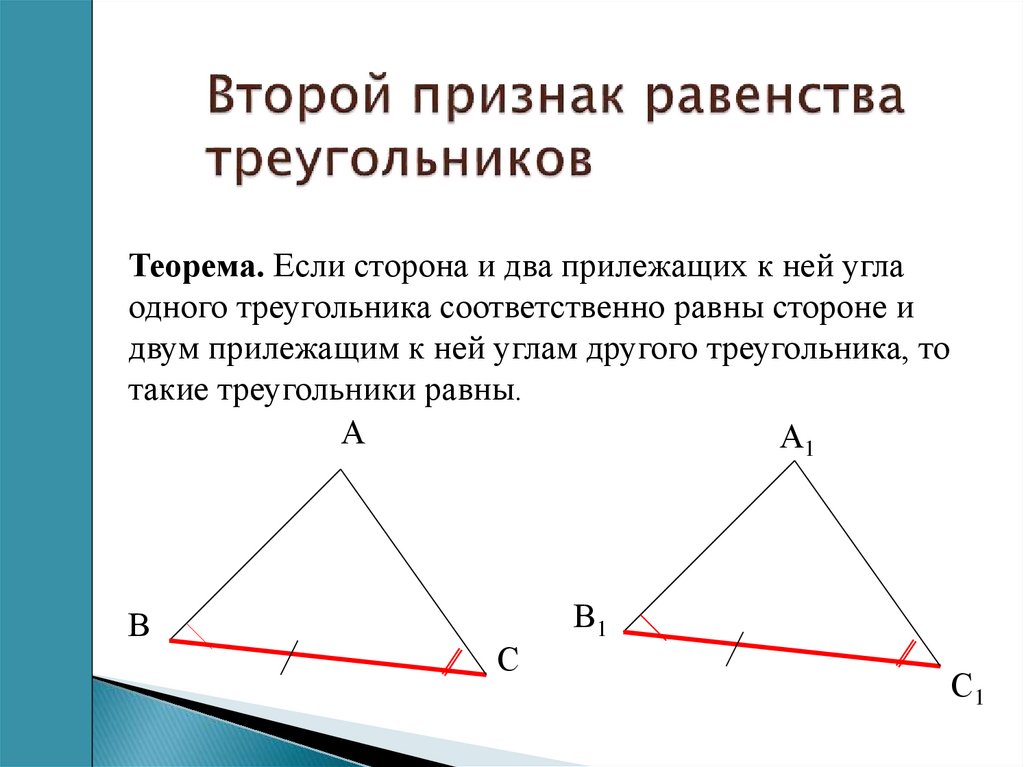
Второй признак равенства треугольников

Если сторона треугольника и два прилежащие к ней углы равны стороне другого треугольника и двум прилежащим углам, то эти два треугольника равны.

Отсюда вытекает следующее теоремма:

Если сторона треугольника и два к ней углы равны стороне другого треугольника и двум углам, то эти два треугольника равны.

Третий признак равенства треугольников

Если три стороны треугольника равны трём сторонам другого треугольника, то такие треугольники равны.

Задача 1
Дано:
ABC — равнобедренный треугольник.
АМ и BN биссектрисы угла.
Доказать: AM = BN.

Доказательство:
Треугольники AMB и BNA — равны (по второму признаку — угол-сторона-угол) потому что:
1. ∠CAB = ∠CBA
2. AB – в обеих треугольниках.
3. ∠MAB = ∠NBA = ¹/₂ ∠CAB.
Отрезки AM и BN являются соответствующими в этих равных треугольниках, и, следовательно, AM = BN.

---

Задача 2
Дано:
ABC — треугольник,
CM — медиана,
AA₁ ⊥ CM и BB₁ ⊥ CM.
Доказать: АА₁ = ВВ₁.

Доказательство:
1. ∠BB₁M = ∠AA₁M = 90&deg,
2. ∠AMA₁ = ∠BMB₁ как вертикальные,
3. AM = BM.
Следовательно △AA₁M = △BB₁M (по второму признаку).
Тогда AA₁ = BB₁ как соответствующие стороны в этих треугольниках.

---

Задача 3
Докажите, что перпендикуляры, проведённые из любой точки биссектрисы угла по отношению к его сторонам, вырезают на них равные отрезки.

Доказательство:
Давайте предположим, что ∠AOB точка M — неопределённая точка на биссектрисе OL.(fig.40)
Возьмём, что MP ⊥ OA и MQ ⊥ OB. Для того, чтобы доказать, что OP = OQ, достаточно доказать что △OPM = △OQM.

Но △OPM = △OQM(по второму признаку), потому что
1. OM — общая сторона,
2. ∠QOM = ∠POM (OL есть биссектриса),
3. ∠OQM = ∠OPM = 90°, откуда OP = OQ

Задача 4
Докажите, что если в треугольнике высота и биссектриса, проведенные из одной вершины, равны, то треугольник равнобедренный.

Доказательство:
Обозначим, что △ABC высота и биссектриса, проведённые из вершины C, совпадают (рис. 41).
Для того, чтобы доказать, что AC = BC, т.е. △ABC является равнобедренным, достаточно доказать, что △APC = △ BPC.
Но △APC = △BPC (по второму признаку) потому что
1. ∠ACP = ∠BCP (CP — биссектриса)
2. ∠ACP = ∠CPB = 90° (CP — высота)
3. CP — общая сторона
Следователвно AC = BC ⇒ ABC — равнобедренный

---

Задача 5

Дано:
AB = A₁B₁
BC = B₁C₁
AM = A₁M₁ — медианы
Докажите △ABC = △A

1B₁C₁

Доказательство:
Давайте посмотрим на треугольники △ABM и △A₁B₁M₁.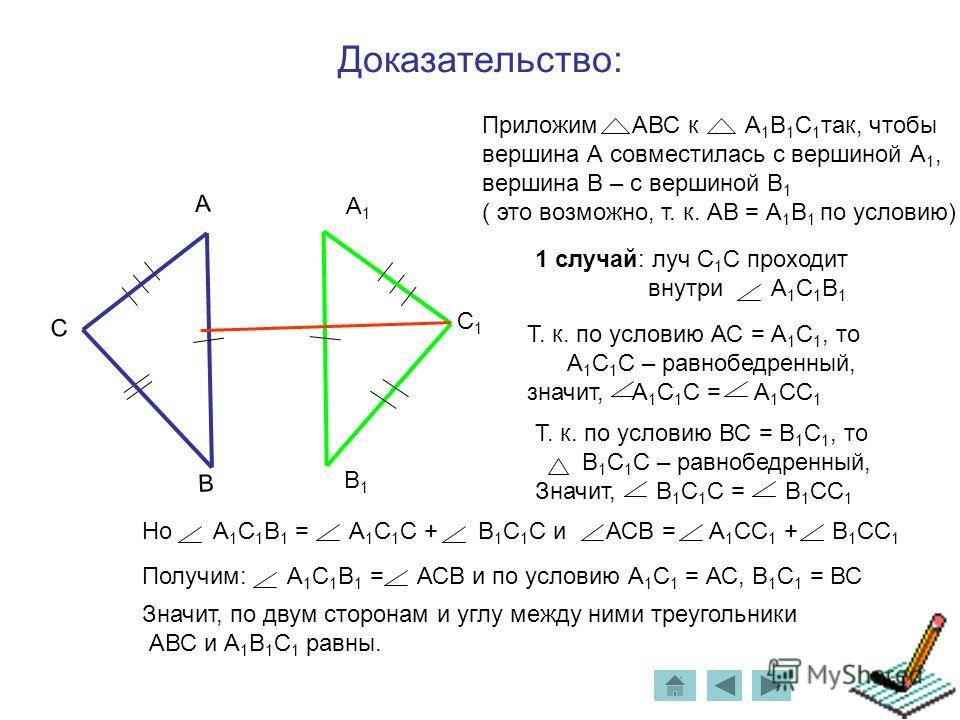
1. AB = A₁B₁
2. AM = A₁M₁
3. BM = $\frac{1}{2}$BC
B₁M₁ = $\frac{1}{2}$B₁C₁
Но BC = B₁C₁ следовательно
BM = B₁M₁

⇒ △ABM = △A₁B₁M₁(по третьему признаку).
Следовательно, ∠ABC = ∠A₁B₁C₁

Давайте посмотрим на треугольники △ABC и △A₁B₁C₁
1. AB = A₁B₁
2. BC = B₁C₁
3. ABC = A₁B₁C₁
Тогда, △ABC = △A₁B₁C₁ — равны по первому признаку.

Задачи на равенство треугольников по первому признаку

Первый признак равенства треугольников – доказательство: второй и третий признаки, теорема и определение

С далеких времен и по сей день поиск признаков равенства фигур считается базовой задачей, которая является основой основ геометрии, сотни теорем доказываются с использованием признаков равенства.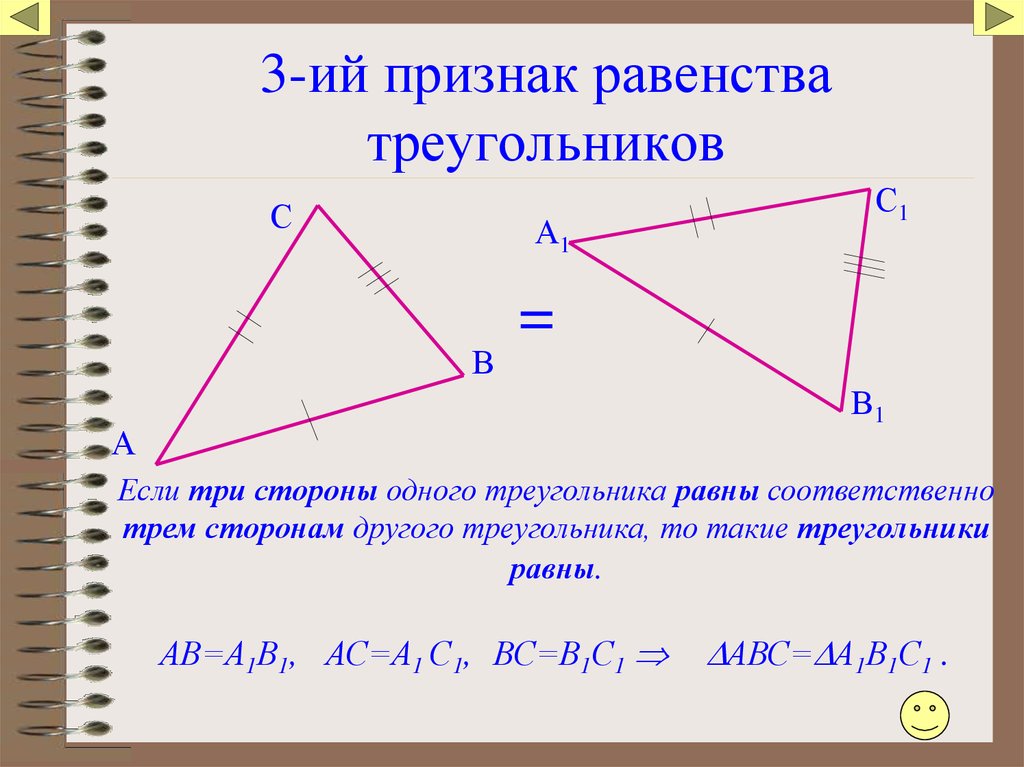 Умение доказывать равенство и подобие фигур важная задача во всех сферах строительства….

Содержание

Применение навыка на практике

Предположим, что у нас есть фигура, начерченная на листе бумаги. При этом у нас есть линейка и транспортир, с помощью которых мы можем замерять длины отрезков и углы между ними. Как перенести на второй лист бумаги фигуру таких же размеров или увеличить ее масштаб в два раза.

Мы знаем, что треугольник это фигура, состоящая из трех отрезков, называемых сторонами, образующими углы. Таким образом, существует шесть параметров три стороны и три угла, которые определяют эту фигуру.

Однако, замерив величину всех трех сторон и углов, перенести данную фигуру на другую поверхность окажется непростой задачей. Кроме того, есть смысл задать вопрос: а не достаточно ли будет знания параметров двух сторон и одного угла, или всего лишь трех сторон.

Замерив длину двух сторон и угол между ними, затем отложим этот угол на новом листке бумаги, так мы сможем полностью воссоздать треугольник. Давайте разберемся, как это сделать, научимся доказывать признаки, по которым их можно считать одинаковыми, и определимся с тем, какое минимальное число параметров достаточно знать, чтобы получить уверенность в том, что треугольники одинаковы.

Важно ! Фигуры называются одинаковыми, если отрезки, образующие их стороны, и углы равны между собой. Подобными называются те фигуры, у которых стороны и углы пропорциональны. Таким образом, равенство это подобие с коэффициентом пропорциональности 1.

Какие существуют признаки равенства треугольников, дадим их определение:

• первый признак равенства: два треугольника можно считать одинаковыми, если равны две их стороны, а также угол между ними.
• второй признак равенства треугольников: два треугольника будут одинаковыми, если одинаковы два угла, а также соответствующая сторона между ними.
• третий признак равенства треугольников: треугольники можно считать одинаковыми, когда все их стороны имеют равную длину.

Как доказать, что треугольники равны. Приведем доказательство равенства треугольников.

Доказательство 1 признака

Долгое время среди первых математиков данный признак считался аксиомой, однако, как оказалось, его можно геометрически доказать, опираясь на более базовые аксиомы.

Рассмотрим два треугольника KMN и K1M1N1. Сторона КМ имеет такую же длину как и K1M1, а KN = K1N1. А угол MKN равен углам KMN и M1K1N1.

Если рассматривать KM и K1M1, KN и K1N1 как два луча, которые выходят из одной точки, то можно сказать, что между этими парами лучей одинаковые углы (это задано условием теоремы). Произведем параллельный перенос лучей K1M1 и K1N1 из точки K1 в точку К. Вследствие этого переноса лучи K1M1 и K1N1 полностью совпадут. Отложим на луче K1M1 отрезок длиной КМ, берущий свое начало в точке К. Поскольку по условию полученный отрезок и будет равен отрезку K1M1 то точки М и M1 совпадают. Аналогично и с отрезками KN и K1N1. Таким образом, перенося K1M1N1 так, что точки K1 и К совпадают, а две стороны накладываются, получаем полное совпадение и самих фигур.

Важно! В интернете встречаются доказательства равенства треугольников по двум сторонам и углу при помощи алгебраических и тригонометрических тождеств с численными значениями сторон и углов. Однако исторически и математически данная теорема была сформулирована задолго до алгебры и раньше, чем тригонометрия. Для доказательства этого признака теоремы использовать что-либо, кроме базовых аксиом, некорректно.

Доказательство 2 признака

Докажем второй признак равенства по двум углам и стороне, основываясь на первом.

Доказательство 2 признака

Рассмотрим KMN и PRS. К равен Р, N равен S. Сторона КN имеет такую же длину, как и РS. Необходимо доказать, что KMN и PRS одинаковы.

Отразим точку М относительно луча КN. Полученную точку назовем L. При этом длина стороны КМ = КL. NKL равен PRS. KNL равен RSP.

Поскольку сумма углов равна 180 градусов, то KLN равен PRS, а значит PRS и KLN- одинаковые (подобные) по обеим сторонам и углу, согласно первому признаку.

Но, так как KNL равен KMN, то KMN и PRS две одинаковые фигуры.

Это интересно! Чему равна и как найти площадь равностороннего треугольника

Доказательство 3 признака

Как установить, что треугольники равны. Это прямо вытекает из доказательства второго признака.

Длина KN = PS. Поскольку К = Р, N = S, KL=KM, при этом КN = KS, MN=ML, то:

Это означает, что обе фигуры являются подобными друг другу. Но так как их стороны одинаковы, то и они также равны.

Из признаков равенства и подобия вытекает множество следствий. Одно из них заключается в том, что для того, чтобы определить, равны два треугольника или нет, необходимо знать их свойства, одинаковы ли:

• все три стороны,
• обе стороны и угол между ними,
• оба угла и сторона между ними.

Использование признака равенства треугольников для решения задач

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Следствия первого признака

В ходе доказательства можно прийти к ряду интересных и полезных следствий.

1. Параллелограмм. Тот факт, что точка пересечения диагоналей параллелограмма делит их на две одинаковые части следствие признаков равенства и вполне поддается доказательству.Стороны дополнительного треугольника (при зеркальном построении, как в доказательствах, которые мы выполняли) параллельны сторонам главного (стороны параллелограмма).
2. Если есть два прямоугольных треугольника, у которых одинаковые острые углы, то они подобны. Если при этом катет первого равен катету второго, то они равны. Понять это довольно легко у любых прямоугольных треугольников есть прямой угол. Поэтому признаки равенства для них более просты.
3. Два треугольника с прямыми углами, у которых два катета имеют одинаковую длину, можно считать одинаковыми. Это связано с тем, что между двумя катетами угол всегда равен 90 градусов. Поэтому по первому признаку (по двум сторонам и углу между ними) все треугольники с прямыми углами и одинаковыми катетами равны.
4. Если есть два прямоугольных треугольника, и у них один катет и гипотенуза равны, значит и треугольники одинаковы.

Докажем эту простую теорему.

Есть два прямоугольных треугольника. У одного стороны a, b, c, где с гипотенуза, a, b катеты. У второго стороны n, m, l, где l гипотенуза, m, n катеты.

По теореме Пифагора один из катетов равен:

,

.

Таким образом, если n = a, l = с (равенство катетов и гипотенуз), соответственно и вторые катеты будут равны. Фигуры, соответственно, будут равны по третьему признаку (по трем сторонам).

Отметим еще одно важное следствие. Если есть два равных треугольника, и они подобны с коэффициентом подобия k, то есть попарные отношения всех их сторон равны k, то отношение их площадей равно k2 .

Первый признак равенства треугольников. Видеоурок по геометрии 7 класс

Геометрия 7 Первый признак равенства треугольников

Вывод

Рассмотренная нами тема поможет любому ученику лучше разобраться в базовых геометрических понятиях и повысить свои навыки в интереснейшем мире математики.

Объяснение урока: Критерии сходства треугольников и их применение

В этом объяснении мы узнаем, как использовать свойства подобных треугольников для решения задач.

Мы можем начать с понимания значения подобного.

Определение: подобные треугольники

Два треугольника подобны, если соответствующие углы конгруэнтны и длины их соответствующие стороны находятся в той же пропорции.

Говоря более просто, можно сказать, что подобные треугольники имеют одинаковую форму, но они могут быть разного размера. Кстати, треугольники одинаковой формы и одного размера определяются как конгруэнтные.

Ниже приведен пример двух подобных треугольников.

Пары углов 𝐴 и 𝐷, 𝐵 и 𝐸, и 𝐶 и 𝐹, равны меры. Длины соответствующих сторон, 𝐴𝐵 и 𝐷𝐸, 𝐴𝐶 и 𝐷𝐹, и 𝐵𝐶 и 𝐸𝐹 находятся в той же пропорции. В этом примере мы также можем сказать, что масштабный коэффициент от △𝐴𝐵𝐶 в △𝐷𝐸𝐹 равно 12.

Теперь мы исследуем геометрию подобных треугольников.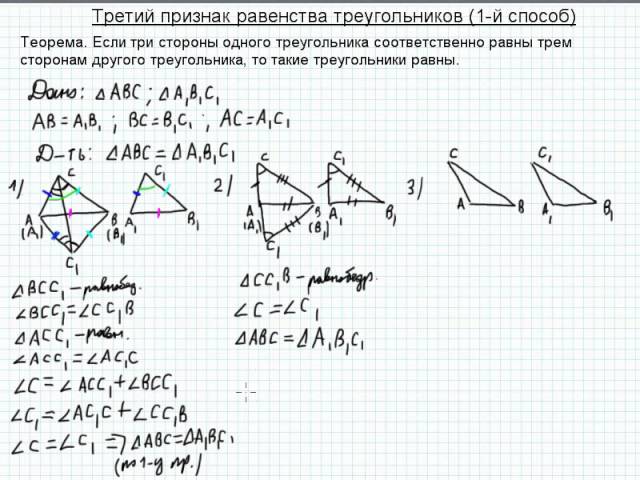 Мы можем взять треугольник, например треугольник 𝐹𝐺𝐻.

Выполнение расширения коэффициента масштабирования 𝑘 приведет к следующему треугольник 𝐹′𝐺′𝐻′.

При расширении все длины сторон умножаются на масштабный коэффициент, и все меры углов сохраняются. Если масштабный коэффициент больше 1, то фигура увеличена. А если масштабный коэффициент меньше 1, то цифра уменьшенный.

Можно сказать, что треугольник 𝐹𝐺𝐻 подобен треугольнику 𝐹′𝐺′𝐻′, и мы можем записать это как △𝐹𝐺𝐻∼△𝐹′𝐺′𝐻′.

Когда мы пишем отношения подобия между треугольниками, порядок надпись важна, так как она указывает на углы и стороны, которые соответствуют в треугольниках.

Если данная пара треугольников имеет равные соответствующие углы, то длины соответствующих сторон находятся в той же пропорции. И если треугольники имеют длины соответствующих сторон в той же пропорции, то соответствующие углы равны. Чтобы доказать, что два треугольника подобны, вместо того, чтобы доказывать, что все соответствующие углы равны и все длины соответствующих сторон пропорциональны, существует ряд критериев подобия, которые мы можем использовать.

Первый критерий, который мы могли бы использовать, это критерий угол-угол (AA).

Определение: критерий сходства угол-угол (AA)

Если две пары соответствующих углов в паре треугольников конгруэнтны, то треугольники подобны.

Мы можем начать со следующей пары треугольников.

Здесь дано, что 𝑚∠𝐵=𝑚∠𝐸 и 𝑚∠𝐶=𝑚∠𝐹. Мы можем показать, что всего с двумя заданными парами углы равны, третья пара углов, 𝑚∠𝐴 и 𝑚∠𝐷, также должны быть равны.

Мы можем вспомнить, что сумма внутренних углов треугольника равна 180∘. Следовательно, для определения меры угла 𝐴, мы могли вычислить 𝑚∠𝐴+𝑚∠𝐵+𝑚∠𝐶=180𝑚∠𝐴=180−(𝑚∠𝐵+𝑚∠𝐶).∘∘

В △𝐷𝐸𝐹 мы могли бы вычислить меру ∠𝐷 как 𝑚∠𝐷+𝑚∠𝐸+𝑚∠𝐹=180𝑚∠𝐷=180−(𝑚∠𝐸+𝑚∠𝐹).∘∘

Поскольку мы знаем, что 𝑚∠𝐵=𝑚∠𝐸 и 𝑚∠𝐶=𝑚∠𝐹, мы можем сказать, что 180−(∠𝐵+∠𝐶)=180−(∠𝐸+∠𝐹).∘∘

Следовательно, 𝑚∠𝐴=𝑚∠𝐷.

Таким образом, когда две пары соответствующих углов в треугольнике равны, третья пара соответствующих углов также равна и треугольники похожи.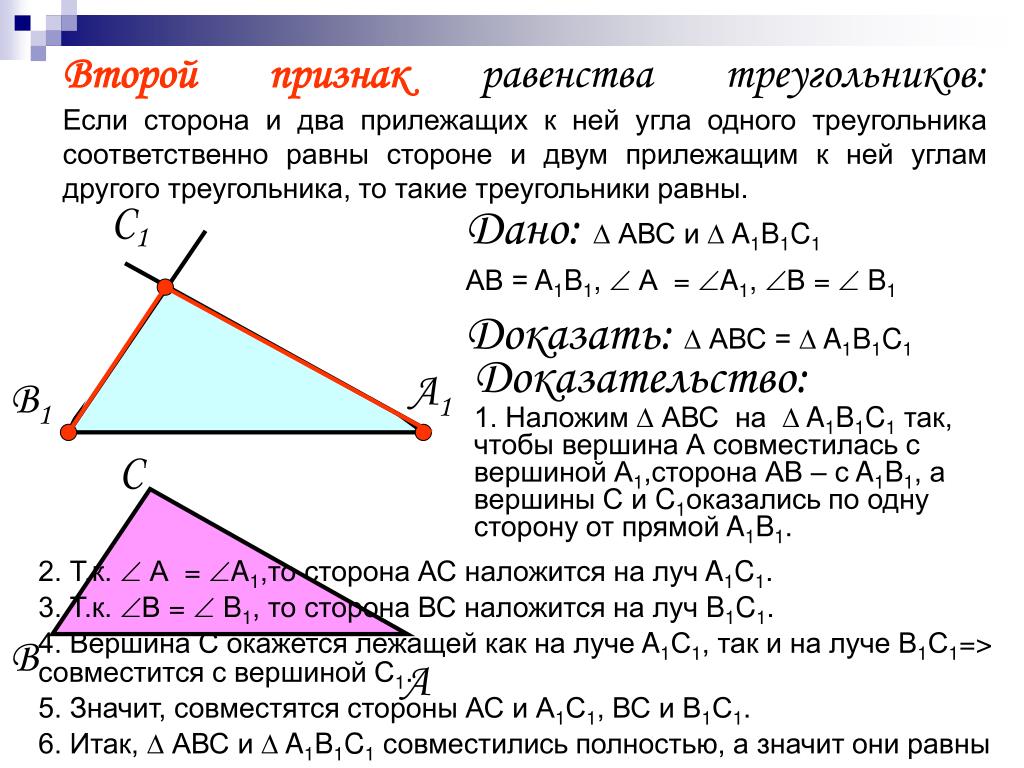

Второй критерий сходства касается сторон треугольников.

Определение: Критерий сходства сторон (SSS)

Если все три пары соответствующих длин сторон двух треугольников равны пропорциональны, то эти треугольники подобны.

Мы можем применить этот критерий следующим образом. Мы можем взять треугольники 𝑃𝑄𝑅 и 𝐾𝐿𝑀.

Если мы сможем показать, что стороны этих треугольников пропорциональны отношения такие, что 𝑃𝑄𝐾𝐿=𝑄𝑅𝐿𝑀=𝑅𝑃𝑀𝐾, тогда △𝑃𝑄𝑅∼△𝐾𝐿𝑀.

Например, мы можем рассмотреть треугольники ниже, △𝐴𝐵𝐶 и △𝐷𝐸𝐹.

Мы можем написать, что 𝐴𝐵𝐷𝐸=𝐵𝐶𝐸𝐹=𝐴𝐶𝐷𝐹, поскольку 63=105=94,5.

Все пропорции соответствующих сторон эквивалентны 21=2. Следовательно, △𝐴𝐵𝐶∼△𝐷𝐸𝐹.

Обратите внимание, что также допустимо написать 𝐷𝐸𝐴𝐵=𝐸𝐹𝐵𝐶=𝐷𝐹𝐴𝐶.

Нам просто нужно убедиться, что мы сохраняем все стороны каждого треугольника как числители или как знаменатели.

Поскольку между всеми соответствующими длины сторон треугольника, треугольники подобны.

Теперь мы обсудим окончательный критерий сходства.

Определение: Критерий подобия сторона-угол-сторона (SAS)

Если длины двух сторон в одном треугольнике пропорциональны длинам двух сторон другого треугольника и углы между ними равны равны, то эти треугольники подобны.

Мы можем проиллюстрировать этот критерий следующим рисунком.

Здесь у нас есть две пары соответствующих длин сторон в той же пропорции, 𝐴𝐵𝑋𝑌=𝐵𝐶𝑌𝑍, поскольку 106=63,6.

Обе эти пропорции эквивалентны 53. И, в обоих треугольников, углы между этими сторонами равны. Таким образом, △𝐴𝐵𝐶∼△𝑋𝑌𝑍.

Чтобы выполнить критерий правила SAS, нам достаточно двух пар сторон в пропорция, но пара углов должна быть углами между этими сторон в каждом треугольнике. Обратите внимание, что это правило отличается от правила соответствия SAS. критерий, где мы должны показать, что соответствующие стороны равны чтобы треугольники были равны.

Теперь мы рассмотрим несколько примеров того, как мы можем применять эти критерии сходства. доказать, что пары треугольников подобны.

Пример 1. Доказательство подобия двух треугольников

На рисунке показан треугольник 𝐴𝐷𝐸, где отрезок 𝐵𝐶 параллелен 𝐷𝐸.

1. Какой угол эквивалентен ∠𝐴𝐵𝐶? Почему?
   1. ∠𝐴𝐷𝐸, потому что углы равны
   2. ∠𝐴𝐷𝐸, потому что углы чередуются
   3. ∠𝐴𝐶𝐵, потому что углы чередуются
   4. ∠𝐴𝐸𝐷, потому что углы равны
   5. ∠𝐴𝐶𝐵, потому что углы равны
2. Какой угол эквивалентен ∠𝐴𝐶𝐵? Почему?
   1. ♂, потому что углы соответствуют
   2. ♂, потому что углы соответствуют
   3. ♂, потому что углы являются чередующимися
   4. ♂, потому что углы чередуются
   5. ♂, потому что равенство соответствуют
3. Следовательно, треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 похожий? Если да, то как?
   1. Да, похожи по критерию SSS.
   2. Да, они похожи по критерию SAS.
   3. Да, похожи по критерию АА.
   4. Нет, они не похожи.

Ответ

Часть 1

На диаграмме мы видим, что есть пара параллельных линий сегменты, 𝐵𝐶 и 𝐷𝐸. Линия ⃖⃗𝐴𝐷 — их трансверсаль; следовательно, угол, равный ∠𝐴𝐵𝐶, равен ∠𝐴𝐷𝐸.потому что углы равны

Часть 2

Чтобы найти угол, эквивалентный ∠𝐴𝐶𝐵, мы используем свойства углов параллельных прямых, а также поперечный ⃖⃗𝐴𝐸. Таким образом, угол что эквивалентно ∠𝐴𝐶𝐵 ∠𝐴𝐸𝐷.потому что углы соответствуют

Часть 3

Теперь мы показали, что существуют две пары соответствующих углы равны в треугольниках 𝐴𝐵𝐶 и 𝐴𝐷𝐸: 𝑚∠𝐴𝐵𝐶=𝑚∠𝐴𝐷𝐸,𝑚∠𝐴𝐶𝐵=𝑚∠𝐴𝐸𝐷.

Критерий сходства АА утверждает, что если две пары соответствующих углы в паре треугольников равны, то треугольники похожий. Следовательно, мы можем дать ответ, что треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 похожи на критерий АА.

Теперь рассмотрим другой пример.

Пример 2. Доказательство подобия двух треугольников

На рисунке показаны два треугольника 𝐴𝐵𝐶 и 𝐷𝐸𝐶, где отрезок 𝐴𝐵 параллелен 𝐷𝐸.

1. Какой угол эквивалентен ∠𝐴𝐵𝐶? Почему?
   1. ∠𝐶𝐷𝐸, потому что углы равны
   2. ∠𝐶𝐷𝐸, потому что углы параллельны
   3. ∠𝐶𝐸𝐷, потому что углы равны0094
   4. ∠𝐷𝐶𝐸, потому что углы вертикально противоположны
2. Какой угол эквивалентен ∠𝐵𝐴𝐶? Почему?
   1. ♂, потому что углы являются альтернативными
   2. T𝐶𝐷𝐸, потому что углы соответствуют
   3. ♂, потому что углы соответствуют
   4. ♂, потому что углы чередуются
   5. ♂, потому что углы верны. напротив
3. Следовательно, треугольники 𝐴𝐵𝐶 и 𝐷𝐸𝐶 похожий? Если да, то как?
   1. Да, похожи по критерию SSS.
   2. Да, они похожи по критерию SAS.
   3. Да, похожи по критерию АА.
   4. Нет, они не похожи.

Ответ

Часть 1

На схеме сегменты линий 𝐴𝐵 и 𝐷𝐸 отмечены как параллельные. Если рассматриваем ∠𝐴𝐵𝐶, тогда, используя свойства углов параллельных прямых, пересекаемых секущей, мы можно определить, что угол, который является его эквивалентом, равен ∠𝐶𝐸𝐷.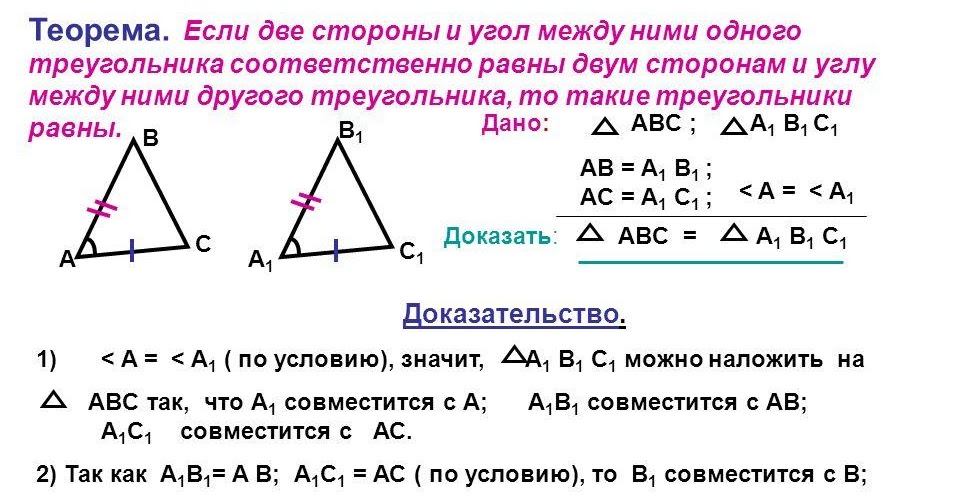 потому что углы настоящие

Часть 2

Используя те же свойства, с поперечной 𝐴𝐷, угол что эквивалентно ∠𝐵𝐴𝐶 Мы показали, что 𝑚∠𝐴𝐵𝐶=𝑚∠𝐶𝐸𝐷,𝑚∠𝐵𝐴𝐶=𝑚∠𝐶𝐷𝐸.

Можно вспомнить критерий сходства АА, который гласит, что если два пары соответствующих углов в паре треугольников равны, то треугольники подобны. Следовательно, мы можем дать ответ, что треугольники 𝐴𝐵𝐶 и 𝐷𝐸𝐶 похожи по критерию АА.

Мы можем обобщить методы, использованные в предыдущих двух вопросах, в Следствие подобия треугольников.

Определение: Следствие сходства треугольников

Если длины двух сторон в одном треугольнике пропорциональны длинам двух сторон другого треугольника и углы между ними равны равны, то эти треугольники подобны.

На каждом из приведенных выше рисунков мы можем утверждать, что если ⃖⃗𝐷𝐸⫽𝐵𝐶 и пересекается ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶 в 𝐷 и 𝐸 соответственно, то △𝐴𝐷𝐸∼△𝐴𝐵𝐶.

В следующем примере мы рассчитаем коэффициент масштабирования между парой подобных треугольников.

Пример 3: Нахождение масштабного коэффициента сходства

На рисунке 𝐶𝐵=5,7 и 𝐵𝐸=9,12. Поскольку треугольники 𝐶𝐵𝐴 и 𝐸𝐵𝐷 похожи, каков масштабный коэффициент?

Ответ

Мы можем начать с обозначения заданных длин на рисунке.

Нам дано, что △𝐶𝐵𝐴 похоже на △𝐸𝐵𝐷. Напомним, что подобные треугольники имеют соответствующие пары углов, которые равны и соответствующие стороны длины, которые находятся в пропорции.

Мы можем использовать порядок букв, чтобы определить, что длины 𝐶𝐵 и 𝐸𝐵 соответствуют. Таким образом, мы можем записать долю их длины от △𝐶𝐵𝐴 до △𝐸𝐵𝐷 как 𝐸𝐵𝐶𝐵=9,125,7=85.

Мы можем дать ответ в виде дроби или десятичной дроби; таким образом, шкала множитель от треугольника 𝐶𝐵𝐴 к треугольнику 𝐸𝐵𝐷 равно 1,6.

Обратите внимание, что масштабный коэффициент в обратном направлении, от △𝐸𝐵𝐷 в △𝐶𝐵𝐴, будет записано как пропорция 𝐶𝐵𝐸𝐵=58.

Теперь рассмотрим пример, в котором сначала нужно доказать, что два треугольника похожи, а затем использовать эти свойства, чтобы помочь нам определить недостающие длины.

Пример 4. Вычисление неизвестных по сходству и нахождение периметра Треугольник

На рисунке показан треугольник 𝐴𝐵𝐶.

1. Определите значение 𝑥.
2. Определите значение 𝑦.
3. Вычислите периметр △𝐴𝐵𝐶.

Ответ

Внутри большего треугольника 𝐴𝐵𝐶 мы видим, что существует меньший треугольник, который мы можем пометить точками 𝐷 и 𝐸 для определения △𝐴𝐷𝐸.

Чтобы найти недостающие длины, мы сначала определяем, △𝐴𝐵𝐶 и △𝐴𝐷𝐸 похожи. Подобные треугольники имеют соответственные углы, которые равны, и соответствующие длины сторон, которые находятся в пропорция.

Заметим, что на рисунке 𝐷𝐸 и 𝐵𝐶 отмечены как параллельные. Это означает, что мы можем идентифицировать две пары соответствующих углов используя трансверсали ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶.

Мы можем написать, что ∠𝐴𝐷𝐸=∠𝐴𝐵𝐶 и что ∠𝐴𝐸𝐷=∠𝐴𝐶𝐵.

Критерий подобия AA утверждает, что если две пары соответствующих углы в паре треугольников равны, то треугольники похожий. В качестве альтернативы мы могли бы также показать, что, поскольку угол 𝐴 является общим для обоих треугольников, то ∠𝐵𝐴𝐶=∠𝐷𝐴𝐸. Любые две пары из этих трех пары углов было бы достаточно, чтобы доказать, что △𝐴𝐷𝐸∼△𝐴𝐵𝐶.

Пропорция соответствующих сторон может быть записана как 𝐴𝐵𝐴𝐷=𝐵𝐶𝐷𝐸=𝐴𝐶𝐴𝐸.

Теперь мы можем использовать это отношение пропорциональности, чтобы найти недостающие длины, 𝑥 и 𝑦.

Часть 1

Длина, 𝑥, составляет часть 𝐴𝐶 и соответствующая сторона в треугольнике 𝐴𝐷𝐸 сторона 𝐴𝐸.

При работе с подобными треугольниками мы обычно имеем или можем вычислить длины двух соответствующих сторон. Это позволяет нам найти пропорцию или масштабный коэффициент между данными треугольниками. Здесь нам даны длины 𝐷𝐸 и 𝐵𝐶. Следовательно, мы можем написать, что 𝐴𝐶𝐴𝐸=𝐵𝐶𝐷𝐸.

Длина 𝐴𝐶 может быть записана в терминах 𝑥 как (6+𝑥). Мы заменяем в значения длин, чтобы дать 6+𝑥6=74.

Умножение обеих частей на 6 и упрощение дают 6+𝑥=424𝑥=424−6𝑥=4,5.

Следовательно, мы нашли значение 𝑥 равным 4,5.

Часть 2

Неизвестная длина 𝑦 является частью отрезка 𝐴𝐵. Соответствующая сторона в △𝐴𝐷𝐸 это 𝐴𝐷. Мы можем использовать отношение пропорциональности: 𝐴𝐵𝐴𝐷=𝐵𝐶𝐷𝐸.

Мы можем представить длину 𝐴𝐵 как (𝑦+5). Подставляя значения длин и упрощая, имеем 𝑦+55=74𝑦+5=354𝑦=354−5=3,75.

Следовательно, значение 𝑦 равно 3,75.

Часть 3

Периметр — это расстояние по внешней стороне фигуры. Таким образом, чтобы вычисляем периметр △𝐴𝐵𝐶, мы иметь следующее: периметр=𝐴𝐵+𝐵𝐶+𝐶𝐴.

Подставляя длины из рисунка, имеем периметр=(5+𝑦)+7+(𝑥+6).

Мы рассчитали 𝑥=4,5 и 𝑦=3,75; следовательно, мы можем упростить до дайте периметр=5+3,75+7+4,5+6=26,25.

Тогда мы можем дать ответ, что периметр △𝐴𝐵𝐶 — 26.25.

В следующем вопросе мы будем использовать подобие треугольников, чтобы позволить нам составить и решить алгебраические уравнения, чтобы найти неизвестную длину.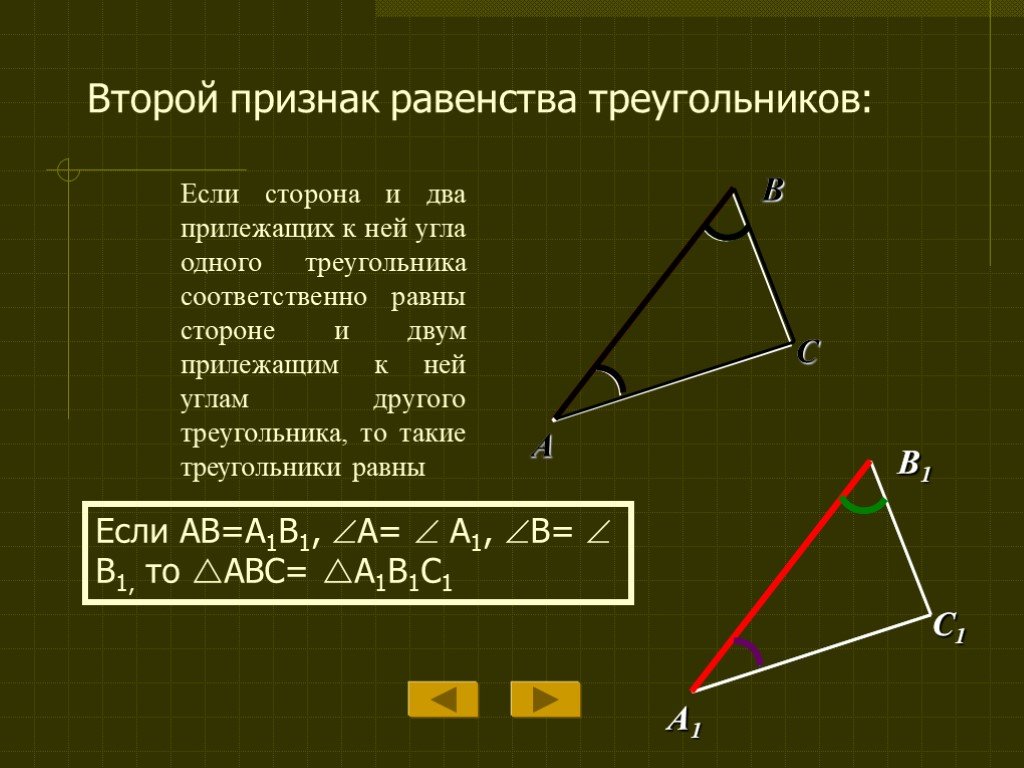

Пример 5. Составление и решение уравнения с использованием подобия для поиска неизвестного

Треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 подобны. Найдите 𝑥 с точностью до целого числа.

Ответ

Внутри большего треугольника 𝐴𝐵𝐶 на рисунке мы обратите внимание, что существует меньший треугольник, 𝐴𝐷𝐸. Мы не может сразу вычислить длины 𝐸𝐷 и 𝐶𝐵; тем не менее, мы можем использовать данную информацию что эти два треугольника подобны.

В подобных треугольниках пропорции сторон одинаковы. Следовательно, мы можно записать отношение соответствующих сторон как 𝐵𝐶𝐷𝐸=𝐴𝐶𝐴𝐸.

Затем мы можем подставить данные длины из рисунка, будучи обратите внимание, что 𝐴𝐶=5+2=7см. Это дает нам 𝑥+24𝑥−15=75.

Упрощая, имеем 5(𝑥+2)=7(4𝑥−15)5𝑥+10=28𝑥−10510=23𝑥−105115=23𝑥5=𝑥.

Таким образом, мы можем дать ответ, что значение 𝑥 равно 5.

Теперь мы увидим пример того, как мы можем использовать сходство треугольников с найти измерения в реальной ситуации. Всегда полезно сначала отображать полученную информацию в эскизе.

Пример 6. Использование подобия двух треугольников для нахождения косвенных измерений

Мужчина ростом 1,97 м стоит 3,49м от уличного фонаря и бросает тень длиной 2,73 м. На какой высоте лампа? Округлите свой ответ до ближайший десятый.

Ответ

Было бы полезно начать с наброска имеющейся у нас информации. было дано.

Затем мы можем смоделировать ситуацию, используя треугольники с линией, соединяющей вершина света к вершине тени.

Полезно пометить точки. Здесь мы можем определить их как 𝑃, 𝑄, 𝑅, 𝐿 и 𝑀. Можно предположить, что человек и уличный фонарь встречает горизонтальную землю на 90∘ и что уличный фонарь и человек вертикальны и параллельны.

Нам нужно проработать высоту светильника, длину 𝑃𝑄. Если бы у нас была длина 𝑃𝑅, мы могли бы применить теорему Пифагора. Однако, возможно, наилучший подход состоит в том, чтобы посмотреть, образовался ли треугольник. со светом и тенью, △𝑃𝑄𝑅, похоже к меньшему треугольнику, созданному человеком и тенью, △𝐿𝑀𝑅.

Напомним, что у подобных треугольников соответствующие углы равны. и соответствующие длины сторон, которые пропорциональны. Один из способов, которым мы Доказать, что два треугольника подобны, можно, показав, что есть две пары соответственных углов, которые равны, т. критерий АА.

Мы можем написать, что ∠𝑃𝑅𝑄=∠𝐿𝑅𝑀,∠𝑅,∠𝑃𝑄𝑅=∠𝐿𝑀𝑅,90.поскольку оба треугольника равны обоим∘

Так как мы нашли два соответствующих угла, которые конгруэнтны, то мы доказали, что △𝑃𝑄𝑅∼△𝐿𝑀𝑅.

Чтобы вычислить длину 𝑃𝑄, мы можем используйте соответствующую сторону в △𝐿𝑀𝑅, сторона 𝐿𝑀. Мы знаем, что пропорция между этими стороны будут такими же, как пропорция между соответствующими стороны, 𝑄𝑅 и 𝑀𝑅, длина которых нам дана.

Следовательно, 𝑃𝑄𝐿𝑀=𝑄𝑅𝑀𝑅.

Затем мы подставляем значения длины, отмечая, что 𝑄𝑅=3,49+2,73=6,22 м. Это дает нам 𝑃𝑄1,97=6,222,73𝑃𝑄=6,222,73×1,97=4,4884…. м

Высота лампы была определена как 𝑃𝑄, и мы округлить это значение до десятых, чтобы получить ответ для высота светильника, которая составляет 4,5 м.

Мы также можем отметить частный случай сходства треугольников, который включает высота прямоугольного треугольника.

Рассмотрим следующий рисунок.

Самый большой прямоугольный треугольник 𝐴𝐵𝐷 делится на два меньших треугольники. Обратите внимание, что 𝐴𝐶 образует высота этого треугольника, так как это перпендикуляр, проведенный из вершина треугольника на противоположную сторону.

Обратите внимание, что сумма углов на прямой равна 180∘, мы также можем констатировать что ∠𝐴𝐶𝐷=90∘.

Рассмотрим углы в этих треугольниках, начиная с ∠𝐴𝐷𝐵. Мы можем нарисовать 3 треугольника отдельно, с прямым углом в том же положении.

Поскольку 𝐷 — общий угол между △𝐴𝐵𝐷 и △𝐶𝐴𝐷, и у них обоих есть под углом 90∘, то по Критерий подобия АА, △𝐴𝐵𝐷∼△𝐶𝐴𝐷.

Далее мы замечаем, что угол при 𝐵 является общим для обоих треугольники 𝐴𝐵𝐷 ​​и 𝐶𝐵𝐴.

Так как эти треугольники также имеют угол 90∘, затем по АА критерий подобия, △𝐴𝐵𝐷∼△𝐶𝐵𝐴.

Если любые два треугольника подобны третьему треугольнику, то все три треугольники подобны. Следовательно, △𝐴𝐵𝐷∼△𝐶𝐴𝐷∼△𝐶𝐵𝐴.

Следовательно, мы можем определить второе следствие сходства треугольников ниже.

Определение: Следствие сходства треугольников

В любом прямоугольном треугольнике высота гипотенузы разделяет треугольник на два треугольника, которые подобны друг другу и подобны оригинальный треугольник. △𝐴𝐵𝐷∼△𝐶𝐴𝐷∼△𝐶𝐵𝐴

Теперь мы увидим, как мы можем применить это следствие в следующем примере.

Пример 7. Использование подобия треугольников, образованных высотой прямоугольного треугольника

На данном рисунке изображен прямоугольный треугольник 𝐴𝐵𝐶, где 𝐶𝐷 перпендикулярно 𝐴𝐵.

1. Используя сходство, выразите 𝑎 через 𝑐 и 𝑑.
2. Используя сходство, выразите 𝑏 через 𝑐 и 𝑒.
3. Выразите сумму 𝑎 и 𝑏 через 𝑐.

Ответ

На рисунке видно, что 𝐶𝐷 является высота прямоугольного треугольника 𝐴𝐵𝐶. Мы можем вспомнить, что в любом прямоугольный треугольник, высота гипотенузы делит треугольник на две части треугольники, которые подобны друг другу и подобны исходному треугольнику.

Следовательно, мы можем написать, что △𝐴𝐵𝐶∼△𝐶𝐵𝐷∼△𝐴𝐶𝐷.

Часть 1

Мы можем нарисовать 3 треугольника отдельно и в одной ориентации с выровненными соответствующими углами.

Как нам нужно отношение между сторонами длин 𝑎, 𝑐 и 𝑑, мы используем △𝐴𝐵𝐶 и △𝐶𝐵𝐷 для формирования отношения подобия.

Мы знаем, что когда треугольники подобны, соответствующие стороны в той же пропорции. Итак, у нас есть это 𝐶𝐵𝐷𝐵=𝐴𝐵𝐶𝐵𝑎𝑑=𝑐𝑎.

Затем мы упрощаем это уравнение, чтобы получить 𝑎=𝑐𝑑.

Таким образом, мы выразили 𝑎 через 𝑐 и 𝑑.

Часть 2

Мы используем △𝐴𝐵𝐶 и △𝐴𝐶𝐷, чтобы сформировать следующее сходство отношение, для сторон длин 𝑏, 𝑐 и 𝑒.

Отсюда имеем 𝐴𝐶𝐴𝐷=𝐴𝐵𝐴𝐶𝑏𝑒=𝑐𝑏𝑏=𝑐𝑒.

Итак, имеем 𝑏, выраженное через 𝑐 и 𝑒.

Часть 3

Мы можем записать сумму 𝑎 и 𝑏, подставив значения 𝑎=𝑐𝑑 и 𝑏=𝑐𝑒, которые мы вычислили в частях 1 и 2. Это дает нам 𝑎+𝑏=𝑐𝑑+𝑐𝑒=𝑐(𝑑+𝑒).

Используя рисунок, мы видим, что 𝑐=𝑑+𝑒; следовательно, 𝑎+𝑏=𝑐×𝑐=𝑐.

На самом деле, мы можем признать, что это верно, используя пифагорейскую теорема. Это означает, что для любого прямоугольного треугольника квадрат гипотенуза равна сумме квадратов двух других сторон. Используя сходство, мы продемонстрировали справедливость этого теорема. Мы можем выразить сумму 𝑎 и 𝑏 с точки зрения 𝑐 как 𝑎+𝑏=𝑐.

Подведем итоги.

Ключевые моменты

• Два треугольника подобны, если соответствующие углы равны и соответствующие длины сторон пропорциональны.
• Мы можем доказать, что два треугольника подобны, используя один из следующие критерии подобия:
  • Угол-Угол (AA): Если две пары соответствующих углов в два треугольника равны, то эти треугольники подобны.
  • Сторона-сторона-сторона (SSS): если все три пары соответствующих сторон длины двух треугольников пропорциональны, то эти два треугольника похожи.
  • Сторона-Угол-Сторона (SAS): Если две длины сторон в одном треугольнике пропорциональны двум длинам сторон другого треугольника и углы между ними равны, то оба треугольники подобны.
• В любом прямоугольном треугольнике высота гипотенузы разделяет треугольник на два треугольника, которые подобны друг другу и аналогично исходному треугольнику.
• Мы можем моделировать ситуации из реальной жизни с участием подобных треугольников с помощью рисуя эскиз и используя пропорциональность сторон и эквивалентность углов, чтобы найти неизвестные измерения.

Свойство равенства углов, противоположных равным сторонам треугольника

• Математические сомнения
• Геометрия
• Треугольники
• Свойства

Если две стороны треугольника равны, то равны и углы, противолежащие тем же двум сторонам.

Длины двух сторон треугольника могут быть равны. Это возможно только в случае как равностороннего, так и равнобедренного треугольника.

Благодаря свойству равенства двух сторон в треугольнике углы, противолежащие им, также геометрически равны. Эта теорема также может быть доказана в геометрии на основе свойства симметрии.

Таким образом, становится ясно, что углы, противоположные двум сторонам равной длины, в треугольнике равны.

Доказательство

Для доказательства этой теоремы нам нужно построить либо равносторонний, либо равнобедренный треугольник.

$\Delta ABC$ — треугольник, две стороны которого имеют одинаковую длину. Следовательно, треугольник $ABC$ называется равнобедренным. В этом равнобедренном треугольнике длины сторон $\overline{AC}$ и $\overline{BC}$ равны.

$AC = BC$

Из точки $C$ проведите перпендикуляр к стороне $\overline{AB}$. Он делит сторону $\overline{AB}$ ровно в ее середине, а точкой пересечения является $D$.

Следовательно, $AD = BD$.

Аналогично, прямая $\overline{DC}$ делит $\Delta ABC$ на два прямоугольных треугольника $\Delta DAC$ и $\Delta DBC$. Теперь перпендикулярная прямая $\overline{DC}$ является общей стороной обоих прямоугольных треугольников.

Теперь сравните длины трех сторон обоих треугольников.

1. $AC = BC$
2. долларов США =
долларов США
3. ДС =
ДС $

Сравнение длин сторон обоих треугольников показало, что эти два треугольника одинаковы, но представлены по-разному.

Таким образом, $\Delta DAC$ и $\Delta DBC$ известны как конгруэнтные треугольники, и они также представляют критерий прямоугольной стороны гипотенузы (RHS).

$\Delta DAC \cong \Delta DBC$

В этом случае $\angle DAC$ — это угол, противоположный стороне $\overline{BC}$, а $\angle DBC$ также является углом, противоположным стороне $\overline{AC}$. Два угла равны из-за конгруэнтности.

$\угол DAC = \угол DBC$

Следовательно, если две стороны треугольника равны, то равны и противоположные им углы.