Порядок выполнения арифметических действий и альтернативная математика.: biglebowsky — LiveJournal
?- Общество
- Образование
- Cancel
Сегодня мне попалось занятное обсуждение во френд-ленте: оказывается, значительное количество людей воспринимает запись вида 1/2a совершенно «альтернативным» способом.
Порядок выполнения действий в математическом выражении начинают изучать в 3м классе общеобразовательной школы http://festival.
1september.ru/articles/638450/В итоге получается следующее http://www.askamathematician.com/2011/04/q-how-do-you-calculate-6212-or-48293-whats-the-deal-with-this-orders-of-operation-business/
Однако, у некоторых людей это трансформируется в голове совершенно удивительным образом.
Например, так: «меня в школе учительница учила что деление делается в последнюю очередь…умножение всегда перед делением…» https://ru.pokerstrategy.com/forum/thread.php?threadid=774835&page=2
Ну, или так.
— «Напомню, что умножение имеет приоритет перед делением»
— «Умножение имеет приоритет перед делением? Это где такое написано? :)»
— «В учебнике. Порядок выполнения действий […]» http://dimka-jd.livejournal.com/3865176.html
Кроме того, массово высказывается совершенно удивительная гипотеза (обалдеть, как у людей фантазия работает!).
То есть 1/2a =альтернативно равно= 1/(2*a) = 1/2/a
Численный пример «концепции слитности». Пусть a=10 Тогда
1/2a=5
1/2a=альтернативно равно=1/20
В комментариях обсуждается задачка вида «10a:10a=?»
Соответственно
10a:10a=a2
10a:10a=альтернативно равно=1
Ссылки по теме
http://p-i-f.livejournal.com/9437853.html
http://dimka-jd.livejournal.com/3865176.html
https://ru.pokerstrategy.com/forum/thread.php?threadid=774835
http://engineerblog.ru/6-2-1-2-holywar/
Примечания.
* Я не рискнул использовать для произвольной величины букву «x» — боюсь, кто нибудь перепутает ее со знаком умножения…
org/wiki/Возведение_в_степеньUpdate. Комментарий из дискусии.
Приводится в качестве примера линуксоидный калькулятор «Qalculate!», и он для обсуждаемой ситуации может быть настроен «на вкус» пользователя.
Pedro says:
December 17, 2016 at 12:00 am
Software documentation
https://qalculate.github.io/manual/qalculate-expressions.html
Implicit Multiplication and Parsing Modes
The evaluation of short/implicit multiplication, without any multiplication sign (ex. “5x”, “5(2+3)”), differs depending on the parsing mode. In the conventional mode implicit multiplication does not differ from explicit multiplication (“12/2(1+2) = 12/2*3 = 18”, “5x/5y = 5*x/5*y = xy”). In the “parse implicit multiplication first” mode, implicit multiplication is parsed before explicit multiplication (“12/2(1+2) = 12/(2*3) = 2”, “5x/5y = (5*x)/(5*y) = x/y”). The default adaptive mode works as the “parse implicit multiplication first” mode, unless spaces are found (“1/5x = 1/(5*x)”, but “1/5 x = (1/5)*x”).
Subscribe
Предисловие к «Термодинамике и Статистической механике» Дэвида Гудштайна
Людвиг Больцман, который потратил значительную часть своей жизни на изучение стат. механики, покончил свою жизнь самоубийством в 1906г. Пауль…
Неконтролируемое увеличение цен на газ в РФ
Я скрываюсь от коронавируса на даче под Звенигородом. Вчера мне пришел e-mail — ультиматум из газового хозяйства: я должен в течении 20 суток…
Распродажа земель в водоохранной зоне Московской области
Я скрываюсь от коронавируса на даче под Звенигородом, и мне сегодня пришло официальное письмо от «команды губернатора Подмосковья». «Изменения в…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Предисловие к «Термодинамике и Статистической механике» Дэвида Гудштайна
Людвиг Больцман, который потратил значительную часть своей жизни на изучение стат.
механики, покончил свою жизнь самоубийством в 1906г. Пауль…Неконтролируемое увеличение цен на газ в РФ
Я скрываюсь от коронавируса на даче под Звенигородом. Вчера мне пришел e-mail — ультиматум из газового хозяйства: я должен в течении 20 суток…
Распродажа земель в водоохранной зоне Московской области
Я скрываюсь от коронавируса на даче под Звенигородом, и мне сегодня пришло официальное письмо от «команды губернатора Подмосковья». «Изменения в…
механики, покончил свою жизнь самоубийством в 1906г. Пауль…| Почему умножение и деление «приоритетнее» сложения и вычитания | [Nov. 14th, 2019|02:32 am] Darkhon |
https://a-rodionova.livejournal.com/67729.html#t592017 Месяц назад на Рамблере появилась сообщение о том, что появившийся в твиттере пример 8:2(2+2) (https://twitter. Почему умножение и деление «приоритетнее» сложения и вычитания Пусть выражением 20+10 =30 записано решение задачи. Слагаемыми являются известные числа, известные по условиям задачи, типа такой: вчера выкопали 20 кг моркови, сегодня — 10. Какой урожай моркови? Теперь представим, что слагаемые неизвестны, но по условию задачи известно, что 20 — это 10*2, а 10 — это 30:3. Так и записываем сумму: 10*2+30:3=? Нам надо получить сумму двух неизвестных чисел, чтобы подсчитать урожай. Для того, чтобы теперь найти сумму, нужно в первую очередь вычислить слагаемые, которыми здесь являются произведение и частное. Всё очень просто. Повторю. Т.к. невозможно вычислить сумму неизвестных чисел, записанных в виде неизвестного произведения и частного без нахождения произведения и частного, то это и является той незыблемой основой первоочередного выполнения умножения и деления, когда произведение и частное являются слагаемыми. А действие сложения в таких выражениях всегда является заключительным. Некогда математики договорились, что для того, чтобы подобные выражения и формулы не пестрели трёхэтажными и выше скобками, не писать, а лишь подразумевать скобки для умножения и деления, т. к. произведения и частные, которые являются слагаемыми, всегда находятся в первую очередь, что всем (некогда было) ясно и без скобок (как «Волга впадает в Каспийское море»). Ставь скобки или нет, всё равно сначала будешь делить и умножать, а потом складывать и вычитать. Вот так надо понимать, почему умножение и деление «приоритетнее» сложения и вычитания. Первоочерёдность теперь обозначается нелепым словом «приоритетность», т. е. вы должны умножение и деление делать первыми потому, что они «приоритетнее» сложения! И самим не смешно, т. к. на деле выясняется, что умножения и деление — это вспомогательные действия, которые нужно сделать, чтобы найти сумму? Как раз сложение имеет настоящую важность. Если бы не нужно было находить сумму, то умножать/делить было бы не нужно. Будем считать, что поняли, почему умножение и деление «приоритетнее» сложения. Основу первоочерёдности умножения и деления нельзя изменить. Слово «приоритетность» теперь все понимают как обозначение некой таинственной важности умножения и деления, из-за которой им присвоили более «высокий» «приоритет». Сложение и вычитание становятся как бы «ущербными» действиями, имея самый низкий «приоритет» в «табеле о рангах». Эмоциональная нагрузка заменяет смысловую. Чтобы избавиться от эмоций, надо просто заменить слово «приоритетность» на, скажем, «очерёдность» (первоочерёдность, равноочерёдность), чтобы мозг не буксовал. Или восстановить прежнюю терминологию (не помню, что использовалось вместо «приоритетности»). Почему умножение и деление «равноприоритетны» В примере решения задачи есть действия деления и умножения. На этот случай имеется правило, что умножение и деление — равноприоритетны, т. Действительно, абсолютно неважно, какое из слагаемых вычисляется первым, какое — вторым, т. к. очерёдность вычислений слагаемых не влияет на сумму. Неважность очерёдности действий умножения и деления при вычислении слагаемых в выражении — это основа безочерёдности этих действий, что значит, произведения и частные в выражении можно вычислять в любом порядке, как удобно, не соблюдая правило «слева направо». Понятно, что в выражении, где есть несколько слагаемых в виде произведений, частных, а также других действий, взятых в скобки, так же неважно для правильного ответа, в каком порядке вычислять слагаемые. Не обязательно начинать вычислять сначала все слагаемые в скобках, потом все частные и произведения, порядок — произвольный, как удобно. А также необязательно находить сразу все слагаемые, несмотря на «пониженную приоритетность» сложения/вычитания. Пожалуйста, можете выполнять сложение по мере вычисления неизвестных слагаемых. Почему «равноприоритетны» сложение и вычитание (на примере выражения без умножения и деления) Т.к. вычитание есть сложение с отрицательными числами, и от перемены мест слагаемых сумма не изменяется, то вычитание и сложение могут проводиться в любой очерёдности, т. Например: 10+20-10 можно посчитать в таком порядке: 10+(20-10), в таком: -10+10+20, в таком: -10+20+10, в таком 10-10+20. Во всех случаях ответ будет одинаков — 20. Порядок вычисления не влияет на сумму, поэтому у действий сложения и вычитания — произвольная очерёдность, которую устанавливает тот, кто находит значение выражения. Сложение и вычитание не имеет очерёдности согласно переместительному свойству сложения, поэтому правило «слева направо» выполнять необязательно. Т. к. сложение — это увеличение количества, а вычитание — уменьшение, то ребёнок не может сразу понять, почему в реальности разные действия (сложение и вычитание) формально являются одним и тем же. назначение правила «слева направо» Мы выяснили, что если в выражении два и более слагаемых, неважно, простых или сложных, то сложение (вычитание) данных и найденных слагаемых можно производить в любом порядке. Зачем же в таких выражениях бывает нужно применять очерёдность вычисления «слева направо»? Иногда порядок нахождения суммы «слева направо» имеет смысл. Любое математическое, как арифметическое, так и алгебраическое, выражение определяется и составляется исходя из условий задачи. Выше я уже показала, что произвольность в очерёдности (а также хоть «справа налево») не вредит вычислению ответа, когда находятся неизвестные произведения и частные. В выражениях, где члены НЕ являются слагаемыми, например 8:2*4, нужно выполнять действия «слева направо». Хотя умножение и деление имеют своими корнями сложение/вычитание, но в отличие от вычитания и сложения, они не являются одним и тем же действием. Умножение — это сложение одинаковых чисел, а деление — это разложение суммы на равные количественные доли. Как говорят — обратное действие. В данном примере 8 делится пополам. Одна часть = 4. Эта часть обратно складывается, но не 2 раза, чтобы опять получилась 8, а 4 раза, что в сумме даёт 16. Взаимосвязь, как обратимость, деления и умножения видна в примерах, где делитель равен множителю: 8:2*2=8. Мы разделили 8 на 2 части, потом часть сложили 2 раза, и получили 8. В общем, насчёт обратимости понятно: на сколько частей разобрали, столько и собрали. Не в этом дело. Но во взаимосвязь умножения и деления дети тоже должны вникнуть, выявить её на опыте (упражнениях), а не просто знать о ней, т. Из примера видно, что 8 является делимым, а 2 является делителем. Делитель, как теперь называется, это — «оператор действия», т.е. это то, что делит (на определённое его величиной количество частей). Поэтому 2 не может быть одновременно множителем (точнее — умножаемым) для 4. Не должно быть «или-или», т. е. двусмысленности назначения члена выражения. Множителем (умножаемым) для 4 (здесь 4 — оператор умножения) станет частное от деления 8 на 2, т. е. тоже 4. Следовательно, последовательность записи действий слева направо определяет так сказать статус каждого члена выражения: что есть делимое, делитель, множитель. А это не просто «статус», а так сказать, «положение обязывает». Делителю — делить, умножаемому — умножаться, множителю — умножать. Значит, в порядке записи обозначен порядок действий. Сама запись есть способ обозначения порядка действий. Способ, который устраняет неоднозначность, порождаемую безочерёдностью («равноприоритетностью») умножения и деления. *** Я разъяснила объективные основания «приоритетности» всех арифметических действий. Надеюсь теперь всем понятно, почему не может быть ни различных, ни других правил «приоритетности». Порядок действий не зависит от человека. От человека зависит лишь его формулировка в виде правил. При желании каждый может формулировать правила «своими словами», формулируя своё понимание очерёдности. Повторю, что это отрывок, где я показываю смысл правил BODMAS/PEMDAS, т.к. без смысла они становятся догмой. Но весь сыр-бор разгорелся по причине того, что никто, включая решивших правильно, не понимает смысла опущенного перед скобками знака умножения. Опущенный знак умножения имеет назначение скобок, поэтому в «спорном примере» делителем 8 является произведение 2(2+2). Или, выражаясь на математическом новоязе, опущенный знак умножения делает действие умножения «приоритетнее» деления, т.к.
Телеграмм-канал для своих, не скопипащенных, постов: t. | |
com/pjmdolI/status/1155599063242485762 ) пользователи решают по разному: одни делят 8 на 2 и умножают на (2+2), ответ: 16, другие делят 8 на произведение 2(2+2), ответ — 1. Первых — большинство. Правильный ответ — 1. Я хотела написать пост на эту тему. Пока помещаю отрывок из него, где объясняю правила порядка действий.
е. их можно выполнять в произвольной последовательности. 
к. это одно и то же действие. Такова основа безочерёдности выполнения действий сложения и вычитания, которую в псевдоматематическом новоязе назвали равной приоритетностью сложения и вычитания. Не может одно и то же действие быть «разноприоритетным», если уж на то пошло.
Поэтому самое главное, что ребёнку надо пояснить, почему разное — одинаково, так, чтобы, наоборот, не запутать его. Если он сам не поймёт, не увидит одинаковость с точки зрения именно арифметики, как бы условности исключительно для удобства счёта реальных вещей, то он просто зазубрит, мол, «что это одно и тоже», чего нельзя допускать, ибо он отчается понять, что повлечёт за собой цепь непониманий. Поэтому пояснять надо в своё время. Думаю, что одинаковость будет ясна в полной мере после понимания, что такое отрицательные числа как уяснения их назначения (практического использования) — «ниже нуля и выше нуля». До этого вычитание для ребёнка будет самостоятельным арифметическим действием, как он видит на практике, противоположностью сложения по результату. Поэтому детям сначала надо соблюдать правило «слева направо» в выражениях, где есть сложение и вычитание, чтобы получить правильный ответ. Но не делать правило догмой, а лишь подспорьем при неуверенности. Положительные слагаемые они могут складывать произвольно, они могут сложить все слагаемые, из которых потом вычитать все вычитаемые, чтобы убедиться, что сумма не меняется, и на наглядных практических примерах с теми же счётными палочками, понять — почему.
В примерах, подобных 10+20-10 они могут сначала выполнить вычитание, т. е. второе действие, или сначала от 10 — 10, и всё это можно воспроизвести на практике, с помощью тех же счётных палочек. Затем в выражения можно добавлять слагаемые/вычитаемые в виде неизвестных произведений и частных. После изучения отрицательных чисел и накопления опыта действий с ними они легко могут осознать тождественность вычитания и сложения как арифметического действия, убедившись в этом на практике.
Поэтому составление и запись выражения отражает логику решения данной задачи, последовательность ответов на предварительные вопросы, получив которые, человек может получить ответ, ради которого он решал задачу и даже ставил её. Поэтому каждый член выражения, являющийся количественной характеристикой, имеет и смысловое значение, отвечая на вопрос: «количество чего?» (только в абстрактных примерах этот вопрос не ставится, число имеет только величину, или «значение», и не имеет качественной, или смысловой, характеристики). Т. к. арифметические действия записываются в порядке осознания задачи и решения предварительных вопросов, то тем самым фиксируется смысловая нагрузка членов выражения, следовательно, фиксируется смысл действия — на какой вопрос будет получен ответ. Следовательно, очередность действий в порядке записи выражения («слева направо») позволяет решающему задачу человеку сохранять логику решения, последовательно отвечая на предварительные вопросы. Только для этой цели требуется соблюдать очерёдность «слева направо».
Но и в этом случае, уверенный в себе человек, хорошо понимающий смысл задачи, может не соблюдать этого правила, если ему удобно считать (ведь считать не означает — решать) в другой последовательности, как какой-либо абстрактный пример. Для этой же цели учащиеся осваивают способы «упрощения выражений» и свойства арифметических действий. Такой человек всегда может объяснить метод своего решения, как свои допущенные на время условности. Большинство людей уверенность путают с самоуверенностью, поэтому для страховки им лучше соблюдать очерёдность действий, чтобы не запутаться в задаче и не получить абсурд в виде «полтораземлекопа». В физике адекватность составленного выражения решению задачи проверяется размерностью.
И теперь уже не только ради сохранения смысла членов выражения, а потому, что другой порядок действий даст неправильный ответ. Правило «слева направо» придаёт строгую очерёдность «безочерёдным» делению и умножению. Почему?
к. без этого не смогут владеть этими инструментами математики в полной мере.
Это есть основание правила «слева направо». Менять этот порядок, например выполнять сначала умножение 2*4, значит — фактически решать не данный, а другой пример, в котором бывший делитель (2) становится множителем для 4, а полученное произведение — делителем 8. В первом случае мы находим произведение, во-втором, частное. Т.е. изменение порядка действий изменяет пример. Другой пример — другой ответ. Если же нам нужен именно «другой пример», то нет проблем — произведение 2*4 берётся в скобки: 8:(2*4), или знак деления заменяется на горизонтальную черту. В данном случае скобки «аннулируют» очерёдность «слева направо», т. к. меняют «статус» двойки с делителя, данный ему порядком записи, на умножаемое. Чтобы оно благополучно умножилось. В алгебраических выражениях, типа a:bc, чтобы обозначить делителем b, нужно делимое и делитель взять в скобки(а:b)c, или заменить знак деления на горизонтальный. Хотя проще всего в таких случаях поставить знак умножения между b*c. Точнее, при записи алгебраического выражения его просто не надо опускать.
Но принято его опускать, поэтому скобки — в помощь.
согласно правилам, действия в скобках первичны. В данном случае опущенный знак умножения меняет порядок вычисления «слева направо» на «справа налево», определяя делителем произведение. Постараюсь дописать текст, т.к. мне надо было понять, как вообще и почему мог произойти такой «спор». Для меня это как гром с ясного неба.
me/warrax_newsОбъяснение для родителей, учителей и детей
PEMDAS появляется в начальной и средней школе и является популярной аббревиатурой, используемой для того, чтобы помочь учащимся запомнить порядок операций. В этой статье мы объясним, что означает PEMDAS, предоставим вам рабочие примеры и практические вопросы, чтобы помочь вашим ученикам в классе.
Что такое PEMDAS?
PEMDAS — известная аббревиатура, используемая для того, чтобы помочь учащимся запомнить порядок операций.
PEMDAS означает:
- Скобки
- Экспоненты
- Умножение
- Подразделение
- Дополнение
- Вычитание
Что такое правило PEMDAS?
Правило PEMDAS сообщает учащимся, как решать математические задачи с несколькими операциями и в каком порядке их следует выполнять, чтобы получить правильный ответ.
Важно отметить, что обратные операции умножения и деления, а также сложения и вычитания в этом списке взаимозаменяемы и выполняются слева направо по мере их появления в выражении.
Во избежание путаницы некоторые учителя предпочитают отображать PEMDAS, как показано ниже, с M/D (для умножения и деления) и A/S (для сложения и вычитания) на одном уровне:
| P | Сложниц: () [] {} |
| E | Экспоненты: 2 2 4 3 |
| M/D | справа |
| A/S | Сложение и вычитание: + – слева направо |
В чем разница между PEMDAS и DMABODMAS?
PEMDAS, BODMAS и BIDMAS — это аббревиатуры, которые служат одной и той же цели — помочь учащимся запомнить порядок операций при решении математических уравнений с несколькими операциями. Эти сокращения различаются в зависимости от того, где они используются.
Например, PEMDAS обычно используется математиками в США, а BODMAS и BIDMAS обычно используются в Великобритании.
Канада и Новая Зеландия часто используют BEDMAS. Выделенные термины в таблице ниже показывают, чем они отличаются.
Обратите внимание, что термины «круглые скобки» и «квадратные скобки», а также термины «показатели степени», «порядки» и «индексы» относятся к одним и тем же понятиям.
| PEMDAS | BODMAS | BIDMAS |
| Parentheses Exponents Multiplication Division Addition Subtraction | Brackets Orders Division Multiplication Addition Subtraction | Brackets Indices Division Multiplication Addition Subtraction |
Посмотрите, как порядок операций разбит на простые шаги в нашей программе индивидуального обучения Third Space Learning.Почему PEMDAS важен?
PEMDAS важен, потому что важен порядок операций! Порядок операций — это набор правил для решения математических уравнений и выражений с несколькими операциями. Этот набор правил гарантирует, что все математические уравнения решаются одинаково. Если уравнения решать просто в том порядке, в котором они появляются, вы можете получить неправильный ответ.
Учащиеся могут обращаться к правилам PEMDAS для решения уравнений или вычисления выражений в правильном и последовательном пошаговом процессе. PEMDAS важен, потому что он позволяет учащимся запомнить этот набор правил в правильном порядке.
Как вы помните PEMDAS?
PEMDAS может быть запоминающимся для многих, но некоторые учащиеся могут предпочесть мнемоническое устройство, которое поможет им легко вспомнить каждую букву PEMDAS. Наиболее распространенным является «Прошу прощения, моя дорогая тетя Салли».
Некоторые учителя предлагают своим ученикам придумать свое собственное мнемоническое устройство для PEMDAS, которое может мотивировать учащихся легче запомнить аббревиатуру. Студенты могут придумать глупые мнемоники, такие как Purple Elephants March Down A Street 9.0064 .
Когда дети узнают о PEMDAS в школе?
PEMDAS и порядок работы чаще всего преподаются в 5-м и 6-м классах по всей стране в школах, соответствующих Common Core и другим стандартам.
Это закладывает прочную основу для изучения учащимися более сложных математических понятий, включающих алгебраические выражения, в средней и старшей школе. Эти более сложные уравнения и выражения могут включать квадратные корни, десятичные числа, переменные, целые числа и т. д., но правила PEMDAS и порядок арифметических операций останутся неизменными.
PEMDAS в 5-м классе
PEMDAS и порядок операций впервые появляются в Common Core Standards в 5-м классе в разделе «Операции и алгебраическое мышление».
- 5.OA.A.1 Используйте круглые и фигурные скобки в числовых выражениях и вычисляйте выражения с этими символами.
- 5.OA.A.2 Напишите простые выражения, которые записывают вычисления с числами, и интерпретируйте числовые выражения без их вычисления.
Учащиеся должны уметь оценивать выражения, содержащие круглые скобки ( ), квадратные скобки [ ] или фигурные скобки { }, а также понимать, как определить, в каком порядке следует оценивать каждую часть выражения. У учащихся может возникнуть соблазн пройтись по выражению слева направо, но PEMDAS поможет им не забывать этого делать.
Учащиеся также должны уметь представлять математические выражения в письменной форме. Используемая ими формулировка должна передавать порядок, в котором должны оцениваться части выражения.
Например, мы можем описать выражение 3 x (5 + 2) как «, умноженное на три суммы пяти и двух. » Если бы мы описали это как «трижды пять плюс два», это не передало бы того факта, что сложение (которое находится в скобках) нужно выполнить перед умножением.
PEMDAS для 6-го класса
PEMDAS для 6-го класса находится в домене выражений и уравнений. Понимание учащимися порядка операций расширяется по мере того, как они работают с более сложными числовыми выражениями, включающими переменные, которые представляют собой букву, используемую в качестве неизвестного числа в выражении (например, 4 + x = 7).
Учащиеся должны хорошо понимать порядок операций при переходе к более сложному содержанию. Учащиеся и преподаватели будут использовать PEMDAS при соблюдении этих стандартов более высокого уровня, чтобы подтвердить свои знания о порядке операций.
- 6.EE.A.1 Напишите и оцените числовые выражения, включающие целые числа.
- 6.EE.A.2 Напишите, прочитайте и оцените выражения, в которых буквы обозначают числа.
- 6.EE.A.3 Применение свойств операций для создания эквивалентных выражений.
- 6.EE.A.4 Определите, когда два выражения эквивалентны.
Примечание.
В стандарте 6.EE.A.2 есть несколько подстандартов, включающих числовые выражения, которые также требуют понимания учащимися порядка операций.
Рабочие примеры PEMDAS
Рабочие примеры PEMDAS для 5-го класса
Вопрос 1: 6 x 4 + 8 ÷ 2
Шаг 1: В этом примере мы видим сложение, деление и умножение, в этой последовательности. Согласно PEMDAS, нам нужно выполнить любое умножение или деление слева направо, как они появляются, перед любым сложением или вычитанием.
После выполнения умножения у нас осталось 24 + 8 ÷ 2
Шаг 2: Теперь, когда у нас осталось сложение и деление, мы сначала выполняем деление.
После деления остается 24 + 4
Ответ: 24 + 4 = 28
Вопрос 2: (8 + 5) – 3 x 2 2
5 90 В этом примере мы видим операции сложения, вычитания и умножения именно в таком порядке, но у нас также есть набор скобок и показатель степени.
Следуя PEMDAS, нам нужно сначала выполнить что-либо в скобках, а затем вычислить показатели степени, прежде чем переходить к операциям.
После вычисления в скобках у нас осталось 13 – 3 x 2 2
Шаг 2: Теперь переходим к показателю степени.
После вычисления значения степени у нас осталось 13 – 3 x 4
Шаг 3: В нашем выражении осталось умножение и вычитание, поэтому нам нужно выполнить умножение перед вычитанием. Здесь вы чаще всего обнаружите, что студенты делают ошибку. Сначала они захотят выполнить вычитание (13 — 3 = 10), а затем умножение (10 x 4 = 40), но это даст им неверный ответ 40.
После первого умножения у нас останется 13 – 12.
Ответ: 13 – 12 = 1
Вопрос 3: 5 x [3 + (3 2 – 8)]
5 Часто, когда пятиклассники становятся более опытными в этом содержании, они сталкиваются с более сложными выражениями, включающими больше группирующих символов.
Вместо круглых скобок они также могут видеть квадратные скобки [ ] и фигурные скобки { }. Их всегда следует выполнять, начиная с самого внутреннего символа группировки, которым должны быть круглые скобки.Шаг 1: Мы переключаем наше внимание на самый внутренний символ группировки, круглые скобки. Внутри скобок мы видим показатель степени, а также вычитание. Сначала нам нужно вычислить значение показателя степени.
После вычисления значения показателя степени у нас осталось 5 x [3 + (9 – 8)]
Шаг 2: Теперь, когда мы вычислили показатель степени, мы выполняем операцию в скобках, которая вычитание.
После вычитания у нас осталось 5 х [3 + 1]
(Обратите внимание, что я удалил круглые скобки, так как в них осталось только одно число.)
Шаг 3: Теперь, когда мы вычислили внутреннюю часть скобок, мы переходим к следующему символу группировки, который это скобки. Мы рассматриваем их так же, как круглые скобки, поэтому нам нужно выполнить сложение внутри них, прежде чем мы сможем выполнить умножение в нашем выражении.
После выполнения сложения в скобках у нас осталось 5 х 4
Ответ: 5 x 4 = 20
Рабочие примеры PEMDAS для 6-го класса
В 6-м классе учащиеся используют ту же концепцию PEMDAS и порядок операций, но они имеют дополнительный уровень сложности по мере их введения к переменным, которые представляют собой буквы, используемые вместо неизвестных чисел.
Вопрос 1: 6 x y 2 если y = 3
Шаг 1: Первое, что нам нужно сделать, чтобы найти значение этого выражения, это заменить нашу переменную ее значением. В этом примере нам дано значение нашей переменной y, равное 3,9.0005
После замены нашей переменной у нас останется 6 x 3 2
Шаг 2: Далее мы следуем правилу PEMDAS для вычисления показателей степени перед любыми операциями.
После того, как мы вычислим показатель степени, у нас останется 6 x 9
Ответ: 6 x 9 = 54
Вопрос 2: 3n + 8 x (4y – 3), если n = 2 и y = 1
В 6-м классе учащиеся также знакомятся с новым способом чтения и записи умножения.
Когда они узнают о переменных, они также узнают, что такой термин, как 3n, представляет умножение. Число 3 и переменная рядом с ним предназначены для умножения. Точно так же, если учащиеся видят число рядом со скобкой, например 2 (4), это также представляет собой умножение, поэтому этот пример будет равен 8.
Шаг 1: Во-первых, нам нужно ввести значения наших переменных.
Поскольку n = 2 и y = 1, наше выражение принимает вид 3(2) + 8 x (4 x 1 – 3)
Шаг 2: Теперь давайте поработаем с нашими группирующими символами. Член 4y стал 4 x 1, что, как мы знаем, равно 4. Таким образом, у нас осталось 4 – 3 в скобках, что равно 1.
3(2) + 8 x (1)
Шаг 3: Теперь нам остается умножение, сложение и умножение именно в таком порядке. Если вокруг одного числа (в данном примере 1) оставлены круглые скобки, оно не имеет значения, если только оно не находится непосредственно рядом с другим числом, как мы видим 3(2).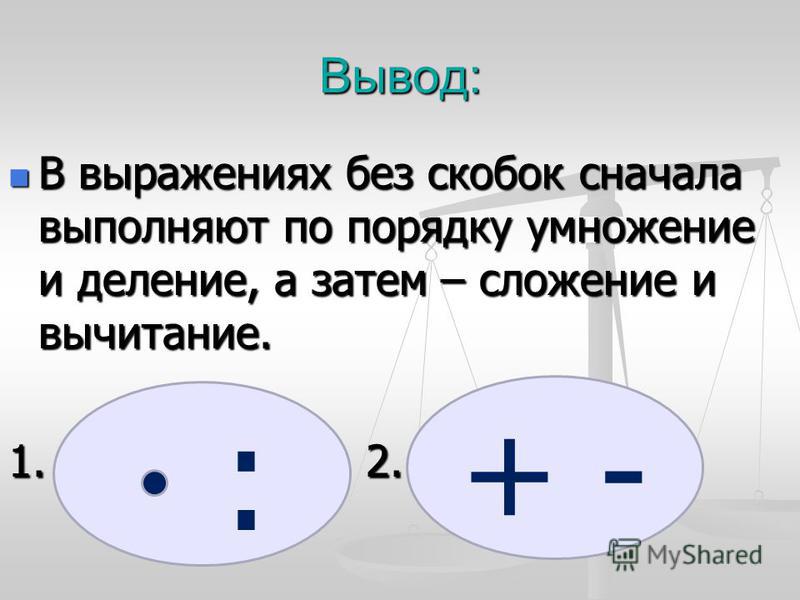
Как упоминалось выше, это означает умножение.
Давайте выполним умножение, которое идет первым слева направо, чтобы соответствовать нашему правилу PEMDAS.
У нас осталось 6 + 8 x (1)
Шаг 4: Теперь, когда у нас осталось сложение и умножение, мы можем выполнить другую часть умножения.
Осталось 6 + 8
Ответ: 6 + 8 = 14
Практические вопросы PEMDAS
Ниже мы включили вопросы PEMDAS, подходящие для учащихся 5-х и 6-х классов, включая ответы.
Вопросы PEMDAS для 5 класса:
7 + 3 x 4 ÷ 2
Ответ: 13
8 x (12 – 9) + 4 ÷ 2 7 – 4)
Ответ: 57
9 x [18 – (2 x 3)] ÷ 4
Ответ: 27
5 3 – [3 x (1 + 2)]
0 2 Ответ: 44Вопросы PEMDAS для 6-го класса:
5x – 4 2 если x = 8
Ответ: 24
4(9 – 2 2 ) x 3y если y = 4
Ответ: 240
Какой показатель делает уравнение верным?
(9 – 6) 3 + _______ = 43
Ответ: 4 2
Какое число делает неравенство верным?
7 + [(4 – 2) x 2] 3 > 6 + [(13 – 9) x _____] 2
а) 3 б) 2 в) 4 г) 5
: 90 Ответ ) 2
Напишите <, > или =, чтобы числовое выражение стало верным.
3(8 – 3) + 5 2 ____ 5[2 + 3] + 4 2
Ответ: <
Часто задаваемые вопросы о PEMDAS
Что означает PEMDAS?
PEMDAS расшифровывается как Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
Вы сначала умножаете или делите при использовании PEMDAS?
Умножение и деление выполняются слева направо. Например, в следующем выражении 6 x 2 ÷ 3 x 4 мы должны выполнить умножение, затем деление, затем умножение.
Как вы помните PEMDAS?
Пожалуйста, извините, моя дорогая тетя Салли.
Почему PEMDAS важен?
PEMDAS — важная аббревиатура, используемая для того, чтобы помочь учащимся запомнить правила порядка операций. Это предотвращает разные ответы для одних и тех же математических уравнений.
Как правильно: BODMAS или PEMDAS?
И BODMAS, и PEMDAS верны и используются в разных регионах мира. BODMAS распространен в Великобритании, а PEMDAS используется в США. BODMAS означает скобки, порядок, деление, умножение, сложение, вычитание.
Что такое GEMS?
GEMS расшифровывается как группировка, экспоненты, умножение или деление, вычитание или сложение. Группировка относится ко всем символам группировки — скобкам, фигурным скобкам, фигурным скобкам и т. д. GEMS — это новая аббревиатура, которая была введена вместо PEMDAS. Их можно использовать взаимозаменяемо.
арифметика — можете ли вы опровергнуть это правило PEDMSA? — (деление перед умножением, вычитание перед сложением)
Чтобы расширить ответ Losethegame
Losethegame ответил: «Я попал сюда, погуглив тот же вопрос, хотя я не уверен, что (м)кто-либо из комментаторов ответил на него конкретно.
Я думаю, что вы правы в том, что ваше правило не может быть нарушено. Вероятно, это может быть доказано алгебраически, потому что a*(b/c)=(a/c)*b и a+(b-c)=(a-c)+b…?»
Я согласен, что это, вероятно, может быть доказано алгебраически с помощью методов, подобных тому, что упоминает Losethegame (хотя пример с LoseGame может быть ошибочным, поскольку, как указывает пользователь 21280, Losethegame меняет операнды местами). Но развивая идею алгебраического доказательства (и без замены операндов!), я могу придумать какую-нибудь алгебру, которая могла бы это доказать. (Предоставленный пользователь 21280 считает, что мои примеры не учитывают все возможности. Его ответ с использованием логических формул мог бы).
Дано уравнение, в котором умножение предшествует делению, например. 3*4/2 неважно, что вы сделаете первым. Так что буквальный PEMDAS или PEDMAS подойдет. Принимая во внимание уравнение, в котором деление идет текстуально перед умножением, например. 6/2*3 тогда имеет значение, что вы сделаете первым.
Традиционное прочтение PEMDAS или PEDMAS делает это правильно (потому что они сказали бы сначала сделать первое, а это деление), буквальное PEDMSA делает это правильно. Буквальное прочтение PEMDAS может привести к ошибкам.
Вычитание и деление разделяют это свойство. Допустим, мы составим небольшое уравнение из той части уравнения, в которой операторы конкурируют друг с другом. Если вычитание конкурирует со сложением, и вычитание происходит первым (текстуально, в уравнении), оно должно быть выполнено первым. Если деление конкурирует с умножением, а деление идет первым, деление должно быть выполнено первым. В то время как если бы сложение конкурировало с вычитанием, то независимо от того, происходит ли оно первым текстуально или нет, не имеет значения, выполняется ли сначала сложение или вычитание. Точно так же, если умножение конкурирует с делением, если умножение идет первым текстуально, то не имеет значения, выполняется ли сначала деление или умножение. Таким образом, литерал PEDMSA всегда работает (т.
е. строго выполняет деление перед умножением, вычитание перед сложением). Как и традиционное/правильное прочтение PEMDAS/PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют одинаковый приоритет и сначала выполняют первое, аналогично сложению и вычитанию.
Так, например.
Взятие 1*2/3 , так что a*b/c
Следование PEDMSA буквально дает 1*(2/3) , так что a(b/c) Следуя PEDMSA, мы традиционно получаем (1*2)/3 , поэтому (ab)/c
И мы знаем алгебраически, что a(b/c) = (ab)/c
1*2/ 3 а* б/к знак равно 1*2/3 сб/с
Принимая 1/2*3 так a/b*c Это оценивается одинаково независимо от того, следуете ли вы строго упорядоченному PEDMSA или традиционному PEMDAS, т. Е. Делаете ли вы сначала деление, как правило, или сначала вы выполняете первое из умножения и деления, это (a/b)*c в обоих случаях так явно одно и то же.
1/2*3 (а/б)*в знак равно 1/2*3 (а/б)*в
С 1+2-3 , если мы делаем a+ b-c , который заказан PEDMSA, т.е. a+(b-c) , это тот же результат, что и при традиционном PEMDAS (a+b)-c. Мы знаем алгебраически a+(b-c)=a+b-c=(a+b)-c
Я помню, как мой учитель математики указал, что одна вещь, которую вы хотите остерегаться / знать, это -(a+b) , которое мы просверлили, было -a-b настолько сильно отличается от -а+б . Вычитания всегда должны выполняться первыми и по порядку… и если сначала выполняется вычитание или сначала сложение и вычитание, то мы сохраняем это правило.
1+2-3 а+(б-в) знак равно 1+2-3 (а+б)-в
И для этого то же самое. алгебраически
1-2+3 (1-2)+3 (a-b)+c знак равно 1-2+3 (1-2)+3 (а-б)+в
И, наверное, наконец. 1-2-3 и 1/2/3 И независимо от того, выполняете ли вы строго предписанную PEDMSA или традиционную PEMDAS, это (1-2)-c и (1/2)/3 так же есть.