Что выполняется вперед, деление или умножение? — «Семья и Школа»
Содержание
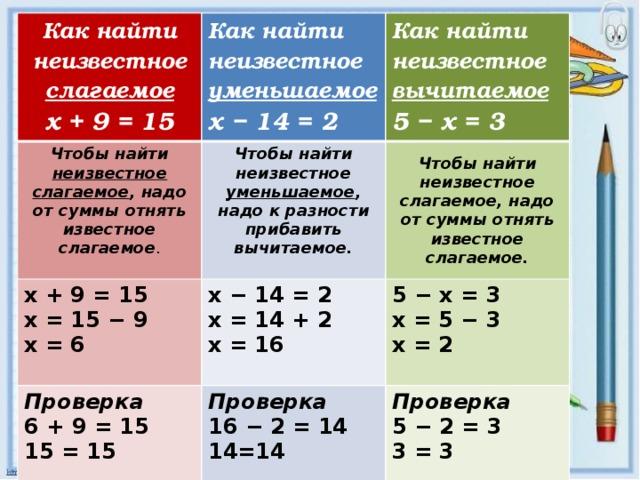
Действия какой ступени выполняются в первую очередь?
Меню раздела
- Математика
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5
Ответьте на вопрос: —
Какой порядок действий при решении длинного выражения?
Порядок выполнения действий при решении выражения.
В математике последовательность выполнения действий разделена на две ступени:
к первой ступени относятся действия — сложение и вычитание, ко второй ступени — умножение и деление.
При нахождении значения выражения в первую очередь выполняются действия заключённые в скобки (если имеются), далее выполняются действия второй ступени и в последнюю очередь действия первой ступени.
Порядок действий обозначается слева направо.
Пример:
1. Слева направо обозначим действия в скобках.
2. Вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия второй ступени.
Действия второй ступени — умножение и деление.
3. Вновь вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия первой ступени.
Действия первой ступени — сложение и вычитание.
Всего 10 действий. Выполняем их по проставленному порядку.
Выполним действия в скобках:
18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8
- 27 — 25 = 2
- 6 + 4 = 10
После выполнения действий в скобках выражение стало выглядеть так:
18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8
Теперь выполним все действия второй ступени — умножение и деление:
18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8
- 8 : 2 = 4
- 2 · 8 = 16
- 4 · 10 = 40
- 16 : 8 = 2
После выполнения действий второй ступени выражение стало выглядеть так:
18 + 4 — 16 + 40 + 2
Теперь выполним все действия первой ступени — сложение и вычитание:
18 + 4 — 16 + 40 + 2
- 18 + 4 = 22
- 22 — 16 = 6
- 6 + 40 = 46
- 46 + 2 = 48
18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8 = 48
Коротко:
Известные и великие математики
ученые средневековья и современности, и их вклад в мировую науку
Пафнутий Чебышёв
Русский математик и механик
Дата рождения: 16 мая 1821
Место рождения: Акатово, Боровский уезд, Калужская губерния, Российская империя
Дата смерти: 8 декабря 1894 (73 года)
Биография
Первоначальное воспитание и образование получил дома: грамоте его обучила мать Аграфена Ивановна. Арифметике, французскому языку и музыке обучала двоюродная сестра Авдотья Квинтилиановна Сухарёва.
Одним из детских увлечений будущего учёного было изучение механизмов игрушек и автоматов, которые сам
придумывал и изготовлял их.
Арифметике, французскому языку и музыке обучала двоюродная сестра Авдотья Квинтилиановна Сухарёва.
Одним из детских увлечений будущего учёного было изучение механизмов игрушек и автоматов, которые сам
придумывал и изготовлял их.
В 1832 году семья переехала в Москву. В Москве с Пафнутием математикой и физикой занимался П. Н. Погорельский — один из лучших учителей Москвы, у которого в том числе учился, в пансионе Вейденгаммера, и И. С. Тургенев. Латынь Пафнутию Чебышёву преподавал в то время студент-медик, а в будущем главный врач Шереметевской больницы А. Т. Тарасенков.
Летом 1837 года Чебышёв поступил в Императорский Московский университет на вторе физико-
математическе отделение философского факультета и начал изучение математики . Существенное влияние на
формирование круга научных интересов молодого Чебышёва оказал его учитель — профессор прикладной
математики и механики Московского университета Николай Дмитриевич Брашман.
В 1841 году Пафнутий Чебышёв его окончил.
В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел, геометрии, теории эллиптических функций и практической механике.
В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории
вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского
университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на
тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел,
геометрии, теории эллиптических функций и практической механике.
В 1849 году Чебышёв защитил в Петербургском университете докторскую диссертацию «Теория сравнений», после чего в 1850 году он стал профессором Петербургского университета; данную должность он занимал до 1882 года. Работая в Петербургском университете, Чебышёв близко сошёлся с профессором прикладной математики О. И. Сомовым, который тоже был учеником Н. Д. Брашмана, и эти отношения переросли в глубокую дружбу. В семейном плане Чебышёв был одинок, и это обстоятельство также способствовало его сближению с большой семьёй Сомова.
Интерес к механизмам сохранялся у Чебышёва и в зрелые годы. В 1852 году Чебышёв совершил научную
командировку в Великобританию, Францию и Бельгию, в ходе которой он ознакомился с практикой зарубежного
машиностроения, с музейными коллекциями машин и механизмов, с работой заводов и фабрик, а также
встречался с крупнейшими математиками и механиками: О. Коши, Ж. Лиувиллем, Ж. -А. Серре, Л. Фуко, Ш.
Эрмитом, Дж. Сильвестром, А. Кэли, Т. Грегори. После этого он некоторое время преподавал практическую
механику в Петербургском университете и Александровском лицее.
Коши, Ж. Лиувиллем, Ж. -А. Серре, Л. Фуко, Ш.
Эрмитом, Дж. Сильвестром, А. Кэли, Т. Грегори. После этого он некоторое время преподавал практическую
механику в Петербургском университете и Александровском лицее.
В 1853 году академики П. Н. Фусс, В. Я. Струве, Б. С. Якоби, В. Я. Буняковский представили Чебышёва к избранию в адъюнкты Петербургской академии наук, особо отметив важность его работ в области практической механики. В том же году он был избран в адъюнкты, а в 1856 году стал экстраординарным академиком.
В 1858 году в связи с его работами по теории шарнирных параллелограммов и теории приближения функций академики В. Я. Буняковский, М. В. Остроградский, Э. Х. Ленц, Б. С. Якоби, А. Я. Купфер, О. В. Струве подписали представление к избранию Чебышёва ординарным академиком. И 1859 году Чебышёв избран ординарным академиком. Стал почётным членом Московского университета.
С 22 февраля 1860 года — ординарный профессор.
С 10 июля 1863 года — член Учёного комитета Министерства народного просвещения.
С 30 августа 1863 года — действительный статский советник.
Чем знаменит:
- В 1840/1841 учебном году, участвуя в студенческом конкурсе Императорского Московского университета, Пафнутий Чебышёв получил серебряную медаль за работу по нахождению корней уравнения n-й степени которую написал ещё в 1838 году и сделаную на основе алгоритма Ньютона
- Работы по теории вероятностей — изъяв из неё расплывчатые формулировки и неправомерные утверждения и превратив её в строгую математическую дисциплину
- Работы по теории чисел
- Работы по математическому анализу
- Работы по прикладной математике и механике
- Работы по «стопоходящей машины»
- Создатель автоматического арифмометра
- оздатель модели инвалидной коляски
- оздатель
- Работы по
- Назад
- Вперед
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Подростку оторвало три пальца У подростка взорвалась бомба Восьмиклассник подорвался на кофемолке Не рой себе яму, тебе будут угрожать! Алло, Майя! Взорвалась прямо во рту Продырявили «Северный поток-2» Прекращение торгов долларом Застрелил дочь из ружья Изрезал ножом собственную дочь В составе России В школе № 26 отравились дети Кадыров заявил о перевыполнении плана призыва в Чечне на 254% Мальчика наградили орденом Мужества Избили, задушили и положили в ванну Все наши прежние действия покажутся детскими шалостями
Запомнить меня
Регистрация
Таблица деления | Таблица умножения
Деление в математике – это действие, противоположное умножению.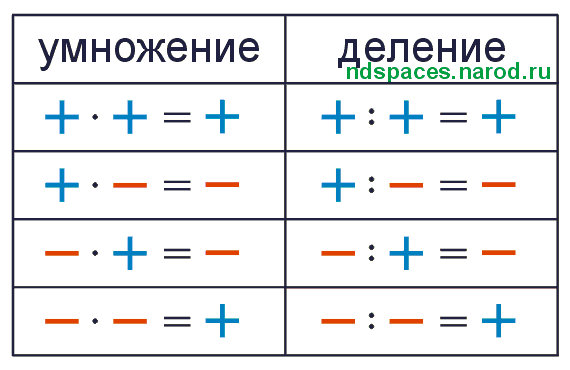
Смысл слова «деление» в русском языке намного шире, более того иногда оно применяется с разными оттенками и смыслами, а порой возможны и совсем необычные повороты, как, например, во фразе «клетка размножается путем деления», но на этой странице речь пойдет именно о делении в математике в общепринятом на сегодня смысле. Во многих случаях речь будет идти о ситуации, когда происходит преобразование единого целого или совокупности множества составных частей в самостоятельные или отдельно рассматриваемые части. Также в математике часто можно встретить термин «операция деления». Какой же практический смысл этого действия? Представим, что в корзинке есть 12 яблок. Если разделить яблоки поровну между Васей, Петей и Колей, то по сколько яблок достанется каждому? Итак по условию задачи 12 яблок мы будем делить между тремя мальчиками, тогда в результате каждому из них достанется по 4 яблока. В письменном виде это можно записать как 12 : 3 = 4.
То же самое выражение можно записать дробью, где над чертой будет 12, а под чертой 3. При любой из этих записей справедливо следующее: в операции деления все числа представлены в виде делимого, делителя и частного.
На первом месте (или в верхней части дроби) будет всегда находиться делимое. На втором месте (в этом примере под чертой) – делитель. После знака равно всегда находится результат деления (частное). Следует отметить, что делителей может быть несколько. Например, 10 : 2 : 5=1. Здесь только одно делимое, одно частое, но два делителя (2 и 5). Для лучшего понимания необходимо хорошо разобраться, где находится делимое, где делитель, а где частное. Для быстрого счета в уме таблицу деления часто запоминают наизусть также, как и таблицу умножения. Как правило, если таблица умножения «отскакивает от зубов», проблем с таблицей деления не возникает. Но стоит отметить, что есть и другие способы быстрого деления в уме (способы счета описаны в специальном разделе).
Также деление может быть представлено в виде квадратной таблицы. В зависимости от того, что на что мы будем делить, результат может быть получен различный. Ниже представлен пример записи результатов в такой таблице.
В данной таблице в строке указано делимое, в столбце делитель, в ячейках на пересечении – частное. Так как не всегда в результате получаются целое число и при этом не все люди, изучающие деление, уже умеют использовать десятичные дроби, запись в ячейках сделана с помощью знака /. Существует и другой способ записи, когда в столбцах указано делимое, в строке — делитель. Частное по-прежнему находится в ячейках на пересечении.
Как видим, таблица уже приняла совсем другой вид. Поэтому, с такой таблицей нужно быть внимательным, желательно в начале её использования произвести проверку умножением. К примеру, мы выполняли действие 10 : 5 = 2. С помощью умножения можно проверить, правильно ли мы записали ответ: 2 х 5 = 10. Следовательно, все было выполнено верно. Также, для поиска ответа можно воспользоваться обыкновенной таблицей Пифагора. Сразу стоит отметить, что в таблице в примере ниже высота всех строк и ширина всех столбцов одинаковая. Это важно, и поможет при соотнесении умножением с площадью прямоугольника. Рассмотрим пример деления 45 на 9 (45 : 9).
Следовательно, все было выполнено верно. Также, для поиска ответа можно воспользоваться обыкновенной таблицей Пифагора. Сразу стоит отметить, что в таблице в примере ниже высота всех строк и ширина всех столбцов одинаковая. Это важно, и поможет при соотнесении умножением с площадью прямоугольника. Рассмотрим пример деления 45 на 9 (45 : 9).
Находим ячейку со значением 45. Поднимаемся или идем мысленно в бок до цифры 9. Дорисовываем (опять же мысленно или с помощью карандаша) до прямоугольника и находим оставшееся значение, равное 5. Как видим, операция деления довольно проста, особенно, если до этого была хорошо изучена тема умножения или под рукой имеется соответствующая табличка.
Откройте для себя происхождение деления и умножения
В сегодняшней статье мы объясним происхождение математических символов деления и умножения.
Символ деления:
Существует множество способов обозначения деления, и мы собираемся объяснить происхождение некоторых наиболее часто используемых и известных всем символов.
Горизонтальная черта дробей, введенная арабами, была впервые использована в Европе математиком Фибоначчи в тринадцатом веке, хотя ее использование не получило распространения до шестнадцатого века.
Наклонная черта, вариант горизонтальной, была введена Де Морганом в 1845 году. Это был типографский ресурс в печатных книгах, позволяющий писать дробь одной строкой. Символ, который сегодня широко используется для обозначения деления:
Другим одним из знаков была скобка, хотя в настоящее время она используется мало. Чтобы выразить 21, разделенное на 3, мы напишем 21) 3 и поместим результат деления справа после еще одной скобки: 21) 3 (7,
9).0005 Этот знак встречается в произведении Arithmetica integra (1544) немецкого математика Михаэля Штифеля.
Этот же математик также использовал заглавные буквы M и D для обозначения умножения и деления в своей работе Deutsche Arithmetica (1545). Другие авторы также использовали D, в том числе использование в качестве перевернутой D, например, французы, Ж. Э. Галлимар (1685-1771), и другие авторы, упавшие d, такие как португальцы, Ж. А. да Кухна (1744-1787).
Э. Галлимар (1685-1771), и другие авторы, упавшие d, такие как португальцы, Ж. А. да Кухна (1744-1787).
Один из до сих пор используемых символов деления — полоса с точками вверху и внизу. Он был введен швейцарским математиком Иоганном Генрихом Раном в его работе 9.0016 Немецкая алгебра (1659). Этот знак деления очень нагляден, вплоть до того, что черта дроби является общей нормой.
Этот символ не имел большого успеха ни в Швейцарии, ни в Европе. Впрочем, так было и в Великобритании, и в США. В частности, этот символ до сих пор используется в калькуляторах для деления.
Немецкий математик Готфрид В. Лейбниц ввел две точки ( : ), и в настоящее время это наиболее широко используемый символ. Согласно Лейбницу, одно из преимуществ использования этого символа состоит в том, что деление может вестись вдоль той же линии и сохраняет связь деления с умножением, для чего Лейбниц использовал точку.
Что касается гномона или угла, который мы используем для разделения факторов деления (делимое, делитель и частное), информации немного.
Но Бойер в своей History of Mathematics , стр. 282, говорит: «Арабы, а через них позже и европейцы, переняли большую часть своих арифметических ухищрений от индусов, и поэтому весьма вероятно, что метод «длинное деление», известное как «метод галеры» по своему сходству с кораблем с развернутыми парусами, также происходит из Индии». Судя по всему, в «методе галеры» использовался угол, аналогичный используемому в настоящее время.
Символ умножения:
Во времена вавилонян использовали идеограмму: «а-ду». В манускрипте Бахшиили , старейшем манускрипте по индийской математике, они помещают рядом один фактор и ничего больше. Индийский математик Бхаскара Ачария (1114–1185) использовал слово «бхавита» или «бха» сразу после факторов.
Другие математики использовали букву М для умножения и букву D для деления, как мы уже говорили ранее.
В старые времена арифметики многие алгоритмы использовали крест Сан-Андрес для решения продуктов деления и умножения и пропорций. Возможно, по этой причине в 1631 году Утред выбрал этот крест как символ умножения.
Возможно, по этой причине в 1631 году Утред выбрал этот крест как символ умножения.
Он получил широкое признание, за исключением математиков Готфрида В. Лейбница и Исаака Ньютона, которые не чувствовали себя полностью комфортно с этим символом. Лейбниц в 1698 году в одном из своих писем к математику Иоганну Бернулли пишет: «Мне не нравится символ × как символ умножения, так как его можно принять за х; … Я часто просто связываю две величины точкой, а умножение обозначаю RS · PQ».
По этой причине Лейбниц ввел точку как символ умножения.
Были и другие символы для умножения. Например, швейцарский математик Иоганн Ран (1622–1676) использовал звездочку * в своей работе Teutsche Algebra (1659). А также Лейбниц, который ранее использовал упавшую C открытой стороной вниз в своей Dissertatio комбинаторного искусства (1666).
Я надеюсь, что этот пост о делении и умножении и символах, которые мы используем для их выражения, был интересен.
Если вы хотите узнать больше о делении и умножении, зарегистрируйтесь в Smartick и попробуйте его бесплатно.
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения от Smartick (посмотреть все)
Как познакомить с умножением и делением на начальных уровнях
Умножение и деление — это следующий шаг после сложения и вычитания, и его следует преподавать по ступенчатой спирали в течение всех лет начальной школы. Оба понятия можно и нужно вводить вместе, уже во втором классе.
Прежде чем овладеть таблицей умножения, учащиеся должны сначала понять понятия умножения и деления. С этой целью мы требуем, чтобы учащиеся овладели четырьмя понятиями, выраженными в следующих утверждениях «Я могу»:
- Я могу использовать сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.

- Я могу разделить заданное количество конкретных предметов, объяснить, можно ли это сделать одинаково, и найти количество в каждой группе. Например. Найдите количество яблок в каждой группе, если 12 яблок разделить на 3 группы.
- Я могу найти количество групп, зная количество конкретных объектов и число в каждой группе. Например. Найдите количество групп, если 12 яблок разделить на группы по 3.
- Я могу определить, состоит ли группа объектов (до 20) из четного или нечетного числа членов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.
Давайте рассмотрим эти задачи более подробно:
Во-первых, мы хотим, чтобы учащиеся привыкли к графическим обозначениям того, что мы пытаемся выполнить, т. е. распределяем предметы по группам для облегчения подсчета. Будьте последовательны в соглашении, например. «3 группы по 4» выражается как 3×4, а 3×4 изображается как 3 ряда по 4.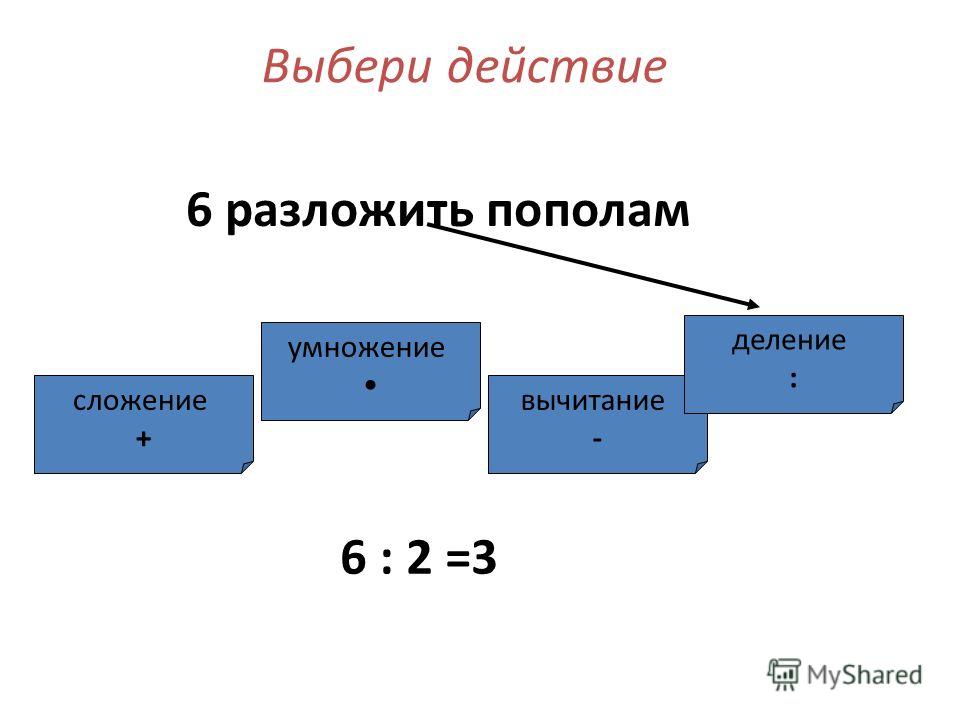
Как только мы сможем «интерпретировать», что означает произведение 3 и 4, мы введем простейшую стратегию для нахождения общего числа, то есть общее число для 3 групп по 4 равно 4 + 4 + 4 (равные слагаемые) .
Для учащихся не критично знать окончательный ответ (т.е. 12), получение концепции — это то, чего мы хотим достичь.
После того, как учащиеся поймут, как группировать предметы для их подсчета, следующим логическим шагом будет изучение дополнительной задачи деления – здесь у нас есть сумма, и мы хотим разбить ее на группы. Одно и то же уравнение деления может иметь две разные интерпретации.
1 – Количество элементов в каждой группе
2 – Количество групп
Мы видим, что одно и то же уравнение 12 ÷3 означает две разные вещи. На этом этапе важно понимать разницу между этими двумя сценариями, так как это повторится позже, когда они будут изучать дроби.
Как и в случае с умножением, более важно увидеть, как работает расположение объектов для обоих сценариев, чем получить правильный ответ «4» в данный момент.
Здесь мы хотим ввести родственную концепцию — видя, что группа объектов является четной, если объекты могут быть организованы в две равные группы.
Старайтесь избегать таких правил, как «числа, оканчивающиеся на четное число или нуль, четны». Вместо этого сосредоточьтесь на понимании того, что если в группе четное количество элементов, ее можно поровну разделить на две группы.
После того, как объекты разделены на две группы, мы можем легко увидеть, что сумма состоит из суммы двух равных чисел, в данном случае 12 = 6 + 6,
Видео объяснение и план урока (ресурс участника)
- https://teachablemath.com/lesson-plans/grade-2-lesson-plans/grade-2-semester-1-week-10-11/
Common Core Standards
- C3 Определить, состоит ли группа объектов (до 20) из четного или нечетного числа членов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.
Предмет: Математика Урок: 88 | Школа: | |||
Дата: | ФИО учителя: Мамаева А. | |||
Класс: 3 | Количество присутствующих: | Количество отсутствующих: | ||
Раздел (сквозная тема): | Раздел 3A – Внетабличное умножение и деление. | |||
Тема урока: | Закрепление устных приёмов умножения и деления. Графика. | |||
Цели обучения, которым посвящен урок: | 3.1.2.7 — выполнять устно внетабличное умножение и деление в случаях вида: 17·5, 96:6, 75:15, 84:4 3.1.2.9 — применять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100 3. | |||
Развитие навыков: | 1.2Операции над числами 2.1 Числовые и буквенные выражения 2.2 Равенства и неравенства. Уравнения | |||
Предполагаемый результат: | Все учащиеся смогут: выполнять устно умножение и деление внетабличных случаях вида: 17 · 5; 96 : 6; 75 : 15; 84 : 4; применять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Большинство учащихся смогут: объяснять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Некоторые учащиеся смогут: группировать случаи устного умножения и деления во внетабличных случаях вида: 17 · 5; 96 : 6; 75 : 15; 84 :4. | |||
Языковая цель | Учащиеся могут: объяснять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Предметная лексика и терминология: Правило умножения и деления суммы на число, подбор частного. Серия полезных фраз для диалога/письма Обсуждение: Объясните, какое правило лежит в основе конкретного приема: деление суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Как вы считаете, для чего нужно знать правила и свойства действий? Как выполнить проверку своих вычислений? | |||
Письмо: Запишите вычисления и их проверку | ||||
Материал прошедших уроков: | Приемы внетабличного умножения и деления | |||
Ход урока: | ||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | ||
0-3 мин | Мотивация Педагог показывает графические рисунки. детей в беседу о таком виде изобразительного искусства. Графика (др.греч. γρᾰφικός письменный, от др.греч. γράφ ω – записывать, писать) – вид изобразительного искусства, использующий в качестве основных изобразительных средств линии, штрихи, пятна и точки. Цвет также может применяться, но, в отличие от живописи, здесь он традиционно играет вспомогательную роль. В современной графике цвет может быть не менее важен, чем в живописи. При работе в графике обычно используют один или два цвета, кроме основного черного или красно-коричневого цвета сангины, можно использовать белый, в особенности на тонированной бумаге. Но при работе пастелью может использоваться вся цветовая палитра, как в живописи; согласно современной музейной классификации, работа пастелью на бумаге тоже относится к графике. контурной линии, в графическом искусстве широко используются штрих и пятно, также контрастирующие с белой (а в иных случаях также цветной, черной, или реже – фактурной) поверхностью бумаги – главной основой для графических работ. Сочетанием тех же средств могут создаваться тональные нюансы. Наиболее общий отличительный признак графики – особое отношение изображаемого предмета к пространству, роль которого в значительной мере выполняет фон бумаги (по выражению советского мастера графики В. А. Фаворского, – «воздух белого листа»). В графике, в частности, в гравюрах, может использоваться большое число цветов (при создании некоторых гравюр может использоваться более десятка печатных форм, каждая из которых «добавляет» свой цвет). | |||
Середина урока 4-6 мин 7-11 мин 12-29 мин 31-37 мин | Актуализация. На этом уроке можно провести математический диктант «Да – нет» с проверкой. • Произведение 29 и 3 равно 87. • Число 5 увеличили в 19 раз. Получили 85. • Сумму 17 и 5 увеличили в 4 раза. Получили 98. • Одну седьмую часть от 56 увеличили в 12 раз. Получили 96. • Первый множитель равен одной пятой от 25, второй множитель равен 11. Тогда произведение равно 55. • Произведение 12 и 8 меньше 100. • Разность 570 и 370 увеличили в 4 раза. Получили 900. • Делимое равно 720, делитель равен разности 20 и 11. Тогда частное равно 9. • Первый множитель равен сумме чисел 37 и 4. Второй множитель равен 2. Тогда произведение равно 82. «Найди лишнее слово». Далее педагог предлагает выполнить задание №2 (а, б) в учебнике. В каждом из этих пунктов примеры подобраны на применение одного из свойств действий. Поэтому комментирование решений позволит выявить, что за свойство лежит в основе. Параллельно с комментированием педагог на доске вывешивает буквенные записи свойств. Постановка цели (проблемная ситуация). Для каждого случая внетабличного умножения и деления предлагает восстановить алгоритм. Например, для случая 25·3 1. Прочитать каждый шаг алгоритма. 2. Составить алгоритм. 3. Объяснить выполнение шагов алгоритма. Шаги предлагает на карточках: Карточка 1. Сложите полученные произведения. Запишите ответ. Разложите число на сумму разрядных слагаемых. Умножьте на это число поразрядно. Карточка 2. Разложите число на сумму разрядных слагаемых. Умножьте на это число поразрядно. Полученные произведения сложите. Запишите ответ. Для всех остальных случаев надо построить алгоритм на сегодняшнем уроке. Проверяет, все ли усвоили. Самостоятельная работа. Предлагает выполнить задание №3 в учебнике. После сравнения с эталоном (решенными уже примерами) составляет план коррекции. Коррекция затруднений Педагог проверяет правильность выполнения. – У кого возникли затруднения? – В каком месте вы допустили ошибку? – В чем причина допущенной ошибки? – Те, у кого не возникло затруднений в самостоятельной работе, сформулируйте цель вашей деятельности. (Выполнить дополнительные задания). – Какова дальнейшая цель работы у тех, кто выявил затруднения? (Исправить ошибки). – Используем алгоритм исправления ошибок. – Каждый проговаривает свою учебную задачу. Работа над ранее изученным Педагог дает задания индивидуально, в зависимости от уровня продвижения ребенка. Предлагает выполнить задание №6. Рассматривая вычисления в первой строчке, делается вывод, что при умножении 111на однозначное число, количество сотен, десятков и единиц равно этому числу. Предлагает выполнить задание №8. Для решения задачи составляется граф.Пять точек соединяются попарно. Получается из одной точки проводим 4 линии. 5∙4=20 Второй способ. Рассуждаем: каждый отдал по 4 фотографии. Друзей 5 значит 4∙5=20 Педагог предлагает задание в тетради с критериями оценивания. Предлагает в тетради решить и проверить простые уравнения, содержащие изученные приемы. х :5=19 750:х=5 23·х=69 Я могу: решить простое уравнение на умножение и деление; выполнить устно умножение и деление; выполнить проверку. Составь вопросы по теме урока. В каждом уроке нового или закрепления учащиеся составляют вопросы. Это позволит помочь провести рефлексию усвоения темы. Со словами, приведенными в учебнике надо составить вопросы. Можно использовать прием: ромашка или кубик Блума. | Учебник Тетрадь Учебник Тетрадь Учебник Тетрадь | ||
Конец урока 38-40 мин | Рефлексия. Определяет домашнее задание с учетом индивидуальных трудностей детей. – Какие задачи мы ставили перед собой в начале урока? – Удалось ли достичь этих задач? – Возникали у вас затруднения? – Вы смогли их преодолеть? – Чем интересен был сегодняшний урок? Предлагает оценить свою работу при помощи линейки успеха. | Самооценивание | ||
Какие пользовательские опции программы доступны?
💡 Для назначения пользовательской программы у вас должна быть лицензия Premium . Бесплатная программа включает только программные назначения по умолчанию, которые перечислены в нашем Руководстве по программе. Обратите внимание, что всем ученикам 4 класса и выше по умолчанию назначается одна и та же программа: Сложение, вычитание, умножение и деление.
В этой статье объясняется, какие параметры доступны при назначении пользовательской программы: операции , набор задач , порог беглости и опция только оценка.
Обратите внимание, что XtraMath в настоящее время не предлагает ни программ, в которых выполняются смешанные операции в одном упражнении, ни вариантов выбора конкретных фактов для работы.
В пользовательской программе вы можете выбрать, какие операции будут включены в назначенную программу. Операции выполняются одна за другой, по порядку, поэтому, если вы выберете Умножение учащийся будет просто выполнять умножение, но если вы выберете Умножение и деление , он будет выполнять умножение и, закончив его, перейдет к делению.
Варианты операций в настоящее время:
- Сложение
- Вычитание
- Умножение
- Деление
- Сложение и вычитание
- Сложение, вычитание и умножение Сложение,
- 0040
- Умножение и деление
Набор задач определяет какие факты будут отработаны в каждой операции. Варианты набора задач в настоящее время:
- Начало (в настоящее время только для сложения и вычитания, включает факты, сумма которых равна 10, и обратное значение)
- Обычный (все операции, факты до 9)
- Расширенный (все операции, факты до 12-е)
Более подробное объяснение этих опций см. в нашем XtraMath Glossary and Icon Guide.
в нашем XtraMath Glossary and Icon Guide.
Порог беглости определяет, сколько времени учащийся должен ответить на каждую задачу. Меньшее число означает более сложную программу, так как у учащегося меньше времени на беглый ответ. Порог тайм-аута — это когда правильный ответ отображается во время викторины, если учащийся еще не ввел ответ.
Параметры порога беглости в настоящее время:
- 6 секунд (таймаут 20 секунд)
- 3 секунды (таймаут 10 секунд)
- 2 секунды (таймаут ~7 секунд)
- 1,5 секунды (таймаут 5 секунд)
Если вы примените настройку Assessment Only к студенческой программе, они будут переходить от викторины по размещению одной операции к другой. Они не будут практиковаться или викторины прогресса, только викторины размещения. За программой «Только оценка», как правило, должна следовать обычная программа (без оценки), чтобы учащийся мог улучшить свою начальную беглость речи.
За программой «Только оценка», как правило, должна следовать обычная программа (без оценки), чтобы учащийся мог улучшить свою начальную беглость речи.
15 забавных и эффективных способов научить детей умножению
Вы учитель математики в начальной школе? Вы пытаетесь понять, как научить своих учеников умножению? Что ж, тогда вы попали в нужный пост. Мы обсудим простые и забавные способы научить ваших юных учеников умножению.
Математика редко является любимым предметом учащихся. Но он устанавливает основы большинства повседневных действий. Будь то измерение времени или подсчет денег, все это математика.
Среди четырех основных элементов математики (сложение, вычитание, умножение и деление) умножение является наиболее важным. Он закладывает основу для многих передовых математических понятий, таких как алгебра и исчисление.
Кроме того, обучающие столы улучшают память и математические способности детей. Таким образом, обучение ваших дошкольников беглому умножению дает им уверенность в решении сложных математических задач и совершенствовании их в математике. Кроме того, это дает студентам смелость заниматься математикой в высших учебных заведениях.
Кроме того, это дает студентам смелость заниматься математикой в высших учебных заведениях.
Как учитель математики в начальной школе, вы должны сделать умножение веселым и увлекательным занятием для вашего класса. Если вы заинтересуете своих учеников математикой сейчас, вы можете дать им несколько успешных учебных лет вперед. Но не переживайте, мы здесь, чтобы помочь!
Как мы уже неоднократно говорили, игры и развлечения могут помочь учащимся учиться. Таким образом, вы также можете использовать забавные и инновационные стратегии, чтобы научить своих учеников умножению.
Давайте рассмотрим несколько увлекательных и простых способов научить дошкольников умножению.
Дополнительная литература: Как помочь детям с математикой: 6 инновационных подходовКак научить умножению за 9 простых шагов
Начальная школа — это ступенька в академическом развитии ребенка. Он учит жизненно важным предметам, таким как умножение, которые могут помочь выучить много новых предметов.
Поэтому учителя начальных классов должны сделать предмет интересным для учащихся. Поскольку основы умножения вращаются вокруг запоминания таблиц, учителя мало что могут сделать, чтобы сделать этот предмет интересным. Учащиеся должны изучать таблицы самостоятельно, чтобы продвигаться вперед в своих классах.
Но есть несколько стратегий, которые учителя могут использовать для упрощения обучения умножению в своем классе. Вот лучшие стратегии обучения умножению учащихся начальной школы:
SplashLearn пробуждает любознательность на протяжении всей жизни своей игровой программой обучения PreK-5, которую любят более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.
Попробуйте бесплатно
Шаг 1. Препятствуйте запоминанию Студенты часто испытывают трудности с запоминанием. Им сложно изучить и реализовать все таблицы в задаче. Некоторые дети так боятся запоминания таблиц, что боятся заниматься математикой.
Некоторые дети так боятся запоминания таблиц, что боятся заниматься математикой.
Чтобы предотвратить это, лучше всего показать вашему классу взаимосвязь между умножением и сложением. Эта стратегия также может помочь учащимся понять концепцию умножения, которая представляет собой просто повторяющееся сложение.
Используйте соответствующие примеры, чтобы показать вашему классу, как умножение основано на сложении. Поскольку ваш класс уже изучил сложение на предыдущих уроках, обучение умножению займет меньше времени.
Вы можете написать эти уравнения на доске, чтобы помочь отстающим учащимся с наглядностью:
3 x 3 равно 3 + 3 + 3
Или
4 x 2 равно 4 + 4
Шаг 2. Покажите волшебство нуля Прежде чем приступать к комплексным числам, вы должны показать своим ученикам, как работает ноль в математике. Вы можете показать им, что прибавление числа к нулю не меняет его значения. Но умножение числа на ноль также делает его равным нулю.
Здесь вы можете использовать этот наглядный пример:
n + 0 = n
Но . . .
n x 0 = 0
Вы также можете использовать примеры, чтобы учащиеся поняли, как ноль действует при умножении. Например, попросите учеников сосчитать количество стульев в классе, скажем, 25. После этого попросите их сосчитать стулья с обезьянами на них; это ноль.
Шаг 3. Определите свойство единицыКак и ноль, единицу также легко умножить. Любое число, которое умножается на единицу, сохраняет свое значение:
n x 1 = 1
Вы можете использовать примеры из реальной жизни, чтобы показать вашему классу свойство номер один. Например, строка в календаре показывает семь дней одной недели.
Шаг 4. Начните с простых чиселЧтобы упростить изучение таблиц, начните с простых чисел, которые учащиеся смогут быстрее запомнить.
Например, после изучения числа ноль и свойства единицы, вы можете показать классу таблицы чисел 10 и 11.
Итак, n x 10 = n0
Или
n x 11 = nn
Шаг 5: Показать переместительное свойствоУмножение также является коммутативным, как и сложение. Это означает, что порядок факторов не меняет ответ.
Простыми словами, вы можете умножать два числа в любом порядке, и ответ будет одинаковым. Например, ответом для 2 x 5 или 5 x 2 будет одно и то же число 10.
Это свойство может показать вашим учащимся, что умножение проще, чем кажется.
Шаг 6: Покажите взаимосвязь между таблицамиЕще один простой шаг в обучении умножению — показать вашему классу взаимосвязь между таблицами.
Например, вы можете выделить, что когда учащиеся изучают таблицы до 8, они автоматически изучают таблицу 9, поскольку число 9 встречается во всех таблицах, учащиеся могут пропустить изучение этой таблицы.
Это небольшое облегчение может помочь мотивировать учащихся, когда они борются с умножением.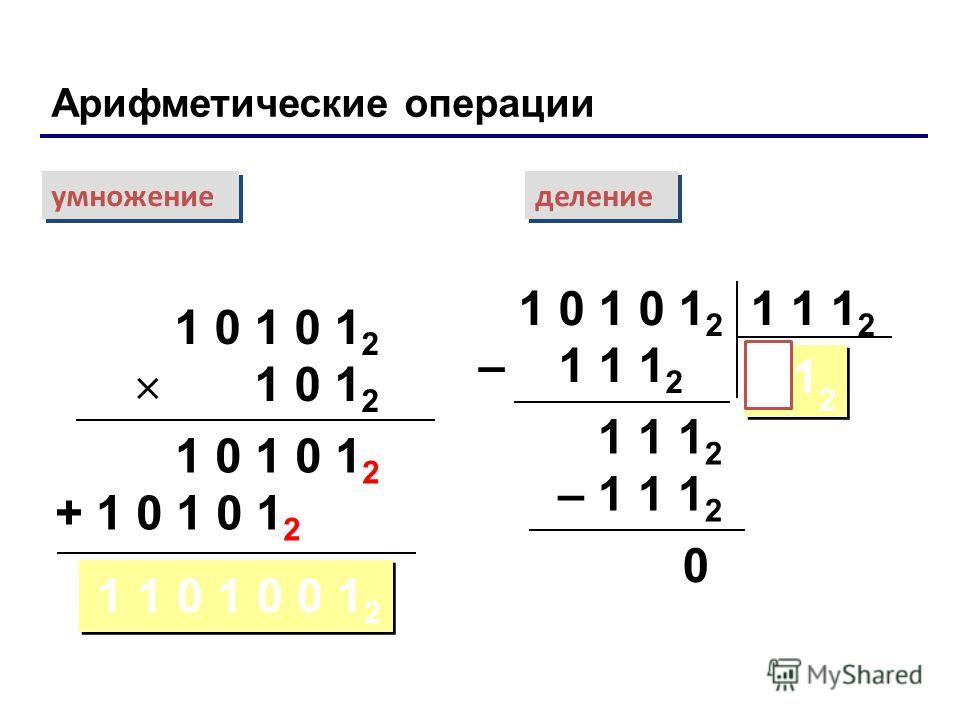
Если дети попытаются запомнить таблицы, они тоже скоро их забудут. Поэтому вместо того, чтобы заставлять своих учеников запоминать таблицы, расскажите им о значении умножения, и они смогут использовать его в реальных ситуациях.
Например, вы можете принести своим ученикам коробку пончиков и попросить их подсчитать количество пончиков в коробке. Теперь покажите своим ученикам, что если они умножат количество строк на столбцы, они смогут вычислить пончики быстрее, чем считать каждый пончик.
Шаг 8: Разложите числоЕсли ваши ученики не умеют умножать большие числа, вы можете показать им, как разбивать числа.
Например, вместо умножения 8 x 9 они могут умножаться как 8 x (5 + 4).
Они также могут реализовать это свойство следующим образом: (8 x 5) + (8 x 4) : 40 + 32.
Шаг 9. Используйте наглядные материалы Многие исследования подтвердили, что учащиеся лучше учатся с помощью наглядных материалов. Таким образом, использование наглядных средств обучения является одним из лучших способов обучения умножению.
Таким образом, использование наглядных средств обучения является одним из лучших способов обучения умножению.
Например, учащиеся могут научиться умножению с помощью анимированных игр. Игры позволяют учащимся понять причину умножения. Кроме того, визуальные эффекты помогают быстрее выучить таблицы.
6 забавных способов научить отстающих учеников умножениюЧтобы упростить умножение для ваших учеников, вам нужно выйти за рамки обычных стратегий обучения. Чтобы сделать изучение умножения приятным и простым, вот несколько забавных учебных заданий:
Занятие №1: Веселые виртуальные игрыСегодня невозможно оторвать детей от экранов. Таким образом, вы можете использовать экраны в своих интересах для обучения умножению.
Обращение к обучению на основе игр может сделать обучение умножению увлекательным. Эти игры могут улучшить уровень концентрации учащихся и математические навыки. Самое приятное то, что подобные игры устраняют страх неудачи, с которым борются многие ученики.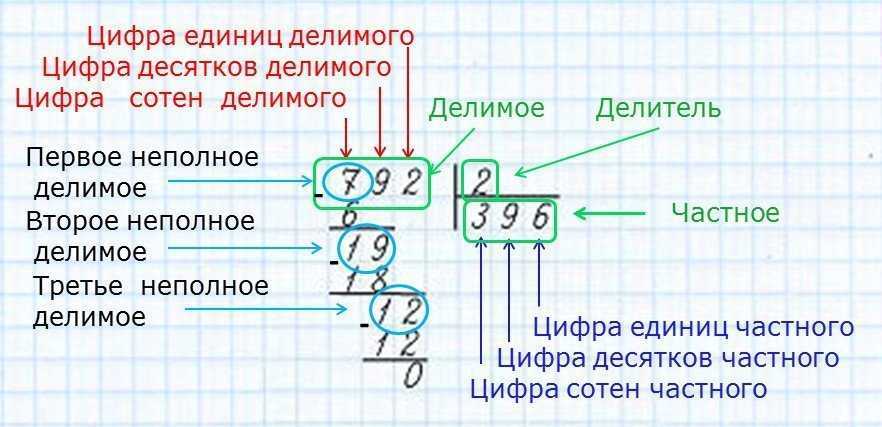 Обучающие игры на умножение обеспечивают безопасную среду, в которой учащиеся могут ввести неправильный ответ, но при этом чувствовать мотивацию попробовать еще раз.
Обучающие игры на умножение обеспечивают безопасную среду, в которой учащиеся могут ввести неправильный ответ, но при этом чувствовать мотивацию попробовать еще раз.
Вы можете избавиться от страха перед умножением в классе с помощью математических игр. Например, вы можете разыграть в своем классе простое упражнение «Константный калькулятор».
Предложите учащимся использовать константную функцию на калькуляторах, чтобы найти кратность любого числа, чтобы понять связь между сложением и умножением.
Вот как это работает:
- Выберите число, например 7, и введите его в калькулятор.
- Сначала нажмите кнопку +, затем кнопку =. Калькулятор должен еще раз показать семь.
- Далее, продолжайте нажимать кнопку =. Семь будет постоянно добавляться постоянной функцией, отображая возрастающие кратные числа (7, 14, 21, 28 и т. д.)
- Вы можете попросить учащихся перечислить обнаруженные ими множители, а затем предложить им найти закономерности в своих список.

Каждый ребенок любит музыку. И намного легче выучить все, что рифмуется и имеет биты. Итак, вы можете найти несколько хороших песен об умножении и проигрывать их в своем классе для увлекательного изучения математики. Вы даже можете предложить ученикам подпевать во время обучения.
На YouTube можно найти различные песни на умножение с анимационными видеороликами. Некоторые из лучших каналов песен и веб -сайтов умножений:
- Умножение Unplugged
- Песни для обучения
- Rock ‘n Learn
- Flocabulary Multiplication Multiplication

Вот как это работает:
- Разделите свой класс на две команды.
- Постройте две шеренги учеников, по одной шеренге, представляющей каждую команду, и поставьте их лицом друг к другу.
- Преподаватель может показать уравнение или назвать факт умножения.
- Ученик из первой пары (дети смотрят друг на друга) выкрикивает решение.
- Балл присуждается учащемуся, ответившему правильно первым.
- Преподаватель переходит к следующей паре, когда оба ученика садятся.
- Преподаватель продолжает в том же духе, пока не будут адресованы все ученики в очереди.
- Побеждает ряд с наибольшим количеством очков.
Вы можете поручить роль счетовода ученику, если в вашем классе нечетное количество учеников. Объединение студентов одного академического уровня для соревнования друг с другом также может принести им пользу.
Увлекательное занятие №5: Карточные игры Вы также можете использовать карточки для обучения своих учеников умножению. Multiplication War — это старая, но веселая автомобильная игра, которая может превратить обучение умножению в увлекательное занятие.
Multiplication War — это старая, но веселая автомобильная игра, которая может превратить обучение умножению в увлекательное занятие.
Вот как это работает:
В этой игре участвуют два игрока. Карты сдаются лицом вниз в две стопки одним учеником после того, как они перетасованы. Оба ученика переворачивают верхнюю карту из своей стопки лицевой стороной вниз после обратного отсчета (3, 2, 1, ВПЕРЕД!).
Набор выигрывает тот ученик, который первым правильно умножит оба числа на карточках. Когда все карточки будут использованы, побеждает студент с наибольшим количеством наборов.
Обязательно присвойте номера тузу, даме и королю, если вы планируете использовать их из колоды. Например, туз может стоить ноль, валет — один, дама — одиннадцать, а король — двенадцать. Не забудьте убрать джокеров!
Увлекательное занятие № 6: Умножение именных бирок Это упражнение — отличный способ научить детей умножать. Это может помочь студентам выучить таблицы, даже не пытаясь.
Вот как это работает:
Сделайте бирки для умножения для себя и всех в классе. Каждый должен ходить по «имени» в течение дня. Чье-то имя на этот день было бы 24, если бы, например, на нем была бирка «8 x 3». Каждый день выделяйте определенное время, чтобы студенты могли встать и представиться друг другу. Доброе утро; меня зовут 80 (8 х 10) или 25 (5 х 5).
Связанное чтение: Простые способы сделать математику увлекательной для детейЗаключение
Как видите, выяснить, как научить умножению, — это не просто наука. Использование творческого подхода к обучению учащихся умножению поможет им выучить и запомнить концепции.
Инновационные методы могут сделать математику простой и интересной для учащихся. Итак, используйте визуальные эффекты, игры, занятия и различные стратегии, чтобы сделать умножение увлекательным.
Для игр на умножение вы всегда можете воспользоваться бесплатными играми SplashLearn. У нас есть широкий выбор бесплатных игр для дошкольников и учащихся начальной школы.
У нас есть широкий выбор бесплатных игр для дошкольников и учащихся начальной школы.
Как я могу научить умножению учащихся, которые испытывают страх перед математикой?
- Вот как научить умножению учащихся, которые кажутся перегруженными этой темой, за 4 простых шага:
Шаг 1. Разделите информацию на удобные части.
Шаг 2: Используйте простое визуальное представление, чтобы придать контекст факту.
Шаг 3: Покажите учащемуся, как использовать более простые факты в качестве трамплина для более сложных.
Шаг 4: Работайте над освоением каждой таблицы отдельно.
Как я могу научить своих учеников с СДВ/СДВГ умножать?
Разложите карточки по одной, чтобы ваши ученики могли их умножить, объяснив, что вы хотите, чтобы они попрактиковали (например, 9 x таблиц), и установив таймер на одну минуту. Дайте им ответы на любые вопросы, в которых они ошиблись, чтобы у них было больше шансов ответить правильно в следующий раз, когда назовут этот номер.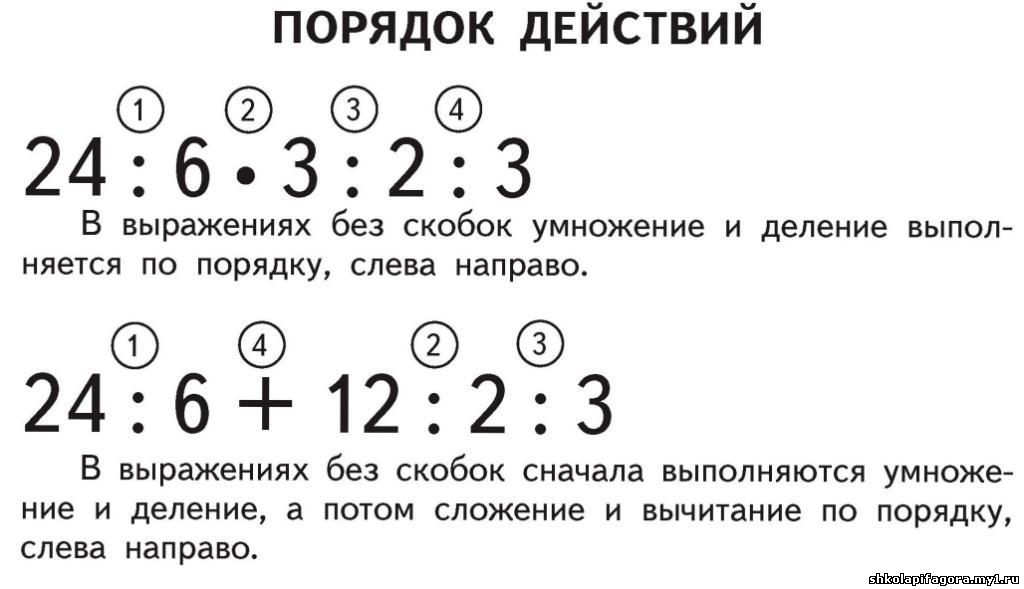

 М.
М. 2.2.2 — решать простейшие уравнения, содержащие действия умножения и деления; уравнения сложной структуры видах· (25:5)=60; (24·3):х=6;х: (17·2)=2;k+124 : 4 = 465
2.2.2 — решать простейшие уравнения, содержащие действия умножения и деления; уравнения сложной структуры видах· (25:5)=60; (24·3):х=6;х: (17·2)=2;k+124 : 4 = 465
 Вовлекает
Вовлекает Кроме
Кроме





